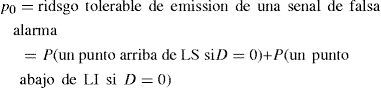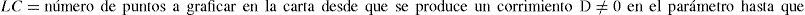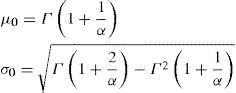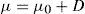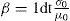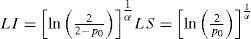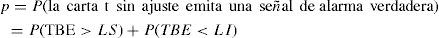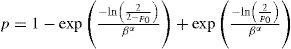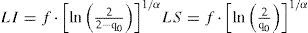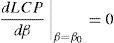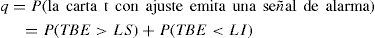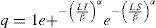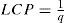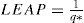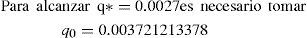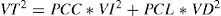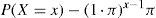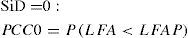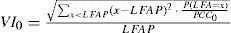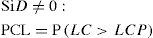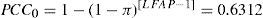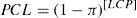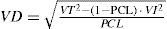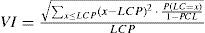Desempeño de cartas de control estadístico con límites bilaterales de probabilidad para monitorear procesos Weibull en mantenimiento

Resumen

Una manufactura con óptimos estándares de calidad está apuntalada por la alta confiabilidad de sus equipos y sistemas, entre otros pilares esenciales. Ingeniería de mantenimiento tiene la responsabilidad de planear el control y mejoramiento continuo de su equipamiento crítico mediante algún enfoque, como Six Sigma. Este se nutre de numerosas herramientas estadísticas destacando, entre ellas, a las cartas de control estadístico de procesos. Si bien sus primeras aplicaciones fueron en producción, otros diseños surgieron para adaptarse a nuevas necesidades como el monitoreo de los equipos y sistemas en el hábitat fabril. El tiempo entre fallas suele ajustarse a un modelo Exponencial o Weibull. Las cartas t y t ajustada, con límites probabilísticos de control, son alternativas aptas para monitorear el tiempo medio entre fallas. Desafortunadamente, es difícil encontrar publicaciones de ellas aplicadas a modelos Weibull, muy útiles en contextos como mantenimiento. Además, la literatura limita el estudio de su desempeño al análisis de la métrica estándar: longitud de corrida promedio, dando así una visión parcial. El objetivo de este trabajo es explorar el desempeño de las cartas t y las cartas t ajustada mediante el uso de tres métricas, dos no convencionales. Para ello, incorpora el concepto de variabilidad lateral, en sus formas variabilidad derecha e izquierda. Mayores precisiones del comportamiento de estas cartas permitieron entender las condiciones bajo las cuales son convenientes: si el objetivo principal del monitoreo recae en detectar deterioros, se recomienda la carta t con ajuste. En cambio, cuando la prioridad es detectar mejoras, la carta t sin ajuste es la mejor opción. No obstante, la velocidad de respuesta de ambas cartas es muy variable de corrida en corrida.

Abstract

Manufacturing with optimal quality standards is underpinned to the high reliability of its equipment and systems, among other essential pillars. Maintenance Engineering is responsible for planning control and continuous improvement of its critical equipment by any approach, such as Six Sigma. This is nourished by numerous statistical tools highlighting, among them, statistical process control charts. While their first applications were in production, other designs have emerged to adapt to new needs as monitoring equipment and systems in the manufacturing environment. The time between failures usually fits an exponential or Weibull model. The t chart and adjusted t chart, with probabilistic control limits, are suitable alternatives to monitor the mean time between failures. Unfortunately, it is difficult to find publications of them applied to the models Weibull, very useful in contexts such as maintenance. In addition, literature limits the study of their performance to the analysis of the standard metric average run length, thus giving a partial view. The aim of this paper is to explore the performance of the t chart and adjusted t chart using three metrics, two unconventional. To do this, it incorporates the concept of lateral variability, in their forms left and right variability. Major precisions of the behavior of these charts allow to understand the conditions under which are suitable: if the main objective of monitoring lies in detecting deterioration, the t chart with adjustment is recommended. On the other hand, when the priority is to detect improvements, the t chart without adjustment is the best choice. However, the response speed of both charts is very variable from run to run.

Introducción

En el contexto mundial competitivo actual, el control y mejoramiento continuo de los procesos críticos de una empresa mediante un programa sistemático como por ejemplo, Six Sigma, se reconoce no solo como una necesidad, sino también como una estrategia de negocios, una ventaja competitiva (Gutiérrez y de la Vara, 2009). Ingeniería del mantenimiento no escapa a esta realidad; por el contrario, desempeña una función cada vez más comprometida dentro de las empresas. Esto se ve reflejado en los diversos cambios que sus prácticas diarias experimentan desde hace años.

La obtención de una manufactura con estándares de calidad óptimos está respaldada esencialmente por la alta confiabilidad de su equipamiento y sistemas, entendiéndose esta como su capacidad para suministrar largos períodos de desempeño satisfactorio sin fallas. Ingeniería de mantenimiento tiene entonces la responsabilidad clave de elaborar y ejecutar un plan de control y mejoramiento continuo de la confiabilidad de sus activos críticos, identificando y tratando adecuadamente deterioros o aspectos posibles de mejora.

Si bien las primeras aplicaciones de la metodología Six Sigma surgieron en manufactura, se han extendido a otras áreas y continúa creciendo. Un programa Six Sigma comprende una serie de etapas bien definidas: definir, medir, analizar, mejorar y controlar. Cada una de ellas se nutre de una gran diversidad de herramientas estadísticas. La última se apoya en el control estadístico de procesos (CEP) destacando, como su principal herramienta, las cartas de control.

Cartas de control

Son métodos gráficos para monitorear y diagnosticar el desempeño de un proceso en el tiempo, detectando posibles corrimientos de magnitud D en los valores nominales de sus principales parámetros; por ejemplo, en la media o desviación estándar de una variable descriptiva de su desempeño (Surucu y Sazak, 2009; Ryan, 2011). Las cartas bilaterales tienen un doble rol: permiten detectar corrimientos por abajo (D < 0) y por arriba (D > 0) del valor nominal del parámetro, lo que señala deterioros y mejoras en el desempeño. Las cartas bilaterales son entonces claves en todo programa de mejoramiento continuo y, en particular, del pensamiento Six Sigma. Lecturas periódicas del desempeño del proceso se vuelcan a un estadístico de control cuya estructura matemática depende del tipo de carta. Sus valores, representados en la gráfica mediante puntos, se comparan con dos líneas horizontales: los límites de control superior (LS), para detectar corrimientos D > 0, e inferior (LI), para corrimientos D < 0.

Con reglas de decisión preestablecidas, si el parámetro ha sufrido cambios (D ≠ 0) la carta emite una señal de alerta y se concluye que el proceso está fuera de control con una consecuente toma de acciones en función del tipo de cambio, perjudicial o beneficioso. De lo contrario (D = 0), se concluye que el proceso está bajo control en cuyo caso sigue su curso normal. La regla de decisión estándar para cartas de control bilaterales indica que un solo punto fuera de alguno de los límites es señal de alerta y debe actuarse en consecuencia. Aún cuando D = 0, la carta puede emitir una señal de falsa alarma. Para minimizar su riesgo, se fija de antemano la probabilidad p₀ definida, bajo la regla de decisión estándar para cartas bilaterales por:

A partir de p₀ y los principios estadísticos se establecen los límites de control. La teoría general de las cartas de control nace de la mano de Shewhart en la segunda década del siglo pasado con el objeto de monitorear procesos de manufactura que pueden modelarse con una distribución de probabilidad normal.

Con el tiempo y el avance tecnológico, otros diseños emergieron para cubrir nuevas necesidades y contextos de uso más allá de la producción, por ejemplo en mantenimiento, para monitorear la confiabilidad de los equipos y sistemas en su hábitat fabril. La variable de monitoreo más usual es TBE (Time Between Events). Si bien este término se usa en un contexto más amplio, en confiabilidad representa el tiempo entre fallas consecutivas del equipo o sistema. Desde el punto de vista estadístico, la inestabilidad del activo se manifiesta mediante una distorsión de la variable TBE en su media, variabilidad o distribución, situaciones que pueden ser detectadas con una carta de control. Es un excelente recurso para combinar con actividades de mantenimiento preventivo permitiendo reducir costos y tiempo (Linderman et al., 2005; Zhao et al, 2012).

Si las fallas del proceso se pueden describir por un proceso de Poisson, lo que implica que la tasa de fallas es constante, la distribución exponencial es adecuada para modelar datos TBE (Xie et al., 2002; Zhao et al., 2012). Sin embargo, las maquinarias sufren procesos de envejecimiento o desgaste con lo cual la tasa de fallas crece con el tiempo. En estos casos, los modelos de probabilidad Weibull son los más indicados. Su versatilidad le ha permitido ganar un lugar protagónico en varios contextos de uso: mantenimiento, producción y servicios. Así lo evidencia la literatura y el ámbito empresarial que, desde hace décadas, muestran interés por ellos y no cesa en la actualidad (Lai et al., 2006).

Diseños de cartas de control

En presencia de procesos asimétricos como, por ejemplo, los que pueden modelarse por la distribución de probabilidad de Weibull, las cartas de Shewhart no se comportan bien. Causan, entre otras desventajas, un incremento sustancial en la probabilidad de emisión de una señal de falsa alarma y la posibilidad de un límite de control inferior inexistente con lo cual, la detección de mejoramientos del proceso, clave en un programa Six Sigma, no es factible. Numerosos diseños surgen para corregir estos y otros problemas. Sin pretender hacer una lista exhaustiva, se citan las cartas: CUSUM, EWMA, no paramétricas, basadas en el método de las varianzas ponderadas y con límites de probabilidad.

Los esquemas CUSUM y EWMA son muy veloces para detectar pequeños cambios en los parámetros de interés del proceso. Si bien su diseño surgió para monitorear procesos normales, con el tiempo se extendió a modelos asimétricos (Hawkins y Olwell, 1998; Castagliola et al., 2006; Ryan, 2011). Las cartas no paramétricas tienen la ventaja de que no se basan en una premisa acerca del modelo de probabilidad que rige a la variable de monitoreo. Los trabajos de Bakir (2004) y Chakra-borti y van de Wiel (2008) se basan en conocidos tests no paramétricos. Alemi (2004) propuso una sencilla y atractiva carta no paramétrica con base en el gráfico de caja (box plot). Un interesante trabajo para monitorear tiempos de falla puede encontrarse en Li et al. (2012). Las cartas no paramétricas son insensibles ante la presencia de valores atípicos (outliers) como los que pueden producirse con una variable de monitoreo que se modela con una distribución de probabilidad asimétrica como Weibull, por lo que varios autores mostraron interés en cartas con límites de control construidos con base en el método de la varianza ponderada, entre ellos Khoo et al. (2009) y Castagliola y Khoo (2009).

El interés de este trabajo se enfoca en las cartas con límites bilaterales de probabilidad. Conservan los principios de las cartas de Shewhart, pero corrigen sus problemas ante procesos asimétricos, su diseño es más amigable que el de otras cartas mencionadas. Una interesante variedad de diseños, refinamientos y aplicaciones de cartas con límites de probabilidad emergen a fines de la década de los 80 y en forma ininterrumpida hasta nuestros días como respuesta a la necesidad de monitorear procesos de alto rendimiento o alta calidad (high-quality o high-yield processes), que se caracterizan por tener una tasa de fallas muy baja, propias de un ambiente Six Sigma. Entre sus diseños, aptas para ambientes de producción automática, se cuenta con las cartas CCC (Cumulative Count Control Chart) y su extensión CCC-r. También, sus equivalentes continuas: las cartas CQC (Cumulative Quantity Control Chart) y CQC-r (Xie y Goh, 2006).

Basadas en las cartas CQC y su extensión, surgen en la última década otros esquemas con límites de probabilidad para usarse en contextos más allá de la producción. Se trata de las cartas t (t chart) y su extensión a cartas t_r (t_r chart) introducidas por Xie et al. (2002) con el objeto de monitorear la confiabilidad de los equipos y sistemas de una empresa a través de la media de la variable TBE y suponiendo que estos tiempos pueden modelarse con la distribución de probabilidad exponencial o Weibull. En el caso de la carta t, la gráfica registra directamente las observaciones TBE. En cambio, en la carta t_r, se maneja el “tiempo total transcurrido hasta la obtención de r fallas”. Estas cartas no son exclusivas del área de mantenimiento, pueden utilizarse también en servicios (Santiago y Smith, 2013). En la literatura, las cartas CCC, CQC, t y sus extensiones suelen agruparse dentro de un grupo más general de cartas llamado cartas TBE (TBE Charts) (Liu et al, 2006).

Desempeño de las cartas de control

A la hora de seleccionar una carta, es imprescindible examinar su desempeño en términos de su velocidad de respuesta ante un corrimento D en el parámetro. La métrica usual es la longitud de corrida promedio (LCP), representa la media de la variable longitud de corrida (LC) definida por:

LCP es una función que depende del corrimiento D. Cuando D = 0, LCP toma aquí la notación LFAP para representar la longitud de falsa alarma promedio, la media de la variable longitud de falsa alarma (LFA). La carta tendrá un mejor desempeño cuanto mayor sea su LFAP y menor su LCP para un rango de valores D de interés.

Desafortunadamente, la variable LC está afectada por una alta variabilidad (Ryan, 2011; Govindaraju y Lai, 2004) por lo que el mero uso de LCP es insuficiente para mostrar el comportamiento real de la carta, solo brinda una visión parcial. Sin embargo, en la literatura, numerosos estudios de desempeño aún se focalizan, exclusivamente en el análisis de LCP. Afortunadamente, el número de publicaciones con análisis más completos está creciendo. Lo más usual es complementar la LCP con otras medidas de resumen de uso corriente en la disciplina estadística (Luceño y Puig, 2000; Tang y Cheong, 2004; Zhang et al., 2006; Chakraborti, 2007). En otros enfoques, una medida alternativa a LCP apta para corridas cortas de producción fue propuesta por Govindaraju (2005). Gráficos amigables introducidos por Radson y Boyd (2005) permiten comparar rápidamente varios diseños a la vez. Govindaraju y Lai (2004) redefinen la LC modificando la regla de decisión estándar. En cartas donde el tiempo para graficar dos puntos consecutivos varía de un par a otro como en las cartas CCC, CQC, t y sus extensiones, si el factor tiempo es de interés, la métrica ATS (Average Time to Signal) es adecuada; o, en sus formas particulares, ANI (Average Number Inspected) para las cartas CCC y CCC-r y AQI (Average Quantity Inspected) para la carta CQC (Sharma et al., 2006; Liu et al., 2006; Lai y Govindaraju, 2008; Lai et al, 2001).

Quintana et al. (2009) y (2011) presentan un método no convencional al demostrar que las varianzas de LC y LFA pueden descomponerse en dos varianzas laterales, a izquierda y derecha de LCP y LFAP, respectivamente. A partir de este resultado proponen, para cada estado del proceso (D = 0 y D ≠ 0), una terna diferente de medidas de resumen, una convencional y dos no. Para D = 0, la terna está integrada por: LCP, la variabilidad izquierda y la proporción de corridas tempranas (con LC inferior a LCP). En cambio, para D ≠ 0: LCP, la variabilidad derecha y la proporción de corridas tardías (con LC superior a LCP). La información combinada de las 3 medidas permite caracterizar, para cada estado del proceso, el desempeño real de la carta de forma más completa y precisa.

Cartas con límites de probabilidad

Desafortunadamente, las cartas con límites de probabilidad presentan una desventaja. Es de sentido común pretender de una carta que su LCP sea inferior a LFAP para todo corrimiento D ≠ 0. En términos gráficos, significa que se pretende que la curva LCP tenga su máximo en D = 0. Se dice entonces que la carta presenta un desempeño con LCP no sesgada (ARL unbiased) (Ryan, 2011). Esta propiedad no se satisface en las cartas con límites de probabilidad. No obstante, como solución, es posible ajusfar sus límites. Una alternativa es asignar valores desiguales a las probabilidades en (1) (Chen y Cheng, 2011). Otra muy usual es incorporar un factor de ajuste a las líneas de control recurriendo a métodos clásicos de análisis matemático para la búsqueda de los valores óptimos de funciones (Sharma, 2003; Tang y Cheong, 2004; Zhang et al, 2006).

Sin embargo, independientemente de la alternativa aplicada, se observa en la literatura que el estudio de su desempeño se limita al análisis de LCP. Surgen dudas entonces sobre su desempeño real en relación con otras medidas de desempeño muy significativas. En particular, es difícil encontrar publicaciones, salvo en Sharma et al. (2003) aunque no en forma completa, que traten la carta t con LCP no sesgada para monitorear tiempos TBE modelados según Weibull, muy útiles en contextos como mantenimiento y servicios.

Objetivo y alcance del trabajo

El objetivo del presente trabajo fue realizar un estudio comparativo del desempeño de las cartas bilaterales t con y sin ajuste de sus límites de control con base en la metodología propuesta por Quintana et al. (2009) para monitorear la media de los tiempos TBE cuando se modelan mediante una distribución de probabilidad Weibull de dos parámetros. Esto fue motivado por la falta de publicaciones con análisis de su desempeño más allá de LCP, la repercusión de las cartas con límites de probabilidad en el ambiente Six Sigma, el alcance de los modelos Weibull en mantenimiento y el creciente interés por el uso de cartas de control en contextos más allá de producción. Mayores precisiones del comportamiento de estas cartas permiten entender las condiciones bajo las cuales son convenientes.

La distribución Weibull de dos parámetros depende de los parámetros de forma α y escala β. Dado que su media está en función de ambos, un cambio en ella puede generarse por un cambio en uno solo de sus parámetros o en ambos. Se contempla aquí el control de la media de TBE a través de β, ya que generalmente, un cambio en la operación del proceso provoca un cambio en β. A lo largo del trabajo, α se supone conocido. En cuanto a la carta con ajuste, el enfoque usado es la incorporación de un factor de ajuste a las líneas de control de la carta t.

La estructura del presente artículo es de la siguiente manera: en la primera sección (desarrollo) se presentan los supuestos en los que se basa el trabajo, las expresiones matemáticas de los límites de control y de las medidas LCP y LFAP para las cartas t con y sin ajuste con sus respectivas justificaciones, las medidas de resumen propuestas por Quintana et al. (2009) para evaluar el desempeño de una carta con una breve descripción del por qué de su elección y el cálculo de ellas para las cartas t con y sin ajuste. En la segunda sección (discusión y análisis de resultados) se presentan los gráficos que permiten comparar el desempeño de ambas cartas en términos de cada una de las medidas de resumen presentadas y el análisis de los resultados encontrados. En la tercera sección (conclusiones) se presentan los aportes del trabajo y futuras líneas de investigación.

Desarrollo

Supuestos del trabajo

Dado que el diseño de la carta t depende del modelo de probabilidad de las observaciones TBE y que tanto los parámetros del modelo Weibull como el corrimiento D en la media pueden tomar cualquier valor positivo dentro de una escala continua, es necesario establecer algunos supuestos y restricciones:

• 
  ▪

  Los valores convenidos para α son: 1, 2, 3, 4, 6 y 8

  Este conjunto es suficiente para evaluar las diferencias en el comportamiento de las cartas y la mayoría de las aplicaciones. El caso α = 1 coincide con el modelo de probabilidad exponencial.

• 
  ▪

  Sea β₀ = 1 donde β₀es el valor nominal de β cuando D = 0.

  Este supuesto no causa pérdida de generalidad. Se justifica en que, si TBE se ajusta a un modelo Weibull con parámetros α y β, TBE/ β sigue un modelo Weibull con parámetros α y β = 1.

• 
  ▪

  Sean μ₀y σ₀los valores nominales de la media y la desviación estándar de la variable TBE que se ajusta a un modelo de probabilidad Weibull con parámetros α y β₀ = 1:

  

  Es importante notar que estos valores dependen de α.

• 
  ▪

  Sea μ la media desplazada de TBE. Su forma de expresión usual es

  

  donde D = dσ₀ con d = 0, +0.25, +0.50, ±1, +1.5 y ±2. Cabe observar que μ depende tanto de D como de α.

• 
  ▪

  Los valores β desplazados toman la forma

  

  Estos valores también dependen de D y α. La identidad (5) se justifica fácilmente: reemplazando μ por βΓ1+1α en (4) y teniendo en cuenta (3) se despeja β. En particular y como es de esperar

  

  Además, si D > 0 entonces β > 1 y μ > μ₀. Luego, en términos de TBE, el tiempo medio entre fallas es más amplio, lo cual implica que se produce un mejoramiento en el desempeño del equipo. En cambio, si D < 0, β < 1 y μ < μ₀; es decir, el tiempo medio entre fallas se ha reducido lo que equivale a un deterioro de su desempeño.

• 
  ▪

  Sea p₀ = 0.0027 siendo p₀la probabilidad dada por(1)

  Se convino en tomar este valor estándar para mantener la consonancia con las cartas de Shewhart.

Límites de control de la carta t sin ajuste

Las cartas con límites de probabilidad se caracterizan por la sencillez de su diseño. En el caso de la carta t, su estadístico de control es directamente TBE, la variable a monitorear. Ante cada falla del equipo o sistema se registra, mediante un punto en la gráfica, el tiempo transcurrido desde su última falla. Las líneas de control LS y LI se muestran en (10) y se justifican como sigue (Xie et al., 2002).

La expresión (1) se reescribe en función de TBE como sigue

En cartas bilaterales, lo usual es considerar ambas probabilidades iguales. Chen (2011) considera probabilidades desiguales para que la carta tenga un desempeño con LCP insesgada. En este trabajo, para obtener una carta con esta propiedad se ha optado por la incorporación de un factor de ajuste a los límites de control manteniendo las probabilidades de (7) iguales

Como TBE se ajusta a un modelo Weibull, su función de distribución de probabilidad acumulada es

A partir de (6) y (9), se resuelve (8). Al despejar LS y LI se obtiene

LCP en la carta t sin ajuste

Como cada tiempo de falla se considera independiente de los anteriores, la variable LC definida en (2) se ajusta a un modelo de probabilidad geométrico con parámetro p definido como sigue para cada corrimiento D

Considerando (9)

Se reemplaza LS y LI por (10)

De la naturaleza geométrica de la variable LC

Es importante notar que LCP depende de D y α.

LFAP en la carta t sin ajuste

Si D = 0, considerando (6) se reemplaza β por β₀ = 1 en (11) y se obtiene p = p₀. Al igual que LC, LFA se ajusta a un modelo de probabilidad geométrico. Luego, reemplazando p por p₀ en (12), sigue la primera igualdad de (13). Dado el supuesto p₀ = 0.0027, sigue la segunda igualdad de (13). Esto significa que, se espera en concepto de promedio, una falsa alarma cada 370 puntos graficados en la carta aún cuando D = 0, análogo a lo que se espera en una carta estándar de Shewhart.

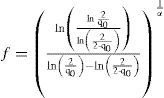
Límites de control de la carta t con ajuste

Al igual que en la carta t, el estadístico de control de la carta t con ajuste es directamente TBE, la variable a monitorear. Para transformar la carta t en una que tenga desempeño con LCP no sesgada, la alternativa elegida aquí es multiplicar los límites (10) por una constante apropiada, el factor/de ajuste:

donde q₀ es la probabilidad admisible y fijada de antemano de que la carta t con ajuste emita una señal de falsa alarma. El rol del factor f es provocar que la curva LCP alcance su máximo en D = 0, es decir en β₀ = 1 (Sharma et al., 2003). Esto implica

La búsqueda del factor f requiere de la resolución de (15). Para ello, es necesario que LCP se exprese en función de β. La variable LC de la carta t con ajuste sigue también un modelo de probabilidad geométrico con parámetro q definido para cada corrimiento D por:

Considerando (9)

Se reemplaza LS y LI por (14) y se obtiene

De la naturaleza geométrica de la variable LC

Tomando en cuenta las dos últimas expresiones se resuelve (15). Al despejar/se obtiene (17). Aplicando criterios clásicos de análisis matemático como el de la derivada primera, se comprueba que LCP presenta su máximo en β₀ = 1.

LCP en la carta t con ajuste

Como se explicó anteriormente, de la naturaleza geométrica de la variable LC

donde q está dada por (16). Al igual que con la carta t sin ajuste, LCP depende de D y α.

LFAP en la carta t con ajuste

Si D = 0, teniendo en cuenta (6) se reemplaza β por β₀ = 1 y/por (17) en (16). Se obtiene q = q*, la probabilidad real de que la carta t con ajuste emita una señal de falsa alarma dada por:

De la naturaleza geométrica de LFA y reemplazando q por (19) en (18) se obtiene

Desafortunadamente, la incorporación del factor de ajuste causa un inconveniente. A diferencia de lo que ocurre con la carta t sin ajuste y contrario a lo que es de esperar, de (19) se observa que q*≠ q₀. Esto significa que, aún fijando inicialmente una probabilidad q₀ de falsa alarma en 0.0027 como en la carta t sin ajuste, la probabilidad real de que la carta t con ajuste emita una falsa alarma (q*) difiere de 0.0027. Luego, de (20) resulta que LFAP ≠ 370.37, lo que provoca que las cartas t con y sin ajuste no sean comparables cuando se fijan p₀y q₀ en el mismo valor dado que las LFAP de ambas cartas son desiguales.

Afortunadamente, de (19) se observa que q* es una función que depende de q_0, pero no de α. Esta ventaja permite remendar el problema modificando estratégicamente el valor de q₀. La corrección consiste en fijar q₀ en un valor conveniente tal que q* = 0.0027. La engorrosa expresión de q* en (19) requiere que se trabaje numéricamente con la ayuda de algún software adecuado como EXCEL o MATHEMATICA:

Luego

Desempeño de las cartas

El desempeño de las cartas se evaluó siguiendo la metodología propuesta por Quintana et al. (2009) que contempla el uso de una terna de medidas de resumen integrada por un promedio, una medida de variabilidad lateral y una proporción, diferente para cada estado posible (D = 0 y D ≠ 0), a partir de los argumentos que se describen brevemente a continuación.

La alta variabilidad de LC y LFA hacen que, el uso de LCP y LFAP como únicas medidas del desempeño de una carta, sean insuficientes. El coeficiente de variación de una variable aleatoria, métrica usual en estadística para medir su variabilidad relativa, es igual al cociente entre la desviación estándar y la media de la variable. Sin embargo, el coeficiente de variación (VT) de LC o LFA no es una medida completamente adecuada para evaluar la dispersión en la velocidad de respuesta de una carta, dado que LC y LFA presentan una acentuada asimetría. Para solucionar este problema, Quintana et al. (2009) demuestran que el coeficiente VT puede ser descompuesto en dos componentes discriminando las LFA inferiores a LFAP de las superiores si D = 0. Asimismo, si D ≠ 0, discrimina las LC inferiores a LCP de las superiores:

donde

• PCC = proporción de corridas más cortas (más tempra nas) que LCP (o LFAP)

• PCL = proporción de corridas más largas (más tardías) que LCP (o LFAP)

• PCC + PCL = 1

• VI = variabilidad relativa o coeficiente de variación a la izquierda de LCP (o LFAP)

• VD = variabilidad relativa o coeficiente de variación a la derecha de LCP (o LFAP)

Importancia de las variabilidades laterales según el estado del proceso

Debido a la naturaleza asimétrica de las variables LFA y LC, las variabilidades laterales no contribuyen en iguales proporciones a VT y no revisten la misma importancia para ambos estados (D = 0 y D ≠ 0) si se tiene en cuenta lo que mide una y otra variable. No toda la variabilidad contenida en VT es perjudicial. Teniendo en cuenta que, la carta es más eficiente cuando, en lo que respecta a LCP y LFAP, mayor es LFAP si D = 0 y menor es LCP si D ≠ 0, se deduce:

• 
  ▪

  Si D = 0, las corridas con longitudes superiores a LFAP contribuyen a engrosar VT favoreciéndola. El hecho de que VD sea grande no es motivo de preocupación. VI es el único componente realmente perjudicial que incrementa VT, dado que proviene de las corridas con longitudes inferiores a LFAP.

• 
  ▪

  Si D ≠ 0, la situación es a la inversa. Las corridas con longitudes inferiores a LCP son bienvenidas. Luego, el hecho de que VI sea grande no es un problema. VD es el único componente realmente preocupante que incrementa VT, dado que proviene de las corridas con longitudes superiores a LCP.

Medidas de resumen para evaluar el desempeño de una carta de control

De lo analizado se concluye que, cuando D = 0, LFAP y VI son indicadores adecuados para evaluar el desempeño de la carta. En cambio, LCP y VD son aptos para D ≠ 0. Resulta conveniente completar la primera dupla anterior con PCC para evaluar el grado de incidencia de valores altos de VI. Análogamente, para D ≠ 0, la dupla se completa con PCL para evaluar el grado de incidencia de valores altos de VD. En resumen, para evaluar el desempeño de una carta, se proponen las ternas:

• 
  ▪

  LFAP, VI y PCC para D = 0

• 
  ▪

  LCP, VD y PCL para cada corrimiento D ≠ 0

La carta tendrá mejor desempeño cuanto mayor sea su LFAP y menor sea el resto de las medidas para un rango de valores D de interés. Análogo a las cartas de Shewhart, cada tiempo de falla se considera independiente de los anteriores. Luego, tanto LFA como LC siguen el modelo de probabilidad geométrico. En símbolos:

donde

• X = LFA o LC según sea D = 0 o D ≠ 0, respectivamente

• π = p₀ o q* para la carta t sin ajuste o con ajuste, respectivamente si X = LFA

• π = po q para la carta t sin ajuste o con ajuste, respectivamente si X = LC

Luego, su función de distribución acumulada es una suma finita de una progresión geométrica:

donde [x], parte entera de x.

Las expresiones de las medidas de resumen propuestas surgen a partir de la demostración de la igualdad (22) en el trabajo de Quintana et al. (2009) (el operador P(·) significa probabilidad):

El numerador de (25) es la desviación estándar a la izquierda de LFAP.

El numerador de (27) es la desviación estándar a derecha de LCP.

PCC₀ para D = 0

La primera igualdad de (28) se justifica a partir de (24) teniendo en cuenta (23). De (13) y (21), LFAP = 370.3 para ambas cartas. De lo visto, p₀= q*= 0.0027 (siempre y cuando se fije q₀ en 0.003721213378). Luego, sigue la segunda igualdad de (28).

donde π = p₀ o q* según se trate de la carta t sin o con ajuste, respectivamente.

VI₀ para D = 0

De (13), (21) y (28), LFAP = 370.37 y PCC₀ = 0.6312 para ambas cartas. Luego de trabajar numéricamente (25) con el software MATHEMATICA, se obtiene:

VI₀ = 0.6461

PCL para D ≠ 0

A partir de (23), (26) se convierte en

donde π = p o q según se trate de la carta t sin o con ajuste, respectivamente. Es importante notar que PCL depende de D y α.

VD para D ≠ 0

Si bien (27) define a VD, involucra el engorroso cálculo de una suma infinita. Una alternativa más sencilla es despejar VD de (22)

Dado que LC es una variable geométrica con parámetro π, su media es 1π y su desviación estándar,1−π/π. Luego, el coeficiente de variación total VT esVT=1−π con π = p o q para la carta sin ajuste o con ajuste, respectivamente

La expresión de VI surge a partir de la demostración de la igualdad (22) en el trabajo de Quintana et al. (2009):

Al igual que PCL, cabe destacar que el valor de VD depende de D y α.

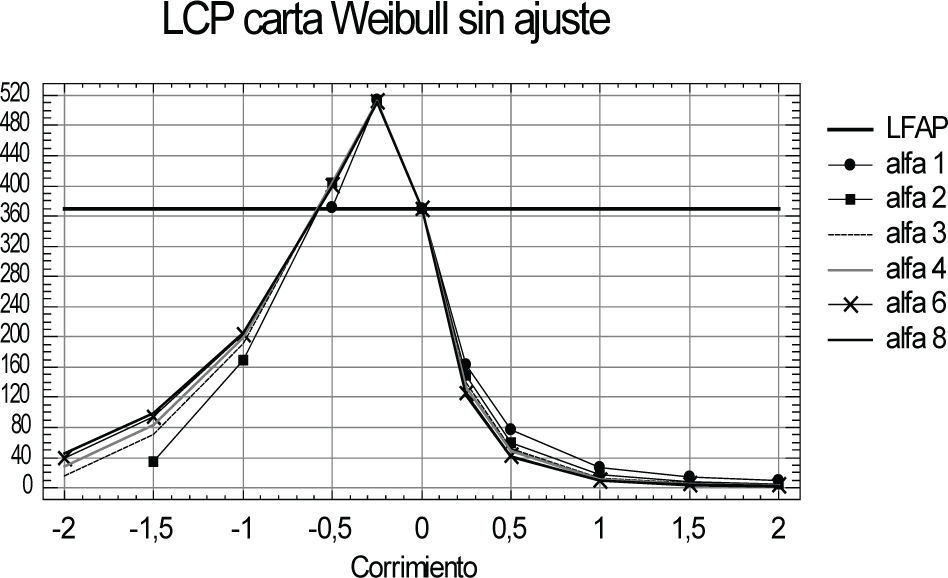
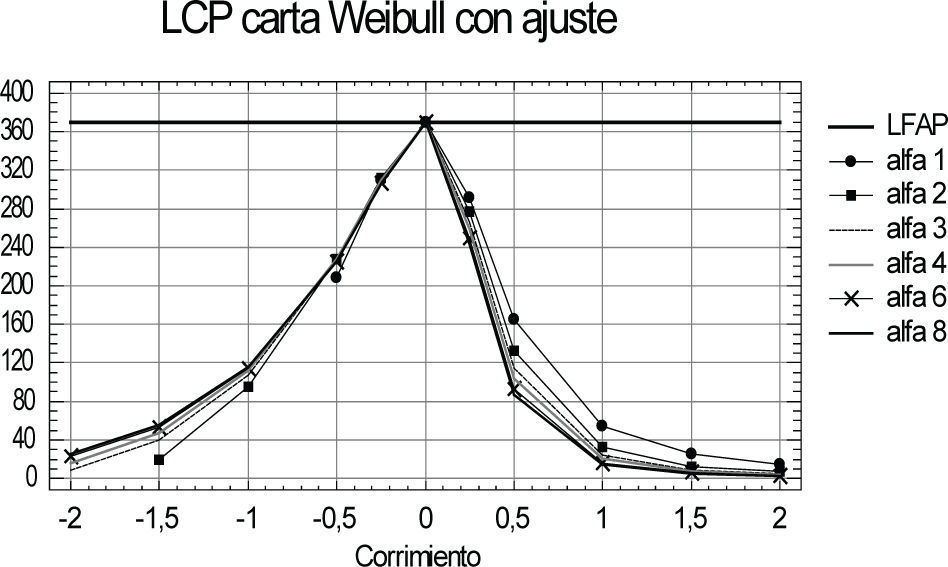
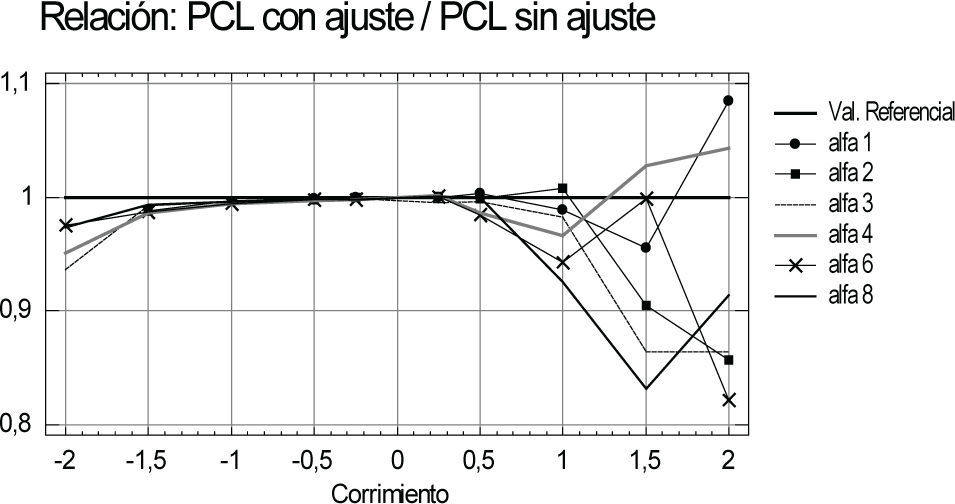
Gráficos

Es importante notar que los cálculos de LCP, PCL y VD para ambas cartas dados por (12), (18), (29) y (30) se deben realizar para cada par de valores (D, α) con D ≠ 0, contemplados en la sección supuestos del trabajo. Dada la numerosa cantidad de combinaciones posibles y para facilitar el análisis de las conclusiones, se presentan gráficos apropiados. En las figuras 1, 4 y 5 se aprecian los resultados de la carta t sin ajuste. En la figura 2, los de LCP para la carta t con ajuste. Para comparar las cartas, se grafican las relaciones:

• LCP con ajuste / LCP sin ajuste (figura 3)

• VD con ajuste / VD sin ajuste (figura 6) y

• PCL con ajuste / PCL sin ajuste (figura 7)

Figura 1.

LCP cuando D ≠ 0 para la carta t sin ajuste

Figura 2.

LCP cuando D ≠ 0 para la carta t con ajuste

Figura 3.

Relación LCP con ajuste LCP sin ajuste para D≠0

Figura 4.

VD cuando D ≠ 0 para la carta t sin ajuste

Figura 5.

PCL cuando D ≠ 0 para la carta t sin ajuste

Figura 6.

Relación VD con ajuste VD sin ajuste para D≠0

Figura 7.

Relación PCL con ajuste PCL sin ajuste para D≠0

Discusión y análisis de resultados

Para D ≠ 0, el ajuste de los límites de control ha dado sus frutos como se observa en las figuras 1 y 2. En la carta t sin ajuste (figura 1), para pequeños deterioros del equipo o sistema (D < 0 muy pequeño), LCP supera significativamente al valor LFAP preasignado de 370 puntos. Esto significa que, ante pequeños deterioros, la carta tarda más en emitir una señal que cuando no se producen. De la figura 2, la ventaja del ajuste es evidente, mantiene a LCP por debajo de ese nivel, cualesquiera sean D y α.

La naturaleza asimétrica de Weibull hace que, para valores D de igual magnitud pero distinto sentido, las LCP de ambas cartas difieran significativamente, aunque con menor intensidad en la carta t con ajuste y ser mayores para D < 0. Esto significa que, a igual tenor de D, ambas cartas son mucho más veloces para detectar mejoramientos que deterioros. No obstante, estas discrepancias se suavizan conforme aumenta la magnitud de D. Se observa además que, para la mayoría de los corrimientos D, el valor LCP de cada carta no difiere significativamente de un valor α a otro, para los contemplados en este trabajo.

El comportamiento de LCP en la carta t con ajuste varía según el signo de D (figura 3). Para D < 0 (deterioros), es claramente ventajosa, significativamente más sensible, más rápida que la carta t sin ajuste. Su LCP es aproximadamente 40% inferior a la del caso sin ajuste.

En cambio, para D > 0 (mejoramientos), la carta t con ajuste se torna perjudicial. Su LCP es significativamente superior a la de la carta t sin ajuste, especialmente para corrimientos D > 0 muy pequeños, aunque, la magnitud del incremento disminuye conforme aumenta D y también con α. En conclusión, la carta t con ajuste trae como contrapartida una carta menos sensible, más lenta que la carta t sin ajuste para detectar mejoramientos del equipo o sistema.

En cuanto a las otras medidas de desempeño, en la carta t sin ajuste se aprecia una muy elevada variabilidad derecha (figura 4). Para deterioros (D < 0), es del orden de 140% aproximadamente. Para mejoramientos (D > 0), disminuye levemente hasta alcanzar un mínimo de 110%. Esos altos niveles de VD están acompañados por una proporción de corridas largas PCL de 37% aproximadamente, para D < 0, y oscilando entre 30% y 40%, para D > 0 (figura 5).

La carta t con ajuste, para D < 0, mantiene los mismos niveles elevados de VD de la carta t sin ajuste y también casi iguales valores PCL. Similar comportamiento se aprecia para corrimientos positivos de magnitud pequeña (0 < D < lσ) (figuras 6 y 7).

Para la mayoría de los corrimientos positivos de mayor magnitud (D > 1σ), el incremento en LCP de la carta con ajuste está acompañado de un leve incremento en los valores VD (inferior a 20%) (figura 6). Sin embargo, este aumento no es preocupante dado que está atenuado por una reducción en PCL (inferior a 20%) (figura 7). Es decir, si bien la LC carta t con ajuste es más variable que la del caso sin ajuste, menor es la probabilidad de que presente una corrida más larga que el promedio.

En resumen, el ajuste de los límites de control solo alcanza para corregir aquellos valores LCP de la carta t sin ajuste que están por encima del valor LFAP preasignado, pero no para disminuir sus elevados niveles de VD.

Conclusiones

El principal objetivo de este trabajo fue realizar un análisis y comparación de las ventajas y desventajas del uso de cartas de relativa sencillez que surgieron en años recientes en concordancia con la evolución de la metodología Six Sigma y de particular interés en mantenimiento, evaluando no solo la tradicional LCP, sino también otras facetas poco exploradas de la velocidad de respuesta de una carta de control.

Atendiendo a la velocidad media de respuesta, si el objetivo principal del monitoreo del equipo o sistema recae en detectar deterioros, se recomienda la carta t con ajuste. En cambio, cuando la prioridad es detectar mejoramientos, la carta t sin ajuste es la mejor opción. Sin embargo, en un programa Six Sigma, el interés recae en detectar tanto deterioros como mejoramientos del proceso, para no desatender información valiosa que pueda dar lugar a una oportunidad de mejora. De usar estas cartas, se sugiere su uso simultáneo.

No obstante, la velocidad de respuesta de ambas cartas es muy variable de corrida en corrida. Con frecuencia el costo que se paga por una carta con diseño de relativa sencillez, como las presentadas en este trabajo, es la obtención de una carta menos veloz y más variable que otras disponibles en la literatura, entre las que se destaca, la carta CUSUM Weibull (Quintana y García, 2010). Es bien conocido que las cartas CUSUM son rápidas en la detección de corrimientos muy pequeños aunque su diseño es más complejo.

Desde el punto de vista operacional, las cartas t con y sin ajuste son más recomendables que la carta CUSUM Weibull. La primera razón es que el diseño de las cartas t requiere del proceso menos información que CUSUM. Esto es particularmente útil en situaciones donde no se tiene plena claridad de cuál magnitud del corrimiento D es la más crítica; es decir, a partir de qué valor D se pueden obtener serios perjuicios en el proceso si el cambio no es detectado a tiempo (requerimiento indispensable para diseñar una carta CUSUM). Esto ocurre, por ejemplo, en la puesta en marcha de un equipo o sistema nuevo o cuando no se cuentan con suficientes registros de su historial de funcionamiento. Como consecuencia, para determinar los límites de control, es más simple llevarlo a cabo con la carta t que con CUSUM. La segunda razón es que el cómputo de las medidas de desempeño de la carta es más sencillo en las cartas t, dado que se disponen de fórmulas precisas para ello. Por el contrario, para la carta CUSUM, es necesario recurrir a algoritmos aproximados.

Sin pretender hacer una enumeración exhaustiva, otras alternativas existentes en la literatura son: la carta t_r (extensión de la carta t), las cartas no paramétricas y las que se basan en el método de la varianza ponderada. Se dispone de estudios de sus desempeños aunque generalmente solo en términos de LCP y ATS. En el caso de las cartas no paramétricas, pocas publicaciones hacen comparaciones con cartas diseñadas para procesos Weibull y menos si se trata de aplicaciones a mantenimiento. En cambio, en el caso de las cartas basadas en el método de la varianza ponderada, la literatura evidencia interés sobre su aplicación a procesos Weibull, aunque con análisis limitados de su desempeño. Por ello, el análisis de las características, bondades y limitaciones de las cartas alternativas nombradas, más allá de las medidas convencionales de desempeño, es de sumo interés para los autores de este trabajo en una futura investigación, con el objeto de comparar con las cartas t presentadas aquí y orientar sobre la alternativa más conveniente a las condiciones y limitaciones de un proceso, con especial énfasis en mantenimiento.