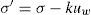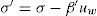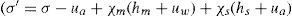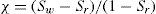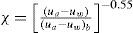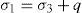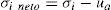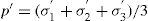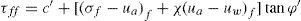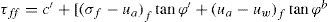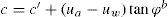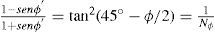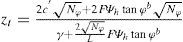El comportamiento de resistencia y cambios volumétricos de un suelo saturado están controlados por los esfuerzos efectivos, sin embargo, para el caso de los suelos no saturados no ha sido posible esclarecer este argumento. No existe una ecuación de esfuerzos efectivos para los suelos no saturados que sea aplicable a todos los tipos de suelos. Bishop (1959) propuso una ecuación para esfuerzos efectivos para suelos no saturados, esta ecuación contiene el parámetro χ; para determinar este parámetro existen varias ecuaciones pero ninguna comprende todos los casos. Por otra parte, en la mecánica de suelos se ha considerado que la resistencia cortante de los suelos finos se incrementa con la succión; sin embargo, esto no es el caso para todos los tipos de suelos. Existen algunos suelos cuya resistencia alcanza un máximo para cierta succión y luego se reduce para valores mayores de succión, no obstante, tales casos aún no han sido completamente documentados y analizados. Este artículo presenta una serie de pruebas triaxiales con succión controlada en laboratorio hechas en una arena limosa. Las pruebas se hicieron para las trayectorias de humedecimiento y secado. La succión se controló mediante circulación de aire con humedad relativa constante. La curva de retención de agua fue también obtenida para ambas trayectorias de humedecimiento y secado con la técnica del papel filtro, y para la trayectoria de secado se hicieron pruebas con el cilindro extractor de membrana. Los resultados de las pruebas triaxiales se muestran en diagramas p'-q y se ha podido observar que la resistencia del suelo crece a un máximo para cierta succión y luego decrece para valores mayores de succión, también se han incluido los valores de χ obtenidos de algunas ecuaciones existentes para este parámetro y resultados experimentales.
The behaviour of resistance and volumetric changes of a saturated soil are controlled by effective stress, however in the case of unsaturated soils it has not been possible to clarify this argument. There is not an equation for the effective stress of unsaturated soil that is applicable to all soil types. Bishop (1959) proposed an equation for effective stress to unsaturated soils, this equation contains the parameter χ, to determine this parameter there are several equations but none covers all the cases. Moreover, the soil mechanics has considered that the shear strength of fine soils increases with suction, but this is not the case for all soil types. There are some soils whose resistance reaches a maximum for certain suction and then decreases for higher values of suction. However, such cases have not yet been fully documented and analyzed. This article presents a series of triaxial tests with controlled suction made in a silty sand. The tests were made on wetting and drying trajectories. The suction was controlled by circulation of air with constant relative humidity. The water retention curve was obtained for both trajectories of wetting and drying with filter paper technique and other tests were made with the cylinder membrane extractor for drying trajectory. The results of triaxial tests are shown in p'-q diagram, and can be observed that the resistance of soil increases to a maximum for certain suction and then decreases for higher values of suction, it also includes the χ values obtained from some existing equations for this parameter and experimental results.
Terzaghi (1936) establece el principio de los esfuerzos efectivos, y en mecánica, se han definido esos esfuerzos como los que controlan la resistencia al cortante y los cambios de volumen de los suelos, éstos últimos generalmente se han relacionado con el fenómeno de consolidación. En este principio, Terzaghi considera que tanto las partículas sólidas y el agua son incompresibles, además de que puede ser despreciada el área de contacto entre dos partículas. La ecuación de esfuerzos efectivos para suelos saturados se escribe de la siguiente forma:
En la ecuación anterior a representa el esfuerzo efectivo y es el resultado de la diferencia entre el esfuerzo total a y la presión intersticial o de poro uw. Posteriormente Skempton (1960) propone la ecuación (2) para explicar el comportamiento de la resistencia de los suelos en la que introduce un parámetro k que toma en cuenta el efecto de las áreas de contacto despreciado por Terzaghi.
Para Skempton σ′ es el esfuerzo efectivo y σ es el esfuerzo total, donde k=1 – a tan ψ / tan ϕ. En esta expresión a es el área entre partículas por unidad de área, ψ es el ángulo de fricción del material de las partículas sólidas y ϕ es el ángulo de fricción entre las partículas del suelo.
Lade y De Boer (1997) proponen para el comportamiento volumétrico de los suelos saturados k=1 − (1 − n) Cs / Ce′, donde n es la porosidad, Cs es la compresibilidad del material sólido de las partículas de suelo y Ce es la compresibilidad de la estructura del suelo.
Para el caso de los suelos no saturados se tiene la controversia con respecto a la existencia de una ecuación de esfuerzos efectivos que pueda explicar ese comportamiento. Croney et al. (1958) establece una ecuación de esfuerzos efectivos para un suelo no saturado:
En la ecuación anterior σ′ es el esfuerzo normal efectivo, σ es el esfuerzo normal total, β′ es un factor de unión, que representa una medida del número de vínculos bajo tensión entre las partículas y uw es la presión de poro.Bishop (1959) sugiere otra ecuación de esfuerzos efectivos para suelos no saturados (4), en esta ecuación se incluye un parámetro hidromecánico χ, que es difícil de evaluar.
En la ecuación de Bishop, σ′ es el esfuerzo efectivo, σ − ua es el esfuerzo neto, (ua – uw) es la succión y] es el parámetro de Bishop, siendo unitario para suelos saturados, y por tanto, esta ecuación se reduce a la de Terzaghi y se toma como cero para suelos secos. El producto χ (ua – uw) representa el esfuerzo cohesivo. A la ecuación de Bishop le siguieron otras de la misma forma; Aitchison (1961) define que el esfuerzo efectivo está dado por la ecuación:En la ecuación (5) ψ es un parámetro que varía de cero a uno y p″ es definida como la deficiencia de la presión de agua en los poros. Jennings (1960) también establece la siguiente ecuación:Para Jennings p″ es la presión de agua negativa en los poros, pero tomada como valor positivo, y β es un factor estadístico del mismo tipo, tal como el área de contacto, que debe ser medido experimentalmente. Burland (1964 y 1965) sugiere que el comportamiento mecánico de los suelos no saturados debe ser relacionado con las variables (σ′ – ua) y (ua – uw) siempre que sea posible. Richards (1966) propone una ecuación (7), con dos componentes de succión para estimar el esfuerzo efectivo.donde χm es parámetro de esfuerzo efectivo para la succión mátrica, hm es la succión mátrica, χs es el parámetro de esfuerzo efectivo para la succión salina y hs es la succión salina. Aitchison (1965) presenta la ecuación (8), similar a la de Richards:En la ecuación anterior, P”m es la succión mátrica, P”s es la succión salina y χm y χs son los parámetros para cada una de las succiones mátrica y osmótica, respectivamente, y varían entre cero y uno. Más ecuaciones han sido propuestas (Garven y Vanapalli, 2006) y recientemente se ha tratado de relacionar experimentalmente la curva característica de retención de agua del suelo con su comportamiento a la resistencia cortante (Thamer et al., 2006).Para determinar el parámetro J de Bishop existen varias ecuaciones, la (9) y (10) propuestas por Vanapalli et al. (2000), la (11) por Öberg y Sällfours (1997) y la (12) por Khalili y Khabbaz (1998):
En las ecuaciones anteriores Sw es el grado de saturación, k es un parámetro de ajuste que varía con el índice de plasticidad (Vanapalli y Fredulund, 2000), Sr es el grado de saturación residual, (ua – uw) es la succión y (ua – uw)b representa el valor de la succión para el punto de entrada de aire. Sin embargo, no hay una ecuación adecuada para todos los tipos de suelos y valores de succión, por esta razón es necesario realizar más experimentación y desarrollar la base teórica del comportamiento de suelos.El objetivo de este trabajo es presentar resultados experimentales de laboratorio, en los que se observa la variación de los esfuerzos efectivos utilizando algunas de las ecuaciones que incluyen al parámetro χ de Bishop. Los resultados se presentan en diagramas de esfuerzo efectivo contra el esfuerzo desviador, p′– q, para las trayectorias de secado y humedecimiento de una arena limosa no saturada. Para este propósito se realizaron pruebas de compresión triaxial controlando la succión en probetas remoldeadas de ese suelo y se obtuvieron las curvas de retención de agua para ambas trayectorias con las técnicas del papel filtro y del cilindro extractor de membrana.
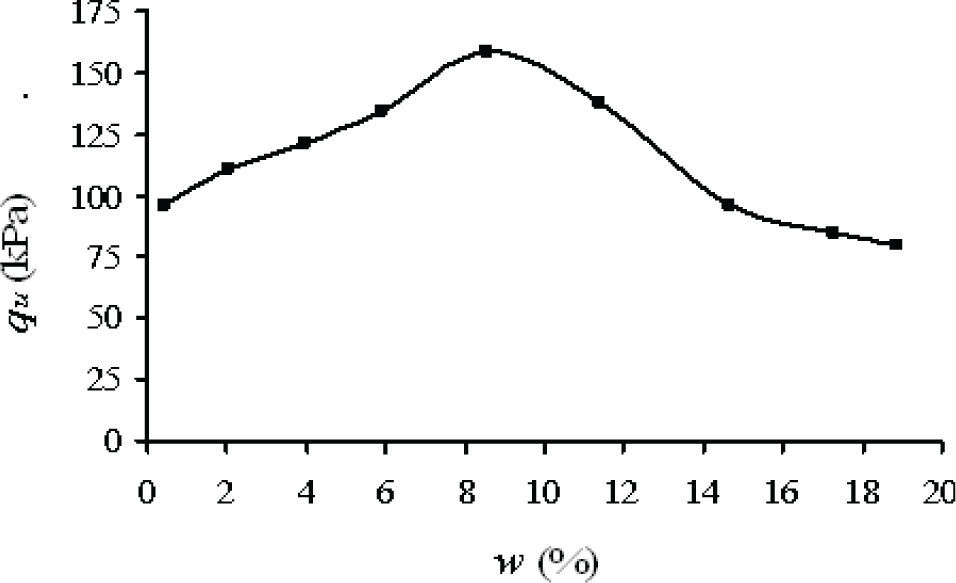
Materiales y métodosEl suelo estudiado en este trabajo es una arena limosa (SM). La granulometría fue seleccionada con 79% de arena y 21% de limo, sus coeficientes de curvatura y uniformidad fueron 1.47 y 7.50, respectivamente, y no presentaba plasticidad. Por otra parte, se requería de un suelo que presentara incrementos de resistencia a medida que la humedad fuera cambiando y luego de alcanzar un máximo de resistencia para cierta humedad la resistencia disminuyera al seguir modificándose la humedad, para lograr este objetivo se realizaron pruebas de compresión simple en la trayectoria de secado. Las probetas se fabricaron en un molde de media caña de diámetro 3.6cm y la altura de 7.2cm, la humedad inicial de remoldeo fue de 19.53%; cada probeta se hizo con 5 capas de suelo, cada capa de 0.343 N de suelo húmedo se aplicó en caída libre 10 veces un pisón metálico de 8.88 N por capa, la altura de caída fue de 0.497m, y entre capas se realizó anclaje por medio de escarificación. Los resultados de estas pruebas se indican en la figura 1.
En la figura 1, puede observarse que para la trayectoria de secado la resistencia alcanza un máximo para cierta humedad, y al continuar el proceso de secado disminuye. Está serie de pruebas de compresión simple resultó importante para continuar con las pruebas triaxiales consolidadas y drenadas, ya que a partir de éstas se tuvo la tendencia de comportamiento en este caso de estudio.
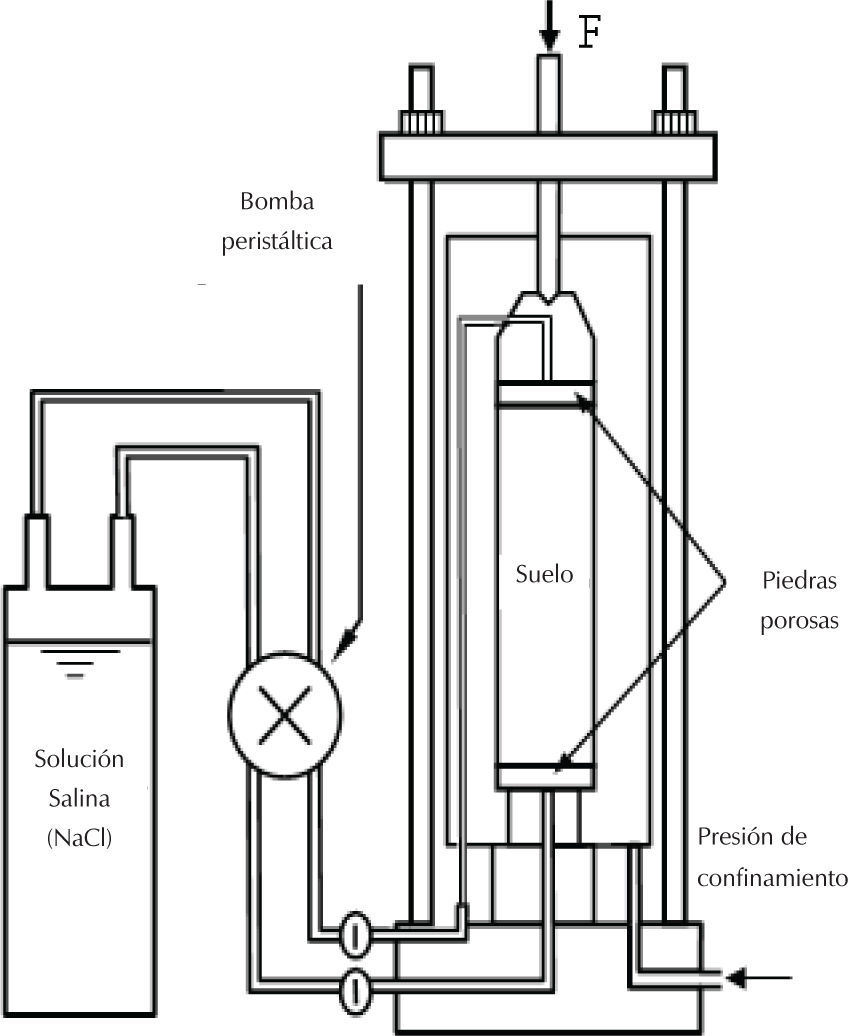
Pruebas de compresión traxial con succión controladaEn un equipo convencional de pruebas triaxiales, la succión cambia a medida que se aplican las diferentes etapas de carga. En este trabajo se controla la succión con una bomba peristáltica, que hace circular aire con humedad relativa constante, esta humedad se obtiene de la evaporación de agua generada en un recipiente con solución de cloruro de sodio; el recipiente no se llena totalmente para tener un espacio en que se aloje la evaporación del agua de la solución a una temperatura de 20°C. La concentración de sal se determina para cierta succión que se desee inducir a la probeta de suelo. El recipiente en su parte superior está provisto de una tapa con dos orificios, de uno de ellos succiona el aire húmedo con la bomba peristáltica y se lleva a uno de los extremos de la probeta de suelo colocada en la cápsula triaxial. Por el otro extremo de la probeta se conecta otra manguera para continuar con el flujo del aire en la misma dirección de circulación, ésta se lleva hasta la bomba peristáltica y se retorna hasta el recipiente, de tal forma que se tiene un circuito cerrado en condiciones isotérmicas e isobáricas. El flujo de bombeo fue de 8.81ml/min que corresponde a una velocidad de 15rpm de la bomba peristáltica (marca Dynamax modelo RP-1 peristaltic diseñada para transferencia de fluidos). Se describe el sistema en la figura 2.
En la parte inferior y superior de las probetas de suelo se colocaron dos papeles filtro para determinar la humedad obtenida por contacto con la muestra de suelo y con ello determinar la succión al final de la prueba triaxial. Con este equipo se realizaron dos series de pruebas de compresión triaxial del tipo consolidadas drenadas (CD), teniendo un esfuerzo de confinamiento de 150kPa y con una velocidad de deformación aplicada de 0.001mm/min. Las probetas fueron preparadas por presión en forma estática en cinco capas de 0.70 N de peso cada capa, con una presión de 3140kPa. De esta forma se controló el peso específico seco de 14.889kN/m3 y la humedad de remoldeo de 19.53%. Una serie de probetas de suelo fue realizada para la trayectoria de humedecimiento y otra para la trayectoria de secado. Al final de cada prueba se verificó la succión con la metodología del papel filtro de acuerdo a la norma ASTM D 420-D-5611. En la figura 3 se indica la calibración del papel filtro utilizado (Schleicher and Schuell Núm. 589).
En este equipo también se ensayó una serie de tres probetas saturadas, permitiendo su consolidación y drenaje, los esfuerzos de confinamiento fueron de 50, 100 y 150kPa, el procedimiento de su preparación fue el descrito en el párrafo anterior, sólo que en esta condición no se hace circular la humedad relativa con la bomba peristáltica.
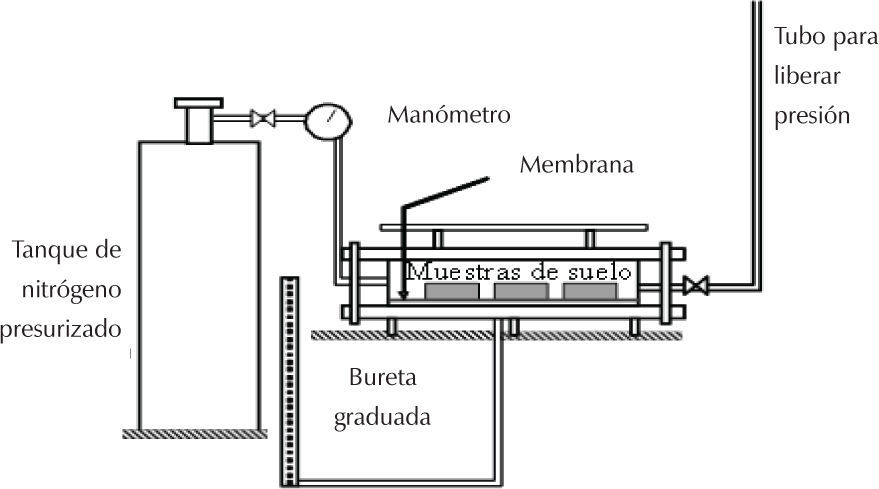
Para determinar las curvas de retención de agua se utilizó la técnica de papel filtro para las trayectorias de secado y humedecimiento, la determinación de la curva de retención para la trayectoria de secado también se realiza con el cilindro extractor de membrana para un intervalo de succiones del orden de 1.0kPa hasta 4200kPa. Este equipo es un contenedor en el que se colocan las muestras de suelo en condiciones iniciales de saturación por inmersión, posteriormente se presuriza con nitrógeno.
El procedimiento con este equipo fue el siguiente: se prepararon muestras de suelo colocadas en anillos de aluminio y compactadas por presión en forma estática, controlando el peso específico seco (14.889kN/m3) y la humedad de remoldeo (19.53%). En el fondo del cilindro extractor se coloca una membrana porosa con la característica de que sólo deja pasar el agua, de esta manera y a medida que se aplican incrementos sucesivos de presión con el nitrógeno se van deshidratando las muestras de suelo colocadas sobre esa membrana. El agua se drena por un orificio en el fondo del cilindro extractor y se deposita en una bureta graduada (0.1ml), en esta bureta se observan los cambios de volumen por el agua que se drena de las muestras, debido a una presión dada por el nitrógeno, cuando ya no hay cambios en el volumen se abre el cilindro extractor, se mide la disminución de altura de las muestras de suelo y se pesan. Por diferencias en el en peso, se determina la disminución en el grado de saturación y la presión aplicada por el nitrógeno se considera como la succión. Se repite este proceso hasta llegar a los límites de capacidad de la membrana, ya que con presiones ligeramente superiores a los 4000kPa tienden a romperse. En la figura 4 se presenta el equipo descrito.
Resultados y discusiónSe ensayaron 10 probetas remoldeadas de arena limosa en compresión triaxial consolidadas y drenadas, se mantuvieron con un esfuerzo de confinamiento de 150kPa durante la prueba, sus resultados están en la figura 5, se indica el esfuerzo desviador residual contra la succión y se incluyen las trayectorias obtenidas para procesos de humedecimiento y secado. En ambas trayectorias se obtuvo un valor máximo de resistencia en términos del esfuerzo desviador para cierto valor de succión, y luego se observa decremento de resistencia para valores mayores de succión.
De acuerdo con las curvas esfuerzo desviador-succión se puede ver que para succiones mayores del orden de 2000kPa el esfuerzo desviador es mayor en la trayectoria de secado, y para succiones del orden de los 600kPa se intersecan las curvas q-s, de tal forma que la resistencia es mayor en la trayectoria de humedecimiento para succiones menores a ese valor.
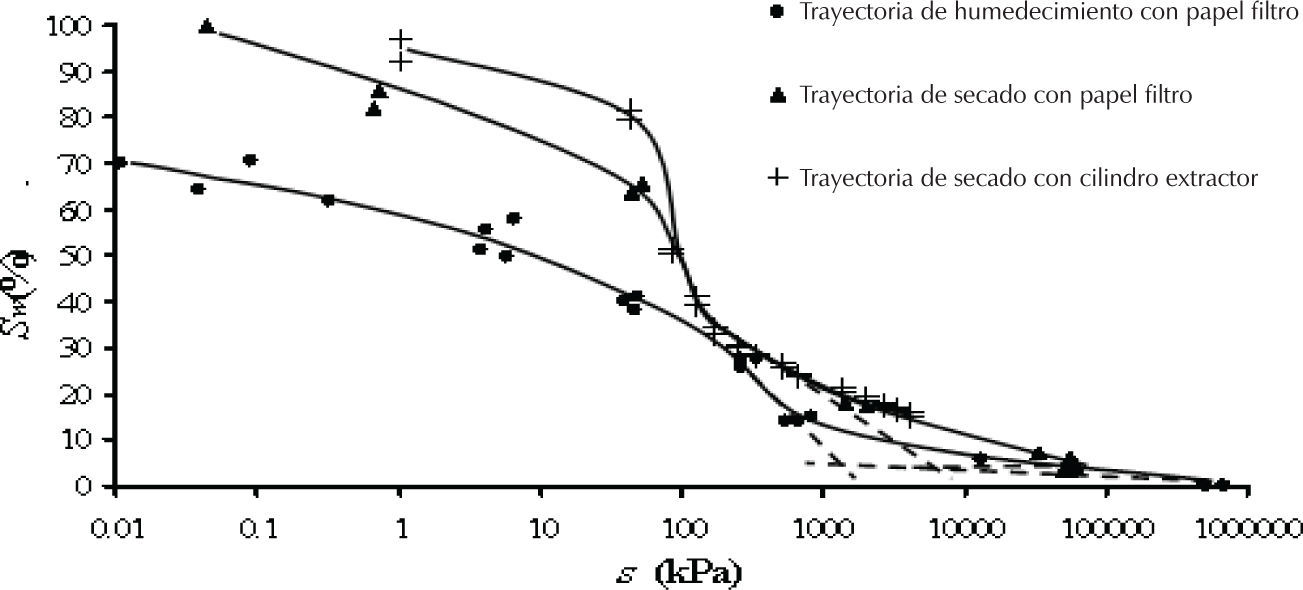
La forma de retener agua del suelo es el resultado de la distribución de sus poros y de su sensibilidad a sufrir cambios de volumen bajo esfuerzos, que se puede representar con las curvas de retención en las que se grafica la succión (s) y el grado de saturación (Sw). Para el suelo estudiado (SM), se obtuvieron las curvas de retención de agua para las trayectorias de humedecimiento y secado, estas curvas son una relación entre el grado de saturación y la succión mátrica, sin embargo, en este trabajo experimental no se incluye el efecto de los cambios de volumen que ocurre en los poros del suelo. Para el caso de la trayectoria de secado se utilizó además de la técnica de papel filtro, el cilindro extractor, que tiene un intervalo limitado de manejo de succiones con respecto a la técnica del papel filtro. Las curvas de retención obtenidas se muestran en la figura 6.
Como se muestra en la figura anterior, para cualquier grado de saturación la curva de retención de agua en proceso de secado presenta valores mayores de succión que la curva de humedecimiento. En la curva de secado puede observarse que ocurren pérdidas grandes de agua para valores de succión menores a 2100kPa, llegando a tener un grado de saturación de aproximadamente 17.5%; para poder drenar el agua después de ese valor de succión se requieren cantidades mayores de energía, ya que para llegar a un grado de saturación cercano a cero se requieren aproximadamente 1 000 000kPa de succión. En la curva de la trayectoria humedecimiento, el suelo ensayado se encuentra inicialmente en un estado de succiones altas, cercanas a 670 000kPa y cuando comienza el humedecimiento, el grado de saturación se incrementa lentamente hasta valores de succión del orden de 675kPa para un grado de saturación de aproximadamente 14.0%; para valores menores de succión el grado de saturación se incrementa más rápidamente.
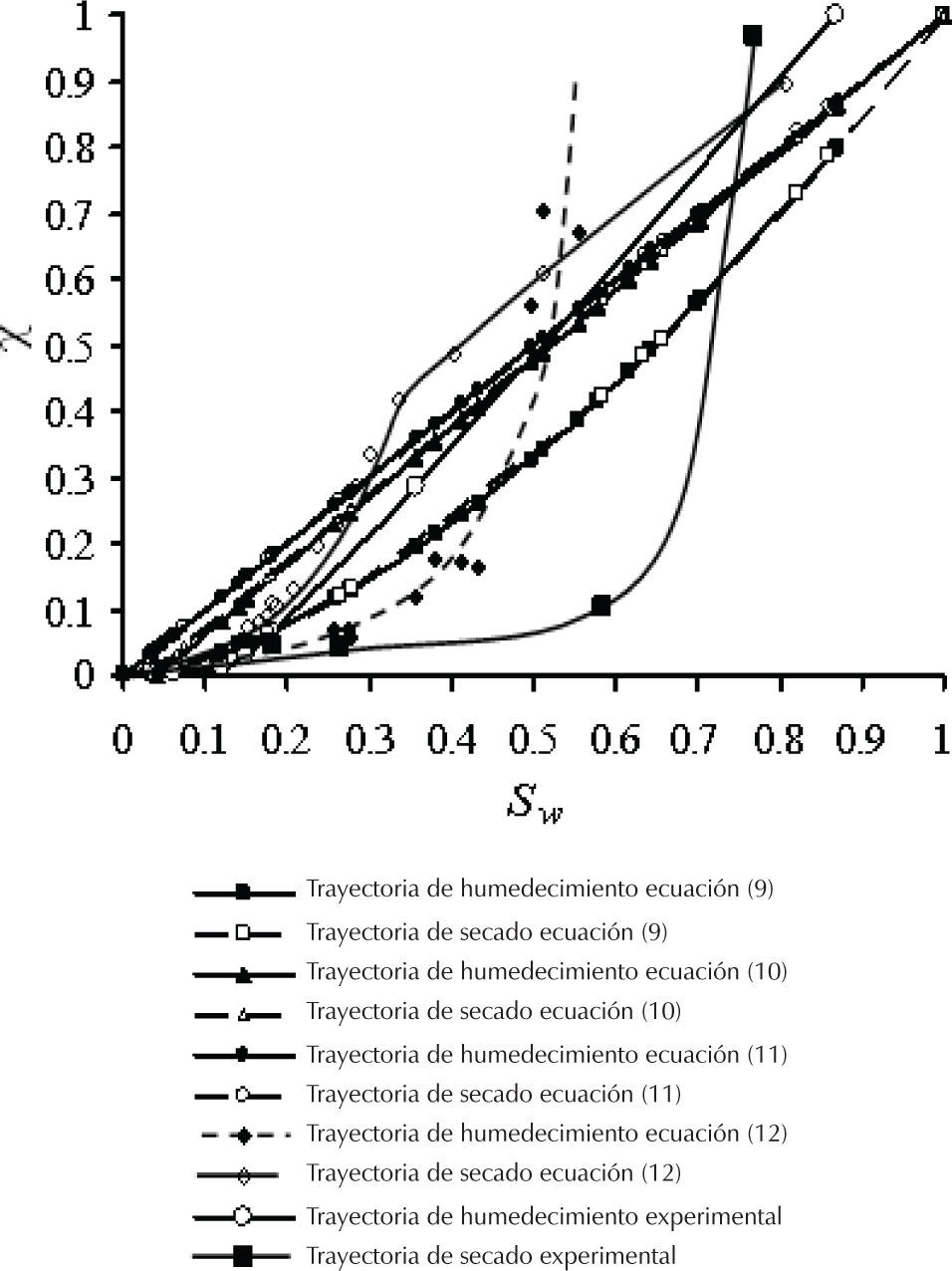
Para estimar los esfuerzos efectivos se requieren calcular los valores del parámetro χ de Bishop. Este cálculo se ha realizado para la trayectoria de humedecimiento y secado a partir de los datos de la curva característica y de los datos de las pruebas triaxiales con las ecuaciones (9), (10), (11) y (12). De esta forma, con cada ecuación se obtienen dos series de valores del parámetro χ. La figura 7 contiene los resultados de χ y los valores experimentales del mismo.
Valores del parámetro χ de Bishop, estimado con las ecuaciones (9) y (10) de Vanapalli, la ecuación (11) de Öberg y Sällfours y la ecuación (12) de Khalili y Khabbaz para las trayectorias de secado y humedecimiento de una arena limosa (SM). Las Trayectorias sin número de ecuación corresponden a valores experimentales del parámetro χ
En la elaboración de la figura 7, con respecto a la ecuación (9), se utilizó el valor de ajuste κ=1.6; la selección de este valor corresponde a la mejor alineación posible a una recta que pase por el origen de los valores del esfuerzo efectivo en un diagrama p′−q, como será explicado más adelante.
Los grados de saturación residuales utilizados en la ecuación (10) fueron obtenidos de las curvas características, siendo el grado de saturación residual Sr=0.04 para la trayectoria de humedecimiento y Sr=0.0325 para la trayectoria de secado. Éstos se obtienen trazando un par de líneas tangentes en el cambio de curvatura de las curvas características; una tangente se traza en el tramo de mayor pendiente de la curva y otra en el tramo final de la misma, en donde la succión presenta mayores valores y en el punto de su intersección se encuentra el Sr, los trazos de esas tangentes se indican en la figura 6.
Se puede ver en la figura 7 que los valores de χ varían de una ecuación a otra, esto indica que las ecuaciones no son aplicables para todos los casos. Conocidos los valores del parámetro χ, para cada ecuación es posible estimar los valores de los esfuerzos efectivos. Se puede hacer aplicando las siguientes expresiones:
En estas ecuaciones, i varia de 1 a 3, σ1 es el esfuerzo vertical total, σ3 es el esfuerzo de confinamiento, ua es la presión de aire en los poros, q es el esfuerzo desviador de los ensayes triaxilaes, σ′es el esfuerzo efectivo y s es la succión.Para determinar cuál de las ecuaciones de χ representa de mejor forma los esfuerzos efectivos, se considera, según la teoría del estado crítico, que las probetas ensayadas se han llevado hasta la falla o rotura y que han alcanzado el estado crítico.
En este estado se tiene una determinada relación entre las componente desviadora e isótropa de esfuerzos que se puede definir como M, esta relación corresponde a la pendiente de una recta que pasa por el origen en un diagrama p′−q. En estos diagramas, p′ representa la componente isótropa y q la componente desviadora. Entonces resulta conveniente representar los resultados en diagramas de este tipo para observar su alineación con esa recta de pendiente M. Para calcular p′ se tiene la siguiente relación:
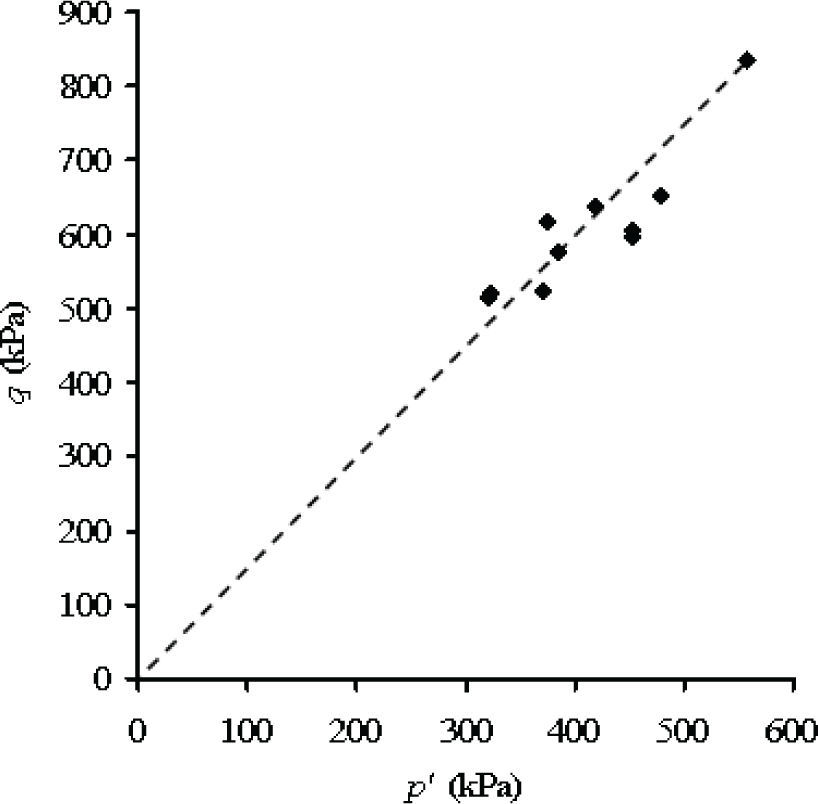
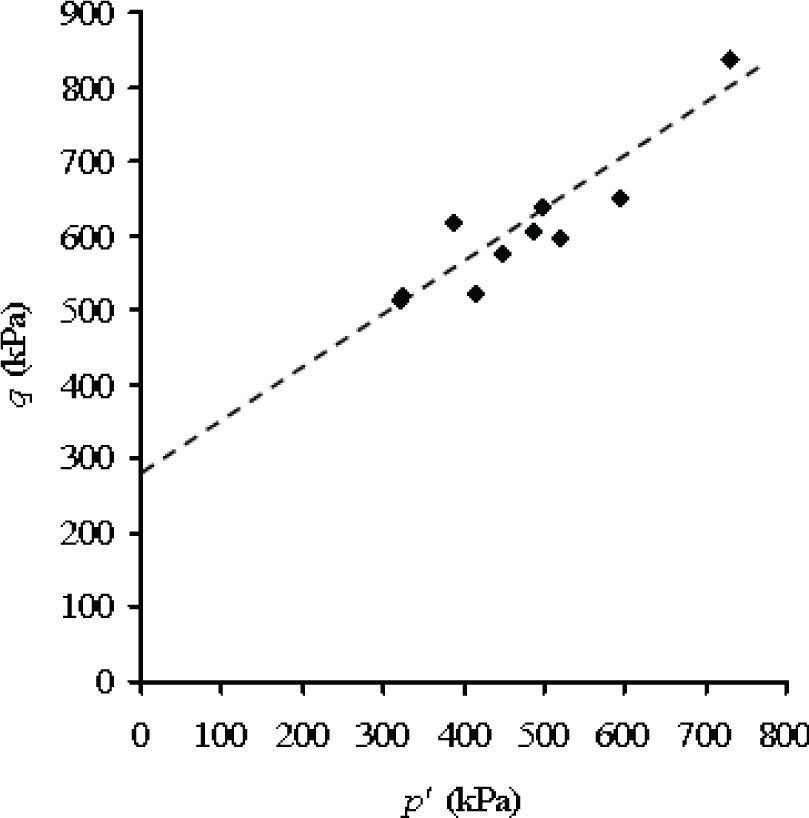
Los resultados de las pruebas triaxiales se pueden representar en las figuras 8, 9, 10 y 11 que corresponden a cada una de las ecuaciones del parámetro χ antes citadas, en ese orden.
Diagrama p′−q obtenido con los valores de χ para la ecuación (9) de Vanapalli et al. (2000) para las trayectorias de secado y humedecimiento de una arena limosa (SM)
Diagrama p′−q obtenido con los valores de χ para la ecuación (10) de Vanapalli et al. (2000) para las trayectorias de secado y humedecimiento de una arena limosa (SM)
Diagrama p'-q obtenido con los valores de c para la ecuación (11) de Öberg y Sällfours (1997) para las trayectorias de secado y humedecimiento de una arena limosa (SM)
Diagrama p'-q obtenido con los valores de c para la ecuación (12) de Khalili y Khabbaz (1998) para las trayectorias de secado y humedecimiento de una arena limosa (SM)
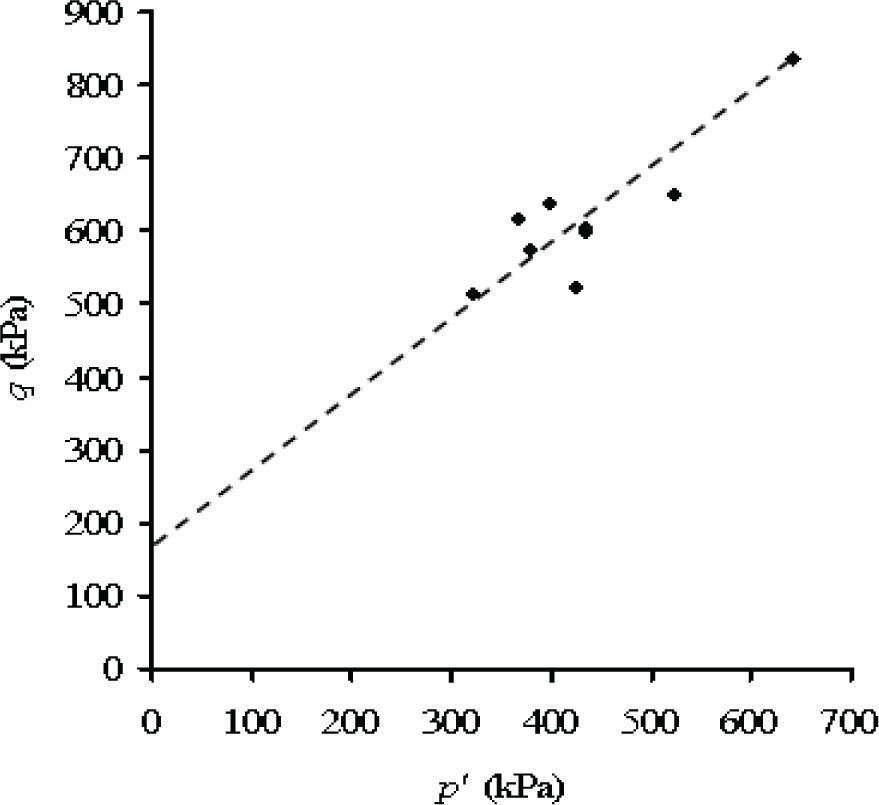
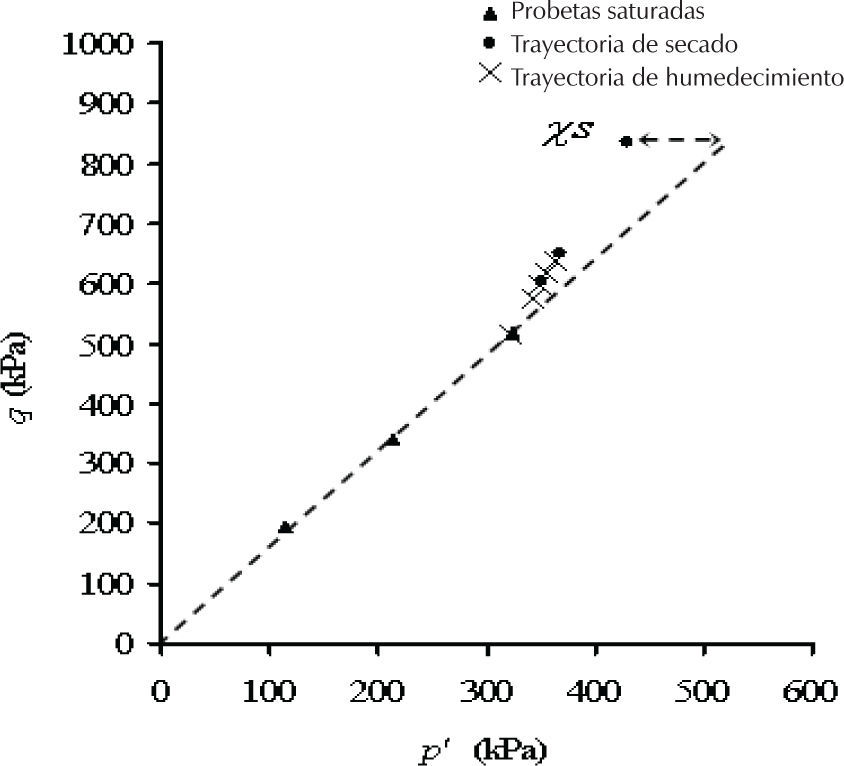
En la figura 7, los valores de χ experimentales se han obtenido a partir del conocimiento de M del diagrama p′−q de la serie de probetas saturadas de ensayes triaxiales, realizadas a presiones de confinamiento de 50, 100 y 150 kPa. En este caso la recta que representa los pares (p′, q) pasa por el origen, y si en este diagrama se representan los pares (σneto, q) la diferencia entre las abscisas de estos puntos con esa recta representa el esfuerzo cohesivo χs, y como s es determinada en laboratorio, entonces es posible conocer χ. Este procedimiento es equivalente a despejar el parámetro χ de la ecuación (15), (figura 12).
Una ecuación que realmente represente los esfuerzos efectivos alinearía los puntos experimentales en una recta que pase por el origen en un diagrama p'-q, según la teoría del estado crítico, la dispersión con respecto a esa recta es mayor con las ecuaciones menos adecuadas. Se puede observar que el esfuerzo efectivo depende en parte del parámetro χ, y que de las ecuaciones aquí utilizadas para el suelo analizado, la de menor dispersión fue la ecuación (9) de Vanapalli et al. (2000), con el valor de ajuste κ=1.6; en tanto que para las otras ecuaciones hay una mayor dispersión, presentando una ordenada al origen en los diagramas p′-q.
Aplicación: determinación de la presión activa actuante en una estructura de contenciónEn la mecánica de suelos se han considerado tres tipos de problemas relacionados con la resistencia del suelo en equilibrio, el equilibrio plástico: análisis de presión de tierras, determinación de capacidad de carga y análisis de estabilidad de taludes. En el caso de los suelos no saturados se asume que existe presión negativa del agua en los poros o succión. En este trabajo se presenta una de las aplicaciones del parámetro χ de Bishop para determinar la distribución de presiones de tierra en estado activo actuantes en el respaldo de una estructura de retención.
Cuando una estructura de retención permite que el suelo retenido se deforme hacia el frente el esfuerzo horizontal se reduce, pudiendo alcanzar un valor límite correspondiente al estado de equilibrio plástico. Como resultado de esto el esfuerzo horizontal debe ser el esfuerzo principal menor (σh =σ3) y el esfuerzo vertical el esfuerzo principal mayor (σν = σ1). El esfuerzo horizontal corresponde al estado activo y puede ser calculado a partir del esfuerzo vertical y establecer la distribución de presiones que empujan a la estructura.
Bishop (1959) presentó una ecuación para determinar la resistencia cortante de un suelo no saturado en la que incluyó el parámetro c, esta ecuación es la siguiente.
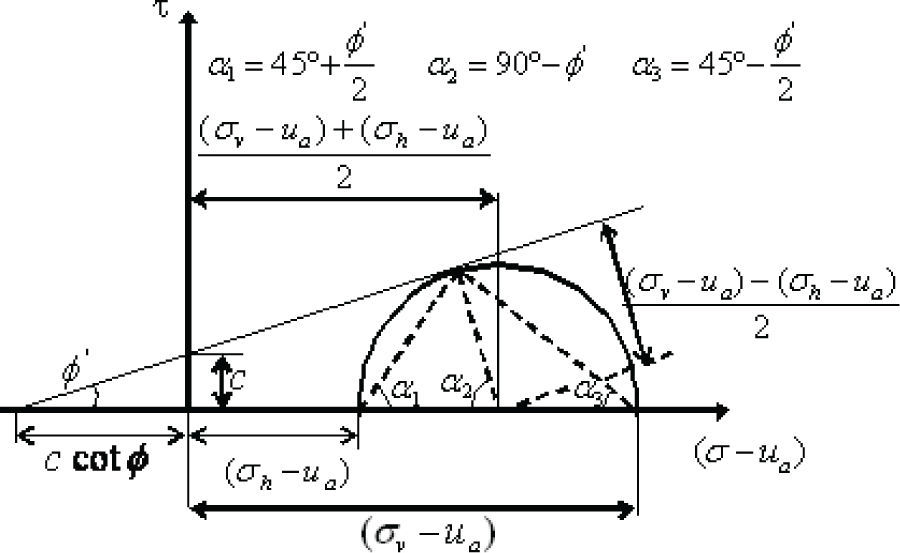
En la ecuación anterior, τff es la resistencia cortante en la falla, c′ es la cohesión efectiva, (σf - ua)f es el esfuerzo normal neto en el plano de falla, (ua - uw)f es la succión mátrica en el plano de falla, χ es el parámetro relacionado con el grado de saturación del suelo y φ′ es el ángulo de fricción interna asociado con el esfuerzo normal neto.Fredlund et al. (1978) estableció una ecuación para la resistencia al esfuerzo cortante de los suelos no saturados tomando en cuenta la succión mátrica, esta ecuación se escribe a continuación.
En donde, τff es la resistencia cortante en la falla, c′ es la cohesión efectiva, (σf−ua)f es el esfuerzo normal neto en el plano de falla, uaf es la presión del aire en los poros en el plano de falla, φ′ es el ángulo de fricción interna asociado con el esfuerzo normal neto, (ua − uw)f es la succión mátrica en el plano de falla y φb es el ángulo de fricción que indica la razón en que cambia la resistencia cortante con respecto a la succión mátrica. Las variables descritas en esta ecuación se pueden representar en las figuras 13 y 14 utilizando los círculos de Mohr.La presión activa está representada por (σh – ua) en la figura 14, para obtener una ecuación que permita su cálculo se puede establecer la siguiente relación trigonométrica.
En la ecuación (18) y según la figura 13, la cohesión total está representada por:Sustituyendo la ecuación (20) y las relaciones (21) y (22) en la (19) la presión activa puede ser calculada con la ecuación (23).Igualando las ecuaciones (17) y (18) se llega a tener la siguiente relación:La utilidad de la expresión (24) está en el cálculo de φb y se calcula con el parámetro x determinado con la ecuación (15), como fue descrito anteriormente, y del ángulo φ' obtenido de pruebas triaxiales consolidas drenadas.Envolvente de falla Mohr-Coulomb para suelos no saturados, Fredlund et al. (1978)
A continuación se presenta el análisis de la distribución de la presión activa de tierras, considerando una distribución lineal decreciente de la succión mátrica hasta llegar a un valor cero en la superficie del nivel de aguas freáticas. Esta distribución es la que actuaría en el respaldo de una estructura de retención, considérese la figura 15.
En la figura 15 la distancia desde la superficie hasta el nivel freático de agua es L y ψh representa la succión mátrica en la superficie del suelo correspondiente a una distribución lineal e hidrostática, F es un factor que relaciona la succión mátrica en la superficie correspondiente a una distribución de succión no lineal.
Introduciendo el factor F en la ecuación (23) la presión activa actuante en el respaldo de una estructura se expresa con la ecuación (25).
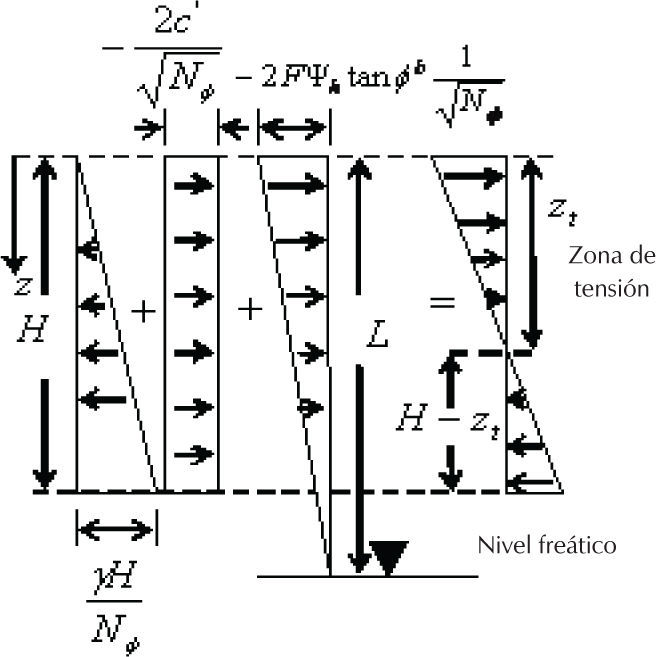
La presión activa definida por la ecuación (25) no considera los casos en que se presente agrietamiento. Las componentes de la presión activa de la ecuación anterior se representan en la figura 16.
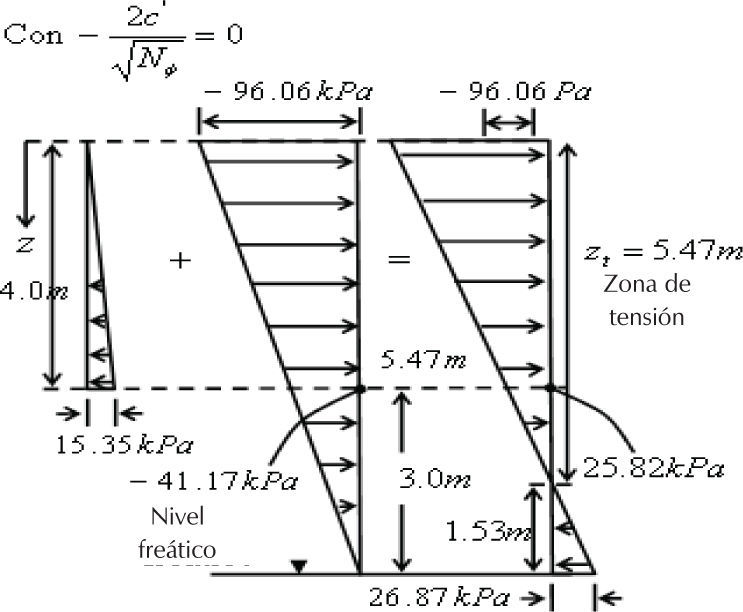
En la figura 16, H representa la altura de una estructura de retención y puede observarse que en la distribución resultante de la presión activa en la parte superior del suelo puede quedar una zona de tensión, cuya profundidad es zt, que puede ser calculada al igualar a cero el esfuerzo total horizontal y la presión del aire ua en la ecuación (25), resultando la ecuación (26).
Para ejemplificar numéricamente el procedimiento de cálculo arriba descrito se determinará la distribución de la presión activa actuante en el respaldo de una estructura de retención con respaldo vertical liso y se hará uso de la arena limosa estudiada en este trabajo, considerándola como el suelo de relleno.La altura de la estructura propuesta es H=4.0m, el ángulo de fricción interna es φ′=39.25°, la cohesión efectiva es c′=0, el peso específico promedio del suelo es γ=17.06 kN/m3, el grado de saturación medido en la superficie es Sw=17.46%, el parámetro χ=0.061 obtenido con la ecuación (9) para κ=1.6. La distribución de la succión mátrica en una sección del suelo de relleno actuante en el respaldo de la estructura se presenta en la figura 17.
Aplicando las expresiones indicadas en la figura 16 resultan los valores de las componentes de la presión activa de la figura 18 y la profundidad de la zona de tensión se calculó con la expresión (26).
ConclusionesEn este trabajo se ha encontrado que el cálculo del esfuerzo efectivo no se mantiene porque los valores de χ varían al calcularse con las ecuaciones utilizadas por diferentes autores. Los valores de χ calculados con esas ecuaciones también varían con respecto a los determinados experimentalmente. Estos últimos indican la existencia de valores distintos de χ para un mismo grado de saturación, según se trate de la trayectoria de humedecimiento o secado.
Para el suelo estudiado (SM), el criterio de Vanapalli correspondiente a la ecuación (9) para la determinación del parámetro χ fue el más adecuado, debido a que los puntos determinados en los diagramas p'-q presentan menor dispersión con respecto a la recta que pasa por el origen y de acuerdo a la teoría del estado crítico.
Los autores agradecen a la Universidad Autónoma de Querétaro, México por las facilidades en el uso de laboratorios.
Ingeniero Civil con grado de maestría en ciencias de ingeniería (1998) con línea terminal en mecánica de suelos. Es profesor en el Departamento de Ingeniería Civil de la Universidad de Guanajuato, México, desde 1990. Actualmente es estudiante de doctorado en ingeniería en la Universidad Autónoma de Querétaro, México.
Citación Chicago Leal-Vaca Julio César, Gustavo Gallegos-Fonseca, Eduardo Rojas-González. Estimación de esfuerzos efectivos a partir del parámetro χ de Bishop en una arena limosa. Ingeniería Investigación y Tecnología, XIV, 02 (2013): 139–151.
Citación ISO 690 Leal-Vaca, J.C., Gallegos-Fonseca G., Rojas-González E. Estimación de esfuerzos efectivos a partir del parámetro χ de Bishop en una arena limosa. Ingeniería Investigación y Tecnología, volumen XIV (número 2), abril-junio 2013: 139–151.
Es ingeniero civil con grado de maestría en ciencias de ingeniería en mecánica de suelos(2002). Es profesor de la Facultad de Ingeniería en la Universidad Autónoma de San Luís Potosí, México desde 1993.
Es profesor investigador en la Facultad de Ingeniería de la Universidad Autónoma de Querétaro, México.