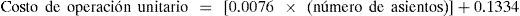El propósito de esta investigación fue evaluar una nueva estrategia para atender las operaciones aéreas en un aeropuerto con problemas de saturación para reducir los costos de operación de las aeronaves y las demoras de los pasajeros. El continuo crecimiento de la actividad aérea genera problemas de saturación en los principales aeropuertos del mundo, produciendo incrementos en los costos de operación de las aeronaves y molestias en los pasajeros. En la estrategia evaluada la regla tradicional para atender a las aeronaves, primeras llegadas-primeras salidas, fue sustituida por una secuencia que reduce los costos de operación y las demoras. Para realizar dicha evaluación fue desarrollado un modelo de simulación de eventos discretos aplicado al Aeropuerto Internacional de la Ciudad de México. Los resultados mostraron que al aplicar la estrategia propuesta se pueden obtener beneficios significativos, del orden de 28.6 millones de pesos anuales.
The objective of this research was to evaluate a strategy for attending the takeoffs and landings at a congested airport, in order to reduce aircraft operating costs and passenger delay times. The continuous growth of air transport activity has created congestion at major airports worldwide, this situation produces increases in the aircraft operating costs and passenger discomfort. In the strategy evaluated the traditional rule for attending to aircraft, on a first-come-first-served basis, was substituted with a sequence that reduces operating costs and passenger delays. In order to perform this evaluation a discrete-event simulation model was developed for the Mexico City International Airport. Results showed that it is possible to obtain significant benefits if the proposed strategy is applied, an annual benefit of around 28.6 million pesos could be achieved.
Los problemas de saturación en el transporte se presentan cuando la demanda de la infraestructura excede su capacidad, originando demoras en los viajes como uno de sus principales síntomas (Roosens, 2008). Desde hace varios años ha sido reportada la falta de suficiente capacidad aeroportuaria para cumplir con las demandas del transporte aéreo. Esto ha generado problemas de saturación y demoras en las redes de transporte aéreo en los principales aeropuertos del mundo (Hamzawi y Lack, 1992). La saturación afecta a varios de los subsistemas de los aeropuertos y, en mayor medida, a sus pistas, las cuales son el elemento crítico para determinar la capacidad máxima de cualquier aeropuerto.
Hoy en día la saturación de los centros de concentración y distribución aérea (hubs) representa uno de los principales problemas que enfrenta el transporte aéreo, debido a que genera inconvenientes en los aeropuertos, por ejemplo, demoras, cancelaciones y pérdida de conexiones, que en consecuencia afectan a las aerolíneas y a los pasajeros (Flores, 2010). La saturación incrementa los costos de operación de las aerolíneas y los pasajeros son afectados negativamente al perder tiempo, como resultado de la formación de líneas de espera.
La asignación y autorización de los aterrizajes y despegues de aeronaves se realizan mediante el control del tránsito aéreo (CTA) de acuerdo con la secuencia de cada solicitud. Aunque hay ciertas excepciones, la regla seguida es la de primeras llegadas primeras salidas (o FCFS, First-Come-First-Served) (FAA, 2010). Sin embargo, esta regla no considera que los costos de operación y las capacidades de los distintos tipos de aeronaves pueden ser muy diferentes (Herrera y Moreno, 2011).
Con el objeto de reducir el desequilibrio entre la relación demanda/capacidad de los aeropuertos se proponen diversas soluciones. Además, se desarrollan distintas herramientas de apoyo para los CTA, más eficientes y efectivas en la toma de decisiones, como un intento por equilibrar la demanda con la capacidad existente. Sin embargo, todas estas herramientas han sido aplicadas respetando la regla de prioridad para el servicio de las aeronaves FCFS. Una excepción parcial se presentó en Estados Unidos, en donde se utiliza un administrador para el tránsito de las aeronaves –Traffic Management Advisor, TMA– (Janic, 2009).
Además, existen otros trabajos de investigación que abandonan el principio FCFS, pero sólo consideran el caso de los aterrizajes. Por ejemplo, Soomer y Koole (2008) utilizan el problema del aterrizaje de aeronaves para ilustrar diversas definiciones de equidad que se oponen al principio tradicional. Otro proyecto de investigación se enfoca en la problemática de la programación de los aterrizajes en los aeropuertos (Wen, 2005). Por último, Lee (2008) desarrolló un algoritmo de programación dinámica para determinar el costo mínimo de llegada programada, utilizando los costos de las demoras de las aeronaves.
En una investigación previa se desarrolló una estrategia para atender los despegues y aterrizajes con objeto de reducir los costos operación de las aeronaves y las demoras de los pasajeros en aeropuertos saturados (Herrera y Moreno, 2011). Aunque se cuantificaron los beneficios potenciales de aplicar dicha estrategia, éstos sólo se determinaron para dos tamaños específicos de colas y para cierto tipo de aeronaves.
En este estudio se desarrolló un modelo de simulación de eventos discretos para el Aeropuerto Internacional de la Ciudad de México (AICM), con objeto de calcular los beneficios no solamente en un tamaño específico de línea de espera, si no en un día típico de operación para obtener elementos que respaldan la implementación de la estrategia. Este modelo permitió estimar el tamaño de las líneas de espera y su composición, considerando las diferentes clases de aeronaves.
La aplicación de modelos de simulación en las pistas de aeropuertos saturados es más bien limitada, aunque se desarrollaron algunos modelos (Janic, 2009), éstos se han centrado únicamente en los aterrizajes de las aeronaves. El modelo de simulación utilizado para evaluar la estrategia señalada aquí considera ambas operaciones, despegues y aterrizajes.
El AICM es una importante infraestructura en el ámbito mundial; durante 2009 estuvo ubicado en la posición 50 en cuanto a la atención de pasajeros (24.2 millones) y en la posición 29 de acuerdo con las operaciones realizadas –348,306– (Air Transport World, 2010). En relación con la carga aérea, se ubicó en la posición 49 (382,417 toneladas) durante 2008 (Air cargo World, 2009).
MetodologíaEl comportamiento de un sistema a través del tiempo se puede estudiar por medio de un modelo de simulación que suele tomar la forma de un conjunto de supuestos acerca de un sistema, los cuales usualmente se expresan mediante relaciones matemáticas y lógicas. Los modelos de simulación son una herramienta para predecir los efectos de cambios en sistemas ya existentes o en aquellos que se van a construir. En general, no es necesario tener una correspondencia uno a uno entre cada elemento del sistema real y el modelo. Sin embargo, es importante establecer qué aspectos del sistema real necesitan incorporarse al modelo de simulación y cuáles se pueden ignorar. Por un lado, el modelo debe ser tan simple como sea posible con objeto de tener ventajas al trabajar con él. Por otro lado, debe ser lo suficientemente detallado para permitir obtener conclusiones válidas acerca del sistema real (Law y Kelton, 2006).
Existe una secuencia de pasos a seguir para construir un modelo de simulación y llevar a cabo experimentos con él. Los pasos para desarrollar el modelo de simulación fueron los siguientes (adaptados de Hillier y Lieberman, 2006; Law y Kelton, 2006):
- 1.
Formulación del problema
- 2.
Recolección y procesamiento de información operacional del aeropuerto
- 3.
Establecimiento del modelo conceptual
- 4.
Construcción del modelo de simulación en un programa de cómputo
- 5.
Realización de pruebas piloto y validación del modelo
- 6.
Realización de corridas con el sistema de interés
- 7.
Análisis de resultados
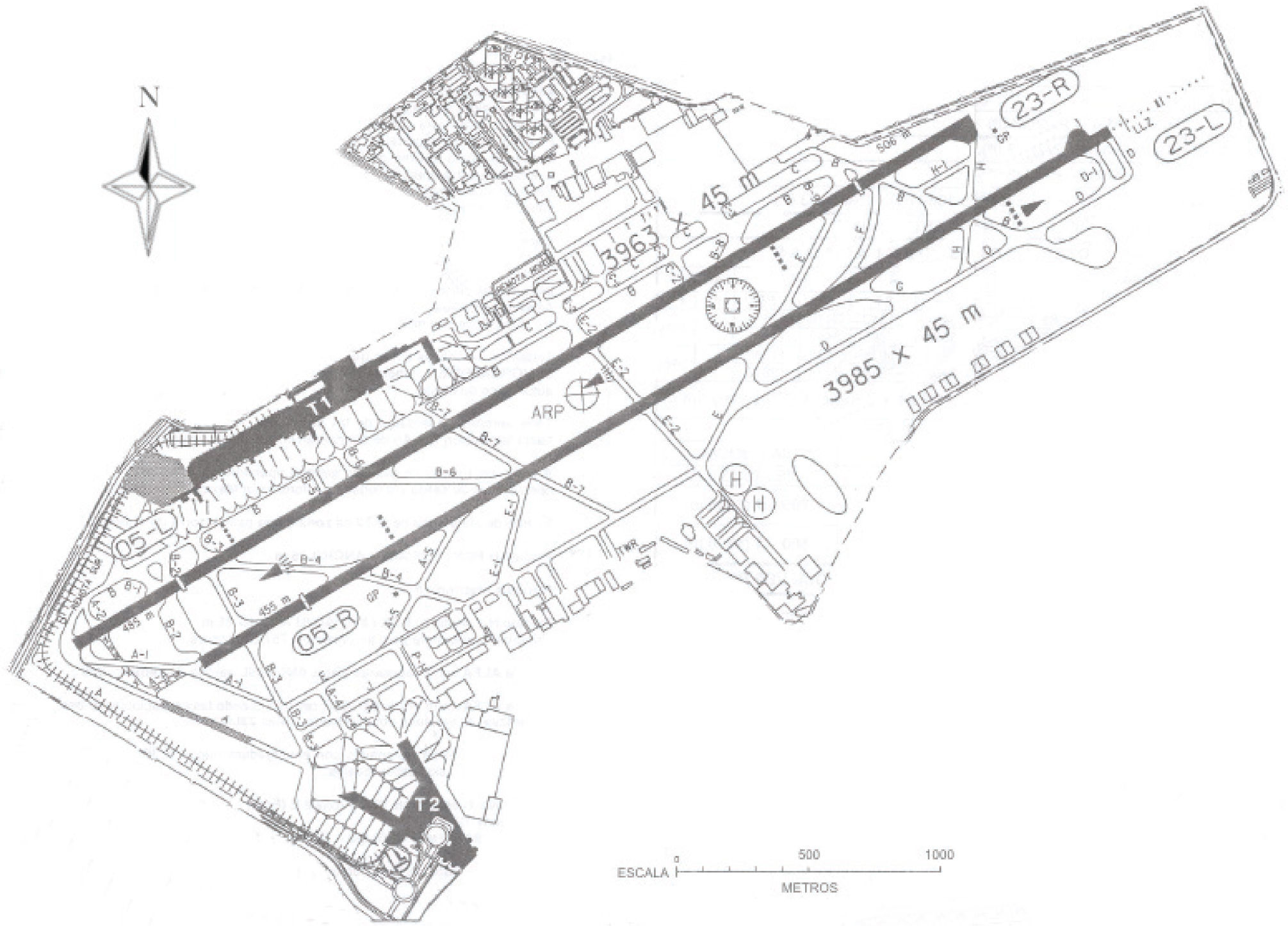
El objetivo del modelo fue simular los despegues y aterrizajes de aeronaves en las pistas 05-L y 05-R del AICM (figura 1), con objeto de evaluar los beneficios de la estrategia para reducir los costos operación y las demoras de los pasajeros (Herrera y Moreno, 2011). El modelo aplica la regla de prioridad FCFS e identifica los diferentes tipos de aeronaves en el sistema. También, clasifica los diferentes tipos de operaciones en las pistas, como despegues o aterrizajes, y estima los tamaños de las líneas, así como los tiempos de espera. Utilizando estos valores, se estimaron los costos de operación de las aeronaves y las demoras de los pasajeros. Después se aplicó la estrategia propuesta y se compararon los resultados de ambas políticas para determinar los beneficios.
Aeropuerto Internacional de la Ciudad de México
En este inciso se revisaron las operaciones aéreas realizadas en el AICM. Además, se determinó la capacidad de sus pistas y se establecieron las distribuciones empíricas de los tiempos de llegada y salida de los principales tipos de aeronaves. Posteriormente, se verificó que estas distribuciones se comportaban como alguna distribución teórica conocida, utilizando para ello pruebas de bondad de ajuste.
Comportamiento general de las operaciones de aeronavesUna revisión de la actividad aérea del AICM durante 2010 mostró que en promedio se realizaron 888 operaciones/ día; también se observó un equilibrio entre la cantidad de llegadas y salidas (50.04% y 49.96%, respectivamente).
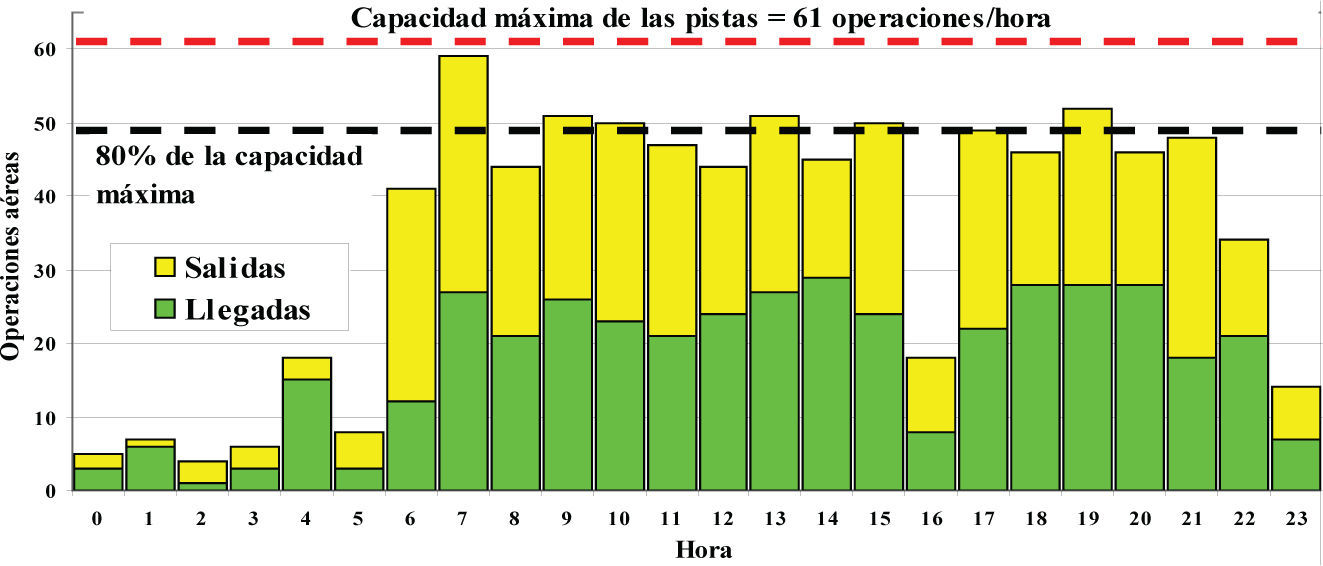
Con relación a los movimientos de aeronaves durante un día típico de 2011, se observó que existen dos comportamientos (figura 2). El primero fue antes de las 6:00 horas, en este caso se realizaron muy pocas operaciones aéreas (5.7%); el segundo comportamiento se presentó después de las 6 y hasta las 24 horas, intervalo en el cual se realizó la mayoría de las operaciones (94.3%).
También, durante este día típico se detectaron 36 tipos distintos de aeronaves que realizaron operaciones en las pistas del aeropuerto; sin embargo, sólo seis tipos concentraron 80% de todas las operaciones aéreas. En cuanto a las distintas clases de aeronaves clasificadas por su estela de turbulencia, 14% fueron pequeñas, 80.8% grandes y 5.2% pesadas.
Distribuciones empíricas de los tiempos de llegada y salida para los principales tipos de aeronaves y pruebas de bondad de ajusteCon base en información operativa detallada, proporcionada por Servicios a la Navegación en el Espacio Aéreo Mexicano (SENEAM), se calcularon los tiempos entre llegadas y salidas, de los aterrizajes y los despegues, para las principales aeronaves que operan en este aeropuerto. Después, esta información se resumió en histogramas de distribución de frecuencias y de éstos, se obtuvieron las funciones de densidad de probabilidad (fdp) empíricas asociadas. Mediante pruebas de bondad de ajuste, se evaluaron las fdp empíricas respecto a las fdp teóricas conocidas.
Con objeto de determinar cuál distribución de probabilidad representaba mejor a cada conjunto de datos, se consideraron más de 20 diferentes tipos de distribuciones. Sin embargo, sólo siete de ellas fueron las mejores (beta, Erlang, gamma, Johnson SB, lognormal, Pearson tipo 6 y Weibull).
Como se mencionó, se observaron dos comportamientos en la operación normal del AICM, por esta razón también se consideraron dos grupos diferentes de distribuciones, uno entre las 00:00 y 6:00 horas y el otro entre las 6:00 y 24:00 horas (tablas 1 y 2).
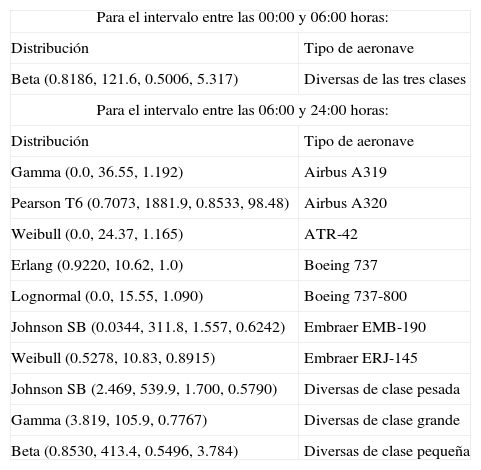
Funciones de densidad deprobabilidad para las llegadas
| Para el intervalo entre las 00:00 y 06:00 horas: | |
| Distribución | Tipo de aeronave |
| Beta (0.8186, 121.6, 0.5006, 5.317) | Diversas de las tres clases |
| Para el intervalo entre las 06:00 y 24:00 horas: | |
| Distribución | Tipo de aeronave |
| Gamma (0.0, 36.55, 1.192) | Airbus A319 |
| Pearson T6 (0.7073, 1881.9, 0.8533, 98.48) | Airbus A320 |
| Weibull (0.0, 24.37, 1.165) | ATR-42 |
| Erlang (0.9220, 10.62, 1.0) | Boeing 737 |
| Lognormal (0.0, 15.55, 1.090) | Boeing 737-800 |
| Johnson SB (0.0344, 311.8, 1.557, 0.6242) | Embraer EMB-190 |
| Weibull (0.5278, 10.83, 0.8915) | Embraer ERJ-145 |
| Johnson SB (2.469, 539.9, 1.700, 0.5790) | Diversas de clase pesada |
| Gamma (3.819, 105.9, 0.7767) | Diversas de clase grande |
| Beta (0.8530, 413.4, 0.5496, 3.784) | Diversas de clase pequeña |
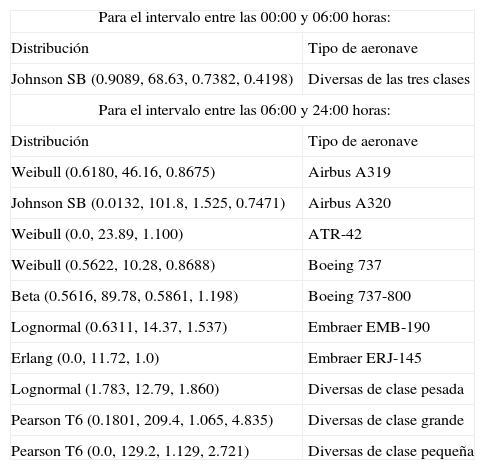
Funciones de densidad deprobabilidad para las salidas
| Para el intervalo entre las 00:00 y 06:00 horas: | |
| Distribución | Tipo de aeronave |
| Johnson SB (0.9089, 68.63, 0.7382, 0.4198) | Diversas de las tres clases |
| Para el intervalo entre las 06:00 y 24:00 horas: | |
| Distribución | Tipo de aeronave |
| Weibull (0.6180, 46.16, 0.8675) | Airbus A319 |
| Johnson SB (0.0132, 101.8, 1.525, 0.7471) | Airbus A320 |
| Weibull (0.0, 23.89, 1.100) | ATR-42 |
| Weibull (0.5622, 10.28, 0.8688) | Boeing 737 |
| Beta (0.5616, 89.78, 0.5861, 1.198) | Boeing 737-800 |
| Lognormal (0.6311, 14.37, 1.537) | Embraer EMB-190 |
| Erlang (0.0, 11.72, 1.0) | Embraer ERJ-145 |
| Lognormal (1.783, 12.79, 1.860) | Diversas de clase pesada |
| Pearson T6 (0.1801, 209.4, 1.065, 4.835) | Diversas de clase grande |
| Pearson T6 (0.0, 129.2, 1.129, 2.721) | Diversas de clase pequeña |
Para algunos tipos de aeronaves hubo menos de diez registros de operaciones realizadas por día, en estos casos las fdp se establecieron para las diferentes clases de aeronaves, agrupando diversos tipos. Este fue el caso de las distribuciones para el intervalo entre las 00:00 y 06:00 horas, tanto para llegadas como para salidas.
Observe que para el intervalo entre las 06:00 y 24:00 horas, las siete primeras distribuciones corresponden a tipos de aeronaves específicos, que representan 85.9% del total de todos los tipos detectados. El resto de las aeronaves se agrupó por clase, como se señaló en el párrafo anterior.
Por último, se aplicaron las pruebas de bondad de ajuste Anderson-Darling y Kolmogorov-Smirnov para obtener una evaluación formal de las distribuciones que mejor se ajustaban. En todos los casos se obtuvieron valores satisfactorios al compararse con los valores críticos, considerando un nivel de significancia α = 0.05. Los tamaños de las muestras fluctuaron entre 11 y 88 aeronaves.
Modelo conceptualEl AICM tiene dos pistas paralelas con una separación de 310 metros (figura 1). Esta separación no es suficiente para permitir las operaciones simultáneas de aeronaves, sólo permite operaciones secuenciales. Cuando los despegues y aterrizajes se realizan en las pistas 05-L y 05-R, en buenas condiciones meteorológicas, la capacidad máxima del conjunto de ambas pistas es 61 operaciones por hora.
Por lo general, los despegues se realizan en la pista 05-L y los aterrizajes en la 05-R, la cual está equipada con el sistema de aterrizaje por instrumentos. Sin embargo, en ocasiones algunos pilotos solicitan despegar en la pista 05-R, principalmente cuando sus aeronaves están muy cerca de su capacidad máxima de peso; y también en ocasiones algunos aterrizajes se realizan en la pista 05-L.
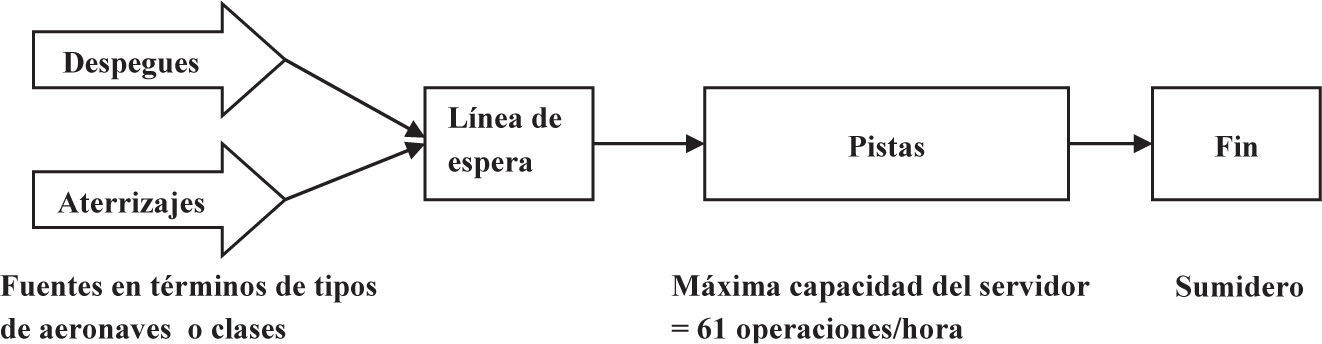
El modelo propuesto representa las características operacionales del aeropuerto cuando las pistas 05-L y 05-R están en servicio. La figura 3 muestra los elementos del sistema que forman el modelo conceptual utilizado.
Construcción del modelo de simulación en un programa de cómputoEn esta etapa, el modelo conceptual especificado se codificó en un programa de cómputo1. Para ello, las distribuciones de llegadas y salidas obtenidas en los incisos anteriores se incorporaron al modelo conceptual. La disciplina utilizada en el modelo, tanto para las llegadas como para las salidas, fue la regla tradicional FCFS.
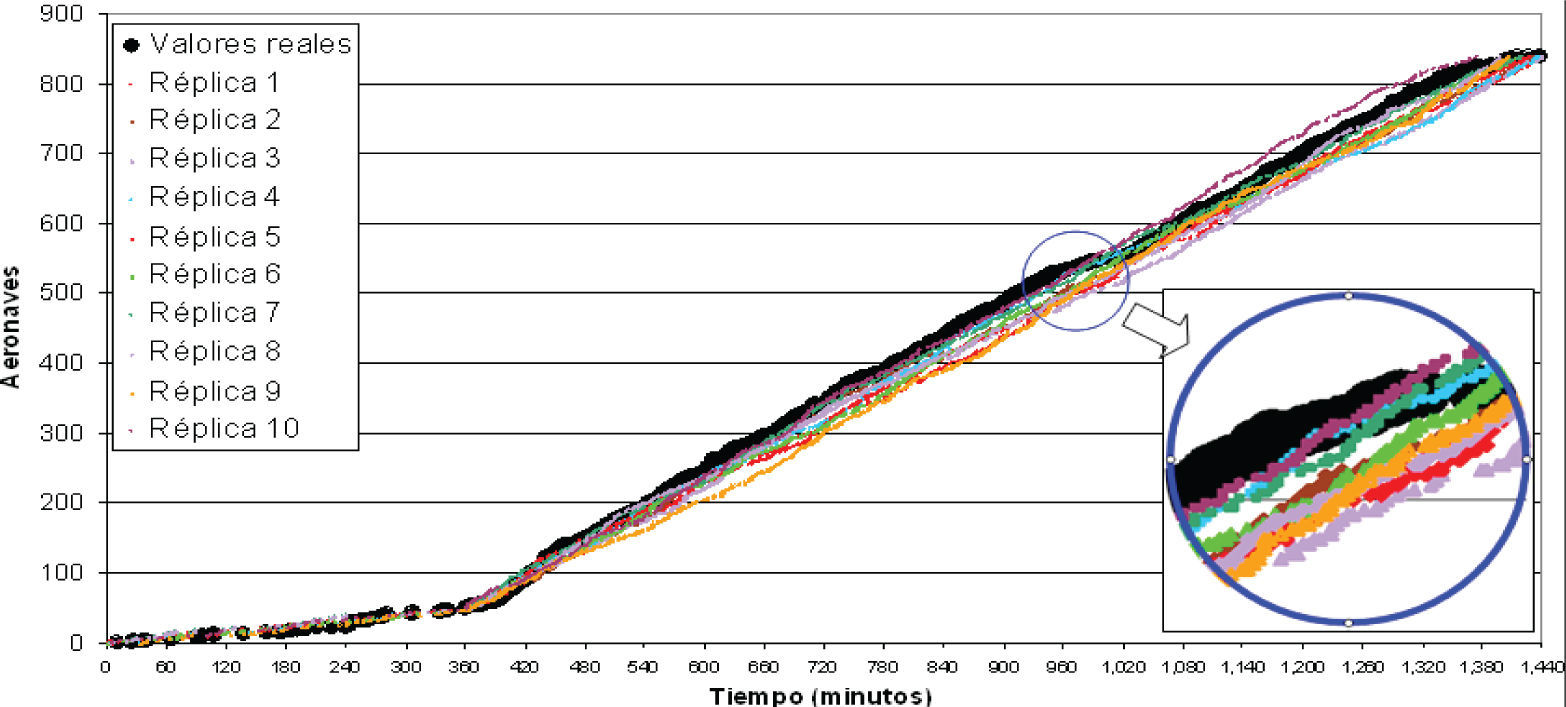
Pruebas piloto y validación del modeloInicialmente, se realizaron algunas pruebas piloto y ajustes menores para afinar el modelo. Después, con objeto de validarlo, se compararon los resultados de varias corridas con la información del sistema real. La figura 4 muestra una comparación entre los tiempos reales de llegadas y salidas de aeronaves (aterrizajes y despegues) observados en las pistas del AICM y los tiempos estimados por el modelo de simulación. Observe que se graficaron los resultados de 10 réplicas y que en cada una se consideró una operación diaria de 24 horas (1,440 minutos).
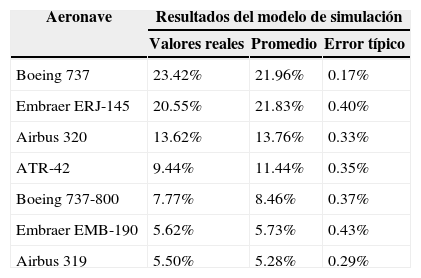
También es importante que el modelo de simulación genere los diferentes tipos de operaciones aéreas (aterrizajes y despegues) y los principales tipos de aeronaves, de acuerdo con las proporciones reales. En el primer caso, el modelo de simulación generó en promedio 49.86% de llegadas y 50.14% de salidas, valores que son muy similares a los reales (50.04% y 49.96%, respectivamente). En relación con los principales tipos de aeronaves, la tabla 3 muestra las proporciones de operaciones de acuerdo con los valores reales y las generadas con el modelo de simulación. Los resultados del modelo fueron obtenidos promediando los valores de diez réplicas. Esta tabla también presenta el error típico de dichos valores. Observe que los valores obtenidos con el modelo de simulación son muy similares a los valores reales y que en todos los casos el error típico nunca fue mayor a 0.43%. La evaluación formal de las fdp utilizadas en el modelo de simulación se realizó mediante las pruebas de bondad de ajuste como se señaló en incisos anteriores. Todos estos resultados validan el modelo de simulación, ya que aseguran que las operaciones aéreas se presentan en el momento y proporciones adecuados.
Participación de los principales tipos de aeronaves en las operaciones del AICM, considerando los valores reales y los resultados del modelo de simulación
| Aeronave | Resultados del modelo de simulación | ||
|---|---|---|---|
| Valores reales | Promedio | Error típico | |
| Boeing 737 | 23.42% | 21.96% | 0.17% |
| Embraer ERJ-145 | 20.55% | 21.83% | 0.40% |
| Airbus 320 | 13.62% | 13.76% | 0.33% |
| ATR-42 | 9.44% | 11.44% | 0.35% |
| Boeing 737-800 | 7.77% | 8.46% | 0.37% |
| Embraer EMB-190 | 5.62% | 5.73% | 0.43% |
| Airbus 319 | 5.50% | 5.28% | 0.29% |
Se realizaron 40 réplicas con el modelo de simulación para la política actual (FCFS) y considerando una operación diaria de 24 horas. Como resultado se obtuvieron los tiempos de entrada y salida para las líneas de espera y las pistas. También se identificaron los distintos tipos de aeronaves y el tipo de operación realizada por cada una de ellas.
Posteriormente, se aplicó la estrategia propuesta para atender los despegues y aterrizajes, con objeto de reducir los costos de operación de las aeronaves y las demoras de los pasajeros (Herrera y Moreno, 2011). Después, se determinaron los beneficios en términos de reducción de costos de operación y demoras. Para ello, a los valores del modelo de simulación se les restaron los obtenidos con la estrategia propuesta.
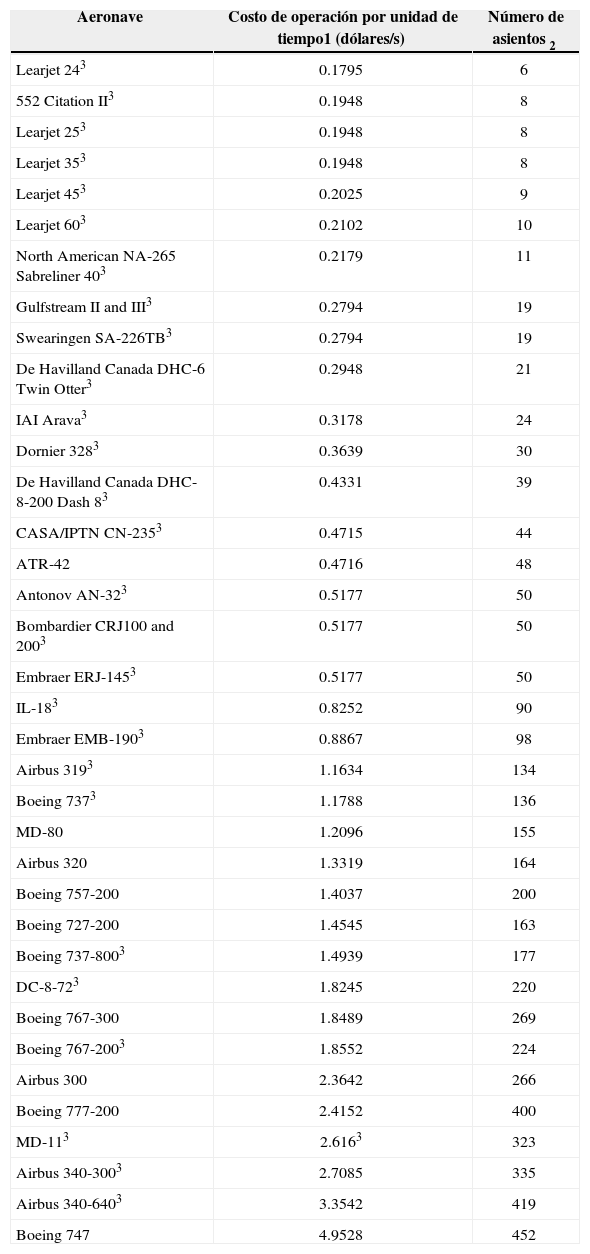
Con objeto de aplicar la estrategia propuesta fue necesario conocer, para cada aeronave en la línea de espera, su tiempo de operación particular, el costo de operación por unidad de tiempo (costo unitario) y el número de asientos. Todas las líneas de espera consideradas para aplicar la estrategia se formaron en un breve intervalo de menos de un minuto. El tiempo de operación particular para cada aeronave se obtuvo utilizando la información generada por el modelo de simulación, este tiempo es igual a la diferencia entre los tiempos de entrada y salida a las pistas. En relación con el costo de operación por unidad de tiempo y el número de asientos, los valores utilizados se muestran en la tabla 4. Es conveniente mencionar que los costos unitarios se obtuvieron actualizando al 2011 los valores establecidos en 2000 por la Organización de Aviación Civil Internacional (OACI); y debido a que dicha información no incluye todos los tipos de aeronaves, los costos de operación unitarios para las aeronaves faltantes se obtuvieron aplicando la expresión siguiente.
Costos de operación por unidad de tiempo y número de asientos para los diferentes tipos de aeronaves que operan en el AICM
| Aeronave | Costo de operación por unidad de tiempo1 (dólares/s) | Número de asientos 2 |
|---|---|---|
| Learjet 243 | 0.1795 | 6 |
| 552 Citation II3 | 0.1948 | 8 |
| Learjet 253 | 0.1948 | 8 |
| Learjet 353 | 0.1948 | 8 |
| Learjet 453 | 0.2025 | 9 |
| Learjet 603 | 0.2102 | 10 |
| North American NA-265 Sabreliner 403 | 0.2179 | 11 |
| Gulfstream II and III3 | 0.2794 | 19 |
| Swearingen SA-226TB3 | 0.2794 | 19 |
| De Havilland Canada DHC-6 Twin Otter3 | 0.2948 | 21 |
| IAI Arava3 | 0.3178 | 24 |
| Dornier 3283 | 0.3639 | 30 |
| De Havilland Canada DHC-8-200 Dash 83 | 0.4331 | 39 |
| CASA/IPTN CN-2353 | 0.4715 | 44 |
| ATR-42 | 0.4716 | 48 |
| Antonov AN-323 | 0.5177 | 50 |
| Bombardier CRJ100 and 2003 | 0.5177 | 50 |
| Embraer ERJ-1453 | 0.5177 | 50 |
| IL-183 | 0.8252 | 90 |
| Embraer EMB-1903 | 0.8867 | 98 |
| Airbus 3193 | 1.1634 | 134 |
| Boeing 7373 | 1.1788 | 136 |
| MD-80 | 1.2096 | 155 |
| Airbus 320 | 1.3319 | 164 |
| Boeing 757-200 | 1.4037 | 200 |
| Boeing 727-200 | 1.4545 | 163 |
| Boeing 737-8003 | 1.4939 | 177 |
| DC-8-723 | 1.8245 | 220 |
| Boeing 767-300 | 1.8489 | 269 |
| Boeing 767-2003 | 1.8552 | 224 |
| Airbus 300 | 2.3642 | 266 |
| Boeing 777-200 | 2.4152 | 400 |
| MD-113 | 2.6163 | 323 |
| Airbus 340-3003 | 2.7085 | 335 |
| Airbus 340-6403 | 3.3542 | 419 |
| Boeing 747 | 4.9528 | 452 |
Nota 1: Costos unitarios obtenidos de actualizar al 2011 los establecidos por la OACI para 2000 (ICAO, 2000). El componente relacionado con el precio de la turbosina fue actualizado utilizando el índice de precios del combustible de aviación (368.3 puntos) establecido (el 11 de marzo de 2011) por la Asociación del Transporte Aéreo Internacional (IATA, 2011).
Nota 2: El número de asientos en cada aeronave puede cambiar dependiendo de la configuración de clases establecida por cada aerolínea. Los valores mostrados son cifras típicas obtenidas de los fabricantes de aeronaves.
Nota 3: Para estas aeronaves los costos unitarios se estimaron utilizando la ecuación 1.
en donde, el costo de operación unitario está en dólares/ segundo. Esta ecuación se obtuvo mediante la correlación lineal entre los costos de operación unitarios actualizados de la OACI y el número de asientos de las aeronaves2.Se observó que el número de asientos es una variable significativa que puede explicar el valor de los costos de operación unitarios por unidad de tiempo, dado que mediante el análisis de regresión se obtuvo un valor p igual a 1.5361 × 10–6.
Los resultados mostraron que al aplicar la estrategia propuesta se pueden obtener beneficios diarios de 4,749.17 dólares en los costos de operación y de 10,763.24 pasajeros-minuto en las demoras. También, se observó que las primeras seis horas de operación del AICM sólo contribuyen con 0.46% de los beneficios, en relación con los costos de operación y demoras. Durante este intervalo sólo fueron observadas líneas de espera de dos aeronaves. En contraste, después de este periodo se presentaron líneas de espera de dos, tres, cuatro y cinco aeronaves. Aunque la mayoría de ellas fueron de dos aeronaves (81.04%); las líneas de espera de tres (16.94%), cuatro (1.97%) y cinco (0.04%) aeronaves contribuyeron con 43% de los beneficios, tanto de los costos de operación como de las demoras. Además, se observó que en promedio 46.7% de las colas generadas por el modelo de simulación no produjeron beneficios cuando se aplicó la estrategia propuesta.
La afectación más crítica en la operación de aeronaves se presentó en las líneas de espera de cinco aeronaves, pero aún en este caso la secuencia de atención, cuando se comparó con la secuencia original, se modificó en promedio 117.61 segundos y, en el caso de colas de dos aeronaves, la modificación fue tan solo 58.61 segundos en promedio.
Análisis de resultadosLos resultados mostraron que al aplicar la estrategia propuesta es posible obtener un beneficio anual de 20.66 millones de pesos3 (1.733 millones de dólares) en los costos de operación, y de 65,476.3 pasajeros-hora en la reducción de demoras.
Debido a la reducida actividad de las operaciones aéreas durante las primeras seis horas de operación en el AICM hubo muy pocas líneas de espera durante este intervalo (en promedio 1.38 líneas de espera por día) y por esto solamente se obtuvieron beneficios marginales en ese periodo. Observe que en comparación durante el intervalo entre las 06:00 a las 24:00 horas, se presentó un promedio de 199.3 colas por día.
Si todas las colas generadas bajo la política FCFS hubieran sido de dos aeronaves, se esperaría que aproximadamente 50% de éstas presentaran la secuencia que corresponde a las demoras y costos de operación mínimos, pero debido a que existen algunas colas de 3, 4 y 5 aeronaves, este porcentaje se reduce a 46.72%. En el caso de colas con más de dos aeronaves, la probabilidad de que originalmente presenten la secuencia que genera las demoras y costos de operación mínimos es menor a 50%, debido a que existen otras alternativas (permutaciones).
DiscusiónDurante 2009 se realizaron 348,306 operaciones aéreas en el AICM (posición 29 en el ámbito mundial), abajo de 20 aeropuertos de Estados Unidos, seis europeos, uno canadiense y uno asiático (Air Transport World, 2010).
Existen algunos aeropuertos en Estados Unidos, Europa y Asia que manejan un número similar de operaciones al del AICM, por ejemplo, en Europa, el aeropuerto de Munich (posición 23, con 396,805 operaciones), y el Leonardo da Vinci en Roma (posición 34 con 324,487 operaciones); en Estados Unidos, Nueva York (La Guardia), Miami (Florida), Van Nuys (California), Logan (Boston), Washington Dulles (Virginia), Memphis (Tennessee), que manejan prácticamente el mismo número de operaciones que el AICM (±3%); y en Asia, el Aeropuerto Internacional de Tokio (posición 33, con 335,716 operaciones). En todos estos casos podrían esperarse beneficios similares a los del AICM, considerando únicamente el número de aterrizajes y despegues.
Por otro lado, en un reporte relacionado con la comparación de rendimientos en centros en ruta seleccionados de Estados Unidos y Europa (Benzle et al., 2003), hay evidencia de que los aeropuertos en estas regiones tienen una variabilidad horaria similar a la del AICM (figura 2). Por esta razón, se esperaría que si la estrategia propuesta fuera aplicada, también algunos aeropuertos en Estados Unidos y Europa podrían presentar beneficios reducidos durante el intervalo entre las 00:00 y 06:00 horas; y durante el intervalo entre las 06:00 y 24:00 horas se presentarían los beneficios principales.
Observe que durante las primeras seis horas de operación diaria del AICM solamente se realizan 5.7% de las operaciones totales, pero éstas sólo contribuyen con 0.5% del total de los beneficios. Esto se debe a que en la operación de los sistemas de transporte las demoras empiezan a presentarse cuando la demanda excede aproximadamente tres cuartos de la capacidad disponible del sistema, y los resultantes incrementos en las demoras promedio crecen exponencialmente conforme la relación demanda/capacidad se aproxima a 100% (Hamzawi, 1992). En el AICM durante el intervalo entre las 00:00 y 06:00 horas, la demanda es muy baja (figura 2) con una relación promedio demanda/ capacidad igual a 13.1%.
Es posible cuantificar en términos monetarios la reducción de las demoras, si se conoce el valor del tiempo de los usuarios del aeropuerto. Una estimación de este valor para los usuarios del AICM es de 121.24 pesos/hora. El cual se obtuvo al actualizar4 al 2010 el valor estimado por Alberro (2008). Utilizando este valor el beneficio anual derivado de la reducción en las demoras de los pasajeros se estimó en 7.93 millones de pesos. Sin embargo, debe señalarse que el valor del tiempo de los pasajeros puede tener diferencias significativas entre diferentes regiones y países. Su valor depende principalmente de la metodología utilizada para estimarlo. Por ejemplo, para España se propuso la utilización de un valor del tiempo de los usuarios en sus aeropuertos igual a 16 €/hora (Fernández, 2009), equivalente a aproximadamente 299.6 pesos/hora5, el cual es un valor 2.4 veces más alto que el obtenido para el AICM.
ConclusionesMediante el modelo de simulación se estimó que es posible obtener beneficios significativos en el AICM si se aplica la estrategia propuesta. Se estimaron beneficios anuales del orden de 20.66 millones de pesos ahorrados en costos operación de las aeronaves y de 65,476.3 pasajeros-hora en reducción de demoras. Integrando ambos resultados en términos monetarios se obtuvo un beneficio anual aproximado de 28.6 millones de pesos. Observe que estos beneficios podrían alcanzarse sin afectar en gran medida la operación aérea, generalmente la modificación de la secuencia de atención sólo cambió el inicio de los servicios en aproximadamente un minuto y en los casos más críticos alrededor de dos minutos.
Los resultados mencionados son una referencia de los beneficios potenciales que podrían lograrse en algunos aeropuertos de Estados Unidos, Europa y Asia, debido a que las características operacionales del AICM son similares a las de estos aeropuertos. Sin embargo, las proporciones de las clases de aeronaves, clasificadas por estela de turbulencia en cada aeropuerto y el valor del tiempo de los pasajeros en cada país, podrían cambiar significativamente los resultados; el primero, en los beneficios relacionados con los costos de operación y el segundo, en la cuantificación monetaria de las demoras. Por otro lado, el modelo de simulación desarrollado tiene el potencial de evaluar otros cambios operativos en el AICM, por lo que en futuras líneas de investigación puede aportar información para mejorar su operación.
AgradecimientosLos autores agradecen el apoyo brindado por la Universidad Autónoma de Querétaro y el Instituto Mexicano del Transporte.
Citación estilo Chicago Herrera-García, Alfonso, Eric Moreno-Quintero, Carlos Daniel Martner-Peyrelongue. Evaluación de una nueva estrategia de atención a los despegues y aterrizajes en el Aeropuerto Internacional de la Ciudad de México, para reducir los costos de operación de las aeronaves y las demoras de los pasajeros. Ingeniería Investigación y Tecnología, XV, 01 (2014): 51-61.
Citación estilo ISO 690 Herrera-García A., Moreno-Quintero E., Martner-Peyrelongue C.D. Evaluación de una nueva estrategia de atención de los despegues y aterrizajes en el Aeropuerto Internacional a la Ciudad de México, para reducir los costos de operación de las aeronaves y las demoras de los pasajeros. Ingeniería Investigación y Tecnología, volumen XV (número 1), enero-marzo 2014: 51-61.
Obtuvo el grado de ingeniero en aeronáutica (1985) por el Instituto Politécnico Nacional, y el grado de maestro en sistemas de transporte y distribución de carga (1998) por la Universidad Autónoma de Querétaro. Durante trece años laboró en la industria de aviación (1984-1996); también se ha desempeñado como profesor en la Facultad de Ingeniería de la Universidad Autónoma de Querétaro, en donde estudia el doctorado en ingeniería. Durante catorce años ha trabajado en el Instituto Mexicano del Transporte y actualmente tiene el puesto de investigador titular ``C''. Su principal línea de investigación es el transporte aéreo.
Es matemático por la UAM-Iztapalapa (1980), maestro en investigación de operaciones por la Facultad de Ingeniería de la UNAM (1987) y doctor en transporte por la Universidad de Leeds, Reino Unido. Actualmente es profesor de tiempo libre en la Facultad de Ingeniería de la Universidad Autónoma de Querétaro e investigador titular del Instituto Mexicano del Transporte. Su principal línea de trabajo es la modelación matemática de sistemas de transporte.
Licenciado en diseño de asentamientos humanos por la Universidad Autónoma Metropolitana; estudió el posgrado en planificación urbana y regional en el Instituto Nacional de Administración Pública, en Madrid, España y obtuvo el grado de doctor en ciencias sociales por la Universidad Autónoma Metropolitana. Es profesor en la Facultad de Ingeniería de la Universidad Autónoma de Querétaro y autor de numerosos artículos y publicaciones. Actualmente es el coordinador de Integración del Transporte en el Instituto Mexicano del Transporte y posee Nivel II, SNI. Su línea de investigación es la integración logística, modal y territorial de los sistemas de transporte.
En este trabajo fue utilizado el programa de simulación Flexsim, versión 5.
Se obtuvo un coeficiente de determinación R2=0.8176.