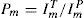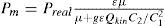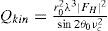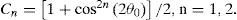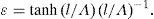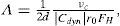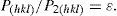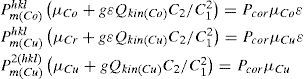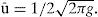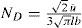A method to correct pole densities (PD) for primary and secondary extinction applied for maxima of pole figures (PF) measured by X-ray diffraction, was extended to correct the whole 111 and 200 PFs for nickel samples after 75% cold rolling and subsequent annealing at 600°C during 30 minutes. The PDs were corrected, and parameters of primary and secondary extinction were calculated using the PDs obtained in PFs measured for the first order reflections with two wavelengths (Cu Kα and Co Kα - radiations) and for the second order reflections with Cu Kα – radiation. Three orientation distribution functions (ODF) were calculated, namely: the first one from 111, 200 and 220 PFs; the second one from 222 and 400 PFs (the second order reflections) and 220 PF (440 reflection is absent for the radiations used); the third one from corrected 111 and 200 PFs and not corrected 220 PF (for lack of the second order reflection). Essential differences between the obtained ODFs indicate the necessity to take into account the extinction phenomenon in analysis of textured materials. The obtained parameters of extinction were used for the evaluation of microstructure details of textured nickel depending on grains orientation that is not easily obtained by conventional metallographic methods.
Un método para corregir densidades de polos (DP) por extinción primaria y secundaria en máximos de figuras de polos (FP) medidos por difracción de rayos X, se extendió a todos los datos de las FP 111 y 200 de muestras de níquel con 75% laminación en frío y recocido posterior de 600°C durante 30 minutos. Las DP fueron corregidas, y los parámetros de extinción primaria y secundaria fueron calculados utilizando las DP medidas en FP para las reflexiones de primer orden con dos radiaciones (Cu Kα y Co Kα) y para las reflexiones de segundo orden con radiación de Cu Kα. Se calcularon tres funciones de distribución de orientación (FDO): la primera a partir de FP para reflexiones 111, 200 y 220, la segunda a partir de las FP 222, 400 (los segundos ordenes) y 220 (en ausencia de segundo orden) y la tercera con las FP para las reflexiones 111 y 200 corregidas por extinción y la FP 220 no corregida (en ausencia de segundo orden). Las diferencias esenciales entre las FDO obtenidas, indican la necesidad de tomar en cuenta el fenómeno de extinción en el análisis de materiales con textura. Los parámetros de extinción obtenidos fueron utilizados para evaluar los datos de la microestructura para níquel en función de la orientación de los granos, que no es fácil obtener por métodos convencionales metalográficos.
In poly crystal line materials, grains are rarely randomly distributed from the point of view of crystallo-graphic orientation. The preferred crystallographic orientation, or texture, arises during the manufacturing processes owing to anisotropic properties of individual grains and in turn, it affects different material properties (Bunge, 1987) and the correct evaluation of texture is important for materials research. The common method for quantitative texture analysis by X-rays diffraction (XRD) from a crystalline medium is based on the measurement of pole figures (PF) (Bunge, 1996; Kocks et al., 1998; Randle et al., 2000) that are characterized by pole densities (PD) obtained from the measured X-ray reflected intensities. The data of two-dimensional PFs are used for calculating a three-dimensional representation of the orientation density in terms of the orientation distribution function (ODF).
Since the initial information to obtain a PF is the data of reflected intensities, the fact that in PF measurements the extinction phenomenon can be present should be taken in to account. Indeed, it has been shown that extinction is present in PF measurements, and specially in those of low index reflections (Kryshtab et al., 2004; Tomov, 2011; Palacios-Gómez et al., 2010) with X-ray as well as with neutron diffraction, and a brief proof of the presence of this phenomenon can be easily done by comparing the PDs from PFs for higher order reflections with those for the first order reflections; here only PDs in maxima of PFs have been analyzed. If this phenomenon is present, it cannot be avoided and it reduces PDs in PFs for the first order reflection as compared to PDs in PFs for higher order reflections.
On the other hand, neither PFs nor ODFs contain information of microstructure details such as grain size and lattice perfection of grains. The conventional method for evaluation of microstructure in polycrystalline materials using XRD is based on the diffraction peak broadening (Warren, 1969; Langford, 1978) and kinematics cattering theory (Krivoglaz, 1996). It is impossible to use this method in the case of real crystals with low dislocation density, where full-width at half maximum of the peak reaches the instrumental breadth (Authier et al., 1980). In such crystals the X-ray dynamic scattering processes come into being and lead to the extinction phenomenon. The characteristics of extinction have been introduced into the kinematic theory in the form of two different phenomena (Darwin, 1922; Zachariasen, 1963) as the primary extinction, which depends on the size of coherently diffracting crystallites, and the secondary extinction, which depends on disorientation of crystallites. Therefore, the characteristics of extinction relate to the crystal microstructural feature and can be used for its evaluation.
An original technique for correction of the PD in the maximum of a PF and for the evaluation of grain microstructure using the characteristics of the primary and secondary extinctions was proposed by (Kryshtab et al., 2004), and was applied to an aluminum sample. Whereas the problem of the separation of contributions of PD and extinction phenomenon in XRD measurements of textured materials, when primary and secondary extinctions are present simultaneously, cannot be solved exactly, some reasonable assumptions were proposed in the above mentioned work. These assumptions were used for a material (aluminum) that has the K-absorption edge distant from wavelengths of X-ray radiation commonly used for PFs measurements.
In the present work, for further development of the mentioned technique (Kryshtab et al., 2004) we extend the validation of the approximations for a material, namely nickel, whose wavelength of its K-absorption edge lies very close to the wavelengths used for PFs measurements. It is expected that not only PDs, but also the parameters of primary and secondary extinction can change throughout the PFs. The corrections of PDs in the whole PFs, particularly for 111 and 200 PFs were performed, and the determined parameters of the primary and secondary extinction were used to estimate the grains microstructure. Changes of microstructure characteristics depending on grain orientations were also shown. Using the data of measured PFs, and of PFs partially corrected by this technique, three ODFs were calculated as follows: one from 111, 200 and 220 PFs (the first order reflections); another one from 400 and 222 PFs (the second order reflections) as well as 220 PF (the second order 440 reflection for this direction is absent owing to wide Bragg angle with radiations used); and the last one from the corrected 111 and 222 PFs and not corrected 220 PF (it cannot be corrected by the applied method for lack of the second order reflection), respectively.
Experimental detailsSamples of commercial nickel after 75% cold rolling with and without consequent annealing were used for PFs measurements by the XRD technique. A nickel sample after cold rolling was heated in a furnace at the heating rate of 10°C/min up to 600°C and held at this temperature during 30 minutes. A nickel powder standard sample was also measured with the same conditions of the textured samples for PFs normalization, defocusing and background correction. For texture analysis a one-axis D8 Advance Bruker X-ray diffractometer with an Euler cradle and with two non-polarized Cu Kα and Co Kα radiations was used. Pole figures for <111>, <100> and <110> crystallographic directions were measured for the first and second order reflections using a 5×5 deg (tilt and rotation) collection grid. The samples were oscillated along the direction of rolling with amplitudes of 4–6mm in order to average over a significant number of diffracting grains. Measurement duration for weak second order reflections was several times longer as compared with the duration for low index reflections. Data analysis was performed using the pop LA (preferred orientation package – Los Alamos) texture package. The WIMV algorithm was used to convert the normalized PFs data to complete ODF data.
In order to get the information about grain size and shape distribution, metallographic studies were carried out on the face of one of the edges of a sample, after polishing and etching it with a mixture of HNO3 acid diluted with H2O (2:1) at room temperature, and using the optical microscope OLIMPUS model PM3 with a Hitachi camera KP-D50.
Results and discussionThe images of the cross-section microstructure of Ni samples after the rolling and subsequent annealing at 600°C are shown in Figure 1.
After the cold rolling the grains have heterogeneous sizes and elongated shape with a length of up to 500μm in the rolling direction and 80μm in the transversal direction. The annealing process results in changes of grains shape and size. Grains become almost equiaxial with a length up to 70μm. Taking into account the grains size and the absorption coefficients of the radiations used, the X-ray beam was reflected from the grains of the sample surface. Therefore, oscillation amplitudes of 4–6mm were chosen to include as many grains as possible along the rolling direction of samples for PFs measurements. The presence of texture in the samples studied was confirmed by the comparison of peak intensities distribution in XRD patterns measured with Cu Kα- radiation and the simulated one for Ni powder.
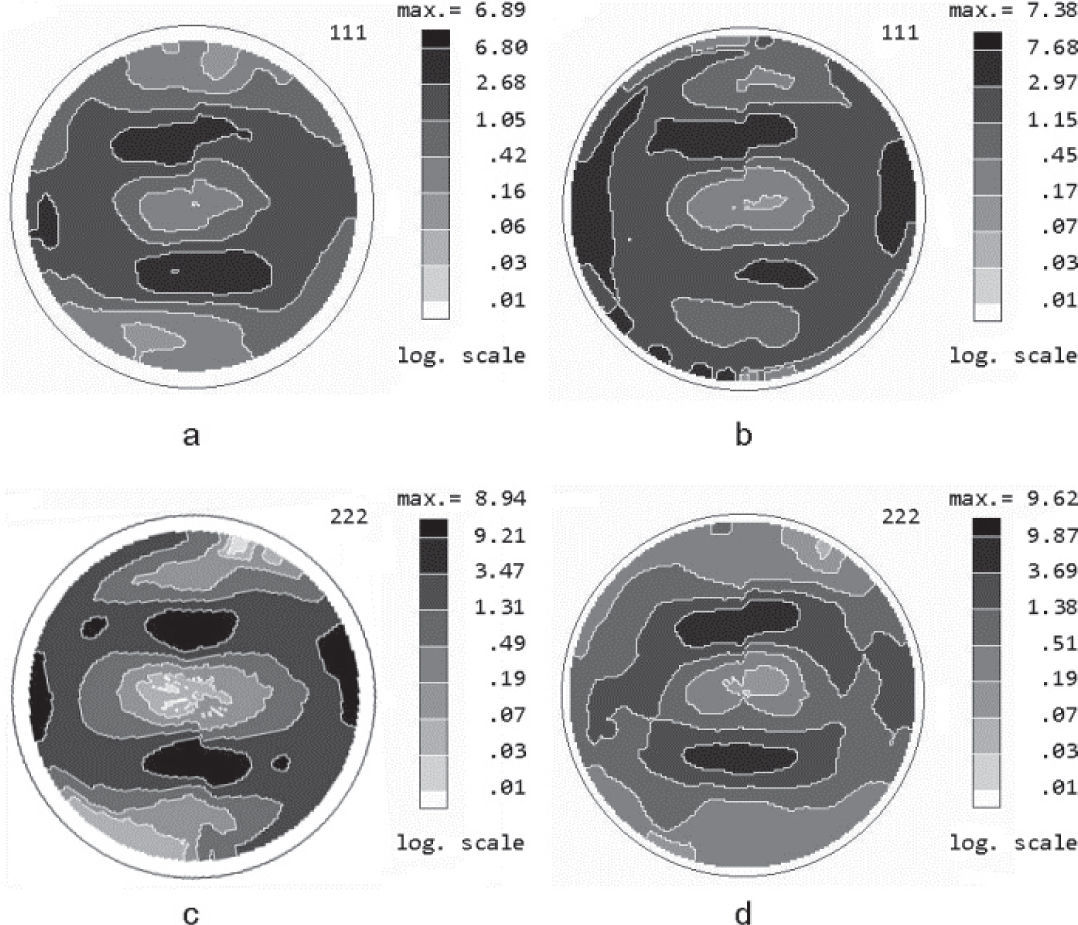
Pole figures for cold rolled nickel sampleThe normalized {111} PFs for the nickel sample after 75% cold rolling measured using Cu Kα and Co Kα- radiations for the first order 111 reflection and for the second order 222 reflection are shown in Figure 2. We observed an insignificant difference between PDs in maxima of PFs measured for the same order reflection with different radiations and more essential difference between the PDs in maxima of PFs measured for the first and second order reflections. It should be noted that PDs in maxima of PFs measured for both reflections with Cu Kα-radiation are somewhat less than the ones measured with Co Kα - radiation.
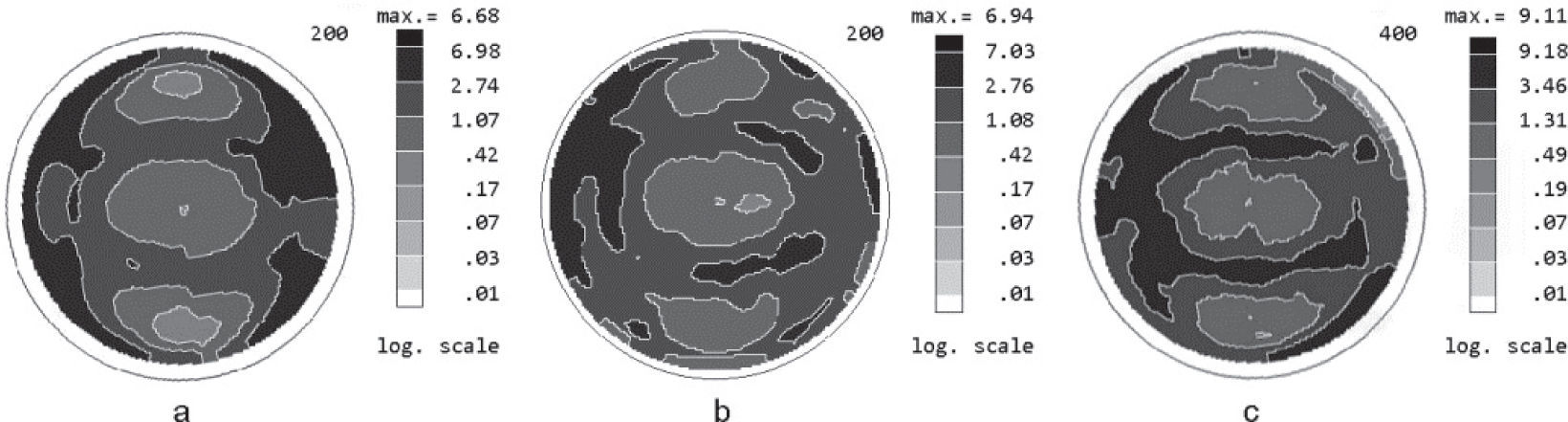
Similar results were also observed for the normalized {200} PFs measured using Cu Ka and Co Kα- radiations for the first order 200 reflection and for the second order 400 reflection (Figure 3). It should be noted that a 400 reflection with Co Kα-radiation was not measured owing to the wide Bragg angle for this reflection.
Smaller values of PDs obtained in the maxima of PFs for the first order reflections than those for the second order reflections for both crystallographic direction sindicate the presence of extinction phenomenon even in the Ni sample after common cold rolling.
Theoretical basisThe normalized PD (Pm) at a general point of the PF measured by XRD technique is defined as:
Where ImT and ImP are the integrated intensities measured for the textured sample and for a powder standard sample of the same material, respectively.
Applying the theory of (Zachariasen, 1963) for the secondary extinction in mosaic crystals, it was shown (Kryshtab et al., 2004) that when primary and secondary extinction phenomena are present simultaneously, the measured PD for any point of the PF is:
Where Preal is the true PD, ε is the primary extinction coefficient, g is the secondary extinction coefficient, μ is the linear absorption coefficient, Qkin is the integrated reflectivity per unit volume given by:
Where r0 is the classical radius of the electron, υc is the unit cell volume, λ is the radiation wavelength, θ0 the diffraction angle, FH the structure factor, and C1 and C2 are polarization factors defined as:
As one can see from Eq. (2), the measured PD depends on the values of the primary extinction coefficient, the secondary extinction coefficient and the extra term QkinC2/C12.
Let us now analyse how different factors can affect the measured PD.
- (i)
Preal is a constant value for a given crystallographic direction <hkl> and certain point of the PF. This means that for every point of the pole figure Eq. (2) is also valid for different wave lengths and reflection orders with the same value of Preal.
- (ii)
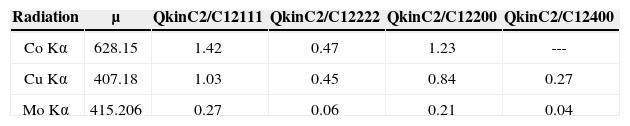
The secondary extinction coefficient is a characteristic of the crystallites disorientation and for a given crystallographic direction and certain point of the PF is also a constant value. It does not depend on the order of reflection and radiation wavelengths used. However, the influence of the secondary extinction on Pm is equivalent to an extra term to the linearabsorption coefficient μ and for different wavelengths and order reflection it is determined by the ratio between the values of μ and QkinC2/C12. The calculated values of the linear absorption coefficients μ and extra term of QkinC2/C12 for nickel for different wavelengths and reflections are listed in Table 1.
Table 1.Calculated values of the absorption coefficient μ(cm−1) and the extra term of QkinC2/C12 (cm−1) for nickel for CoKα-, CuKα-, and MoKα- radiations and for different reflections
Radiation μ QkinC2/C12111 QkinC2/C12222 QkinC2/C12200 QkinC2/C12400 Co Kα 628.15 1.42 0.47 1.23 --- Cu Kα 407.18 1.03 0.45 0.84 0.27 Mo Kα 415.206 0.27 0.06 0.21 0.04
As one can see, the value of the extra term decreases for the second order reflections and its contribution in absorption part of intensity is less for Co Kα - radiation. Therefore, if only secondary extinction is present, the measured PD must be less in PF measured with Cu Kα - radiation as compared with PD in PF measured with Co Kα - radiation and also it must be higher for the second order reflection as compared with the one for the first order reflection. This is precisely what we observed in the measured PFs (Figures 2 and 3).
- (i)
The value of the primary extinction coefficient is not a constant; it depends on crystal perfection and can be evaluated within the framework of the dynamic diffraction theory (Pinsker, 1978). The primary extinction coefficient depends on the size of coherently diffracting crystallites (domains) l and the extinction length Λ as:
For a given grain microstructure the coherent domain size for a given crystallographic direction and certain point of the PF is a constant value, but the extinction length depends on the reflection and wavelength of the radiation used. For the symmetrical Bragg (reflection) case and non-polarized radiation Λ can be calculated according to (Kryshtab et al., 2002) as:
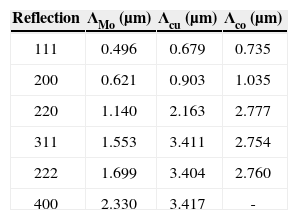
where r0 is the classical radius of the electron, υc is the unit cell volume, d is the spacing of the lattice planes (hkl), Cdyn=(1+cos 2θ)/2 is the polarization factor for dynamical scattering, FH is the structure factor that depends on the atomic scattering amplitude and on the dispersion corrections, which are determined by the ratio of the K-absorption edge wavelength (for NiλK=0.149nm) and the wavelength of the radiation used. The calculated values of extinction length for Ni samples, taking into account the structure factors with dispersion corrections and the temperature Debye factor (International Tables for X-ray Crystallography, 1992) for different reflections with the different radiations used, are listed in Table 2.From Eq. (5) and Table 2 one can see that the influence of the primary extinction on measured PD is stronger in PF measured with Cu Kα - radiation as compared with PD in PF measured with Co Kα - radiation (lower value of PDCu) and this influence decreases considerably for the second order reflection. So, if we take into account only the primary extinction, the measured PD also must be less in PF measured with Cu Kα - radiation as compared with PD in PF measured with Co Kα - radiation and it should increase for the second order reflection as compared with the one for the first order reflection.
Therefore, the obtained results can be completely explained considering the presence of extinction phenomenon in PFs measurements.
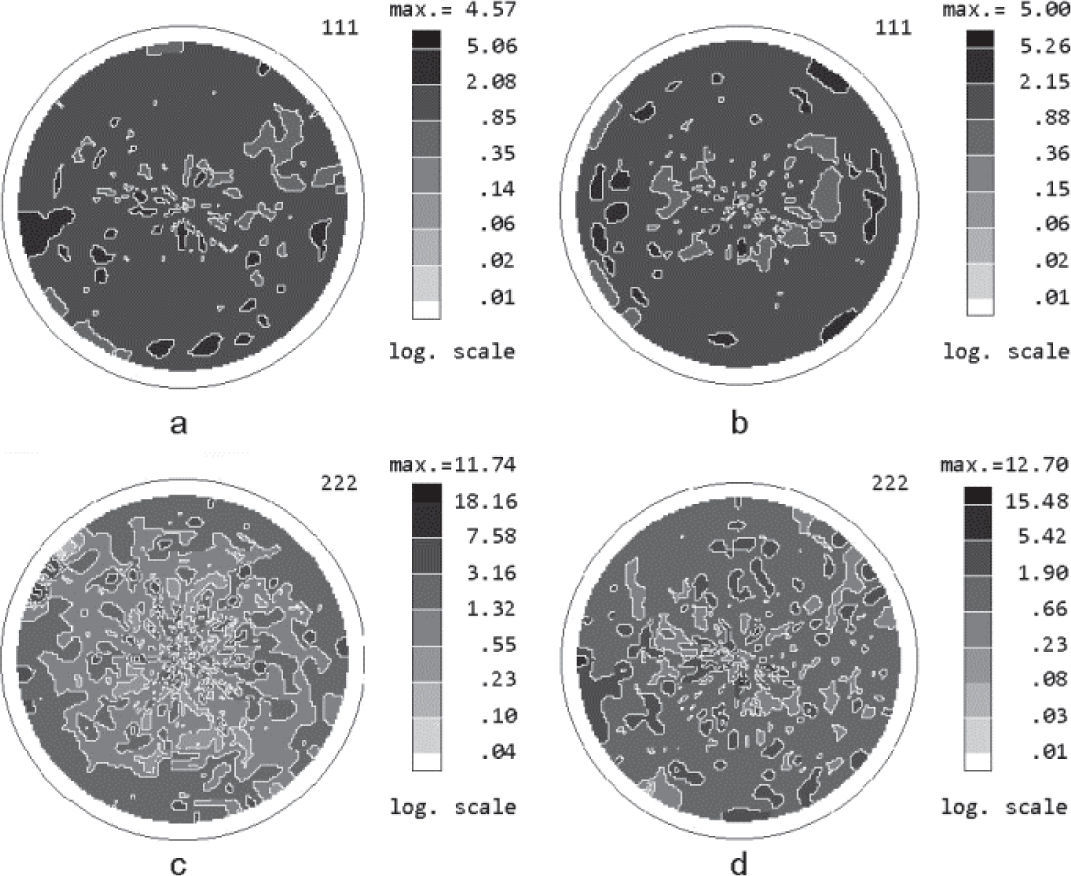
Pole figures for annealed nickel sampleThe normalized PFs for the nickel sample after a cold rolling and subsequent annealing at 600°C during 30 minutes measured using Cu Kα and Co Kα - radiations for the first order 111 reflection and for the second order 222 reflection are shown in Figure 4. For annealed nickel sample, once again, an insignificant difference between PDs in maxima of PFs measured for the same order reflection with different radiations with a lower value of PD for PFs measured with Cu Kα - radiation was observed. At the same time the difference between the PDs in maxima of PFs measured for the second order reflection increased in about 2.5 times as compared to the PDs in maxima of PFs measured for the first order reflection.
This shows a stronger influence of extinction phenomena on the measured diffracted intensities from the textured annealed sample and consequently on measured PDs for this sample as compared with the sample after a cold rolling. It should be noted that a comparison of PDs in maxima of PFs measured only for the first order reflection for the sample after a cold rolling (Pmax, roll=7.38) and for the sample after a cold rolling and subsequent annealing (Pmax, ann=5.0) can lead to the conclusion that the annealing results in a texture decrease for <111> direction. But the comparison of PDs in maxima of PFs measured for the second order reflection, where the influence of extinction is weak, shows another result of the annealing, (Pmax, roll=9.62 and Pmax, ann=12.70), i.e. the annealing results in the texture increase for <111> direction. Therefore, in the case of a strong influence of extinction phenomenon on the measured PDs the interpretation of obtained results can be incorrect.
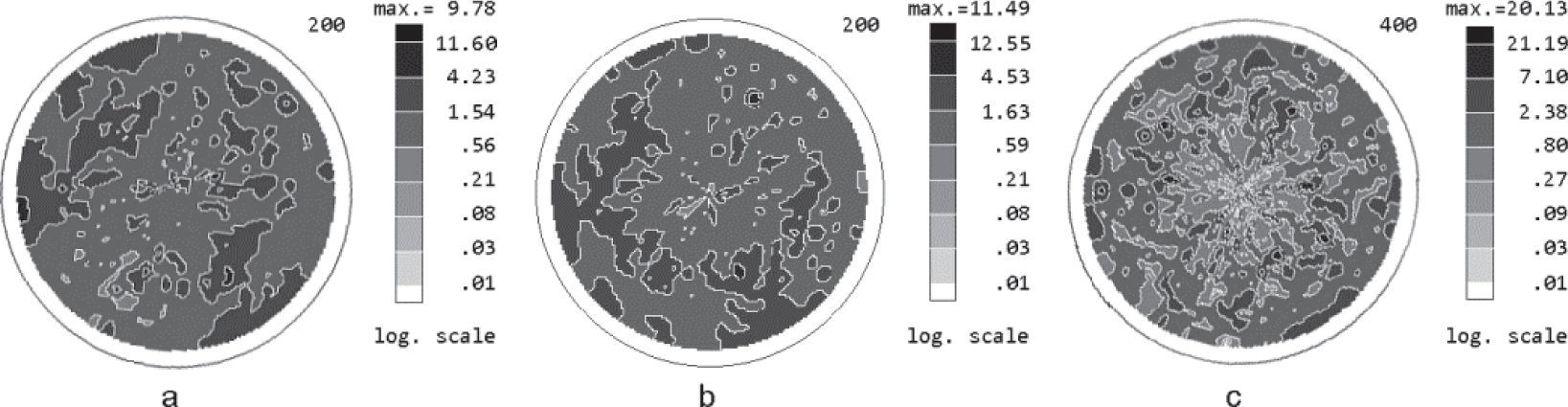
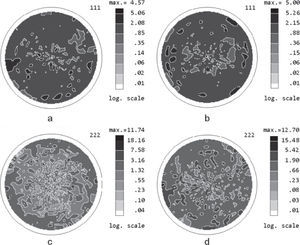
The normalized PFs for the nickel sample after cold rolling and annealed at 600°C measured for the first order 200 reflection using Cu Kα - and Co K α - radiations and for the second order 400 reflection with Cu K α - radiation (400 reflection with Co Kα - radiation was not measured) are shown in Figure 5.
For this <100> crystallographic direction the difference between the PDs in maxima of PFs measured for the first and the second order reflections increased in about 2 times. A comparison of PDs in maxima of PFs measured for the first order reflection for the sample after a cold rolling, and for the sample after a cold rolling and annealing shows that the annealing results in an increase of texture in 1.4 times. At the same time, a comparison of PDs in maxima of PFs measured for the second order reflection, shows that texture increased in more than 2 times, that is more close to the real result.
For the second order reflections the extinction phenomenon is not completely excluded, (at least the secondary extinction is present) and for the refinement of texture analysis data it is necessary to correct PFs taking into account the characteristics of the primary and secondary extinction. The applied XRD technique (Kryshtab et al., 2004) can be used to correct the PDs in PFs measured for nickel samples after the evaluation of validity of the proposed assumptions, since the nickel K-absorption edge is very close to the wavelength of the radiations used.
Evaluation of the assumptions- (i)
The main assumption was used for the coefficient of the primary extinction (ε), that for low index reflections this coefficient depends insignificantly on the wavelength used, and thus, the average value can be used for different wavelengths. This coefficient depends on the value of the extinction length, Eq. (5), which in turn depends on the structure factor, Eq. (6). The structure factor depends on the atomic scattering amplitude, which for a given reflection is a constant for different wavelength and also on the dispersion corrections, which are determined by the ratio of the wavelengths of the K- absorption edge for the sample and the radiation used. Therefore, the variations of the extinction length for a given reflection in dependence on the wavelength used should be examined for nickel sample. From Table 2 one can see that the extinction lengths for the first order reflections (111 and 200 reflections) do not change essentially for Co Kα and Cu Kα radiations, but for Mo Kα - radiation this difference is more than 25%. Thus, the first assumption is valid for Ni with the use of Co Kα- and Cu Kα - radiations.
- (ii)
The next important assumption of the proposed technique, was that for the second order reflection the primary extinction coefficient (ε) is equal to unity. As mentioned above, the ratio between the measured PDs in the maxima of PFs for the first (P(hkl)) and the second (P2(hkl)) order reflections is less than 1/2 (the increase of PD for the second order reflection in more than 2 times). In the case when the secondary extinction is not taken into account (g=0 in Eq. (2)), the ratio is connected with the primary extinction coefficient as:
So, the value of ε for the first order reflections is less than 0.5 and the ratio l/Λ is about 2 (International Tables for X-ray Crystallography, 1992). Taking into account the calculated values of extinction length Λ for the first and the second order reflections (Table 2) and that the coherent domain size l is some constant value for a given grain microstructure and a given crysta- llographic direction, one can see that the ratio l/Λ for the second order reflections with Cu K α - radiation will decrease to 0.3−0.4 owing to the increase of extinction length in about five times. For this value of ratio the value of the primary extinction coefficient e is about 0.96−0.95. Therefore, the approximation that the primary extinction coefficient approaches to the unit can be used for nickel samples in the case of Cu K α - radiation.
Correction of pole figures and orientation distribution functionThereby, a system of three equations can be used for PDs correction in PFs for nickel samples, as it was proposed by (Kryshtab et al., 2004) with the result:
In a system two equations for PDs measured for the same first order reflection with Co Kα - and Cu Kα - radiations, and one equation for PDs measured for the second order reflection with Cu Kα - radiation are used. In the equations Pm is the measured PD and Pcor is the corrected PD, others symbols are defined in Eq. (2), (3) and (4).
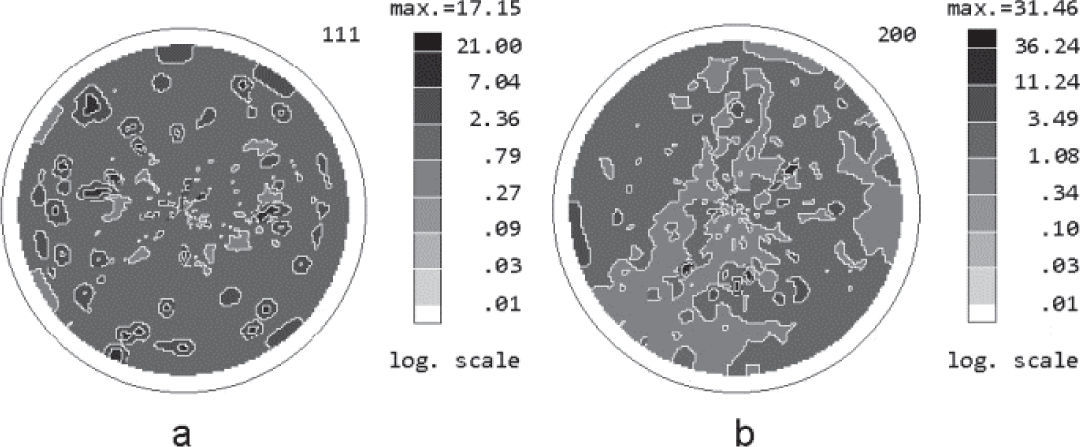
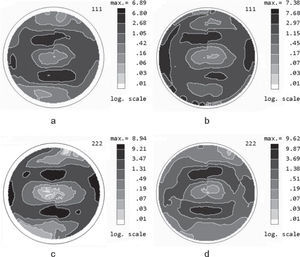
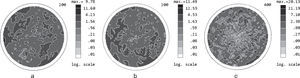
Figure 6 shows the wholly corrected PFs for 111 and 200 reflections for the nickel sample after 75% cold rolling and annealing at 600°C. PDs were corrected in every point of the measured PFs, solving a system of three equations (8).
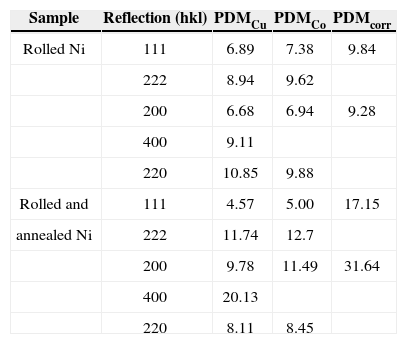
The values of PDs in the maxima of normalized PFs measured for different reflection with Cu Kα - and Co Kα - radiations as well as corrected ones for nickel samples after cold rolling and cold rolled with subsequent annealing at 600°C are listed in Table 3.
PDs in the maxima of PFs measured for different reflection with Cu Kα (PDMCu) and Co Kα (PDMCo) radiations as well as corrected ones (PDMcorr) for nickel samples after a cold rolling and cold rolled with subsequent annealing at 600°C
| Sample | Reflection (hkl) | PDMCu | PDMCo | PDMcorr |
|---|---|---|---|---|
| Rolled Ni | 111 | 6.89 | 7.38 | 9.84 |
| 222 | 8.94 | 9.62 | ||
| 200 | 6.68 | 6.94 | 9.28 | |
| 400 | 9.11 | |||
| 220 | 10.85 | 9.88 | ||
| Rolled and | 111 | 4.57 | 5.00 | 17.15 |
| annealed Ni | 222 | 11.74 | 12.7 | |
| 200 | 9.78 | 11.49 | 31.64 | |
| 400 | 20.13 | |||
| 220 | 8.11 | 8.45 |
In the corrected PFs the values of PDs in maxima increased. For example, the corrected PD in the maximum of corrected PF for 111 reflection (Figure 6a) increased in 3.75 times and for 200 reflection (Figure 6b) it increased in 3.2 times as compared with the PDs obtained in the PFs measured for the first order reflections with Cu Kα radiation (Figures 4a and 5a) indicating a stronger influence of extinction phenomenon on PF measurements for 111 reflection.
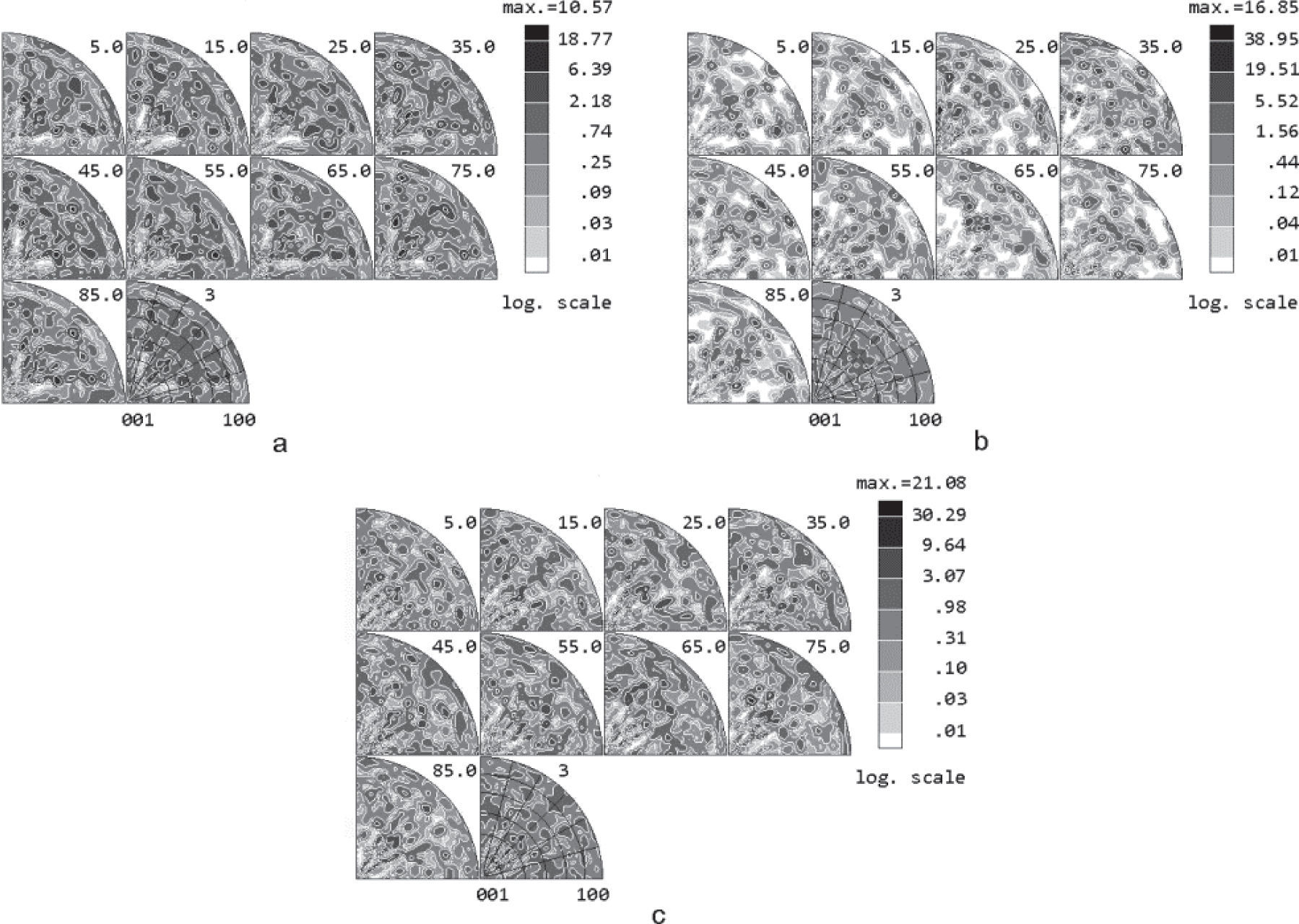
The data of normalized PFs measured for the first order 111, 200 and 220 reflections; measured for the second order 222 and 400 reflections and for 220 reflection (440 cannot be measured); and PFs corrected for 111 and 200 reflections and measured for 220 reflection (it was impossible to correct 220 reflection for lack of 440 reflection for radiations used) were used for the calculation of three ODFs. The results are presented in Figure 7.
Calculated ODFs for nickel sample after 75% cold rolling and annealing at 600°C using PFs measured for the first order reflections (a); for the second order reflections with Cu-Kα radiation (b); and corrected PFs for 111 and 200 reflections and measured with Cu Kα-radiation PF for 220 reflection (c)
As one can see, not only the details somewhat changed in calculated ODFs, but also the values of orientation density increased in more than 1.5 times in ODF calculated from the PFs for second order reflections and in 2 times in ODF calculated from the corrected ones with respect to this value in ODF obtained from the PFs for first order reflections, which have the strongest influence of extinction phenomenon on the diffracted intensity. It should be noted that PF for 440 reflection, for which the influence of extinction phenomenon should decrease considerably, and corrected PF for 220 reflection were not used for ODF calculations by the above mentioned reasons, which leads to somewhat less value of orientation density with respect to the real one. The obtained results show that the use of only the first order reflections for PFs measurements, for which the presence of extinction phenomenon is evident, can lead to an incorrect interpretation of the treatment process, as it was observed for <111> crystallographic direction, to a considerable decrease of PDs in PFs and the values of orientation density in ODFs.
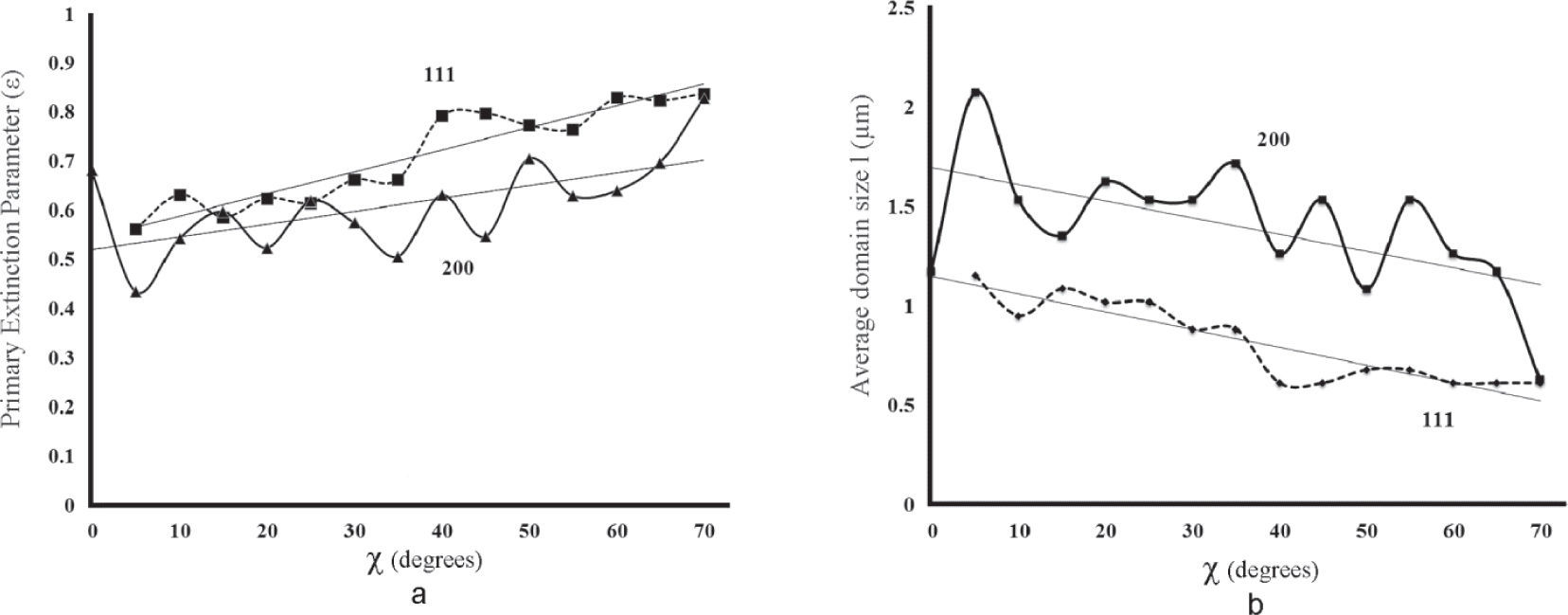
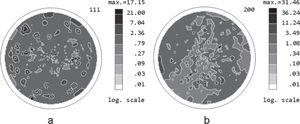
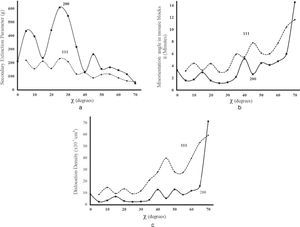
Evaluation of grain microstructureSolving system of equations (8) for correction of PDs, the coefficients of primary and secondary extinction are also calculated. The coefficients of the primary extinction and the values of extinction length for the given reflection and radiation (Table 2) were used for the evaluation of the average coherent domain size in dependence on grains orientation (each orientation of the sample at its inclination and rotation). In Figure 8 the calculated parameter of the primary extinction ε and the evaluated average size of coherent domain l are pre-presented in dependence on the grains orientation, described by the sample tilt angle χ and averaged over the whole range of sample rotation φ, for 111 and 200 reflections for nickel sample after 75% cold rolling and annealing at 600°C.
Calculated parameter of the primary extinctione for nickel sample after 75% cold rolling and annealing at 600°C for 111 and 200 reflections (a) and calculated average size of coherent domain l in these directions (b) in dependence on grains orientation. Straight lines indicate only the tendencies
The domain size is determined as the average length of the coherently diffracting crystallite in the direction normal to the diffracting planes. As one can see from Figure 8, the domain sizes are larger for the <100> direction as compared to the ones for the <111> direction and changed in dependence on the grain crystallographic orientation in such a way that the size is larger in the grains with the diffracting planes parallel to rolling surface and continually decreases in grains with the diffracting planes inclined to rolling surface for the both above mentioned directions. It needs to be pointed out, that not every point of the PF gave acceptable solutions for system of equations (8), in particular, in the points of the PF, where measured intensities from the textured sample are low up to underground. Also, it must be mentioned that the observed variations in the calculated dependences apparently are not related to real changes in the parameter of the primary extinction and the evaluated average domain size, since the solution of system of three equations (8) is obtained using the values of three PDs affected with measurement errors that propagate with slight increments or decrements to Pcorr. One more reason that can generate these variations is the texture inhomogeneity that affects the averaged value of PD at sample rotation φ, which was used for the calculations.
The evaluated average domain size (coherently diffracting crystallite) (Figure 8b), which was used for the calculation of dislocation density is almost a hundred times smaller than the real grain size (Figure 1b).
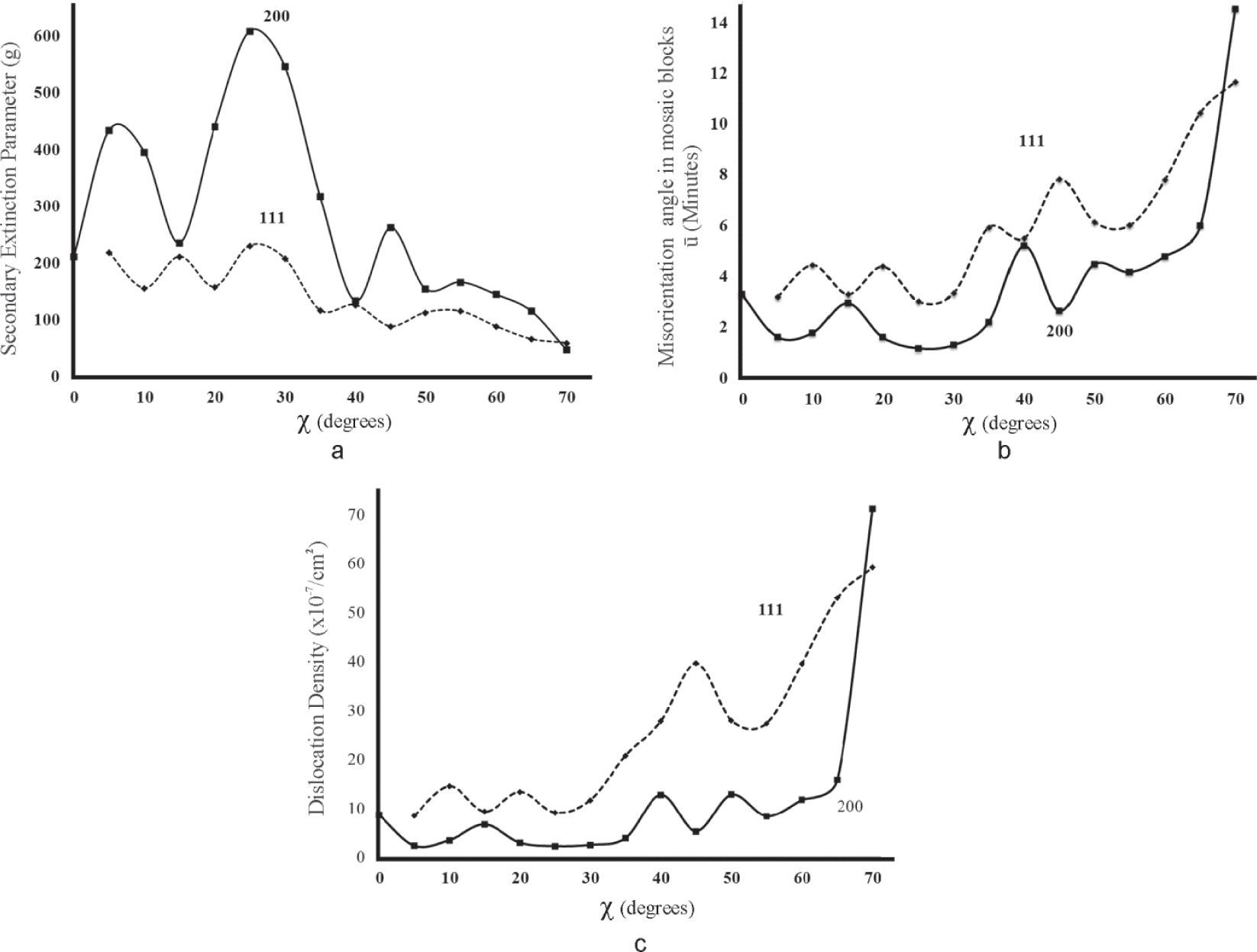
The determined values of the secondary extinction g (Figure 9a) give us the possibility to calculate the average angle of domains disorientation ū (Figure 9b) assuming a Gaussian distribution of the domains (Ivanov et al., 1983) that can be observed in many cases, according to:
Within the framework of the mosaic crystal model it is possible to calculate the dislocation density ND in domain boundaries using the calculated values of l and ū as (Larson et al., 1969):
where b is the magnitude of Burgers vector. For nickel that has the f.c.c. structure, the absolute value of Burgers vector for perfect dislocations is taken as b=(a/2) [220] (a=0.3523nm is the lattice constant). The calculated dislocation densities ND in domain boundaries in dependence on grains orientation for rolled and annealed Ni sample are shown in Figure 9c. Figures 8 and 9 include only acceptable results for the values of ε and g.This difference appears in the grain with some amount of dislocations not only in domain boundaries, but also with individual dislocations in the grain. Therefore, the dislocation density in domain boundaries is somewhat overestimated owing to this reason. The model of the mosaic crystal used does not take into account this situation and, unfortunately, a complete theory for the estimation of the dislocation density at their heterogeneous distribution does not exist. This is the subject of further investigations.
ConclusionsIn the present work the influence of extinction phenomenon on the data of PFs measurements for the first order reflections is demonstrated.
The evaluation of the approximations used in the applied XRD technique for quantitative texture analysis, when extinction phenomenon is present, demonstrated their validity for PD correction and determination of the primary and secondary extinction coefficients for a textured material, whose wavelength of the K-absorption edge lies very close to the wavelengths used for PFs measurements, for two determined X-ray radiations.
It was shown that even in the measurements of PFs for a sample with common cold rolling the extinction phenomenon can be present.
The correction of PDs, taking into account the extinction phenomenon, was performed in whole PFs measured for 111 and 200 reflections. A comparison of ODFs calculated using PFs, strongly affected, slightly affected and corrected for extinction, presents differences, which show the necessity to take into account the extinction phenomenon for the refinement of quantitative texture analysis by XRD.
The characteristics of microstructure and their dependences on grains orientations with respect to sample surface for different crystallographic directions, determined from the coefficients of the primary and the secondary extinctions, can be used for the evaluation of microstructure modification in grains at technological processes.
The authors would like to thank the CONACyT in Mexico for financial support of this work by the projects N 83425 and N 83781.
He is Ph. D. candidate in the School of Physics and Mathematics, National Polytechnic Institute (IPN). He is Master of Science in Physics by the School of Physics and Mathematics, National Polytechnic Institute (IPN) (2007), has a Bachelor degree in Physics and Mathematics (2001) by the IPN. He taught at the senior high school level education institute of the Federal District teaching physics and mathematics (2005). He currently works as professor in the School of Chemical Engineering and Extractive Industries ESIQIE-IPN, teaching applied differential equations, vector calculus, precalculus and differential and integral calculus.
Chicago citation style Cadena-Arenas, Antonio, Tetyana Kryshtab, Jesús Palacios-Gómez, Andriy Kryvko. Extinction Phenomenon in X-Ray Diffraction Technique for Texture Analisis. Ingeniería Investigación y Tecnología, XV, 02 (2014): 241–252.
ISO 690 citation style Cadena-Arenas A., Kryshtab T., Palacios-Gómez J., Kryvko A. Extinction Phenomenon in X-Ray Diffraction Technique for Texture Analisis. Ingeniería Investigación y Tecnología, volume XV (issue 2), April-June 2014: 241–252.
He studied BS in Physics and Mathematics at the School of Physics and Mathematics (ESFM), National Polytechnic Institute (IPN) and Doctorate in Natural Sciences at the Technical University of Aachen, Germany. He teaches at the School of Physics and Mathematics, National Polytechnic Institute (IPN) since 1969. Field of research: interaction of radiation with matter and the development of methods for studying diffraction structural materials; the extinction observed in X-ray diffraction and neutron measurement in polar figures textured materials. He has published a paper a year internationally and attended on average one international and one national event per year. He has developed a set of practices XRD in condensed matter for final year students of the Bachelor in Physics and Mathematics. He is a member of the National System of Reserchers (SNI) in México.
She has worked for 33 years as a researcher in the area of Solid State Physics in characterizing the structure and microstructure (dislocations, point defects, residual stresses, etc.) Single crystals, polycrystals with texture, thin films and heterostructures with wells and quantum dots based semiconductor by X-ray diffraction. Her scientific career began at the Institute of Semiconductor Physics of the National Academy of Sciences of Ukraine, Kiev, Ukraine. Since 1999, she works at the School of Physics and Mathematics, National Polytechnic Institute (IPN) as Professor. She has published 116 articles in international and national journals indexed and arbitrated, which have been cited 120 times, and 5 books specializing in radiation diffraction in solids. She has participated in over 70 international and national conferences and had over 150 confer on research projects. She assisted in the preparation of seven M. Sc thesis and 3 Ph. D. thesis. She is a level II member of SNI.
He obtained his Ph.D. in Mathematics at the National Polytechnic Institute IPN, Mexico City. He is a Bachelor in Actuarial Science by the University of Mexico; M. Sc. in Mathematics by the National Polytechnic Institute IPN, Mexico; BS in Physics and Mathematics by the National Polytechnic Institute (IPN), Mexico City, Mexico. AWARDS: Best average in 2007 in the Ph.D. program (Mathematics) IPN; Excellent performance and best average mastery in 2004, IPN. He has published 15 articles in international and national journals indexed and arbitrated. He is currently a research professor of the School of Mechanical and Electrical Engineering, IPN. Fields of study: ordinary differential equations, partial differential equations, asymptotic methods.