Factores de fiabilidad y eficiencia en la toma de decisiones para la rehabilitación de tuberías

Resumen

La metodología que se ha desarrollado propone una secuencia de rehabilitaciones en la red de distribución de agua, identificando jerárquicamente los grupos de tuberías que deben ser objeto de renovación, tomando en consideración todos los factores asociados tanto endógenos como exógenos y las limitaciones técnicas en el funcionamiento de la red de agua, considerando los presupuestos anuales disponibles para la rehabilitación de tuberías. El objetivo de este trabajo es desarrollar un modelo para facilitar la toma de decisiones de los gestores en las redes de abastecimiento, considerando una restricción presupuestal, qué cantidad de metros lineales de cada grupo de tuberías proporciona un máximo beneficio con relación a la valoración de los factores de influencia, de los beneficios obtenidos y el costo de la rehabilitación. Para lograr esto utilizaremos la herramienta de algoritmos genéticos a través de Evolver y lógica difusa, la utilización de EPANET para determinar el costo del “ahorro” de la energía eléctrica y del caudal recuperado de las fugas. Dicho modelo se aplicará a un caso de estudio en la ciudad de Celaya, Guanajuato, México.

Abstract

The methodology that has been developed suggests a sequence of interventions in the water distribution network, identifying the hierarchy of groups of pipes that must be renewed, taking into consideration all the factors associated, both endogenous and exogenous, and the technical limitations in the functioning of the water network considering the annual budget available for the rehabilitation of pipelines. The aim of this work is to develop a model to facilitate the decision-making to the managers of water distribution systems, considering a budget constraint, the amount of linear meters of each group of pipes that provides a maximum benefit in relation to the valuation of influence factors, the benefits and the cost of the rehabilitation. To accomplish this, we use the genetic algorithms tool through Evolver and fuzzy logic, using EPANET to determine the cost of “saving” electricity and the recovered leakage flow. This model is applied to a case study in the city of Celaya, Guanajuato, Mexico.

Introducción

Para los gestores de sistemas de abastecimiento de agua que operan y toman decisiones respecto al sistema, identifica factores que influyen en la determinación de prioridades en la renovación de las tuberías no es tarea sencilla, dado que la selección debe apoyarse, en primera instancia, en la identificación de aquellos criterios fundamentales a la hora de seleccionar la tubería que debe ser considerados prioritarios para su renovación (Alonso et al., 2008) aunado a la disponibilidad de los recursos financieros requeridos y los recursos financieros disponibles para las empresas que operan los sistemas de abastecimiento de agua. El objetivo es mejorar la fiabilidad y el funcionamiento de la red.

Se pretende conformar un modelo que nos permita decidir, con base en una restricción presupuestal, qué cantidad de metros lineales de cada grupo de tuberías analizadas nos proporciona un mayor beneficio, según la valoración de los factores de influencia, el costo de rehabilitación y de los beneficios obtenidos con la misma. Para esto, utilizaremos la herramienta de algoritmos genéticos a través del método “recipe” del software Evolver para determinar el ahorro de la energía eléctrica y del caudal recuperado de las fugas al rehabilitar las tuberías, también se utiliza el software Epanet para el análisis de redes hidráulicas. Dicho modelo se aplica a un caso de estudio.

Desarrollo del modelo

El caso de estudio se realiza para ocho grupos de tuberías de la red de abastecimiento de la ciudad de Celaya, Guanajuato, donde se cuenta con una restricción presupuestal de 270,000 dólares anuales, monto disponible en el programa de rehabilitación de tuberías por parte del organismo operador. Por lo tanto, la función objetivo es:

sujeta a

donde

• X_i es la cantidad de metros lineales de tubería,

• B_t se refiere a los beneficios totales,

• C_t a los costos totales,

• C_s a los costos de sustitución.

Para determinar los costos se cuenta con los costos unitarios de rehabilitación para cada grupo de tubería, así como los valores de factores de influencia de cada uno de ellos, como se muestra en la tabla 1.

Tabla 1.

Concentrado de valores de los factores de influencia

ID Línea	Edad Per. Inst.	Historial fugas	Perdida capacidad	IDN	IIQfuga	Tiempo renovación	Influencia rotura Q	Impacto medio amb.	Total
AC (A1)	6.40	10.00	3.98	4.10	0.00	7.19	3.26	6.00	40.93
AC (A2)	3.60	9.19	4.64	5.80	2.45	0.00	3.04	4.80	33.52
FoFo (C1)	10.00	8.36	5.02	5.20	0.55	6.33	4.46	4.80	44.72
Fo Ga (C1)	10.00	9.25	4.73	4.60	4.62	3.85	4.57	10.00	51.62
Fo Ga (C2)	6.40	9.92	4.10	5.50	3.72	10.00	4.10	4.20	47.94
PVC30	3.60	6.78	4.92	3.60	3.24	0.00	0.12	6.00	28.26
PVC20	1.60	7.26	4.27	5.50	10.00	0.00	1.76	0.00	30.39
Polietileno	0.40	9.10	2.86	10.0	2.23	0.00	1.12	0.00	25.71

Con la valoración de los factores de influencia y con el costo de rehabilitación unitario se calcula el factor del costo, la tabla 2 muestra el costo total del factor de costo, en donde la primera columna se refiere al costo de rehabilitación por metro lineal para cada uno de los grupos de tuberías, en la segunda columna el factor de costo, que es el resultado del costo unitario dividido entre la suma de los valores de los factores influencia de la tabla 1. La columna tres se refiere a los metros lineales de cada grupo de tuberías, la cuarta columna contiene los metros lineales a modificar y que maximizan los beneficios cumpliendo con las restricciones. Como se observa, para rehabilitar la longitud total de los ochos grupos de tuberías se requieren aproximadamente 3,846,153 dólares, pero sólo se disponen de 270,000 dólares anuales.

Tabla 2.

Factor de costo, longitudes totales y costo total

ID	Edad tubería (años)	Costo $/ML	Factor	m.1 (a modificar)	Costo total
AC (A1)	40	$477	11.65	12605	$6,012,585.00
AC (A2)	30	$537	16.02	7243	$3,889,491.00
FoFo (C1)	50	$594	13.28	11613	$6,898,122.00
Fo Ga (C1)	50	$550	10.65	8600	$4,730,000.00
Fo Ga (C2)	40	$480	10.01	7540	$3,619,200.00
PVC30	30	$491	17.37	25201	$12,373,691.00
PVC20	20	$471	15.50	11548	$5,439,108.00
Polietileno	20	$480	18.67	13865	$6,655,200.00
				Total	$49,617,397.00

Los beneficios logrados por el “ahorro” de la energía al rehabilitar las tuberías, es decir, lo que se consume de energía en “alimentar” las fugas, se determina simulando tres escenarios de operación de las redes de abastecimiento para cada grupo de tuberías mediante Epanet. Para cada grupo de tuberías en Epanet, los tres escenarios planteados son: la red operando con una eficiencia de 85%, red en el estado que se encuentra actualmente, y en el último se aplica la curva de bombeo original, pero con la red en el estado en que se encuentra actualmente. A continuación se ilustra con un ejemplo el procedimiento para determinar el beneficio del ahorro de la energía, de uno de los sectores (sector San Juanico).

En la figura 1 se muestra la presión nodal simulada con la red a 85% de eficiencia, que es el nivel deseado y con el cual se realiza el cálculo. En la figura 2 se muestra la presión nodal del estado actual de la red, que incluye las fugas. El caudal total a través de la red, es igual a la demanda total diaria de 1381.61 m³ y todas las presiones nodales tienen por lo menos 10 mca.

Figura 1.

Presión nodal con 85% de eficiencia en la red

Figura 2.

Presión nodal, estado actual de la red

Cuando las fugas en los nodos tienen asociado un coeficiente de emisor para representar el escenario actual y la curva original de las estaciones de bombeo, se aplica (Colombo y Kerney, 2002) el caudal total a través del sistema y dicho caudal se incrementa a 18.82 lps., mientras que todos los requisitos de la demanda se cumplen, pero la presión cae significativamente como se muestra en la figura 3. A pesar de que la satisfacción de las demandas nodales es un requisito típico del modelado (Le Gauffre et al., 2002a), en compensación para las fugas, la magnitud de las pérdidas aumenta, hasta que el volumen del sistema se convierte en 21.80 lps., y cumple con las presiones nodales mínimas; el adicional de 2.98 lps., está asociado con la presión que depende de la demanda ejercida por las fugas y por consiguiente la energía aplicada para “alimentar las fugas”.

Figura 3.

Caída de presión en la red, aplicando curva de bombeo original

Epanet calcula el costo de la energía para los diferentes escenarios. Los resultados obtenidos se presentan en la tabla 3.

Tabla 3.

Costo diario de la energía para los diferentes escenarios planteados

Sector	Q85% eficiencia costo día	Q sin cumplir presiones (a) costo día	Q cumpliendo presiones (b) costo día	Diferencia b-a
AC (A1)	$621.31	$875.00	$1,231.00	$356.00
AC (A2)	$701.24	$1,023.22	$1,424.22	$401.00
FoFo (C1)	$567.30	$831.31	$1,214.31	$383.00
Fo Ga (C1)	$444.65	$630.54	$1,008.54	$378.00
Fo Ga (C2)	$678.95	$944.22	$1,345.22	$401.00
PVC30	$1,388.42	$2,019.41	$2,496.41	$477.00
PVC20	$538.26	$787.19	$1,191.19	$404.00
Polietileno	$174.84	$259.51	$504.51	$245.00

Cálculo del caudal fugado

El procedimiento para determinar el caudal fugado es análogo al que se realizó para el cálculo del costo de la energía, con la diferencia de que ahora se realiza la comparación de los volúmenes demandados en las condiciones actuales en que se encuentra la red, versus los volúmenes demandados por la red con un 85% de eficiencia. El resultado de la comparación del balance de masa de cada uno de los escenarios (tabla 4), se multiplica por el precio promedio del costo del m³ de agua.

Tabla 4.

Caudales diarios para los tres escenarios planteados

Sector	Q85% eficiencia lps	Q sin cumplir Presiones (a)	Q cumpliendo Presiones(b)	Diferencia b-a
AC (A1)	13.44	1559.18	1908.06	348.88
AC (A2)	13.48	1379.95	1788.97	409.02
FoFo (C1)	9.83	1129.18	1506.05	376.87
Fo Ga (C1)	10.63	1138.71	1511.04	372.33
Fo Ga (C2)	48.55	4538.44	4904.06	365.62
PVC30	54.38	5473.63	5934.89	461.26
PVC20	37.84	3975.66	4375.62	399.96
Polietileno	15.99	1626.41	1883.66	257.25

Cálculo del riesgo de la consecuencia de fallo

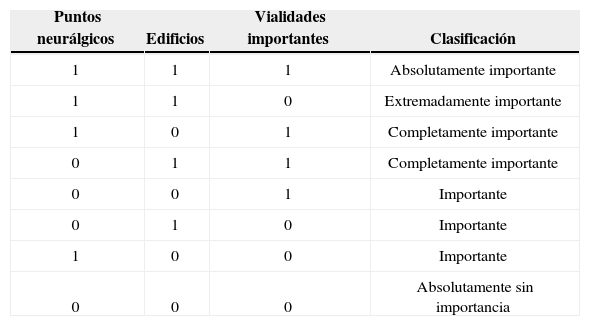
Es necesario calcular el costo, antes de que se presente un fallo, del riesgo de la consecuencia de fallo por no rehabilitar la tubería, de tal manera que se supone que al rehabilitar la tubería evitaremos el fallo y su posible consecuencia en el entorno (Nafi, 2006), lo cual se considera como un beneficio, dentro de los beneficios en la función objetivo. Para considerar como beneficio la inversión en la rehabilitación de las tuberías, se seleccionan tuberías con nivel de riesgo alto y nivel de consecuencia importante. La clasificación para la determinación de las consecuencias de riesgo se realiza mediante las escalas cualitativas (Werey, 2003), con base en la importancia de los factores y de su densidad en las tuberías; por ejemplo, para las tuberías donde se localice al menos un punto “neurálgico”, como edificios de dimensiones importantes próximos a las tuberías o vialidades importantes. Se asigna al punto más elevado en la escala de esa clasificación y así sucesivamente, según el grado de importancia del factor, como muestra en la tabla 5.

Tabla 5.

Escala cualitativa de las consecuencias de riesgo

Puntos neurálgicos	Edificios	Vialidades importantes	Clasificación
1	1	1	Absolutamente importante
1	1	0	Extremadamente importante
1	0	1	Completamente importante
0	1	1	Completamente importante
0	0	1	Importante
0	1	0	Importante
1	0	0	Importante
0	0	0	Absolutamente sin importancia

De acuerdo con lo descrito, se aplica al caso de estudio y se obtienen los resultados mostrados en la tabla 6.

Tabla 6.

Resultados de la clasificación de las consecuencias de riesgo

ID	Puntos neurálgicos 38,461 dólares	Edificios 61,538 dólares	Vialidades importantes 32,307 dólares	Escala cualitativa
AC (A1)	0	0	0	Absolutamente sin importancia
AC (A2)	0	1	0	Importante
FoFo (C1)	0	0	0	Absolutamente sin importancia
Fo Ga (C1)	0	0	0	Absolutamente sin importancia
Fo Ga (C2)	1	1	0	Extremadamente importante
PVC30	1	0	1	Completamente importante
PVC20	0	0	0	Absolutamente sin importancia
Polietileno	0	0	1	Importante

La probabilidad de fallo se calcula con la ecuación 4, donde se asigna un valor de probabilidad correspondiente a K₁ = 1, K₂ = 0.8, K₃ = 0.6, K₄ = 0.4, K₅ = 0.2. A cada grupo de tuberías se le asigna un valor según el criterio del evaluador y las características de cada grupo de tuberías (Dridi et al., 2005). Para determinar la probabilidad de fallo se multiplica la probabilidad determinada por el valor del peso asignado; el resultado es la probabilidad de fallo como se muestra en la siguiente expresión

Los factores considerados en la influencia de fallos son: tipo de material, presión hidrostática, edad de la tubería, historial de fugas, medio ambiente, tipo de unión y continuidad en la operación. Los resultados de la probabilidad de fallo para el grupo de tuberías del caso de estudio se muestran en la tabla 7.

Tabla 7.

Concentrado del cálculo de la probabilidad de fallo

ID	Tipo del material			Presión hidrostática			Edad de la tubería			Historial de fugas			Medio ambiente			Tipo de unión			Continuidad en la operación			∑
	W	K	P = F1*W1	W	K	P = F1*W1	W	K	P = F1*W1	W	K	P = F1*W1	W	K	P = F1*W1	W	K	P = F1*W1	W	K	P = F1*W1
	0.1	0.2	0.02	0.1	0.2	0.01	0.2	0.2	0.03	0.2	0.4	0.06	0.1	0.6	0.06	0.1	0.4	0.02	0.1	0.2	0.02	0.22
	0.1	0.4	0.04	0.1	0.4	0.04	0.2	0.4	0.06	0.2	0.4	0.08	0.1	0.4	0.04	0.1	0.2	0.02	0.1	0.2	0.02	0.30
	0.2	0.2	0.03	0.1	0.2	0.02	0.2	0.6	0.12	0.1	0.2	0.02	0.2	0.2	0.03	0.2	0.2	0.03	0.1	0.4	0.02	0.27
	0.3	0.6	0.15	0.1	0.2	0.02	0.2	0.4	0.06	0.1	0.4	0.04	0.2	0.2	0.03	0.2	0.2	0.03	0.1	0.6	0.02	0.35
	0.3	0.4	0.10	0.2	0.4	0.06	0.2	0.2	0.04	0.2	0.2	0.04	0.2	0.4	0.06	0.2	0.2	0.03	0.1	0.6	0.02	0.35
	0.1	0.2	0.01	0.2	0.6	0.12	0.1	0.2	0.01	0.1	0.2	0.02	0.1	0.6	0.03	0.1	0.4	0.04	0.02	0.4	0.06	0.29
	0,1	0.2	0.01	0.2	0.4	0.08	0.1	0.2	0.01	0.1	0.4	0.04	0.1	0.2	0.02	0.1	0.2	0.01	0.02	0.2	0.04	0.21
	0.1	0.4	0.02	0.1	0.4	0.04	0.1	0.2	0.01	0.1	0.2	0.01	0.2	0.4	0.08	0.3	0.6	0.15	0.01	0.6	0.06	0.37
	1		0.38	1		0.39	1		0.34	1		0.31	1		0.35	1		0.33	1		0.26

La probabilidad de fallo para cada uno de los grupos de tuberías se obtienen de la tabla 7, una vez que se determina la probabilidad se realiza la siguiente clasificación para determinar la escala cualitativa de la probabilidad de riesgo. El rango de los cuartiles se determina de acuerdo con el rango de probabilidad total (Tuhovcak et al., 2007); en nuestro caso, el rango es de 20 a 40, donde el rango de menor importancia en la clasificación es de 20–25, lo que se clasifica como alto, y así sucesivamente, hasta llegar a la clasificación de absolutamente alto que es el mayor valor del rango de probabilidad. Los resultados obtenidos se muestran en la tabla 8.

Tabla 8.

Clasificación de la probabilidad de fallo

ID	Probabilidad de fallo	Escala cualitativa
AC (A1)	0.22	Alto
AC (A2)	0.30	Completamente alto
FoFo (C1)	0.27	Completamente alto
Fo Ga (C1)	0.35	Extremadamente alto
Fo Ga (C2)	0.35	Extremadamente alto
PVC30	0.29	Completamente alto
PVC20	0.21	Alto
Polietileno alta densidad	0.37	Absolutamente alto

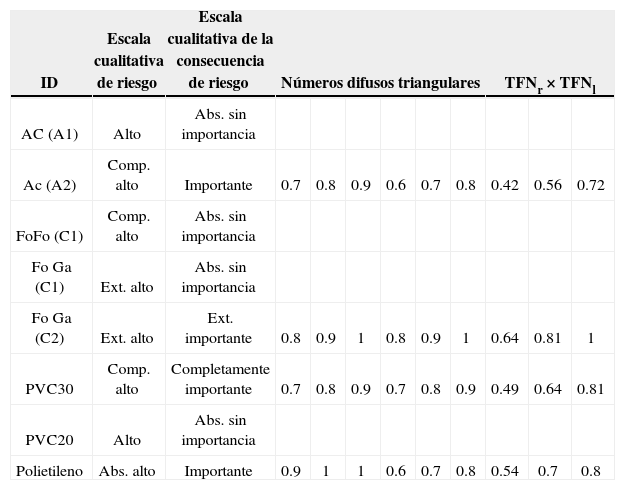
Una vez que se tiene la clasificación y la valoración de las escalas cualitativas de la probabilidad de riesgo y la consecuencia de riesgo, se procede a la determinación del conjunto de números difusos (Mogolia et al., 2006), donde se obtiene el riesgo de los números difusos triangulares (TFN_rl) para cada grupo de tuberías mostrado en la tabla 9. En la figura 4 se muestra el ejemplo de la estimación de cinco-tuplas de riesgo del conjunto difuso, en este caso para el grupo de tuberías de PVC 30 (tabla 10), donde el número difuso triangular de la probabilidad de fallo (TFN_r) es [0.7, 0.8, 0.9], dado que la probabilidad de riesgo es completamente alto y el número difuso triangular de la consecuencia de fallo (TFN_l) es [0.7, 0.8, 0.9], con la consecuencia de riesgo completamente importante.

Tabla 9.

Resultados de los números difusos triangulares

ID	Escala cualitativa de riesgo	Escala cualitativa de la consecuencia de riesgo	Números difusos triangulares						TFNr × TFNl
AC (A1)	Alto	Abs. sin importancia
Ac (A2)	Comp. alto	Importante	0.7	0.8	0.9	0.6	0.7	0.8	0.42	0.56	0.72
FoFo (C1)	Comp. alto	Abs. sin importancia
Fo Ga (C1)	Ext. alto	Abs. sin importancia
Fo Ga (C2)	Ext. alto	Ext. importante	0.8	0.9	1	0.8	0.9	1	0.64	0.81	1
PVC30	Comp. alto	Completamente importante	0.7	0.8	0.9	0.7	0.8	0.9	0.49	0.64	0.81
PVC20	Alto	Abs. sin importancia
Polietileno	Abs. alto	Importante	0.9	1	1	0.6	0.7	0.8	0.54	0.7	0.8

Figura 4.

Estimación de cinco-tuplas de riesgo del conjunto difuso

Tabla 10.

Estructura de la obtención del riesgo difuso

x = TFNrl =	[0.49, 0.64,0.81]
P	MB			B			M			A			MA
TFNL	0	0	0.25	0	0.25	0.5	0.25	0.5	0.75	0.5	0.75	1	0.75	1	1
Inferencia	0				0			0.65			0.75			0.16
XL =	[0,0,0.65,0.75,0.16]			cardinalidad, C = 1.56
X =	[0,0,0.42,0.48,0.10]

Esto se obtiene de la tabla 10, donde se definen los números difusos triangulares para una probabilidad de riesgo completamente alto y una consecuencia de riesgo completamente importante. Al realizar la operación (TFN_r * TFN_l), se obtiene el correspondiente riesgo x TFN_rl [0.49, 0.64, 0.81].

Una vez que se determina el TFN_rl, se realiza la conversión al riesgo difuso X normalizado de las cinco-tuplas del conjunto difuso (Kleiner y Adams, 2001), obteniendo el resultado del riesgo difuso X [0, 0, 0.42, 0.48, 0.10], donde tomamos la probabilidad más alta (muy alta en la escala del nivel de riesgo), que en este caso es 0.16 (tabla 9); este valor se aplica para determinar el costo de la consecuencia de fallo, donde: MB (muy bajo), B (bajo), M (medio), A (alto), MA (muy alto).

Para la determinación del costo de la consecuencia de fallo para cada una de las tuberías, en la tabla 11 se concentra el grupo de tuberías con cada uno de los costos de las consecuencias de fallos, definidos previamente, en donde se asigna el porcentaje de la probabilidad de la consecuencia de fallo obtenida en el riesgo difuso X en la escala cualitativa más alta, considerando sólo los valores de las probabilidades de la escala cualitativa del nivel de riesgo muy alto.

Tabla 11.

Resultados del cálculo del costo de la consecuencia de fallo

ID	Agencia de autos $500,000.00	Edificios proximidad $800,000.00	Vialidades importantes $420,000.00	Costo consecuencia de fallo
AC (A1)	0	0	0	$0.00
AC (A2)	0	0.27	0	$216,000.00
FoFo (C1)	0	0	0	$0.00
Fo Ga (C1)	0	0	0	$0.00
Fo Ga (C2)	0.33	0.33	0	$429,000.00
PVC30	0.1	0	0.1	$92,000.00
PVC20	0	0	0	$0.00
Polietileno	0	0	0.1	$42,000.00

Obtención de resultados

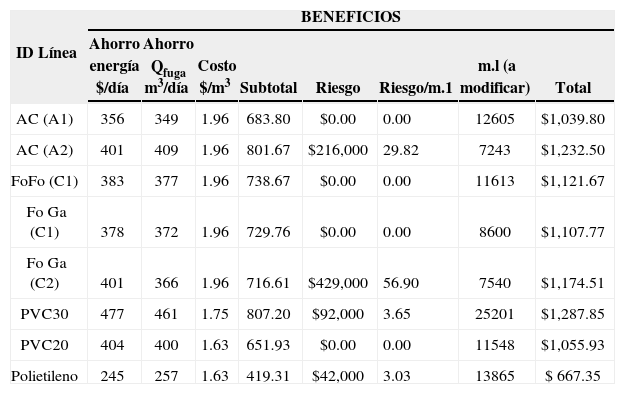
Los costos se determinan a partir del costo de rehabilitación unitario de cada grupo de tubería, por el factor de costo obtenido de la longitud total entre la valoración global en la suma de los factores de influencia. Los beneficios se muestran en la tabla 12.

Tabla 12.

Resultado y cálculo de los beneficio al rehabilitar las tuberías

ID Línea	BENEFICIOS
	Ahorro energía $/día	Ahorro Qfuga m^3/día	Costo $/m^3	Subtotal	Riesgo	Riesgo/m.1	m.l (a modificar)	Total
AC (A1)	356	349	1.96	683.80	$0.00	0.00	12605	$1,039.80
AC (A2)	401	409	1.96	801.67	$216,000	29.82	7243	$1,232.50
FoFo (C1)	383	377	1.96	738.67	$0.00	0.00	11613	$1,121.67
Fo Ga (C1)	378	372	1.96	729.76	$0.00	0.00	8600	$1,107.77
Fo Ga (C2)	401	366	1.96	716.61	$429,000	56.90	7540	$1,174.51
PVC30	477	461	1.75	807.20	$92,000	3.65	25201	$1,287.85
PVC20	404	400	1.63	651.93	$0.00	0.00	11548	$1,055.93
Polietileno	245	257	1.63	419.31	$42,000	3.03	13865	$ 667.35

El método de solución del Evolver es el método de solución “recipe”, el método “recipe” funciona cuando las variables a ajustar son independientes unas de otras. El procedimiento es similar a pesar que cada variable es la cantidad de ingrediente de un pastel, Evolver genera números para estas variables, con el objetivo de encontrar la mejor mezcla. Una vez que se ejecuta el modelo, se obtienen los resultados de la longitud óptima para cada grupo de tubería con la que se maximizan los beneficios. Los resultados se presentan en la tabla 13.

Tabla 13.

Resultados de la longitud óptima para cada grupo de tubería

ID Línea	m.1	Costo total
AC (A1)	593.00	$283,455.00
AC (A2)	1,250.00	$671,843.00
FoFo (C1)	723.00	$430,056.00
Fo Ga (C1)	1,198.00	$659,494.00
Fo Ga (C2)	599.00	$288,113.00
PVC30	750.00	$368,844.00
PVC20	937.00	$441,922.00
Polietileno	741.00	$356,273.00
		$3,500,000.00

Conclusiones

El aspecto económico es relevante y es un factor determinante para la toma de decisiones de los gestores en las empresas de agua, aunado a los costos y beneficios que se encuentran vinculados. De tal manera que se considera de gran ventaja contar con la opción de obtener longitudes de tubería a rehabilitar en cada sector para no enfocar y centrar su rehabilitación a sectores completos solamente. Los resultados muestran que la mayor longitud a rehabilitar es la que pertenece al grupo de las tuberías de asbesto, cemento de 50 años de edad, seguidas por las tuberías de fierro galvanizado de 40 años de edad. De tal manera, se concluye que el modelo desarrollado es una herramienta práctica y tangible para la toma de decisiones, proporcionando la longitud optima de tubería que debe ser rehabilitada, objetivo primordial en toda empresa de agua, considerando los distintos factores de influencia en el deterioro de las tuberías, que a su vez, contribuyen a los fallos de las mismas ocasionando consecuencias considerables y afectando la fiabilidad en el sistema de distribución.