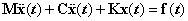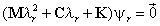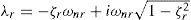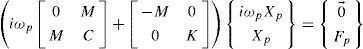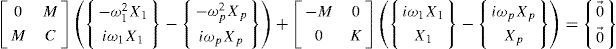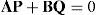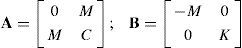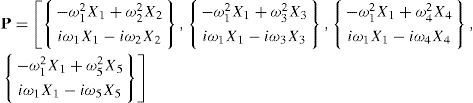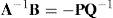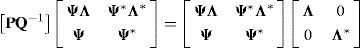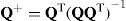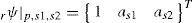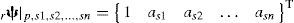Identificación de modos cercanos de vibración de una estructura cuasi-axisimétrica: estudio complementario

Resumen

Se presenta un procedimiento para la caracterización de modos de vibración estructural conocidos como “modos cercanos”, que son aquellos con frecuencias naturales similares y que se presentan comúnmente en estructuras cuasi-axisimétricas.

La caracterización de estos modos normalmente se dificulta debido a que sus regiones de resonancia están traslapadas, y eso impide distinguir las componentes de vibración correspondientes a cada modo empleando los métodos convencionales, diseñados para sistemas de un grado de libertad. El procedimiento que se propone aquí se basa en la estimación simultánea de los parámetros de dos modos cercanos empleando el número mínimo posible de datos de respuesta en el dominio de la frecuencia. Los parámetros modales se relacionan directamente con las diferencias entre la respuesta medida a diferentes frecuencias de excitación. La contribución principal de este trabajo es un método de caracterización modal diseñado específicamente para identificar los parámetros de pares de modos cercanos de vibración, que a diferencia de los métodos establecidos de análisis no requiere que la respuesta en cada resonancia esté dominada por un solo modo. La aplicación del procedimiento a una estructura real demuestra que es posible estimar los parámetros modales asociados con modos cercanos de un sistema empleando un número reducido de datos de su respuesta vibratoria, y proporciona resultados satisfactorios aún en presencia de ruido en las mediciones.

Abstract

A procedure for the characterization of so-called close vibration modes is presented. These are modes with similar natural frequencies that commonly appear in quasiaxisymmetric structures. Their characterization is usually hindered because their resonance regions overlap significantly, and thus conventional characterization methods based on single-degree-of-freedom curve fits cannot be used. The proposed procedure is based on performing simultaneous estimations of the parameters of the two modes, employing the fewest possible response data points in the frequency domain. The modal parameters are directly related with the differences between the response measurements at different excitation frequencies. The main contribution of this work is a modal characterization method that is designed specifically for the identification of close vibration modes and which, in contrast with the well established analysis methods, does not require that each resonance region be dominated by a single mode of vibration. The application of the procedure to the case of a real structure demonstrates that it is possible to estimate the modal parameters of close vibration modes using a reduced set of vibration response data, and yields satisfactory results even in the presence of measurement noise.

Introducción

Las geometrías axisimétricas son idealizaciones comúnmente empleadas en diseños de ingeniería, dada la abundancia de componentes con formas circulares, cilíndricas, esféricas o con periodicidad circunferencial que se requieren para la construcción de sistemas mecánicos reales como máquinas y estructuras. Sin embargo, estas geometrías no pueden lograrse estrictamente en la práctica debido a las imperfecciones de los materiales y de los métodos de fabricación, por lo que en general el ingeniero sólo se enfrenta con sistemas cuasi-axisimétricos. Las estructuras de este tipo se caracterizan por poseer modos de vibración que ocurren en pares de “modos cercanos” con frecuencias naturales similares.

Conocer las características de estos modos de vibración (frecuencias naturales, razones de amortiguamiento y formas modales) es importante para aplicaciones como la validación de modelos numéricos, la predicción de respuesta vibratoria, el control de vibraciones (Sun et al., 2006) y la estimación de los efectos de modificaciones estructurales, entre otras. En la mayoría de los casos este proceso de caracterización puede lograrse mediante procedimientos estándar basados en la aplicación iterativa de algoritmos para la caracterización de modos independientes, pero para sistemas con modos cercanos esto no es posible, ya que normalmente dichos modos se excitan de manera simultánea y esto hace difícil identificar las características de cada uno de ellos por separado (Reay y Shepherd, 1971).

Aunque existen técnicas para excitar selectivamente este tipo de modo usando fuentes múltiples de excitación (Peeters et al., 2011; Zaveri, 1985), su aplicación práctica está limitada porque se requiere un conocimiento previo de las formas modales, que es precisamente una de las características que se desea conocer mediante las pruebas.

La estrategia en la que se basan los algoritmos existentes para caracterización de modos de vibración se basa en la suposición de que en la región de resonancia de un modo, los cambios de vibración se deben a variaciones de la componente de vibración de dicho modo, siendo la contribución de otros modos prácticamente constante. Este planteamiento fue originalmente introducido por Kennedy y Pancu (1947). Cuando se caracterizan modos cercanos de vibración es necesario aplicar este método de forma iterativa, de manera que en cada iteración se sustraigan de la vibración total las componentes parciales de cada modo de vibración que se hayan podido identificar. Aunque esta estrategia de iteración constituye la base de prácticamente todos los algoritmos existentes para la identificación de modos cercanos, no siempre es posible separar las contribuciones de cada modo y por ende, tampoco lo es determinar con exactitud sus parámetros modales. Esto se agrava en situaciones con ruido en las mediciones, por ejemplo el ajuste de cocientes de polinomios (Richardson y Formenti, 1982) a las funciones de respuesta en el dominio de la frecuencia (FRFs), que constituye uno de los algoritmos estándar de caracterización modal, comúnmente conduce a la identificación de un par de modos cercanos como un único modo, especialmente cuando se realiza con mediciones reales.

Los métodos más recientes de caracterización modal se basan en el uso de funciones de transmisibilidad (FTs), en lugar de FRFs (Devriendt y Guillaume, 2008). Las transmisibilidades se obtienen al dividir entre sí dos FRFs, medidas con la(s) misma(s) fuerza(s) de excitación pero en diferentes puntos de la estructura de prueba. Estas funciones tienen la particularidad de que su valor para cada una de las frecuencias naturales es independiente de la fuerza de excitación. Si se utilizan dos fuerzas de excitación linealmente independientes se observan cruces de las FTs precisamente a las frecuencias naturales de la estructura. Los valores que adquieren estas FTs a esas frecuencias están directamente relacionados con los vectores de forma modal. En Devriendt y Guillaume (2007), Devriendt (2010a) y (2010b) se demuestra el uso de estas funciones para la caracterización modal de estructuras. Un inconveniente que tiene este método de identificación es que cuando los modos de vibración tienen frecuencias naturales similares los cruces no ocurren exactamente a las frecuencias naturales, sino a otras que están más o menos alejadas de éstas dependiendo de la participación relativa de cada modo de vibración. Esto puede conducir a errores considerables en la estimación de las frecuencias naturales (en el eje horizontal de las gráficas de las FTs contra frecuencia) y de las formas modales (en el eje vertical de dichas gráficas).

Para superar las limitaciones de los métodos convencionales de caracterización modal, Vélez-Castán et al. (2010) propusieron un procedimiento que utiliza datos de vibración provenientes de pruebas con excitación en un solo punto. La estrategia de análisis se basa en la identificación simultánea de pares de modos de vibración y no de modos independientes. El procedimiento de identificación se diseñó para estructuras con pares de modos cercanos y no requiere que cada región de resonancia esté dominada por un solo modo, como es el caso para los métodos convencionales.

Una de las limitaciones para la aplicación práctica de los resultados de Vélez-Castán et al. (2010) es que no se toman en cuenta los efectos de errores aleatorios en las mediciones. En la práctica es común que este tipo de información contenga algún tipo de contaminación aleatoria, como por ejemplo la causada por ruido en la instrumentación. Aunque estos efectos pueden ser pequeños en comparación con la magnitud de las señales de vibración, dado que el método que se propuso se basa en la inversión de matrices, es posible que estos errores conduzcan otros considerables en la predicción de parámetros modales.

Para resolver este tipo de dificultad práctica, algunos métodos de caracterización modal utilizan una gran cantidad de información redundante que se procesa, por ejemplo, mediante algoritmos de ajuste por mínimos cuadrados con el fin de reducir errores aleatorios. Sin embargo, en Vélez-Castán et al. (2010) no se proponen soluciones a este problema práctico; por ejemplo, no se describe la manera en que el procedimiento propuesto pueda hacer uso de medicines redundantes para mejorar la estimación de parámetros modales.

En el presente artículo se utilizan como base los resultados de Vélez-Castán et al. (2010) para desarrollar un procedimiento robusto de caracterización modal con el cual es posible utilizar información redundante, reduciendo así el efecto de fuentes aleatorias de incertidumbre en las mediciones. También se explica la manera en que otro tipo de información redundante (mediciones en más puntos que los estrictamente necesarios) puede emplearse para describir con mayor exactitud las formas modales de vibración. La explicación de cada paso del procedimiento y de sus fundamentos analíticos está encaminada a facilitar su aplicación práctica. Se presentan de manera condensada las deducciones analíticas en las que se basa el procedimiento que se propone, así como la deducción del mínimo número de datos de vibración requeridos para la identificación de modos cercanos.

El artículo está organizado de la siguiente manera: en la siguiente sección se presentan las ecuaciones de movimiento de los sistemas que son el objeto de este trabajo, así como la relación de éstas con los parámetros modales. Posteriormente se presenta el desarrollo de un procedimiento para determinar las características individuales de dos modos cercanos de vibración usando mediciones de la respuesta vibratoria en el dominio de la frecuencia. La aplicación del procedimiento a una estructura real se presenta en dos etapas que se describen a continuación: la primera consiste en el modelado de la estructura por el método de elementos finitos, que sirve como base para la planeación de las pruebas experimentales en cuanto a la determinación de puntos de excitación y de medición de respuesta. La segunda etapa consiste en la ejecución de las pruebas. Con base en los resultados experimentales se determinan los parámetros de un par de modos cercanos de la estructura de prueba.

Asimismo se presenta un análisis comparativo entre los parámetros modales obtenidos numérica y experimentalmente. Finalmente se presentan las conclusiones del trabajo.

Desarrollo

Ecuación de movimiento y parámetros modales

El comportamiento de un sistema vibratorio, como lo son una estructura o un componente estructural sometido a una fuerza de excitación oscilatoria, se rige por la siguiente ecuación de movimiento, que relaciona las fuerzas internas del sistema con las fuerzas externas de excitación, f (t):

En esta ecuación, M, C y K son las matrices de masa, amortiguamiento y rigidez del sistema y representan sus propiedades inerciales, disipativas y elásticas, respectivamente; son de dimensiones N × N donde N es el número de grados de libertad del sistema. El vector x tiene dimensiones N × 1 y representa los desplazamientos asociados con los distintos grados de libertad. El punto indica diferenciación con respecto al tiempo.

Los parámetros modales del sistema son la solución del siguiente problema de valores y vectores característicos:

En esta ecuación los valores característicos, λ_r representan las frecuencias naturales complejas del sistema; los vectores característicos, Ψ_r, representan las formas modales asociadas con cada una de estas frecuencias, 0→ es un vector de ceros y r indica el número de modo.

Cada frecuencia natural compleja está relacionada con la frecuencia natural ω_nr, y la razón de amortiguamiento ζ_r, de un modo de vibración mediante la siguiente ecuación:

donde i=−1.

Los parámetros modales ω_nr, ζ_r y Ψ_r, de cada uno de los modos de vibración son los parámetros a identificar mediante el procedimiento que se describe en las siguientes sub-secciones.

Caracterización de modos cercanos a partir de la respuesta vibratoria del sistema

Es común obtener los parámetros modales de un sistema a partir de los resultados de pruebas de vibración, en las que una fuerza controlada se aplica a la estructura para medir su respuesta vibratoria en uno o más puntos. Los resultados en el dominio de la frecuencia se pueden expresar mediante funciones de respuesta (FRFs) que expresan la amplitud y el ángulo de fase de la respuesta a una fuerza de excitación unitaria, y que son funciones de la frecuencia de excitación. Existen varios métodos usados convencionalmente para determinar parámetros modales estructurales (por ejemplo, McConnell, 2008; Ewins, 2000; Brandt, 2001; He y Zhu, 2001).

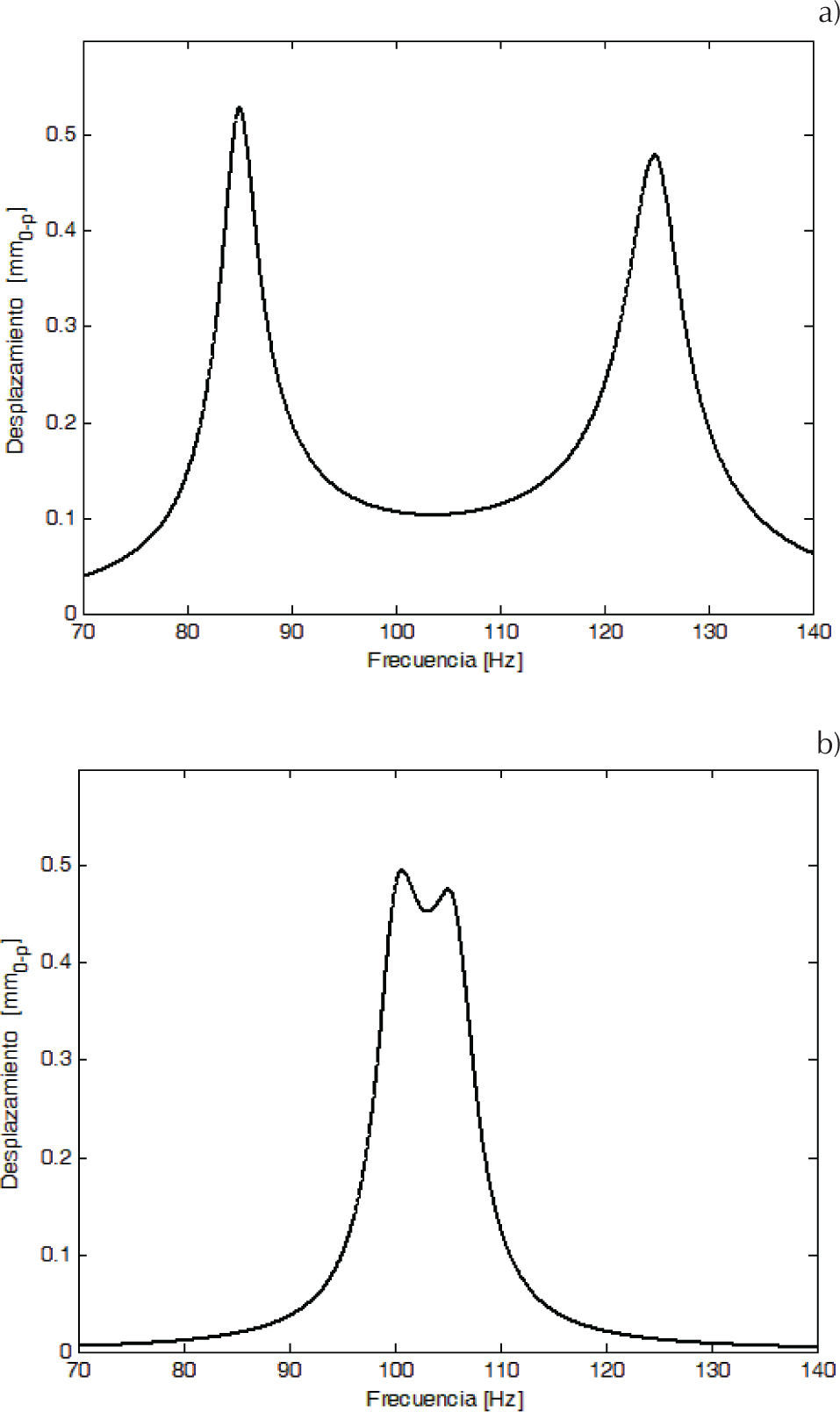
Sin embargo, estos métodos pueden conducir a errores considerables cuando se aplican a sistemas cuasi-axisimétricos. Esto se debe a la dificultad para distinguir las componentes modales de vibración de los modos con frecuencias naturales cercanas (modos cercanos), que son característicos de este tipo de sistema. La dificultad se debe a que los métodos convencionales utilizan la respuesta resonante del sistema. Mientras las regiones de resonancia de todos los modos estén bien separadas (figura 1a) cada modo puede identificarse por separado debido a que no existe traslape con las resonancias de otros modos. Sin embargo, cuando las frecuencias naturales son similares existe un traslape considerable de las regiones de resonancia (figura 1b) y la identificación de los parámetros asociados con los modos individuales se dificulta.

Figura 1.

Respuesta resonante típica para: a) modos “distantes”, b) modos “cercanos”

Dentro de un intervalo de frecuencias que contenga sólo las dos resonancias correspondientes a un par de modos cercanos, un sistema se comporta como si tuviera sólo dos grados de libertad. A continuación se desarrolla un procedimiento para determinar los parámetros modales para sistemas con modos cercanos, empleando un número reducido de FRFs medidas.

Fundamento teórico del procedimiento propuesto

Al igual que el procedimiento desarrollado por Dobson (1987) el que se propone aquí utiliza las diferencias entre las FRFs medidas a diferentes frecuencias como base del proceso de caracterización. Sin embargo, a diferencia, éste es aplicable a sistemas con modos cercanos.

Para la identificación de dos modos cercanos se considera que el sistema tiene efectivamente dos grados de libertad y que la respuesta se mide en dos puntos del sistema. El procedimiento puede repetirse para diferentes intervalos de frecuencia y para abarcar otros grupos de modos cercanos, hasta identificar todos los modos de interés.

Para una fuerza de excitación armónica, la ecuación (1) puede escribirse en el espacio de estados como:

donde 0 y 0→ representan una matriz y un vector de ceros, respectivamente. En esta ecuación todas las matrices son de dimensiones 2 × 2 y los vectores de dimensión 2 × 2. Los vectores X₁ y F₁ representan los desplazamientos y las fuerzas de excitación para una frecuencia de excitación ω₁.

Si se escribe la ecuación (4) para una frecuencia de excitación distinta, digamos ω_p, entonces se tiene:

En pruebas de vibración es común determinar la respuesta por unidad de la fuerza de excitación. Cuando se hace esto, las FRFs del sistema toman el lugar de los desplazamientos y los vectores de fuerza de excitación son independientes de la frecuencia y están formados por ceros, excepto por el elemento correspondiente al grado de libertad en el que se aplica la excitación, que toma el valor de uno. En este caso, los vectores F₁ y F_p de las ecuaciones (4) y (5) son iguales.

Tomando esto en consideración, los miembros izquierdo y derecho de la ecuación (5) pueden sustraerse de los correspondientes de la ecuación (4), llegándose a la siguiente expresión:

Si se mide la respuesta a cuatro frecuencias distintas (2 ≤ p ≤ 5) además de una frecuencia de referencia, ω₁, es posible escribir una versión ampliada de la ecuación (6) de la siguiente manera:

donde las matrices A, B, P y Q de dimensiones 4 × 4, se definen como:

Como las matrices P y Q contienen únicamente información sobre la respuesta medida y las frecuencias de excitación, pueden determinarse directamente de los resultados de las pruebas. Contrariamente, las matrices A y B dependen de las matrices de masa, amortiguamiento y rigidez del sistema, que son desconocidas.

Usando la ecuación (7) es posible establecer la siguiente igualdad:

Por otro lado, con base en las definiciones dadas en las ecuaciones (8) y (9), las matrices de valores y vectores característicos del sistema, Λ y Ψ respectivamente, se relacionan con las matrices A y B mediante:

Las ecuaciones (12) y (13) pueden emplearse para establecer una relación directa entre los resultados de las pruebas, contenidos en las matrices, P y Q y los parámetros modales del sistema. El uso combinado de estas ecuaciones resulta en:

Esta ecuación es de la forma TΨ = ΨΛ, que corresponde a un problema clásico de valores y vectores característicos de una matriz cuadrada, T. Por lo tanto, las matrices de frecuencias naturales complejas y de formas modales del sistema se pueden determinar al calcular los valores y vectores característicos del producto PQ⁻¹. Este producto a su vez se obtiene de las FRFs del sistema medidas a cinco frecuencias de excitación diferentes.

Es posible utilizar más de cinco frecuencias de medición para el cálculo de los parámetros modales (p > 5), de manera que se consideren frecuencias adicionales del intervalo de pruebas. En estos casos las matrices P y Q son, en general, rectangulares y de dimensiones 4 × (p – 1) y la ecuación (12) se escribe:

Donde Q⁺ representa la pseudo-inversa de la matriz Q, que se calcula mediante:

Claramente, la ecuación (12) es sólo un caso particular de la ecuación (15) en el que únicamente se consideran cinco frecuencias de medición. Por esta razón, en el resto del trabajo se utilizará la ecuación (15) para el cálculo de los parámetros modales, que se obtendrán entonces de la solución al siguiente problema de valores y vectores característicos:

Los valores y vectores característicos representan entonces una solución optimizada, con base en un criterio de mínimos cuadrados, en la cual se consideran los datos de respuesta a todas las frecuencias de medición.

Un planteamiento adecuado de este problema requiere que tanto las frecuencias de prueba como los puntos de medición de respuesta se elijan de manera que el producto PQ⁺ dé como resultado una matriz bien condicionada, con el fin de reducir los efectos que el ruido en las mediciones pueda tener sobre los parámetros estimados.

Procedimiento para la caracterización de modos cercanos de vibración

Mediante el procedimiento que se presentó en la sección anterior es posible utilizar mediciones de FRFs para determinar las frecuencias naturales y las razones de amortiguamiento de dos modos cercanos de un sistema, así como los elementos de sus vectores de forma modal correspondientes a dos puntos de medición: un punto de referencia al que se designará como punto “primario” y otro para el cual se desea conocer la vibración relativa al primero y que se designará como punto “secundario”.

La aplicación repetida del procedimiento para diferentes puntos secundarios hace posible conocer las formas modales en más puntos a través del sistema. Sin embargo es importante utilizar el mismo punto primario para todas las pruebas, de manera que pueda calcularse la vibración de todos los demás puntos relativos a éste, y así se obtengan resultados consistentes que permitan definir cada forma modal como un vector con información referente a todos los puntos de interés.

El procedimiento para caracterizar los modos cercanos de vibración inicia con la selección de los puntos y frecuencias de prueba (planeación de las pruebas), continúa con la medición de las FRFs del sistema, el cálculo de sus parámetros modales en dos puntos y finalmente la repetición de los pasos necesarios para determinar las formas modales en un mayor número de puntos, con el fin de obtener una mejor descripción de ellas. A continuación se explica cada paso del procedimiento.

Paso 1 - Planeación de pruebas

El objetivo de la planeación de pruebas es garantizar que las mediciones proporcionen información útil para determinar los parámetros modales del sistema. Durante la planeación se seleccionan el intervalo de frecuencia de las pruebas, el punto de excitación y los puntos primario y secundario(s) en los que se medirán las FRFs.

La planeación de pruebas de vibración, y particularmente de las pruebas encaminadas a la determinación de parámetros modales, está ampliamente documentada. El lector interesado encontrará más detalles al respecto en McConnell (2008) y Ewins (2000).

Para los propósitos del procedimiento que se discute aquí, el punto de excitación y los puntos de medición de respuesta deben elegirse de manera que no coincidan con alguno de los nodos de los modos de vibración que se desea caracterizar, ya que de ocurrir esto la respuesta medida no contendrá componentes de vibración de dichos modos o éstas no serán detectadas por los sensores de vibración.

En ambos casos será imposible determinar los parámetros de todos los modos de interés.

Aunque no existe algún método para determinar con exactitud las ubicaciones de los nodos, es práctica común emplear modelos numéricos para tener una noción de ellas, y así contar con una guía para evadir los nodos durante la selección de puntos de prueba.

Para la selección de puntos de excitación y de medición de respuesta se utilizan las formas modales calculadas numéricamente. La determinación de puntos óptimos se realiza mediante un algoritmo basado en el concepto de «independencia efectiva», introducido por Kammer (1991), cuyo objetivo es seleccionar grados de libertad del sistema, con respecto a los cuales los vectores de forma modal sean (aproximadamente) ortogonales entre sí.

La optimización facilita la tarea de asociar las distintas formas modales con sus frecuencias naturales correspondientes.

Paso 2 - Medición de FRFs

Las FRFs pueden medirse por cualquier método convencional y empleando cualquier técnica de excitación adecuada al sistema que se estudie. El lector interesado podrá encontrar una descripción de estas técnicas en McConnell (2008); Ewins (2000); Brandt (2011); He y Zhu (2001).

Paso 3 - Selección del intervalo de frecuencia de análisis

La selección del intervalo de frecuencia se hace con base en las frecuencias naturales calculadas para el modelo numérico. Alternativamente, puede basarse en la respuesta del sistema a un barrido sinusoidal preliminar en el que se identifiquen de forma aproximada las frecuencias naturales de los modos de interés. El intervalo de frecuencia considerado para el análisis debe ser tal que las componentes predominantes de vibración sean las correspondientes a los dos modos cercanos que se desea caracterizar.

Esto se debe a que el procedimiento que se describió en la sección anterior presupone un sistema de dos grados de libertad, y por consiguiente la existencia de sólo dos modos de vibración. Eligiendo un intervalo de frecuencias de prueba que abarque únicamente las regiones resonantes de los dos modos cercanos de interés es posible reducir la participación relativa de otros modos del sistema y lograr condiciones más acordes con las premisas del procedimiento.

Paso 4 - Selección de datos de vibración

Los datos de vibración son valores de las FRFs para los puntos primario y secundario en cada prueba y están asociados con al menos cinco frecuencias distintas. Las frecuencias deben estar lo suficientemente espaciadas entre sí para que los valores correspondientes de las FRFs sean notablemente distintos (ver siguiente paso). Esto es para evitar la singularidad del producto.

Paso 5 - Cálculo de las matrices P y Q del producto PQ⁺

Una vez que se seleccionaron las frecuencias y los valores de las FRFs que se utilizarán, se determinan las matrices P y Q usando las ecuaciones (10) y (11) respectivamente, y posteriormente la matriz que resulta del producto PQ⁺. Si esta matriz es singular o casi singular (puede emplearse el número de condición de la matriz para evaluar esta característica), deberán repetirse los pasos 4 y 5 de este procedimiento con otras frecuencias de prueba y con los valores de las FRFs correspondientes a estas frecuencias.

Paso 6 - Cálculo de valores y vectores característicos de PQ⁺

Los valores característicos de este producto son las frecuencias naturales complejas del sistema, de las cuales pueden determinarse las frecuencias naturales y las razones de amortiguamiento de cada modo. Los vectores característicos tienen el siguiente formato: rΨ = {_rΨ₁ λ₁, _rΨ₂λ_rrΨ_1rΨ₂}^T, donde los elementos 1 y 3 corresponden al punto primario de medición y los elementos 2 y 4 corresponden al punto secundario. La información que debe retenerse de este vector son los elementos 3 y 4, que representan la porción de desplazamientos de la forma modal. Estos elementos forman un vector de dimensión 2 que debe multiplicarse por un factor de escala adecuado para que su primer elemento siempre sea la unidad. A este proceso se le llama normalización. La información sobre la forma modal para este par de puntos es entonces:

donde los subíndices p y s1 del miembro izquierdo de la ecuación indican que el primer elemento del vector corresponde al punto primario y el segundo al punto secundario utilizado en esta primera prueba.

Paso 7 - Determinación de formas modales en puntos adicionales

Repetir desde el paso 2 con un punto secundario diferente para determinar las formas modales en más de dos puntos.

Las frecuencias naturales y razones de amortiguamientos de los dos modos cercanos son independientes del punto secundario elegido en cada prueba. Sin embargo, los vectores de forma modal cambian al elegirse otro punto secundario. Si en una segunda prueba se determina la siguiente forma modal:

entonces el vector de forma modal para el punto primario y los dos puntos secundarios será:

Si se realizan pruebas para n puntos secundarios, manteniendo siempre el mismo punto primario, entonces se tendrá el siguiente vector de forma modal:

Hasta este punto se han determinado los parámetros modales de dos modos cercanos del sistema. Si existen más pares de estos modos deben elegirse los intervalos de frecuencia apropiados para cada par y repetir el procedimiento que se detalló en los pasos anteriores.

Si en cada prueba se utiliza un intervalo amplio de frecuencia que abarque la totalidad de modos de interés, entonces las mismas FRFs pueden utilizarse para caracterizar todos los pares de modos cercanos, siempre y cuando se sigan las recomendaciones hechas en el paso 3 para la selección de los intervalos de frecuencia para cada par de modos.

En las siguientes secciones se presenta una ampliación del caso de estudio presentado en Vélez et al. (2010), haciendo énfasis en el procedimiento que se presentó anteriormente.

Verificación experimental: pruebas de vibración

Se describen las pruebas que se realizaron para verificar la aplicabilidad del procedimiento que se presentó en la sección anterior a una estructura real.

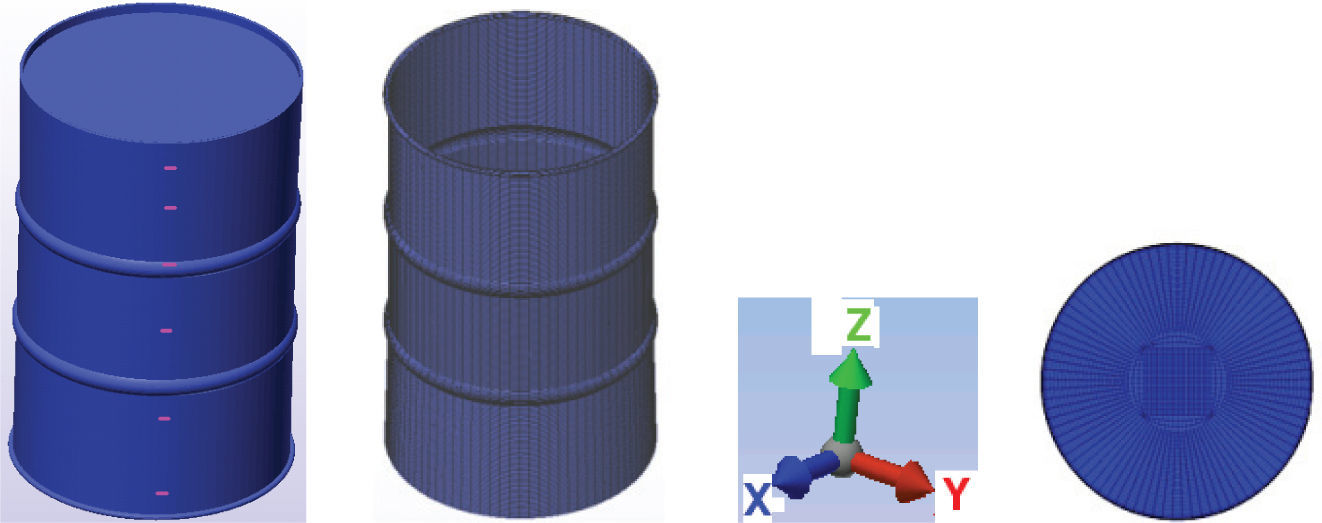
Planeación de pruebas

La planeación de las pruebas experimentales, como se mencionó en la sección anterior, tiene como objetivo garantizar que la información obtenida mediante las pruebas sea la necesaria para determinar los parámetros modales del sistema. Para esto se requiere conocer inicialmente los puntos de medición de FRFs y el intervalo de frecuencia de las pruebas. Los puntos de medición de respuesta deben considerarse de forma tal que se evite coincidencia con nodos de las formas modales de interés. Para conocer esas ubicaciones, en este estudio se utilizó el modelo discreto que se presenta en la figura 2, el cual se analizó por el método de elemento finito mediante el software Algor.

Figura 2.

Geometría empleada para el modelado numérico

Dada la relación de espesor con el resto de dimensiones geométricas del modelo, los elementos usados para el modelo son tipo placa de 4 nodos. El modelo discreto completo consiste de 20076 elementos y 20119 nodos. El comportamiento del material se considera lineal y sin amortiguamiento; además se incluye no-linealidad geométrica en la respuesta. Los cálculos se realizaron sólo para perturbación lineal con el objeto de obtener las formas y las frecuencias naturales modales. Para este fin no se requieren cargas de excitación, resultados dinámicos previos del modelo ni condiciones iniciales de movimiento.

Tabla 1.

Consideraciones para el modelo numérico

Tipo de elemento	Placa
Material	Acero rolado en fréo (AISI 1018)
Densidad de masa	7870 Kg/m^3
Módulo de Young	2.05 × 1011N/m^2
Módulo cortante	8×10^10 N/m^2
Relación de Poisson	0.29

El modelo representa al tanque montado en una suspensión suave, la cual emula la suspensión empleada en las pruebas experimentales que se muestran en la figura 3a. No se impusieron restricciones de movimiento al modelo numérico (montaje libre).

Figura 3.

Pruebas de vibración: a) montaje, b) puntos óptimos para excitación y para medición de respuesta, c) instrumentación

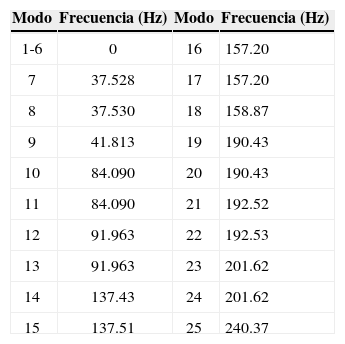
Se calcularon 25 formas modales, las primeras seis de las cuales corresponden a modos rígidos de la estructura y no se consideran en el estudio de identificación de modos cercanos. Las restantes son las que se presentan en la figura 4; las frecuencias naturales obtenidas del modelo discreto se presentan en la tabla 2.

Figura 4.

Formas modales calculadas

Tabla 2.

Frecuencias naturales del modelo numérico

Modo	Frecuencia (Hz)	Modo	Frecuencia (Hz)
1-6	0	16	157.20
7	37.528	17	157.20
8	37.530	18	158.87
9	41.813	19	190.43
10	84.090	20	190.43
11	84.090	21	192.52
12	91.963	22	192.53
13	91.963	23	201.62
14	137.43	24	201.62
15	137.51	25	240.37

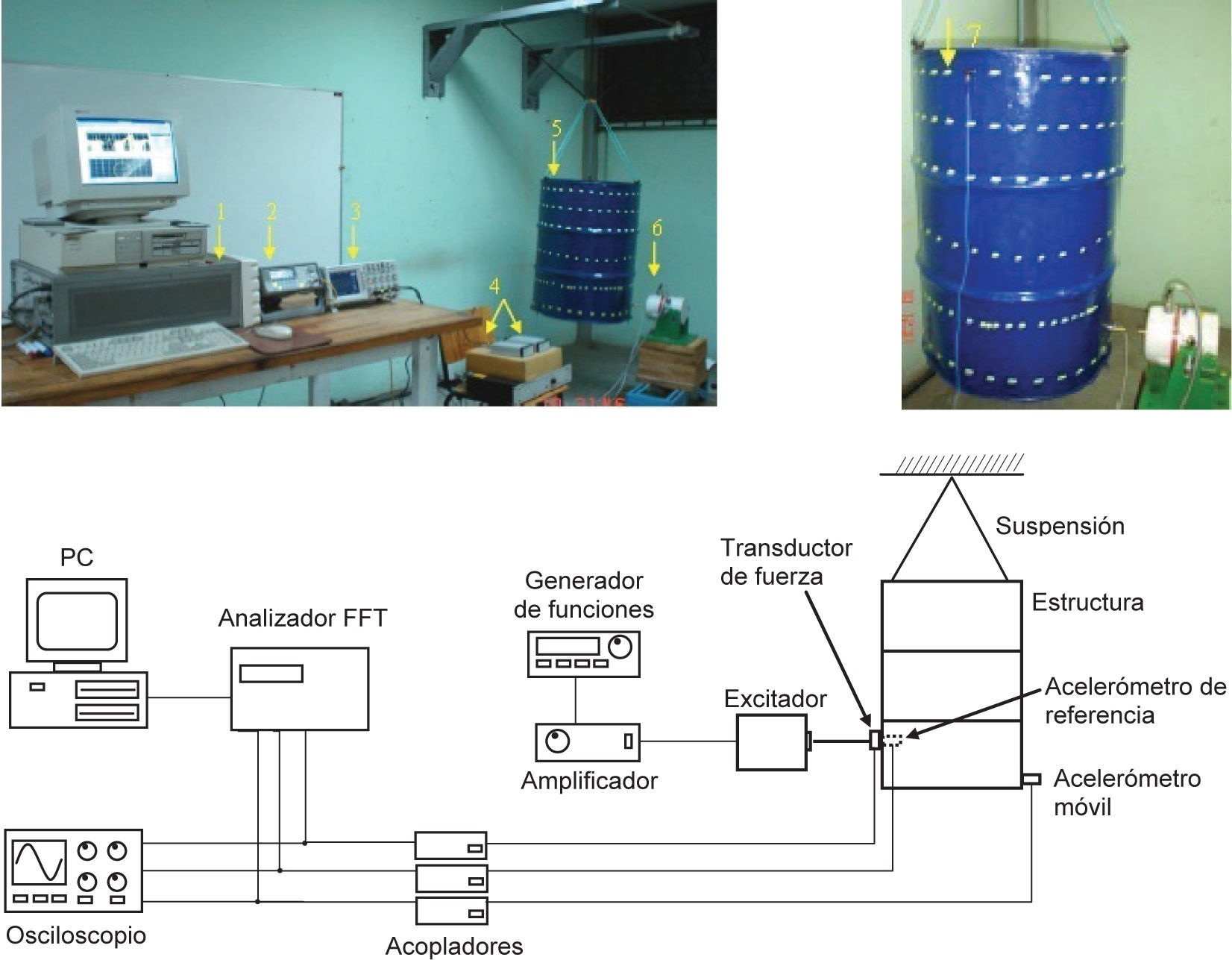
Las formas modales que se calcularon con el modelo discreto son la base para determinar los puntos óptimos de excitación y de medición de respuesta. Para este fin se empleó el criterio de independencia efectiva que se describió en el paso 1 del procedimiento para la caracterización de modos cercanos de vibración. En la figura 3b se observa el montaje de la estructura con el dispositivo de excitación montado sobre el punto óptimo de excitación y los puntos de medición de respuesta se encuentran señalados con marcas de color claro sobre la estructura. En la figura 3c se muestra un esquema de la instrumentación y el montaje que se utilizó para las pruebas.

Las frecuencias naturales que se obtuvieron del modelo se utilizaron para determinar el intervalo de frecuencias de prueba. Se eligió el intervalo de 0-170 Hz que abarca las frecuencias naturales de tres pares de modos cercanos y de cuatro modos adicionales.

Medición de FRFs

Se realizaron pruebas de barrido con excitación sinusoidal, en las que se obtuvo la respuesta de la estructura para el intervalo de frecuencias que abarca las resonancias de los primeros 10 modos. En la figura 3a se muestra la instrumentación empleada en las pruebas. La señal de excitación proviene de un generador de funciones (2) marca Agilent, modelo 33120A, que proporciona una señal sinusoidal de frecuencia variable a un amplificador de potencia, marca LDS, modelo PA-1OOE, el cual a su vez alimenta el excitador electromagnético (6) marca LDS, modelo V406. El excitador se utiliza para aplicar fuerzas sinusoidales a la estructura de prueba (5) a través de una varilla delgada de conexión. La fuerza de excitación se mide con un transductor tipo ICP marca Kistler, modelo 9712A500, y la respuesta de la estructura se mide con dos acelerómetros tipo ICP (7) marca Kistler, modelo 8628B50: uno fijo al punto primario, que es en el que se aplica la excitación, y otro que se reubica en cada prueba a un nuevo punto secundario que se toma del conjunto de puntos seleccionados en la etapa de planeación.

Las señales de los acelerómetros y del transductor de fuerza se filtran y se amplifican por medio de acopladores electrónicos (4) marca Kistler, modelo 5118A, y la señal acondicionada se alimenta a un osciloscopio (3) marca Tektronix, modelo TDS2004, para monitoreo constante de la respuesta, así como a un analizador digital de señales tipo FFT (1) marca Hewlett-Packard, modelo 3566A, conectado a una computadora personal HP Vectra 486. El analizador convierte la señal de vibración del dominio del tiempo al de la frecuencia y despliega diagramas de amplitud y ángulo de fase contra frecuencia de excitación. Esta información es la que se utiliza para iniciar la estimación de parámetros modales.

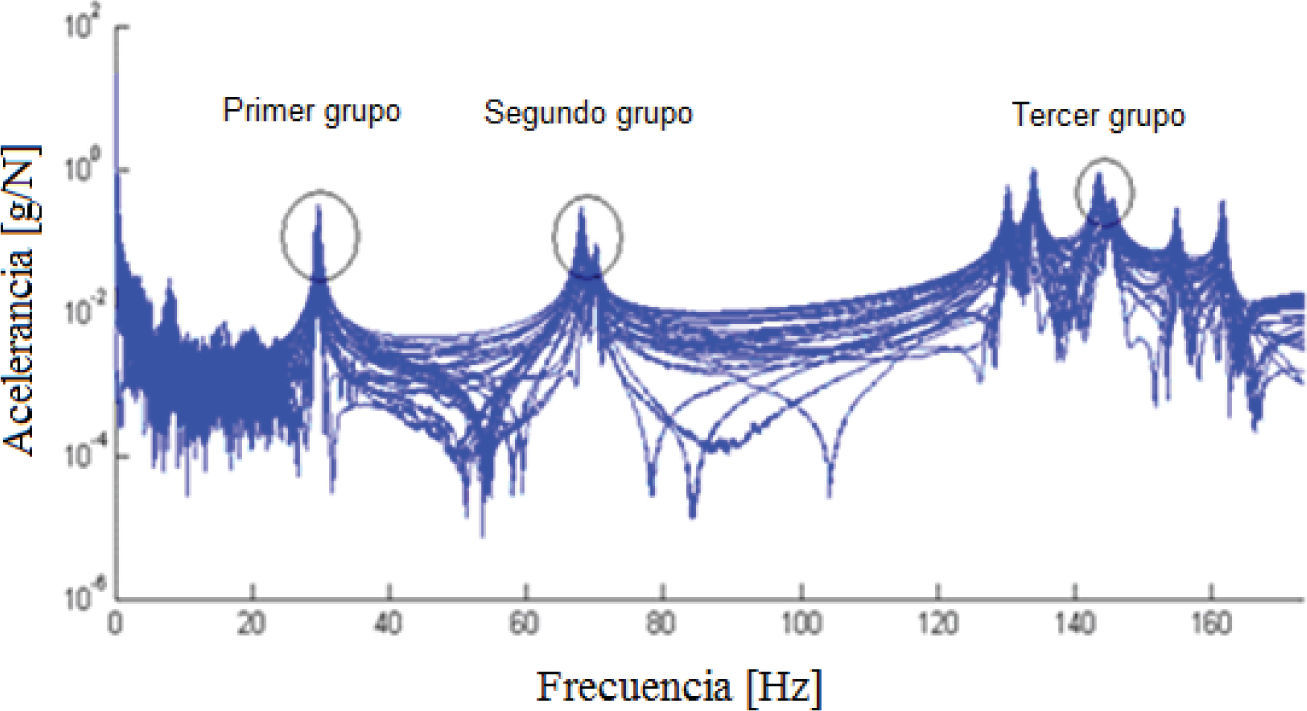
Para la validación experimental del procedimiento de caracterización modal se midieron FRFs en 30 puntos de la estructura. En la figura 5 se presentan las FRFs (acelerancias), con el objetivo de evidenciar las frecuencias naturales de la estructura real y la existencia de modos cercanos.

Figura 5.

Grupos de modos cercanos de la estructura de prueba

Discusión y análisis de resultados

El objetivo del análisis de las FRFs fue determinar los parámetros modales de los modos que forman el primer grupo (figura 5). Sus resonancias en las FRFs medidas aparecen indicadas como 1A y 1B en la figura 6. Aunque no es posible identificar visualmente las frecuencias naturales de dos modos cercanos a partir de un diagrama de Bode, las de estos dos modos parecen estar ubicadas entre los 29 y los 30 Hz. En cada FRF, las alturas de los picos correspondientes a cada modo son funciones de su forma modal en el punto de medición de la FRF.

Figura 6.

Resonancias de los modos 1A y 1B

Efectos de ruido e incertidumbre en las mediciones

La técnica de barrido sinusoidal reduce el efecto de ruido en las estimaciones de frecuencia, amplitud y ángulo de fase de las señales de vibración, en comparación con el caso de otro tipo de prueba como las de excitación por impacto o de excitación con ruido aleatorio. Esto se debe a que para cada frecuencia los parámetros de vibración se obtienen del ajuste por mínimos cuadrados de una función armónica a la señal correspondiente a varios ciclos de vibración. En este proceso el ruido aleatorio que está presente en los diferentes ciclos tiende a cancelarse, por lo que en el ajuste predomina la porción repetitiva de la señal, que está asociada con la vibración de la estructura.

En la figura 5 puede observarse que el efecto del ruido disminuye hacia el lado alto del espectro de frecuencia, lo cual es típico en señales de aceleración, cuya amplitud es proporcional al cuadrado de la frecuencia de vibración. Contrariamente, la razón de amplitud de vibración a nivel de ruido es más desfavorable en el lado bajo del espectro. Sin embargo, como puede obser varse en la figura 5, aún a frecuencias inferiores a las correspondientes al primer par de modos cercanos, las fluctuaciones en las FRFs causadas por el ruido en las mediciones están alrededor de dos órdenes de magnitud por debajo del nivel de vibración resonante pico. Debido a que los parámetros modales se identifican a partir de la respuesta en dicha región, la incertidumbre en los valores de las FRFs en esta región debida a ruido en las mediciones es del orden del 1-2%.

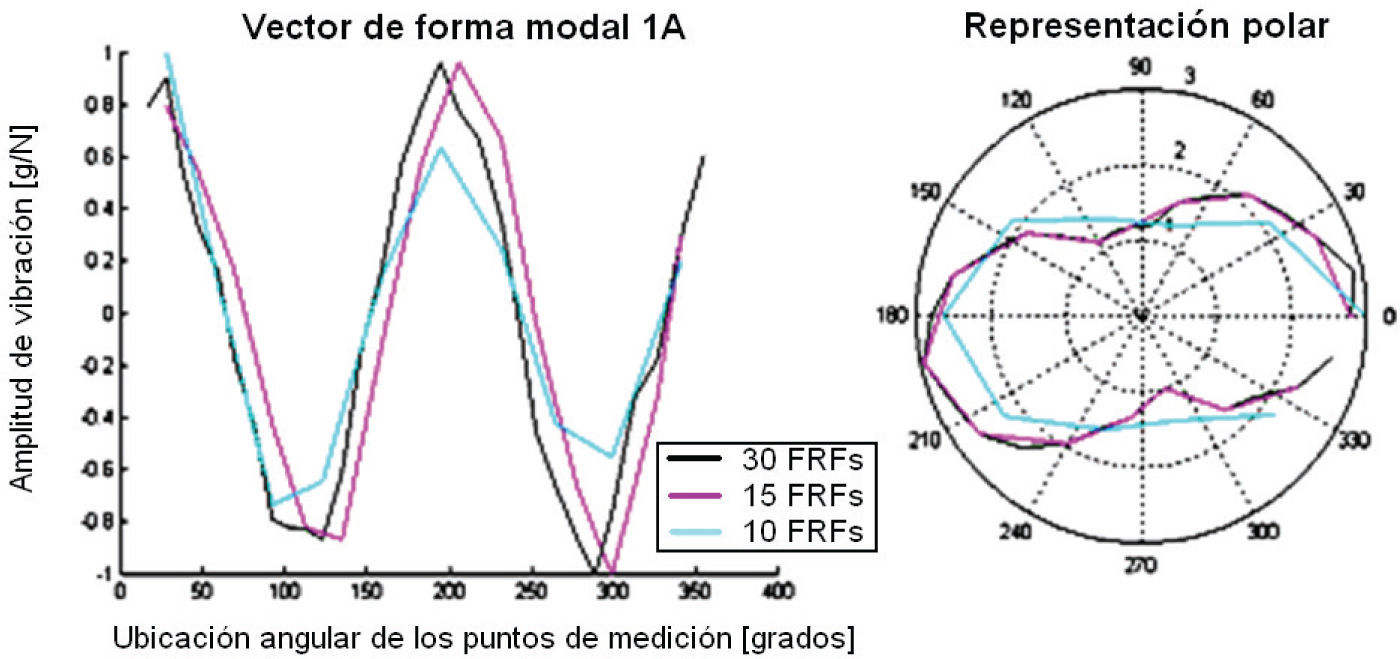
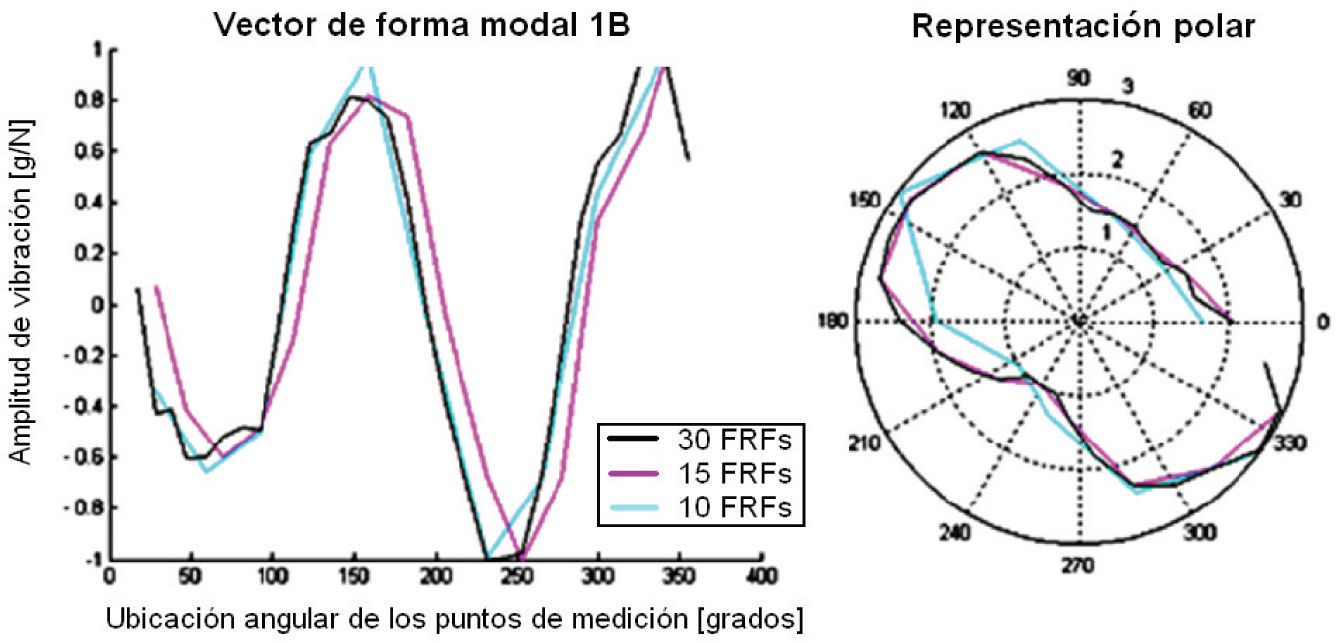
Estimación de frecuencias naturales y amortiguamientos

Las frecuencias naturales y los amortiguamientos de los modos 1A y 1B se determinaron siguiendo los pasos del procedimiento descrito en secciones anteriores. La estimación de estos parámetros puede realizarse con un mínimo de dos FRFs, sin embargo, para estudiar la relación entre las estimaciones y el número de FRFs empleadas en el proceso, éste se repitió usando 10, 15 y 30 FRFs en cálculos independientes de las matrices P y Q de la ecuación (17). Las frecuencias naturales y razones de amortiguamiento para los dos modos se obtuvieron a partir de dicha ecuación en los tres casos y se presentan en la tabla 3. Como se observa, el número de FRFs no afecta significativamente las estimaciones de los parámetros.

Tabla 3.

Frecuencias naturales y razones de amortiguamiento

	Modo 1A		Modo 1B
Número de FRFs	wn [Hz]	z	wn [Hz]	z
10	29.164	0.0033	29.795	0.0030
15	29.213	0.0034	29.815	0.0031
30	29.208	0.0036	29.812	0.0031
Modelo numérico	37.528	-	37.530	-

La discrepancia entre las frecuencias naturales y las razones de amortiguamiento de los modos 1A y 1B son relativamente pequeñas y reflejan el hecho de que la estructura no es perfectamente axisimétrica. La no-uniformidad del material, la presencia de pequeñas deformaciones geométricas (abolladuras) en la lámina y las posibles fluctuaciones en el espesor de la capa de pintura aplicada a la estructura, por ejemplo, pueden causar variaciones de los parámetros modales como las observadas en las pruebas.

Las diferencias entre los parámetros modales obtenidos numéricamente y los obtenidos mediante las pruebas están relacionadas con el proceso de modelado. El modelo numérico se basa en la suposición de que el material es homogéneo y que la estructura es perfectamente cilíndrica. Más aún, para especificar las propiedades del material se utilizan fuentes de información estándar como tablas de ingeniería o especificaciones del fabricante, pero no se toman en cuenta cambios como los debidos a envejecimiento o a endurecimiento por deformación, ni los efectos de abolladuras en la superficie de la estructura. En el modelo numérico también se considera típicamente una suspensión idealizada (en el caso presente un montaje libre), mientras que las pruebas se realizan con una suspensión de flexibilidad finita. Por estas razones, los resultados obtenidos con el modelo numérico se utilizan solamente para formarse un primer criterio sobre el comportamiento de la estructura en el intervalo de frecuencia de interés. Es práctica común corregir estos modelos empleando la información obtenida de pruebas de vibración, las cuales están exentas de las suposiciones mencionadas anteriormente. Las frecuencias naturales pueden utilizarse para la corrección de las propiedades elásticas e inerciales del modelo numérico, y para incorporarle las características de amortiguamiento obtenidas experimentalmente. Este proceso de refinamiento del modelo no se abordará aquí, pero el lector interesado podrá encontrar más información al respecto en Sedlar et al. (2012); Mottershead y Friswell (1993 y 1995); Wang et al. (2011).

Estimación de formas modales

La estimación de formas modales a partir de datos experimentales se limitó a los puntos de prueba más cercanos al borde circunferencial en el lado abierto de la estructura, que es el anillo inferior en las figuras 3a y 3b. Esto es porque en dichos puntos se observan las mayores amplitudes de vibración y por lo tanto las mediciones presentan una menor influencia porcentual del ruido en las señales provenientes de los acelerómetros. Asimismo, para estos puntos se obtienen las formas modales que son características de sistemas axisimétricos y cuasi-axisimétricos (Blevins, 1995), las cuales consisten en lóbulos cuyo número se incrementa conforme aumenta la frecuencia natural. Esto lo confirman los resultados numéricos que se presentan en la figura 4.

En las figuras 7 y 8 se presentan las formas modales obtenidas de la solución de la ecuación (17), usando 10, 15 y 30 FRFs medidas, respectivamente. Aunque se aprecia que las formas modales no son idénticas para los tres casos, la apariencia general de las curvas y su orientación para cada uno de los modos no varía significativamente con un incremento en el número de las FRFs consideradas.

Figura 7.

Representaciones cartesiana y polar del modo 1A (1er. grupo)

Figura 8.

Representaciones cartesiana y polar del modo 1B (1er. grupo)

Naturalmente, las curvas correspondientes a los casos con más FRFs presentan un mayor grado de detalle debido a que se trazan con un mayor número de puntos (uno por FRF).

Las formas modales experimentales para los modos 1A y 1B coinciden con las predicciones obtenidas para los modos 7 y 8 usando el modelo numérico: en ambos casos son curvas de dos lóbulos con una orientación que difiere 45 grados entre los dos modos cercanos.

En la tabla 4 se comparan las formas modales numéricas y experimentales correspondientes a los dos modos cercanos que se caracterizaron. En la columna de resultados numéricos los esquemas indican con círculos las líneas de desplazamiento nulo para ambos modos y con elipses las formas modales escaladas arbitrariamente para su mejor visualización.

Tabla 4.

Comparación de formas modales

MODO	NUMÉRICA	EXPERIMENTAL
1A
1B

Las formas modales obtenidas numérica y experimentalmente consisten en desplazamientos radiales de la estructura. Estos desplazamientos son funciones armónicas de la posición angular de cada punto, medida en dirección circunferencial sobre el plano que contiene los puntos de medición. Este es un resultado común en estructuras axi-simétricas de distintos tipos, incluyendo las de geometría cilíndrica como la estudiada aquí, de manera que los resultados obtenidos son consistentes con las predicciones teóricas (Dobson, 1987).

Conclusiones

Se presentó un procedimiento para la estimación de los parámetros modales de modos cercanos de vibración. Este procedimiento hace posible la estimación simultánea de los parámetros de dos modos cercanos, por lo que no requiere que cada resonancia esté dominada por un solo modo, como es el caso para los métodos convencionales.

El procedimiento se basa en la suposición de que en la región de resonancia que abarca un par de modos cercanos, la estructura puede modelarse como un sistema de dos grados de libertad. Utilizando mediciones de su respuesta vibratoria en esta región es posible establecer un problema estándar de valores y vectores característicos, cuya solución son las frecuencias naturales complejas y las formas modales de los dos modos cercanos.

Procedimiento de cálculo

Se demostró analíticamente que para identificar simultáneamente los parámetros de dos modos cercanos son necesarias las mediciones de la respuesta (FRFs) para al menos cinco frecuencias de excitación distintas. El uso de más mediciones hace posible optimizar las estimaciones por el criterio de mínimos cuadrados. Las frecuencias para la estimación de los parámetros modales deben elegirse de manera que el producto PQ+ tenga un número de condición lo más bajo posible. Para la estimación se utilizan las diferencias entre las respuestas medidas a diferentes frecuencias de excitación.

Para la estimación de formas modales es útil incorporar más mediciones, ya que el número de puntos con los cuales se define la forma modal crece con el número de mediciones empleadas para el cálculo. Sin embargo, el utilizar pocas mediciones no introduce errores significativos en las formas modales calculadas para los puntos de medición.

Validación experimental

Se demostró a través de pruebas con una estructura real sencilla que el procedimiento de cálculo propuesto es útil para determinar los parámetros de modos con un traslape significativo de sus regiones de resonancia.

Se estableció un procedimiento práctico para la aplicación de los resultados de esta investigación al estudio de estructuras reales. Dicho procedimiento abarca: la planeación de pruebas, la medición de FRFs, la selección de intervalos de frecuencia para el análisis, la selección de datos de vibración, el cálculo de matrices auxiliares para el cálculo de los parámetros modales, la determinación de dichos parámetros y el refinamiento de los vectores de forma modal.

La naturaleza de las formas modales obtenidas experimentalmente son consistentes con la predicha en la literatura para estructuras axisimétricas o cuasi-axisimétricas como la que se empleó en la parte experimental de este trabajo.