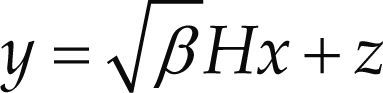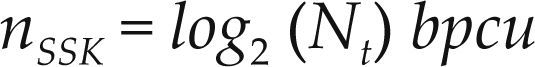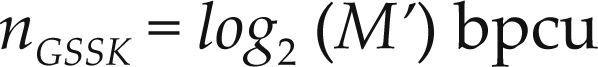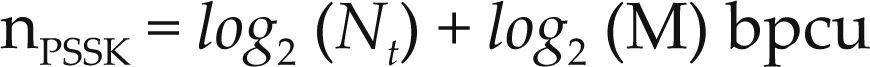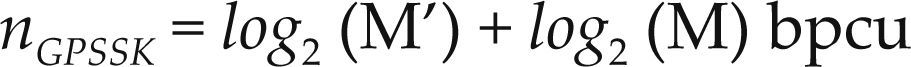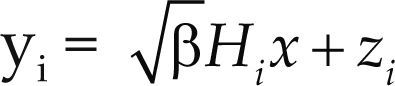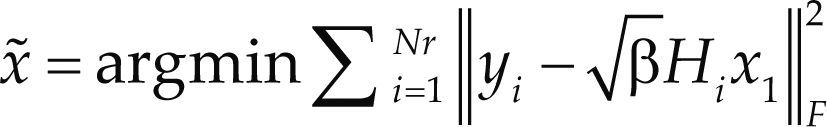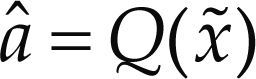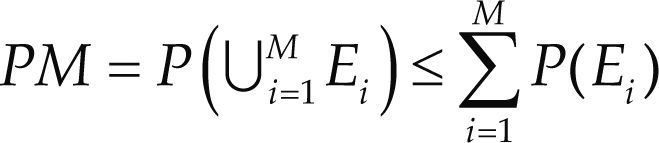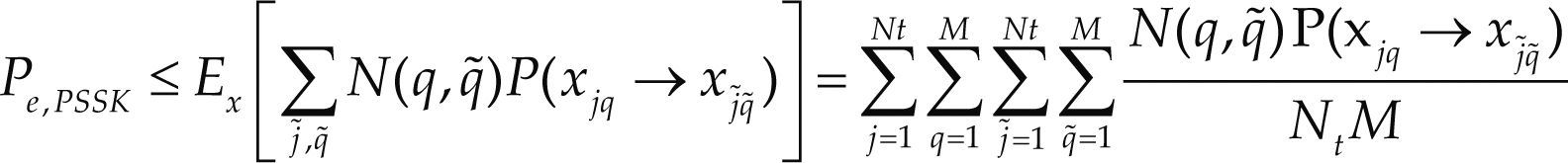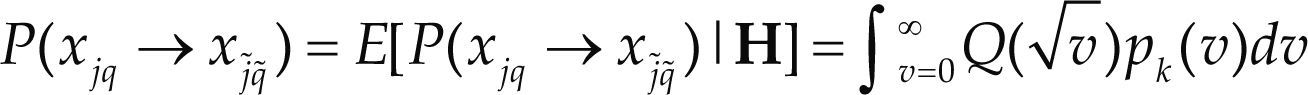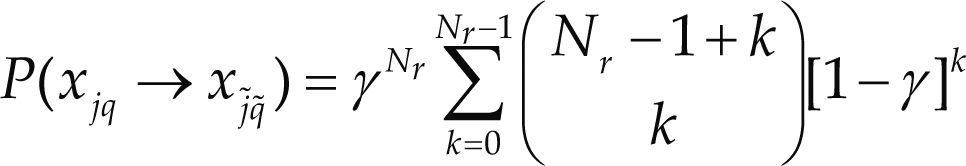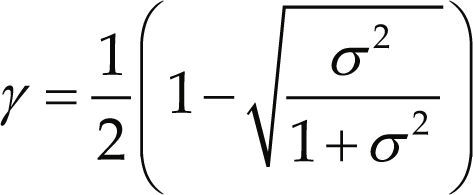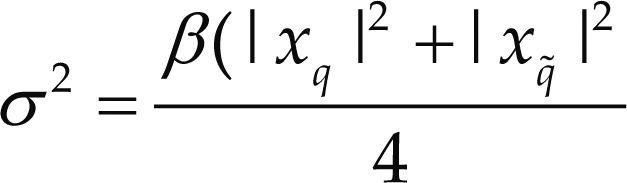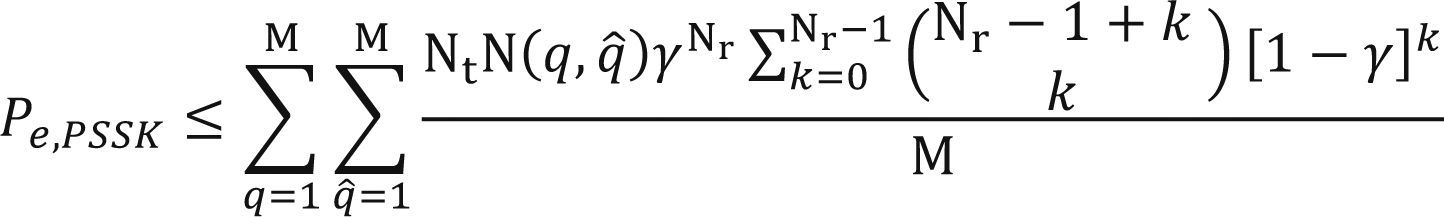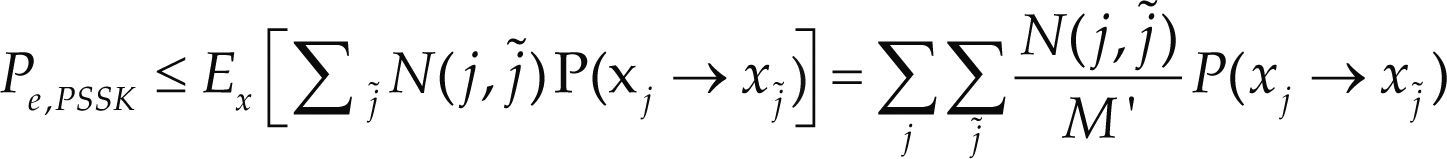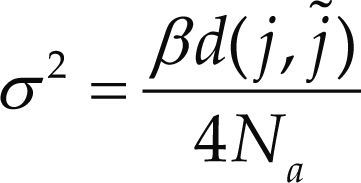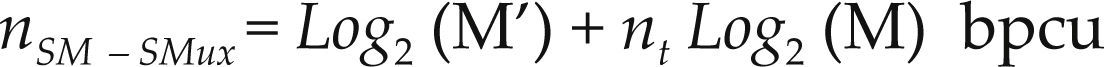En este trabajo se presenta un marco general para el análisis de los esquemas de transmisión Multiple Input-Multiple Output (MIMO) monousuario con modulación espacial (SM). Se presenta un análisis comparativo de los cuatro esquemas SM básicos considerando el desempeño en tasa de bits erróneos (BER), complejidad en la detección, eficiencia espectral y cantidad total de antenas transmisoras utilizadas. Los resultados muestran que los sistemas que utilizan un solo transmisor RF tienen un mejor desempeño mientras que las versiones generalizadas tienen una mejor eficiencia espectral. Se muestra que todos los esquemas SM tienen una complejidad de detección menor en comparación con el esquema convencional de multiplexaje espacial (SMux) que usa cancelación sucesiva de interferencias (SIC), sin embargo la cantidad de antenas de transmisión utilizadas para los sistemas SM es significativamente mayor que la requerida por el esquema convencional SMux. Adicionalmente se analiza un esquema que combina las técnicas SM y SMux. Estos resultados pueden ser útiles como criterios de diseño en sistemas de comunicaciones inalámbricas de la siguiente generación.
This paper introduces a general framework for the analysis of single user Multiple Input-Multiple Output (MIMO) transmission schemes using Spatial Modulation (SM). We present a comparative analysis for the four basic SM schemes considering: Bit Error Rate (BER) performance, detection complexity, spectral efficiency and total amount of transmit antennas used. Results show that single RF chain schemes have better performance while generalized versions have better spectral efficiency. Results also show that all SM schemes have reduced detection complexity when compared to the conventional Spatial Multiplexing/Successive Interference Cancelation (SMux/SIC) scheme, however the amount of transmit antennas used for SM schemes is significantly higher than the required by the conventional SMux scheme. Additionally, a scheme which combines SM and SMux techniques is analyzed. These results can be useful as design criteria for the next generation of wireless communication systems.
La creciente demanda de servicios de comunicación inalámbrica exige de las futuras redes mayor capacidad de transmisión y mejores eficiencias espectral y energética. Una de las tecnologías ampliamente reconocida para la implementación de las futuras redes se conoce como Multiple Input-Multiple Output (MIMO). Esta técnica consiste en el uso de múltiples antenas tanto en el transmisor como en el receptor.
Recientemente una nueva técnica de modulación conocida como modulación espacial (SM) se propone en la implementación de sistemas de transmisión MIMO. La idea básica detrás de la modulación espacial es que se considera a un arreglo de antenas transmisoras como una constelación espacial, donde cada antena transmisora (Tx) representa un punto de esa constelación. Idealmente, desde cada antena Tx hasta cada antena receptora (Rx) existe la única “huella de canal”, que identifica a ese enlace, por lo tanto, asumiendo que el canal cambia de forma relativamente lenta y que el receptor conoce el estado del canal, el receptor puede determinar cuál es la antena Tx que se encuentra activa en un momento dado. En un esquema de transmisión SM básico, únicamente una antena Tx se activa en un tiempo dado. Dependiendo del símbolo que se desee transmitir se activará una antena diferente, de esa manera, adicionalmente a la transmisión de un símbolo modulado en amplitud y fase (símbolo QAM), se trasmite información en la constelación espacial.
En general, se les denomina esquemas SM mono- usuario a aquellos sistemas que utilizan la modulación espacial para trasmitir información desde un único transmisor hacia un único receptor. El esquema SM más simple se denomina Spatial Shift Keying (SSK), (Jeganathan et al., 2009). Este esquema utiliza el único transmisor RF y solo usa la constelación espacial para modular, sin embargo, una desventaja del esquema SSK es que el tamaño de la constelación espacial se determina por la cantidad de antenas Tx, esta característica impone un límite en las implementaciones prácticas para constelaciones grandes. Para superar esta limitante se han propuesto versiones generalizadas a los esquemas SM, en las cuales varias antenas de transmisión se activan simultáneamente. Adicionalmente, la capacidad del sistema se puede incrementar al considerar la transmisión de símbolos QAM en cada antena transmisora activa. Estos esquemas extienden la constelación espacial a una constelación tridimensional amplitud-fase-espacio (AFE), lo que los hace más eficientes espectralmente. En la tabla 1 se muestra una clasificación de los sistemas SM-MIMO monousuario.
Como se observa en la tabla 1, las técnicas que solo utilizan modulación espacial son: Space Shift Keying (SSK) y SSK generalizado (GSSK), mientras que las técnicas que utilizan una constelación AFE son; Phase Space Shift Keying (PSSK) la cual se conoce como SM, y PSSK generalizado (GPSSK). Adicionalmente existen propuestas de sistemas de transmisión que combinan los esquemas SM con los sistemas convencionales que utilizan multiplexaje espacial (SMux).
Las técnicas de transmisión SM se consideran como una alternativa en el diseño de futuros sistemas de comunicación MIMO (Cheng et al., 2014), por lo que actualmente existe un gran interés en el estudio y desarrollo de sistemas de transmisión SM-MIMO. El curso actual de las investigaciones sobre el tema, abarca en su gran mayoría aspectos de optimización de los esquemas de transmisión monousuario, sin embargo, existen todavía aspectos del sistema que debido a su complejidad no se investigan completamente, en particular, cuando se trata de esquemas multiusuario y multi-célula (Di Renso et al., 2014).
En este artículo se presenta un análisis comparativo de los esquemas SM-MIMO monousuario. Con este análisis se pretende esclarecer las ventajas y desventajas que tiene cada una de las técnicas SM MIMO básicas comparadas entre ellas. Se presenta un modelo general para representar los esquemas SM-MIMO básicos y se compara el desempeño en tasa de bits erróneos (BER), la complejidad de los detectores, la eficiencia espectral y el número de transmisores de RF de las cuatro técnicas básicas SM y del esquema convencional SMux que utiliza cancelación sucesiva de interferencias (SIC). Adicionalmente se analiza el esquema que combina ambas técnicas. Finalmente se discuten las tendencias en el área.
En este artículo se utiliza la siguiente notación. Las letras en negrita y minúsculas denotan vectores, mientras que las letras en negrita y mayúsculas denotan matrices. Las notaciones (·)T, (·)H, (:) y ∥·∥F denotan transposición, transpuesta conjugada, coeficiente binomial y norma de Frobenius de un vector o matriz. CN(m,σ2) se utiliza para representar la distribución gaussiana compleja de una variable aleatoria, teniendo distribuciones independientes en la parte real e imaginaria denotados por N(m, σ2/2), con media m y varianza σ2/2, P(·) representa la probabilidad de eventos. La esperanza matemática respecto a x se denota como Ex[·].
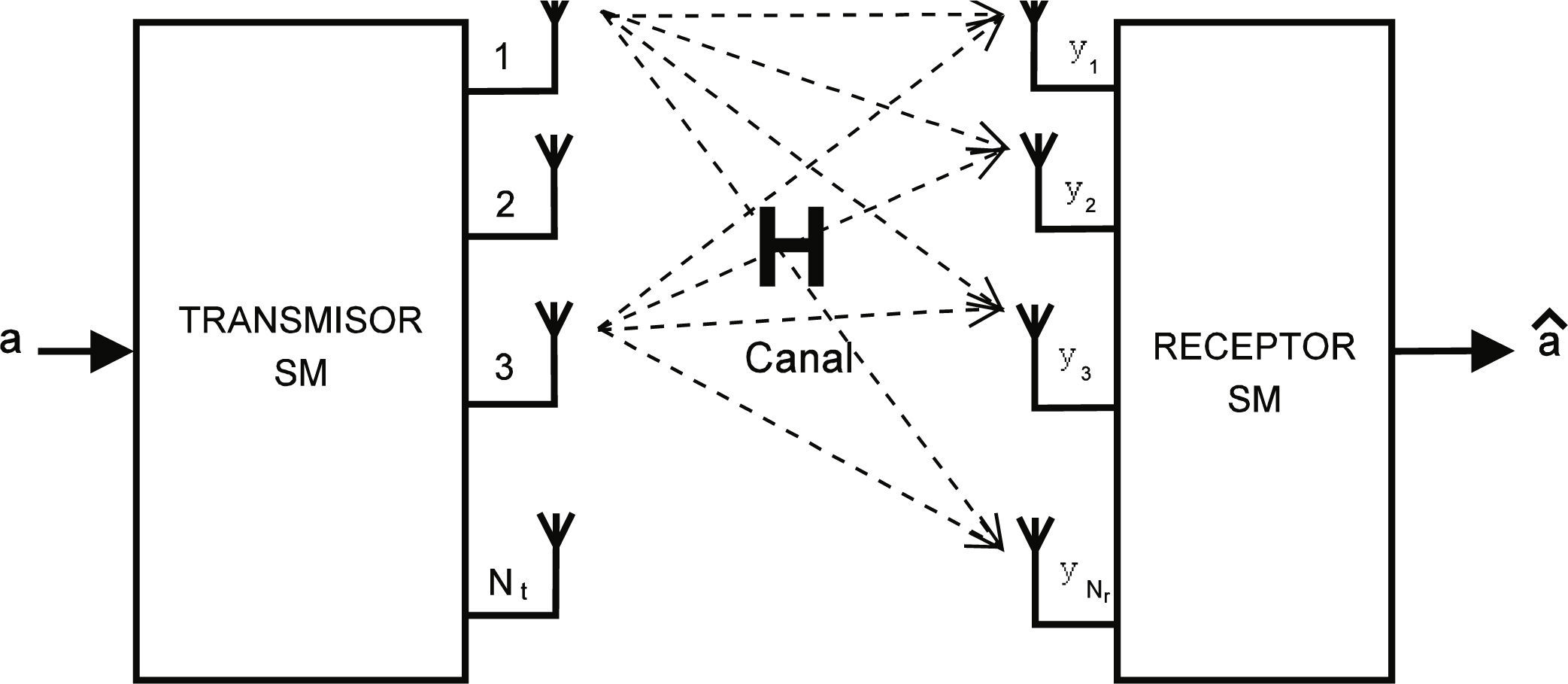
Modelo de sistemaLa figura 1 muestra el modelo de sistema para los esquemas SM-MIMO monousuario. El sistema consiste de un enlace inalámbrico MIMO con Nt antenas transmisoras, Nr antenas receptoras y Na antenas activas. El transmisor recibe una secuencia aleatoria de bits a= [a1, a2, ... ak], donde grupos de n bits son mapeados a un vector de constelación x = [x1, x2, ... xNt]T, que indica cuál es la posición de las antenas activas en un momento dado. xi ∈ C es un punto de la constelación que puede ser únicamente espacial, o bien, una constelación C ompuesta AFE. El vector de constelación x se transmite sobre un canal plano H con desvanecimientos tipo Raleigh de dimensiones Nr × Nt. La señal recibida está dada por
Donde
y = [y1, y2,... yNr]T = vector de señales recibidas
z = ruido blanco Gaussiano aditivo o AWGN (Additive White Gaussian Noise)
β = relación señal a ruido o SNR (Signal to Noise Ratio) promedio en cada antena receptora
Se asume que tanto H como z son variables independientes e idénticamente distribuidas (iid) con valores CN (0,1).
En lo sucesivo, independientemente de la cantidad de antenas transmisoras, la potencia total de transmisión está normalizada. Se asume sincronía perfecta entre transmisor y receptor, además de que la información del estado del canal (CSI) se conoce completamente en el receptor.
TransmisiónEn la transmisión cada uno de los cuatro esquemas básicos tiene una regla de asignación diferente. En esta sección se proporcionan ejemplos de reglas de asignación para los cuatro esquemas básicos, considerando tres bits por uso de canal (bpcu).
Spatial Shift Keying (SSK)En SSK (Jeganathan y Ghrayeb, 2009), el dominio espacial es el único utilizado para transmitir información, la cantidad de antenas transmisoras activas en un momento dado es igual a uno (Na= 1), elegida de un total de Nt antenas transmisoras. La cantidad de bits n por uso de canal que este sistema es capaz de transmitir es
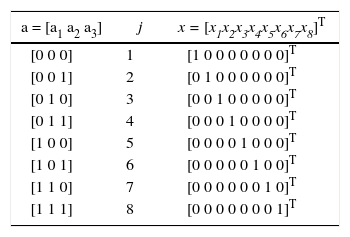
En la tabla 2 se muestra un ejemplo de asignación para el esquema SSK. En este caso se requieren Nt = 8 antenas de transmisión y cada símbolo representa log2(Nt) = 3 bits.
Regla de mapeo para el sistema SSK
| a = [a1 a2 a3] | j | x = [x1x2x3x4x5x6x7x8]T |
|---|---|---|
| [0 0 0] | 1 | [1 0 0 0 0 0 0 0]T |
| [0 0 1] | 2 | [0 1 0 0 0 0 0 0]T |
| [0 1 0] | 3 | [0 0 1 0 0 0 0 0]T |
| [0 1 1] | 4 | [0 0 0 1 0 0 0 0]T |
| [1 0 0] | 5 | [0 0 0 0 1 0 0 0]T |
| [1 0 1] | 6 | [0 0 0 0 0 1 0 0]T |
| [1 1 0] | 7 | [0 0 0 0 0 0 1 0]T |
| [1 1 1] | 8 | [0 0 0 0 0 0 0 1]T |
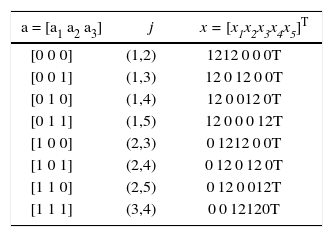
El esquema GSSK (Jeganathan y Ghrayeb, 2008b), es la versión generalizada de SSK. En este caso un número fijo de antenas transmisoras Na se activan simultáneamente de un total de Nt antenas Tx disponibles.
El número de puntos de la constelación espacial M’ se calcula como la combinación donde M’ se elige como M’ = 2k, k entero. Por lo tanto, la cantidad de bits n por uso de canal que pueden transmitirse en GSSK es
En la tabla 3 se muestra un ejemplo de asignación para el esquema GSSK. En este ejemplo se usan Na = 2 antenas activas de un total de Nt = 5 antenas transmisoras disponibles.
Phase Spatial Shift Keying (PSSK)En la literatura se conoce como SM al esquema SSK, el cual transmite simultáneamente un símbolo modulado en amplitud y fase (Mesleh et al., 2006). De acuerdo con la clasificación de la tabla 1, y para evitar confusión, en este artículo se denominó como PSSK a este esquema, reservando el término SM para referirse a la técnica de modulación en general.
En PSSK, el receptor debe detectar tanto el símbolo modulado en amplitud y fase (M-QAM), como el índice de la antena Tx activa. La cantidad de bits n por uso de canal que pueden transmitirse usando esta técnica es
donde M es el orden de la constelación M-QAM. Por ejemplo, cuando se utilizan Nt = 4 antenas Tx, cada antena representa 2 bits, y si se utiliza BPSK (M = 2), se agrega un bit más, por lo que cada símbolo detectado en el receptor representa 3 bits. La tabla 4 muestra un ejemplo de asignación para el esquema PSSK. En este caso, se utilizan 4 antenas transmisoras en combinación con un esquema de modulación BPSK con fases y amplitudes definidas como: ϕ1 = ei0 y ϕ2 = eip. Los valores de xi se definen: xi ∈ {0, ϕ1, ϕ2}.
Regla de mapeo para el sistema PSSK
| a = [a1 a2 a3] | j, símbolo BPSK | x = [x1x2x3x4]T |
|---|---|---|
| [0 0 0] | (1,0) | [e0i 0 0 0]T |
| [0 0 1] | (1,1) | [eπi 0 0 0]T |
| [0 1 0] | (2,0) | [0 e0i 0 0]T |
| [0 1 1] | (2,1) | [0 eπi 0 0]T |
| [1 0 0] | (3,0) | [0 0 e0i 0]T |
| [1 0 1] | (3,1) | [0 0 eπi 0]T |
| [1 1 0] | (4,0) | [0 0 0 e0i]T |
| [1 1 1] | (4,1) | [0 0 0 eπi]T |
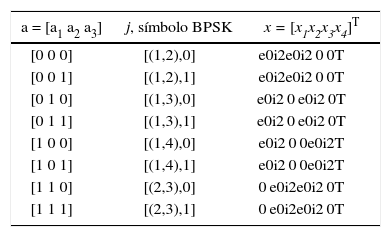
La versión generalizada de PSSK se conoce como Generalized Phase Space Shift Keying (GPSSK), (Ramírez et al., 2011). Al igual que en GSSK, Na es el número fijo de antenas de transmisión activas. La cantidad de bits n por uso de canal que se puede transmitir usando esta técnica es
donde M′≤NtNa y M′ se elige como M’ = 2k, k entero y M es el tamaño de la constelación M-QAM.
La tabla 5 muestra un ejemplo de asignación para GPSSK, que utiliza Na = 2 y Nt = 4 en combinación con un esquema de modulación BPSK con fases y amplitu-des definidas como: φ1=ei02yφ1=eiπ2 . Los valores de - xi se definen: xi ∈ {0, ϕ1, ϕ2}. Todas las antenas trans-miten el mismo símbolo ϕ1. Como en todos los casos, se utilizó una transmisión de 3 bpcu.
Regla de mapeo para el sistema GPSSK
| a = [a1 a2 a3] | j, símbolo BPSK | x = [x1x2x3x4]T |
|---|---|---|
| [0 0 0] | [(1,2),0] | e0i2e0i2 0 0T |
| [0 0 1] | [(1,2),1] | e0i2e0i2 0 0T |
| [0 1 0] | [(1,3),0] | e0i2 0 e0i2 0T |
| [0 1 1] | [(1,3),1] | e0i2 0 e0i2 0T |
| [1 0 0] | [(1,4),0] | e0i2 0 0e0i2T |
| [1 0 1] | [(1,4),1] | e0i2 0 0e0i2T |
| [1 1 0] | [(2,3),0] | 0 e0i2e0i2 0T |
| [1 1 1] | [(2,3),1] | 0 e0i2e0i2 0T |
Consideremos la matriz de canal H formada por vectores H = [H1; H2; ... HNr], donde cada vector fila Hi contiene el valor de todos los canales para cada antena receptora. Entonces la señal recibida por la -ésima antena receptora es
donde el vector de transmisión x se define diferente para cada uno de los esquemas básicos e invariablemente incluye la posición de la o las antenas transmisoras. En el receptor, cada antena receptora calcula el vector síndrome Si,l=∥yi−βHix1∥F2, donde x1 ∈ C es un símbolo de la constelación AFE. La estimación ML se lleva a cabo después de sumar los síndromes de cada antena receptora de la siguiente manera
Finalmente, la detección se realiza por
donde Q(·) es la función de deslizamiento, que determina un punto en la constelación AFE.
Análisis de desempeñoExisten diversos métodos analíticos para el cálculo de la probabilidad de error para los diferentes esquemas SM-MIMO monousuario. Estos métodos se proponen por Di Renso et al. (2011); Jeganathan et al. (2008a), Mesleh (2008) e Ikky y Mesleh (2012), entre otros. En general, la probabilidad de error para diversos esquemas SM se puede derivar utilizando la técnica de cota superior.
Consideremos la detección como el problema de decidir entre M señales ortogonales. Si Ei representa el evento: C(r, si) > C (r, sl), donde C(·) es la correlación entre la señal recibida r y la señal sm; m = 2, 3 ... M, i ≠ l, entonces la probabilidad de error de símbolo se puede calcular como en la ecuación 9 (Proakis, 2001, p. 263-264)
Utilizando este principio, la probabilidad de error en bits para el esquema PSSK se acota como la suma de las contribuciones de cada antena y cada símbolo de la siguiente manera (Jeganathan et al., 2008b)
donde los índices j y q representan el índice de la antena transmisora activa, el símbolo de la constelación M-aria. Nq,q˜ el número de bits erróneos entre el símbolo xq y xq˜, y P(xjq → xj˜q˜) denota la probabilidad de error de una pareja (PEP) para decidir por el vector d ado que se transmite xjq. El PEP condicional considerando el canal de ruido gaussiano es P (xjq → xj˜q˜) |H = Qυ, donde v = |h|2Eb/N0 es la energía efectiva del ruido. Considerando el canal con desvanecimientos H, la probabilidad de error total se calcula como la esperanza matemática del PEP condicional, es decir
donde pk(v) es la función densidad de probabilidad (pdf) de la variable aleatoria ya que h tiene una distribución Rayleigh, |h|2 tiene distribución chi-cuadrada con dos grados de libertad y la variable k debe tener distribución chi-cuadrada. Esta integral, tiene la siguiente solución cerrada (Alouini, y Goldsmith, 1999)
donde
En Jeganathan (2008b) se define σ2 para constelaciones reales como
donde β es la relación señal a ruido promedio. Para BPSK se tiene: σ2=β2. Sustituyendo (12) en (10) se obtiene la expresión analítica para la probabilidad de error de bits en PSSK
De forma similar, para SSK la probabilidad de error se deriva al considerar en (10) una constelación únicamente espacial. Considerando una constelación espacial M’, la ecuación (10) se reduce de la siguiente manera
El PEP, P(xj → xj˜) se calcula como en (12) y (13) y σ2=β2.
Un procedimiento similar se puede utilizar para el esquema GSSK donde se define (Jeganathan et al, 2008a)
donde el parámetro d (j,) es la distancia Euclideana entre los vectores de la constelación que se define como el número de columnas distintas entre hj y hj˜.
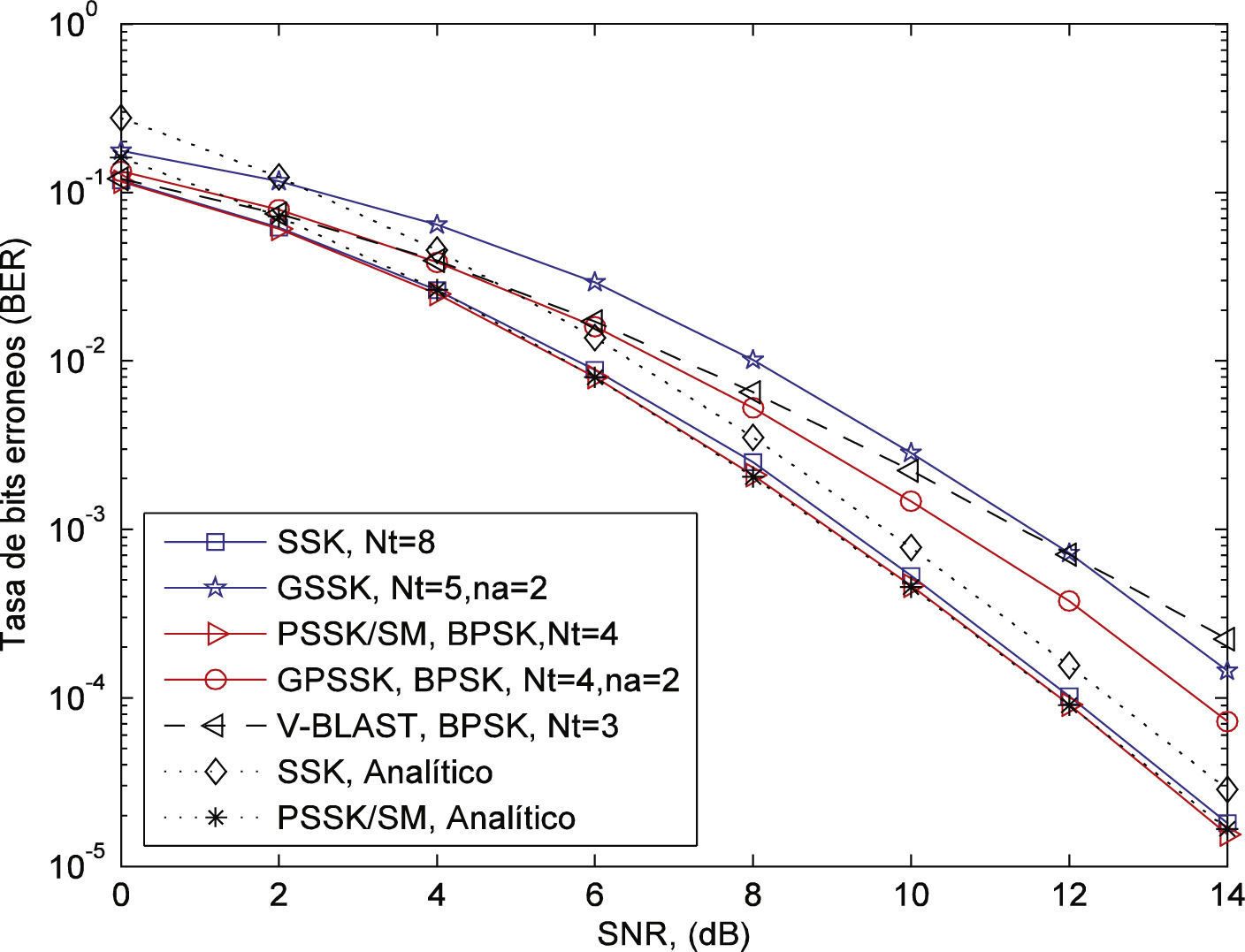
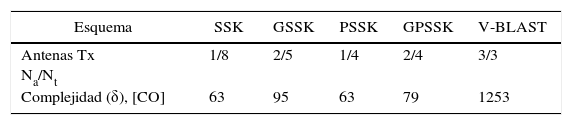
ResultadosPara las simulaciones se consideró una trasmisión de 3 bpcu con SNR variando de 0dB a 14dB. El tamaño de la constelación fue M=8. La cantidad de antenas receptoras Nr = 4, para todos los sistemas. La cantidad de antenas Tx y antenas activas es la que se indica en la tabla 6. La potencia de transmisión fue normalizada y se asume completo conocimiento del estado del canal en el receptor.
La figura 2 muestra el desempeño de los cuatro esquemas SM básicos y del esquema convencional SMux usando la técnica SIC conocida como V-BLAST (Wolniansky et al., 1998). Los resultados muestran que todos los esquemas SM superan la técnica convencional para tasas de error medias y bajas. Los esquemas PSSK y SSK tienen una ganancia aproximada de 2dB para tasas de error de 10-4, comparado con sus versiones generalizadas, GPSK y GSSK, respectivamente. Por su parte, las técnicas que agregan una modulación QAM, tienen ganancias menores a 1dB en comparación con sus contrapartes. Esas ganancias tienden a incrementarse para SNR mayores. La figura 2 también muestra que los resultados analíticos para PSSK obtenidos en (9)-(15) empatan de forma ajustada a los resultados de la simu- lación, mientras que los resultados analíticos obtenidos para SSK de la ecuación (16) presentan una cota superior con una desviación menor a 1dB para tasas de error medias y bajas.
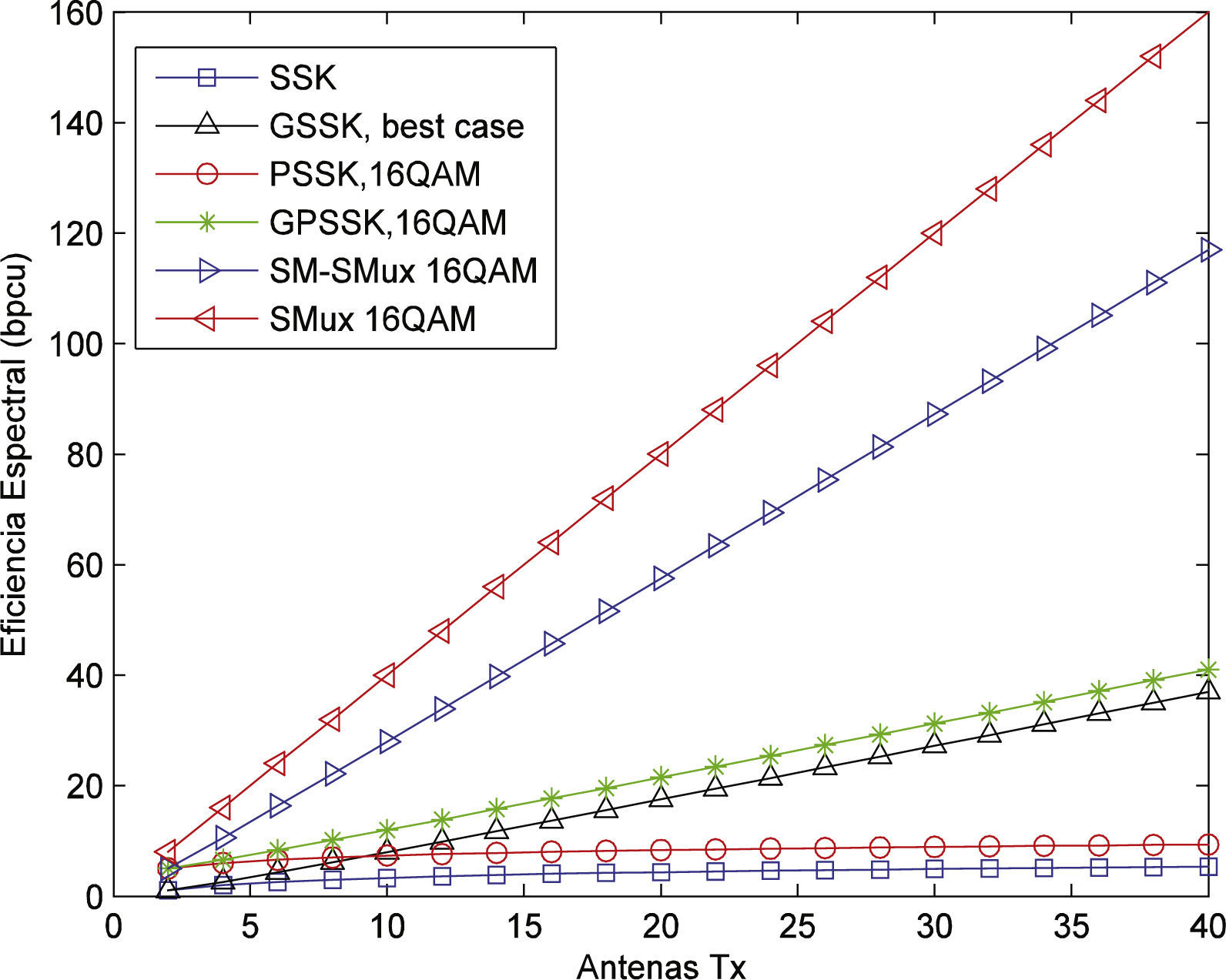
La figura 3 muestra una comparación de la eficiencia espectral en bits por uso de canal (bpcu) para los esquemas analizados. En esta comparación no solo se consideraron las antenas activas sino el total de antenas. Como puede observarse, los esquemas básicos SM tienen una eficiencia espectral menor en comparación con el esquema de convencional SMux. Los esquemas generalizados presentan una mejora en eficiencia espectral en comparación con los esquemas que usan un solo transmisor RF.
La complejidad (δ) en los receptores se calcula como la suma de operaciones complejas (CO) realizadas considerando detección ML, usando (7) y (8). Adicional a las operaciones aritméticas, se considera una comparación como una operación compleja. La tabla 6 muestra una comparación de la complejidad de los cuatro esquemas básicos y del esquema convencional SMux que usa SIC mediante el algoritmo V-BLAST de Wolniansky et al. (1998) para una transmisión de 3 bpcu.
Los resultados obtenidos muestran que los esquemas básicos basados en SM superan en desempeño a la técnica convencional SMux/V-BLAST. Adicionalmente se observa que los esquemas SM tienen una complejidad de implementación reducida. Los esquemas que combinan la modulación de fase y modulación espacial (PSSK y GPSSK) mostraron un desempeño ligeramente superior a sus contrapartes, que solo usan una constelación espacial (SSK y GSSK). Estas técnicas no aumentan la complejidad y no aumentan el número de transmisores RF necesarios. Las versiones generalizadas (GSSK y GPSSK) tienen una mayor eficiencia espectral a expensas de un desempeño menor; además, la complejidad del detector se incrementa y se requieren más transmisores RF para su implementación en comparación con sus respectivas contrapartes SSK y PSSK. La principal desventaja de los esquemas con modulación espacial es su baja eficiencia espectral en comparación con el esquema convencional SMux.
SM y SMux combinadosComo se observa en la figura 2, los esquemas básicos SM tienen un mejor desempeño, además de una menor complejidad en comparación con el esquema convencional que usa SIC/V-BLAST. Sin embargo, como se observa en la figura 3, la eficiencia espectral es consi- derablemente mayor en el esquema convencional para un número limitado de antenas Tx. Una posibilidad para el diseño de sistemas es la combinación de los esquemas SM y SMux. Estos esquemas combinados se proponen recientemente y se les conoce como SM generalizados (Rajab et al., 2013).
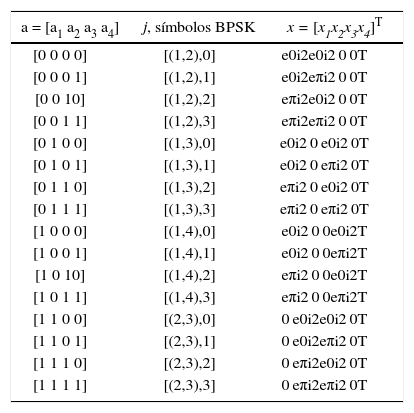
La cantidad de bits n por uso de canal que se pueden transmitir utilizando el esquema combinado SM-SMux es
donde M’ = (Nt / Na), es la combinación Na de Nt y representa el tamaño de la constelación espacial, con la condición: M’ ≤ 2k, donde k es un número entero positivo.
En la tabla 7 se muestra un ejemplo de asignación para el esquema SM-SMux. En este caso el número de antenas transmisoras es Nt = 4, el número de antenas activas es Na = 2 y el tamaño de la constelación M-QAM es M = 2. Para el ejemplo que se muestra en la tabla 7 se utilizó modulación BPSK con fases y amplitudes definidas como φ1=e0i2 y φ2=eiπ2. Los valores de xi se definen como: xi ∈ {0, φ1, φ2.
Regla de mapeo para el sistema combinado SM-SMux
| a = [a1 a2 a3 a4] | j, símbolos BPSK | x = [x1x2x3x4]T |
|---|---|---|
| [0 0 0 0] | [(1,2),0] | e0i2e0i2 0 0T |
| [0 0 0 1] | [(1,2),1] | e0i2eπi2 0 0T |
| [0 0 10] | [(1,2),2] | eπi2e0i2 0 0T |
| [0 0 1 1] | [(1,2),3] | eπi2eπi2 0 0T |
| [0 1 0 0] | [(1,3),0] | e0i2 0 e0i2 0T |
| [0 1 0 1] | [(1,3),1] | e0i2 0 eπi2 0T |
| [0 1 1 0] | [(1,3),2] | eπi2 0 e0i2 0T |
| [0 1 1 1] | [(1,3),3] | eπi2 0 eπi2 0T |
| [1 0 0 0] | [(1,4),0] | e0i2 0 0e0i2T |
| [1 0 0 1] | [(1,4),1] | e0i2 0 0eπi2T |
| [1 0 10] | [(1,4),2] | eπi2 0 0e0i2T |
| [1 0 1 1] | [(1,4),3] | eπi2 0 0eπi2T |
| [1 1 0 0] | [(2,3),0] | 0 e0i2e0i2 0T |
| [1 1 0 1] | [(2,3),1] | 0 e0i2eπi2 0T |
| [1 1 1 0] | [(2,3),2] | 0 eπi2e0i2 0T |
| [1 1 1 1] | [(2,3),3] | 0 eπi2eπi2 0T |
La detección de señales SM-SMux se puede llevar a cabo con el procedimiento general analizado en (6)-(8). Como puede esperarse, la técnica SM-SMux hereda las ventajas y desventajas de cada una de las técnicas básicas que la conforman. En la figura 3 se observa la mejora en eficiencia espectral que ofrece este esquema combinado. En (Castillo et al., 2015b) se puede encontrar una comparación de desempeño de este esquema y el esquema convencional.
TendenciasActualmente existe una gran cantidad de publicaciones donde se proponen mejoras a los esquemas SM-MIMO analizados. Por ejemplo, en Mesleh et al., (2010) proponen un esquema SM con codificación de Trellis (TCM); en la publicación de Shinya et al. (2012) se propone un nuevo esquema STSK (Space Time Shift Keying), donde se plantea el uso de matrices de dispersión para optimizar el sistema. En Luna (2013) el esquema de Tx utiliza una cantidad variable de antenas activas; Mesleh (2015) propuso una técnica conocida como Quadrature Spatial Modulation (QSM); Castillo et al. (2015b) plantearon un esquema que mejora la detección de señales combinadas SM-SMux. En Serafimovski et al. (2013) se puede encontrar una implementación práctica del sistema SM-MIMO.
Desde el surgimiento en 2006 y basados principalmente en los esquemas monousuario, múltiples investigaciones han mostrado que la modulación espacial tiene ventajas sobre las técnicas convencionales de modulación basadas en constelaciones amplitud-fase. Aunque el concepto de modulación espacial ha llegado a un cierto grado de madurez, se requiere mayor investigación sobre la implementación de esta técnica en esquemas multiusuario y multi-célula. Algunos trabajos pioneros en esquemas multiusuario se encuentran en Serafimovski et al. (2012); Kadir et al. (2013) y Castillo et al. (2015a), entre otros.
Antes de que la técnica SM se implemente en sistemas prácticos, se requiere avanzar en las investigaciones considerando escenarios más complejos. Algunas áreas que permanecen como temas abiertos de investigación en esta área son: Di Renso et al., 2014: ventajas y desventajas del uso de transmisor RF único en futuras redes con tecnologías verdes, comunicaciones SM-MIMO multiusuario y multi-célula, y estrategias de beamforming para sistemas SM de onda milimétrica, entre otras.
ConclusionesEn este artículo se presentó un marco general para el análisis de las técnicas de transmisión MIMO monousuario que utilizan modulación espacial. Basados es ese marco general se realizó una comparación de las técnicas básicas de transmisión SM-MIMO monousuario. En general, la modulación espacial extiende la constelación amplitud-fase a una constelación tridimensional amplitud-fase-espacio, adaptándose de manera natural a los esquemas de comunicación MIMO masivo, brindando ventajas en desempeño y una reducción de la complejidad en la detección de señales, en comparación con la técnica convencional SMux/SIC. Cuando se combinan los esquemas SM y SMux se tiene una mayor flexibilidad en el diseño del sistema de comunicación, al mismo tiempo que se heredan las ventajas y desventajas de ambos esquemas. Aunque las técnicas SM-MIMO pertenecen a un campo de investigación todavía en desarrollo, son una alternativa prometedora en la implementación de los futuros sistemas de comunicación inalámbrica.
Agradecemos al CONACYT México por el apoyo brindado para el desarrollo de este artículo.
Citación estilo Chicago
Citación estilo ISO 690
Francisco Rubén Castillo-Soria. Recibió el grado de ingeniero en comunicaciones y electrónica y el grado de maestro en ciencias en telecomunicaciones por el Instituto Politécnico Nacional en México (1999 y 2004, respectivamente). Recibió el grado de doctor en ciencias en electrónica y telecomunicaciones por el Centro de Investigación Científica y de Educación Superior de Ensenada en Baja California, México en 2015. Sus principales áreas de interés son procesamiento de señales en sistemas MIMO-OFDM y modulación espacial.
Jaime Sánchez-García. Recibió el grado de ingeniero en comunicaciones y electrónica del Instituto Politécnico Nacional, México en 1976. Es M en C en electrónica y telecomunicaciones por el CICESE en 1979 y doctorado en ciencias en ingeniería eléctrica por la Universidad de George Washington en 2001. Desde 1979 es investigador en el Departamento de Telecomunicaciones del CICESE en México. Sus principales áreas de interés incluyen redes inalámbricas, radio definido por software, codificación espacio-tiempo, OFDM y MIMO.
Ramón Parra-Michel. Recibió el grado de maestro en ciencias en ingeniería eléctrica, especialidad en comunicaciones por el CINVESTAV-IPN, Guadalajara, en 1998 y el grado de doctor en ingeniería eléctrica con especialidad en procesamiento de señales digitales para las comunicaciones por el CINVESTAV IPN, Ciudad de México, en 2003. Ha colaborado con varias empresas tales como Siemens, Lucent, Mabe, Mixbaal, Hewlett-Packard e Intel. Desde junio de 2006, es profesor titular del CINVESTAV Guadalajara. Sus intereses de investigación incluyen el modelado, simulación, estimación de canal y la implementación digital de algoritmos DSP para sistemas de comunicación.
Jorge Flores-Troncoso. Recibió el grado de ingeniero en electrónica por la Universidad de Zacatecas. El grado de maestro en ciencias y doctor en electrónica y telecomunicaciones en el Centro de Investigación Científica y de Educación Superior de Ensenada en Baja California, México. Actualmente es profesor-investigador en la UAZ y coordinador del Centro de Investigación y Desarrollo en Telecomunicaciones Espaciales. Sus principales áreas de interés son codificación para sistemas MIMO y OFDM.
Gustavo Fernández-Torres. Licenciado en física y matemáticas por la Escuela Superior de Física y Matemáticas del Instituto Politécnico Nacional (ESFM-IPN). Obtuvo la maestría en ciencias por el Centro de Investigación en Matemáticas (CIMAT). Actualmente estudia el doctorado en ciencias en la Facultad de Ciencias de la Universidad Nacional Autónoma de México (FC-UNAM). Las áreas de investigación son: análisis numérico, análisis funcional en teoría de operadores y álgebras de operadores integrales singulares. Es profesor ordinario de carrera en la Facultad de Estudios Superiores (FES) Aragón de la Universidad Nacional Autónoma de México.