Lógica y abstracción en la formación de ingenieros: una relación necesaria

Resumen

Este artículo se enfoca en la lógica y la abstracción vistas como una relación necesaria en los procesos formativos de los ingenieros. Se describe la importancia y la necesidad de formar en esta área del conocimiento y de la relación entre el ejercicio profesional de los ingenieros y el desarrollo y potencialización de su capacidad lógico-interpretativa y abstractiva para la resolución de problemas. Es un trabajo de investigación-revisión-reflexión acerca de la importancia de estos dos componentes, vistos estructuralmente desde el currículo. Es el producto de una primera fase de la investigación sobre “desarrollo de la capacidad lógico-interpretativa y abstractiva como componente básico para el ejercicio profesional de los ingenieros”.

Abstract

This article is about the logic and abstraction seen as a necessary relation in the formative process engineers. It describes the importance and the need for training in this area of knowledge and the relationship between professional exercise of the engineers and the development and/or potentiation of logical-interpretative and abstractive ability for problem solution. It is a research-review-reflection work about the importance of these two components, viewed structurally from the curriculum. It is the product of the first phase of the research “The capacity logical-interpretative and abstractive as a basic component for professional exercise of the engineers”.

Introducción

En el mundo moderno la ingeniería se concibe como una disciplina cada vez más dominada por las técnicas de modelado, una práctica que requiere procesos como comprender el problema, abstraer, modelar y construir, así como evaluar los diseños antes de la fabricación física de un producto. Además, la mayoría de los sectores productivos exigen a los ingenieros habilidades especiales para su ejercicio profesional, como pensamiento lógico, resolución de problemas y capacidad de abstracción. Las personas se sienten atraídas por la ingeniería porque les gusta aplicar la ciencia y usar sus habilidades para resolver problemas. En contraste y de acuerdo con la revisión al estado del arte, la formación que se imparte en la mayoría de programas de ingeniería no orienta a los estudiantes en pro de alcanzar ese objetivo, por lo que la recomendación es estructurar y poner en marcha currículos que orienten al desarrollo y potencialización de sus capacidades en lógica y abstracción, con la meta de lograr profesionales creativos en ingeniería y con las habilidades, destrezas, conocimientos y operaciones necesarias para resolver los problemas de la sociedad de este siglo.

David Parnas, un pionero de la ingeniería de software, dijo alguna vez que para los ingenieros es esencial una sólida formación y comprensión de la lógica y la abstracción, porque junto a la ingeniería son áreas que no se pueden interpretar libremente. La ingeniería trata los procesos necesarios para construir cosas, generalmente con un propósito preconcebido, y quien la practica debe aplicar su ingenio para lograrlo. La abstracción es un proceso mental para eliminar detalles con el objetivo de centrarse en lo realmente importante del problema para generar un modelo abstracto de la solución. Por otro lado, la lógica se enfoca en la esfera de una verdad formal a priori, abarca las matemáticas y es crucial para la ingeniería porque es la base sobre la que se apoya la construcción y explotación de los modelos abstractos o matemáticos.

La capacidad para resolver problemas es un componente importante en el ejercicio profesional de los ingenieros, e inclusive puede ser el núcleo de su ejercicio. Como nunca antes en la historia, esta capacidad en este siglo está dominando cada vez más el contenido intelectual de esta área del conocimiento y los principios de la lógica y la abstracción cobran especial importancia para potencializarla. Las soluciones propuestas a los problemas actuales serán más eficaces si se sustentan en procedimientos y modelos construidos con fundamentos lógicos sólidos, pero en los procesos formativos la revolución y aplicación de la lógica apenas se prevé y la responsabilidad se delega a las matemáticas como un único núcleo alrededor del cual giran los procesos ingenieriles.

Desarrollar la lógica de estos procesos debe ser una etapa natural, porque permitirá a los ingenieros aprovechar de mejor manera sus habilidades y destrezas para resolver los problemas cada vez más complicados de la sociedad actual. Si bien la lógica y la abstracción son cuestiones necesarias para que un estudiante comprenda el mundo y potencialice sus competencias, la mayoría de contenidos curriculares apenas las mencionan, no se estructuran adecuadamente uno con otro ni se proponen como fundamento para desarrollar competencias en los estudiantes, aunque esta posibilidad es una parte importante de la motivación para que decidan iniciar programas en esta área de formación.

En este artículo se describe la importancia y la necesidad de formar adecuadamente a los ingenieros en lógica y abstracción, con el objetivo de capacitarlos para comprender, analizar y modelar los problemas de la información y el conocimiento en la sociedad actual, y para que presenten soluciones eficientes y eficaces. Este trabajo es producto de la primera fase del proyecto de investigación: “desarrollo de la capacidad lógico-interpretativa y abstractiva como componente básico para el ejercicio profesional de los ingenieros”.

Cuestiones clave

Resolver problemas es una de las habilidades más importantes que deben desarrollar los estudiantes en cualquier parte del mundo. En los contextos laborales se paga a los profesionales para resolver problemas y la vida cotidiana gira constantemente alrededor de la resolución de los mismos (Popper, 1999). Cada día nos enfrentamos a problemas, grandes y pequeños, simples y complejos, claros y confusos, pero paradójicamente en las instituciones de formación sus procesos parecen ignorar en gran medida la necesidad de desarrollar y/o potencializar la capacidad lógico-interpretativa y abstractiva en los estudiantes.

De acuerdo con la literatura revisada para el proyecto de investigación, prácticamente no se encontraron referencias de cómo desarrollar esa capacidad, y muy poca información acerca del diseño instruccional orientado a la resolución de problemas. En las primeras ediciones de su libro, Gagné (1960) se refería a la resolución de problemas, pero en ediciones posteriores al parecer se dio por vencido, ya que prefirió enfrentar reglas de orden superior y se adentró en otros terrenos ¿Por qué? Si los problemas son pandémicos y solucionarlos es esencial para la actividad cotidiana y profesional ¿por qué no hace un mayor esfuerzo para formar estudiantes y resolverlos adecuadamente?

Por mucho tiempo, algunos modelos de procesamiento de la información de resolución de problemas han tratado de explicar y aplicar una metodología para el desarrollo de este tema. Ejemplos de ello son el General Problem Solver (Newell y Simon, 1972), un modelo que especifica dos tipos de procesos de pensamiento asociados con la capacidad para resolver problemas: 1) comprender el contexto y 2) aplicar procesos de búsqueda; otro es el IDEAL (Bransford, 1993) que describe la resolución de problemas como un proceso uniforme en etapas: 1) identificar problemas potenciales, 2) definirlos y representarlos, 3) explorar posibles estrategias de solución, 4) actuar de acuerdo con esas estrategias y 5) mirar hacia atrás y evaluar los efectos de esas actividades. Aunque este modelo supone que esos procesos se aplican de manera diferente para cada problema no presenta sugerencias explícitas acerca de qué hacer para saber cómo hacerlo. Gick (1986) sintetiza estos y otros modelos y los simplifica en: 1) construir una representación del problema, 2) buscar soluciones y 3) aplicar y hacer seguimiento a las soluciones. Aunque estas propuestas son útiles descriptivamente tienden a tratar de la misma forma todos los problemas, en un esfuerzo por articular un procedimiento generalizado. La culminación de los conceptos de procesamiento de la información (Smith, 1990) fue otro intento, aunque sin éxito, por articular una teoría uniforme para solucionar problemas.

La suposición subyacente es que la habilidad para resolver problemas es un tipo especial de formación para ingenieros, que resulta de desarrollar la capacidad lógico-interpretativa y abstractiva en los estudiantes. Por otro lado, existen diferentes formas para resolver problemas y cada una requiere distintos tipos de habilidades y destrezas en lógica y abstracción. Estas competencias son las que se adquieren al desarrollar esa capacidad y las que capacitan a un estudiante para adaptarse a una situación problemática, interpretarla, comprenderla, modelarla y luego presentar una solución eficiente y eficaz. Por otro lado, al hablar de los ingredientes necesarios para que los ingenieros resuelvan problemas con éxito se considera útil hacer una distinción entre los principios científicos y las técnicas de resolución de problemas. Los primeros se orientan a las leyes, como la de conservación de la masa, de los gases, de Ohm, de Hooke, las de la termodinámica y así sucesivamente; las segundas incluyen el uso de modelos matemáticos algebraicos y gráficos, la lógica simbólica, la capacidad de abstracción, los diagramas de flujo, el juicio, las técnicas de solución de errores y los programas informáticos, entre muchos otros. Por supuesto, ambos principios se sustentan en bases sólidas de lógica y abstracción.

Además, en general se reconoce que los ingenieros deben utilizar determinadas herramientas matemáticas y lógicas para realizar su función principal: resolver problemas y, al igual que con los principios científicos, las utilizan para correlacionar los diferentes componentes del contexto de la situación problemática. En estos ambientes los principios y herramientas se deben comprender desde dos puntos de vista para seleccionar los datos correlacionales necesarios: 1) con referencia a su uso en la solución de problemas específicos y 2) desde el examen el fondo de los conocimientos disponibles sobre el contexto. Algunas de las herramientas y métodos necesarios son:

• •

  Matemáticas

• •

  Lógica

• •

  Abstracción

• •

  Modelado y simulación

• •

  Modelos matemáticos

• •

  Conceptos de gráficos (diagramas) de flujo

• •

  Iteración

• •

  Técnicas de solución mediante prueba y error.

Para aplicar eficiente y eficazmente estas herramientas y métodos, los ingenieros necesitan desarrollar una capacidad lógico-interpretativa y abstractiva que les permita comprender los problemas para presentar una solución acorde. Esta característica representa una marcada diferencia entre ellos y otros profesionales porque son quienes más la aplican, aunque diversas investigaciones y estudios han demostrado que el ejercicio profesional en cualquier área del conocimiento necesitará en algún momento de ella. Ese proceso requiere la comunión constante entre tres áreas clave: ingeniería, lógica y abstracción, que deben formar parte de sus procesos formativos para lograr los profesionales que la sociedad de la información y conocimiento necesita.

Lógica y abstracción: estado del arte

La primera fase de la investigación consistió en realizar una amplia revisión de la literatura relacionada. Parte de los conceptos y conocimientos encontrados se relacionan a continuación.

En la década de los 60 varios investigadores evaluaron el nivel de comprensión, el alcance y las limitaciones de dominio que las personas logran a partir del desarrollo de la lógica, donde citamos a Piaget (1957);Inhelder y Matalon (1960); Hill (1961); McLaughlin (1963); Inhelder y Piaget (1964); Furth y Youniss (1965); Suppes (1965) y Youniss y Furth (1964, 1967). Sin embargo, estos estudios no reportaron en qué medida las personas comprenden el significado lógico de la temática de investigación, no definieron explícitamente la situación experimental aplicada y no proyectaron el uso de los resultados para proponer cambios en los procesos formativos. Del mismo modo, en la medida que las edades de la población se incrementan, también se requiere información más detallada acerca de sus hábitos lingüísticos y de la comprensión lógica que aplican.

Mediante dos experimentos relacionados Suppes y Feldman (1969) determinaron la forma en que los niños de edad preescolar comprenden el significado de los conectores lógicos y de la lógica misma, con lo que contribuyeron a la acumulación de información sistemática en esta área. McCarthy y Hayes (1969) propusieron que para que un programa de computadora fuera capaz de actuar inteligentemente debe tener una representación general del mundo en términos de las entradas que interpreta y para diseñarlo se requiere saber qué es y cómo se obtiene el conocimiento, un proceso que requiere lógica y abstracción. Sloam (1971) respondió a este trabajo argumentando que los problemas filosóficos acerca del uso de la intuición en el razonamiento, relacionados a través de un concepto de representación analógica para problemas como la simulación de la percepción, la resolución de problemas y la generación de conjuntos útiles se debían estudiar considerando una manera específica de actuar. Concluyó que los requisitos propuestos por McCarthy y Hayes para tomar decisiones inteligentes eran demasiado estrechos y en su lugar propuso requisitos más generales. Pero en su trabajo no mencionó ni aplicó la conceptualización lógico-abstractiva como base para lograrlo.

La capacidad para pensar de forma abstracta es una habilidad necesaria para el desarrollo profesional, pero es común encontrar diferencias en la forma en que la aplican los estudiantes, porque algunos la desarrollan con mayor facilidad que otros e incluso algunos no llegan a desarrollarla (Boroditsky y Ramscar, 2002). Estos estudios demostraron que existen vínculos entre la capacidad abstractiva y el éxito en la resolución de problemas, por lo que desarrollar esa capacidad debería ser un objetivo de los procesos formativos. La capacidad para pensar de esta forma fue identificada por Piaget (1972) como una de las etapas del desarrollo cognitivo de los niños, y describió la cuarta y última etapa de este proceso como de operación formal, observando que solo alrededor de 35% de ellos la alcanza.

En los 80 se realizaron varias investigaciones aplicando modelos computacionales alrededor de las temáticas de la resolución de problemas, del modelado cognitivo y de la memoria a largo plazo. Entre ellas se encuentran las de Schank (1982); Kolodner (1984) y Ross (1984), cuyos resultados les sirvieron a Kolodner et al. (1985) para explorar las formas en que el razonamiento basado en casos puede ayudar en esa resolución. De acuerdo con su modelo, la transferencia de conocimientos entre casos está en gran medida guiada por el proceso mismo de la resolución, además demostró las interacciones entre los procesos de resolución y la memoria por experiencia. Su programa de computador MEDIATOR ilustra el razonamiento basado en casos para interpretar y resolver disputas de sentido común. El resultado de este trabajo fue un modelo de razonamiento basado en casos que integran la solución de problemas, la comprensión y la memoria, pero que no hace referencia a cómo integrar el proceso mental lógico-abstractivo que las personan aplican para resolver esos problemas.

En la década siguiente se investigó activamente acerca del uso del razonamiento abductivo y se presentaron trabajos como el de O'Rorke (1988) cuyo tema central fue el aprendizaje y el descubrimiento, el de Dasigi y Reggia (1989) acerca del procesamiento del lenguaje natural y el de Peng y Reggia (1990) relacionado con el diagnóstico de errores. Estos estudios les sirvieron a Kumar y Venkataram (1994) para proponer un modelo con el objetivo de resolver problemas de diagnóstico, fundamentado en el mecanismo de inferencia abductiva y que se aplicó para añadir algunas características nuevas al modelo general existente de resolución de problemas de diagnóstico. Estos investigadores fueron los primeros en combinar las matemáticas con los algoritmos computacionales y sus resultados demostraron efectividad en la resolución de los problemas de diagnóstico, aunque no se acercaron a la lógica y la abstracción como herramientas que también trabajan desde la abducción.

Gottinger y Weimann (1995) exploraron las diversas técnicas de inferencia para un sistema de apoyo a las decisiones inteligentes basadas en diagramas de influencia y concluyeron que el razonamiento acerca de la acción requiere varios niveles de representación e inferencia que dependen del nivel de incertidumbre y de la complejidad, así como de la novedad de la situación de decisión. Para hacerlo se basaron en la caracterización unificada de procedimientos de inferencia de conocimientos de la lógica probabilísti- ca, en el razonamiento teórico de decisiones, en el trabajo de Jarke y Radermacher (1989) acerca de la lógica de la solución de problemas mediante técnicas para el análisis probabilístico, la toma de decisiones bajo in-certidumbre y la investigación de operaciones, por último, en el trabajo de Gottinger y Weimann (1992) acerca de técnicas basadas en inteligencia artificial para sistemas de apoyo a las decisiones inteligentes. Aunque en este trabajo se aplica la lógica desde la visión de las decisiones inteligentes, no cubre aspectos como la interpretación, el modelado de problemas o la capacidad abstractiva de quien intenta tomar esas decisiones. Lo interesante de esta investigación es la aplicación que hace de los métodos formales.

Morris y Sloutsky (1998) intentaron averiguar si el razonamiento abstracto se desarrolla naturalmente y cómo contribuyen a esto los procesos formativos. Su investigación se centró específicamente en los efectos que una formación prolongada tiene en el desarrollo del razonamiento abstracto-deductivo y, concretamente, en el desarrollo de la comprensión de la necesidad lógica. Plantearon la hipótesis de que el énfasis en la formación en el meta-nivel de deducción en un dominio de conocimiento puede mejorar el desarrollo del razonamiento deductivo, tanto dentro como a través de ese dominio. Este trabajo consistió en dos estudios en los que se examinan el desarrollo de la comprensión de la necesidad lógica en el razonamiento algebraico-deductivo y verbal. Los resultados apoyaron la hipótesis, lo que indica que una formación prolongada con énfasis en el metanivel de la deducción algebraica contribuye al desarrollo de la comprensión de la necesidad lógica, tanto en el razonamiento algebraico-deductivo como en el verbal. También sugirieron resultados indicando que muchos adolescentes, a pesar de estar expuestos a los mismos procesos de formación, no desarrollan naturalmente una comprensión de esa necesidad lógica.

Pietarinen (2003) intentó responder a la cuestión de qué tienen en común la lógica epistémica y la ciencia cognitiva y concluyó que existen tres posibilidades:

• 1)

  nuevas versiones cuantificadas de multi-agentes lógicos epistémicos capturan las locuciones de identificación de los objetos involucrados, dando lugar a aplicaciones de la representación de conocimiento en sistemas multiagente y procesamiento paralelo,

• 2)

  el marco de la semántica de la teoría de juegos para las lógicas consiguientes tiene mayor credibilidad cognitiva como una verdadera semántica para las nociones epistémicas y

• 3)

  algunos hallazgos en neurociencia cognitiva relacionados con las nociones de conocimiento y transformación explícita versus procesamiento implícito contribuyen a los estudios de lógica.

Explora estas conexiones desde las perspectivas lógica y cognitiva, los resultados definieron nuevas extensiones de la lógica epistémica e incrementaron la comprensión formal del procesamiento de la información inconsciente y consciente en el cerebro; con ello se logró que el formalismo susceptible de representación del conocimiento se configure en multiagentes.

Huitt y Hummel (2003) afirman que la mayoría de adultos necesita un entorno especial para alcanzar la cuarta etapa de desarrollo de Piaget, pero no es claro si lo logran gracias a una habilidad innata o si se desarrolla a través de los procesos formativos a los que se exponen. Piaget describe esta etapa como la del uso lógico de símbolos relacionados con conceptos abstractos, descripción que también se podría utilizar para referir la capacidad de interpretar problemas y de producir modelos, una característica importante para el desarrollo profesional de los ingenieros. Pietarinen (2004) argumenta que los hallazgos empíricos acerca de las raras disfunciones neuronales son contribuciones de las investigaciones en lógica y que la fase temprana de la ciencia cognitiva comparte raíces en la fenomenología. En consecuencia, identifica líneas en ese periodo inicial que se originan en la lógica, la inteligencia artificial (IA) y las ciencias computacionales. Otra conclusión a la que llegó es que desde estas fases también se reconoce la importancia de la división entre aspectos implícitos y explícitos del conocimiento en la cognición comprensiva.

Aunque el aporte de este trabajo es importante para reconocer las raíces de la discapacidad lógica en algunas personas, los resultados no se aplican para indicar el mismo proceso en personas sin esa discapacidad.

Egorov (2007) parte de la hipótesis de que la capacidad de pensar lógicamente está determinada por los genes, a los que llama informalmente genes lógicos que hipotéticamente codifican la información de las proteínas. Se pregunta si en los seres humanos realmente existen genes para la lógica, respondiendo que lo más probable es: sí, debido a que estos contribuyen en gran medida al control de la cognición, tal como lo han investigado McLearn et al. (1997), Winterer y Goldman (2003), Oldham et al. (2006), Popesco et al. (2006) y Reuter et al. (2006). Egorov pretende encontrar el origen de la capacidad lógico-interpretativa de las personas y aunque su aporte es importante no aplica el mismo procedimiento para la capacidad abstractiva, lo que no permite hacer una inferencia relacional del desarrollo de ambas capacidades.

A diferencia de otros animales, los seres humanos están equipados con un poderoso cerebro que los dota de conciencia y reflexión, sin embargo, una creciente tendencia en psicología cuestiona los beneficios de esa conciencia. A este tema se refiere la hipótesis de Lieberman et al. (2002). Por otro lado, De Wall et al. (2008), aplican cuatro estudios cuyos resultados sugieren que la conciencia como sistema de procesamiento reflexivo es importante para el razonamiento lógico, de lo que se puede concluir que el sistema de procesamiento reflexivo ayuda a ese razonamiento. Los investigadores se basaron en esto para presentar la hipótesis de que el razonamiento lógico depende en gran medida del procesamiento consciente y propusieron que la forma de probar esta teoría sería logrando que las manipulaciones afecten solo a uno u otro de los dos sistemas de procesamiento y que dejen al otro intacto.

Muchos estudiantes carecen de habilidades para buscar lógicamente la información que requieren, y aunque se encuentre a su disposición no son capaces de leerla, analizarla ni evaluarla críticamente (Serna, 2012a). Para hacer frente a estos problemas, Bouhnik y Giat (2009) desarrollaron un curso universitario con el objetivo de capacitar a los estudiantes para aplicar herramientas lógicas. El curso se desarrolló para dos grupos de estudiantes diferentes, uno orientado a las áreas sociales y otro a las ciencias exactas. El objetivo fue estudiar y comprender los sistemas lógicos basados en el concepto; los resultados demostraron que las habilidades en los razonamientos lógico y crítico de los estudiantes mejoraron con el tiempo, tanto objetiva como subjetivamente. Este trabajo hace varias contribuciones a los campos de formación en tecnologías de la información y comunicaciones (TIC), en lógica aplicada y en pensamiento crítico.

De acuerdo con investigadores como Simon (1996); Harel y Sowder (1998) y Lithner (2000), de las disciplinas relacionadas con la formación en matemáticas, como la filosofía, la psicología y la matemática misma, se derivan razonamientos como inductivo, deductivo, abductivo, plausible y de transformación. Cañadas et al (2009) consideraron la diferenciación general entre los razonamientos inductivo y deductivo desde la tradición filosófica y desde las diferentes disciplinas y contextos en que esa distinción persiste, se esforzaron por centrar su investigación en el proceso del razonamiento inductivo, aunque Ibañez (2001); Marrades y Gutiérrez (2000); Stenning y Monaghan (2005) resaltaron las dificultades prácticas de realizar esa separación. Concluyeron que los estudiantes aplican acciones lógicas con mayor frecuencia en problemas cuyos casos particulares se expresan de forma numérica y que son capaces de identificar la aplicabilidad de ciertos pasos del razonamiento inductivo, que previamente habían utilizado en las aulas.

Halpern y Pucella (2011) examinaron cuatro enfoques para abordar el problema de la omnisciencia lógica, es decir, cómo elegir un enfoque y construir un modelo apropiado para su aplicabilidad potencial:

• 1)

  sintáctico (Eberle, 1974; Moore y Hendrix, 1979; Konolige, 1986),

• 2)

  de la conciencia (Fagin y Halpern, 1987),

• 3)

  del conocimiento algorítmico (Halpern, 1994) y

• 4)

  de los mundos imposibles (Rantala, 1982).

Aunque algunos investigadores aceptan que estos enfoques poseen el mismo nivel de expresividad y pueden capturar todos los estados epistémicos, otros demuestran lo contrario. El objetivo de la investigación de Halpern y Pucella fue hacer frente a la omnisciencia lógica. Teniendo en cuenta la pragmática de esta área y con base en el principio de la falta de omnisciencia lógica en esta situación, identificaron algunos principios que rigen el proceso de cómo elegir un enfoque para una situación modelo y concluyeron que el enfoque de mundos imposibles es especialmente adecuado para representar un punto de vista subjetivo del mundo. Recientemente surgió el interés por investigar en la recopilación de pruebas acerca de los vínculos entre el pensamiento abstracto y el desarrollo de la capacidad abstractiva, y mientras algunas investigaciones concluyen que la lógica y la abstracción son habilidades clave para la formación en ciencias computacionales e ingeniería (Serna, 2011-2012), otras tratan de encontrar un vínculo entre el éxito de las habilidades de abstracción en los cursos de lógica computacional (Bennedsen y Caspersen, 2006; Armoni y Gal-Ezer, 2007), todas con logros diferentes.

La capacidad lógico-interpretativa y abstractiva

De acuerdo con Andrews (2002), ser lógico presupone tener:

• 1)

  sensibilidad para el lenguaje y habilidad para utilizarlo efectivamente, porque la lógica y el lenguaje son inseparables,

• 2)

  gran respeto por el escenario mundial, porque la lógica trata de la realidad y

• 3)

  conciencia viva de cómo los hechos —las ideas— se relacionan con los objetos en el mundo, porque la lógica trata de hallar la verdad.

Desarrollar efectivamente estas capacidades, actitudes, puntos de vistay modalidades prácticas le permite a cualquier persona preparar su mente para trabajar con éxito la lógica, pero para lograrlo eficientemente debe:

• •

  Ser un excelente observador

• •

  Estar atento

• •

  Obtener los hechos directamente

• •

  Comprender las ideas y sus objetos

• •

  Estar consciente de los orígenes de las ideas

• •

  Hacer coincidir las ideas con los hechos

• •

  Hacer coincidir las palabras con las ideas

• •

  Realizar análisis profundos

• •

  Concatenar situaciones para obtener conclusiones

• •

  Comunicarse efectiva y eficientemente

• •

  Evitar el lenguaje vago y ambiguo

• •

  Evitar el lenguaje evasivo

• •

  Tener concentración

• •

  Ser realista

• •

  Buscar la verdad

• •

  Poseer habilidades comunicativas en diversas formas

• •

  Ser buen oyente

• •

  Ser buen lector

• •

  Gustarle escribir

La lógica se refiere a la formalización de las leyes del pensamiento y se centra en la formulación de teorías normativas que establecen cómo se debe pensar correctamente y se relaciona no sólo con el pensamiento abstracto sino también con el que se representa en forma de oraciones y con el que manipula frases para generar un nuevo pensamiento. Si la lógica es una formalización de este tipo, entonces el mejor lugar para encontrarla sería en el cerebro (Gibbs, 1994), pero limitar la observación a su estructura y actividad sería como analizar el hardware cuando el objetivo es el software o como tratar de comprender las interacciones humanas estudiando el movimiento de las partículas atómicas, por esto se recomienda utilizar el sentido común y tener como base la introspección, aunque sea poco fiable (Bransford y Stein, 1993). El optimismo a ultranza puede llevar a que se vea lo que se quiere ver en lugar de ver lo que realmente está ahí y el modelado y la simulación son herramientas a las que se puede recurrir para tener éxito.

De acuerdo con esto, ¿cuáles serían las capacidades lógico-abstractas de las que dependen las personas para su desarrollo cognitivo? ¿Cómo se pueden mejorar esas capacidades? ¿Sería posible enseñar habilidades de pensamiento lógico-abstracto? Con base en algunos estudios de caso, Piaget e Inhelder (1969) y Huitt y Hummel (2003) sentaron las bases para una mejor comprensión del desarrollo cognitivo. En su trabajo, derivaron cuatro etapas para este proceso: 1) senso-motriz, 2) pre-operacional, 3) operacional concreto y 4) operacional formal. En las dos primeras, la inteligencia se demuestra primero mediante actividades motrices y posteriormente con el lenguaje y la manipulación temprana de símbolos; en la tercera se demuestra mediante la comprensión de la conservación de la materia y de la causalidad, y de una habilidad para clasificar objetos concretos, en la cuarta se demuestra una habilidad para pensar de forma abstracta, sistemática e hipotética, se utilizan símbolos relacionados con conceptos abstractos y es una etapa crucial en la que el individuo es capaz de pensar abstracta y científicamente. Aunque existen estudios y evidencias experimentales que apoyan la hipótesis del progreso a través de las tres primeras etapas, parece que no todas las personas progresan hasta la formal operacional a medida que maduran. El desarrollo biológico puede ser un pre-requisito, pero pruebas realizadas en poblaciones de adultos indican que solo entre 30% y 35% alcanza la etapa operacional formal (Kuhn et al., 1977); además, para que los adolescentes y los adultos la alcancen pueden ser necesarias condiciones particulares provenientes del medio ambiente y de procesos formativos.

Hall (1976) menciona que la lógica permite a los humanos examinar las ideas, los conceptos y los procesos mentales, porque se encuentra en todas las esferas de la vida ordinaria. En estas esferas la capacidad lógica y abstracta se expresa utilizando relaciones lógicas en lenguaje natural, un principio necesario para simplificar y comprender la cotidianidad. Wason y Johnson (1972) sostienen que la comprensión de reglas y regulaciones se ha convertido en un problema que afecta la vida de las personas, es decir, se refieren a la forma complicada como se presentan las relaciones lógico-abstractas. Para solucionar este inconveniente algunos investigadores sugieren utilizar un árbol lógico en el que sea posible reflejar con claridad todas esas relaciones. La idea es lograr que esa estructura sea lo suficientemente sencilla y clara luego de eliminar las conexiones complejas entre las cláusulas, porque son las que impiden la comprensión de las reglas lógico-interpretativas y abstractivas involucradas.

Estos conceptos y principios constituyen la base para desarrollar la capacidad lógico-interpretativa y abstractiva de los estudiantes en ingeniería y, aunque esta área ha sido poco investigada, existe una necesidad generalizada de reorientar los procesos formativos para alcanzar su desarrollo. Como se ha podido identificar en el análisis del estado del arte, existen tres posibles hipótesis para lograr el desarrollo de esta capacidad:

• 1)

  es una cuestión genética,

• 2)

  es el resultado de procesos formativos focalizados y

• 3)

  es una combinación de las dos anteriores.

Aunque en la revisión no se encontró la validación de ninguna de ellas, es posible concluir que el desarrollo de esta capacidad es un componente básico para el ejercicio profesional de los ingenieros.

Desarrollo de la capacidad lógico-interpretativa y abstractiva

Idealmente, la práctica de la ingeniería se puede describir como la solución óptima de problemas físico-prácticos mediante un análisis lógico-abstracto y sistemático y la integración de hechos científicos. Sin embargo, el número, la complejidad y la indeterminación de los hechos que se deben manejar en las soluciones es lo suficientemente complejo como para que se agregue invariantemente el juicio y la razón. El juicio es el objeto de la intuición personal y ha dado lugar a la interpretación del concepto de la ingeniería como un arte antes que como una ciencia puramente lógica. El juicio es sin duda un componente conocido de la práctica de esta profesión, debido a que se deben considerar múltiples factores que a menudo son intangibles. Pero es quizá menos reconocido como un factor significativo en el nivel más bajo de los cálculos ingenieriles, donde sólo se presume que están presentes los hechos y la lógica, porque los propios hechos no están completamente claros y normalmente se basan en una serie de hipótesis y supuestos, que a su vez requieren el juicio y la razón.

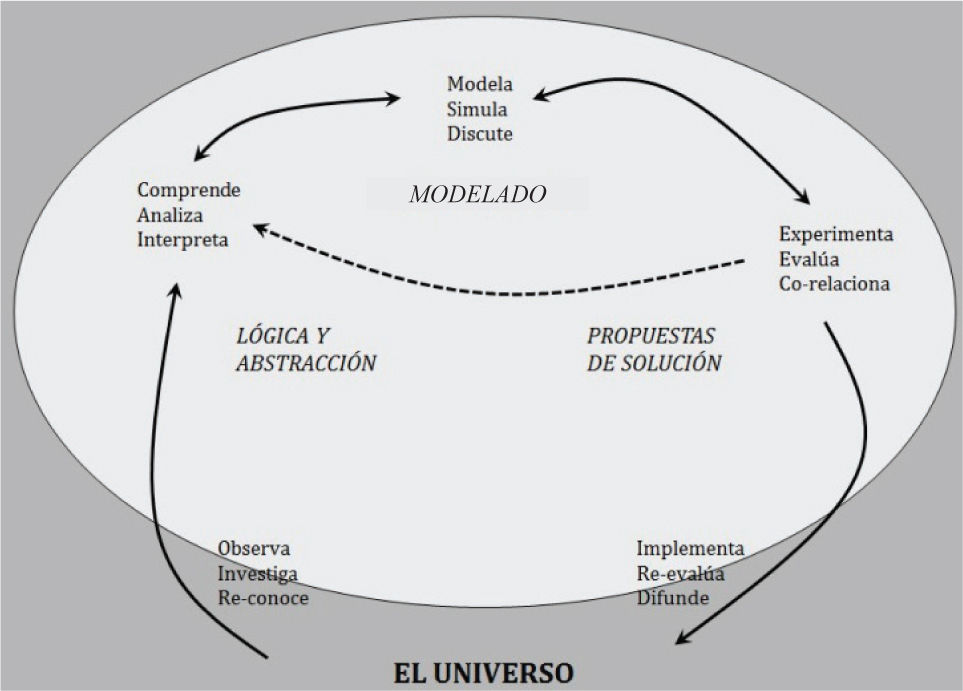
Los ingenieros son seres humanos, por lo tanto su juicio está sujeto a influencias emocionales y, aunque gran parte de los procesos formativos se niegue a aceptarlo, la capacidad lógico-interpretativa y abstractiva puede ser una contribución tan importante a las conclusiones y las decisiones resultantes de un estudio de ingeniería como los hechos y procesos del pensamiento lógico en sí, y esa falta de aceptación de la importancia de la lógica y el pensamiento abstracto impregna todos los resultados de los procesos ingenieriles. Causa de ello es que en el aula rara vez se discute y analiza la influencia de los procedimientos lógicos en los procesos de razonamiento y en su lugar se acrecentan y potencializan las presunciones en las que se basa ese razonamiento. Este proceso lo han descrito algunos investigadores como un condimento de las presunciones injustificadas para conclusiones inevitables. En otras palabras, cuando un individuo piensa lógicamente pero está influenciado emocionalmente tiende a seleccionar aquellas suposiciones que lógicamente lo llevan a la conclusión que desea. Esto se podría evitar si en los procesos formativos de los ingenieros se le da la importancia necesaria a la lógica y a la abstracción, y si se estructuran currículos orientados a desarrollar o potencializar la capacidad lógico-interpretativa y abstractiva en los estudiantes. En la figura 1 se presenta un contexto de aproximación al cómo lograr el desarrollo de esta capacidad, el cual les puede servir a los diseñadores de currículos para tenerlo en cuenta al hacer la integración de contenidos.

Figura 1.

Desarrollo de la capacidad lógico-interpretativa y abstractiva en ingeniería

En esta forma de ver la relación entre el ingeniero y el universo, la mente del profesional es una estructura sintáctica mediante la cual observa, comprende, modela, experimenta e implementa su comprensión y es la forma como se espera que diseñe y presente soluciones a los problemas que investiga o reconoce. Por otro lado, el universo es una estructura semántica que incluye al ingeniero mismo y que le da significado a sus pensamientos. Además, es dinámica porque cambia continuamente y solo existe en el aquí y el ahora. Sin embargo, el profesional puede grabar sus experiencias cambiantes en la mente y formular soluciones generales, después puede utilizar las soluciones que explican los resultados experimentales para alcanzar el objetivo de solucionar la situación problemática previamente reconocida. El ingeniero observa los acontecimientos que tienen lugar en el universo junto con las propiedades que los inician y terminan, asimismo, utiliza su capacidad lógico-interpretativa y abstractiva para derivar conclusiones de esas observaciones. En muchos casos, esas conclusiones son acciones instintivas provocadas por asociaciones estímulo-respuesta, que también se pueden expresar en la forma lógica de simulaciones. Posteriormente, ejecuta acciones para experimentar el modelado y reevaluar los resultados para mejorar sus conclusiones, previo a presentar y difundir nuevamente en el universo el modelo de una solución que procesó a través de la comprensión del contexto.

Las consecuencias de esta secuencia de acciones pueden depender no solo de sus propias acciones, sino también de las acciones de otros agentes o condiciones que están fuera de su control. Aquí cobra importancia una formación estructurada en lógica y abstracción, porque el ingeniero puede no ser capaz de determinar con certeza si esas condiciones se cumplen, pero sí ser capaz de juzgar la posibilidad o probabilidad de ocurrencia. Para lograrlo necesita utilizar las técnicas de la teoría de decisiones y combinar sus juicios de probabilidad y utilidad para elegir el curso de acción que le ofrezca mayor posibilidad de éxito. Entre los criterios que puede utilizar para decidir entre las alternativas para el cumplimiento de sus objetivos tiene a su disposición la experiencia vivida por otros ingenieros en el universo. Aplicando su capacidad lógica para combinar las diferentes alternativas podrá comprender y apreciar sus propias experiencias, metas y creencias y combinarlas con las de los demás, de esta manera podrá evitar el conflicto de soluciones repetidas sobre resultados iguales y aportar el conocimiento adquirido para enriquecer el conocimiento acumulado en el universo.

Conclusiones

Uno de los objetivos de los procesos formativos es preparar a los estudiantes para adaptarse a situaciones problemáticas cambiantes y nuevas. Algunos enfoques pedagógicos buscan equivalencias, aunque su única métrica de aprendizaje sea medir la capacidad que tienen los estudiantes para memorizar la información que se les presenta de forma concreta. Las diferencias for-mativas se hacen más evidentes al evaluarlas desde la perspectiva de qué tan bien se transfiere ese conocimiento a las solución de los nuevos problemas y configuraciones, es decir, a los que se enfrentan en la vida profesional. Algunas características importantes de esos procesos afectan la capacidad del estudiante para transferir lo que aprende. Una de ellas es la cantidad y tipo de aprendizaje inicial, con el que desarrolla experiencia y capacidad para transferir conocimiento.

Los estudiantes de ingeniería se inclinan por los temas complejos y la resolución de problemas, siempre y cuando sean interesantes para ellos, además y en teoría, por la oportunidad de utilizar sus conocimientos para crear productos y beneficios para los demás. Pero si los problemas no les llaman la atención, se incrementa la desmotivación y decae su capacidad para comprenderlos y mucho más para presentar una solución. Algunos estudios proponen una formación utilizando estudios de casos lo más cercanos a la vida cotidiana, porque de esta forma el estudiante desarrolla: 1) su capacidad lógica, para comprenderlos y 2) su capacidad de abstracción, para modelarlos. Por otro lado, el contexto en el que el ingeniero se forma es un agente importante para lograr la transferencia de conocimiento. De acuerdo con los resultados de la revisión a la literatura, es menos probable que un estudiante que se forma en un único contexto logre el objetivo del curso, lo que puede variar cuando está expuesto a múltiples contextos. De esta manera tiene mayores posibilidades para comprender y abstraer las características relevantes del problema y para desarrollar una representación más flexible del mismo.

Si el objetivo de formar es ofrecer a la sociedad profesionales que generen confianza, lo recomendable sería modificar los procesos formativos a los cuales están expuestos. La sociedad de este siglo necesita profesionales confiables desde lo ético y lo humano, pero fundamentalmente que solucionen problemas. La sociedad crea, desarrolla y convive con problemas que exigen soluciones eficientes y eficaces, pero de acuerdo con las tendencias actuales los nuevos profesionales no lo están logrando. Aunque hasta el momento no es posible responder si el desarrollo de la capacidad lógico-interpretativa y abstractiva es una cuestión genética o que se adquiere a través de procesos formativos, sí se puede asegurar que los modelos pedagógicos, los planes de estudio y los programas actuales no están estructurados integralmente para desarrollarla suficientemente, por lo que se necesitan cambios importantes en cada uno de ellos (Serna, 2012a).

Otra recomendación es atender y estructurar soluciones formativas de acuerdo con las necesidades de cada contexto, porque como lo evidencian los estudios neurocientíficos cada persona es un universo, que tiene diferentes motivaciones formativas y diferentes ritmos de aprendizaje y que se desenvuelve en diferentes ambientes al aprender. Por todo esto se necesitan procesos e iniciativas para desarrollar su capacidad lógico-interpretativa y abstractiva, de tal forma que la pueda adaptar y utilizar de acuerdo con sus exigencias y necesidades individuales.

Agradecimientos

Los autores agradecen el financiamiento conjunto de este proyecto al Instituto Tecnológico Metropolitano (ITM) y a la Corporación Universitaria Remington (CUR), en Medellín Colombia.