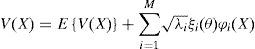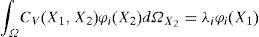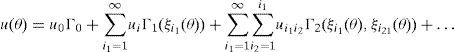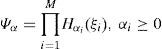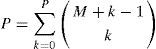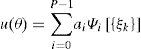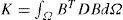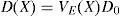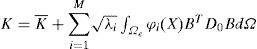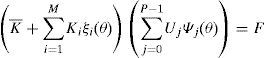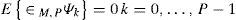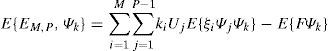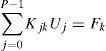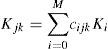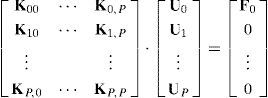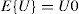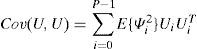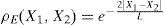Método del elemento finito estocástico en geotecnia. Enfoque espectral

Resumen

En este artículo se exponen las herramientas matemáticas que constituyen la base de la formulación del método del elemento finito estocástico espectral para problemas de elasticidad lineal. Se ilustra el potencial que presenta este método para modelar la variación espacial de las propiedades de materiales heterogéneos y en particular de los suelos, mediante un ejemplo sencillo en el que se analiza cómo se propaga la incertidumbre del módulo de deformación de un material al campo de desplazamientos calculados. Se muestra en particular la influencia de la distancia de correlación sobre la distribución de la incertidumbre. Finalmente, se evalúa la utilidad del método para las aplicaciones en geotecnia y se presentan conclusiones.

Abstract

This paper presents the mathematical tools in which the formulation of Spectral Stochastic Finite Element Method is based. The usefulness of this method to model the spatial variability of heterogeneous materials, and in particular of soils, is illustrated by a practical example in which the propagation of the uncertainty on the deformation modulus to the computed displacement field is assessed. The influence of the correlation length on the distribution of uncertainty is set forth. Finally, the advantages of the method in geotechnical engineering are evaluated and some conclusions are presented.

Introducción

Generalmente, los resultados de los análisis geotécnicos se encuentran afectados por una incertidumbre importante, debido a que los geomateriales son heterogéneos y complejos. Estos resultados dependen de numerosos factores aleatorios (realización de pruebas de laboratorio, remoldeo de muestras, etcétera) que influyen directamente en la determinación de los parámetros de los materiales. Estimar la incertidumbre que afecta dichos resultados ha sido una tarea que ha interesado a los ingenieros geotecnistas desde tiempo atrás. Casagrande (1965) enfatiza, por ejemplo, la importancia de evaluar no sólo los riesgos calculados, inherentes a las obras geotécnicas, sino también los relacionados con las fallas humanas. En los últimos decenios, se ha recurrido a las técnicas probabilistas y estadísticas para modelar la incertidumbre dentro de un marco racional para diversos problemas en el campo de la geotecnia (Auvinet, 2002).

Un método que permite modelar y cuantificar la incertidumbre que induce la dispersión de los parámetros de los materiales en los resultados de los análisis, es el método del elemento finito estocástico (MEFE), el cual es una combinación del método del elemento finito (MEF) con la teoría de la probabilidad (Cambou, 1974; Van-marcke, 1983), donde los parámetros afectados por incertidumbre se representan por medio de variables aleatorias o campos aleatorios. Las principales técnicas usadas en geotecnia hasta el momento, las cuales permiten aplicar el MEFE son los métodos de perturbaciones (variables aleatorias) y de simulación (Monte Carlo: variables y campos aleatorios) (Auvinet, 2002).

Los análisis con el MEFE han permitido ilustrar la influencia de la incertidumbre en los parámetros constitutivos en los desplazamientos, esfuerzos y deformaciones de estructuras térreas (Orlandi, 1996; Bouayed, 1997; Mellah, 1999; Auvinet et al, 2000; Vázquez, 2005) y han resultado ser un camino apropiado para decidir cuáles parámetros deben definirse con especial cuidado en la etapa de diseño. Por ejemplo, con el método de perturbaciones y mediante un análisis elástico lineal, en el que el material se puede caracterizar por dos parámetros: módulo de deformación (E) y relación de Poisson (v), se ha podido poner en evidencia que la relación de Poisson desempeña un papel predominante en la posición y extensión de zonas de tensión en la cortina de presas de tierra y enrocamiento (Louault, 1997; Pérez, 2000). Por otro lado, respecto a los análisis de flujo de agua, se han podido definir técnicas basadas en el MEFE para tomar en cuenta la considerable incertidumbre asociada con la conductividad hidráulica (López, 2010). La importancia de estos resultados para la geotecnia ha alentado la búsqueda de nuevas herramientas numéricas que permitan incorporar otras variantes (como la variación espacial, debida a las condiciones de depósito del suelo) en los análisis estocásticos con el MEF.

Recientemente, los avances computacionales aunados a los métodos numéricos, han permitido el desarrollo de nuevas técnicas matemáticas que hacen posible modelar e integrar cada vez mejor las incertidumbres en los análisis mecánicos con elementos finitos. Tal es el caso del enfoque espectral (Ghanem y Spanos, 1991), cuyas bases matemáticas se fincan en los métodos del análisis funcional y, de manera más específica, en el espacio de funciones de Hilbert. La estrategia consiste en representar el campo aleatorio del parámetro de interés (por ejemplo, el módulo de deformación), por un conjunto de variables aleatorias y funciones ortogonales, lo que permite tratar la variabilidad espacial de las propiedades del material analíticamente. La formulación aleatoria de los desplazamientos se realiza entonces en términos de una nueva dimensión que permite una mejor representación matemática del sistema. Por tal motivo, el MEFE enfoque espectral (MEFEE) resulta ser una técnica numérica atractiva para modelar en geotecnia la incertidumbre de los parámetros constitutivos provocada por la variación espacial, y a su vez, mostrar cómo ésta influye en los resultados de los análisis con el MEF.

En este trabajo se muestra la utilidad de esta técnica para modelar la variabilidad espacial de las propiedades de los geomateriales mediante campos aleatorios. Asimismo, se expone cómo es posible analizar la propagación de la incertidumbre existente en el módulo de deformación de un material en el campo de desplazamientos calculados mediante el método del elemento finito estocástico (MEFE), utilizando el enfoque espectral, método que hasta el momento se ha utilizado poco en geotecnia (Pineda, 2007).

Se señalan las fuentes de incertidumbre más importantes que afectan parámetros como el módulo de deformación y se resumen brevemente los conceptos probabilista que permiten la representación de la incertidumbre. Además, se presentan brevemente los conceptos matemáticos básicos del método del elemento finito estocástico espectral (MEFEE) los cuales se reducen a dos expansiones: Karhunen-Loève y caos polinomial. Se presenta la formulación del enfoque espectral tal como la desarrollaron Ghanem y Spanos (1991). La utilidad de esta técnica se ilustra con el análisis de un sólido cúbico de dimensiones unitarias sujeto a carga axial. Tomando en cuenta las limitaciones prácticas actuales de esta técnica, en este trabajo se limitan los análisis presentados al caso en que el material se puede considerar en primera aproximación como elástico lineal (módulo de deformación y relación de Poisson). La validez de la hipótesis de un comportamiento aproximadamente elástico lineal de los materiales constitutivos en los análisis de esfuerzo-deformación con el MEF de estructuras térreas ha sido confirmada con mediciones de campo (Alberro et al., 1998) a la condición de tomar en cuenta la no-linealidad geométrica (construcción por capas).

Fuentes de incertidumbre en los análisis realizados por el MEF

En los análisis con MEF en geotecnia, los resultados se ven afectados por la incertidumbre asociada a parámetros como el módulo de deformación. Las principales fuentes que dificultan la determinación de este parámetro son:

• a)

  La variabilidad espacial de las propiedades del suelo que depende principalmente de la historia geológica de formación del suelo y, en su caso, del procedimiento constructivo. La evaluación de esta variabilidad está condicionada por la cantidad de información obtenida en la exploración geotécnica.

• b)

  Errores aleatorios y sistemáticos, los primeros se cometen durante la realización de las pruebas de laboratorio; los segundos se deben a un sesgo en la medición, producido por ejemplo, por el remoldeo de muestras o por el uso de correlaciones aproximadas entre propiedades físicas y mecánicas.

Representación de incertidumbre en geotecnia

La teoría más aceptada hasta el momento para representar la incertidumbre en ingeniería es la de la probabilidad (Benjamin y Cornell, 1970). A través de ella, es posible modelar la incertidumbre de los parámetros de los materiales que intervienen en los análisis con elementos finitos por medio de variables o campos aleatorios.

a) Variables aleatorias

Se recurre al concepto de variable aleatoria (función del resultado θ de un experimento) cuando se requiere modelar la incertidumbre asociada a escasa información respecto al parámetro mecánico de interés V para el medio estudiado. La estimación de las características generales de una población (esperanza E{V} y varianza var[V]) se realiza mediante estimaciones puntuales o intervalos de confianza. La representación de la variación espacial mediante variables aleatorias no toma en cuenta la posición específica de las muestras ni la dependencia existente entre ellas.

b) Campos aleatorios

Dentro de la teoría de probabilidad, un concepto adecuado para representar la variabilidad espacial, en un dominio dado, de las propiedades del medio analizado es el de campo aleatorio V(X, θ). La propiedad de interés en cada punto X del medio se considera entonces una variable aleatoria (función del resultado del experimento, θ). Por medio de la función de autocovarianza C_V(X₁, X₂), se describe la correlación espacial entre las distintas variables, quedando el campo definido por esta función, su valor esperado E{V(X, θ)} y su varianza var[V(X, θ)]. Cuando no existe confusión posible en el contexto, el campo se escribe simplemente V(X). Los parámetros y funciones que describen un campo son entonces (Auvinet, 2002):

• □

  Valor esperado: μ_V(X)=E{V(X)}

• □

  Varianza: σ²_V(X) = var[V(X)]. La raíz cuadrada σ_V(X) de la varianza se llama desviación estándar

• □

  Coeficiente de variación: CV_v(X) = σ_v(X)/E{V(X)}

• □

  Función de autocovarianza: C_V(X₁, X₂) = Cov[V(X₁), V(X₂)]=E{[V(X₁)−μ_v(X₁)][V(X₂) − μ_v(X₂)]}

• □

  Autocovarianza normalizada (también llamada coeficiente de autocorrelación): ρ_v(X₁, X₂) = C_v(X₁, X₂)/σ_v(X₁) σ_V(X₂).

Auvinet (2002) ha clasificado los campos como: estimativos o descriptivos.

Estimativos

Cuando no se cuenta con muestreo ni mediciones de campo, se realiza un análisis de incertidumbre a priori. La variación espacial de los parámetros de los materiales es entonces definida generalmente mediante una variable aleatoria para cada subdominio que reúne ciertas condiciones de homogeneidad. El grado de correlación entre diferentes variables estimativas es siempre difícil de estimar. Conviene considerar que existe correlación entre las propiedades de materiales diferentes cuando se tiene el mismo tipo de dudas respecto a su valor, o cuando han sido determinadas experimentalmente por el mismo procedimiento (Auvinet, 2002). Es también posible definir a priori uno o varios campos aleatorios representativos de las variaciones de las propiedades, con una función de autocovarianza estimada a partir de la experiencia obtenida en sitios con características semejantes.

Descriptivos

El campo de tipo descriptivo corresponde a una situación en la que se tiene un número significativo de mediciones en distintos puntos de la masa del suelo, el análisis de incertidumbre es entonces a posteriori. Los parámetros del campo se obtienen directamente a partir de las mediciones o modificando los parámetros de un campo estimativo definido a priori usando un enfoque Bayesiano. El campo aleatorio descriptivo resultante es entonces de tipo condicional con respecto a las mediciones.

Enfoque espectral

Los análisis estocásticos que se realizan con el MEF en geotecnia, mediante el método de perturbaciones, representan generalmente la incertidumbre de los parámetros constitutivos a través de variables aleatorias. El enfoque espectral tiene la ventaja de permitir representar la variabilidad espacial por medio de campos aleatorios Gaussianos¹. En esta sección se describen las herramientas matemáticas que permiten la formulación del MEFEE tal como la desarrollaron Ghanem y Spanos (1991).

Este método se puede utilizar en geotecnia para realizar análisis de incertidumbre en donde la variabilidad espacial de las propiedades de los materiales (por ejemplo el módulo de deformación) se modela como un campo aleatorio Gaussiano, eventualmente después de una transformación del campo real. Posteriormente, las características (esperanza, desviación estándar) del campo aleatorio de la respuesta (desplazamientos, deformaciones, etcétera) son determinadas a través de un análisis de segundos momentos (Sudret y Der Kiureghian, 2000).

En el caso de la elasticidad lineal, el enfoque espectral consiste en utilizar la función de autocovarianza para representar el campo aleatorio del módulo de deformación, a través de una expansión en serie llamada de Karhunen-Loève (Papoulis, 1991) que utiliza un número finito de variables aleatorias; las cuales posteriormente se emplean para representar la respuesta del sistema mediante una expansión en caos polinomial (Wiener, 1938). Se trata de un artificio matemático que permite finalmente, formular el método de elementos finitos estocásticos.

a) Representación de la incertidumbre

En el enfoque espectral el campo aleatorio V(X) del módulo de deformación se representa mediante la expansión en serie de Karhunen-Loève. Esta expansión, considera que el campo es estacionario en el sentido amplio²; se basa en la descomposición espectral de la función de autocovarianza y permite reducir la dimensión del campo aleatorio de forma abstracta a través de un conjunto finito M de variables aleatorias y funciones deterministas ortogonales. Tal serie se expresa de la siguiente manera

donde E{V(X)} representa la esperanza matemática del campo aleatorio; ξ_i(θ) son las coordenadas de realización del campo aleatorio con respecto a un conjunto de funciones deterministas ϕ_i y forman un conjunto de variables aleatorias no correlacionadas con media cero y varianza unitaria; λ_i y ϕ_i son los valores y funciones característicos de la función de autocovarianza, definidas a su vez, por la solución de la ecuación integral, cuya forma es

donde Ω es el dominio espacial en el cual se define el campo aleatorio.

La ecuación (2) se conoce como ecuación integral de Fredholm homogénea de segundo género, en la cual el núcleo C_V(X₁, X₂), está definido por la función de auto-covarianza, que es real, simétrica y positiva; X₁ y X₂ son las coordenadas espaciales. La solución de la ecuación integral puede ser obtenida analítica y numéricamente; ambas soluciones fueron propuestas por Ghanem y Spanos (1991) para el caso de campos aleatorios Gaussianos.

El objetivo de la serie de Karhunen-Loève es discretizar, de forma abstracta, el campo aleatorio en el espacio de funciones de Hilbert. La variabilidad de la propiedad (módulo de deformación) se representa como una suma de proyecciones ortogonales (funciones características) a través de los valores característicos, los cuales expresan la cantidad de varianza que las funciones características llevan a ese espacio (Matthies et al., 2005).

b) Representación de la respuesta

Como la respuesta del sistema es una función de la variabilidad del módulo de deformación, queda expresada en términos de funcionales no lineales, representados a través de un conjunto de polinomios ortogonales de variables aleatorias Gaussianas llamado caos polinomial. La respuesta se expande por medio de estos polinomios sobre el espacio de Hilbert, debido a que la función de autocovarianza no es conocida a priori como en el caso del campo aleatorio del módulo de deformación.

La formulación del caos polinomial está basada en el concepto de caos homogéneo que fue introducido por Wiener, cuyos fundamentos fueron el resultado de investigaciones de funcionales no lineales del movimiento Browniano (Wiener, 1938). Se puede decir que el concepto de caos polinomial es una generalización de las series de Taylor a funcionales no lineales (Cameron y Martin, 1947).

Para representar cada desplazamiento nodal aleatorio dentro de una estructura que capture la variabilidad posible de estos, se requiere crear una base estocástica a través de expansiones no lineales. Así, cada variable aleatoria se puede expandir mediante un caos polinomial de la siguiente manera:

donde: Γp(ξi1(θ),…,ξi(θ)) denota el caos homogéneo de orden p y pyuip son las coordenadas de la variable u(θ) asociadas a este orden (cero, primero, segundo, etcétera). Se define como caos polinomial al conjunto de polinomios multidimensionales y al espacio que ocupan tales polinomios se le llama caos homogéneo.

La construcción del caos polinomial de dimensión finita es a partir de un número M de variables aleatorias Gaussianas ortonormales, ξ_i(θ) que provienen de la expansión en serie de Karhunen-Loéve.

El caos polinomial de dimensión M y orden p se obtiene a partir de polinomios multidimensionales Gaussianos. Cada uno de estos polinomios se define como una secuencia de M enteros no negativos {α₁, …, α_M} de la siguiente manera

donde: Hαi es el polinomio de Hermite unidimensional asociado a la secuencia α, cuyo grado es menor o igual que p.

El número P de coeficientes que conforman el caos polinomial y que contiene toda la estructura probabilista de cada desplazamiento nodal aleatorio, se obtiene mediante una combinación binomial (Benjamin y Cornell, 1970)

Los valores usuales utilizados en las aplicaciones son M = 4 y p = 2,3.

Así, cada desplazamiento expresado en la ecuación (3) se puede escribir en términos de estos coeficientes, como

donde a_i y Ψ_i[{ξ_k}] corresponden a uip y Γp(ξi1(θ),…,ξip(θ)), respectivamente.

c) Formulación del MEFEE

En el análisis lineal por el método del elemento finito clásico se establece un sistema de ecuaciones de equilibrio

F es un vector de fuerzas nodales y volumétricas; U es un vector de desplazamientos nodales y K corresponde a la matriz de rigidez total, con forma

dondeΩ

es el dominio de estudio,

B

es la matriz de forma y

D

es la matriz de elasticidad.

La formulación de la ecuación de equilibrio estocástica del MEFEE se basa en representar la variabilidad espacial de la propiedad del material (módulo de deformación) como un campo aleatorio V_E(X) mediante la expansión de Karhunen-Loéve, quedando la matriz de elasticidad D expresada como

donde D₀ es una matriz de elasticidad calculada con un módulo de deformación unitario. Si la expresión 9 se sustituye en la matriz de rigidez (8), ésta queda expresada por una parte determinista K¯ y una parte estocástica como

De acuerdo con Ghanem y Spanos (1991) la ecuación de equilibrio estocástica se obtiene al sustituir en la ecuación de equilibrio (7) la matriz de rigidez estocástica (10) y los desplazamientos estocásticos representados en términos del caos polinomial(6), finalmente la ecuación se expresa como

siendo F un vector de cargas deterministas.

El punto principal en la formulación del MEFEE es minimizar el error ∈_M,P, resultante del truncamiento de las series, mediante el método de Galerkin (Zienkiewicz y Taylor, 1995) con el fin de obtener la mejor aproximación de los desplazamientos.

Se requiere, entonces, que el residuo ∈_M,P sea cero, es decir, ortogonal al espacio que ocupa el caos polinomial {Ψk}k=0P−1, quedando

donde E{•} denota la esperanza matemática.

Para minimizar el error, ambos lados de la ecuación (11) se multiplican por Ψ_k, y se toman esperanzas, obteniendo

La ecuación (13), que representa la ecuación de equilibrio estocástica global, es una función de la base polinomial sobre el espacio de funciones de Hilbert; donde F_k = E{FΨ_k} es cero si k > 0 para cargas deterministas y E{ξ_i Ψj Ψk} es la esperanza del producto de dos polinomios y una variable aleatoria (Sudret y Der, 2000; Dumitriu et al., 2007), denotada por c_ijk. Agrupando términos en la ecuación (13), se tiene finalmente que la ecuación de equilibrio estocástica es

con

La ecuación (14) establece un sistema de ecuaciones lineales con dimensiones N.P × N.P, donde N está determinado por el número físico de grados de libertad en el modelo de elemento finito y P por el número de coeficientes que se utilizan en la expansión en caos polinomial, dicho sistema se expresa como:

d) Cálculo de la incertidumbre sobre los desplazamientos

Para conocer las características (esperanza y matriz de covarianza) del campo aleatorio de la respuesta, se recurre a un análisis de segundos momentos (Sudret y Der, 2000), ya que los coeficientes de la ecuación (14) por sí solos no dan una idea clara de la incertidumbre sobre los desplazamientos, así se tiene

La expresión (17) representa la esperanza matemática de los desplazamientos U y la expresión (18) define la matriz de covarianza (incertidumbre) sobre los desplazamientos en términos de la norma al cuadro (E{Ψi2}).

Aplicación

Para ilustrar la utilidad del método espectral en la modelación de la variabilidad espacial de las propiedades del suelo, se expone un ejemplo sencillo de interés práctico para la ingeniería y la geotecnia. Este análisis permite observar la propagación de la incertidumbre del módulo de deformación en los desplazamientos horizontales y verticales en un sólido cúbico. Para la realización del ejemplo, se adaptó una subrutina del programa FERUM versión 3 (finite element reliability using matlab), llamada FERUMssfem (Sudret y Der, 2000) que permite realizar análisis de incertidumbre con el MEFEE en dos dimensiones.

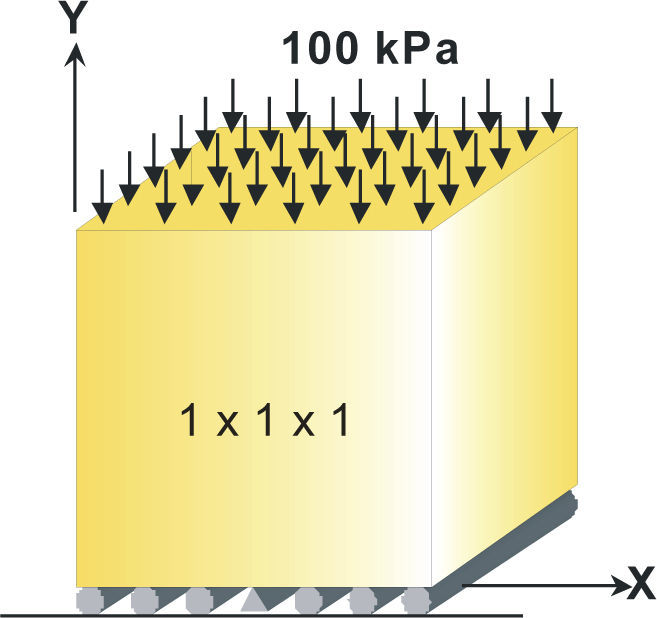
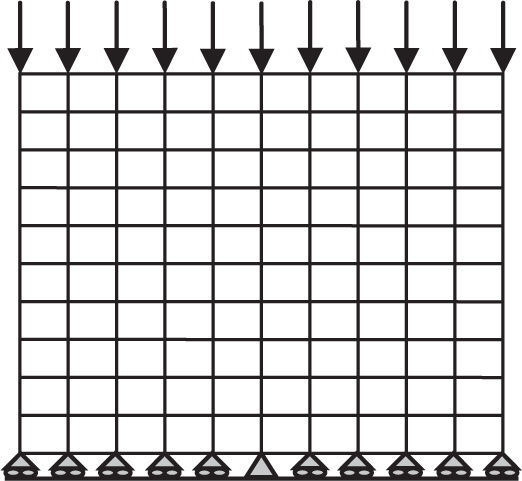
Planteamiento

Se considera un sólido cúbico de dimensiones unitarias (1 x 1 x 1 m), constituido de un solo material con módulo de deformación aleatorio, sometido a presión vertical de 100 kPa. Los apoyos en el extremo inferior restringen el movimiento verticalmente; el central, lo restringe también horizontalmente. En la figura 1 se observan estas condiciones. El análisis se realiza suponiendo en primera aproximación que prevalece un estado de esfuerzos planos. Se evaluará la incertidumbre en los desplazamientos horizontales y verticales con el MEFEE. Para realizar el análisis, el cubo se discretizó con una malla de 100 elementos, la presión se representó como cargas puntuales aplicadas en los puntos nodales superiores de la malla, como se muestra en la figura 2.

Figura 1.

Representación isométrica del sólido cúbico

Figura 2.

Malla de elementos finitos

Se acepta que el módulo de deformación varía en dos dimensiones de acuerdo con un campo aleatorio estacionario. Se ignora la variación en la dirección perpendicular al plano de análisis, lo que equivale a suponer correlación perfecta en esta dirección, es decir, que no existen variaciones del módulo de deformación de un punto a otro en esta dirección. Las características supuestas del campo aleatorio bidimensional del módulo de deformación E son: E{E} = 100 kPa; CV(E) = 0.1; la relación de Poisson (v) se considera determinista con: E{v} = 0.3; CV(v) = 0. Se acepta que la función de autocovarianza normalizada del módulo de deformación es de tipo exponencial:

donde L se define en forma convencional como “distancia de correlación”, y corresponde a la distancia a partir de la cual la correlación se considera despreciable.

Resultados

A través del coeficiente de variación, CV, es posible evaluar la influencia de la incertidumbre del módulo de deformación sobre los desplazamientos horizontales y verticales en todo el cuerpo del sólido. En las curvas de isovalores de las siguientes gráficas se aprecia con claridad tal variación, establecida para distintas distancias de correlación.

En este primer análisis, el campo aleatorio es del tipo “ruido blanco” (sin autocorrelación). Las figuras 3b y 4b muestran que la incertidumbre en los desplazamientos verticales y horizontales es nula, debido a un efecto de promedio espacial o compensación estadística que anula la desviación estándar y, por consecuencia, el CV es igual a cero en todo el cuerpo del sólido. Un material cuyo módulo presenta una variación aleatoria espacial que puede representarse con un campo de ruido blanco se comporta, por tanto, como un material homogéneo no aleatorio.

Figura 3.

Esperanza y coeficiente de variación de los desplazamientos verticales

Figura 4.

Esperanza y coeficiente de variación de los desplazamientos horizontales

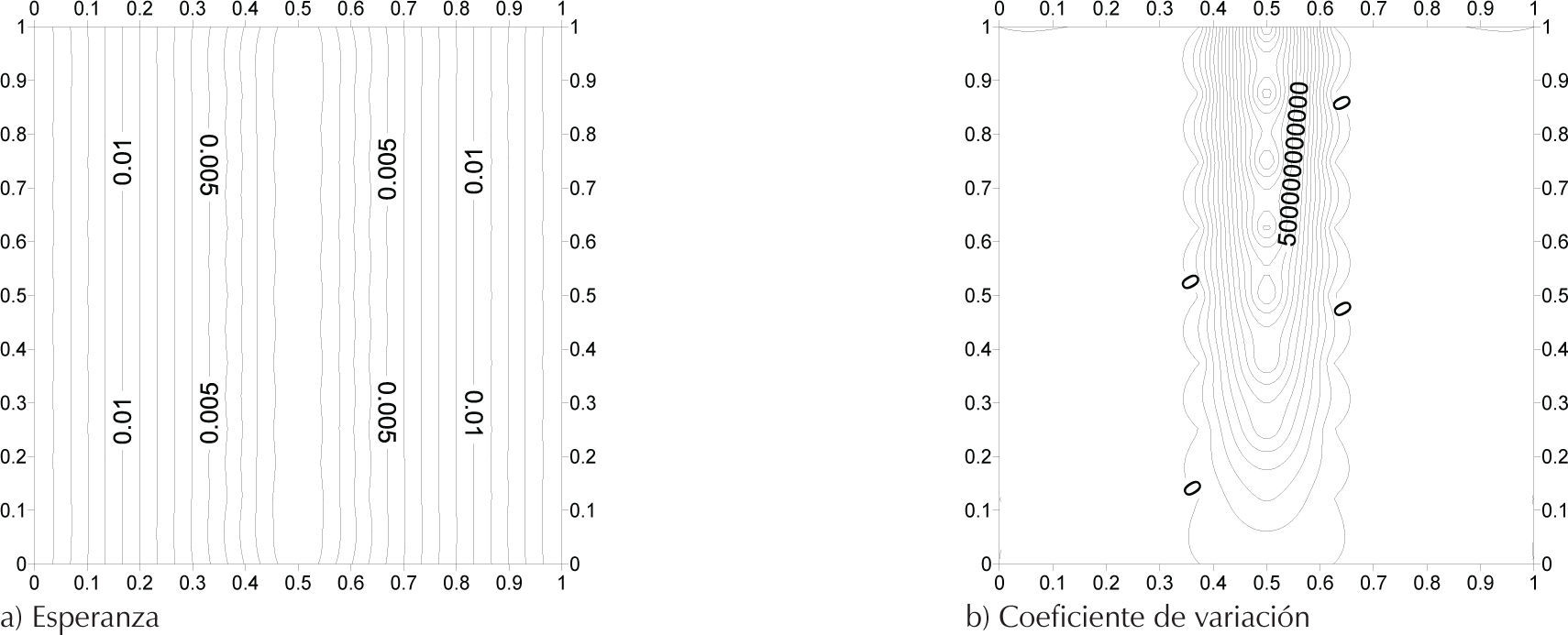
En este segundo análisis, la distancia de correlación (0.64 m) es ligeramente inferior al ancho del sólido (1 m). La figura 5b muestra que, como debía esperarse, la incertidumbre sobre los desplazamientos verticales es nula en la parte inferior del sólido, donde el movimiento fue restringido. En el resto del sólido se observa que la incertidumbre no es uniforme debido al efecto de promedio espacial o compensación estadística. Por ejemplo, la incertidumbre en el punto superior central es menor que en el punto superior de la esquina del sólido debido a que el número de materiales “puntuales” con baja correlación que interactúan es mayor en el punto central que en el de la esquina. Por otra parte, en la figura 6b se observa cómo el CV de los desplazamientos horizontales tiende a infinito sobre el eje de simetría; en este caso, el comportamiento del material es fuertemente heterogéneo lo que da lugar a que se presenten variaciones aleatorias alrededor de su valor esperado (que es nulo), originando una incertidumbre relativa infinita sobre tal eje.

Figura 5.

Esperanza y coeficiente de variación de los desplazamientos verticales

Figura 6.

Esperanza y coeficiente de variación de los desplazamientos horizontales

Distancia de correlación L= 0

Distancia de correlación L= 0.64m

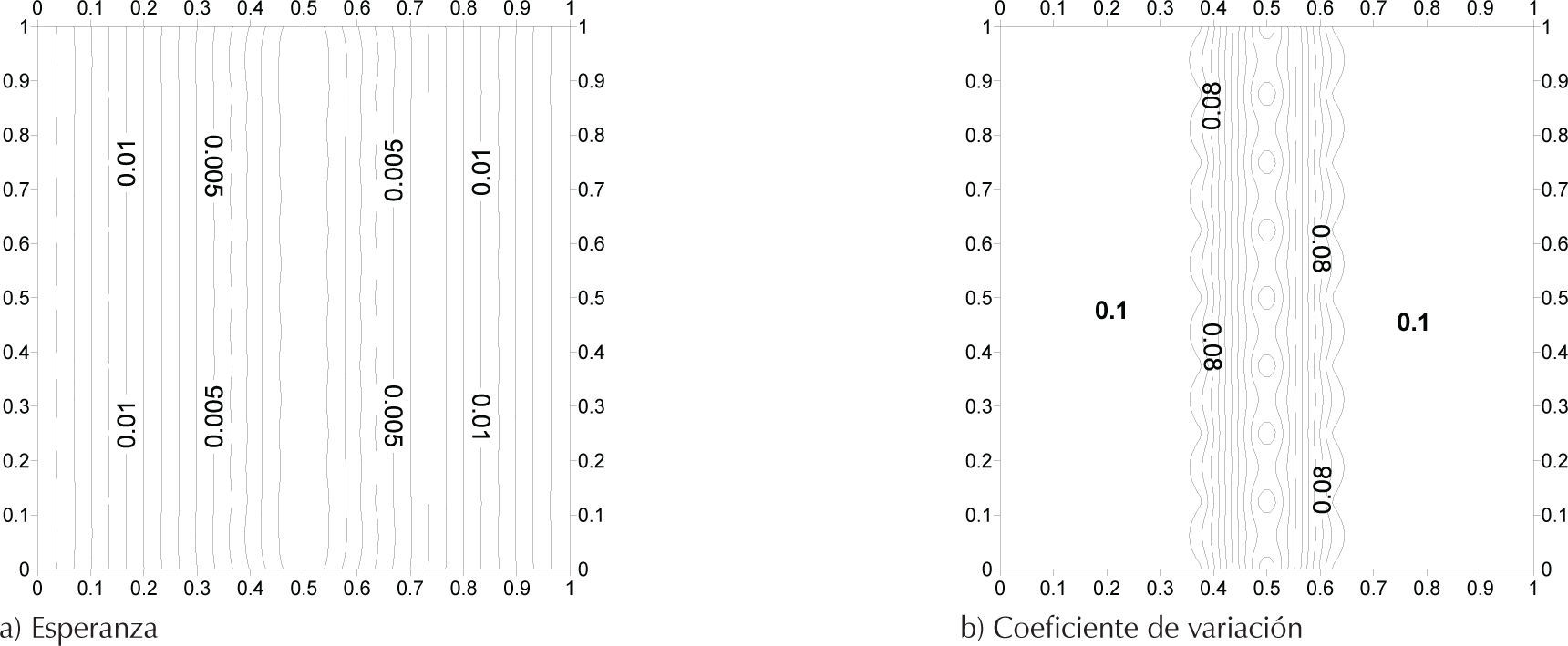
Distancia de correlación infinita

Cuando la distancia de correlación es infinita, el material se comporta como un sólido homogéneo pero aleatorio. En la figura 7b, se observa que, nuevamente, en los nodos donde el movimiento se restringió no existe incertidumbre.

Figura 7.

Esperanza y coeficiente de variación de los desplazamientos verticales

En el resto del espécimen, la misma magnitud de la incertidumbre en el módulo de deformación se refleja directamente en los desplazamientos verticales. Por otro lado, tomando en cuenta que se conserva en este caso la simetría de los desplazamientos horizontales, la incertidumbre sobre el eje del sólido, donde el desplazamiento es necesariamente nulo, es también nula, como se muestra en la figura 8b. En el resto del espécimen, la misma magnitud de la incertidumbre en el módulo de deformación se refleja en los desplazamientos horizontales.

Figura 8.

Esperanza y coeficiente de variación de los desplazamientos horizontales

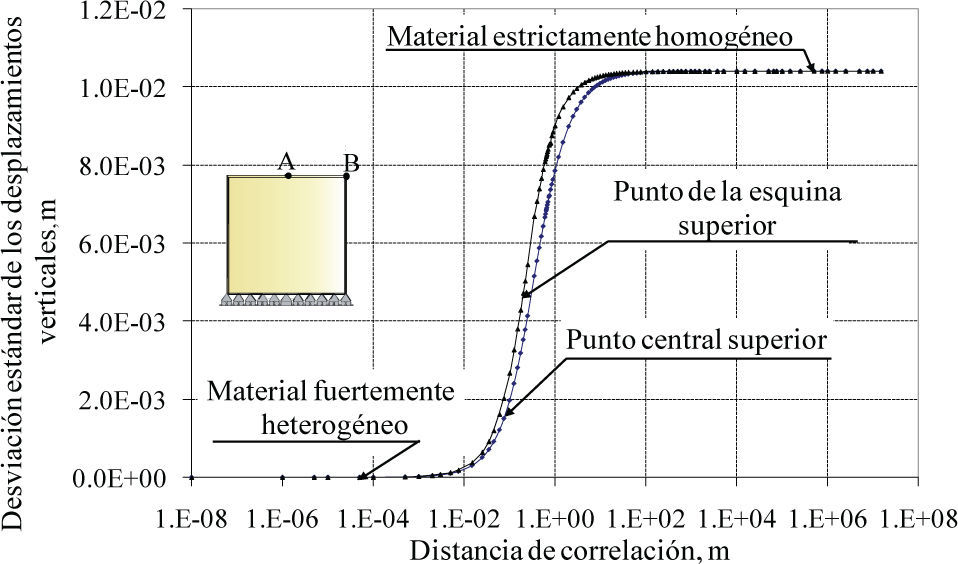
La variabilidad del desplazamiento vertical para el centro superior del cubo (punto A) en función de la distancia de correlación se muestra en la figura 9. Para distancias de correlación pequeñas, la incertidumbre (desviación estándar) sobre este desplazamiento es nula; tal resultado se debe al efecto de compensación estadística ya mencionado, debido a que el material es fuertemente heterogéneo (ruido blanco) pero estadísticamente homogéneo. Conforme la distancia de correlación aumenta, la incertidumbre crece y se presenta una incertidumbre mayor para el punto A que para el B, hasta alcanzar la magnitud de la incertidumbre impuesta en el módulo de deformación, cuando el material se vuelve estrictamente homogéneo.

Figura 9.

Influencia de la distancia de correlación sobre la incertidumbre en los desplazamientos verticales

La incertidumbre (desviación estándar) sobre el desplazamiento horizontal en función de la distancia de correlación para el punto central superior (punto A) se observa en la figura 10. Nuevamente, para distancias de correlación pequeñas, la incertidumbre de tal desplazamiento es nula, existiendo también un efecto de compensación estadística. Posteriormente, la incertidumbre se incrementa y alcanza su máximo valor para una distancia de correlación del mismo orden que la dimensión horizontal del dominio en estudio; conforme la distancia de correlación se sigue incrementando, el material comienza a estabilizarse estadísticamente y la desviación estándar de los desplazamientos comienza a disminuir, hasta alcanzar nuevamente un valor nulo, lo cual representa la homogeneidad estricta del material con rigurosa simetría axial. El comportamiento estadístico del material para el punto superior de la esquina del sólido es similar al del punto superior central del espécimen, a excepción de que para este punto el menor valor alcanzado no es nulo y está condicionado por la incertidumbre impuesta en el módulo de deformación.

Figura 10.

Influencia de la distancia de correlación sobre la incertidumbre en los desplazamientos horizontales

Este sencillo ejemplo muestra que la distancia de correlación constituye un parámetro importante que representa la heterogeneidad local que puede presentar un material estadísticamente homogéneo y condiciona la incertidumbre que se puede esperar en el comportamiento del mismo. Mayor atención debería prestarse a este parámetro, especialmente en los análisis geotécnicos.

Ventajas y limitaciones del método

Una de las ventajas del enfoque espectral en comparación con otras técnicas probabilistas comúnmente empleadas (métodos de perturbaciones) es que permite realizar análisis de incertidumbre que toman en cuenta la variabilidad espacial de las propiedades del suelo mediante campos aleatorios. Tal como se planteó en este trabajo, en su estado actual, el método solamente se aplica a problemas de elasticidad lineal y permite representar la variabilidad espacial de un solo campo aleatorio (módulo de elasticidad, E), cuyas variables aleatorias tienen una distribución Gaussiana. Sin embargo, la formulación del MEFEE se puede extender al caso en el que se considere la relación de Poisson, v, también aleatoria (debido al intervalo de valores que v puede tomar, este parámetro se considera como un campo aleatorio tipo Beta), aún cuando esto ocasiona un mayor esfuerzo de cálculo. Este es el tema de una investigación que están realizando actualmente los autores del presente trabajo. Ghanem (1999) extendió la formulación del MEFEE a problemas de conducción de calor con campos aleatorios lognormales. Por su parte, Matthies y Keese (2005) han planteado la ecuación de equilibrio estocástica del MEFEE para campos no Gaussianos. Recientemente Sett et al. (2011) propusieron una formulación del MEFEE que permitiría abordar el caso elasto-plástico, lo que aumentaría su interés en Geotecnia.

El enfoque espectral presenta, por tanto, un potencial importante. Su mayor inconveniente es probablemente que la representación matemática de los campos aleatorios a la que recurre se aleja del concepto físico, y puede parecer muy abstracta a los ingenieros geotécnicos prácticos.

Conclusiones

Se presentaron brevemente los conceptos probabilistas que permiten modelar la incertidumbre (variación espacial) en los parámetros de materiales y evaluar su influencia sobre los resultados de los análisis con elemento finito (MEF). Asimismo, se presentaron las herramientas matemáticas de una nueva técnica: el enfoque espectral, donde se evaluó su utilidad a través del análisis de un sólido cúbico. Los resultados del ejemplo analizado son de gran utilidad para ilustrar cualitativamente cómo la variabilidad espacial puede afectar los resultados de los análisis con el MEF. Ponen en particular evidencia el fenómeno de compensación estadística y la importancia de la distancia de correlación. Un análisis de incertidumbre que tome en cuenta la variabilidad espacial de las propiedades de los materiales puede resultar particularmente útil en el caso de estructuras térreas, obras que se construyen con materiales, cuyas propiedades tienen un grado alto de incertidumbre debido a su heterogeneidad inherente.

Los comentarios presentados en este trabajo marcan las ventajas y limitaciones del método espectral y deberían ser útiles para el ingeniero deseoso de utilizar este tipo de técnicas.