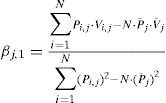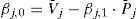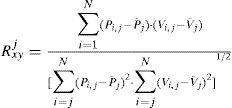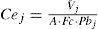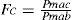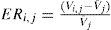Modelación del proceso precipitación-escurrimiento mensual por medio de regresiones

Resumen

Para la solución de los problemas asociados con la evaluación de los recursos hídricos de un río, la modelación del proceso precipitación–escurrimiento (PPE) permite deducir datos faltantes de escurrimiento, así como ampliar su registro, ya que por lo general la información disponible de precipitación tiene más amplitud. También hace posible la estimación de las entradas a embalses, cuando la construcción de estos suspendió a la estación de aforos. El modelo matemático más simple que se puede establecer para el PPE es la regresión lineal o curva, a nivel mensual. Este modelo se describe con detalle y se calibra con el registro conjunto de precipitación y escurrimiento mensuales de la estación hidrométrica Ballesmi, el cual abarca 35 años. Como el escurrimiento de la estación tiene una contribución importante de la descarga de manantiales, primero se corrigió su registro, retirando esa aportación. Para ello se desarrolló un procedimiento basado en los coeficientes de escurrimiento promedio mensual regionales o de una cuenca cercana y similar; en este caso se utilizó la estación de aforos Tancuilín. Ambas estaciones pertenecen a la Región Hidrológica Núm. 26 Parcial (Bajo Río Pánuco) y se ubican dentro del estado de San Luis Potosí. Los contrastes realizados indican que el modelo de regresión mensual, debido a su planteamiento conceptual, reproduce fielmente los volúmenes escurridos promedio mensual y alcanza una excelente aproximación en relación con su dispersión, lo anterior comprobado con base en las medias y las desviaciones estándar.

Abstract

To solve the problems associated with the assessment of water resources of a river, the modeling of the rainfall-runoff process (RRP) allows the deduction of runoff missing data and to extend its record, since generally the information available on precipitation is larger. It also enables the estimation of inputs to reservoirs, when their building led to the suppression of the gauging station. The simplest mathematical model that can be set for the RRP is the linear regression or curve on a monthly basis. Such a model is described in detail and is calibrated with the simultaneous record of monthly rainfall and runoff in Ballesmi hydrometric station, which covers 35 years. Since the runoff of this station has an important contribution from the spring discharge, the record is corrected first by removing that contribution. In order to do this a procedure was developed based either on the monthly average regional runoff coefficients or on nearby and similar watershed; in this case the Tancuilín gauging station was used. Both stations belong to the Partial Hydrologic Region No. 26 (Lower Rio Panuco) and are located within the state of San Luis Potosi, México. The study performed indicates that the monthly regression model, due to its conceptual approach, faithfully reproduces monthly average runoff volumes and achieves an excellent approximation in relation to the dispersion, proved by calculation of the means and standard deviations.

Introducción

La modelación del proceso precipitación–escurrimiento (PPE) es necesaria cuando se deben estimar los recursos hídricos de un río y para ello, es conveniente ampliar su registro. En este caso se puede establecer un modelo del PPE a nivel mensual. En otras situaciones, como en el pronóstico de crecientes o en la estimación del impacto de descargas contaminantes, resulta indispensable la modelación del PPE a nivel diario e incluso horario. Beven (2001) establece y destaca que la razón teórica principal por la cual se requiere modelar el PPE, se debe a la limitación real que se tiene para medir todos los procesos hidrológicos que ocurren en una cuenca al transformar la precipitación en el escurrimiento. También cita ejemplos prácticos y generales asociados a la escasez de datos, donde es imprescindible la modelación del PPE, como en las cuencas sin aforos, las cuales no tienen información hidrométrica, o bien, cuando se debe estimar el impacto en el futuro de los cambios hidrológicos inducidos o probables, entonces las mediciones no son posibles.

Según Beven (2001), una primera clasificación general de los variados enfoques de modelación del PPE, distingue entre modelos globales y distribuidos, los primeros consideran a la cuenca como una unidad y sus variables y parámetros corresponden a los valores promedio de tal área; los segundos dividen la cuenca en áreas elementales y sus variables y parámetros se asocian a cada uno de tales elementos. La segunda diferencia básica es entre modelos determinísticos y estocásticos, los primeros producen una respuesta única para cada simulación que utiliza una serie de datos entrada y parámetros; en cambio los segundos permiten cierta aleatoriedad o incertidumbre en sus respuestas, debido a la variabilidad de sus variables de entrada, parámetros o condiciones de frontera. Otras clasificaciones, más detalladas o exhaustivas de los modelos del PPE se pueden consultar en Haan et al. (1982) y Singh (1995).

Desde que se inició la modelación del PPE hacia mediados de los años sesenta, los modelos conceptuales y los de caja negra son los que más han proliferado. Los primeros emplean representaciones matemáticas simplificadas de los principales procesos hidrológicos que ocurren en la cuenca y los segundos son totalmente matemáticos, se basan únicamente en las mediciones de entrada y salida de la cuenca, sin tomar en cuenta los procesos internos que transforman la precipitación en escurrimiento (Jones, 1997; Shaw et al., 2011). Los modelos que se emplean en este trabajo son del segundo tipo.

El objetivo de este trabajo consiste en describir con detalle el modelo general de regresión polinomial con memoria mensual, que considera a la precipitación como entrada y al escurrimiento como salida o respuesta. El modelo se aplica, para su calibración, a la cuenca de la estación hidrométrica Ballesmi del Río Coy de la Región Hidrológica Núm. 26 Parcial (Bajo Río Pánuco), en el estado de San Luis Potosí, que cuenta con un registro conjunto de precipitación y escurrimiento mensuales de 35 años. La estación de aforos Ballesmi fue seleccionada para este estudio, por tener un área de drenaje pequeña (194 km²) y disponer de tres estaciones pluviométricas, dos de ellas en su cuenca. Debido a que el escurrimiento de esta estación tiene una aportación importante de manantiales, primero se corrige con base en los coeficientes de escurrimiento promedio mensual observados en la estación de aforos Tancuilín, que también pertenece a la región hidrológica citada, es la más cercana, del mismo orden de magnitud (321 km²) y cuyo escurrimiento no está afectado por aportaciones subterráneas (IMTA, 2002). Los contrastes realizados muestran que los modelos de regresión mensuales permiten una buena aproximación para la estimación del escurrimiento mensual, ya que reproducen fielmente los valores promedio mensuales y se aproximan bastante a la dispersión observada.

Resumen de la teoría operativa

Modelo general de regresión

Propuesto y aplicado por Mimikou y Rao (1983) es el modelo matemático más simple que puede plantearse para reproducir el PPE a nivel mensual, sea este lineal o curvo. Su expresión general es:

siendo, V_i,j el escurrimiento mensual del i–ésimo año, con i variando de 1 a N, que es la amplitud del registro conjunto procesado y j es número de mes, con 1 para enero y 12 para diciembre. Es común expresar a V_i,j, en la ecuación 1, en milímetros, lo cual equivale a dividir su valor en miles de metros cúbicos (10³ m³) entre el área de cuenca A en km². P_i,j es la precipitación mensual representativa de la cuenca en milímetros. K y n son los parámetros del modelo y β_j,k son los coeficientes de regresión del modelo, los cuales se obtienen mediante un ajuste de mínimos cuadrados de los residuos.

Selección de los parámetros del modelo

Los parámetros K y n definen la estructura del modelo. El primero determina su orden como ecuación de regresión polinomial y el segundo su memoria con respecto a la precipitación mensual. Entonces, para estimar el valor de K se debe establecer la relación funcional entre el escurrimiento y la precipitación de cada mes, el primero como la variable dependiente en las ordenadas y la segunda como la variable independiente en las abscisas. Como esta relación puede ser lineal o curva, en el primer caso K = 1 y en el segundo K > 1. No es común encontrar valores de K diferentes en cada mes y, por ello, este parámetro es considerado una característica de la cuenca (Mimikou y Rao, 1983).

Cuando alguna relación funcional mensual muestre gran dispersión, se debe establecer la relación entre V_i,j y un valor promedio de las precipitación de los meses j, j–1, …, j–n, con n indicando la memoria del proceso en el mes j. Por lo común, con n = 1 es suficiente para mejorar la relación, en cuencas pequeñas.

Coeficientes de regresión y correlación de la relación funcional

Cuando K = 1 la ecuación 1 es una línea recta, con β_j,0 como ordenada al origen y β_j,1 como pendiente de la recta, cuyas expresiones del ajuste por mínimos cuadrados de los residuos son (Campos, 2003):

En las ecuaciones anteriores, P_i,j es la precipitación mensual cuando n = 0 y puede ser el promedio de la de ese mes y el anterior, si n = .P¯jyV¯j son los valores promedio mensual de la precipitación y el escurrimiento, ambos en milímetros. La medida cuantitativa de la relación funcional entre la precipitación y el escurrimiento, se obtiene a través del coeficiente de correlación lineal (Rxyj), que establece el grado de asociación o dependencia entre ambas variables, con cero para puntos totalmente dispersos y uno cuando todos están sobre la línea recta. Su expresión es:

Cuando la relación funcional entre la precipitación y el escurrimiento es curva (K > 1) se deberá ajustar un modelo de regresión polinomial, parabólico (K = 2) o cúbico (K = 3), cuya solución se obtiene con un planteamiento matricial que se puede consultar en Campos (2003), así como su coeficiente de determinación (R²), el cual indica qué proporción de la variabilidad de la variable dependiente es explicada por la regresión polinomial.

Información hidrométrica procesada

Estación de aforos Ballesmi

Perteneciente a la Región Hidrológica Núm. 26 Parcial (Bajo Río Pánuco) fue seleccionada para este estudio por ser una cuenca pequeña que tiene dos estaciones pluviométricas dentro de ella, Santa Cruz y Aquismón, además de la ubicada en el sitio de tal hidrométrica. Mide los escurrimientos del río Coy afluente del Río Tampaón, su área de cuenca es de 194 km² y su precipitación media anual se estima en los 2000 milímetros (INEGI, 1980). Su registro de volúmenes escurridos mensuales comenzó en noviembre de 1953 y se tiene disponible hasta diciembre de 2002 en el sistema BANDAS (IMTA, 2002), bajo la clave 26241. En el lapso citado, el año de 1979 no tiene datos y los años de 1991, 1998 y 2000 están incompletos. La descripción de su régimen de escurrimiento establece que esta corriente recibe la aportación de los manantiales de El Nacimiento, por ello, primero se debe estimar esa componente subterránea, para eliminarla y después intentar modelar el PPE de manera independiente.

En la figura 1 se muestra la cuenca de la estación Ballesmi y sus respectivas estaciones pluviométricas, cuyos registros de precipitación mensual iniciaron en enero de 1961 y están disponibles hasta diciembre de 2012. Tales registros fueron proporcionados por la Dirección Estatal San Luis Potosí de la CONAGUA. Entonces el registro conjunto de escurrimiento y precipitación mensuales abarcó de enero de 1961 a diciembre de 1997, con dos años faltantes: 1979 y 1991, es decir 35 años.

Figura 1.

Localización de las cuencas y pluviómetros de las estaciones hidrométricas Ballesmi y Tancuilín en la Región Hidrológica Núm. 26 Parcial (Bajo Río Pánuco)

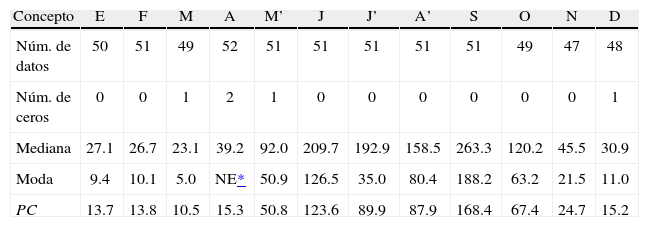
Todos los valores mensuales faltantes de precipitación de la cuenca de la estación de aforos Ballesmi, fueron adoptados igual a la moda de tal mes, estimada con base en la distribución Gamma mixta (Campos, 2005), utilizando todo el registro mensual disponible, por ello variaron de 48 a 52 datos. Cuando la moda no existe se emplea la precipitación confiable (PC), cuya probabilidad de excedencia es de 75%, es decir, que en cada cuatro años solo uno tiene una precipitación menor. En la tabla 1 se citan los resultados de los análisis mensuales, únicamente para la estación pluviométrica Ballesmi.

Tabla 1.

Resultados del ajuste mensual de la distribución Gamma Mixta a los datos de la estación pluviométrica Ballesmi

Concepto	E	F	M	A	M’	J	J’	A’	S	O	N	D
Núm. de datos	50	51	49	52	51	51	51	51	51	49	47	48
Núm. de ceros	0	0	1	2	1	0	0	0	0	0	0	1
Mediana	27.1	26.7	23.1	39.2	92.0	209.7	192.9	158.5	263.3	120.2	45.5	30.9
Moda	9.4	10.1	5.0	NE*	50.9	126.5	35.0	80.4	188.2	63.2	21.5	11.0
PC	13.7	13.8	10.5	15.3	50.8	123.6	89.9	87.9	168.4	67.4	24.7	15.2

*

no existe, la distribución mensual es de tipo J invertida

Estación de aforos Tancuilín

También ubicada dentro de la misma región hidrológica, es la más cercana a la cuenca de la estación Ballesmi, con régimen de escurrimiento no afectado por manantiales (IMTA, 2002) y con área de cuenca reducida. Sus datos generales se han concentrado en la tabla 2. La estación hidrométrica Tancuilín solo tiene la estación pluviométrica del mismo nombre ubicada en su sitio. En la figura 1 se muestra su cuenca.

Tabla 2.

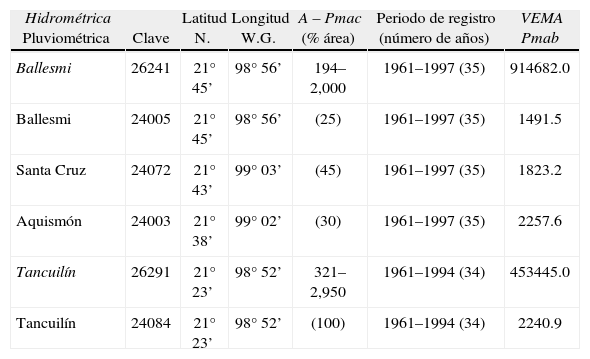
Características generales de las estaciones hidrométricas procesadas y de sus respectivas estaciones pluviométricas

Hidrométrica Pluviométrica	Clave	Latitud N.	Longitud W.G.	A – Pmac (% área)	Periodo de registro (número de años)	VEMA Pmab
Ballesmi	26241	21° 45’	98° 56’	194–2,000	1961–1997 (35)	914682.0
Ballesmi	24005	21° 45’	98° 56’	(25)	1961–1997 (35)	1491.5
Santa Cruz	24072	21° 43’	99° 03’	(45)	1961–1997 (35)	1823.2
Aquismón	24003	21° 38’	99° 02’	(30)	1961–1997 (35)	2257.6
Tancuilín	26291	21° 23’	98° 52’	321–2,950	1961–1994 (34)	453445.0
Tancuilín	24084	21° 23’	98° 52’	(100)	1961–1994 (34)	2240.9

Simbología:

A	= área de cuenca, en km^2
Pmac	= precipitación media anual en la cuenca, en milímetros
% área	= porcentaje de área de cuenca asignado a tal pluviómetro
VEMA	= volumen escurrido medio anual, en miles de m^3
Pmab	= precipitación media anual en la estación base, en milímetros

Se observa en la tabla 2 que el VEMA de la estación de aforos Ballesmi es más del doble del medido en la estación Tancuilín; la cual tiene un área de cuenca más grande un 65% y también mayor Pmac. Lo anterior pone de manifiesto la importancia de la aportación de manantiales en la estación Ballesmi.

Verificación de la homogeneidad de los registros

Antes de realizar alguna estimación estadística con un registro mensual de volumen escurrido o de precipitación, se debe verificar su homogeneidad, lo cual significa que pertenezca a una sola población y que esté libre de componentes determinísticas. Para probar lo anterior, se aplicaron a los registros anuales de escurrimiento y precipitación, siete pruebas (WMO, 1971; Buishand, 1982 y Campos, 2005). La de Von Neumann (VN) que detecta falta de aleatoriedad contra componentes determinísticas no especificadas, dos de persistencia, la de Anderson (PA) y la de Sneyers (PS) y dos de tendencia, la de Kendall (TK) y la de Spearman (TS). La prueba de Cramer (PC) relativa a cambios en la media, se aplicó utilizando dos subperiodos iguales a la mitad del registro, uno al inicio y otro al final. Por último, la prueba de constancia de variabilidad de Bartlett (VB) se aplicó dividiendo cada registro en tres subperiodos.

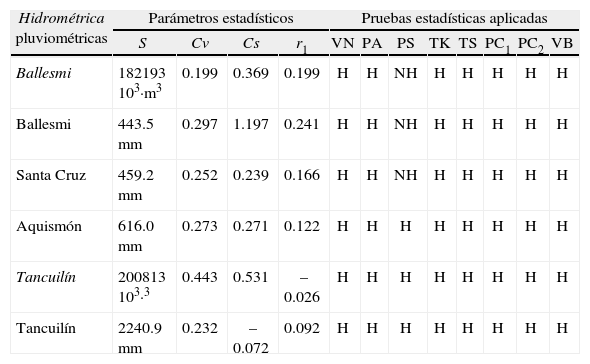
En la tabla 3 se han concentrado los registros conjuntos anuales de la estación de aforos Ballesmi y de los tres pluviómetros de su cuenca y en la tabla 4 se tienen los resultados de las siete pruebas citadas. Se observa que únicamente tres registros de la estación hidrométrica Ballesmi presentan ligera persistencia detectada con la prueba de Spearman.

Tabla 3.

Valores anuales del escurrimiento (10³·³) y la precipitación (mm) en las estaciones de la cuenca de la estación de aforos Ballesmi

Precipitación anual en
Año	VEAO	Ballesmi	S. Cruz	Aquismón
1961	875411	1176.1	1512.9	2075.0
1962	695256	823.8	1223.0	1248.5
1963	667781	1089.5	1296.5	959.2
1964	678010	1005.7	1396.1	1607.2
1965	799757	1413.9	1858.5	2196.6
1966	1014229	1668.4	1735.0	3148.4
1967	1022135	1463.8	1989.0	2162.2
1968	956144	1623.9	2023.6	2634.4
1969	1023727	1511.2	1515.2	2292.9
1970	1048881	1893.0	2388.8	2872.7
1971	967997	1638.9	2111.7	2123.0
1972	1015631	1566.0	2317.1	2974.9
1973	1120103	2216.2	2444.1	2847.2
1974	1053913	1771.8	2026.2	2369.0
1975	1094053	1673.4	2451.2	2172.7
1976	1208742	2360.6	2712.9	3562.1
1977	699825	1127.1	1169.6	1778.6
1978	959427	1603.2	1668.4	2488.3
1980	731731	1100.8	1504.0	1768.2
1981	1106292	1857.0	2515.1	2950.4
1982	579843	1017.1	1117.8	1480.4
1983	858750	1395.2	1771.8	2175.4
1984	1127368	1847.2	2222.2	3168.9
1985	874027	1399.8	2084.6	2533.7
1986	813209	1253.3	1835.0	1776.2
1987	802588	929.0	1348.0	1628.5
1988	944821	1455.2	1630.5	2142.5
1989	811741	1211.7	1532.0	2210.0
1990	978538	1530.3	1304.1	2023.5
1992	1071126	1963.9	2419.5	2607.0
1993	1408598	2955.3	2535.3	3541.5
1994	775327	1380.9	1562.2	1947.0
1995	751937	1089.3	1578.6	2239.5
1996	797767	1080.0	1860.5	1663.0
1997	679166	1111.1	1151.0	1647.5
media	914682	1491.5	1823.2	2257.6

VEAO = volumen escurrido anual observado, en miles de m³

Tabla 4.

Resultados de las pruebas estadísticas específicas aplicadas a los registros anuales de las estaciones hidrométricas Ballemi y Tancuilín y sus estaciones pluviométricas

Hidrométrica pluviométricas	Parámetros estadísticos				Pruebas estadísticas aplicadas
	S	Cv	Cs	r1	VN	PA	PS	TK	TS	PC1	PC2	VB
Ballesmi	182193 10^3·m^3	0.199	0.369	0.199	H	H	NH	H	H	H	H	H
Ballesmi	443.5 mm	0.297	1.197	0.241	H	H	NH	H	H	H	H	H
Santa Cruz	459.2 mm	0.252	0.239	0.166	H	H	NH	H	H	H	H	H
Aquismón	616.0 mm	0.273	0.271	0.122	H	H	H	H	H	H	H	H
Tancuilín	200813 10^3·^3	0.443	0.531	–0.026	H	H	H	H	H	H	H	H
Tancuilín	2240.9 mm	0.232	–0.072	0.092	H	H	H	H	H	H	H	H

Simbología:

S	= desviación estándar
Cv	= coeficiente de variación
Cs	= coeficiente de asimetría
r1	= coeficiente de correlación serial de orden 1
H	= homogénea
NH	= no homogénea

Estimación de la Aportación de Manantiales

El procedimiento que se propone para la estimación de la aportación subterránea en el escurrimiento total observado en la estación de aforos Ballesmi obedece al hecho de no contar con información hidrométrica relativa a las aportaciones de los manantiales y por ello se basa en el comportamiento hidrológico observado en una cuenca cercana, de tamaño similar y que se ubica dentro de la misma subregión geográfica.

Específicamente, el procedimiento sugerido acepta dos suposiciones básicas. La primera consiste en utilizar los coeficientes de escurrimiento promedio mensuales (Ce_j) observados en la estación hidrométrica Tancuilín, para estimar el escurrimiento directo en Ballesmi, función de su área de cuenca y de su precipitación respectiva. En relación con esta consideración, se ha encontrado que los Ce_j muestran similitud en cuencas que pertenecen a la misma subregión geográfica (Campos, 2013). La segunda suposición admite que la aportación de manantiales también varía con la precipitación y entonces cada escurrimiento mensual observado será corregido por una aportación subterránea modificada, con base en su error relativo respecto al promedio mensual observado. El procedimiento sugerido se desarrolla en los 4 pasos siguientes.

Paso 1) Estimación de los Ce_j. Con base en los valores promedio mensuales de escurrimiento (V¯j) y precipitación (Pb¯j) de la estación de aforos Tancuilín se estimarán sus coeficientes de escurrimiento promedio mensuales (Ce_j), con la expresión siguiente:

donde A es su área de cuenca en km² y Fc es su factor de transporte o correctivo, definido como:

En los tres primeros renglones de valores de la tabla 5 se tienen los datos y resultados de la aplicación de la ecuación 5, en la cual, Fc = 1.3164, según magnitudes de la tabla 2.

Tabla 5.

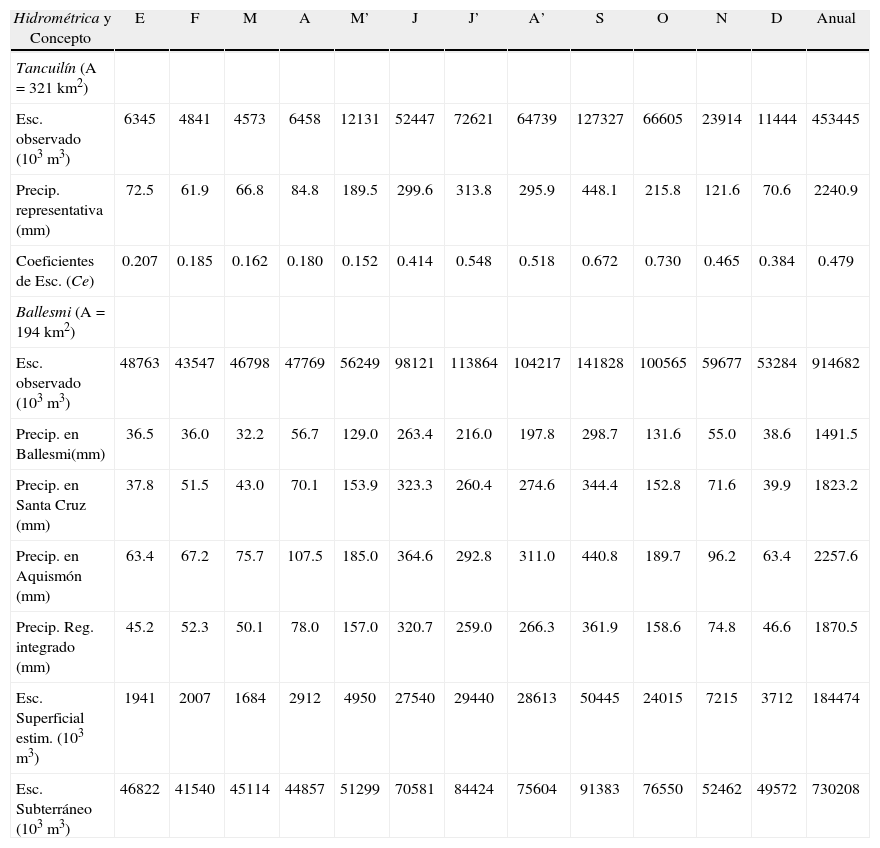
Estimación de los volúmenes de escurrimiento directo y subterráneo en la estación de aforos Ballesmi, con base en los datos de la estación hidrométrica Tancuilín

Hidrométrica y Concepto	E	F	M	A	M’	J	J’	A’	S	O	N	D	Anual
Tancuilín (A = 321 km^2)
Esc. observado (10^3 m^3)	6345	4841	4573	6458	12131	52447	72621	64739	127327	66605	23914	11444	453445
Precip. representativa (mm)	72.5	61.9	66.8	84.8	189.5	299.6	313.8	295.9	448.1	215.8	121.6	70.6	2240.9
Coeficientes de Esc. (Ce)	0.207	0.185	0.162	0.180	0.152	0.414	0.548	0.518	0.672	0.730	0.465	0.384	0.479
Ballesmi (A = 194 km^2)
Esc. observado (10^3 m^3)	48763	43547	46798	47769	56249	98121	113864	104217	141828	100565	59677	53284	914682
Precip. en Ballesmi(mm)	36.5	36.0	32.2	56.7	129.0	263.4	216.0	197.8	298.7	131.6	55.0	38.6	1491.5
Precip. en Santa Cruz (mm)	37.8	51.5	43.0	70.1	153.9	323.3	260.4	274.6	344.4	152.8	71.6	39.9	1823.2
Precip. en Aquismón (mm)	63.4	67.2	75.7	107.5	185.0	364.6	292.8	311.0	440.8	189.7	96.2	63.4	2257.6
Precip. Reg. integrado (mm)	45.2	52.3	50.1	78.0	157.0	320.7	259.0	266.3	361.9	158.6	74.8	46.6	1870.5
Esc. Superficial estim. (10^3 m^3)	1941	2007	1684	2912	4950	27540	29440	28613	50445	24015	7215	3712	184474
Esc. Subterráneo (10^3 m^3)	46822	41540	45114	44857	51299	70581	84424	75604	91383	76550	52462	49572	730208

Paso 2) Precipitación representativa. De acuerdo con la ubicación de las estaciones pluviométricas en la cuenca, se obtienen sus factores de ponderación para obtener el registro integrado. En la cuenca de la estación de aforos Ballesmi, se estimaron valores de 25, 45 y 30% para los pluviómetros de Ballesmi, Santa Cruz y Aquismón, respectivamente, según técnica de los polígonos de Thiessen. En el antepenúltimo renglón de valores de la tabla 5, se exponen los promedios mensuales de precipitación del registro integrado.

Paso 3) Estimación de la Aportación Subterránea. Multiplicando los Ce_j de Tancuilín por el área de cuenca (A, en km²) de Ballesmi y por su precipitación mensual del registro integrado, corregida por Fc = 1.0692, se obtienen las magnitudes estimadas para el volumen escurrido superficial (Vs¯j), mostrados en el penúltimo renglón de la tabla 5. Lo anterior equivale a aplicar la ecuación 5, para obtener V¯j. Restando estos valores al escurrimiento total observado se obtienen las aportaciones subterráneas promedio mensuales (ASP_j), expuestas en el último renglón de la tabla 5.

Paso 4) Corrección del escurrimiento mensual. Primeramente se obtiene el error relativo (ER) de cada escurrimiento mensual observado respecto a su promedio mensual, su expresión es:

Los valores del ER_i,j serán positivos cuando el escurrimiento observado excede al promedio y negativos cuando ocurre lo contrario. Para obtener el volumen escurrido corregido mensual (Vc_i,j), al escurrimiento observado se le resta la aportación subterránea modificada por el ER_i,j, esto es:

El procedimiento sugerido conduce a unos valores promedio mensuales de Vc_i,j denominados VC¯j iguales a los Vs¯j, estimados previamente. Al aplicar el Paso 4, se obtiene el registro mensual de volumen escurrido corregido.

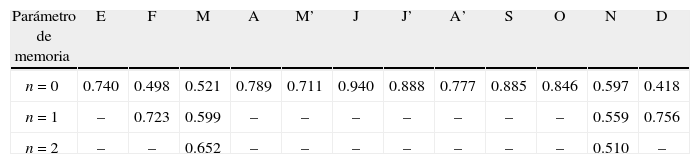
Análisis de los resultados

Relaciones funcionales

En las figuras 2 y 3 se muestran las relaciones funcionales de los meses de marzo y junio, del registro corregido. Se observa que son lineales al igual que las del resto de los meses. Por otra parte, en la tabla 6 se indican los coeficientes de correlación (R_xy) obtenidos al realizar el ajuste lineal de mínimos cuadrados de los residuos (ecuación 4). En todos los ajustes no se eliminaron valores dispersos, por lo tanto el número de parejas (N) siempre fue de 35.

Figura 2.

Relación funcional precipitación-escurrimiento del mes de marzo (con febrero y enero) en la estación hidrométrica Ballesmi

Figura 3.

Relación funcional precipitación-escurrimiento del mes de junio en la estación Ballesmi

Tabla 6.

Coeficientes de correlación (R_xy) de la relación funcional en la estación hidrométrica Ballesmi para el parámetro de memoria (n) indicado

Parámetro de memoria	E	F	M	A	M’	J	J’	A’	S	O	N	D
n = 0	0.740	0.498	0.521	0.789	0.711	0.940	0.888	0.777	0.885	0.846	0.597	0.418
n = 1	–	0.723	0.599	–	–	–	–	–	–	–	0.559	0.756
n = 2	–	–	0.652	–	–	–	–	–	–	–	0.510	–

Los valores de la tabla 6 indican que en los meses de febrero, marzo, noviembre y diciembre se tienen los valores de R_xy más bajos. Para definir el valor mínimo del R_xy que es estadísticamente diferente de cero, se aplicó una prueba basada en la distribución t de Student (Yevjevich, 1972) con un nivel α de significancia de 5%, obteniéndose para N = 35 un valor de R_xy.= 0.33. Entonces, todos los valores de R_xy obtenidos son estadísticamente diferentes de cero, pero podrán mejorar al considerar n = 1. Esto ocurre en febrero y diciembre, pero no en marzo ni en noviembre; para estos meses, se probó mejorar su relación funcional utilizando n = 2, lo cual acontece únicamente en marzo.

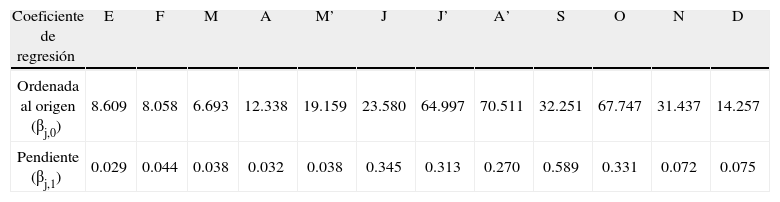
Coeficientes de regresión

Definida la memoria del modelo en cada mes (tabla 6), ahora se muestran en la tabla 7, los coeficientes de regresión obtenidos mediante el ajuste de mínimos cuadrados de los residuos de la ecuación 1 (ecuaciones 2 y 3), con N = 35. Los resultados de la tabla 7 permiten establecer tres tipos de modelos de regresión: (1) los de la época de estiaje (enero a mayo) con pendiente mediana de 0.038 y ordenada al origen mediana de 8.609, similares a la figura 2; (2) los de la época de lluvias (junio a octubre) con pendiente mediana de 0.331 y ordenada al origen mediana de 64.997, similares a la figura 3 y (3) los de la época de transición (noviembre y diciembre) con pendiente del orden de 0.073 y ordenada al origen del orden 20.

Tabla 7.

Coeficientes de regresión (β_j,k) de los modelos mensuales del PPE en la estación hidrométrica Ballesmi

Coeficiente de regresión	E	F	M	A	M’	J	J’	A’	S	O	N	D
Ordenada al origen (βj,0)	8.609	8.058	6.693	12.338	19.159	23.580	64.997	70.511	32.251	67.747	31.437	14.257
Pendiente (βj,1)	0.029	0.044	0.038	0.032	0.038	0.345	0.313	0.270	0.589	0.331	0.072	0.075

Contraste de los modelos de regresión

Contraste de medias y desviaciones estándar mensuales

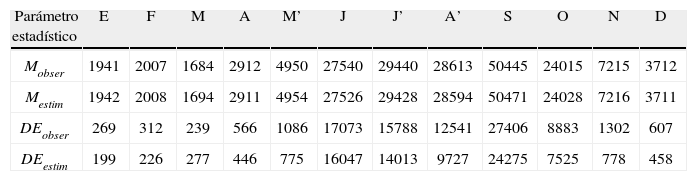
Cada modelo mensual se aplica en el periodo disponible de precipitación para estimar el volumen escurrido mensual; a continuación se cuantifican las medias y desviaciones estándar mensuales, tanto de los escurrimientos estimados como de los corregidos. En la tabla 8 se han concentrado los resultados obtenidos. Se observa que existe una reproducción excelente de las medias durante todo el año; respecto a las desviaciones estándar, todos sus valores son aproximados pero inferiores, excepto en marzo. Las mayores diferencias se presentan en la época de lluvias, específicamente en agosto y noviembre.

Tabla 8.

Valores observados y estimados en miles de m³ de la media aritmética (M) y la desviación estándar (DE) del escurrimiento mensual en la estación hidrométrica Ballesmi

Parámetro estadístico	E	F	M	A	M’	J	J’	A’	S	O	N	D
Mobser	1941	2007	1684	2912	4950	27540	29440	28613	50445	24015	7215	3712
Mestim	1942	2008	1694	2911	4954	27526	29428	28594	50471	24028	7216	3711
DEobser	269	312	239	566	1086	17073	15788	12541	27406	8883	1302	607
DEestim	199	226	277	446	775	16047	14013	9727	24275	7525	778	458

Contraste de escurrimientos anuales

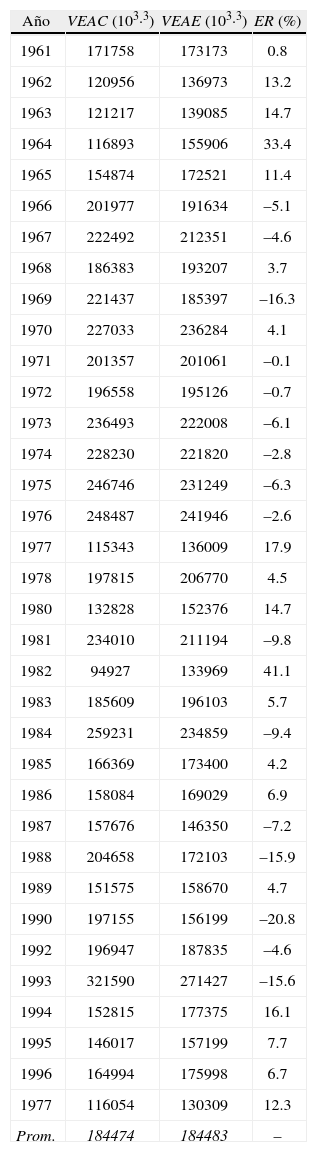
En la tabla 9 se realiza el análisis de los valores anuales, mostrando los errores relativos (ER) estimados con la ecuación 7, del escurrimiento estimado con los modelos de regresión con respecto al escurrimiento corregido. Se deduce de tales resultados que los años con ER extremo por exceso son 1982 y 1964 y por defecto 1990 y 1969; siendo los años 1961 y 1971 los que menor ER presentaron.

Tabla 9.

Errores relativos (ER) de los volúmenes escurridos anuales estimados con los modelos de regresión mensuales de la estación de aforos Ballesmi

Año	VEAC (10^3·^3)	VEAE (10^3·^3)	ER (%)
1961	171758	173173	0.8
1962	120956	136973	13.2
1963	121217	139085	14.7
1964	116893	155906	33.4
1965	154874	172521	11.4
1966	201977	191634	–5.1
1967	222492	212351	–4.6
1968	186383	193207	3.7
1969	221437	185397	–16.3
1970	227033	236284	4.1
1971	201357	201061	–0.1
1972	196558	195126	–0.7
1973	236493	222008	–6.1
1974	228230	221820	–2.8
1975	246746	231249	–6.3
1976	248487	241946	–2.6
1977	115343	136009	17.9
1978	197815	206770	4.5
1980	132828	152376	14.7
1981	234010	211194	–9.8
1982	94927	133969	41.1
1983	185609	196103	5.7
1984	259231	234859	–9.4
1985	166369	173400	4.2
1986	158084	169029	6.9
1987	157676	146350	–7.2
1988	204658	172103	–15.9
1989	151575	158670	4.7
1990	197155	156199	–20.8
1992	196947	187835	–4.6
1993	321590	271427	–15.6
1994	152815	177375	16.1
1995	146017	157199	7.7
1996	164994	175998	6.7
1977	116054	130309	12.3
Prom.	184474	184483	–

VEAC volumen escurrido anual corregido

VEAE volumen escurrido anual estimado

Contraste de escurrimientos mensuales

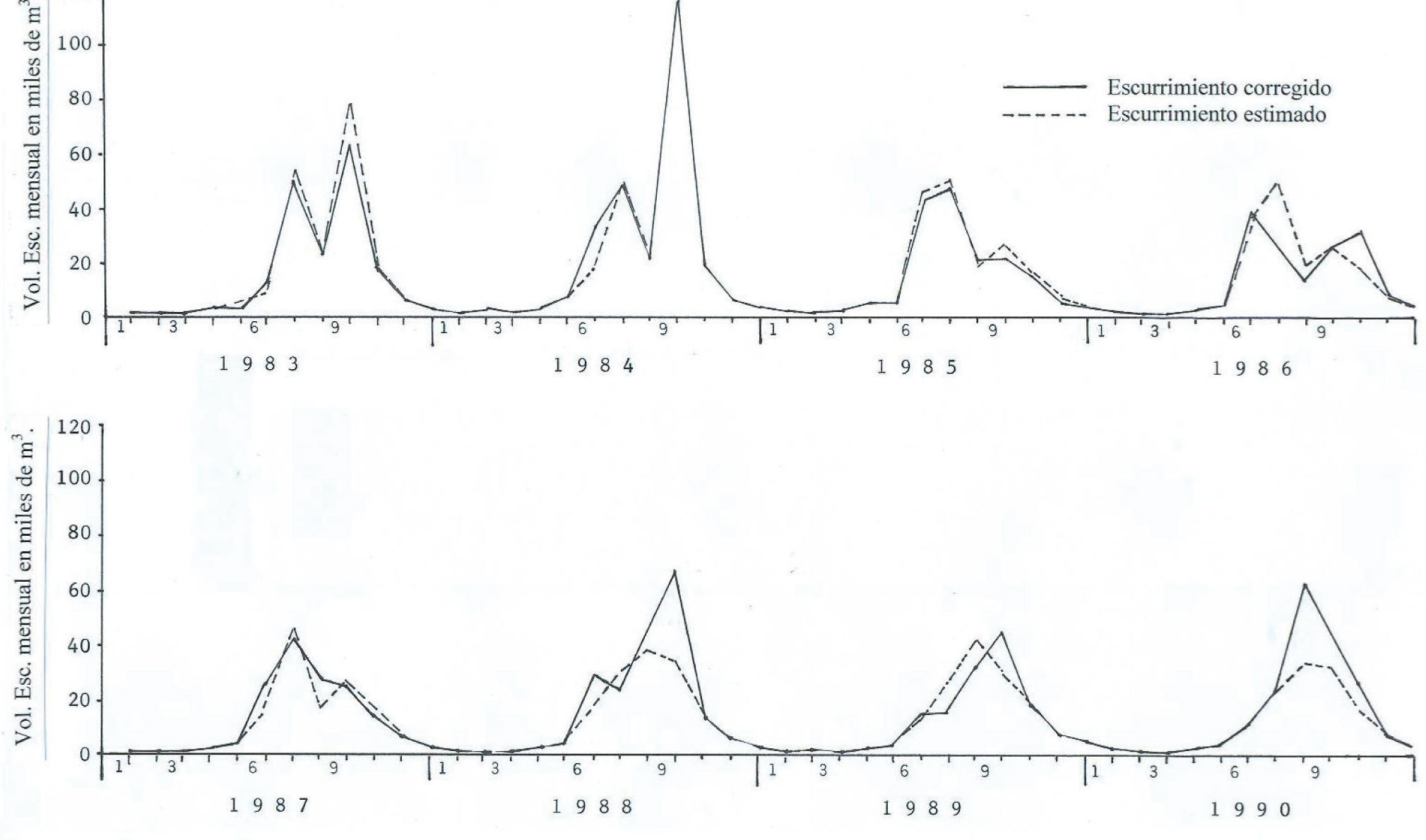
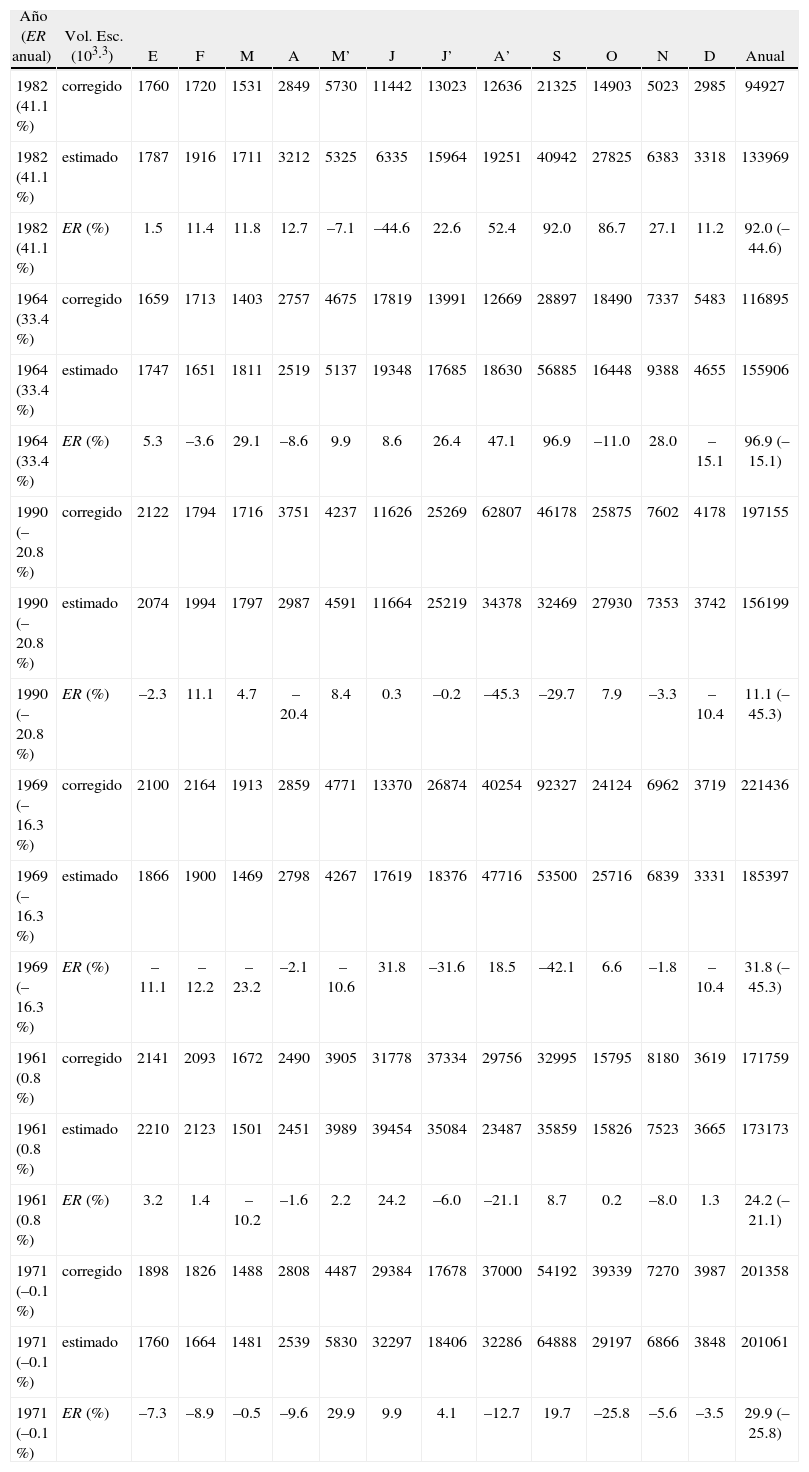
Para los seis años definidos con errores relativos extremos, en la tabla 10 se exponen sus respectivos ER mensuales. Finalmente, en la figura 4 se muestra gráficamente un contraste para un lapso de ocho años, seleccionado de manera arbitraria, pero que incluyera años secos y húmedos observados (tabla 9).

Tabla 10.

Errores relativos (ER) de los volúmenes escurridos mensuales estimados con los modelos de regresión respectivos de la estación de aforos Ballesmi, para los años con ER extremos

Año (ER anual)	Vol. Esc. (10^3·^3)	E	F	M	A	M’	J	J’	A’	S	O	N	D	Anual
1982 (41.1 %)	corregido	1760	1720	1531	2849	5730	11442	13023	12636	21325	14903	5023	2985	94927
1982 (41.1 %)	estimado	1787	1916	1711	3212	5325	6335	15964	19251	40942	27825	6383	3318	133969
1982 (41.1 %)	ER (%)	1.5	11.4	11.8	12.7	–7.1	–44.6	22.6	52.4	92.0	86.7	27.1	11.2	92.0 (–44.6)
1964 (33.4 %)	corregido	1659	1713	1403	2757	4675	17819	13991	12669	28897	18490	7337	5483	116895
1964 (33.4 %)	estimado	1747	1651	1811	2519	5137	19348	17685	18630	56885	16448	9388	4655	155906
1964 (33.4 %)	ER (%)	5.3	–3.6	29.1	–8.6	9.9	8.6	26.4	47.1	96.9	–11.0	28.0	–15.1	96.9 (–15.1)
1990 (–20.8 %)	corregido	2122	1794	1716	3751	4237	11626	25269	62807	46178	25875	7602	4178	197155
1990 (–20.8 %)	estimado	2074	1994	1797	2987	4591	11664	25219	34378	32469	27930	7353	3742	156199
1990 (–20.8 %)	ER (%)	–2.3	11.1	4.7	–20.4	8.4	0.3	–0.2	–45.3	–29.7	7.9	–3.3	–10.4	11.1 (–45.3)
1969 (–16.3 %)	corregido	2100	2164	1913	2859	4771	13370	26874	40254	92327	24124	6962	3719	221436
1969 (–16.3 %)	estimado	1866	1900	1469	2798	4267	17619	18376	47716	53500	25716	6839	3331	185397
1969 (–16.3 %)	ER (%)	–11.1	–12.2	–23.2	–2.1	–10.6	31.8	–31.6	18.5	–42.1	6.6	–1.8	–10.4	31.8 (–45.3)
1961 (0.8 %)	corregido	2141	2093	1672	2490	3905	31778	37334	29756	32995	15795	8180	3619	171759
1961 (0.8 %)	estimado	2210	2123	1501	2451	3989	39454	35084	23487	35859	15826	7523	3665	173173
1961 (0.8 %)	ER (%)	3.2	1.4	–10.2	–1.6	2.2	24.2	–6.0	–21.1	8.7	0.2	–8.0	1.3	24.2 (–21.1)
1971 (–0.1 %)	corregido	1898	1826	1488	2808	4487	29384	17678	37000	54192	39339	7270	3987	201358
1971 (–0.1 %)	estimado	1760	1664	1481	2539	5830	32297	18406	32286	64888	29197	6866	3848	201061
1971 (–0.1 %)	ER (%)	–7.3	–8.9	–0.5	–9.6	29.9	9.9	4.1	–12.7	19.7	–25.8	–5.6	–3.5	29.9 (–25.8)

Figura 4.

Contraste de volúmenes escurridos mensuales corregidos y estimados con los modelos de regresión en la estación hidrométrica Ballesmi para los años indicados

Otras opciones de procesamiento

Por supuesto que el método sugerido para retirar la aportación de manantiales del escurrimiento observado en la estación de aforos Ballesmi, es aproximado y una mejor opción sería analizar con isótopos tal escurrimiento para estimar la proporción de aguas subterráneas (Custodio, 1976; Aggarwal et al., 2012).

Por otra parte, se consideró un mejor planteamiento de análisis, el procesamiento de todo el registro conjunto y su contraste; sin embargo, otra opción consiste en dividir tal registro y calibrar con una mitad y contrastar en la otra. Este último enfoque es el adoptado en la aplicación de la mayoría de los modelos hidrológicos conceptuales. En este trabajo los objetivos centrales fueron la corrección de un registro por aportación de manantiales y la verificación general del modelo más simple del proceso precipitación–escurrimiento mensual.

Conclusiones

Primera: Al observarse una similitud numérica en los coeficientes de escurrimiento promedio mensuales en cuencas que pertenecen a la misma subregión geográfica (Campos, 2013), el procedimiento sugerido para eliminar del volumen escurrido mensual observado la aportación subterránea estimada, se puede considerar aproximado.

Segunda: el modelo matemático más simple del proceso precipitación–escurrimiento (PPE) mensual que se puede establecer es la regresión lineal o curva, la cual, debido a su planteamiento conceptual, reproduce fielmente los volúmenes escurridos promedio mensual y alcanza una excelente aproximación en relación con su dispersión, como se ha demostrado en la tabla 8, con base en las medias y desviaciones estándar.

Tercera: a nivel anual, el contraste entre los escurrimientos observados corregidos y los estimados con los modelos de regresión, según resultados concentrados en la tabla 9, indica que se reproducen sus magnitudes, así como su variabilidad.

Cuarta: finalmente, a nivel mensual y de acuerdo a los indicadores extremos mostrados en la tabla 10 y la figura 4 que muestra un lapso del registro modelado, se considera que la reproducción del escurrimiento es bastante aproximada. Debido a ello, se recomienda la aplicación de este tipo de modelos del PPE, para deducir datos faltantes y ampliar registros de escurrimiento en cuencas de climas húmedos que tienen información de precipitación de mayor amplitud.

Agradecimiento

Se agradece al Ing. Armando Rocha Hernández, Jefe del Centro de Previsión Meteorológica de la Dirección Estatal San Luis Potosí de la CONAGUA, proporcionar al autor toda la información pluviométrica procesada.