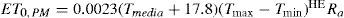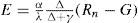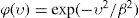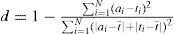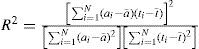Modelos Hargreaves Priestley-Taylor y redes neuronales artificiales en la estimación de la evapotranspiración de referencia

Resumen

Resulta costoso medir directamente la evapotranspiración de referencia (ET₀) con un lisímetro, y al no contar con esta información se utilizó el método de Penman-Monteith modificado por la FAO (ET₀ FAO-56 P-M) para su cálculo. El objetivo del presente trabajo fue realizar una comparación de modelos empíricos como el de Hargreaves, Hargreaves calibrado y Priestley-Taylor, con el modelo de redes neuronales artificiales función de base radial (RNA BR), con las mismas variables de entrada, en la estimación de la ET₀ FAO-56 P-M. Las estimaciones de ET₀ se evaluaron en cuatro estaciones climáticas del Distrito 075, Valle del Fuerte en Sinaloa, México. Las RNABR3 y RNABR7 utilizaron las mismas variables de entrada (o menos) que los métodos convencionales de HARGC y P-T, respectivamente. Los RMSE de HARGC y P-T en el ajuste, variaron de 0.7092 a 0.7848 y de 0.4178 a 0.8207, y en la validación de 1.1898 a 0.6914 y de 0.3800 a 0.6889, respectivamente. De las RNA-BR3 y RNABR7 sus RMSE en el ajuste fueron de 0.5295 a 0.6737 y de 0.3574 a 0.4809, y en la validación de 1.3096 a 0.6254 y de 0.3470 a 0.4919, respectivamente. Los RMSE obtenidos en el ajuste y en la validación de las RNABR3 y RNABR7 definieron que éstas fueron mejores en la estimación de la ET₀ FAO-56 P-M que los métodos convencionales.

Abstract

Directly measuring evapotranspiration accurately through a lysimeter is difficult, and because of data lack the Penman-Monteith method modified by FAO (ET₀FAO-56 P-M) was used to obtain the reference evapotranspiration observed. The objective of the present study was to perform a comparison of empirical models like: Hargreaves, Hargreaves calibrated and Priestley-Taylor with the artificial neural network radial basis function (RNA BR) model with the same entry variables, in the estimation of reference evapotranspiration. The estimations of ET₀were evaluated in four stations of District 075, Valle del Fuerte in Sinaloa, México. RNABR3 y RNABR7 used same entry variables (or less) than HARGC and P-T conventional methods, respectively. HARGC and P-T RMSE's at fitting changed from 0.7092 to 0.7848 and from 0.4178 to 0.8207, and on validation changed from 1.1898 to 0.6914 and from 0.3800 to 0.6889, respectively. RMSE's from RNABR3 and RNABR7 at fitting changed from 0.5295 to 0.6737 and from 0.3574 to 0.4809, and on validation from 1.3096 to 0.6254 and from 0.3470 to 0.4919, respectively. RNABR3, RNABR7 RMSE's obtained fitting as well as validation defined that RNA BR were better on the estimation of ET₀FAO-56 P-M than conventional methods.

Introducción

El método Penman-Monteith (FAO56 P-M) propuesto por la Organización de las Naciones Unidas para la alimentación en el boletín FAO 56 es el único método estándar recomendado para el cálculo de la evapotranspiración de referencia (ET₀), ya que diversos estudios realizados para evaluar diferentes modelos de ET₀ con datos obtenidos de lisímetro de pesada, tales como FAO-24 Penman (Doorenbos y Pruitt, 1980; Jensen et al, 1990); FAO-24 Radiación (Doorenbos y Pruitt, 1980); Hargreaves (Hargreaves y Samani, 1985; Allen et al, 1998), concluyeron que la ecuación de FAO-56 Penman-Monteith fue la mejor (Allen et al., 1998; Steiner et al., 1991; DehghaniSanij et al., 2004; López-Urrea et al, 2006). La evapotranspiración es la principal componente del ciclo hidrológico, por lo que resulta necesario conocerla con anticipación para estimar las necesidades de agua de los cultivos para realizar una planeación acertada de los calendarios de riego y la operación del recurso agua de manera adecuada (Jensen et al., 1990; Ojeda, 2004). Variables climáticas que requieren ser conocidas e influyen en la evapotranspiración son: la temperatura del aire, humedad atmosférica, radiación solar y velocidad del viento (Allen et al., 1998). Debido a que no todas estas variables están disponibles en cualquier estación meteorológica han sido propuestos diferentes modelos para estimar la evapotranspiración de referencia (ET₀) como la ecuación de Hargreaves (1994), que la estima en función de temperatura y tiene resultados razonables de ET₀ (Allen et al., 1998). Otro modelo para estimar la ET₀ es Priestley-Taylor, que relaciona la evapotranspiración con la radiación. Estos demandan el conocimiento de menos datos (Thornley y France, 2007). Mangliulo et al. (2003) utilizan un atmómetro modificado para la estimación de la ET₀, de igual forma Doorenbos y Pruitt (1980) reportaron que existe una alta correlación entre los datos de un tanque evaporímetro y la ET₀ cuando éste se mantiene e instala apropiadamente. En años recientes, las Redes Neuronales Artificiales (RNA) han demostrado ser herramientas excelentes en la investigación, debido a su capacidad para manejar las interrelaciones no-lineales existentes al estimar diversos fenómenos climáticos (Tymvios et al., 2008). Zanetti et al. (2007), evaluaron una RNA multicapa en función de las temperaturas máximas y mínimas del aire para estimar ET₀. De igual manera, Kumar et al. (2002) utilizaron una RNA con el algoritmo backpropagation y además de usar las temperaturas (máximas y mínimas) consideraron: humedad relativa máxima y mínima, velocidad del viento y radiación solar.

Debido a que en México no se encontraron trabajos realizados utilizando redes neuronales artificiales de base radial para estimar la evapotranspiración de referencia, se pretende con este estudio definir si las RNA BR estiman con menor error la evapotranspiración de referencia (ET₀) obtenida con el método de Penman-Monteith, con las mismas (o menos) variables de entrada que utilizan los métodos convencionales de Hargreaves (calibrado y sin calibrar) y Priestley-Taylor, en las condiciones climáticas del distrito de riego 075 ubicado en los Mochis, Sinaloa. Por lo que el objetivo del presente trabajo fue determinar si las RNA de Base Radial con las mismas (o menos) variables de entrada que utilizan los métodos convencionales de: Hargreaves (HARG), Hargreaves calibrado (HARGC) y Priestley-Taylor (P-T), son mejores al estimar la ET₀ obtenida con Penman-Monteith FAO-56.

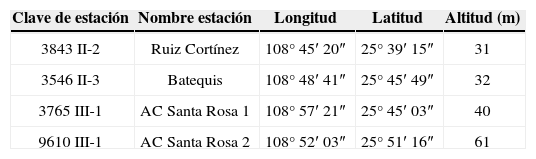
Materiales y métodos

Área de estudio y datos climatológicos

Se utilizaron datos climatológicos de cuatro estaciones: temperaturas máximas y mínimas en °C, radiación global en MJ m⁻² día⁻¹, humedad relativa en % y velocidad del viento en m s⁻¹, que se obtuvieron de la red agroclimática automatizada Valle del Fuerte y fueron proporcionados por el Distrito de Riego 075, en Los Mochis, Sinaloa. Las coordenadas de dichas estaciones se presentan en el cuadro 1.

Cuadro 1.

Nombre, clave, longitud, latitud y altitud de las estaciones objeto de este estudio

Clave de estación	Nombre estación	Longitud	Latitud	Altitud (m)
3843 II-2	Ruiz Cortínez	108° 45′ 20″	25° 39′ 15″	31
3546 II-3	Batequis	108° 48′ 41″	25° 45′ 49″	32
3765 III-1	AC Santa Rosa 1	108° 57′ 21″	25° 45′ 03″	40
9610 III-1	AC Santa Rosa 2	108° 52′ 03″	25° 51′ 16″	61

Estos datos se preprocesaron a nivel diario, comprendieron del periodo abril de 1997 a diciembre de 2001. El conjunto de datos de abril de 1997 a mediados de mayo de 2001 (1484 días), se utilizaron para el ajuste de la evapotranspiración de referencia (ET₀) con los diferentes modelos, así como en el entrenamiento, validación y prueba de las RNA, y de mediados de mayo a diciembre de 2001 (229 días) se utilizó para realizar la validación de los modelos. Los datos se preprocesaron en hojas de cálculo y el software usado para el entrenamiento de las RNA es el toolbox de redes neuronales para Matlab 7.0^MR.

Penman-Monteith FA0 56

Debido a la dificultad de obtener datos de lisímetro de ET₀ se tomaron como datos observados, la evapotranspiración de referencia obtenida por el método FAO-56 Penman-Monteith, recomendado por los expertos como único método estándar para el cálculo de ET₀ (Allen et al., 1998). La ecuación para estimar ET₀ diaria es:

donde:ET₀ =

evapotranspiración de referencia en mm día⁻¹,

R_n =

radiación neta en MJ m⁻² día⁻¹,

G =

densidad de flujo de calor del suelo en MJ m⁻² día⁻¹,

T =

temperatura media del aire a 2 m de altura en °C,

u₂ =

velocidad del viento media a 2 m de altura en m s⁻¹,

e_s =

presión de vapor a saturación a la temperatura del aire T en kPa,

e_a =

presión de vapor actual en kPa,

e_s − e_a =

déficit de presión de vapor en kPa,

Δ =

pendiente de la curva de presión de vapor a saturación en kPa °C⁻¹,

γ =

constante psicométrica en kPa °C⁻¹ (Allen et al., 1998).

Modelos utilizados en la estimación de la evapotranspiración de referencia (ET₀)

Hargreaves (HARG)

La ecuación de Hargreaves es:

donde:T_media =

temperatura media en °C,

T_max y T_min =

temperaturas máximas y mínimas, respectivamente y

R_a =

radiación extraterrestre en mm día⁻¹, este dato se calcula de acuerdo con la metodología propuesta en Allen et al. (1998).

Hargreaves calibrado (HARGC)

De acuerdo con Trajkovic (2007) la ecuación de Hargreaves se puede reescribir como

donde:ET_{0 ′ PM} =

evapotranspiración de referencia calculada con FAO-56 P-M (Allen et al., 1998),

HE =

exponente empírico de Hargreaves, que fue calibrado con los vectores de 1484 datos disponibles para cada una de las estaciones.

Modelo Priestley-Taylor (P-T)

La ecuación de Priestley y Taylor (1972):

donde:E =

evapotranspiración de referencia en mm día⁻¹,

R_n =

radiación neta calculada, MJ m⁻² día⁻¹, con la metodología propuesta en Allen et al. (1998),

G =

densidad de flujo de calor en el suelo en MJ m⁻² día⁻¹,

G =

0 en una escala diaria de acuerdo con Allen et al. (1998),

λ =

calor latente de vaporización igual a 2.45 MJ kg⁻¹, γ=cpPϵλ=0.665×10−3×P, constante psicro-métrica,

c_p =

calor específico a presión constante 1.013 × 10⁻³ en MJ kg⁻¹ °C⁻¹,

ε =

cociente del peso molecular de vapor de agua/aire seco = 0.622, P=101.3293−0.0065z2935.26 presión atmosférica en kPa, z altitud en m.

Red Neuronal Artificial función de base radial (RNA BR)

La red de función de base radial (BR) con n entradas y un escalar como salida se representa en la ecuación 5, tal red implementa un mapeo f_r: Rⁿ → R de acuerdo con:

donde:x ∈ Rⁿ =

vector de entrada,

φ(•) =

función dada de R⁺ a R,

‖•‖ =

norma euclidiana,

λ_i, 0 ≤ i ≤ n_r =

pesos o parámetros,

c_i ∈ Rⁿ, 1 ≤ i ≤ n_r =

conocidas como los centros BR, y

n_r =

número de centros.

Aunque el caso de salida escalar es considerado aquí por simplicidad rotacional. De hecho, una red BR multisalida puede separarse siempre en un grupo de una red BR de una sola salida. En la red BR la forma funcional φ(•) y los centros c_i se asumen fijos. Se suministra un conjunto a la entrada x(t) y la salida deseada correspondiente d(t) para t = 1 hasta N. Los valores de los pesos λ_i se determinan con el método lineal de mínimos cuadrados. Sin embargo, las elecciones de φ(•) y c_i deben considerarse cuidadosamente para que la red BR sea capaz de igualar exactamente la representación de la red neuronal de dos capas.

Resultados teóricos y prácticos de investigación sugieren que la elección de la no-linealidad φ(•) no es crucial para la realización de la red BR. Por ejemplo, sea la elección una función Gaussiana

donde β es una constante real, ésta es una elección típica. Para la no-linealidad φ (υ) → 0, así como (υ) → ∞, (Chen et al, 1991).

Implementación de la red neuronal función de base radial

El código que se usó para implementar la red neuronal en Matlab es el siguiente: net = newrbe(P, T, spread), donde: spread es la constante de extendido de la capa base radial, P son los vectores de entrada, T es el target o vector de salida, newrbe es la función que llama a la red base radial de diseño exacto, que de acuerdo con Demuth et al. (2008) pueden producir un error de cero en los vectores de entrenamiento, la constante de extendido tomó el valor de 100, pues con dicho valor se observó que la red proveía un buen ajuste. Se simularon los datos de salida observados con la red entrenada con el código a = sim(net,P), donde a es la salida de la red.

Escenarios y variables de entrada utilizados en las RNA de base radial

Se utilizaron nueve escenarios de las redes neuronales artificiales de base radial (RNA BR) que a continuación se presentan, así como las {variables de entrada} que se utilizaron en cada una de ellas: La RNABR1 {Tmin, Tmax}, RNABR2 {Tmedia, Ra}, RNABR3 {Tmin, Tmax, Ra}, RNABR5 {Tmedia, Rn}, RNABR6 {Rn, Delta}, RNA-BR7 {Tmin, Tmax, Rn}, RNABR8 {Tmedia, RG, HRmedia, VV}, RNABR9 {Tmedia, RG, DPV, VV}, RNABR10 {Tmin, Tmax, RG, HRmin, HRmax, VV}, donde Tmin y Tmax son temperatura máxima y mínima, respectivamente, Tmedia promedio de las temperaturas, Ra radiación extraterrestre, Rn radiación neta, Delta pendiente de la curva de presión de vapor a saturación, HRmedia promedio de la humedad relativa máxima y mínima, RG radiación global, DPV déficit de presión de vapor, VV velocidad de viento, HRmin y HRmax humedad relativa mínima y máxima, respectivamente.

Índices estadísticos para evaluar los modelos

Se obtuvieron los siguientes estadísticos de prueba para los diferentes modelos:

Error estándar promedio o raíz cuadrada del cuadrado medio del error (RMSE),

Índice de Willmot (Willmot, 1981),

Coeficiente de determinación, R²,

donde:R² =

coeficiente de determinación,

a_i =

dato estimado por el modelo,

t_i =

dato observado,

N =

número de observaciones o estimaciones,

ā =

promedio de los datos estimados por el modelo,

t¯

promedio de los datos observados, (Cai et al., 2007).

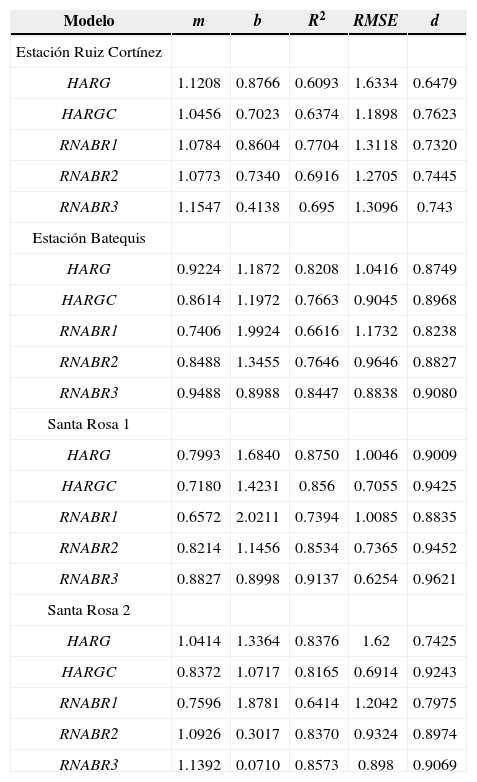
Resultados y discusión

Los valores estimados del exponente HE de HARGC fueron 0.1245, 0.1401, 0.1051, 0.0818 para las estaciones Ruiz Cortínez, Batequis, Santa Rosa 1 y Santa Rosa 2, respectivamente. En el cuadro 2 se observa que HARGC presentó un mejor ajuste que HARG, debido a la calibración del coeficiente HE, esto concuerda con Trajkovic (2007), que comenta que la ecuación de Hargreaves sin calibrar tiende a sobreestimar la evapotranspiración en regiones húmedas y puesto que Valle del Fuerte Los Mochis, Sinaloa es una zona de riego que presenta humedad relativa de 70.4% anual, de acuerdo con Doorenbos y Pruitt (1980), se clasifica como zona de humedad relativa alta.

Cuadro 2.

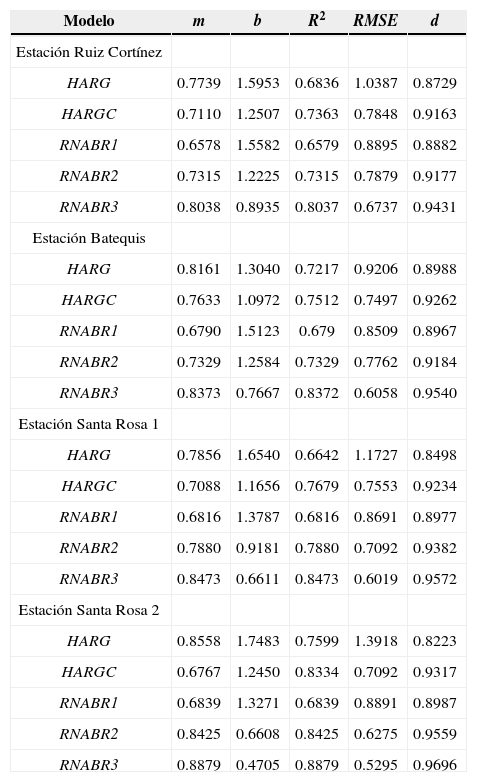
Resumen de estadísticos del ajuste de los métodos que estiman ET₀ diaria HARG, HARGC y RNABR1, 2, 3, comparadas con FAO-56 P-M

Modelo	m	b	R^2	RMSE	d
Estación Ruiz Cortínez
HARG	0.7739	1.5953	0.6836	1.0387	0.8729
HARGC	0.7110	1.2507	0.7363	0.7848	0.9163
RNABR1	0.6578	1.5582	0.6579	0.8895	0.8882
RNABR2	0.7315	1.2225	0.7315	0.7879	0.9177
RNABR3	0.8038	0.8935	0.8037	0.6737	0.9431
Estación Batequis
HARG	0.8161	1.3040	0.7217	0.9206	0.8988
HARGC	0.7633	1.0972	0.7512	0.7497	0.9262
RNABR1	0.6790	1.5123	0.679	0.8509	0.8967
RNABR2	0.7329	1.2584	0.7329	0.7762	0.9184
RNABR3	0.8373	0.7667	0.8372	0.6058	0.9540
Estación Santa Rosa 1
HARG	0.7856	1.6540	0.6642	1.1727	0.8498
HARGC	0.7088	1.1656	0.7679	0.7553	0.9234
RNABR1	0.6816	1.3787	0.6816	0.8691	0.8977
RNABR2	0.7880	0.9181	0.7880	0.7092	0.9382
RNABR3	0.8473	0.6611	0.8473	0.6019	0.9572
Estación Santa Rosa 2
HARG	0.8558	1.7483	0.7599	1.3918	0.8223
HARGC	0.6767	1.2450	0.8334	0.7092	0.9317
RNABR1	0.6839	1.3271	0.6839	0.8891	0.8987
RNABR2	0.8425	0.6608	0.8425	0.6275	0.9559
RNABR3	0.8879	0.4705	0.8879	0.5295	0.9696

m = pendiente, b = intercepto, R² = coeficiente de determinación, RMSE = raíz cuadrada del cuadrado medio del error en mm día⁻¹, d = índice de Willmott

Las tres RNA BR propuestas presentaron RMSE menores que los de HARG (cuadro 2). HARGC fue mejor que RNABR1, muy semejante a la RNABR2, pero no superó a la RNABR3, con base en los RMSE. RNABR3 tienen mejor desempeño en este periodo de ajuste que HARG y HARGC. Contar en la zona de estudio con una RNA BR entrenada, validada y probada con datos de entrada de Tmax y Tmin, dará mejores resultados que el HARG, y dado que el valor de Ra no se obtiene de un instrumento (se calcula), su implementación en RNA BR es fácil y disminuye el error que se comete al estimar la ET₀ FAO56 P-M diaria, lo cual repercute en una mejor estimación de las necesidades de agua de los cultivos. La RNABR3 utiliza un dato menos (temperatura media) que HARG y HARGC.

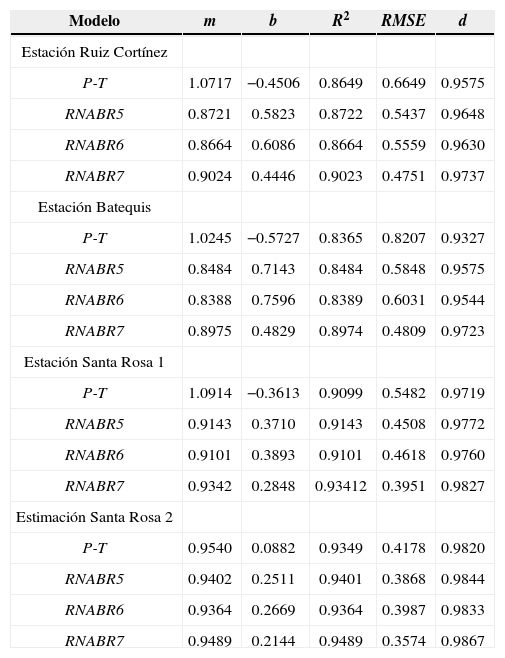
En el cuadro 3 las tres RNA BR propuestas presentaron menos error (RMSE), al utilizar las mismas o menos variables de entrada que P-T. Esto se debe a que la región de estudio es un distrito de riego, donde los cultivos no están estresados hídricamente y la Rn en estas condiciones es la principal componente de la evapo- transpiración, y según Stagnitti et al. (1989) aproximadamente 95% de la demanda evapotranspirativa es proporcionada por el término radiactivo en condiciones de buena humedad del suelo.

Cuadro 3.

Resumen de estadísticos del ajuste de los métodos que estiman ET₀ diaria P-T y RNABR5, 6, 7, comparada con FAO-56 P-M

Modelo	m	b	R^2	RMSE	d
Estación Ruiz Cortínez
P-T	1.0717	−0.4506	0.8649	0.6649	0.9575
RNABR5	0.8721	0.5823	0.8722	0.5437	0.9648
RNABR6	0.8664	0.6086	0.8664	0.5559	0.9630
RNABR7	0.9024	0.4446	0.9023	0.4751	0.9737
Estación Batequis
P-T	1.0245	−0.5727	0.8365	0.8207	0.9327
RNABR5	0.8484	0.7143	0.8484	0.5848	0.9575
RNABR6	0.8388	0.7596	0.8389	0.6031	0.9544
RNABR7	0.8975	0.4829	0.8974	0.4809	0.9723
Estación Santa Rosa 1
P-T	1.0914	−0.3613	0.9099	0.5482	0.9719
RNABR5	0.9143	0.3710	0.9143	0.4508	0.9772
RNABR6	0.9101	0.3893	0.9101	0.4618	0.9760
RNABR7	0.9342	0.2848	0.93412	0.3951	0.9827
Estimación Santa Rosa 2
P-T	0.9540	0.0882	0.9349	0.4178	0.9820
RNABR5	0.9402	0.2511	0.9401	0.3868	0.9844
RNABR6	0.9364	0.2669	0.9364	0.3987	0.9833
RNABR7	0.9489	0.2144	0.9489	0.3574	0.9867

m = pendiente, b = intercepto, R² = coeficiente de determinación, RMSE = raíz cuadrada del cuadrado medio del error en mm día⁻¹, d = índice de Willmott

Esta característica la presenta también el Modelo P-T, ya que, de manera general, tiene RMSE menores (cuadro 3) que HARG y HARGC (cuadro 2). La RNABR7 que tiene las mismas variables que P-T, posee la característica que se acaba de comentar, por esto es la mejor de todas las RNA BR en este proceso de ajuste.

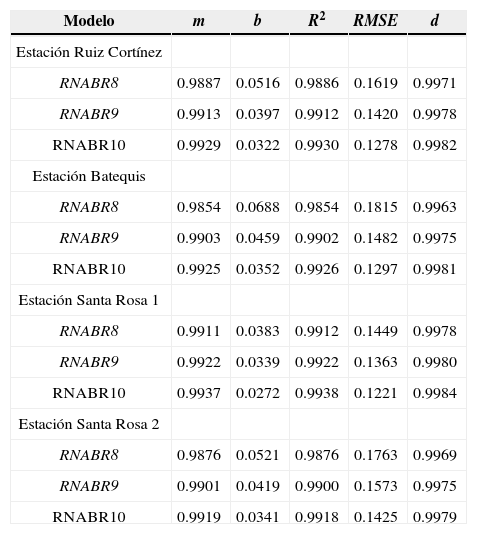
En el cuadro 4 se presentan tres RNA BR a las que se les adicionó el término aerodinámico. De diferente forma, en función a la información que se tenga de la humedad atmosférica se estudiaron estos tres escenarios para conocer su desempeño en la estimación de la ET₀ diaria FAO-56 Penman-Monteith. Todos los indicadores son muy adecuados: m ≈ 1 y b ≈ 0, R² ≈ 1, d ≈ 1 y los errores (RMSE) son menores de dos décimas de mm día⁻¹. La RNABR10 obtuvo valores de R² de 0.99 en todas las estaciones. González et al. (2008), consiguieron una R² semejante en la estación Santa Rosa 1, pero utilizaron una RNA feedforward backpropagation.

Cuadro 4.

Resumen de estadísticos del ajuste de los métodos que estiman ET₀ diaria RNABR8, 9, 10 comparada con FAO-56 P-M

Modelo	m	b	R^2	RMSE	d
Estación Ruiz Cortínez
RNABR8	0.9887	0.0516	0.9886	0.1619	0.9971
RNABR9	0.9913	0.0397	0.9912	0.1420	0.9978
RNABR10	0.9929	0.0322	0.9930	0.1278	0.9982
Estación Batequis
RNABR8	0.9854	0.0688	0.9854	0.1815	0.9963
RNABR9	0.9903	0.0459	0.9902	0.1482	0.9975
RNABR10	0.9925	0.0352	0.9926	0.1297	0.9981
Estación Santa Rosa 1
RNABR8	0.9911	0.0383	0.9912	0.1449	0.9978
RNABR9	0.9922	0.0339	0.9922	0.1363	0.9980
RNABR10	0.9937	0.0272	0.9938	0.1221	0.9984
Estación Santa Rosa 2
RNABR8	0.9876	0.0521	0.9876	0.1763	0.9969
RNABR9	0.9901	0.0419	0.9900	0.1573	0.9975
RNABR10	0.9919	0.0341	0.9918	0.1425	0.9979

m = pendiente, b = intercepto, R² = coeficiente de determinación, RMSE = raíz cuadrada del cuadrado medio del error en mm día⁻¹, d = índice de Willmott

Validación de los modelos

Las tres RNA BR, en las estaciones Ruiz Cortínez y Santa Rosa 2, sus RMSE fueron mejores que los de HARG, y en las restantes fueron RNABR2 y RNABR3 con el conjunto de datos (mayo a diciembre de 2001) que se utilizó en la validación de los modelos (cuadro 5). HAR-GC fue mejor (debido al ajuste del exponente HE), en las estaciones Ruiz Cortínez y Santa Rosa 2, que las tres RNA BR debido a sus RMSE más bajos, en las restantes sólo la RNABR3 presentó RMSE un poco más bajos (cuadro 5). Por lo anterior, la RNABR3 con datos de entrada de temperaturas máximas y mínimas y un dato menos (temperatura media), que los métodos convencionales HARG y HARGC, presentó un mejor desempeño en la estimación de ET₀.

Cuadro 5.

Resumen de estadísticos de la validación de los métodos que estiman ET₀ diaria con HARG, HARGC y RNABR1, 2, 3, comparada con FAO-56 P-M

Modelo	m	b	R^2	RMSE	d
Estación Ruiz Cortínez
HARG	1.1208	0.8766	0.6093	1.6334	0.6479
HARGC	1.0456	0.7023	0.6374	1.1898	0.7623
RNABR1	1.0784	0.8604	0.7704	1.3118	0.7320
RNABR2	1.0773	0.7340	0.6916	1.2705	0.7445
RNABR3	1.1547	0.4138	0.695	1.3096	0.743
Estación Batequis
HARG	0.9224	1.1872	0.8208	1.0416	0.8749
HARGC	0.8614	1.1972	0.7663	0.9045	0.8968
RNABR1	0.7406	1.9924	0.6616	1.1732	0.8238
RNABR2	0.8488	1.3455	0.7646	0.9646	0.8827
RNABR3	0.9488	0.8988	0.8447	0.8838	0.9080
Santa Rosa 1
HARG	0.7993	1.6840	0.8750	1.0046	0.9009
HARGC	0.7180	1.4231	0.856	0.7055	0.9425
RNABR1	0.6572	2.0211	0.7394	1.0085	0.8835
RNABR2	0.8214	1.1456	0.8534	0.7365	0.9452
RNABR3	0.8827	0.8998	0.9137	0.6254	0.9621
Santa Rosa 2
HARG	1.0414	1.3364	0.8376	1.62	0.7425
HARGC	0.8372	1.0717	0.8165	0.6914	0.9243
RNABR1	0.7596	1.8781	0.6414	1.2042	0.7975
RNABR2	1.0926	0.3017	0.8370	0.9324	0.8974
RNABR3	1.1392	0.0710	0.8573	0.898	0.9069

m = pendiente, b = intercepto, R² = coeficiente de determinación, RMSE = raíz cuadrada del cuadrado medio del error en mm día⁻¹, d = índice de Willmott

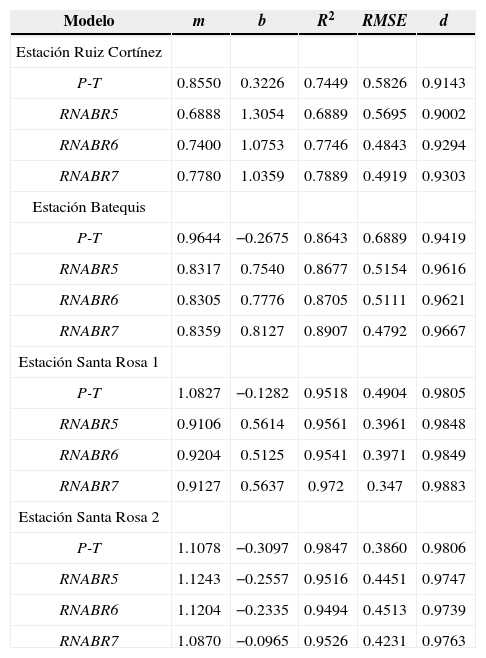
Los valores de RMSE en el cuadro 6 (validación) indican que las tres RNA BR tienen valores más bajos que P-T en las estaciones Ruiz Cortínez, Batequis y Santa Rosa 1. En Santa Rosa 2 P-T estima mejor que las tres RNA BR, puesto que presenta menor RMSE.

Cuadro 6..

Resumen de estadísticos de la validación de los métodos que estiman ET₀ diaria con P-Ty RNABR5, 6, 7 comparada con FAO-56 P-M

Modelo	m	b	R^2	RMSE	d
Estación Ruiz Cortínez
P-T	0.8550	0.3226	0.7449	0.5826	0.9143
RNABR5	0.6888	1.3054	0.6889	0.5695	0.9002
RNABR6	0.7400	1.0753	0.7746	0.4843	0.9294
RNABR7	0.7780	1.0359	0.7889	0.4919	0.9303
Estación Batequis
P-T	0.9644	−0.2675	0.8643	0.6889	0.9419
RNABR5	0.8317	0.7540	0.8677	0.5154	0.9616
RNABR6	0.8305	0.7776	0.8705	0.5111	0.9621
RNABR7	0.8359	0.8127	0.8907	0.4792	0.9667
Estación Santa Rosa 1
P-T	1.0827	−0.1282	0.9518	0.4904	0.9805
RNABR5	0.9106	0.5614	0.9561	0.3961	0.9848
RNABR6	0.9204	0.5125	0.9541	0.3971	0.9849
RNABR7	0.9127	0.5637	0.972	0.347	0.9883
Estación Santa Rosa 2
P-T	1.1078	−0.3097	0.9847	0.3860	0.9806
RNABR5	1.1243	−0.2557	0.9516	0.4451	0.9747
RNABR6	1.1204	−0.2335	0.9494	0.4513	0.9739
RNABR7	1.0870	−0.0965	0.9526	0.4231	0.9763

m = pendiente, b = intercepto, R² = coeficiente de determinación, RMSE = raíz cuadrada del cuadrado medio del error en mm día⁻¹, d = índice de Willmott

Los valores de los RMSE de P-T son menores en la validación (cuadro 6) que en el ajuste (cuadro 3). Para las tres RNA BR, sólo en Santa Rosa 2 los RMSE son menores en el periodo de ajuste con respecto al de validación.

Las RNABR8, 9 y 10 en el proceso de validación (cuadro 7) presentaron RMSE menores a 0.2 mm día^-1, semejantes a los del ajuste, la excepción es en la estación Ruíz Cortínez que son menores de 0.3 mm día⁻¹. Los resultados de los Modelos RNABR8, 9 y 10 en todos sus escenarios (cuadro 7) son similares a lo encontrado por Trajkovic et al. (2003), que utilizó una RNA BR para estimar ET₀ pero de manera mensual con una R² de 0.94. Las RNABR5, 6 y 7 con menos o igual datos que P-T, presentaron mejor capacidad en la estimación de la ET₀ FAO-56 P-M, la mejor fue la RNABR7 (cuadro 6).

Cuadro 7.

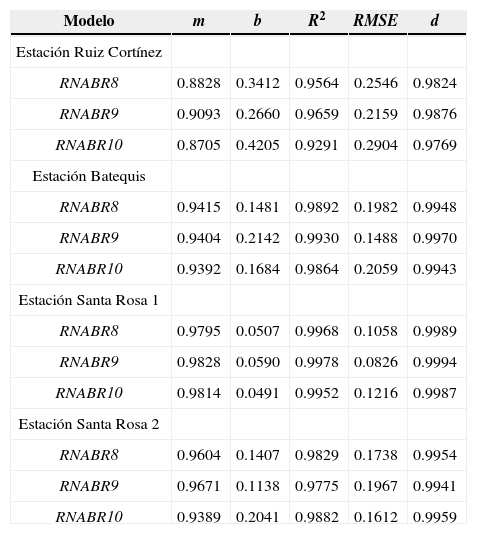
Resumen de estadísticos de la validación de los métodos que estiman ET₀ diaria con RNABR8, 9, 10, comparada con FAO-56 P-M

Modelo	m	b	R^2	RMSE	d
Estación Ruiz Cortínez
RNABR8	0.8828	0.3412	0.9564	0.2546	0.9824
RNABR9	0.9093	0.2660	0.9659	0.2159	0.9876
RNABR10	0.8705	0.4205	0.9291	0.2904	0.9769
Estación Batequis
RNABR8	0.9415	0.1481	0.9892	0.1982	0.9948
RNABR9	0.9404	0.2142	0.9930	0.1488	0.9970
RNABR10	0.9392	0.1684	0.9864	0.2059	0.9943
Estación Santa Rosa 1
RNABR8	0.9795	0.0507	0.9968	0.1058	0.9989
RNABR9	0.9828	0.0590	0.9978	0.0826	0.9994
RNABR10	0.9814	0.0491	0.9952	0.1216	0.9987
Estación Santa Rosa 2
RNABR8	0.9604	0.1407	0.9829	0.1738	0.9954
RNABR9	0.9671	0.1138	0.9775	0.1967	0.9941
RNABR10	0.9389	0.2041	0.9882	0.1612	0.9959

m = pendiente, b = intercepto, R² = coeficiente de determinación, RMSE = raíz cuadrada del cuadrado medio del error en mm día⁻¹, d = índice de Willmott

A su vez, Sudheer et al. (2003) encontraron una R² de 0.8645 en un escenario semejante al RNABR8, éste varió entre 0.9564 a 0.9968. Según los RMSE en esta fase de validación (cuadro 7) resultó mejor el Modelo RNABR9 que el modelo RNABR10, no siendo así en el ajuste. La RNABR9, con las variables de entrada temperatura media, radiación global, déficit de presión de vapor y velocidad del viento fue el modelo de mejor desempeño en la estimación de la evapotranspiración de referencia.

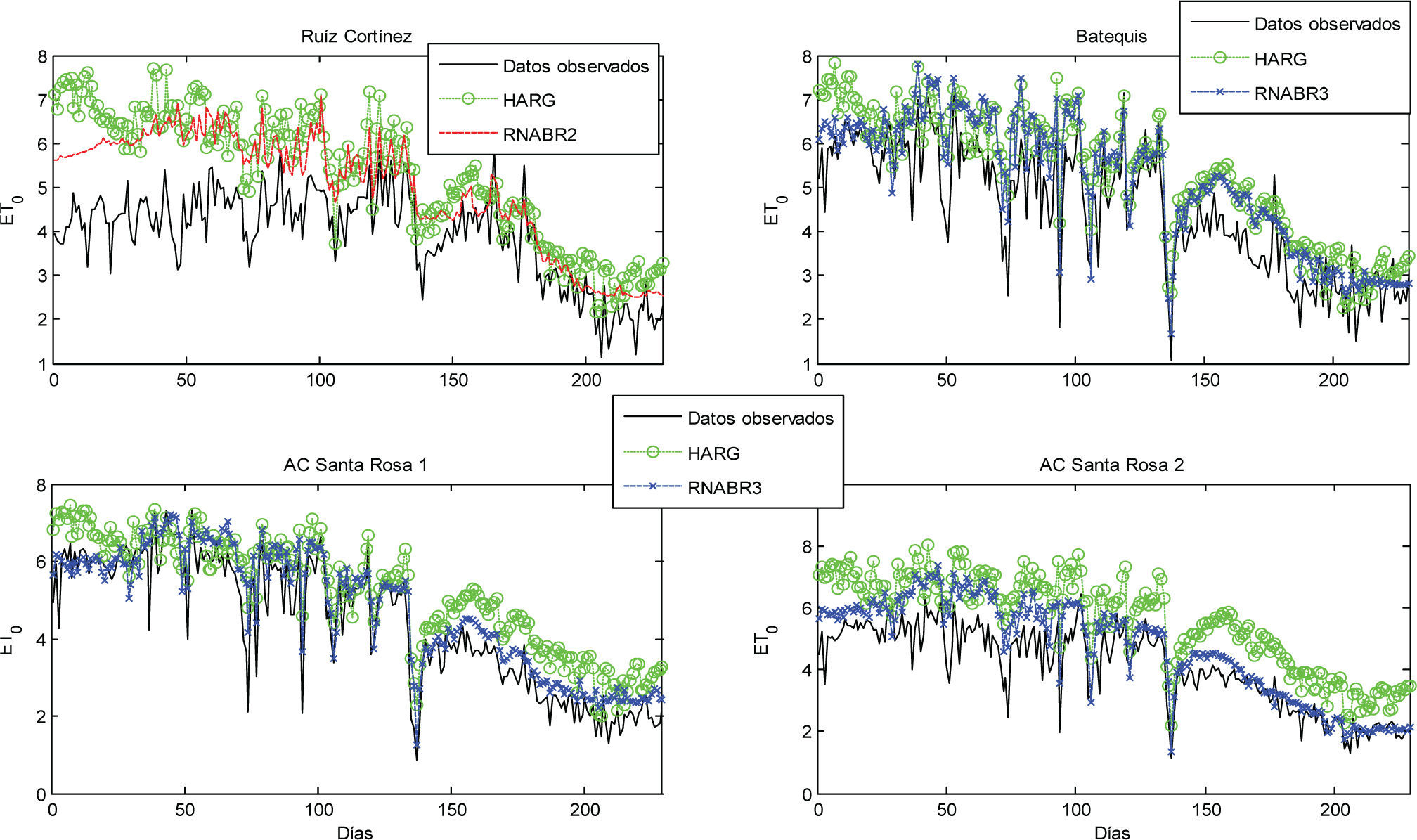
En la figura 1, en las cuatro estaciones, los métodos HARG, RNABR2 y RNABR3 sobreestiman el valor de ET₀ FAO-56 P-M (método base). HARG y RNABR2 en la estación Ruíz Cortínez de mayo a agosto (1 a 120) presentan sus máximas desviaciones, con respecto al método base. La RNABR3 estima mejor la ET₀ FAO-56 P-M en Santa Rosa 1 y 2. Todo lo anterior concuerda con los RMSE (cuadro 5).

Figura 1.

Comparación de los datos ET₀ FAO-56 P-M con los estimados por los métodos HARG, RNABR2 y RNABR3 para el periodo de validación (229 días)

HARGC en las estaciones Ruíz Cortínez y Santa Rosa 2 de la figura 2, presenta un mejor comportamiento que RNABR2 y RNABR3. Aquí también se observa que HARGC y RNABR2 de mayo a julio tienen sus máximas desviaciones. En Batequis y Santa Rosa 1,HARGC y RNABR3 tienen mejor estimación del método base. En las cuatro estaciones, los tres métodos presentan su mejor estimación en los meses de octubre a diciembre (151 a 210). También se resalta que HARGC disminuye la sobreestimación en comparación con HARG.

Figura 2.

Comparación de los datos ET₀ FAO-56 P-M con los estimados por los métodos HARGC, RNABR2 y RNABR3 para el periodo de validación (229 días)

En la figura 3 Santa Rosa 2 P-T presenta mejor estimación que la RNABR7, en las otras estaciones es esta última. Suleiman y Hoogenboom (2007) encontraron que en época de invierno el Modelo P-T subestima a los datos observados de ET₀ en todas sus estaciones, lo que también aquí se presentó (figura 3).

Figura 3.

Comparación de los datos ET₀ FAO-56 P-M con los estimados por los métodos: P-T y RNABR7 para el periodo de validación (229 días)

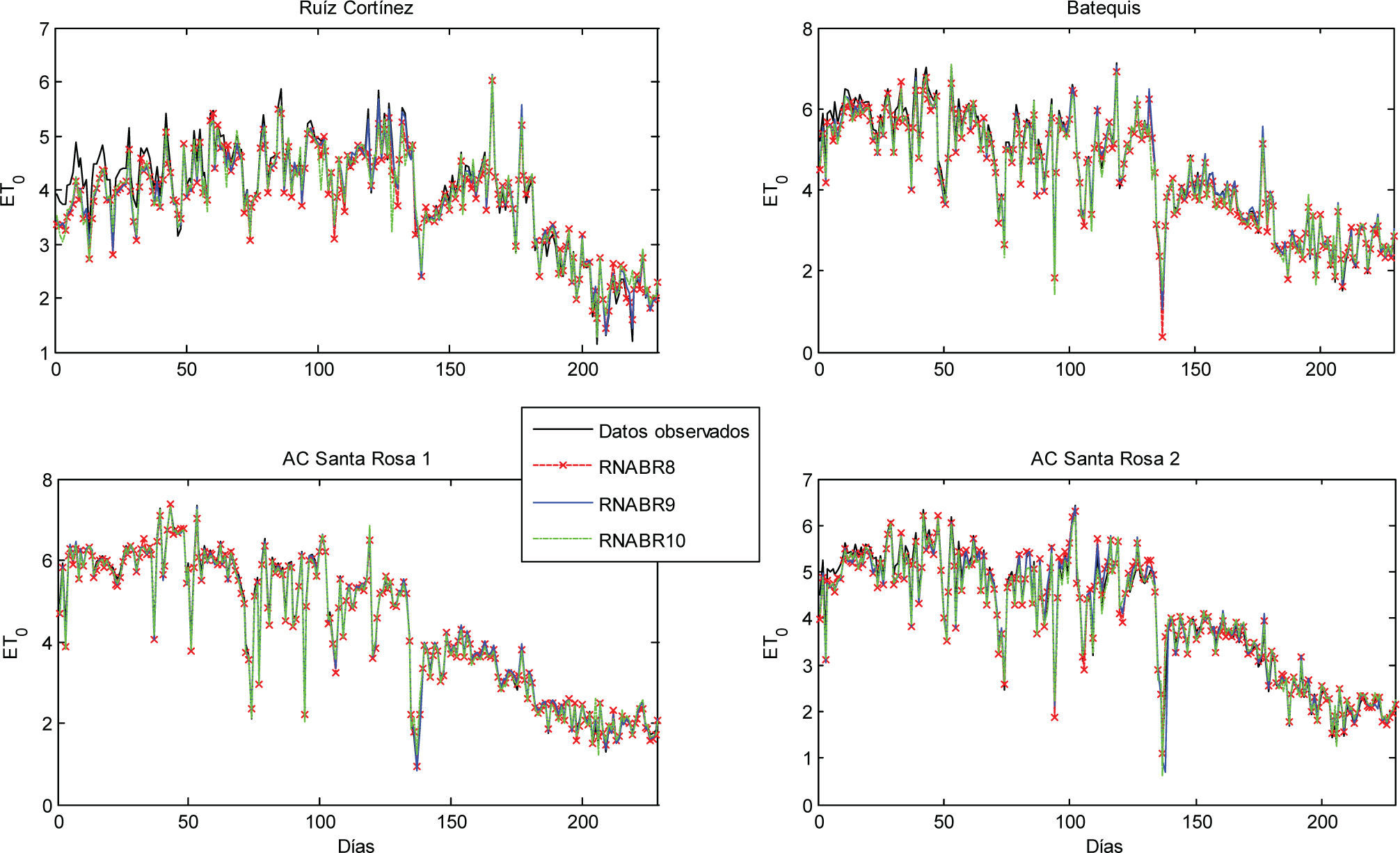
En la figura 4 se confirma lo que se presentó en el cuadro 7, que el Modelo RNABR9 es mejor que el RNA-BR8.

Figura 4.

Comparación de los datos ET₀ FAO-56 P-M con los estimados por los métodos: RNABR8, RNABR9 y RNABR10, para el periodo de validación (229 días)

Por todo lo expuesto aquí, se deriva que los modelos convencionales tienden a sobreestimar o subestimar la ET₀, debido a que tienen parámetros definidos en función de los datos climatológicos que utilicen, si se está estimando en invierno o verano, o si la zona es húmeda o seca, calida o fría. La bondad en el ajuste de los modelos de RNA se debe al entrenamiento, validación y prueba con datos particulares de la región, lo que hace que sean más flexibles y eficientes en la estimación, ya que integran en los pesos de la etapa de entrenamiento, características climáticas de la región y eso repercute en una buena estimación de la ET₀ diaria. Hargreaves calibrado posee también esta flexibilidad de integrar en el ajuste de HE, características climáticas de la región que ayuda en la estimación de la ET₀. El mejor método de los convencionales fue P-T en tres estaciones, le siguió HARGC y al final HARG. En Batequis el primero fue HARGC y P-T fue segundo.

Los modelos RNABR8, RNABR9 y RNABR10 muestran un excelente ajuste, tanto en la simulación como en la validación, ya que considera las variables de entrada que están directamente relacionadas con los dos procesos importantes de la evapotranspiración: el radiactivo y el aerodinámico, la carencia de variables, tales como la velocidad del viento y la humedad atmosférica (humedad relativa o déficit de presión de vapor) limita el desempeño tanto de los modelos convencionales como de las redes neuronales artificiales, pero al retomar el objetivo de estudio, no todas las estaciones cuentan con el total de instrumentos para realizar las mediciones de todas las variables que requiere la estimación de ET₀ FAO-56 P-M y puesto que los instrumentos mínimos con que cuentan cualquier estación son los que miden temperaturas máximas y mínimas que utilizó el modelo de RNABR3 o radiación neta en RNABR7. De ahí la bondad de los modelos y los resultados de los cuadros y figuras, los cuales mostraron que esta información es suficiente para entrenar la red neuronal artificial y obtener buena estimación de la evapotranspiración de referencia diaria. Lo anterior corrobora lo encontrado por Sudheer et al. (2003) y Trajkovic et al. (2003).

Conclusiones

Los resultados indican que al comparar las RNABR3 y RNABR7 con igual (o menos) número de variables de entrada que sus respectivos modelos convencionales, se determinó que ambas fueron mejores en la estimación de la evapotranspiración de referencia calculada con Penman-Monteith FAO-56.