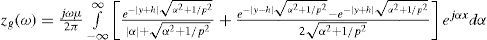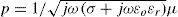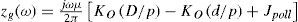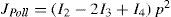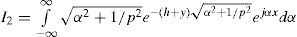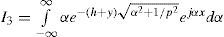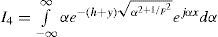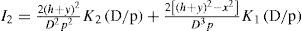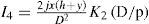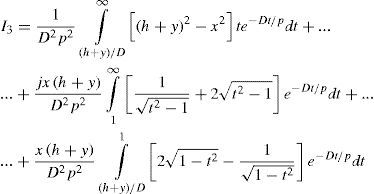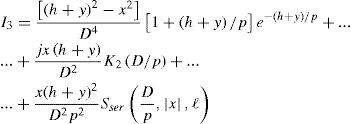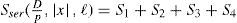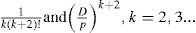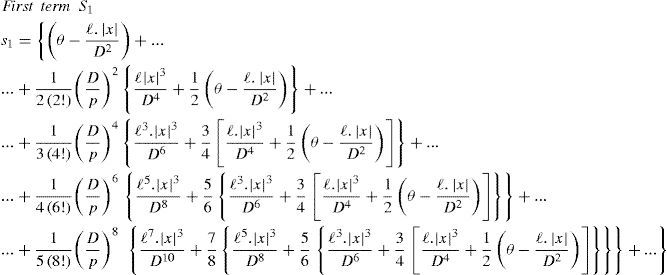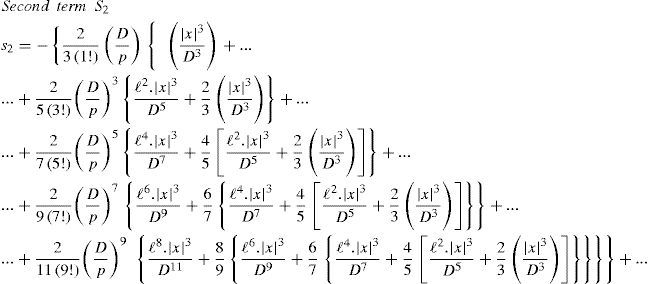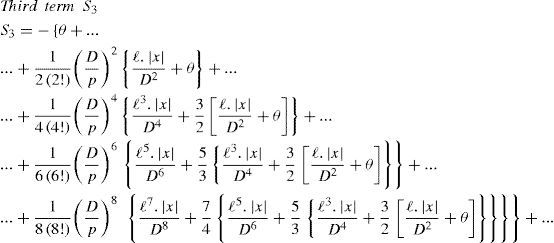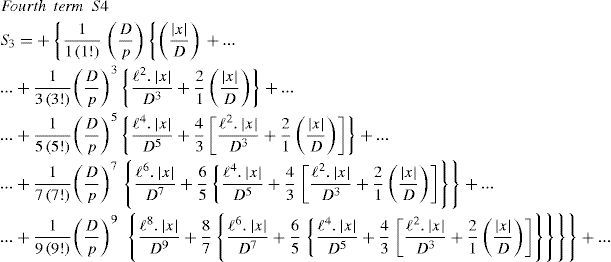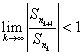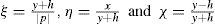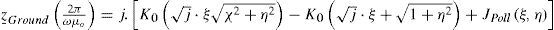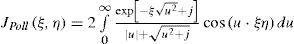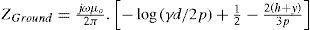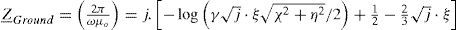In this paper, the Wedepohl-Wilcox series, proposed for calculating ground-return impedances of buried cables and electromagnetic transients, are analyzed in detail. The origin of this series goes back to the original integral derived by Pollaczek. To enhance the analysis developed here, a numerical comparison between the series, the direct numerical integration of Pollaczek integral, and a proposed hybrid numerical algorithm is presented in this paper. The later consists on: a) the use of a vector-type efficient algorithm for the converging series for low frequencies, and b) trapezoidal numerical integration for the high frequency range. In addition, and based on the analysis, a criterion for switching between series and direct numerical integration is proposed here.
En este artículo se analiza con detalle la serie de Wedepohl-Wilcox, propuesta para calcular impedancias de retorno por tierra de cables subterráneos, así como transitorios electromagnéticos. El origen de esta serie se remonta a la derivación original de la integral de Pollaczek. Para mejorar el análisis desarrollado aquí se presenta una comparación numérica entre la serie, la integración directa de la integral de Pollac-zek y se presenta un algoritmo híbrido numérico. Este último consiste en: a) el uso eficiente de un algoritmo vectorizado para series convergentes en el rango de baja frecuencia y b) la integración numérica trapezoidal para el rango de alta frecuencia. Adicionalmente, basándose en este análisis, se propone un criterio para switchear entre la solución de la serie y la integración numérica directa.
One of the most important techniques, over 85 years old, to calculate the influence of the ground-return on aerial and buried electrical conductors was posted by Von F. Pollaczek in June 1926. In this work, Pollaczek presented a set of integral expressions to evaluate the electric field due to an infinite thin filament of current in the presence of an imperfect conducting ground.
Unless, Pollaczek integrals are accurate enough for many power applications, several authors have developed approximate methods and closed-form solutions to avoid facing these rapidly increasing oscillating integrals.
One important publication related to this topic was published in 1973 by Wedepohl and Wilcox, in this publication, a complete mathematical model based on the modified Fourier integral for the synthesis of travelling wave phenomena in underground transmission systems was proposed. An important contribution in Wedepohl and Wilcox (1973) is the solution of Pollaczek’s integral through a set of low frequency infi-nite series. To the best author knowledge, an efficient solution of the series has not been implemented nor included in any commercial software. Besides, it is argued that the series solution is rather complicated and it is better that the impedance is obtained directly from solving the Pollaczek’s integral, numerically.
As a first objective, and inspired on the research in Wedepohl and Wilcox (1973), an efficient numerical implementation of the Wedepohl-Wilcox series solution is developed in this paper for calculating ground-return impedances for underground cables, which can guarantee absolute convergence (Kaplan, 1981).
As a second objective, a comparison with four different algorithms for solving Pollaczek integral is presented for calculating electromagnetic transients. The first one corresponds to the originally proposed in Wede pohl and Wilcox (1973), i.e., solving the series for low frequencies and using a closed-form solution for the high frequency range. The second algorithm is proposed here and corresponds to a hybrid one. This is based on the rapidly converging series for low frequencies, combined with trapezoidal integration of the unexpan-ded integral expression for high frequencies (Wedepohl and Wilcox, 1973). The third and the fourth algorithms consist on trapezoidal numerical integration and Gauss-Kronrod routine, respectively, applied directly to the unexpanded and Pollaczek integral, without using approximating series.
As a third objective, the proposed hybrid algorithm is tested for a wide range of practical application cases on transient analysis. This is achieved by using normalized dimensionless variables according to an interpretation for underground cables of the application limits reported in (Ametani et al., 2009).
The computational analysis of the studied algorithms is presented here regarding accuracy and CPU-time.
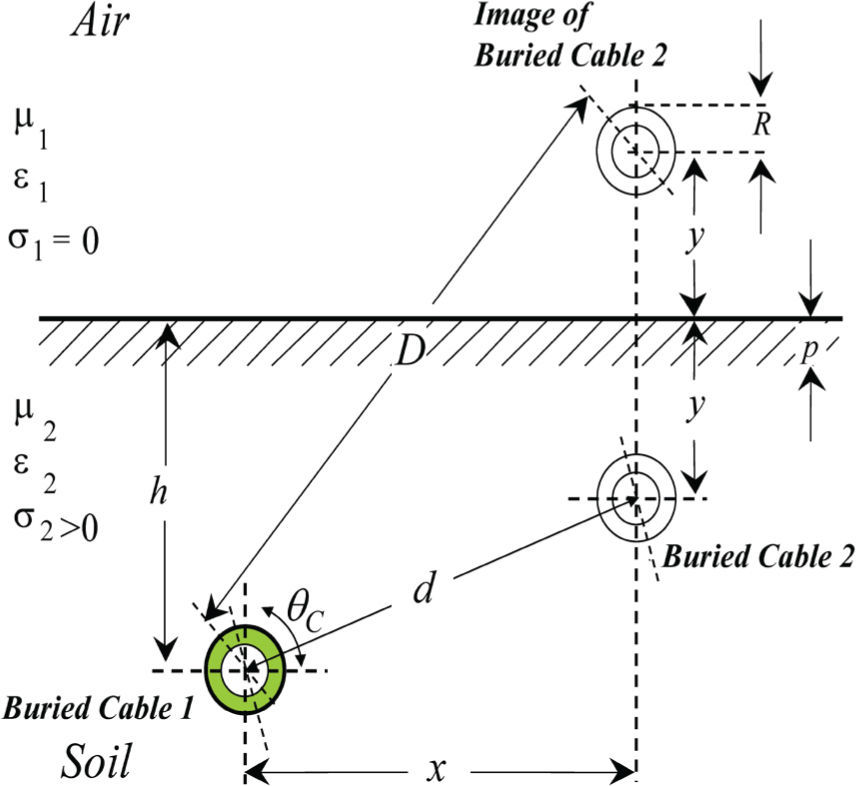
Earth-return impedancesBasic relationsThe self and mutual earth-return impedance for a qua-si-TEMz (transversal electromagnetic with respect to “z” axis) mode is described by (Figure 1 for reference directions) Wedepohl and Wilcox (1973):
where α is the dummy variable, w represents the angular frequency (in rad/s), μ corresponds to the magnetic permeability (H/m) of the soil, and the complex depth or Skin Effect Layer Thickness (considering displacement currents) is given by many authors (Pollaczek, 1926; Wedepohl and Wilcox, 1973; Kaplan, 1981; Ametani et al., 2009; Carson, 1926; Uribe et al., 2004; 2000; Dommel, 1986):
where σ is the ground resistivity (Ω·m) and ε is the relative permitivity (ε0 for the vacuum (F/m) and εr of the soil).
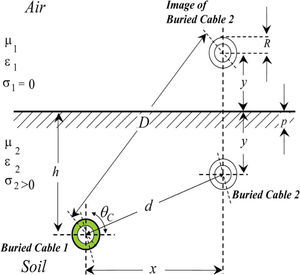
After the second integral in (1a) is expressed via Bessel functions, where K0 is the Bessel function of zero order, thus (1a) becomes (parameters D and d are shown in Figure 1) (Wedepohl and Wilcox, 1973):
where
According to (3b) and (3d), the solution for I2 and I4 is given by
respectively, where K1 and K2 represent modified Bessel functions of first and second order, respectively. For I3, we have
The first part of the integral in (4c) is easily evaluated by traditional integration; the second part corresponds to K2(D/p). In Wedepohl and Wilcox (1973), it is proposed that the third part of (4c) be evaluated by series expansion of the exponential function and then integrated term-by-term to give Sser(D/p, |x|, 1), with ℓ = h + y.
That is
The series term Sser from (4d) is further analyzed in the following sections.
Wedepohl-Wilcox seriesDespite some typographical errors in Wedepohl and Wilcox (1973) regarding the converging series, these can be split up into the following four types of terms:
S1 to S4 are displayed here differently than in Wedepohl and Wilcox (1973) for better clarity of programming implementation, as shown in (6). For instance, an analysis of S1, given by (6a), reveals that the leading terms
can be stored into two separate vectors and used whenever is required. In addition, it can be observed in (6)-(9) the nesting nature of the remaining terms.
It is noted that the aforementioned leading terms are frequency dependent whilst the nested terms depend only on the geometry of the cable system.
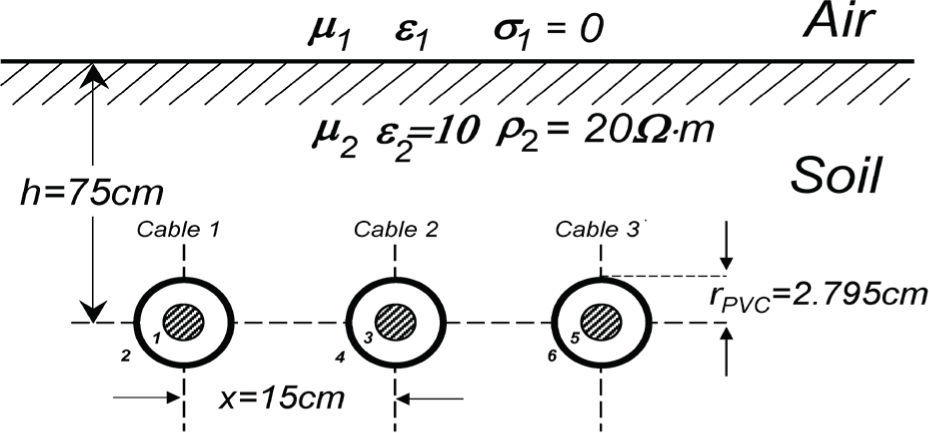
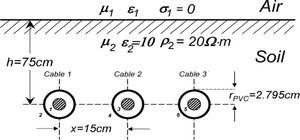
Convergence analysisSeries versus numerical integrationConsider the three cable application case reported in Wedepohl and Wilcox (1973) and reproduced here in Figure 2. For this case, the frequency range has been uniformly sampled from 1Hz to 10MHz by using 100 points.
Underground cable transmission system, taken from Wedepohl and Wilcox (1973)
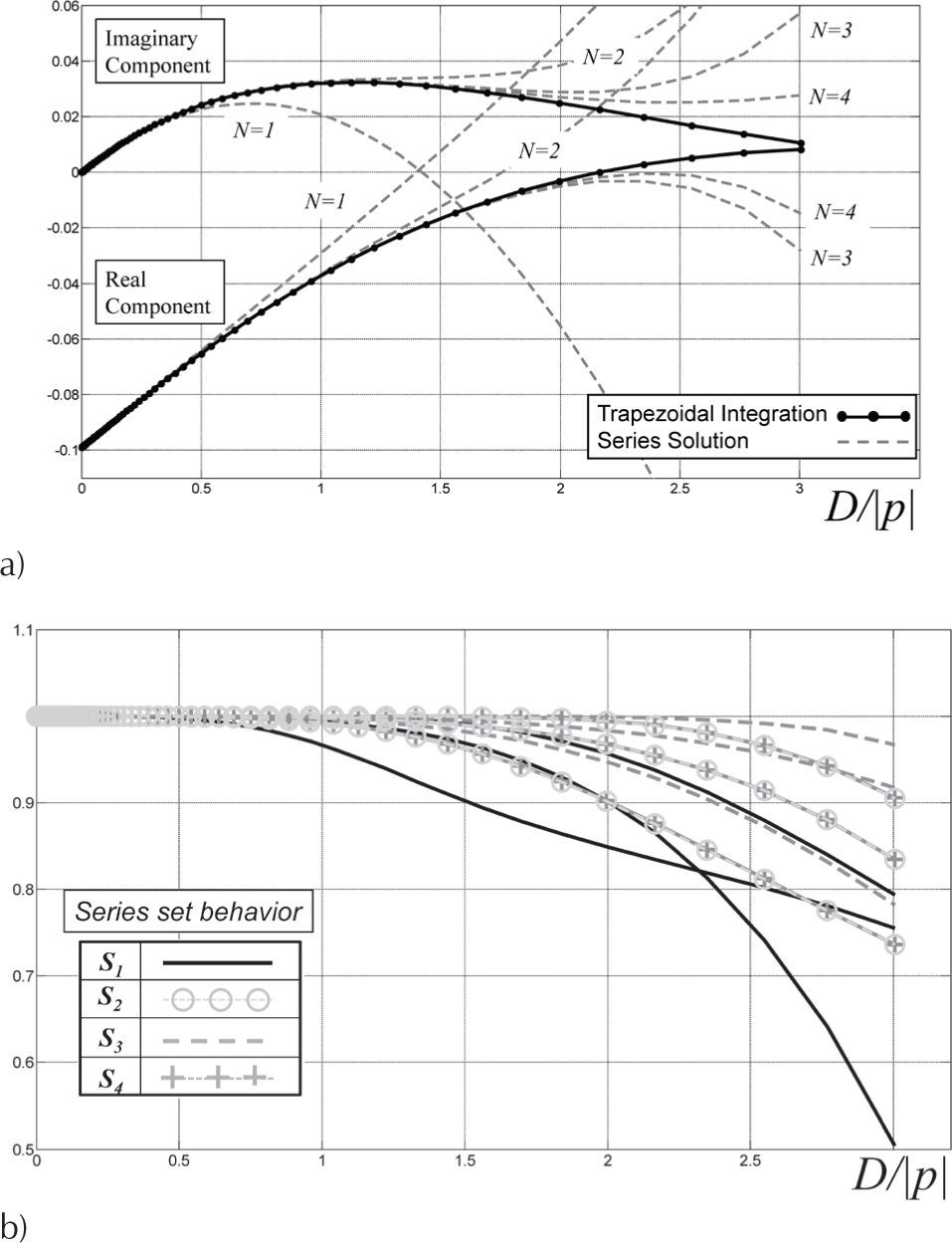
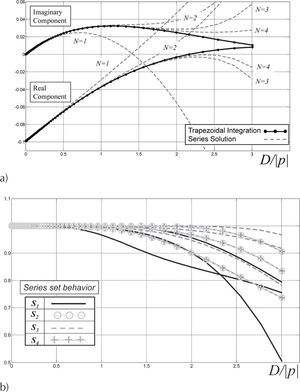
As a first evaluation, we use the series proposed by Wedepohl-Wilcox, Sser, given by (5). The second evaluation corresponds to the trapezoidal-based numerical integration of the third integral in (4c), labeled Sint.. A step equal to 10–4 has been used for calculating Sint.. The behavior of both evaluations is presented in Figure 3a. In this figure, the real and complex components of Sint are presented in black continuous doted line. As for the Sser, the number of terms has been varied and the corresponding result is shown in the gray dashed line. From the results in Figure 3a, it can be noticed that the first four terms of each Sn, n = 1…, 4, give a fairly good agreement compared to Sint. Further evaluations including more than four terms did not change meaningfully the results given by Sser. This obeys to the theory of convergence of a series around a given point (Kaplan, 1981).
Series convergence test, a) comparison between series solution and trapezoidal integration regarding the number of terms, b) ratio test for convergence (Kaplan, 1981)
In addition, the uniform convergence of the sequence of partial sums (or series solution Sn) has been calculated by using the following ratio test (Kaplan, 1981), for n = 1, 2, 3, and 4
The results of evaluating (10) are shown in Figure 3b. From this numerical analysis, one can observe the smooth behavior of the four sets of curves Sn when approximating Sser which indicates a uniform convergence feature, as defined in (Kaplan, 1981).
Proposed hybrid algorithmFrom Figure 3a it can be seen that all four terms of the series give accurate results, at very low computational expenses, up to D/|p| ≈ 2. Therefore, it is proposed here to use this number as a criterion for a hybrid algorithm that switches between series and numerical integration. This criterion contrasts to the one proposed in Wedepohl and Wilcox (1973) where D/|p| = 1/4 is used to switch between series and a closed form solution of (2). Furthermore, in the proposed hybrid algorithm, the displacement current has also been accounted for, as indicated in (1b).
The main numerical characteristics of the results that have been obtained for the particular underground cable system configuration in Figure 2 are general. Thus, it can also be extended to a broad range of cable confi-gurations as explained in the following section.
Broad range algorithmic solutionIt should be mentioned here that the earth-return impedance, given by (1) has been traditionally handled by using true variables. That is, specific physical and geometrical parameters and continuous complex frequency variables are usually involved to calculate the earth return impedance of the system. This consideration is perfectly valid when simulating a transient in that spe-cific system.
Nevertheless, a simple change of variables, as proposed here, leads to a wide range representation of the earth return impedance. The wide range formulation encloses the majority of practical cases and can be also used as benchmark for alternative solution methods.
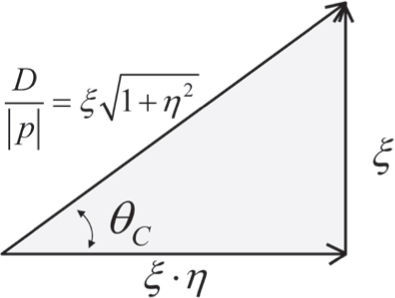
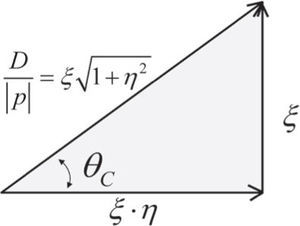
Consider the following normalized dimensionless parameter definitions, which are graphically represented in Figure 4 (Carson, 1926; Uribe, 2004)
Dimensionless normalized vector relations between parameters as described first by Carson’s ground-wave propagation theory (Carson, 1926)
After some mathematical manipulations, one obtains the wide-range representation of (2) as (Uribe, 2004)
where now the term JPoll has been transformed into the following normalized parameter version of the Pollac-zek integral (Carson, 1926; Uribe, 2004)
In obtaining (11c), the change of variable α = u/|p| has been applied also to (1a).
Moreover, the transformation to normalized parameters is of general applicability. For instance, consider the following closed-form expression derived by Wede-pohl-Wilcox from the series expansion (Wedepohl and Wilcox, 1973)
In the normalized parameter form, (11d) becomes now a function of ξ, χ, and η, as follows (Uribe, 2004)
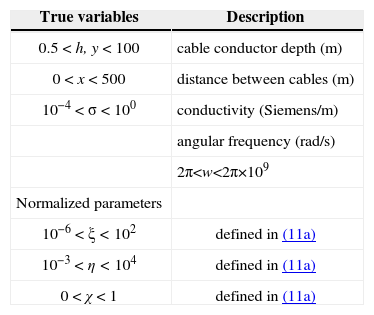
The range for both true and normalized variables is presented in Table 1, following the recommendations from (Ametani et al., 2009). Although the numerical solution of (11c) can be computed, one can take the fast hybrid solution in true variables, as described in the last section “proposed hybrid algorithm”. Then, the result can be transformed into dimensionless variables by using (11a).
Ranges of physical and normalized variables
| True variables | Description |
|---|---|
| 0.5 < h, y < 100 | cable conductor depth (m) |
| 0 < x < 500 | distance between cables (m) |
| 10−4 < σ < 100 | conductivity (Siemens/m) |
| angular frequency (rad/s) | |
| 2π<w<2π×109 | |
| Normalized parameters | |
| 10−6 < ξ < 102 | defined in (11a) |
| 10−3 < η < 104 | defined in (11a) |
| 0 < χ < 1 | defined in (11a) |
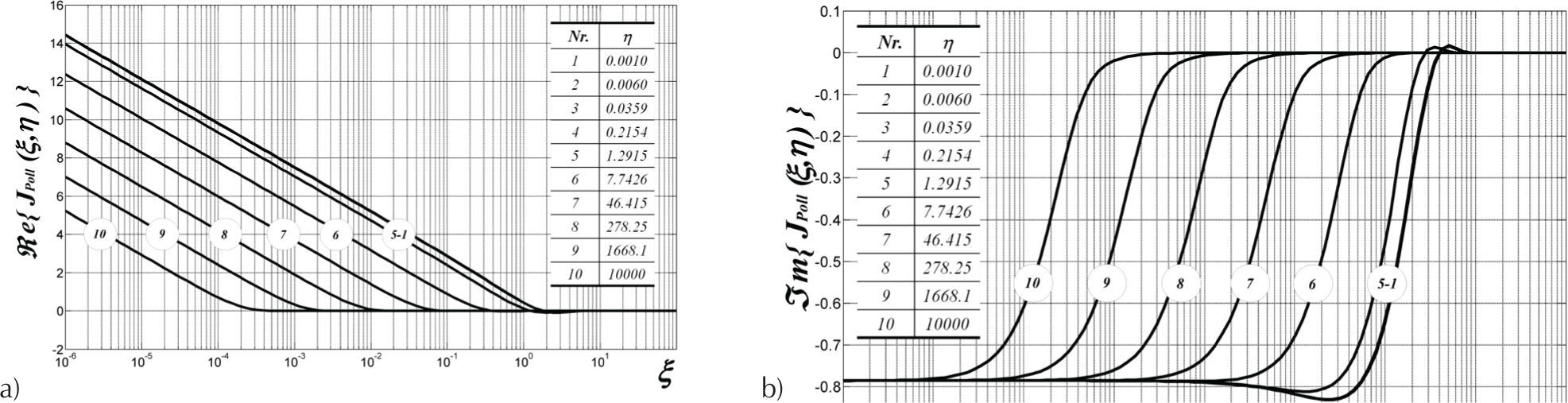
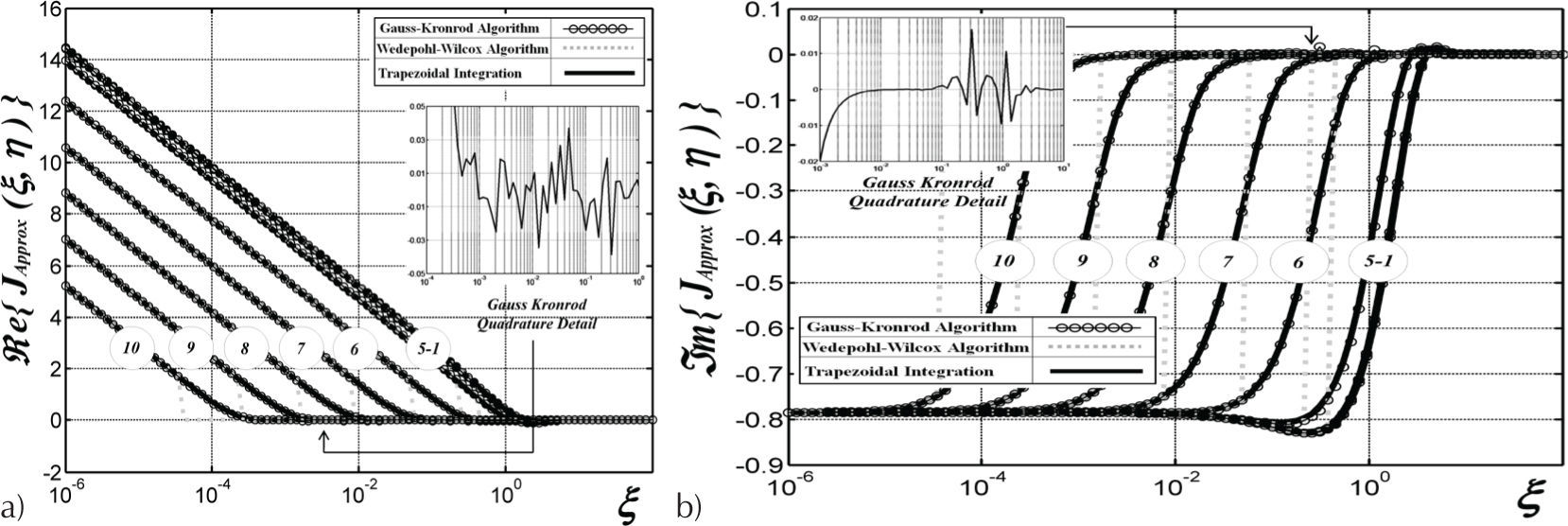
Figure 5 depicts the numerical solution of JPoll(x,h), given by (11c). This solution was obtained with the hybrid algorithm where 100 samples for x and 10 samples for h have been used. The results obtained by the Wedepohl-Wilcox algorithm, by trapezoidal integration, and by the Gauss-Kronrod algorithm can be seen in Appendix A.
For the numerical analysis in the next section, the hybrid algorithm is taken as basis. Firstly, it has a strong fundament on the numerical analysis presented in section “series versus numerical integration”, specifically for the switching criterions. Secondly, it does not show numerical oscillations as other methods (Figure 11, Appendix A).
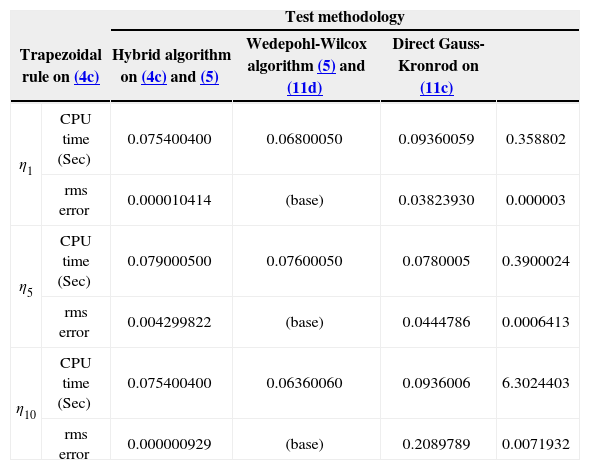
Computational analysisThe computational performance of the aforementioned methodologies for obtaining the wide range solution curves (as shown in Figure 5) is presented in Table 2. The first one corresponds to the trapezoidal integration applied to the third integral in (4c). The second one is the hybrid algorithm proposed here which uses the convergent series from (5) combined with trapezoidal integration on (4c). The third one uses the Wedepohl-Wilcox algorithm using the convergent series at the low frequency range and formula (11d) or (11e) for the high frequency one (Wedepohl and Wilcox, 1973). Finally, the fourth one consists on a widely used method, i.e., Gauss-Kronrod, directly to the wide range formulation (11c) using the default absolute tolerance of 10–10 (using double precision format).
Cpu times and rms error
| Test methodology | |||||
|---|---|---|---|---|---|
| Trapezoidal rule on (4c) | Hybrid algorithm on (4c) and (5) | Wedepohl-Wilcox algorithm (5) and (11d) | Direct Gauss-Kronrod on (11c) | ||
| η1 | CPU time (Sec) | 0.075400400 | 0.06800050 | 0.09360059 | 0.358802 |
| rms error | 0.000010414 | (base) | 0.03823930 | 0.000003 | |
| η5 | CPU time (Sec) | 0.079000500 | 0.07600050 | 0.0780005 | 0.3900024 |
| rms error | 0.004299822 | (base) | 0.0444786 | 0.0006413 | |
| η10 | CPU time (Sec) | 0.075400400 | 0.06360060 | 0.0936006 | 6.3024403 |
| rms error | 0.000000929 | (base) | 0.2089789 | 0.0071932 | |
Table 2 resumes the rms-error (calculated in a classical form (Kaplan, 1981) and the computational times required by the four methods. Only the results for three different values of η, chosen from the curves in Figure 5, are shown in Table 2. To obtain the results in Table 2, Matlab® v7.8 on a 2.4GHz processor with 8GHz RAM was used.
From Table 2 it can be observed that the computational time by the Gauss-Kronrod method is larger than the rest of the methods (much larger for η10), as expected. The Wedepohl-Wilcox solution takes CPU times comparable to trapezoidal and hybrid methods; however, its rms-error increases for larger values of η. This is perhaps due to the “weak” criterion for switching between the series and the closed-formula.
TransientA transient calculation of the underground cable system of 5km length, shown in Figure 2, is presented in the following. The open circuit voltage and the short circuit current responses are both calculated through the inverse Numerical Laplace Transform (cable data are available in Appendix B) (Uribe et al., 2000).
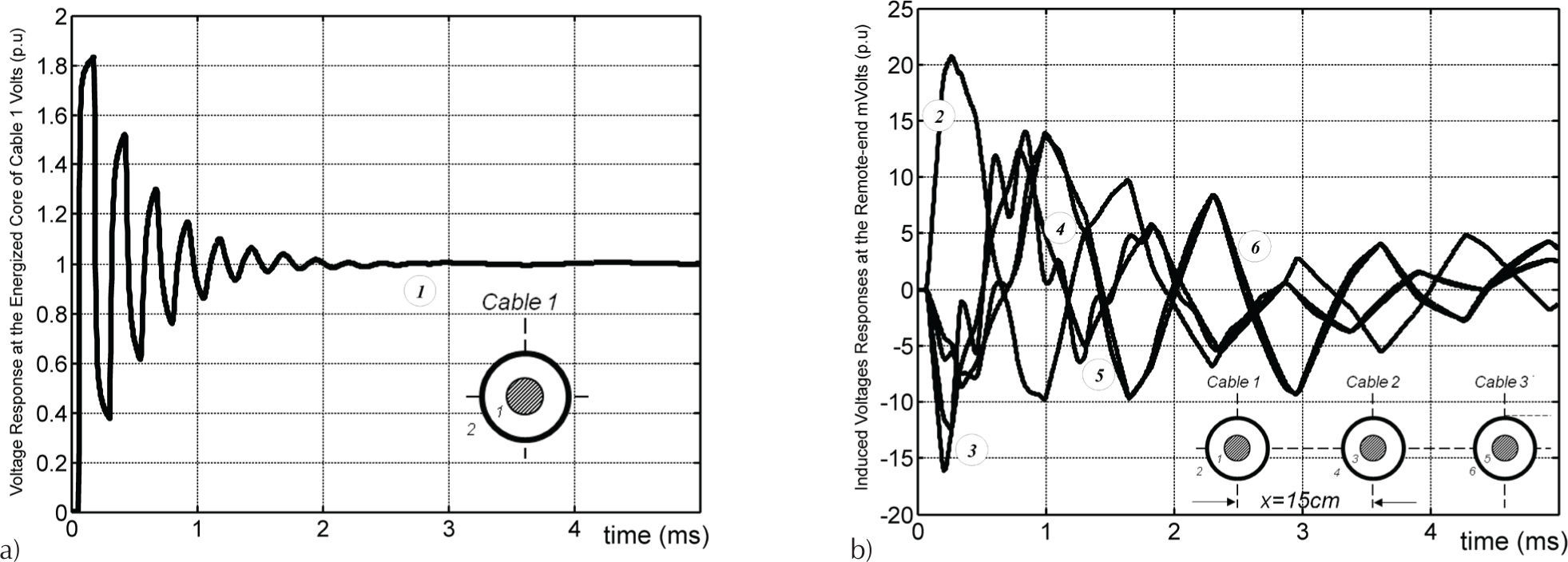
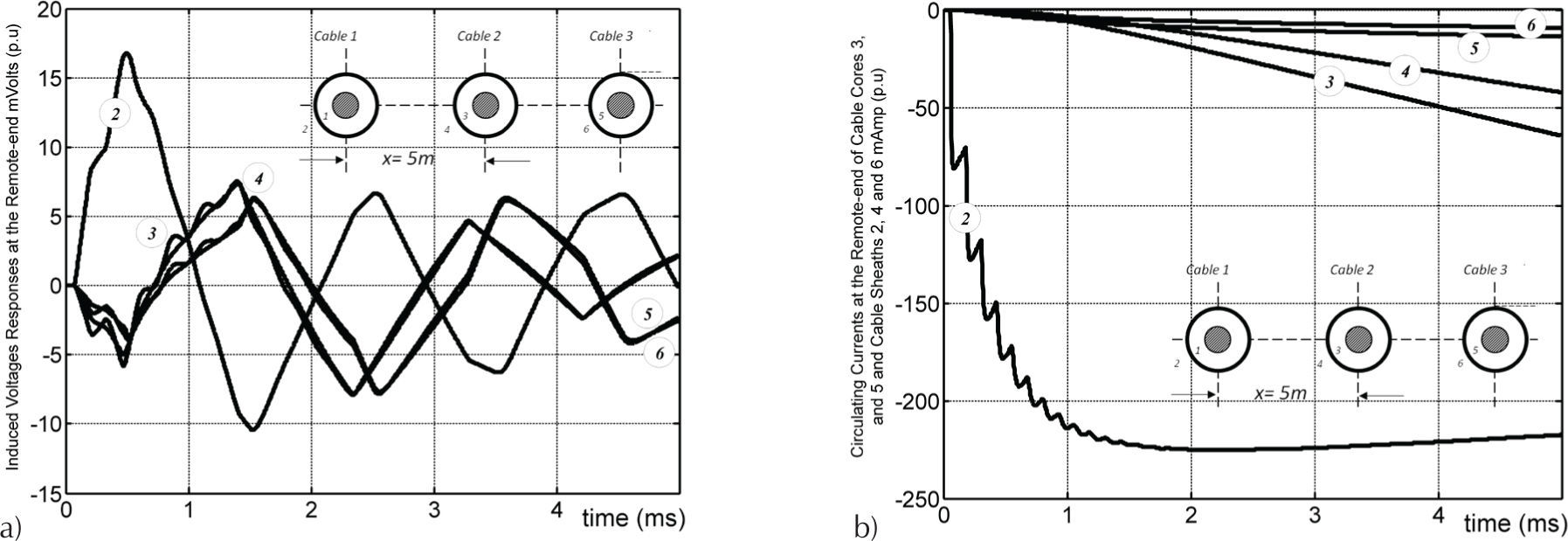
A unit step voltage is injected to the core of cable 1 at the sending end of the underground cable system. The voltages at the receiving end are shown in Figure 6a for the energized core, while Figure 6b presents the induced voltages for cores 3 and 5, and sheaths 2, 4 and 6.
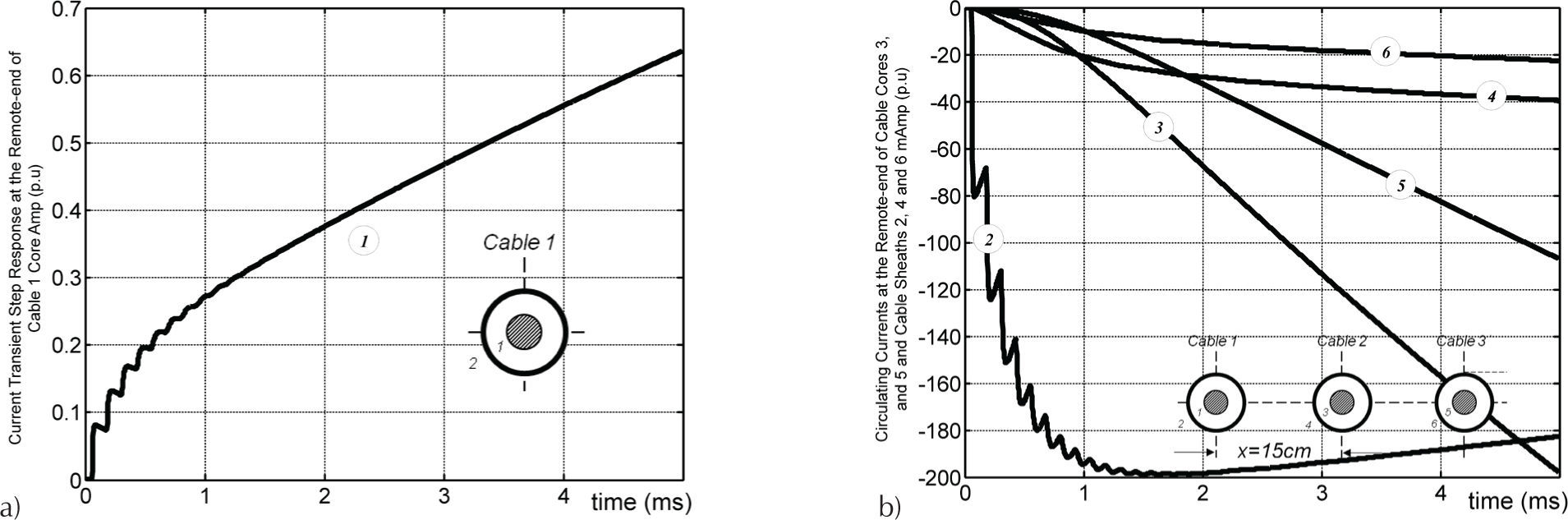
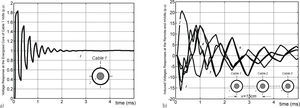
The currents at the receiving end are depicted in Figure 7a for the energized core 1 and in Figure 7b for the circulating currents.
Each core and sheath conductor of the cable system is coupled with each other through four different ground-return loops.
It should be mentioned here that, when the core of cable 1 is energized, the magnitude of the induced voltages and circulating currents for the presented test cases, become naturally smaller as the ground loop distances increases. In these cases, the accuracy of the ground-return impedance calculation becomes important to identify electromagnetic couplings or interference phenomena between underground and overhead transmission or communication systems (Carson, 1926; Dommel, 1986).
Hence, the ground return modeling would directly impact on the estimated voltage or current waveform magnitude responses and on their respective phase behavior.
The transient response corresponding to Figures 6 and 7 have been also obtained with: Gauss-Kronrod direct numerical integration on (11c), the EMTP methodology (Dommel, 1986) and the Wedepohl-Wilcox (1973) derived formula (11d).
In the EMTP methodology the evaluation of the Po-llaczek integral JPoll in (2) is replaced by the evaluation of Carson’s integral (Dommel, 1986).
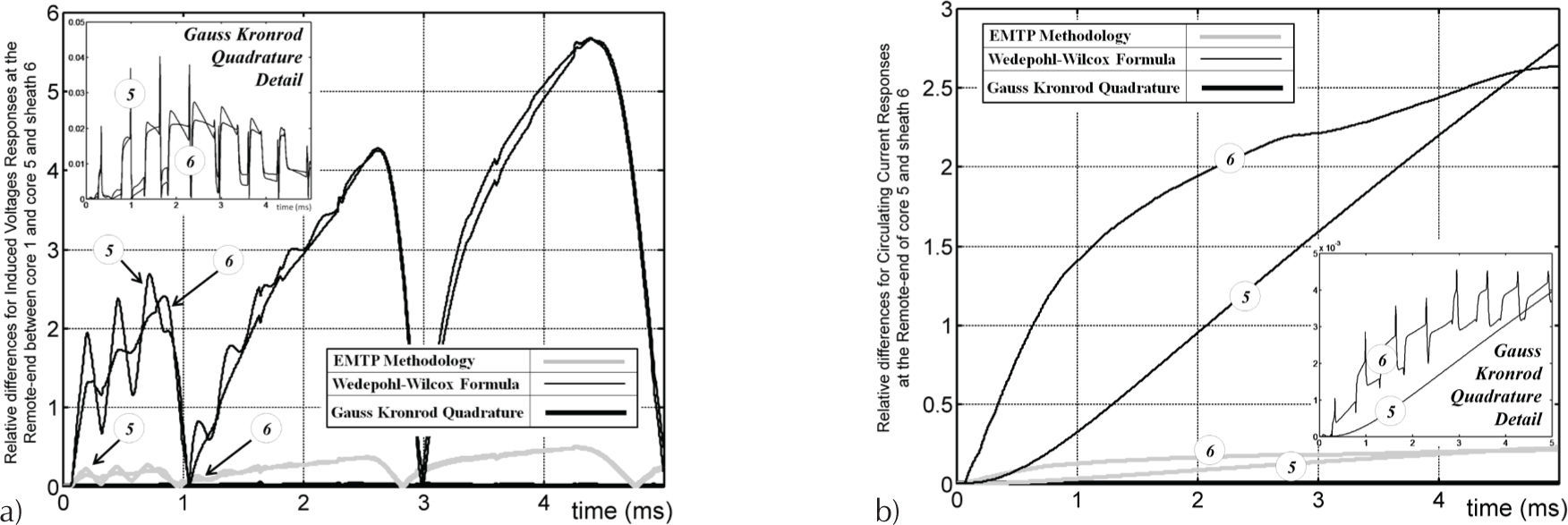
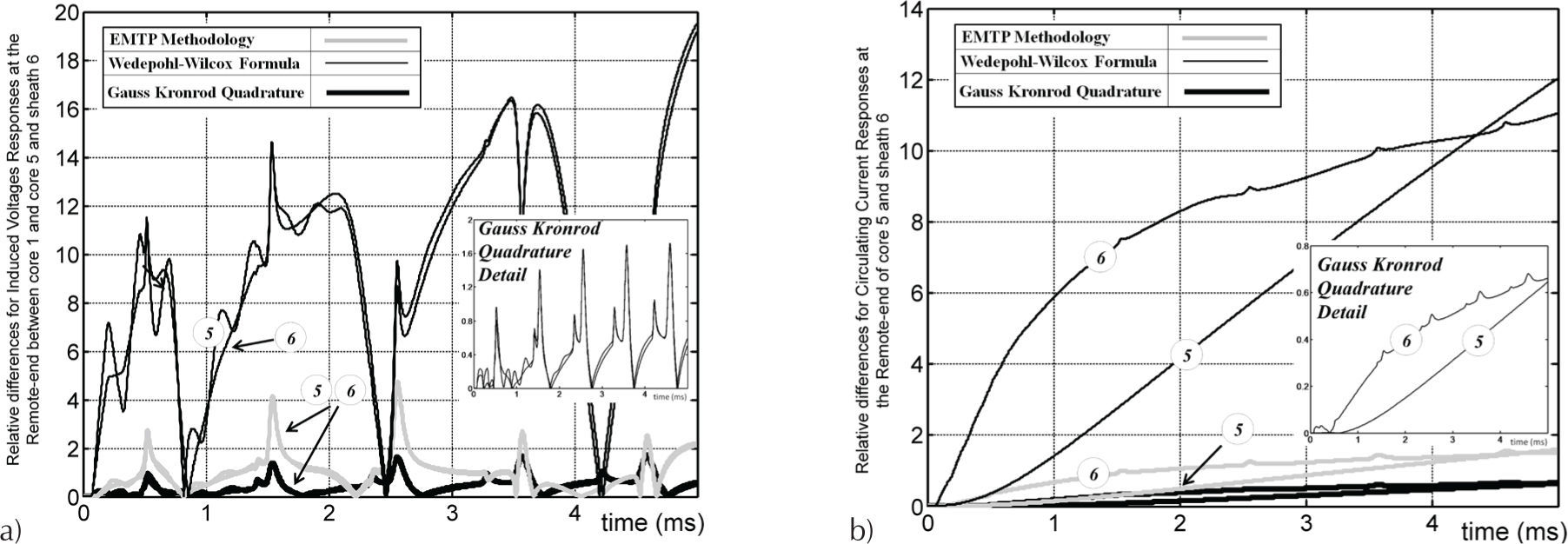
Figure 8a depicts the relative differences for the induced voltage of the loops formed between core-1 on core-5 (circle 5 marker) and on sheath-6 (circle 6 marker), calculated with the aforementioned methods. Figure 8b presents the relative differences for their corresponding circulating currents.
As a second application case, consider again the cable transmission system from Figure 2 (Wedepohl and Wilcox, 1973), but now configured with a separation distance between cables equal to x = 5m.
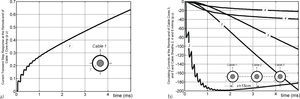
The calculated induced voltages for this second study case are shown in Figure 9a, while the circulating currents are presented in Figure 9b. The corresponding relative differences are shown in Figure 10.
The comparison of Figures 6b and 9a shows that, the greater the distance between cables the lower the induced voltage magnitude, as expected. For this case, the relative differences for the longer formed loops between -core conductor 1 and core conductor 6 and sheath conductor 6 (as shown in Figures 8a and 10a) are more than three times bigger. This confirms that ground return models are highly sensitive on transient applications to the normalized parameters in (11a).
A distinct behavior is presented on the circulating currents in the sheath conductor 2 of the energized cable 1. The greater the distance between cables the greater the magnitude of the current. The relative differences shown in Figures 8b and 10b indicate a poor performance at low frequencies of the ground return models for this example.
ConclusionsThe Wedepohl-Wilcox original infinite series formulation to approximate the ground return impedance, as given by Pollaczek, has been implemented and numerically analyzed in this paper.
An alternative new hybrid method, applicable for both real and wide range dimensionless variables, has also been proposed and also analyzed in this paper. Since the proposed hybrid algorithm can be established for a wide range of physical and geometrical variables, it can be used to define any practical application ranges for approximate formulas and also to assess any other numerical methods (based on quadrature, infinite series, conformal mapping, numerical optimization, etc.) for improving accuracy on transient calculations.
For many years several algorithms to calculate the ground impedance have also been implemented and applied to a transient analysis. From the obtained results, it has been noticed that a precise calculation of such impedance is needed to obtain accurate and reliable time domain transient responses.
The wide range approximate solutions of Pollaczek’s integral calculated via the Wedepohl-Wilcox algorithm, trapezoidal integration, and Gauss-Kronrod algorithm, are depicted in Figure 11. There are some numerical oscillations, that are more noticeable in the real component case of the η10 curve (its value is tabulated in Figure 5), when applying the Gauss-Kronrod algorithm in the following range 10-4 < ξ < 100.
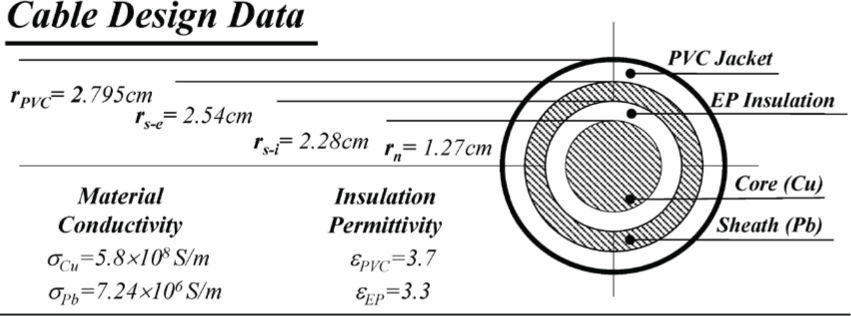
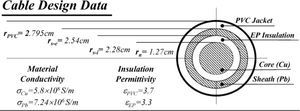
Cable design specifications for the paper transient application cases are depicted in Figure 12.
Original cable data for the electromagnetic transient calculation example, taken from Wedepohl and Wilcox (1973)
Chicago citation style Uribe-Campos, Felipe Alejandro. Numerical Infinite Series Solution of the Ground-Return Pollaczek Integral. Ingeniería Investigación y Tecnología, XVI, 01 (2015): 49-58. ISO 690 citation style Uribe-Campos F.A. Numerical Infinite Series Solution of the Ground-Return Pollaczek Integral. Ingeniería Investigación y Tecnología, volume XVI (issue 1), January-March 2015: 49-58.
Received the B.Sc. and M.Sc. degrees of Electrical Engineering, both from the State University of Guadalajara, in 1994 and 1998, respectively. During 2001 he was a visiting researcher at the University of British Columbia, B.C. Canada. In 2002 he received the Dr. Sc. degree of Electrical Engineering from the Center for Research and Advanced Studies of Mexico. The dissertation was awarded with the Arturo Rosenblueth prize. From 2003 to 2006 he was a full professor with the Electrical Graduate Program at the State University of Nuevo Leon, México. In May 2006, Dr. Uribe joined the Electrical Engineering Graduate Program at the State University of Guadalajara, México, where he is a full time researcher. Since 2004, he is a member of the National System of Researchers of Mexico (SNI). His primary interest is the electromagnetic simulation of biological tissues for early cancer detection, and power system harmonic and transient analysis.