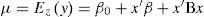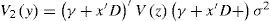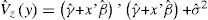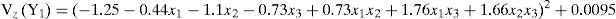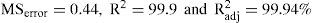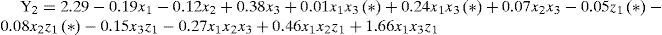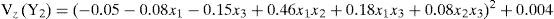Optimization of the Tensile and Flexural Strength of a Wood-PET Composite

Abstract

The large amount of disposable bottles presently produced makes the search for alternative products that reuse these materials imperative. Wood-plastic composites are sustainable, organic materials, that show potential for the development of environmentally friendly products. This paper presents the optimization of tensile and flexural strength of a wood-plastic composite made from polyethylene-terephthalate, as thermoplastic resin, and sawdust as fiberfill. The goal of this study was to establish the operating conditions that provide the optimum properties of the wood-plastic composites, with minimal variance. The particle size of the fiber filler was taken as a noise factor. The response surface methodology, by contour lines, in a combined design of experiment was applied.

Resumen

La gran cantidad de productos desechables producidos en la actualidad hace imprescindible la búsqueda de productos alternativos para la reutilización de estos materiales. Los compuestos de madera-plástico son materiales orgánicos, sustentables y prometedores para el desarrollo de productos amigables con el ambiente. En este trabajo se presenta la optimización de la resistencia a la tensión y flexión de un compuesto de madera-plástico hecho de polietilén-tereftalato como resina termoplástica y aserrín en polvo como fibra de relleno. El objetivo de este trabajo fue establecer las condiciones de procesamiento que proporcionan la máxima resistencia a la tensión y flexión del compuesto de madera plástico, con una variación mínima. El tamaño de partícula de la fibra de relleno se tomó como un factor de ruido. Se aplicó la metodología de superficie de respuesta mediante curvas de nivel en un diseño de experimentos de arreglo combinado.

Introduction

Wood-plastic composites (WPC) are materials that consist primarily of a polymer phase (thermoplastic/thermoset) in which a secondary phase filler is embedded; the filler can be made from fibers, particles or flakes. Traditionally thermoset resins are not normally used in WPC, but the benefits of combining thermoplastic resins with natural fibers are now well recognized. The WPC thermoplastics are environmentally attractive because sawdust is a waste and thermoplastics are recyclable.

The wood fibers were originally used only to reduce the density and cost of plastic articles, but the fibers were also found to improve the mechanical performance of the products. Using wood as a WPC component, the stiffness and other mechanical properties of the compounds can be effectively improved. The natural fiber-reinforced plastics can provide mechanical properties comparable to those of composites reinforced with glass fiber (Herrmann et al., 1998), for example. WPCs have been used primarily in the construction of decorative accessories, windows and doors, where substantial structural performance is not required. Information regarding the WPC engineering with polyolefins is widely available (Clemons, 2002), but the use of PET as a matrix in a WPC has been of interest only recently.

This paper shows an analysis of the tensile and flexural strength of a WPC with polyethylene terephthalate (PET) as thermoplastic resin and sawdust as filler. WPC with other thermoset/thermoplastic resins have been extensively studied (Herrmann et al., 1998). Four operational factors that have an effect on the tensile and flexural strength of a WPC with PET as a thermoplastic resin were determined. One of the four operational factors (particle size of the filler) was considered as an uncontrollable, or noise factor. It is important to note that, in practice, milling and sieving the sawdust to a specific size is very expensive. For this reason, the particle size of the filler is considered a noise factor. Through the response surface methodology in the context of dual robust design (Robinson et al., 2004) we found the level of these three operational controllable factors that maximizes tensile and flexural strength of the WPC, while also being less susceptible to the noise factor variations.

At this time there is only a few articles published on the optimization of mechanical properties of WPC by robust design. There has been some research on improving properties of WPC with different strategies. Shu and Rakesh (2008) examined the injection molding of a WPC with polypropylene (PP) as a thermoplastic resin; this study found the rate of moisture absorption can be reduced by changing operational conditions, while maintaining the same mechanical properties. The experiment was planned as a factorial design and the experimental data were analyzed with analysis of variance (ANOVA) (Montgomery, 2004). Soury et al. (2009) present the application of a micro-multiobjective genetic algorithm, which was applied in optimizing the design of a WPC profile made with PP as a thermoplastic resin; the main objective was to reduce the overall weight of the product and to maintain sufficient capacity, where the optimal design specifications were verified analytically. Shao et al. (2011) investigated the effect of changing the composition of a WPC with recycled polypropylene (RPP) as a thermoplastic resin, on mechanical and physical properties. The study evaluated four parameters: particle size of the filler, dose of coupling agent, lubricant content and the mass ratio of the wood and RPP; the results show that the use of small particle sawdust (less than 125 microns) improved tensile and flexural strength, as well as reduced moisture absorption. Saeed (2013) presents a detailed review about some essential properties of waste and recycled plastics, important for WPC production, and of research published on the effect of recycled plastics on the physical and mechanical properties of WPC. Yong and Qingling (2012) show a study of wood-plastic composites prepared based on in situ formed (PET) sub-micro-fibril reinforced high density polyethylene (HDPE) matrices, using a two-step reactive extrusion technology. They conclude that the use of ethylene -glycidyl methacrylate copolymer- improved phase compatibility in the sub-micro-fibril blends with 75% HDPE and 25% PET

The experimental scheme proposed in this paper is a factorial arrangement that jointly considers control and noise factors, with the latter seen as a random variable. From this scheme, models were obtained for the mean and variance, for both responses (tensile and flexural strength). The robust simultaneous optimization of the two models was achieved by the desirability function (Derringer and Suich, 1980).

Experimental

The global quality of the composites studied here is based on a set of control and noise factors. The robust design is a method that seeks to reduce the variation caused by noise factors and improve the performance of products and processes at low cost. Generating robust products in the presence of noise factors was an innovative idea in the area of quality engineering. In the early 1980s, the engineer Genichi Taguchi substantially contributed to technological development with his methodology. His work created a very important dynamic in the industrial world, and allowed many applications in the design of new products and process improvements. His contribution is known as the robust design parameter (Taguchi and Wu, 1980). Taguchi>s contributions generated significant research activity in the statistics field. Publications regarding new alternatives and approaches based on his work are still appearing today (Robinson et al, 2004; Myers et al, 2004). However, the main contributions of Taguchi led to debates and controversies in academia related to experimental design. A disadvantage of Taguchi’s robust design is the large amount of experimental work to be performed in accordance to his strategy known as double orthogonal array, and the measurement signal to noise ratio (Box et al, 1988; Nair, 1992).

A very good alternative to the Taguchi methods are the response surface models. These include both controllable and noise factors, and their interactions; this type of model is often called a combined array response model (Montgomery, 2004). An important advantage of the response model approach is that both controllable and noise factors can be placed in a single experimental design. This means that the crossed array of Taguchi approach can be avoided. This procedure allows for each treatment to calculate the mean and variance.

Experiment design

In this investigation we propose an optimization procedure to find the best conditions for the average with the lowest variance. This approach leads to the technique known as dual response (Tang and Xu, 2002; Koksoy and Doganaksoy, 2003). Our interest in the experimental analysis is to determine whether there is an interaction effect between the control factors and the noise factor. Several authors have worked on this approach, including Montgomery (2004), Tang and Xu (2002), Myers and Montgomery (2002). The proposed model can be expressed by:

where x' = (x₁x₂, x₃) is the vector of control factors and z' = (z₁) is the noise factor, β and γ are the parameters vector, B is a parameter matrix that represents quadratic effects and interactions between control factors, and D is a triangular matrix of parameters representing the interaction effects between control and noise factors. Model parameters are unknown constants and ε is a random variable with normal probability distribution with mean zero and variance σ². Another relevant statistical assumption concerns the factor z which is a random variable with mean zero and variance σz2. The aim is to find the expected value, mean and variance for in equation (1). That is, using equation (1) two models should be determined, one for the mean (E_z(y)) and another one for the variance (V_z(y)).

The first model is

under the assumption that the random variables z and å have expected value of zero. The estimated model of the expression (2) is:

The model for (V_z(y)) is:

The mean and variance models include only control factors. The estimated model is:

where the V(z) = I.

Materials

Composite specimens were molded with a thermoplastic resin of PET with high and low viscosity, and a sawdust filler. The PET, defined as PET 0.75 and PET 0.84 was obtained from the company INVISTA (Mexico, DF). Sawdust was obtained from a local lumber yard and the additive, which functions as a coupling agent (polyethylene/polypropylene), was obtained from the company CELANESE (Mexico City).

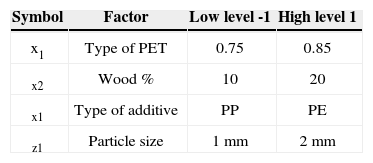
Mixture preparation

A description of the manufacturing process of the samples is shown in Figure 1. First, the sawdust was milled and sieved with an analytical vibrating screen AS 200 to characterize the particle size. The particle sizes used in the experiments were 1, 1.4 and 2 millimeters, corresponding to a mesh size of 18,14 and 10 (ASTM) respectively. The three materials, PET, sawdust, and coupling agent, were dehydrated in a drying oven at a temperature of 100°C for 8 hours. After dehydration each com ponent was weighed using an analytical balance. For the mixing, the ingredients were fed to a single screw laboratory extruder Brabender (PL2200 PLASTICORDER, México). The screw speed was 90 RPM and the temperature profile in the extruder was 240, 250, 260 and 260°C. Sixteen different formulations were made (Table 2). In the sixteen formulations PET, sawdust, and coupling agent concentrations were 2000, 49.6 and 1400 grams respectively.

Figure 1.

Description of the manufacturing process of the specimens

Table 2.

Experimental design 2⁴ and results

Test#	Natural Units				Coded Units				Responses
	PET	Wood	Additive	Particle	x1	x2	x3	zl	¿1	¿2
1	0.75	20	PE	2	-1	1	1	1	11.64	2.79
2	0.85	10	PE	2	1	-1	1	1	19.29	2.85
3	0.85	20	PP	2	1	1	-1	1	11.33	2.57
4	0.75	10	PP	1	-1	-1	-1	-1	12.81	2.11
5	0.75	10	PE	2	-1	-1	1	1	15.24	2.69
6	0.85	20	PE	1	1	1	1	-1	18.09	2.79
7	0.85	20	PP	1	1	1	-1	-1	20.72	2.04
8	0.75	10	PE	1	-1	1	1	-1	18.49	4.38
9	0.75	10	PP	1	-1	1	-1	-1	21.35	3.01
10	0.85	20	PE	2	1	1	1	1	19.21	3.59
11	0.75	10	PE	1	-1	-1	1	-1	21.64	2.64
12	0.75	10	PP	2	-1	-1	-1	1	23.30	4.04
13	0.85	20	PP	1	1	-1	-1	-1	15.71	2.05
14	0.75	10	PP	2	-1	1	-1	1	17.57	2.20
15	0.85	20	PP	2	1	-1	-1	1	14.20	1.21
16	0.85	20	PE	1	1	-1	1	-1	23.10	3.72

Under an inert atmosphere pine wood suffers a slight weight loss. From this result, it was assumed that the 260°C maximum temperature was not enough to degrade the pine sawdust used in the investigation since in rapidly becomes embedded in the PET resin, thus avoiding the interaction with oxygen at high temperatures at the same time. The composite maintained the natural wood color at the end of the processing of the samples (Yi et al, 2012), which confirmed the aforementioned assumption.

The extruder hopper was fed with the ingredients; these were pushed through four heating zones by a single screw. The coupling agent, which has a melting point lower than that of PET, was first melted, making it adhere to the PET and wood before the wood is encapsulated by PET. The literature recommends two different coupling agents. In this study, both coupling agents were evaluated in order to determine which agent worked best with PET. When the material has passed through the four heating zones it is completely mixed and melted allowing to be molded in various geometries.

The extrudate composite was ground to a fine powder. The milling was carried out in a blade mill PAGANI 5HP with a mesh of 5 mm in diameter (diameter of the holes in the mesh). The fine powder was transferred to rectangular plates to mold the specimens that were die cut. The molding was conducted in a hydraulic press with a molding temperature of 260°C for 3 minutes.

Mechanical test

The machined samples were analyzed according to standard ASTM D 638 for tensile properties (ASTM, 2008). Tensile and flexural testing was conducted using an Instron Universal Testing Machine (Model 1196) with a velocity of 1 mm/min. Both variables were measured in kilogram force (kgf/mm²).

Results and discussion

Table 1 shows the four factors and study levels carried out. A non replicable 2⁴ factorial design was used. The objective was to determine whether the change in the level of these factors have a statistically significant effect on the variable response.

Table 1.

Experimental factors and their levels

Symbol	Factor	Low level -1	High level 1
x1	Type of PET	0.75	0.85
x2	Wood %	10	20
x1	Type of additive	PP	PE
z1	Particle size	1 mm	2 mm

Table 2 shows the experimental combinations, in random order, the factors and their levels used in each run in coded units and the values of the two response variables. Using the values of Table 2 a model for each response by least squares method was fitted.

The following model was obtained for Y₁:

According to the ANOVA, the model and most of its terms were statistically significant. The non-significant ones, in equation (6), are marked (*). Relevant information from the statistical analysis is given below.

MS_error = 0.2015, Radj2=98.7%, Standard error σ^=0.45

The mean and variance were determined from model (6). According to equation (2) the model for the mean is

With the assumption that σz2=1 (Montgomery, 2004), according to equation (2), the model for the variance is

The main factor x₁ and the interaction factor x₁x₂ were excluded because they were not statistically significant. Relevant information from the statistical analysis is as follows

The assumptions of normality, constant variance and independence of residuals were met satisfactorily.

For Y₂ the following model was obtained

According to the ANOVA, the model and most of its terms were statistically significant. The non-significant ones, in equation (9), are marked again (*). Relevant information from the statistical analysis:

From equation (9), a model for the mean and variance was determined. According to equation (2) the model for the mean is

with the assumption that σz2=1 (Montgomery, 2004)

According to equation (2), the model for the variance is

Figure 2 describes the contours plot from models (7) and (10). The contours plot show the levels of the factors that provide the highest response of both, tensile and flexural strength. The arrangement of the factors that gives the highest values of both response variables is: PE for the type of additive (1 in coded units), type of PET 0.85 (1 in coded units) and 10% wood. The values obtained were 23 kgf/mm² for tension and 3.3 kgf/mm² for flexural strength.

Figure 2.

Contours plot for the mean

Figure 3 confirms that the above arrangement provides the smallest variance for tensile and flexural strength, described by the models (8) and (11), respectively (lower right corners at the diagrams of the four figures). Finally, considering model (6) for tension and (9) for flexural strength, the optimum (minimum variance) is obtained with small particle sizes of sawdust.

Figure 3.

Contour plot for the variance

Conclusions

This paper describes the results of modeling contour plots for two response variables from a dual robust design. The objective was to determine the arrangement of the levels of the factors studied that maximizes tensile and flexural strength and also provides a production process robust to a noise factor. The experiment evaluated two different types of PET, the percentage of wood contained in the composite and two types of additives. The particle size of sawdust was analyzed as a noise or uncontrollable factor. Multiple linear regression models were adjusted to indicate the suitability of the experimental measurements. Regression models satisfactorily described the experimental data obtained. The three control factors and the noise factor showed a statistically significant effect on the tensile and flexural strength of the composite, as presented in the results section.