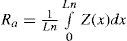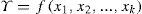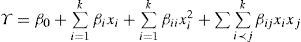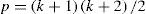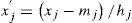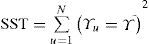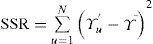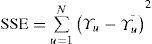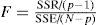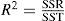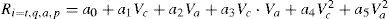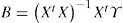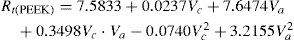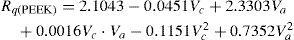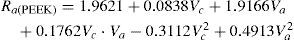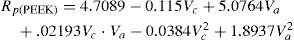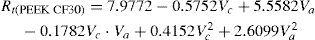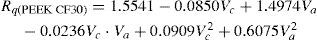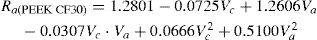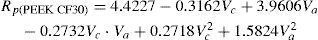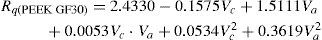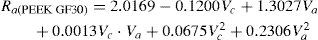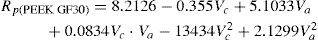Predicción de rugosidad en maquinado de compuestos con base de Peek usando metodología de superficie de respuesta

Resumen

La polieteretercetona (PEEK) pertenece a un grupo de polímeros termoplásticos de alto rendimiento que se utiliza ampliamente en componentes estructurales. Para mejorar las propiedades tribológicas y mecánicas, se añaden fibras cortas a los materiales termoplásticos. Por lo tanto, es necesario investigar el mecanizado de estos compuestos debido a las altas propiedades específicas y a sus usos potenciales. Este trabajo presenta la utilización de la metodología de superficie de respuesta (MSR) para estudiar los aspectos de la maquinabilidad del PEEK no reforzado (PEEK), del PEEK reforzado con 30% de fibras de carbono (PEEK CF30) y del PEEK reforzado con 30% de fibras de vidrio (PEEK GF30) con una herramienta de carburo cementado (K10). Este estudio establece las relaciones entre las condiciones de corte (velocidad de corte V_c y velocidad de avance V_a) y la rugosidad (R_t, R_a, R_q, R_p), desarrollando modelos matemáticos de segundo orden. Se ha utilizado el diseño factorial para establecer el plan de experimentos y el análisis de varianza para comprobar la suficiencia de los modelos. Los modelos de predicción han mostrado validez dentro del rango de parámetros de corte utilizados. En lo que respecta a la influencia de las condiciones de corte, se ha demostrado que la variación de la velocidad de avance, dentro de los valores seleccionados, afecta más a los resultados que la variación de la velocidad de corte. Los resultados de los ensayos han mostrado que los materiales reforzados presentan una peor maquinabilidad en comparación con el termoplástico sin refuerzo. En este caso, el PEEK GF30 es el material que evidencia una peor maquinabilidad.

Abstract

Poly ether etherketone (PEEK) composite belongs to a group of high performance thermoplastic polymers and is widely used in structural components. To improve the mechanical and tribological properties, short fibers are added as reinforcement to the material. Due to its functional properties and potential applications, it's important to investigate the machinability of non-reinforced PEEK (PEEK), PEEK reinforced with 30% of carbon fibers (PEEK CF30), and reinforced PEEK with 30% glass fibers (PEEK GF30) to determine the optimal conditions for the manufacture of the parts. The present study establishes the relationship between the cutting conditions (cutting speed and feed rate) and the roughness (R_a, R_t, R_q, R_p), by developing second order mathematical models. The experiments were planned as per full factorial design of experiments and an analysis of variance has been performed to check the adequacy of the models. These state the adequacy of the derived models to obtain predictions for roughness parameters within ranges of parameters that have been investigated during the experiments. The experimental results show that the most influence of the cutting parameters is the feed rate, furthermore, proved that glass fiber reinforcements produce a worse machinability.

Introducción

La polieteretercetona (PEEK) pertenece a un grupo de polímeros termoplásticos de alto rendimiento. Los compuestos de PEEK se han utilizado ampliamente en automóviles, aeronáutica, biomecánica, robots y máquinas debido a sus altas propiedades específicas respecto a los materiales metálicos convencionales. También encuentran aplicaciones en las industrias naval y militar, en la construcción e ingeniería civil o en la industria química, entre otras.

El material PEEK es el polímero que exhibe propiedades como elevadas resistencias mecánicas, resistencia al desgaste y a la abrasión, resistencia a los agentes químicos y puede trabajar a temperaturas elevadas (Davim et al., 2003; Davim y Mata, 2006). Debido a sus propiedades, este material polimérico se aplica con excepcionales prestaciones en la ingeniería, por ejemplo en la industria aeroespacial, donde el aluminio se ha sustituido por el PEEK debido su mejor comportamiento a temperaturas altas (Davim y Mata, 2007; Davim y Mata, 2008).

Para mejorar las propiedades tribológicas y mecánicas, como la rigidez o el límite elástico, se añaden fibras cortas a los termoplásticos (Davim y Mata, 2005; Davim y Reis, 2004). Las fibras de carbono y de vidrio son los refuerzos más comunes en termoplásticos debido a su alto módulo de elasticidad. Gracias a las altas resistencia y rigidez, los refuerzos de fibra encuentran muchas aplicaciones en componentes resistentes o estructurales. El PEEK reforzado con fibras de vidrio (PEEK GF30) y el PEEK reforzado con fibras de carbono (PEEK CF30) son los mejores materiales para aplicaciones que requieren alta resistencia y rigidez, especialmente a temperaturas por encima de los 150 °C (Harsha y Tewari, 2003; Sinmazcelik y Yilmaz, 2007; Burris y Sawyer, 2007).

Como consecuencia de las propiedades y aplicaciones potenciales, existe una gran necesidad de conocer los procesos de fabricación, en particular los procesos de mecanizado de estos materiales compuestos (Cogswell, 1992; Kukureka et al., 1999; Miravete et al., 2000; Mallick, 2001; Park et al., 2006; Lee et al., 2006; Kim et al., 2006; Verrey et al., 2006).

En la actualidad, crece progresivamente la demanda de componentes fabricados con materiales plásticos reforzados con fibras, debido a su precisión dimensional y a su acabado superficial (Palanikumar et al., 2004; Palanikumar, 2006). El estudio de las superficies constituye una técnica de caracterización de los materiales muy útil en la práctica.

Al mecanizar la polieteretercetona reforzada se evidencia un comportamiento extremadamente abrasivo. Las propiedades y características del material de trabajo se evalúan en términos de “maquinabilidad”, que indica la facilidad relativa con la cual un material se puede maquinar usando las herramientas y los parámetros apropiados. Los criterios más importantes para evaluar la maquinabilidad son la fuerza de corte, la presión específica de corte, la vida de la herramienta, el desgaste de la herramienta y la aspereza superficial o rugosidad. La rugosidad superficial es un parámetro que tiene gran influencia en el comportamiento y la funcionalidad de los componentes mecánicos y en los costos de producción (Abouelatta y Mádl, 2001; Palanikumar et al., 2006), constituyendo una importante variable de control de la calidad. La rugosidad es crítica en los contactos mecánicos, además de otros campos, como la circulación de fluidos y las aplicaciones semiconductoras.

En la mayoría de las aplicaciones se requiere alta calidad en las superficies mecanizadas, incluyendo exactitud dimensional e integridad superficial. Por esta razón, se han llevado a cabo diversas investigaciones con el objetivo de optimizar los parámetros de corte, para obtener una determinada rugosidad (Eriksen, 1999; Abouelatta y Mádl, 2001).

Al hablar de parámetros funcionales de corte nos referimos a la selección de la velocidad de corte, la velocidad de avance y la profundidad de corte. Se han realizado diferentes estudios sobre los parámetros de corte adecuados en la operación de torneado (Yang y Tarng., 1998; El-Sonbaty et al., 2004; Varatharajan et al., 2006), de los que se puede concluir que no existe una referencia universal; antes bien, cada material, según el tipo y porcentaje de fibras de refuerzo, presenta unos valores de velocidad de corte y velocidad de avance más apropiados para conseguir un acabado superficial óptimo y minimizar el desgaste de la herramienta.

Bernardos y Vosniakos presentaron diferentes metodologías que emplearon para predecir la rugosidad superficial (diseño de experimentos, inteligencia artificial, etcétera) y consideraron la influencia de los parámetros de mecanizado, de las propiedades de las herramientas de corte, de las propiedades de la pieza y del fenómeno de corte sobre la rugosidad (Bernardos y Vosniakos, 2003).

Davim y Reis presentaron un estudio sobre la influencia de los parámetros de corte (velocidad de corte y avance) en la rugosidad y en la precisión dimensional torneando tubos de plásticos reforzados con fibras (FRP). Utilizaron matrices ortogonales y análisis de varianza (ANOVA) para investigar las características de corte de los FRP usando insertos de carburos cementados (K15) (Davim y Reis, 2004).

El método de investigación experimental tradicional implica la variación de un parámetro mientras se mantienen otros parámetros en niveles fijos. El método es laborioso, requiere un gran número de experimentos y no incluye efectos interactivos entre los factores controlables. El método de Taguchi, sin embargo, permite enriquecer los métodos de planes de experiencias y tiene por objeto simplificar el protocolo experimental con el fin de poner de relieve los efectos de los factores sobre la respuesta.

La metodología de superficie de respuesta es un conjunto de técnicas matemáticas y estadísticas utilizadas para modelar y analizar problemas en los que una variable de interés es influenciada por otras. El objetivo es optimizar la variable de interés.

Este estudio establece una correlación entre los parámetros de corte (velocidad de corte V_c y velocidad de avance V_a) y la rugosidad (R_t, R_q, R_a, R_p), desarrollando modelos matemáticos de segundo orden. Se ha utilizado diseño factorial para establecer el plan de experimentos y análisis de varianza para comprobar la suficiencia de los modelos.

Trabajo experimental

Materiales ensayados

Para realizar este trabajo de investigación sobre el mecanizado de materiales compuestos, se han utilizado materiales compuestos de matriz polimérica termoplástica, en presentación natural (sin refuerzo) o reforzados con porcentajes fijos de fibras de vidrio o de carbono. En la actualidad, las investigaciones básicas realizadas en tecnología de materiales han permitido procesar materiales termoplásticos que aúnan propiedades y desempeños excelentes en un buen número de aplicaciones y constituyen uno de los mayores focos de atención de la investigación aplicada, especialmente en lo referente al mecanizado por arranque de material.

En concreto, los materiales compuestos de matriz polimérica utilizados en los ensayos son los siguientes:

• a)

  Polieteretercetona (PEEK)

• b)

  Polieteretercetona reforzada con 30% de fibras de vidrio (PEEK GF 30)

• c)

  Polieteretercetona reforzada con 30% de fibras de carbono (PEEK CF 30)

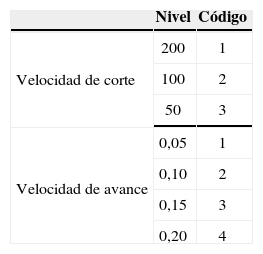
Las propiedades más significativas de estos materiales quedan reflejadas en la tabla 1.

Tabla 1.

Propiedades de los materiales ensayados (ERTA®)

Propiedad	PEEK	PEEK GF30	PEEK CF30	Unidad
Módulo de elasticidad (E)	4400	6300	7700	MPa
Dureza Rockwell	M105	M99	M102	-
Resistencia al impacto	Sin fractura	35	35	kJ/m^2
Temperatura de fusión	340	340	340	°C
Densidad	1.31	1.51	1.41	g/cm^3
Coeficiente de expansión térmica (< 150 °C)	50 x 10^−6	30 x 10^−6	25 x 10^−6	m/m/K
Coeficiente de expansión térmica (> 150 °C)	110 x 10^−6	65 x 10^−6	55 x 10^−6	m/m/K

Preparación de las probetas

Dado que el objetivo de este trabajo de investigación es estudiar el proceso de torneado de piezas pequeñas de materiales compuestos de matriz polimérica termoplástica, se diseñaron probetas de 100 mm de longitud. El material base se adquirió en forma de redondos extruidos de 50 mm de diámetro, de modo que las dimensiones de las probetas son longitud: 100 mm y diámetro inicial: 50 mm.

Máquinas y herramientas

Torno CNC

Para la realización de los ensayos experimentales de torneado se ha utilizado un torno CNC “Kingsbury® MHP 50” de 18 kW de potencia y velocidad máxima de 4500 rpm. El torno CNC posee un controlador Fanuc, una boca de apriete hidráulico, capaz de fijar piezas de hasta 200 mm de diámetro, una torreta para almacenamiento de las herramientas, con capacidad para 12 herramientas de corte. En nuestro estudio se utilizó la herramienta K10 (DCMW 11T304H13A) y un contrapunto con diámetro de 70 mm activado también por accionamiento hidráulico.

Rugosidad superficial

La caracterización de las superficies torneadas se efectuó a través de la técnica más común de análisis de microgeometría de superficies, denominada rugosidad. Las superficies mecanizadas se caracterizaron utilizando los parámetros de amplitud siguientes: R_t, R_q, R_a, y R_p. Para medir los valores de los parámetros de rugosidad, se utilizó un rugosímetro Hommeltester – T 1000, según se puede observar en la figura 2

Figura 2.

Evolución de R_t en función de las velocidades de corte y avance

La rugosidad media aritmética (R_a) indica el valor medio de la rugosidad en una zona de la muestra. Es el parámetro de caracterización de rugosidad que más se utiliza en la mayoría de los procesos de fabricación y se determina mediante la expresión:

donde, Ln es la longitud de evaluación y Z es la distancia entre dos puntos del perfil.

La amplitud máxima del perfil de rugosidad (R_t) corresponde a la distancia entre el pico más alto y el valle más profundo obtenidos en la longitud de medida (Ln), que es independiente de los valores parciales de rugosidad. Se trata de un parámetro que, a diferencia del anterior, tiene un claro significado físico. La altura máxima de picos (R_p) es la distancia del punto más alto del perfil a la línea media. Finalmente, la desviación media cuadrática del perfil (R_q) es el valor cuadrático medio de las desviaciones.

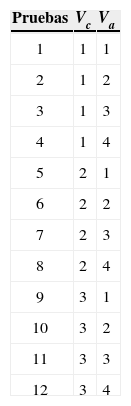
Diseño de experimentos

El proceso de torneado se desarrolló sin lubricante y considerando las doce combinaciones de los tres valores de la velocidad de corte y de los cuatro valores de la velocidad de avance, de acuerdo con la tabla 2. Se utilizó una profundidad de pasada constante de 2 mm. Para los experimentos considerados en este estudio, se empleó un plan experimental basado en el método de Taguchi (1990), lo que permitió reducir el número de ensayos y el costo asociado a los mismos. En la determinación de la primera aproximación del grado de influencia de los parámetros, utilizamos el diseño factorial completo, donde los factores identificados en las pruebas adoptan sus límites superior e inferior. En nuestro caso, sólo se seleccionaron dos factores, de manera que las posibles combinaciones de los niveles coresponden a un total de 12 pruebas. La notación de los parámetros elegidos y sus niveles se resumen en la tabla 2. Los en sayos se realizaron de acuerdo con el plan definido por la tabla 3.

Tabla 2.

Definición de los niveles de los parámetros

	Nivel	Código
Velocidad de corte	200	1
	100	2
	50	3
Velocidad de avance	0,05	1
	0,10	2
	0,15	3
	0,20	4

Tabla 3.

Plan de experimentos

Pruebas	Vc	Va
1	1	1
2	1	2
3	1	3
4	1	4
5	2	1
6	2	2
7	2	3
8	2	4
9	3	1
10	3	2
11	3	3
12	3	4

Método de superficie de respuesta (MSR)

MSR es una herramienta utilizada para establecer la relación entre los factores controlables y las respuestas a fin de explorar el efecto de estos parámetros en las respuestas del proceso de mecanizado.

En muchas áreas de investigación interesa explicar una variable respuesta, Y, a través de k variables explicativas, x_T = [x₁, x₂, …, x_k], mediante un modelo de la forma

La función de respuesta se puede representar con una ecuación polinomial. El éxito en una investigación de una superficie de respuesta depende de que la respuesta se pueda ajustar a un polinomio de segundo grado.

El modelo de segundo orden es el siguiente

Aquí los β_i son los coeficientes de regresión para los términos de primer orden, los β_ii son los coeficientes para los términos cuadráticos puros, los β_ij. son los coeficientes para los términos de producto cruz. Los términos cuadráticos puros y los de producto cruz son de segundo orden. El numero de términos en la ecuación está dado por

Para simplificar los cálculos, las variables independientes se codifican de la siguiente manera

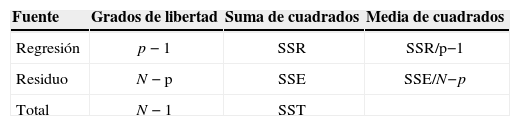
donde m_i es el rango medio de los valores x_j y h_i = (x_imax + x_imin)/2, y m_j es el rango medio de los valores x_jh_j = (x_jmax + x_jmin)/2

Para estimar los coeficientes se requieren N ≥ k + 1 valores de respuesta (Y). El análisis de los datos de las corridas se presenta en una tabla de análisis de varianza. La tabla muestra las diferentes fuentes de variación que contribuyen a la variación total de los datos.

La variación total recibe el nombre de suma de cuadrados total SST y se calcula de la siguiente manera

donde Y_u es el valor observado en el u-ésimo ensayo.

La suma de cuadrados se compone por la suma de cuadrados debido a la regresión y la suma de cuadrados residual. La fórmula de la suma de cuadrados debido a la regresión es

La suma de cuadrados residual, se calcula de la siguiente forma

A continuación la tabla 4 de varianza, presenta el número de términos del modelo ajustado.

Tabla 4.

ANOVA del modelo de regresión múltiple

Fuente	Grados de libertad	Suma de cuadrados	Media de cuadrados
Regresión	p − 1	SSR	SSR/p−1
Residuo	N − p	SSE	SSE/N−p
Total	N − 1	SST

La prueba de significancia de la ecuación de regresión ajustada tiene la siguiente hipótesis nula H₀: todas las β_s(excluyendo β₀) son cero contra la alternativa H_A. Al menos una de las β_s (excluyendo β₀) es diferente de cero. La prueba supone que el error se comporta normalmente y en ella se utiliza el estadístico de prueba F, el cual se calcula

Además de esta prueba se puede hacer un análisis del ajuste del modelo con la R², que es la proporción total de la variación de las Y_u con respecto a la media que se puede explicar con la ecuación de regresión ajustada. Ésta se calcula de la siguiente manera

En esta investigación, se han desarrollado modelos matemáticos de segundo orden basados en el método MSR para estudiar la influencia de los dos parámetros del proceso, a saber, la velocidad de corte (V_c) y avance (V_a), y las cuatro respuestas de rugosidad (R_t, R_q, R_a, y R_p). Las ecuaciones no lineales de la superficie de respuesta de R, R_q, R_a, R_p son

con a₀, a₁, a₂,…, a₅, como los coeficientes del modelo matemático a determinar.

Los valores de los coeficientes de regresión no lineal de la ecuación cuadrática (11) se determina a partir de

donde

• B = la matriz de estimación de los parámetros de la ecuación cuadrática

• X = la matriz de cálculo que incluye términos lineales, cuadráticos y las interacciones

• X^t = la transposición de X e

• Y = la matriz respuesta.

Resultados

Modelos matemáticos de los parámetros de rugosidad

Los modelos matemáticos de predicción para los parámetros de rugosidad de los materiales compuestos PEEK, PEEK FC 30 y PEEK GF 30 son los siguientes

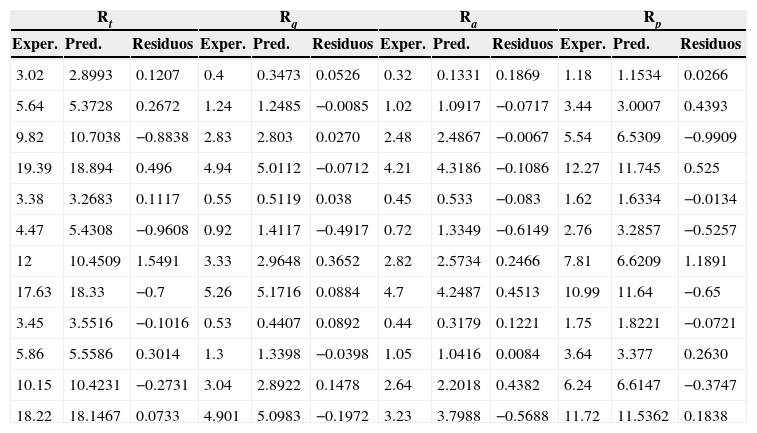
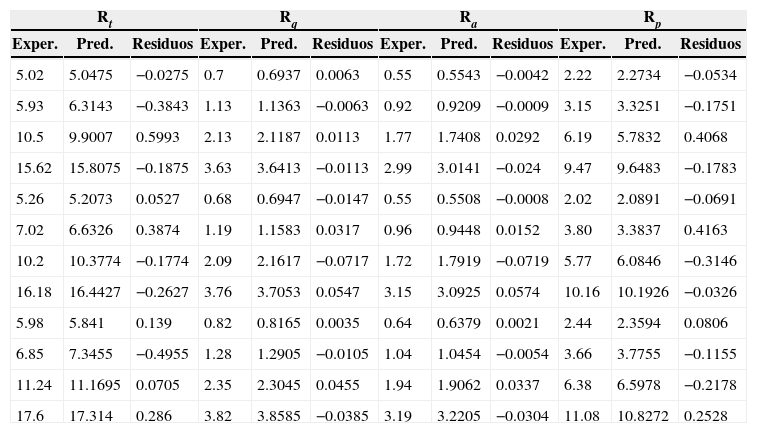
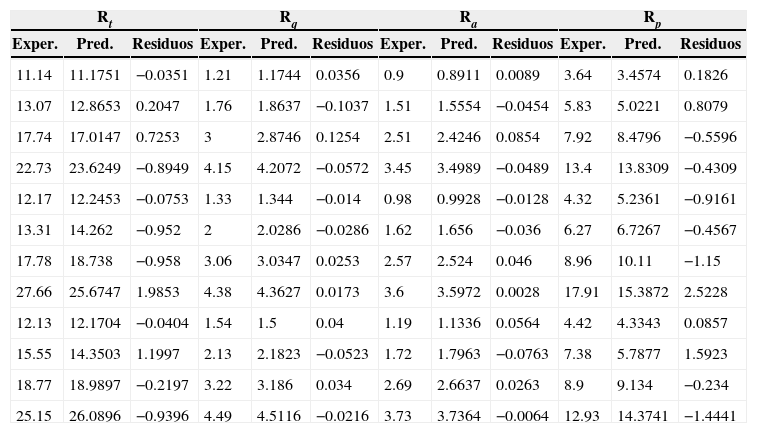
La comparación de las predicciones y los valores experimentales de R_t, R_q, R_a y R_p según el plan factorial completo para los materiales compuestos PEEK, PEEK CF30 y PEEK GF30 se muestra en las tablas 5, 6 y 7.

Tabla 5.

Comparación de las predicciones y los valores experimentales del material PEEK

Rt			Rq			Ra			Rp
Exper.	Pred.	Residuos	Exper.	Pred.	Residuos	Exper.	Pred.	Residuos	Exper.	Pred.	Residuos
3.02	2.8993	0.1207	0.4	0.3473	0.0526	0.32	0.1331	0.1869	1.18	1.1534	0.0266
5.64	5.3728	0.2672	1.24	1.2485	−0.0085	1.02	1.0917	−0.0717	3.44	3.0007	0.4393
9.82	10.7038	−0.8838	2.83	2.803	0.0270	2.48	2.4867	−0.0067	5.54	6.5309	−0.9909
19.39	18.894	0.496	4.94	5.0112	−0.0712	4.21	4.3186	−0.1086	12.27	11.745	0.525
3.38	3.2683	0.1117	0.55	0.5119	0.038	0.45	0.533	−0.083	1.62	1.6334	−0.0134
4.47	5.4308	−0.9608	0.92	1.4117	−0.4917	0.72	1.3349	−0.6149	2.76	3.2857	−0.5257
12	10.4509	1.5491	3.33	2.9648	0.3652	2.82	2.5734	0.2466	7.81	6.6209	1.1891
17.63	18.33	−0.7	5.26	5.1716	0.0884	4.7	4.2487	0.4513	10.99	11.64	−0.65
3.45	3.5516	−0.1016	0.53	0.4407	0.0892	0.44	0.3179	0.1221	1.75	1.8221	−0.0721
5.86	5.5586	0.3014	1.3	1.3398	−0.0398	1.05	1.0416	0.0084	3.64	3.377	0.2630
10.15	10.4231	−0.2731	3.04	2.8922	0.1478	2.64	2.2018	0.4382	6.24	6.6147	−0.3747
18.22	18.1467	0.0733	4.901	5.0983	−0.1972	3.23	3.7988	−0.5688	11.72	11.5362	0.1838

Tabla 6.

Comparación de las predicciones y los valores experimentales del material PEEK CF30

Rt			Rq			Ra			Rp
Exper.	Pred.	Residuos	Exper.	Pred.	Residuos	Exper.	Pred.	Residuos	Exper.	Pred.	Residuos
5.02	5.0475	−0.0275	0.7	0.6937	0.0063	0.55	0.5543	−0.0042	2.22	2.2734	−0.0534
5.93	6.3143	−0.3843	1.13	1.1363	−0.0063	0.92	0.9209	−0.0009	3.15	3.3251	−0.1751
10.5	9.9007	0.5993	2.13	2.1187	0.0113	1.77	1.7408	0.0292	6.19	5.7832	0.4068
15.62	15.8075	−0.1875	3.63	3.6413	−0.0113	2.99	3.0141	−0.024	9.47	9.6483	−0.1783
5.26	5.2073	0.0527	0.68	0.6947	−0.0147	0.55	0.5508	−0.0008	2.02	2.0891	−0.0691
7.02	6.6326	0.3874	1.19	1.1583	0.0317	0.96	0.9448	0.0152	3.80	3.3837	0.4163
10.2	10.3774	−0.1774	2.09	2.1617	−0.0717	1.72	1.7919	−0.0719	5.77	6.0846	−0.3146
16.18	16.4427	−0.2627	3.76	3.7053	0.0547	3.15	3.0925	0.0574	10.16	10.1926	−0.0326
5.98	5.841	0.139	0.82	0.8165	0.0035	0.64	0.6379	0.0021	2.44	2.3594	0.0806
6.85	7.3455	−0.4955	1.28	1.2905	−0.0105	1.04	1.0454	−0.0054	3.66	3.7755	−0.1155
11.24	11.1695	0.0705	2.35	2.3045	0.0455	1.94	1.9062	0.0337	6.38	6.5978	−0.2178
17.6	17.314	0.286	3.82	3.8585	−0.0385	3.19	3.2205	−0.0304	11.08	10.8272	0.2528

Tabla 7.

Comparación de las predicciones y los valores experimentales del material PEEK GF30

Rt			Rq			Ra			Rp
Exper.	Pred.	Residuos	Exper.	Pred.	Residuos	Exper.	Pred.	Residuos	Exper.	Pred.	Residuos
11.14	11.1751	−0.0351	1.21	1.1744	0.0356	0.9	0.8911	0.0089	3.64	3.4574	0.1826
13.07	12.8653	0.2047	1.76	1.8637	−0.1037	1.51	1.5554	−0.0454	5.83	5.0221	0.8079
17.74	17.0147	0.7253	3	2.8746	0.1254	2.51	2.4246	0.0854	7.92	8.4796	−0.5596
22.73	23.6249	−0.8949	4.15	4.2072	−0.0572	3.45	3.4989	−0.0489	13.4	13.8309	−0.4309
12.17	12.2453	−0.0753	1.33	1.344	−0.014	0.98	0.9928	−0.0128	4.32	5.2361	−0.9161
13.31	14.262	−0.952	2	2.0286	−0.0286	1.62	1.656	−0.036	6.27	6.7267	−0.4567
17.78	18.738	−0.958	3.06	3.0347	0.0253	2.57	2.524	0.046	8.96	10.11	−1.15
27.66	25.6747	1.9853	4.38	4.3627	0.0173	3.6	3.5972	0.0028	17.91	15.3872	2.5228
12.13	12.1704	−0.0404	1.54	1.5	0.04	1.19	1.1336	0.0564	4.42	4.3343	0.0857
15.55	14.3503	1.1997	2.13	2.1823	−0.0523	1.72	1.7963	−0.0763	7.38	5.7877	1.5923
18.77	18.9897	−0.2197	3.22	3.186	0.034	2.69	2.6637	0.0263	8.9	9.134	−0.234
25.15	26.0896	−0.9396	4.49	4.5116	−0.0216	3.73	3.7364	−0.0064	12.93	14.3741	−1.4441

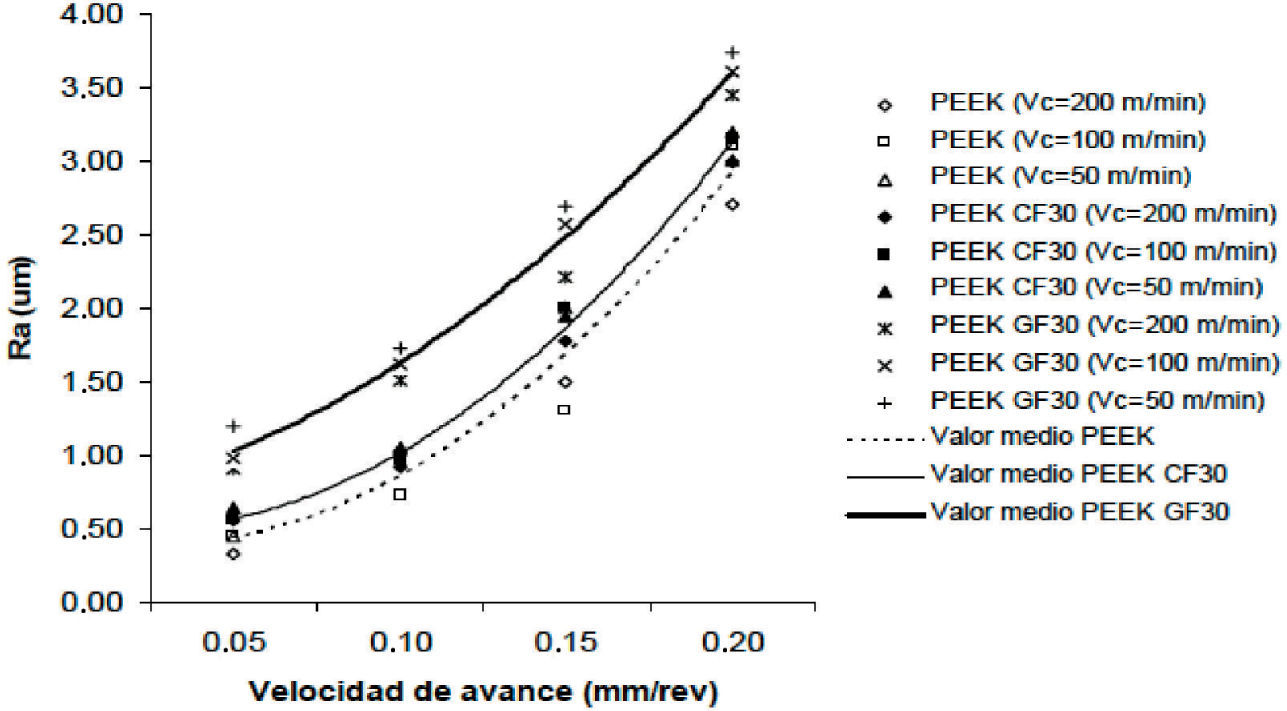
La figura 1 muestra la evolución de R_a en función de los parámetros de corte para los dos tipos de herramientas utilizados en los ensayos. Como se puede observar, es el PEEK GF30 reforzado con fibras de vidrio, el material con el que se obtiene un peor acabado superficial. El PEEK CF30 reforzado con fibras de carbono presenta valores ligeramente mayores en relación con el PEEK. La rugosidad aumenta significativamente al aumentar la velocidad de avance y disminuye ligeramente con la velocidad de corte.

Figura 1.

Evolución de R_a en función de las velocidades de corte y avance

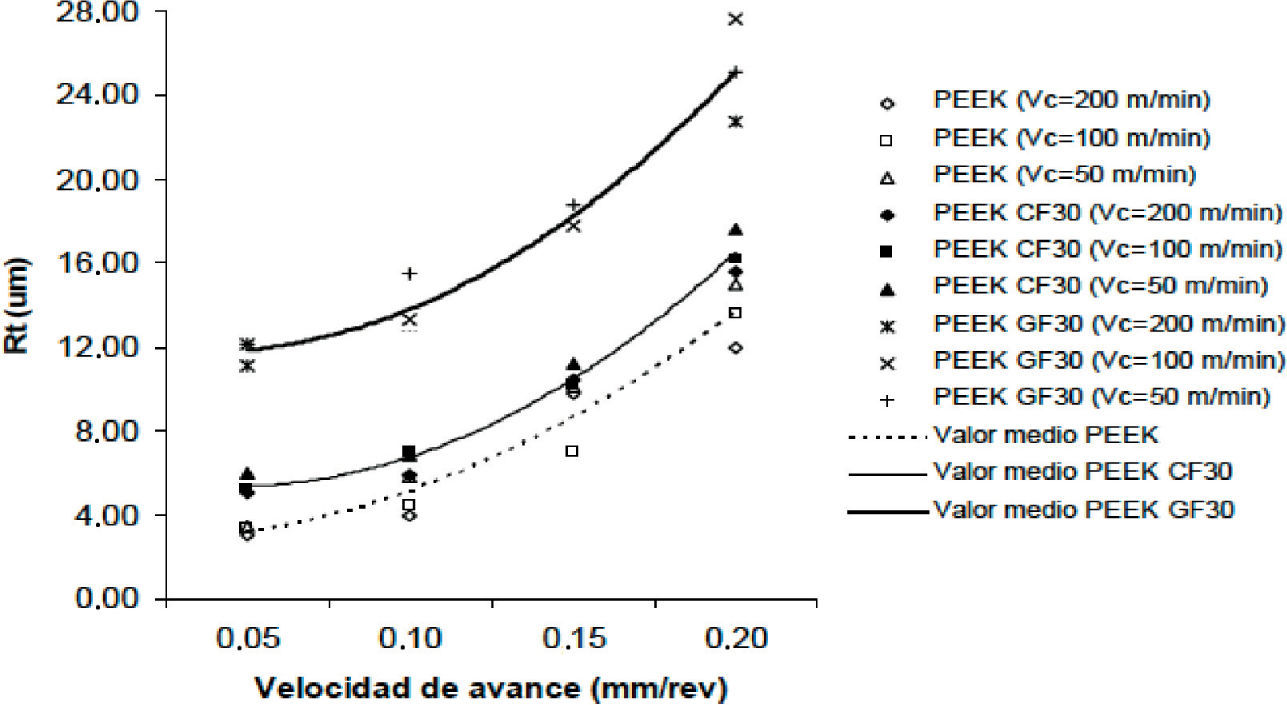
La figura 2 muestra la evolución de R_t en función de los parámetros de corte. Se pueden hacer comentarios similares a lo especificado para el caso de R_a, tanto en lo que respecta a la variación de R_t con los parámetros funcionales de corte e influencia de las fibras de refuerzo.

En las tablas 5, 6 y 7 se presentan los valores del resto de parámetros de rugosidad medidos (R_p, R_q) en función de las condiciones de corte para cada uno de los materiales ensayados. Como se puede verificar, la dependencia con la velocidad de avance y la velocidad de corte es similar a los casos estudiados (R_a y R_t). Se pueden efectuar también análogos comentarios sobre los materiales.

Se puede verificar, que es posible obtener valores mayores de la precisión dimensional IT (peor calidad) para el material reforzado con fibras de vidrio (PEEK GF30), en comparación con el PEEK no reforzado y con el PEEK CF30 reforzado con fibras de carbono. Con el PEEK CF30, a pesar de la presencia de las fibras de refuerzo, se pueden conseguir precisiones dimensionales comparables o ligeramente peores que con el PEEK.

Trabajando con velocidades de avance bajas en los dos materiales se pueden conseguir calidades utilizadas en la construcción mecánica cuidada (IT7 e IT8) e incluso en la construcción de gran precisión (IT5 e IT6), especialmente para V_a = 0.05 mm/rev en los tres materiales y también V_a = 0.10 mm/rev en el caso del material no reforzado. Para velocidades de avance más elevadas (V_a = 0.15 mm/rev y V_a = 0.20 mm/rev) se obtienen calidades aptas para construcción mecánica corriente (IT9 e IT10). En el caso del material no reforzado (PEEK) se obtienen casos de IT9 e IT10 sólo para V_a = 0.20 mm/rev. Por lo demás, el efecto de la velocidad de corte se puede considerar irrelevante.

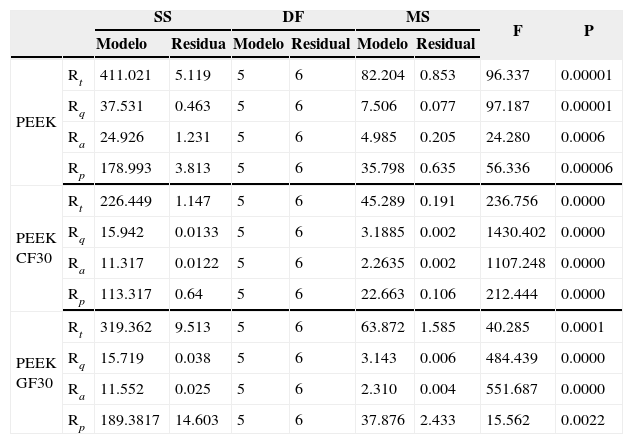
Verificación de los modelos matemáticos

El análisis de varianza (ANOVA), tal como se explica por Montgomery, se utilizó para comprobar la adecuación de los modelos desarrollados para un determinado intervalo de confianza (Montgomery, 2003) y (Myers y Montgomery, 1995). El cuadro consta de ANOVA, suma de los cuadrados y los grados de libertad.

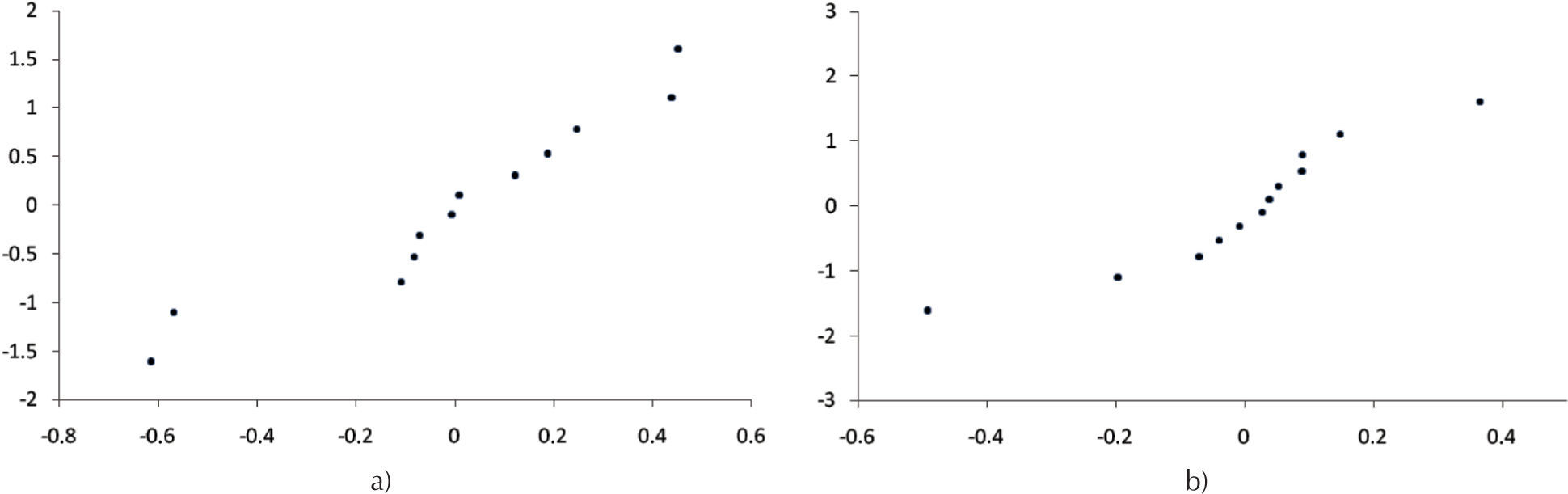
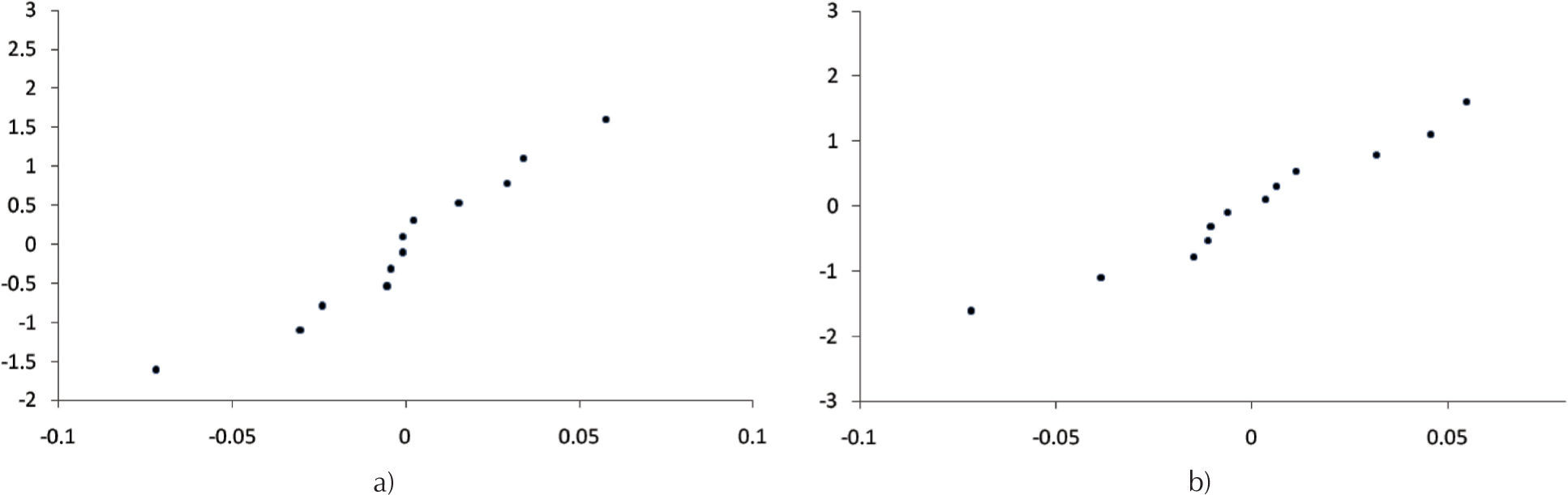
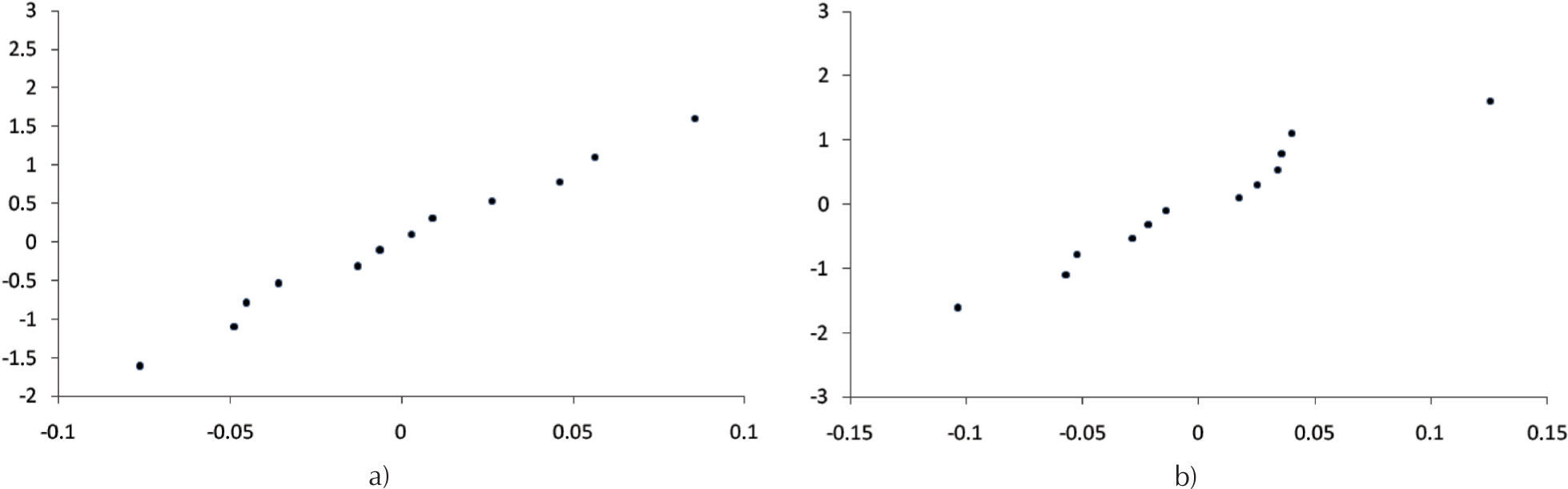
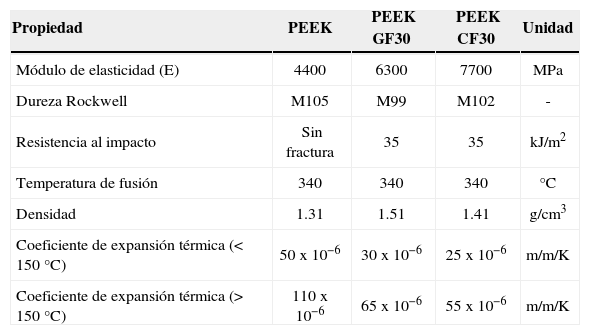
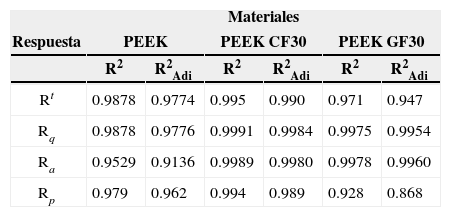
La adecuación de los modelos matemáticos desarrollados se presenta en el tabla 8. La calidad del ajuste de los modelos también fue probado por los coeficientes de determinación (R²) y (R²_Adj). Los valores de R² y R²_Adj de los modelos matemáticos no lineales (tabla 9) indican la correlación entre las variables independientes y las variables dependientes; además es necesario que los residuos deban ser distribuidos normalmente para que el análisis de regresión sea válido. Como ejemplo, las figuras 3, 4 y 5 presentan la probabilidad normal de R_a y R_q para los tres diferentes compuestos. Las figuras indican que los residuos siguen una línea recta, que denota una distribución normal. Resultados similares se obtienen para los casos de R_t y R_p.

Tabla 8.

Resultados de ANOVA de los modelos no lineales de los materiales compuestos

		SS		DF		MS		F	P
		Modelo	Residua	Modelo	Residual	Modelo	Residual
PEEK	Rt	411.021	5.119	5	6	82.204	0.853	96.337	0.00001
	Rq	37.531	0.463	5	6	7.506	0.077	97.187	0.00001
	Ra	24.926	1.231	5	6	4.985	0.205	24.280	0.0006
	Rp	178.993	3.813	5	6	35.798	0.635	56.336	0.00006
PEEK CF30	Rt	226.449	1.147	5	6	45.289	0.191	236.756	0.0000
	Rq	15.942	0.0133	5	6	3.1885	0.002	1430.402	0.0000
	Ra	11.317	0.0122	5	6	2.2635	0.002	1107.248	0.0000
	Rp	113.317	0.64	5	6	22.663	0.106	212.444	0.0000
PEEK GF30	Rt	319.362	9.513	5	6	63.872	1.585	40.285	0.0001
	Rq	15.719	0.038	5	6	3.143	0.006	484.439	0.0000
	Ra	11.552	0.025	5	6	2.310	0.004	551.687	0.0000
	Rp	189.3817	14.603	5	6	37.876	2.433	15.562	0.0022

Tabla 9.

Valores de R² y R² ajustada de los modelos no lineales de los materiales compuestos

	Materiales
Respuesta	PEEK		PEEK CF30		PEEK GF30
	R^2	R^2Adi	R^2	R^2Adi	R^2	R^2Adi
R^t	0.9878	0.9774	0.995	0.990	0.971	0.947
Rq	0.9878	0.9776	0.9991	0.9984	0.9975	0.9954
Ra	0.9529	0.9136	0.9989	0.9980	0.9978	0.9960
Rp	0.979	0.962	0.994	0.989	0.928	0.868

Figura 3.

Prueba de normalidad para los errores del modelo desarrollado por el PEEK: a) R_a; b) R_q

Figura 4.

Prueba de normalidad para los errores del modelo desarrollado por el PEEK CF30: a) R_a; b) R_q

Figura 5.

Prueba de normalidad para los errores del modelo desarrollado por el PEEK GF30: a) R_a; b) R_q

Conclusiones

Con el fin de analizar los efectos de los parámetros del proceso (velocidad de corte y velocidad de avance) en las respuestas (R_t, R_q, R_a, R_p), los experimentos se planificaron según el método de diseño factorial completo.

En lo que respecta a la influencia de las condiciones de corte (parámetros funcionales de corte), se ha demostrado que la variación de la velocidad de avance, dentro de los valores seleccionados, afecta más a los resultados (fuerzas de corte, acabado superficial) que la variación de la velocidad de corte. A medida que aumenta la velocidad de avance, aumentan las fuerzas de corte y la rugosidad de las superficies mecanizadas, obteniéndose, por tanto, resultados peores.

Se ha verificado el efecto de las fibras de refuerzo en los dos grupos de materiales. La presencia de las fibras se traduce en mayores valores de las fuerzas de corte (fuerza de mecanizado, potencia de corte y fuerza específica de corte) y de la rugosidad (R_a y R_t). Este hecho es particularmente importante, ya que el mecanizado resulta más difícil, requiere mayor consumo de energía y el acabado es generalmente peor. Por tanto, los materiales reforzados presentan una peor maquinabilidad en comparación con el termoplástico sin refuerzo. En este caso, el PEEK GF30 reforzado con fibras de vidrio, es el material que evidencia una peor maquinabilidad.

Se han desarrollado modelos matemáticos no lineales de segundo orden para R_t, R_q, R_a y R_p utilizando la metodología de superficie de respuesta. La calidad del ajuste de los modelos se ha probado por los coeficientes de determinación R² y R²_Adj, también se ha utilizado análisis de varianza para comprobar la suficiencia de los modelos. Los modelos de predicción han mostrado validez dentro del rango de parámetros de corte utilizados. Este trabajo de investigación propone el diseño y la implementación de modelos matemáticos tendientes a optimizar los procesos de mecanizado de elementos mecánicos. Las conclusiones a las que se llega tienen interés no sólo para futuras investigaciones que profundicen en ciertos aspectos o versen sobre cuestiones con otros enfoques complementarios, sino también para la industria, en la medida en que los resultados obtenidos plantean ciertas pautas a seguir desde el punto de vista práctico.

Nomenclatura

R_a

Rugosidad media (μm)

R_q

Media aritmética de las desviaciones del perfil (μm)

R_t

Distancia entre el punto más alto y el más bajo del registro (μm)

R_p

Distancia del punto más alto del perfil a la línea media (μm)

R²

Coeficiente de correlación

R²_adj

Coeficiente de correlación ajustado

SS

Suma de cuadrados

DF

Grados de libertad

MS

Varianza

F

Test de Fischer

P

Contribución