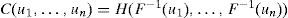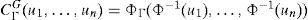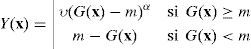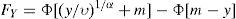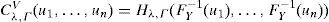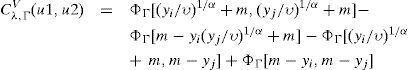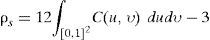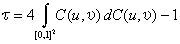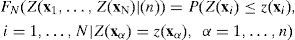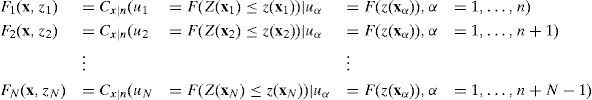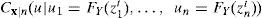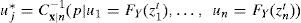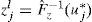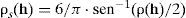Simulación de campos aleatorios con dependencia no multi-gaussiana empleando cópulas

Resumen

Los campos aleatorios se usan comúnmente en ingeniería civil para describir la variación espacial de las propiedades de los materiales. En este artículo se emplea un modelo de cópulas para simular campos aleatorios con dependencia no multi-Gaussiana. Se generan simulaciones de distintos campos aleatorios siguiendo la metodología propuesta y luego se examinan las correspondientes cópulas empíricas bivariadas. Se muestra que los resultados son satisfactorios en términos de la reproducción de las correspondientes cópulas teóricas. Con este simulador es posible incorporar un mayor grado de realismo en el modelo de variabilidad espacial, por ejemplo en problemas de flujo de agua en suelos donde la presencia de zonas continuas más permeables gobierna el comportamiento hidráulico de la masa de suelo, o bien, en problemas de estabilidad de taludes donde la extensión de la superficie de falla puede ser controlada por la presencia de zonas continuas más débiles, por mencionar solo algunos.

Abstract

Random fields are models commonly used in civil engineering to describe spatial variability of material properties. A copula model is used in this paper to simulate random fields with non multi-Gaussian dependence. Simulations of several random fields are conducted following the proposed methodology and bivariate empirical copulas are then examined. Satisfactory results are obtained in terms of the reproduction of the corresponding theoretical copulas. By means of such simulator, it is possible to incorporate a higher degree of realism in the spatial variability model, for example in seepage flow problems wherein the presence of higher permeable continuous zones control the hydraulic behavior of the soil mass or in slope stability problems where the extension of failure surfaces may be controlled by the presence of weaker continuous zones, to mention only a few.

Introduction

Un campo aleatorio es una colección de variables aleatorias indexadas espacialmente, es decir, a cada punto del campo se asocia una variable aleatoria simple. De hecho, un campo aleatorio es un modelo probabilista que se utiliza para representar fenómenos que varían espacialmente. Modelos de este tipo se emplean por ejemplo en geotecnia para representar las variaciones espaciales de las propiedades de los suelos (Griffiths y Fenton, 1993; 1997; Auvinet, 2002; López-Acosta y Auvinet, 2004). Con este enfoque, el valor observado en una ubicación particular se interpreta como una muestra de su distribución de probabilidad. Una configuración específica de los valores se conoce como realización del campo aleatorio. Un campo aleatorio puede considerarse entonces como un conjunto de realizaciones.

La simulación o generación de realizaciones del campo aleatorio se realiza comúnmente en una malla de puntos sobre el dominio de interés. El proceso se reduce por tanto a generar cierto número de variables aleatorias conjuntamente distribuidas. Cuando la densidad de probabilidad conjunta de estas variables es gaussiana se dice que el campo aleatorio es multi-gaussiano y la distribución espacial de los valores simulados adquiere características propias de esta ley de probabilidad. Entre ellas, destacan la simetría de la dependencia, la alta entropía de las realizaciones y en consecuencia la conectividad nula de los valores en las colas de la distribución. En muchas ocasiones, estas características no son representativas de la variabilidad espacial que presentan los geomateriales (Journel y Alabert, 1989; Auvinet, 2002; Sánchez-Vila et al., 2006).

En diversas aplicaciones en ingeniería, para mejorar la representatividad del modelo de variabilidad espacial es necesario recurrir a una hipótesis de dependencia no multi-gaussiana, como en los casos en que la continuidad de los valores extremos o la asimetría de la dependencia impongan un efecto determinante en la respuesta del modelo físico. Esta situación se presenta en problemas de flujo de agua en suelos donde la existencia de zonas continuas permeables y zonas continuas impermeables gobierna el comportamiento hidráulico de la masa de suelo, o bien, en problemas de estabilidad de taludes donde la extensión de la superficie de falla puede controlarse por la presencia de zonas continuas más débiles, por mencionar solo algunos casos de interés práctico.

Se han desarrollado diversas metodologías para simular campos aleatorios con dependencia no multi-gaussiana. Entre las más utilizadas se encuentran: el método de expansión en series (Ghanem y Spanos, 1991; Pineda-Contreras y Auvinet, 2013), el método de múltiples covarianzas indicadoras (Journel, 1983; Journel y Alabert, 1989) y el método de la representación isofactorial de la ley de probabilidad (Chilès y Delfiner, 1999; Emery, 2002). Una herramienta común en estas metodologías es el uso de ciertas variantes de una técnica de interpolación ampliamente utilizada en geoestadística conocida como Kriging (Matheron, 1965).

Se puede mostrar que ninguno de los formalismos utilizados en las metodologías anteriores logra una distribución de probabilidad multivariada tan flexible como la que se obtiene empleando algunos modelos de cópulas multivariadas. Además, las cópulas tienen propiedades deseables tanto para la interpolación geoestadística como para la simulación de campos aleatorios, que no tienen las técnicas de interpolación del tipo Kriging (Bárdossy, 2006; Bárdossy y Li, 2008).

En este artículo se emplea un modelo de cópulas para simular campos aleatorios con dependencia no multi-gaussiana. La discusión del tema se divide en cuatro secciones principales. La primera sección presenta la introducción formal del modelo de cópulas empleado. La siguiente presenta un algoritmo para la simulación no condicional de campos aleatorios mientras que la tercera sección describe el algoritmo para la simulación condicional de estos campos. Una serie de ejemplos se discuten en la última sección con el propósito de mostrar y validar la utilidad de la metodología propuesta.

Cópulas

En un contexto probabilista, una cópula C(·) se puede interpretar como una función de distribución de probabilidad (bivariada o multivariada) H(·), con distribuciones de probabilidad marginales uniformes que une (acopla) una función de distribución multivariada H(·) con sus funciones de distribución marginales F₁, … F_n. Su expresión matemática es (Sklar, 1959; Joe, 1997; Nelsen, 2006):

donde:

F⁻¹₁, …, F⁻¹_n son los inversos de las funciones de distribución marginales de H(·). Si F₁, …, F_n son todas continuas, entonces C(·) es única.

Las cópulas son de interés como funciones aleatorias en modelos de variabilidad espacial debido a que expresan la dependencia entre variables aleatorias sin la influencia del tipo de distribuciones marginales. Además, las cópulas son invariantes a transformaciones monótonas estrictamente crecientes. Por ejemplo, si Y(x) = ln(K_s(x)), entonces tanto K_s(x) como Y(x) comparten la misma cópula. Con esto, las medidas de correlación y asimetría expresadas únicamente en función de cópulas son invariantes.

Cópula gaussiana

La cópula gaussiana multivariada se puede formular fácilmente. Por ejemplo, si en la ecuación 1, H(·) = Φ _Γ (·), es la función de distribución multivariada Gaussiana con media cero, matriz de correlación Γ y con F₁ = … = F_n = Φ donde Φ es la función de distribución univariada gaussiana, entonces la cópula gaussiana C^G_Γ (·), se puede escribir como:

Cópula V-transformada

La cópula V-transformada multivariada se obtiene aplicando una transformación no lineal a un campo aleatorio gaussiano G(x) con media cero, varianza unitaria y matriz de correlación Γ, tal que (Bárdossy y Li, 2008; Li y Bárdossy, 2009):

donde ν es una constante positiva y m y α son reales. Cuando ν = 1 y α = 1, se obtiene la distribución χ² no centrada multivariada para Y(x). Además, el efecto no lineal de la transformación desaparece cuando m → ±∞ y la cópula resultante converge a la cópula gaussiana.

El efecto de la transformación en la ecuación 3 produce una función de distribución multivariada para el campo aleatorio Y(x) con funciones de distribución marginales idénticas dadas por:

La cópula V-transformada multivariada con parámetros λ = {v, m, α} se puede escribir entonces como:

donde H_λ,Γ (·), es la función de distribución multivariada de Y(x).

Para n = 2, la cópula V-transformada bivariada es:

donde Φ₂(·), es la función de distribución gaussiana bivariada con coeficiente de correlación ρ.

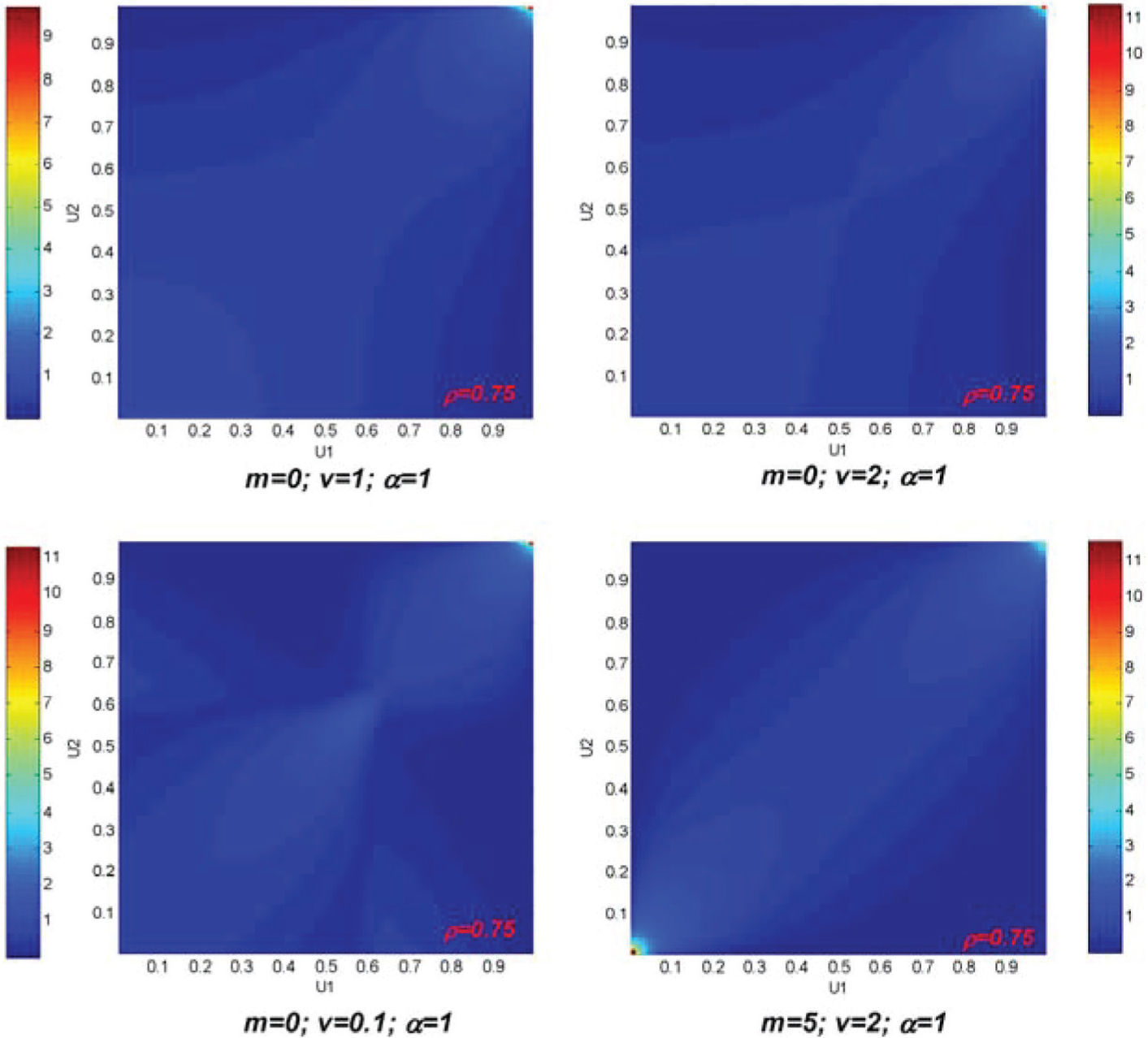
La cópula V-transformada bivariada se puede construir numéricamente transformando un número suficientemente grande de pares de valores de la distribución bivariada gaussiana para un coeficiente de correlación ρ y fijando los parámetros m, v y α. Para cada par se obtienen los valores correspondientes de la distribución acumulativa univariada de Y(x); es decir, u1_i, u2_j = F_Y(y1_i,y2_j), (u1_i para y1 and u2_j para y2), donde (u1_i,u2_j) son valores uniformemente distribuidos Є[0,1]. También se pueden obtener las densidades de probabilidad de la cópula (Bárdossy y Li, 2008). La figura 1, por ejemplo, muestra densidades de probabilidad de la cópula V-transformada teórica bivariada para diferentes valores de sus parámetros λ.

Figura 1.

Densidades de probabilidad de la cópula V-transformada para diferentes parámetros m, v con α = 1

De estas cópulas se pueden observar las características de la dependencia entre variables para cada percentil de sus funciones de distribución marginales. Por ejemplo, se puede observar que la densidad de probabilidad para valores en los percentiles superiores de la variable u2, dado un valor en los percentiles superiores de la variable u1 es muy grande y que este comportamiento no se repite para valores en los percentiles inferiores. Por lo tanto, la forma de la dependencia es asimétrica, excepto en el caso m = 5; v = 2; α = 1, el cual tiende a la cópula gaussiana.

Simulación no condicional

Las realizaciones no condicionales de un campo aleatorio se pueden generar aplicando la V-transformación a las realizaciones de un campo aleatorio gaussiano. Sin embargo, por el efecto de la transformación, la matriz de correlación de G(x) no se conserva en Y(x). Por lo tanto, se requiere encontrar una matriz de correlación para G(x) tal que provea la estructura de correlación prescrita para Y(x).

El conjunto de parámetros λ controlará la asimetría de la dependencia imponiendo correlación fuerte/débil en las colas de la distribución marginal. La asimetría resultante en la dependencia espacial se puede cuantificar empleando funciones de asimetría. El conjunto de valores Є[0,1], que se obtiene de la distribución marginal de Y(x) se puede utilizar para imponer una distribución marginal de cualquier tipo al campo aleatorio. La explicación detallada de estos temas se presenta en esta sección.

La función de correlación

Algunas medidas de dependencia adicionales al coeficiente de correlación de Pearson son el coeficiente de correlación ρ_S de Spearman (Hoeffding, 1940; Quesada-Molina, 1992):

y el coeficiente de correlación τ de Kendall (Hoeffding, 1948):

Ambos coeficientes tienen la ventaja de depender únicamente de la jerarquía o “ranks” (u,v) de las variables aleatorias de la cópula bivariada C(u,v) y además son invariantes a transformaciones monótonas tales como: Y(x) = ln(K_s(x)).

Entonces, tanto K_s(x) como Y(x) pueden compartir funciones de correlación idénticas.

Cada coeficiente ρ de la cópula bivariada C(u,v) se puede relacionar con una distancia en el correlograma de G(x). Entonces, obteniendo ρ_S para diferentes ρ, la curva ρ_S-ρ se puede utilizar para determinar una función de correlación prescrita para Y(x), a partir de un modelo de correlación apropiado para G(x). El procedimiento se puede resumir como sigue:

• 1)

  Ajustar una curva a la relación ρ_S-ρ.

• 2)

  Sustituir los valores ρ_S en la curva ajustada en el paso anterior para obtener los valores r del coeficiente de correlación de Pearson a las distancias en ρ_S. Esta es la curva r-h.

• 3)

  Ajustar una curva a la curva r-h usando una combinación lineal de funciones de correlación válidas.

Cabe mencionar que la función de correlación prescrita para Y(x) se logra como un promedio de un conjunto de realizaciones y que esta curva suele ser el mejor ajuste por mínimos cuadrados.

La asimetría de la dependencia

En un campo aleatorio no multi-gaussiano las dependencias de los valores mayores y menores de la mediana de la distribución marginal pueden ser diferentes. Esto representa la asimetría de la dependencia. Algunas medidas de asimetría se pueden encontrar en la literatura científica (Haslauer et al., 2008; Li y Bárdossy, 2009; Manner, 2010). Estas funciones permiten cuantificar la asimetría como una función de la distancia, de manera similar a las funciones de correlación, agrupando pares de valores (u,v) obtenidos de la función de distribución marginal separados a una misma distancia. Para observar las características de la asimetría se pueden utilizar las cópulas empíricas bivariadas (Nelsen, 2006; Bárdossy, 2006), como se muestra en los ejemplos ilustrativos.

La función de distribución marginal

Los valores del campo aleatorio Є[0,1] que se obtienen de la distribución marginal de Y(x) se pueden utilizar para cambiar a una distribución marginal de cualquier tipo. Por ejemplo, haciendo: Y(x) = Φ^–1(u = F_Y(y(x))) donde Φ(·) es la función de distribución gaussiana univariada. Por lo tanto, un campo aleatorio puede tener funciones de distribución marginales gaussianas, la función de correlación del campo observado y una dependencia no multi-gaussiana, la cual estará controlada por los parámetros λ en la V-transformación. Además, haciendo: Y′(x) = –Y(x) ambos campos aleatorios pueden compartir primeros y segundos momentos pero exhibir la asimetría opuesta, porque esta transformación es monótona.

Simulación condicional

En esta sección se presenta el algoritmo que permite simular campos aleatorios condicionales empleando cópulas. El algoritmo es general y permite incorporar cualquier modelo válido de cópulas para describir variabilidad espacial.

Planteamiento

Considérese el condicionamiento del campo aleatorio Z(x) en N localidades i dado un conjunto α con n observaciones. La función de distribución N-variada acumulativa condicional (CCDF) de Z(x) se puede escribir:

La ecuación 9 muestra que el valor simulado en la ubicación i donde i = 1,…,N se puede generar por muestreo a partir de la CCDF en etapas sucesivas que involucran una CCDF en cada ubicación i con un nivel de condicionamiento incremental (Devroye, 1986). En términos de cópulas, esta secuencia incremental se puede escribir:

donde F(·) es la función de distribución marginal y C_x|n(·) es la cópula condicional (Bárdossy y Li, 2008). El proceso de simulación se restringe a observaciones locales x_i, para i = 1,…, n cercanas al nodo por simular debido al efecto de pantalla (“screen”) o de sombra. Los valores u_α incluyen tanto observaciones como valores simulados en etapas anteriores. El proceso de simulación se realiza visitando las localidades no observadas de la malla siguiendo una trayectoria aleatoria. El proceso de simulación se completa después de visitar todos los nodos de la malla.

Algoritmo

La simulación condicional de campos aleatorios empleando cópulas se puede efectuar implementando el siguiente algoritmo. Por razones ilustrativas se considera el modelo de cópula V-transformada multivariada.

• 1)

  Obtener los valores de la función de distribución acumulativa (CDF) u_i∈[0,1], con i = 1,…, n empleando la función de distribución acumulativa marginal empírica, del campo aleatorio Z(x), tales que ui=Fˆ(zi).

• 2)

  Obtener los valores teóricos z^t_i, utilizando los valores u_i de la etapa anterior y la función de distribución univariada del modelo de cópula, por ejemplo el de la cópula V-transformada z^t_i = F^–1_Y (u_i) con i = 1,…, n.

• 3)

  Preparar cada nodo por similar j para j = 1,…, N sobre una trayectoria aleatoria l.

• 4)

  Hacer j = 1.

• 5)

  Elegir n observaciones cercanas al nodo por similar j y obtener la cópula condicional para un intervalo de valores de u_i∈[0,1] utilizando:

  

• 6)

  Muestrear con el método de Monte Carlo el valor u^*_j utilizando la cópula condicional:

  

  donde p es una variable aleatoria uniforme p u^*_j [0,1].

• 7)

  Asignar el valor muestreado u^*_j al nodo j correspondiente. Ahora, este puede ser considerado en la vecindad de los nodos subsecuentes por similar.

• 8)

  Hacer j = j + 1.

• 9)

  Si j ≤ N, obtener z^t_j = F^–1_Y(u^*_j) y seguir los pasos 5 a 7. De lo contrario ir al paso 10.

• 10)

  Obtener el valor simulado z^l_j para cada ubicación j de la realización l empleando la función de distribución marginal empírica:

  

Se obtienen múltiples realizaciones independientes visitando los nodos con distintas trayectorias aleatorias l. Observe que el primer nodo por simular en cada realización se condiciona a n observaciones cercanas. Además, se puede ver en el paso 6 que el valor simulado u^*_j ∈ [0,1]. Por lo tanto, la distribución marginal del campo aleatorio simulado es la distribución uniforme. Luego, utilizando la función de distribución empírica del paso 10 se obtiene la distribución marginal original del campo observado.

Implementación

Las estrategias de búsqueda para seleccionar los valores cercanos en la vecindad del nodo por simular son idénticas a las que utiliza el programa SGSIM de la librería GSLIB (Deutsch y Journel, 1992). La implementación del algoritmo para la simulación de campos aleatorios empleando cópulas se ha codificado en FORTRAN para LINUX y se ejecuta en el cluster “Tonatiuh” del Instituto de Ingeniería de la UNAM.

Ejemplos ilustrativos y discusión

Esta sección presenta ejemplos de aplicación que muestran y validan la utilidad de la metodología propuesta. En los ejemplos se simulan campos aleatorios condicionales con funciones de distribución Gaussianas, pero con diferentes asimetrías. También se verifican las cópulas empíricas con el objetivo de mostrar características de dependencia no multi-gaussiana en las realizaciones generadas.

Parámetros descriptivos

Considérese un campo aleatorio condicional Z(x) con funciones de distribución marginales gaussianas y estructura de correlación descrita por un coeficiente de correlación de Spearman dado por:

donde ρ(h) es un correlograma exponencial con distancia de correlación isotrópica a = 10 m y h es un vector. La ecuación 14 simplemente expresa el coeficiente de correlación ρ_s(·) de Spearman en función del coeficiente de correlación ρ(·) de Pearson (Krusal, 1954), debido a que las funciones de correlación válidas encontradas en la literatura científica se expresan en términos del coeficiente de correlación ρ(·) de Pearson.

Se considera además que la asimetría del campo se puede describir con la cópula V-transformada. Los distintos casos de asimetría considerados en los ejemplos se muestran en la tabla 1. Note que en ausencia de observaciones directas el primer valor simulado en la trayectoria aleatoria (paso 6) se puede generar por muestreo de la distribución uniforme. Después, el proceso de simulación continúa como se ha expuesto.

Tabla 1.

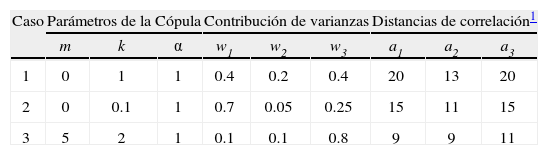
Modelo de correlación anidado para cada uno de los casos analizados. Las contribuciones de las varianzas y las distancias de correlación corresponden a las covarianzas Gaussiana, esférica (Deutsch y Journel, 1992) y exponencial, respectivamente

Caso	Parámetros de la Cópula			Contribución de varianzas			Distancias de correlación^1
	m	k	α	w1	w2	w3	a1	a2	a3
1	0	1	1	0.4	0.2	0.4	20	13	20
2	0	0.1	1	0.7	0.05	0.25	15	11	15
3	5	2	1	0.1	0.1	0.8	9	9	11

1

Las distancias de correlación son isotrópicas y están dadas en metros

Realizaciones generadas y validación

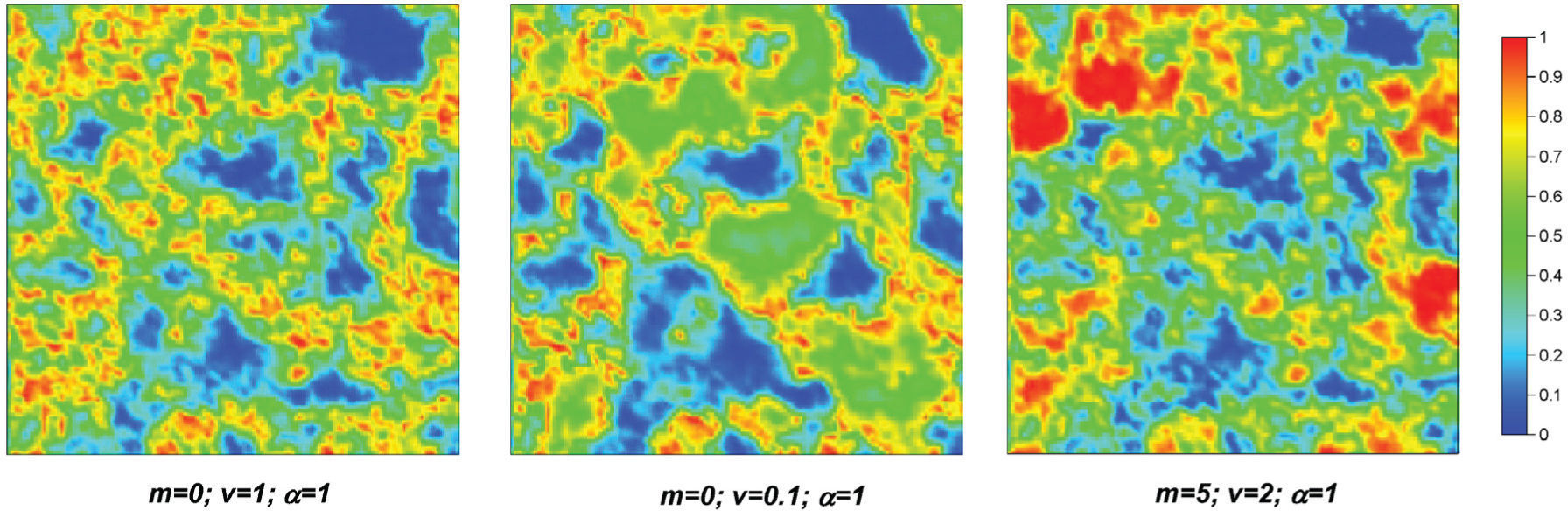
La estructura de correlación prescrita para el campo aleatorio en los diferentes casos de asimetría se obtiene siguiendo el procedimiento descrito anteriormente. La contribución de varianzas y las distancias de correlación de los diferentes modelos de correlación anidados se muestran en la tabla 1. Con estos modelos de correlación, los parámetros de la cópula V-transformada indicados en la misma tabla y siguiendo el algoritmo propuesto se generaron 15 realizaciones de cada campo aleatorio sobre una malla cuadrada de 75 m por lado espaciada regularmente cada 1 m. La segunda realización de cada conjunto se muestra en la figura 2 y sus descriptores estadísticos en la figura 3.

Figura 2.

Realizaciones representativas de distintos campos aleatorios empleando la cópula V-transformada

Figura 3.

Histogramas y funciones de correlación empíricas en la dirección horizontal

La inspección visual de las realizaciones en la figura 2 muestra que la continuidad en los percentiles superiores es mayor que para los percentiles inferiores, excepto en el caso 3 en donde los valores para ambos percentiles aparecen como cúmulos aislados. Esta condición corresponde aproximadamente al caso gaussiano.

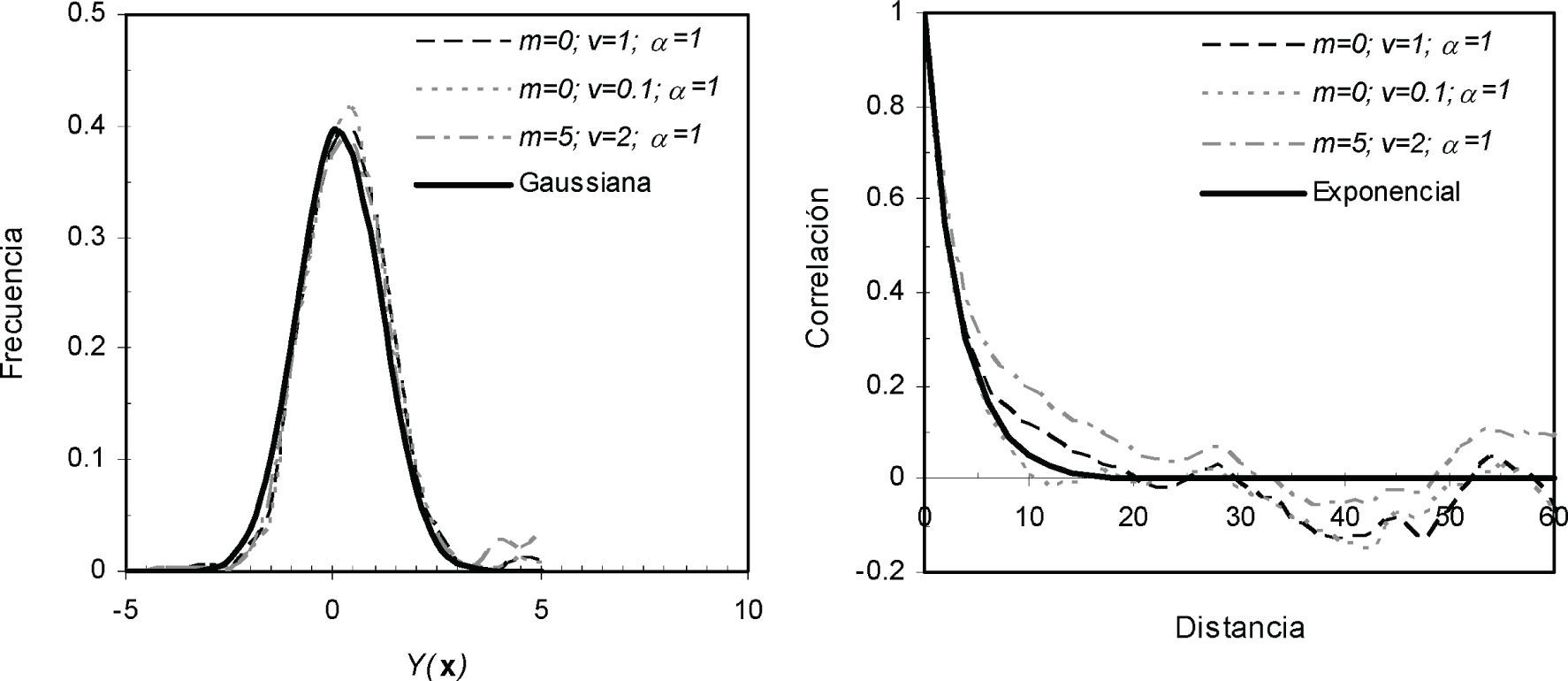
En la figura 3 se observa que el histograma de cada realización es muy cercano a la densidad gaussiana. Esto indica que la distribución de los valores en la simulación condicional es muy cercana a la distribución uniforme, como se esperaba. Por otra parte, las funciones de correlación experimentales de las realizaciones siguen aproximadamente la función de correlación teórica prescrita.

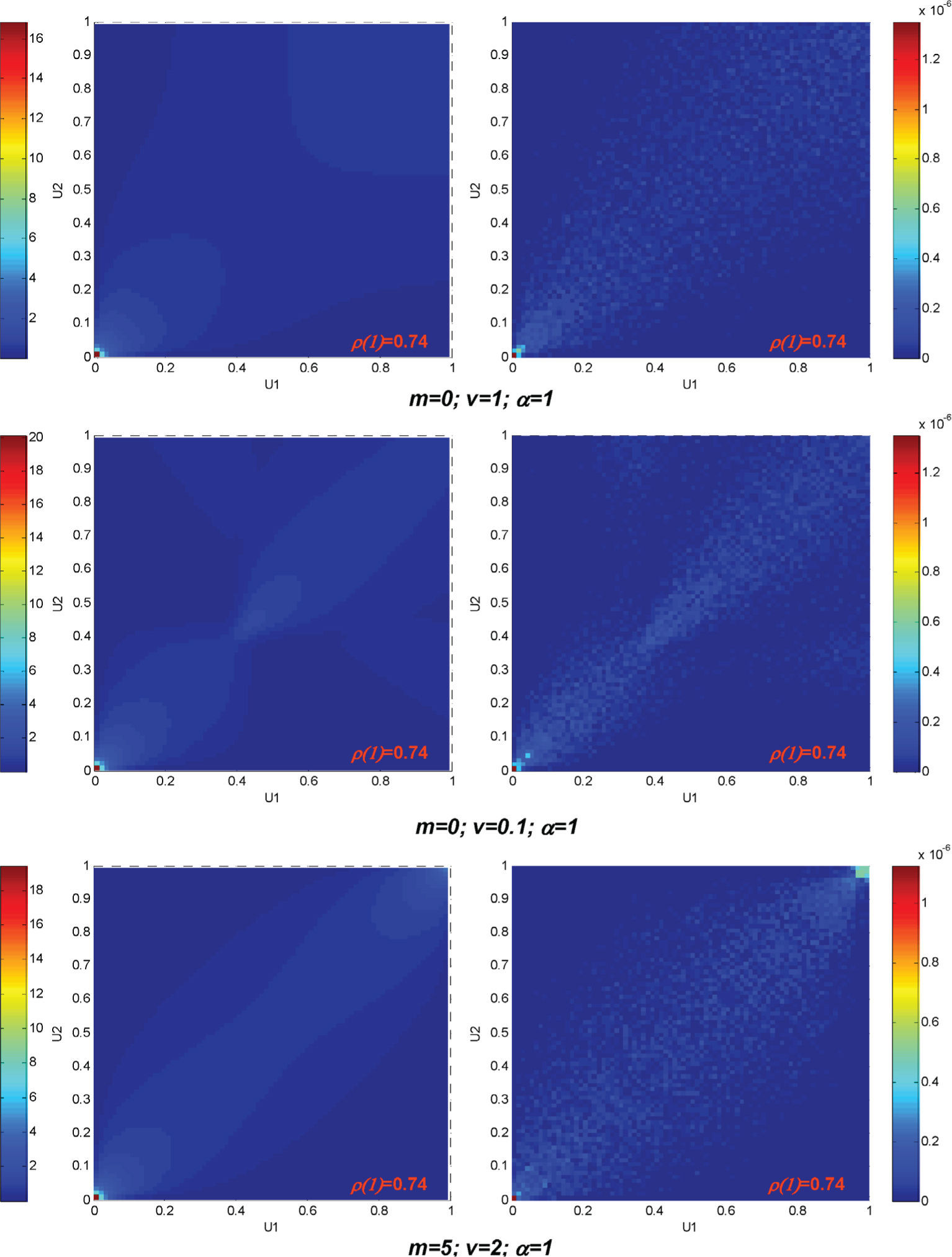
Se obtuvieron además las densidades de las cópulas bivariadas empíricas de estas realizaciones (Nelsen, 2006; Bárdossy, 2006), para la dirección horizontal y magnitud entre pares de valores igual a 1m, es decir, cuando ρ(h) ≈ 0.74. En las cópulas empíricas mostradas en la figura 4 se puede destacar claramente la condición de asimetría con respecto a la diagonal con pendiente de − 45° en los casos 1 y 2. En todos los casos las cópulas empíricas se asemejan a sus correspondientes cópulas teóricas. La asimetría que se observa en las cópulas empíricas confirma lo que la inspección visual de las realizaciones inicialmente sugería, es decir, una mayor continuidad en los percentiles superiores que en los inferiores.

Figura 4.

Densidades de probabilidad de las cópulas empíricas bivariadas (derecha) y las correspondientes versiones teóricas (izquierda) de las realizaciones mostradas en la figura 3

De esta manera se verifica que el simulador de campos aleatorios empleando cópulas produce resultados satisfactorios debido a que las cópulas bivariadas están bastante bien aproximadas.

Conclusiones

En este trabajo se describió una metodología que permite la simulación de campos aleatorios empleando cópulas. Con este simulador es posible incorporar un mayor grado de realismo en los modelos de variabilidad espacial, por ejemplo, en problemas de flujo de agua en suelos donde la presencia de zonas continuas más permeables gobierna el comportamiento hidráulico de la masa de suelo, o bien, en problemas de estabilidad de taludes donde la extensión de la superficie de falla puede ser controlada por la presencia de zonas continuas más débiles, por mencionar solo algunos casos.

Se generaron simulaciones de distintos campos aleatorios siguiendo la metodología propuesta y luego se examinaron las correspondientes cópulas empíricas bivariadas. Se encontraron resultados satisfactorios en términos de la reproducción de las cópulas teóricas correspondientes. Los resultados sugieren que la metodología propuesta es una interesante alternativa para modelar la variabilidad espacial con campos aleatorios empleando cópulas.

Debe reconocerse que la simulación de campos aleatorios empleando cópulas puede resultar muy demandante computacionalmente en mallas con un gran número de nodos. En general, el tiempo de cálculo necesario para simular un campo aleatorio no multi-gaussiano es considerablemente mayor al que se necesita para simular uno multi-gaussiano. El algoritmo aquí presentado se podría optimizar para reducir el tiempo de cálculo.

Otra herramienta de gran interés práctico en ingeniería es la simulación de campos aleatorios condicionados a variables con distinto origen (variables secundarias) y, más aún, cuando estas variables son dinámicas. Un simulador de campos aleatorios de este tipo se presentará en publicaciones subsecuentes.

Agradecimiento

Este trabajo fue financiado parcialmente con la beca CEP-UNAM otorgada al primer autor, lo cual se agradece profundamente.