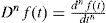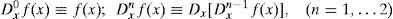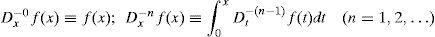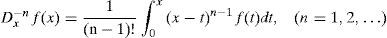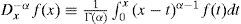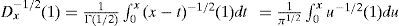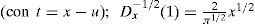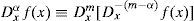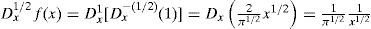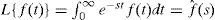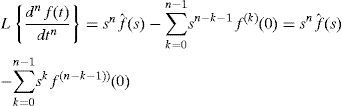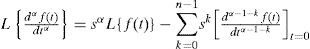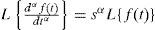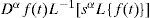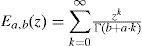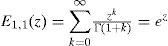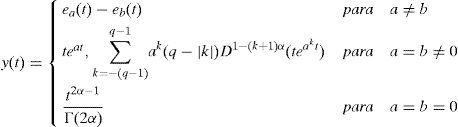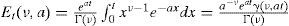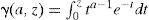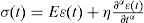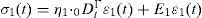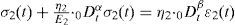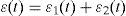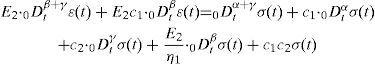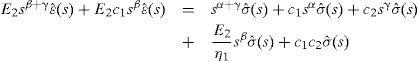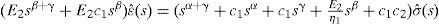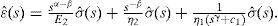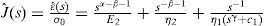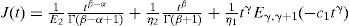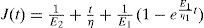Simulación del fenómeno de creep en suelos arcillosos mediante reología y ecuaciones diferenciales fraccionarias

Resumen

En este trabajo se presentan conceptos básicos acerca del cálculo fraccional y la reología fraccionaria utilizados en el estudio del comportamiento viscoelástico de materiales y la aplicación de dicha metodología en el modelado del fenómeno de creep. También se presenta la solución de una ecuación diferencial fraccionaria que modela dicho fenómeno. Las curvas que se obtuvieron experimentalmente se reproducen adecuadamente utilizando la solución de la ecuación diferencial fraccionaria que modela el fenómeno de creep. Por último, se presentan comentarios y conclusiones acerca del beneficio de emplear ecuaciones diferenciales fraccionarias en la simulación de fenómenos y problemas que se presentan en ingeniería.

Abstract

In this paper, basic concepts about fractional calculus and fractional rheology used in the study of viscoelastic behavior of materials and the application of this methodology in modeling the creep phenomenon are presented; also the solution of a differential equation fractional modeling this phenomenon is commented. The curves obtained experimentally were adequately reproduced using the solution of fractional differential equation that models the phenomenon of creep. Finally, conclusions and comments about the benefit to use fractional differential equations in the simulation of phenomena and problems that arise in engineering are presented. Keywords: fractional calculus, fractional derivative, fractional rheology, creep, viscoelasticity, clayey soils.

Introducción

En las últimas décadas, las ecuaciones constitutivas para materiales viscoelásticos que involucran derivadas fraccionarias han cobrado un creciente interés. La motivación para el uso de arreglos constitutivos fraccionarios es en gran parte el hecho de que se requieren menos parámetros para representar el comportamiento viscoelástico de materiales que los requeridos, cuando se usan los arreglos tradicionales de orden entero. Los arreglos fraccionarios permiten variar de una manera más amplia los parámetros reológicos y manipularlos usando las transformadas de Fourier y Laplace.

Hasta el momento, la actividad experimental (a nivel internacional) para determinar el comportamiento reológico clásico de los suelos es amplia. También se está trabajando en la determinación experimental de propiedades reológicas fraccionarias en materiales vinculados con la industria del alimento, agricultura (Neaman y Singer, 2004), textiles, e incluso en propiedades de tejidos biológicos (Jäger y Lackner, 2008) que se emplean en bioingeniería, por ejemplo de arterias y huesos humanos (Robert et al., 2006).

A continuación se hace una breve introducción al concepto de reología fraccionaria y se presentan los conceptos básicos de cálculo fraccionario.

Reología clásica

En el área de interés se han llevado a cabo estudios de características de resistencia de mezclas de suelos y asfaltos, bajo ciertas condiciones de esfuerzos (Abdel-hady y Herrin, 1965). Aplicando esfuerzos constantes se observa la evolución de las deformaciones en el tiempo, por ejemplo pruebas de creep. En Sheldon (2008) se presentan estudios de materiales viscoelásticos que poseen mezclas de propiedades viscosas y elásticas. Como es usual, esto se caracteriza mediante conjuntos de resortes y amortiguadores.

En lo referente a actividades experimentales, se tiene una amplia gama de investigaciones, como el estudio de propiedades reológicas de suelos húmedos bajo esfuerzos constantes y oscilatorios (Teamrat y Dani, 2001). Se ha estudiado el efecto de cambios en la estructura del suelo por la actividad y procesos agrícolas. También se han investigado las propiedades reológicas de suelos, al ensayar especímenes en pruebas de torsión con régimen cinemático, (Meschyan y Taslagyan, 2005). Aigner et al. (2009) realizaron estudios multi-escala para predicción del comportamiento de mezclas de concreto y asfalto. Se incluyen estudios del efecto de temperatura en las propiedades viscoelásticas. En Ariaratnam et al. (2003) se presenta una evaluación de propiedades reológicas de flujos de retorno en perforaciones horizontales direccionales, muy útil en fracturamiento hidráulico.

Reología fraccionaria

En este tema se tienen trabajos sobre visco-elasticidad en arterias mediante experimentos de relajación (Craiem y Armentano, 2007). Para el ajuste de las curvas experimentales se emplean pruebas uniaxiales y modelos de ecuaciones diferenciales fraccionarias. También se han realizado estudios de visco-elasticidad en huesos, utilizando modelos reológicos fraccionarios (Liu y Xu, 2008). Asimismo, se tienen estudios con cálculo fraccionario donde se modelan ecuaciones constitutivas ligadas a teorías moleculares para describir el comportamiento macroscópico de medios visco-elásticos (Bagley, 1986).

En Schmidt y Gaul (2001) se presenta una implementación para análisis, utilizando el método del elemento finito de relaciones constitutivas que involucran ecuaciones diferenciales fraccionarias. Con este tipo de ecuaciones, el número de parámetros necesarios para ajustar curvas experimentales es menor que con ecuaciones diferenciales con derivadas de orden entero. También, se han hecho estudios de materiales con microestructura desordenada basados en geometría fractal y cálculo fraccionario (Carpinteri et al., 2004). Se analiza también el efecto del tamaño de partículas en el comportamiento estructural de muestras de materiales heterogéneos y su relación con el número de parámetros necesarios para el ajuste a curvas experimentales; todo esto es muy útil en estudios de fracturamiento. En Koh y Kelly (1990) se presenta una aplicación de derivadas fraccionarias para análisis de modelos con aislamiento de base para analizar problemas de aislamiento de vibraciones.

Antecedentes de cálculo fraccionario y ecuaciones diferenciales fraccionarias

El concepto de cálculo fraccionario no es nuevo existe hace más de tres siglos. Es una generalización de la diferenciación y la integración ordinarias (enteras) a órdenes no-entero (reales e incluso, complejos). El nacimiento del cálculo fraccionario se data en 1695. En ese año, L’Hôpital planteó en una carta a Leibniz (Arafet et al., 2008) la cuestión de cómo debería entenderse la expresión, introducida por el propio Leibniz:

Leibniz trabajó en el tema y consideró “derivadas de orden general”, además de introducir la notación D^1/2f (x) para denotar la derivada de orden 1/2. Desde entonces destacados matemáticos, como Euler, Laplace, Fourier, Abel, Liouville, Riemann, Laurent y Weyl, han contribuido al desarrollo del cálculo fraccionario. Muchos encontraron, utilizando su propia notación metodológica, las definiciones que se ajustan al concepto de integral o derivada de orden no entero. Las definiciones más conocidas en el mundo del cálculo fraccionario son las de Riemann-Liouville and Grunwald-Letnikov (Arafet et al., 2008).

Hoy en día existe una vasta literatura sobre el tema llamado cálculo fraccionario (CF), cálculo fraccional o cálculo generalizado (Fractional Calculus, Differintegral Calculus). En distintas áreas de la ciencia se han escrito diversos artículos mostrando las más variadas aplicaciones (Denath, 2003). Entre las aplicaciones más comunes del CF se encuentran: la reología, biología cuántica, electroquímica, teoría de la dispersión, difusión, teoría del transporte, probabilidad y estadística, teoría del potencial, elasticidad, viscosidad y teoría de control automático; dos aplicaciones recientes son: en matemáticas financieras y en la teoría de fractales. Por ejemplo, se ha demostrado que los arreglos de orden fraccionario son más apropiados que los de orden entero para describir las propiedades de algunos materiales como los polímeros.

Actualmente existen paquetes desarrollados para el cálculo fraccionario y para el control automático fraccionario (por ejemplo la aplicación gratuita Ninteger para Matlab, disponible en internet). A continuación se presenta la definición formal de derivada fraccionaria, comenzando por mostrar algunos casos simples que ayudan a comprender lo que es una derivada fraccionaria.

Presentación de conceptos elementales de derivada fraccionaria basados en la integral de Riemann-Liouville

Integral de Riemann-Liouville

Recordando algunas notaciones de cálculo elemental, la n-ésima derivada de una función f está definida recursivamente por:

Análogamente, la n-ésima integral de f está definida por

Puede probarse que la segunda integral en (2) se puede reducir a una integral sencilla y está dada por:

donde (n − 1)! ≡ (n − 1) · (n − 2) ··· 2 · 1

El propósito es generalizar (2) y (3) sustituyendo n por un número real positivo α. Para ello se hace uso de la ya conocida función gamma de Euler. Para cualquier α > 0, se define la integral fraccionaria de orden α de una función f (continua) como:

La ecuación (4) se llama integral fraccionaria de Riemann-Liouville (Rocha, 2003). Note que cuando α=n, la definición anterior se reduce a la fórmula usual dada en (3). Por ejemplo, sea f(x) = 1 y α = 1/2. Entonces:

Para comparar, se remarca que Dx-0(1)=1 (lo que significa que no se está transformando la función) mientras que Dx-1(1)=x (lo cual es solo una antiderivada de 1).

La derivada fraccionaria puede definirse en términos de la integral fraccionaria (Rocha, 2003). Sea m el menor entero positivo mayor o igual que un número positivo α (por ejemplo, m = 1 cuando α = 1/2). Entonces Dxm es solo la m-ésima derivada usual y m − α ≥ 0. Para cualquier α > 0, la derivada fraccionaria de orden α de una función f (continua) se define como:

Observe que Dx-(m-α) es la integral fraccionaria de orden m − α.

Continuando con el ejemplo anterior, donde f(x) = 1, la derivada fraccionaria de orden 1/2 de f es:

Este resultado es absolutamente inesperado, ya que la derivada usual de una constante es 0, lo cual ilustra una de las muchas diferencias entre los operadores de derivación clásicos y fraccionarios.

La transformada de Laplace

La transformada de Laplace es una función de transformación que comúnmente se utiliza en la solución de ecuaciones diferenciales lineales. Con ella, es posible en muchos casos, evitar trabajar directamente con ecuaciones de orden diferencial trasladando el problema a un dominio en donde la solución se presenta algebraicamente. La definición formal de la transformada de Laplace está dada por:

donde [0 < t < ∞) y fˆ(s) es una función en la variable s cuyo dominio consta de todos los valores de s para los cuales la integral (5) existe, es decir, la transformada de Laplace de una función f(t) existe si (5) es una integral convergente. El requerimiento para que suceda esto es que f(t) no crezca a una velocidad mayor que la velocidad a la cual decrece el término exponencial e^–st.

Otra propiedad muy importante de la transformada de Laplace es su aplicación a la derivada de orden entero n de una función f(t), la cual está dada por:

De forma análoga, la transformada de Laplace aplicada a derivadas fraccionarias está dada por:

para todo α (exponente fraccionario de la diferencial), donde n es un entero tal que (n − 1) < α < n. Si se consideran las condiciones iniciales igualadas a cero (Hartley et al., 1995), la fórmula anterior se reduce a la expresión:

De manera que la derivada generalizada puede ahora expresarse como:

la cual resulta de mucho interés, pues es otra forma de expresar la derivada fraccionaria de una función f(t).

Función Mittag–Leffler

La solución de ecuaciones diferenciales fraccionarias comúnmente se expresan en términos de la función Mittag-Leffler (MLF) o sus derivadas (Diethelm et al., 2004), que es una generalización de la función exponencial e^z. La función MLF está definida por la serie de potencias:

donde a, b ∈ ℜ y z ∈ ⊄

La función MLF juega el mismo papel en las ecuaciones diferenciales fraccionarias al papel que juega la función exponencial en las ecuaciones diferenciales ordinarias. Para el caso particular, cuando los parámetros a y b son iguales a 1.0, la función MLF se reduce a la definición de la función exponencial:

Ecuaciones diferenciales fraccionarias

En estas ecuaciones, como su nombre lo indica, el orden de las derivadas es fraccionario y, por tanto, aparecen en ella términos con derivadas fraccionarias. A manera de ejemplo se presenta una ecuación de este tipo y sus soluciones para diferentes casos:

[D2α+aDα+bD0]+y(t)=0

donde α es el orden de la derivada (D) fraccionaria, y sus soluciones son:

donde:

q	1/α,eb(t)=∑k=0q-1bq-k-1Et(-kα,bq)
e^at	es la función exponencial
Et(v, a)	es la función Et y Γ(z) son la función gama.

La función E_t surge de la integral de e^at y se define como:

en donde γ(a, z) es la función gama incompleta definida por:

Las funciones especiales, como Γ(z), γ(a, z), E_α,β (z) y E_t resultan muy útiles en la solución de ecuaciones diferenciales fraccionarias, usando la transformada de Laplace. Puede consultarse la referencia de Podlubny (1994), en donde se trata detalladamente la aplicación de la transformada de Laplace en la solución de ecuaciones diferenciales fraccionarias.

Reología clásica y fraccionaria

La reología es una parte de la mecánica del medio continuo que estudia la relación entre el esfuerzo y la deformación en los materiales que son capaces de fluir. Una de las tareas más importantes en reología es encontrar ecuaciones constitutivas para modelar el comportamiento de los materiales. Por ejemplo, Terzaghi explicó mediante un arreglo reológico el estado de esfuerzos para cualquier tiempo t en suelos saturados de agua, bajo la premisa de que en un suelo cien por ciento saturado y sin drenaje, el esfuerzo octahédrico generado se toma totalmente en el agua; una vez permitido el drenaje, el agua deja de tomar dicho esfuerzo y este se toma conforme pasa el tiempo en el esqueleto sólido (proceso de consolidación) (Terzaghi, 1943).

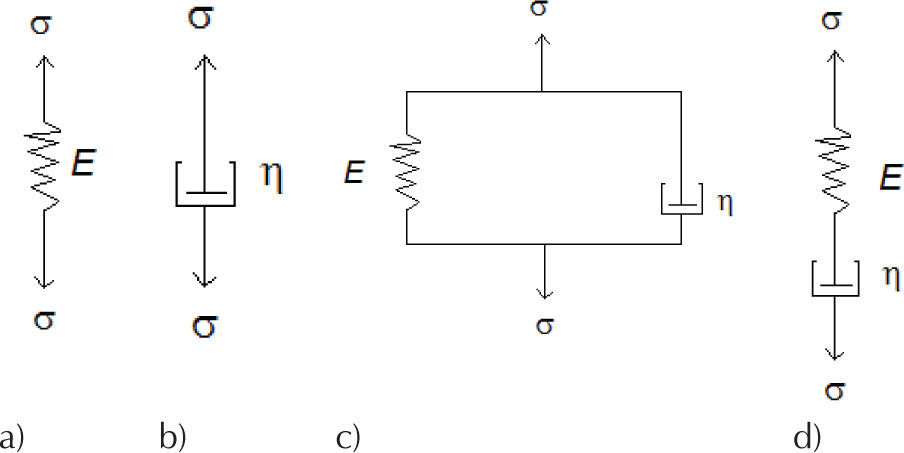
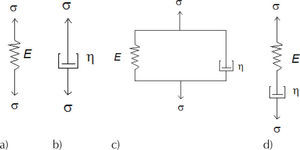
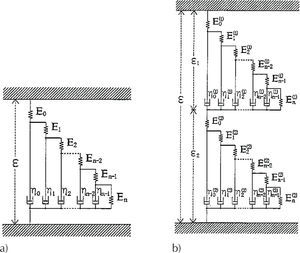
En la figura 1 se presentan algunos arreglos mecánicos simples utilizados para simular el comportamiento viscoelastico de algunos materiales.

Figura 1.

Arreglos mecánicos simples, a) resorte de Hook, b) amortiguador de Newton, c) resorte y amortiguador en paralelo, Kelvin y d) resorte y amortiguador en serie, Maxwell

En (Gurtin y Sternberg, 1962) se presentan los conceptos referentes a la teoría de viscoelasticidad lineal y en particular una sección en donde se tratan las relaciones esfuerzo-deformación en forma de ecuaciones diferenciales de una ley integral de creep o de relajación.

Reología fraccionaria

Los arreglos reológicos, como los arreglos clásicos de Kelvin-Voigt y Maxwell (figura 1), se pueden modificar para tratarse como arreglos reológicos fraccionarios (Meral et al., 2010); se conocen como arreglo fraccionario de Kelvin-Voigt FVM (Fraccional Voigt Model) y arreglo fraccionario de Maxwell FMM (Fraccional Maxwell Model) (Liu y Xu, 2006). Estos arreglos dan mayor versatilidad en la simulación del comportamiento de materiales complejos, tales como los suelos, debido a que resultan más eficientes, pues requieren menos parámetros que un modelo clásico equivalente para simular adecuadamente un material viscoelástico.

La ecuación diferencial del arreglo Kelvin (Gurtin y Sternberg, 1962) (figura 1) expresada con la derivada entera es:

Ahora, escribiendo la misma ecuación pero con derivada fraccionaria (Meral et al., 2010) resulta:

donde α es el exponente fraccionario arbitrario.

En la ecuación (13) se observa la generalización de un arreglo clásico a uno fraccionario. Las constantes E y h (módulos de rigidez y viscosidad, respectivamente), que representan las propiedades viscoelásticas del material aparecen en ambas ecuaciones, lo que cambia es el orden de la derivada en el término de velocidad de deformación ∂^αε/∂t^α en donde α es un número real que representa el orden de la derivada, que en el caso de la ecuación clásica vale 1.0. Estrictamente hablando, cuando α < 1 no puede hablarse de una velocidad de deformación, por lo que su sentido físico desaparece. Sin embargo, como se verá a continuación, una derivada fraccionaria de la deformación es una transición entre un sólido perfecto (resorte, para un valor de derivada fraccionaria igual a cero) y un elemento de Newton (amortiguador, para un valor de derivada fraccionaria igual a uno), lo cual implica que tiene ambos comportamientos. Por tanto, un elemento amortiguador fraccionario es una generalización de un elemento viscoso a uno viscoelástico fraccionario.

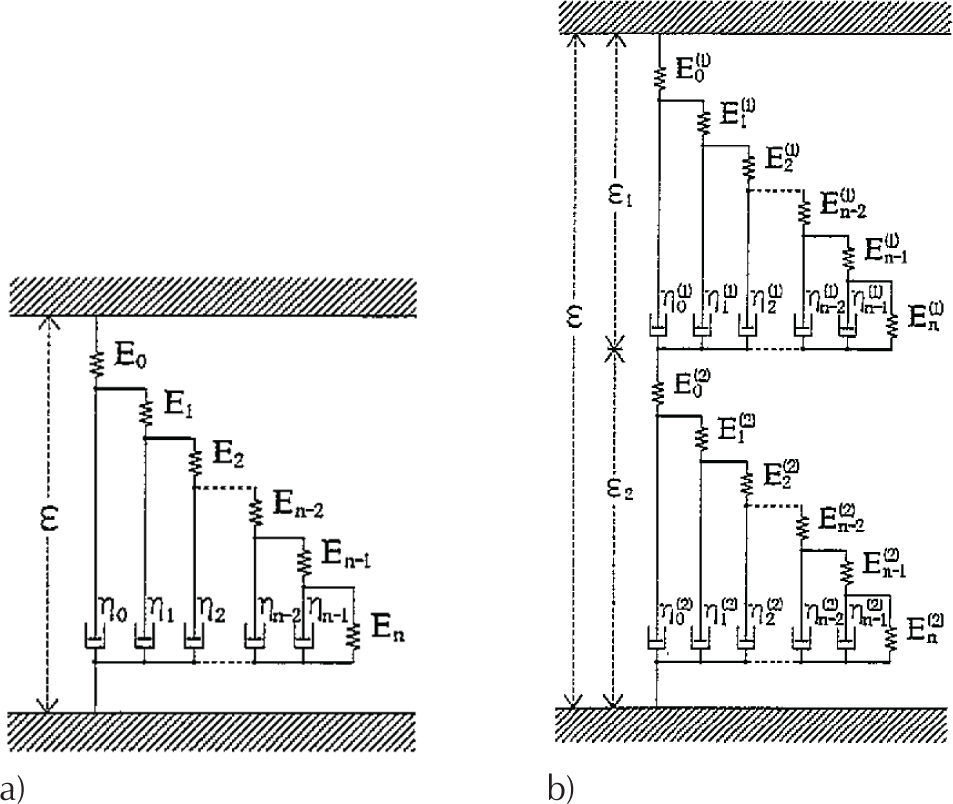
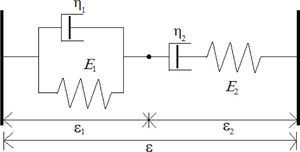
De acuerdo con Schiessel y Blumen (1993), un elemento amortiguador fraccionario puede entenderse como un arreglo finito (en realidad es infinito, pero puede acotarse) de resortes y amortiguadores como el que se presenta en la figura 2a. De forma similar, pueden generalizarse los arreglos como los de Kelvin y Maxwell. En la figura 2b se presenta el esquema generalizado de Maxwell. Plantear una ecuación diferencial que modele a un arreglo como los que se presentan en la figura 2 se torna complicado, y es por ello que las ecuaciones diferenciales fraccionarias permiten trabajar con relativa facilidad fenómenos tan complejos como el de creep.

Figura 2.

Diagramas de arreglos mecánicos finitos usados para simular, a) un elemento amortiguador generalizado y b) un arreglo de Maxwell generalizado

Más adelante se presenta la ecuación diferencial fraccionaria correspondiente al arreglo reológico fraccionario de Burgers, el cual requiere de cuatro constantes viscoelásticas y tres exponentes fraccionarios. Se le llama de orden superior (Liu y Xu, 2006) ya que el orden de la derivada fraccionaria mayor es β + γ, el cual puede alcanzar un valor máximo de 2 si se considera que las derivadas fraccionarias pueden tomar valores entre 0 y 1.

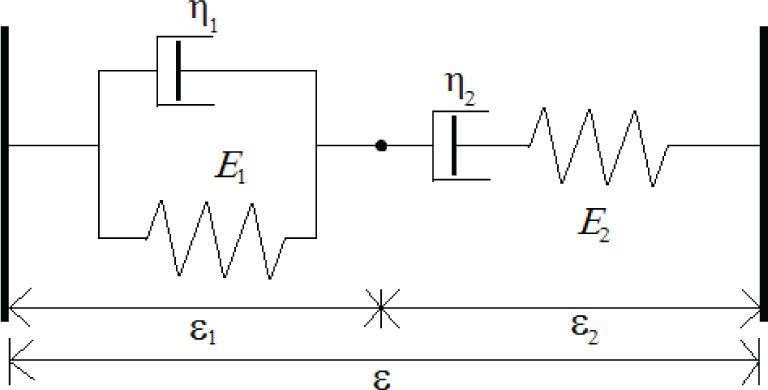
Arreglos reológicos fraccionarios de orden superior

Construyendo arreglos en serie y en paralelo a partir de los modelos FVM y FMM es posible obtener arreglos reológicos fraccionarios de orden superior, tal como el de Burgers, los cuales permiten una simulación más compleja del comportamiento viscoelástico de los materiales (Liu y Xu, 2006). En la figura 3 se presenta el esquema de los arreglos Kelvin y Maxwell en serie FVMS (Fraccional Voigt-Maxwell in Series).

Figura 3.

Arreglo en serie (FVMS)

Ecuación constitutiva del modelo FVMS

En el modelo FVMS se tienen los arreglos FVM y FMM conectados en serie y por tanto, se tienen dos ecuaciones simultáneas como se muestra a continuación (Liu y Xu, 2006).

En el cuerpo de Kelvin-Voigt, la ecuación diferencial es:

y en el cuerpo de Maxwell, la ecuación es:

donde

t	= tiempo
σi(t)	= esfuerzo aplicado como función del tiempo
0D^αt	= derivada fraccionaria con exponente α
Ei y ηi	= módulos de rigidez y viscosidad, respectivamente
α, β y γ	= exponentes fraccionarios arbitrarios
ε1(t), ε2(t)	= funciones de deformación para los cuerpos de Kelvin y Maxwell respectivamente.

Por otro lado, se tiene que las deformaciones en todo el cuerpo son:

Sustituyendo (14) y (15) en (16) y haciendo los arreglos algebraicos necesarios, se tiene:

donde c₁ = E₁/η₁, c₂ = E₂/η₂

La solución de la ecuación diferencial del arreglo FVMS para el fenómeno de creep se puede obtener aplicando la transformada de Laplace a (17):

es decir,

donde s es el parámetro de transformación,

fˆ(s)=L{f(t)}:=∫0∞e-stf(t)dt es la función imagen de f(t).

De (18) se obtiene:

Suponiendo que σ(t) = σ₀H⁰ (una función de tipo escalón), puede obtenerse:

La transformada inversa de Laplace término a término de la ecuación (19) resulta en:

donde

E_a,b(z) es la función Mittag-Leffler.

Cuando α, β y γ son iguales a 1, la ecuación (20) se reduce a la solución de la ecuación diferencial clásica (21) con derivadas enteras:

Análisis paramétrico del modelo FVMS

En esta sección se presenta un análisis paramétrico de la ecuación (20), con el objeto de observar la sensibilidad de dicha ecuación ante la variación de los exponentes fraccionarios y las constantes viscoelásticas. Para facilitar la observación de la variación de los parámetros fraccionarios, la función J(t) se analiza separando cada uno de sus tres términos, de forma que:

J(t)=J0(t)+J1(t)+J2(t)

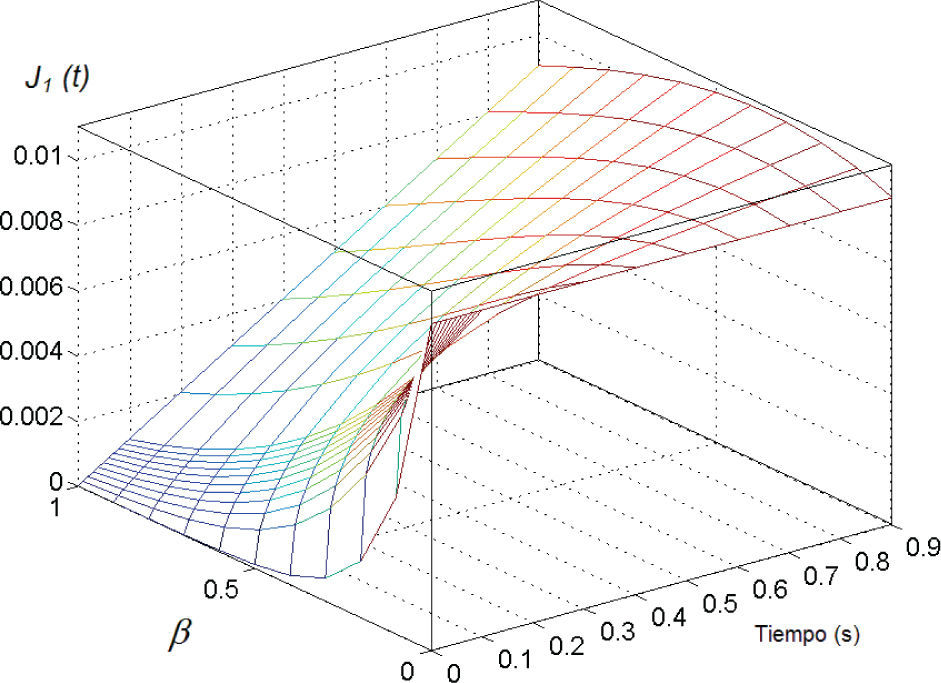
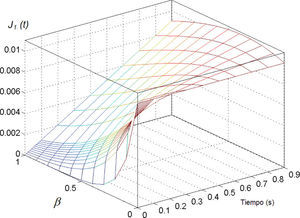
En primer lugar, se presenta el análisis paramétrico del segundo término de la ecuación (20), J₁(t) = 1/η₂ · t^β/Γ(β+1). En la figura 4 se presenta la gráfica tridimensional de J₁(t) variando t y β. A manera de ejemplo, el valor de η₂ se fijó en 100. Puede apreciarse la variación de la función J₁(t) al variar tanto el tiempo t como el exponente fraccionario β. Cuando β = 0, J₁(t) se comporta como una función constante con valor 1/η₂ = 0.01. Al variar el exponente fraccionario, la función J₁(t) se comporta como una parábola dependiente del parámetro β y la función Γ. Cuando β = 1, J₁(t) se comporta como una recta con pendiente igual a 0.01.

Figura 4.

Análisis paramétrico del término J₁(t)

Interpretación física. Cuando β = 0, el elemento fraccionario se comporta como un sólido perfecto (elemento de Hooke), mientras que cuando β = 1 el elemento fraccionario se comporta como un fluido (elemento de Newton). Para valores intermedios, 0 < β < 1, se tiene una transición suave, en donde participan combinados en un arreglo jerárquico elementos amortiguadores y resortes como el mostrado en la figura 2. En ese arreglo, dependiendo del valor de las constantes viscoelásticas, se obtendrá el valor de β para un elemento amortiguador fraccionario equivalente. Por tanto, cuando β → 1 se incrementa la participación de los elementos viscosos (amortiguadores).

El primer término de la ecuación (20), J₀(t) = 1/E₂ · t^β–α/Γ(β − α + 1), presenta el mismo comportamiento que el del caso anterior, con la diferencia de que ahora se ve afectado por el exponente fraccionario α. En este caso se debe cumplir que β ≥ α para que exista estabilidad termodinámica. Fijar los valores de α y β de manera que se cumpla la igualdad β = α resulta de gran utilidad para simular la deformación instantánea en los materiales, ya que su contribución a la función J(t) en este caso, es de una función escalón con valor 1/E₂.

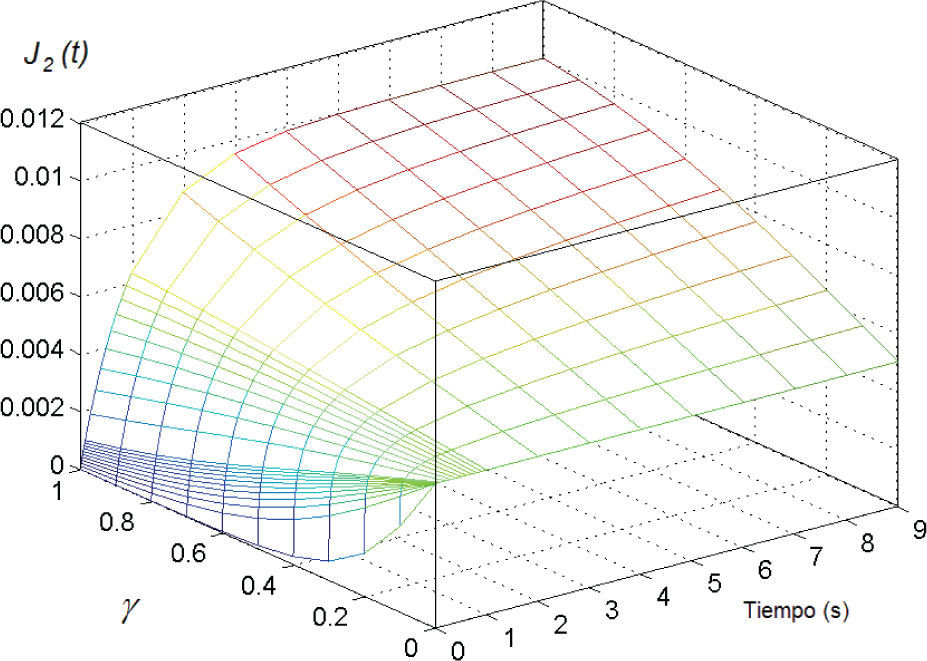
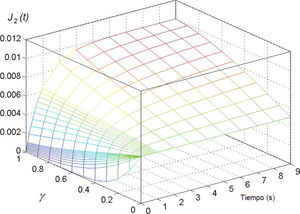
A continuación se muestra el análisis paramétrico del tercer término de la función J(t), J₂(t) = 1/η₁· t^γE_γ,γ+1(–c₁t^γ), donde c₁ = E₁/η₁. A manera de ejemplo, los valores de E₁ y η₁ se fijaron en 100, dando c₁ = 1. En la figura 5 se presenta la variación de la función J₂(t) al variar los parámetros t y γ. Observando la gráfica de la figura 5, puede apreciarse que cuando γ = 0, la función toma la forma de una constante con valor igual a J₂(t) = 0.005. Cuando γ = 1, J₂(t) toma la forma de una parábola asintótica, en este caso a un valor de 0.01. Para valores intermedios, 0 < γ < 1, la función J₂(t) toma la forma de parábolas asintóticas a constantes con valores intermedios a los presentados para γ = 0 y γ = 1.

Figura 5.

Análisis paramétrico del término J₂(t)

Interpretación física. Puede interpretarse físicamente como la deformación dada en el elemento amortiguador fraccionario y está restringida por el elemento elástico (resorte); en este caso, la deformación en el arreglo no es inmediata, sino que existe un tiempo de retardo en donde después de cierto tiempo la deformación máxima se alcanza. Cuando γ = 1, se tiene el arreglo clásico de Kelvin y la deformación máxima la rige el elemento elástico.

En este caso, la función J₂(t) tiende a una asíntota con un valor constante de 0.01. Cuando γ = 0 el arreglo se transforma en un arreglo de dos elementos elásticos en paralelo, por lo que la deformación es inmediata y no existe un tiempo de retardo. La función J₂(t) adquiere un valor máximo instantáneo, en este caso de 0.005, debido a la contribución de los dos elementos elásticos, la cual se mantiene constante en el tiempo. La suma algebraica de las funciones J₀(t), J₁(t), J₂(t) dan como resultado un efecto total sobre la función J(t).

Con el análisis paramétrico antes presentado se tiene una mejor comprensión del comportamiento que exhibe J(t) al variar principalmente los exponentes fraccionarios, ya que dependiendo del valor que tomen estos, J(t) puede evolucionar en el tiempo de formas muy variadas.

Ajustes de curvas experimentales con el modelo FVMS

Con el objetivo de aplicar el modelo FVMS se diseñó una serie de pruebas sobre especímenes de mezclas de bentonita y caolín formados en el laboratorio. Como trabajo previo a este artículo puede consultarse la referencia Hermosillo et al. (2010).

Se consolidaron tres mezclas de caolín y bentonita [M₁ (90% caolín + 10% bentonita), M₂ (80% caolín + 20% bentonita) y M₃ (70% caolín + 30% bentonita)) con el fin de disponer de materiales con diferentes índices de plasticidad. Previo a los ensayos de creep se realizaron pruebas de resistencia del tipo CU (consolidadas no drenadas) para determinar la carga máxima de resistencia (P) correspondiente a cada material. Durante la etapa de consolidación se determinó que el esfuerzo de preconsolidación promedio para todos los materiales fue entre 0.3 y 0.4 kgf/cm², por lo que los ensayos de creep se realizarían a un esfuerzo efectivo de 1 kgf/cm² para garantizar que el creep se desarrollara sobre el tramo virgen de la curva de compresibilidad.

Ensayos de creep

Consolidadas las muestras y la obtención previa de la carga de resistencia para cada material, se realizaron 6 ensayos de creep con el material M₁, 5 ensayos con el M₂ y 3 con el M₃, aplicando diferentes porcentajes de la carga de resistencia (P), correspondiente a cada material.

La carga que se aplicó a cada una de las muestras se generó colocando pesas en el sistema mecánico de las cámaras triaxiales (figura 6). Gracias a la instrumentación electrónica de las cámaras se pudieron registrar los desplazamientos inducidos y las presiones aplicadas en las muestras durante el tiempo que duraron las pruebas de creep. El comportamiento de los materiales observado mediante las curvas de deformación contra tiempo, se logró reproducir usando la ecuación fraccionaria de creep, como se presenta en el siguiente apartado; la reproducción adecuada del comportamiento de esas curvas mediante el modelo fraccionario se comenta más adelante.

Figura 6.

Muestra montada en cámara triaxial y aplicación de carga para generar creep

Empleo del modelo reológico fraccionario y obtención de parámetros

Con la ecuación (20) se realizaron los ajustes a cada una de las curvas obtenidas de las pruebas de creep. Para el ajuste de curvas se utilizó una herramienta numérica en Matlab llamada CFTOOL, la cual está diseñada para realizar ajustes de series de datos con funciones definidas por el usuario, determinando los valores de las constantes de la función que mejor ajustan a dicha serie (minimiza una función de distancia entre la serie de datos y la función definida por el usuario).

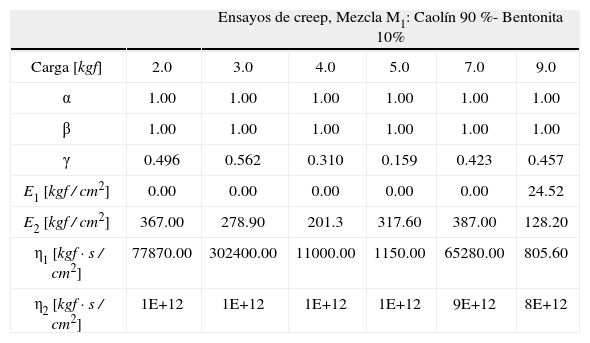
En las tablas 1, 2 y 3 se presenta un resumen de los parámetros para las mezclas M₁ y M₂ y M₃.

Tabla 1.

Parámetros fraccionarios obtenidos con el ajuste de curvas, material M₁

		Ensayos de creep, Mezcla M1: Caolín 90 %- Bentonita 10%
Carga [kgf]	2.0	3.0	4.0	5.0	7.0	9.0
α	1.00	1.00	1.00	1.00	1.00	1.00
β	1.00	1.00	1.00	1.00	1.00	1.00
γ	0.496	0.562	0.310	0.159	0.423	0.457
E1 [kgf / cm^2]	0.00	0.00	0.00	0.00	0.00	24.52
E2 [kgf / cm^2]	367.00	278.90	201.3	317.60	387.00	128.20
η1 [kgf · s / cm^2]	77870.00	302400.00	11000.00	1150.00	65280.00	805.60
η2 [kgf · s / cm^2]	1E+12	1E+12	1E+12	1E+12	9E+12	8E+12

Tabla 2.

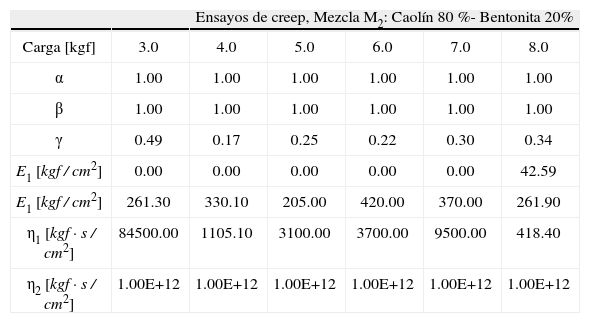
Parámetros fraccionarios obtenidos con el ajuste de curvas, material M₂

		Ensayos de creep, Mezcla M2: Caolín 80 %- Bentonita 20%
Carga [kgf]	3.0	4.0	5.0	6.0	7.0	8.0
α	1.00	1.00	1.00	1.00	1.00	1.00
β	1.00	1.00	1.00	1.00	1.00	1.00
γ	0.49	0.17	0.25	0.22	0.30	0.34
E1 [kgf / cm^2]	0.00	0.00	0.00	0.00	0.00	42.59
E1 [kgf / cm^2]	261.30	330.10	205.00	420.00	370.00	261.90
η1 [kgf · s / cm^2]	84500.00	1105.10	3100.00	3700.00	9500.00	418.40
η2 [kgf · s / cm^2]	1.00E+12	1.00E+12	1.00E+12	1.00E+12	1.00E+12	1.00E+12

Tabla 3.

Parámetros fraccionarios obtenidos con el ajuste de curvas, material M₃

	Ensayos de creep, Mezcla 3 (M3): Caolín 70 %-Bentonita 30%
Carga [kgf]	3.25	4.5	5.6
α	100	1.00	0.90
β	1.00	1.00	0.90
γ	0.21	0.22	0.26
E1 η1 [kgf / cm^2]	0.00	0.00	20.24
E2 [kgf / cm^2]	270.60	254.20	196.0
η1 [kgf · s / cm^2]	2050.00	1800.00	469.20
η2 [kgf · s / cm^2]	1.00E+12	1.00E+12	1.00E+12

En las tablas 1 a 3 puede notarse que para el amortiguador fraccionario del cuerpo de Maxwell se tienen valores de la constante η2 muy grandes, respecto a los demás, lo cual indica que este elemento no influye en el comportamiento visco-elástico del modelo por tener una viscosidad que tiende al infinito. También puede notarse que los valores de α y β son iguales a 1, lo cual implica que el primer término en la ecuación (20) tiene un valor constante 1/E₂ que corresponde a la deformación elástica instantánea de la probeta al aplicar una carga instantánea. Se puede ver que para cargas menores que 70%, el valor de la constante viscoelástica E₁ es nulo y eso implica que solo participa el amortiguador fraccionario en el arreglo de Kelvin. Para cargas cercanas al esfuerzo de resistencia se tiene una deformación instantánea mayor y la constante E₁ adquiere un valor pequeño que influye en el comportamiento a largo plazo en la curva tiempo-deformación.

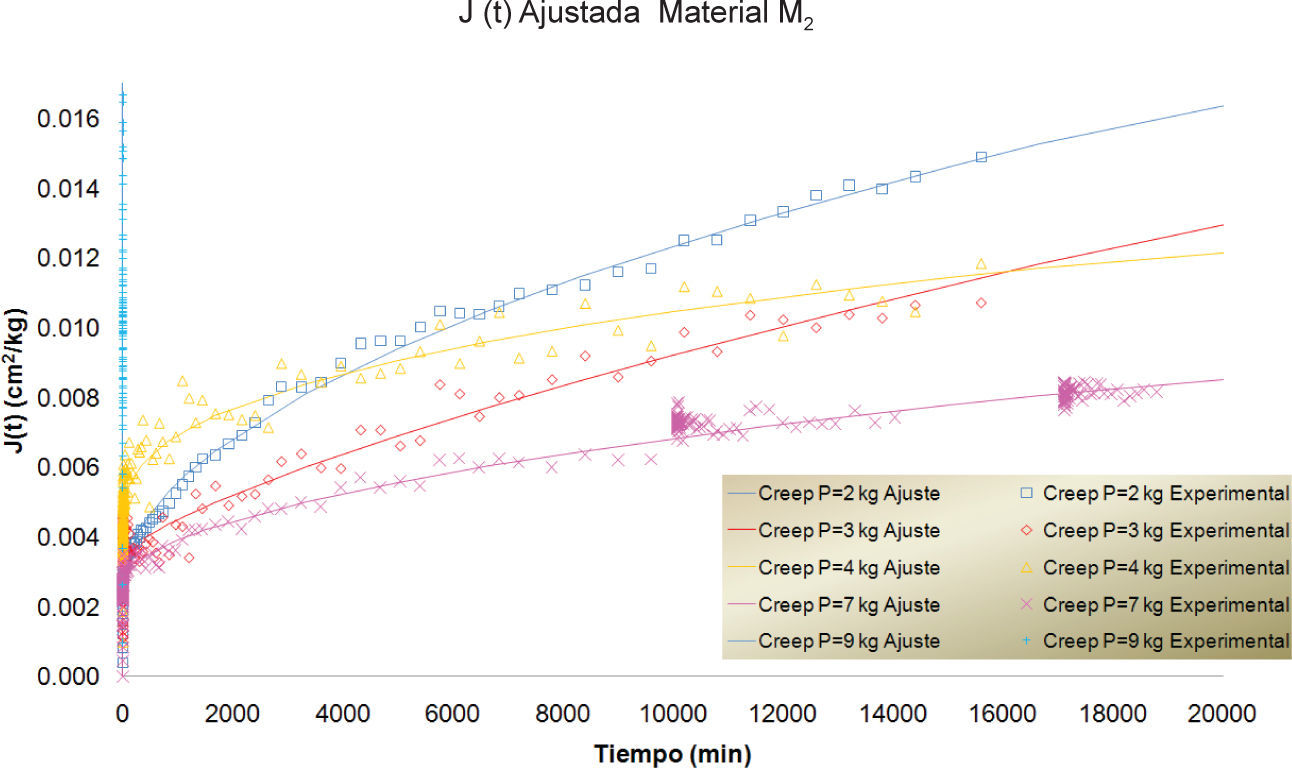
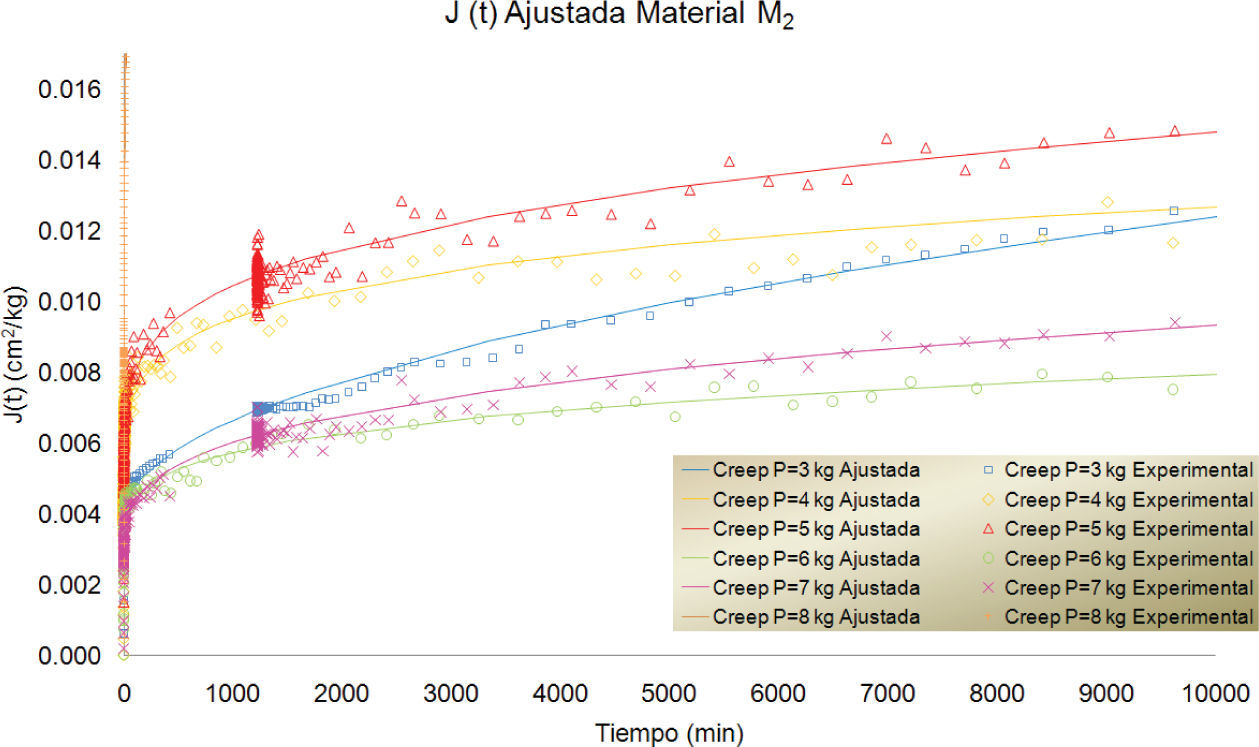
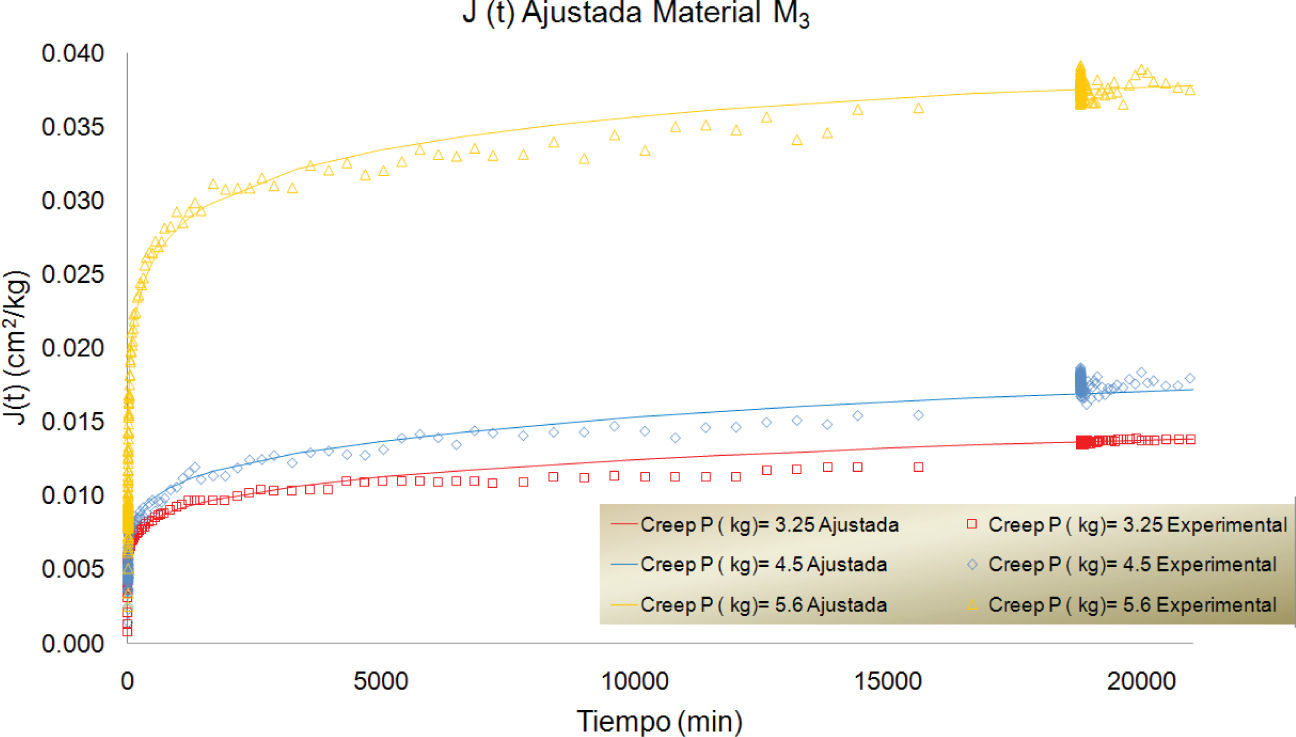
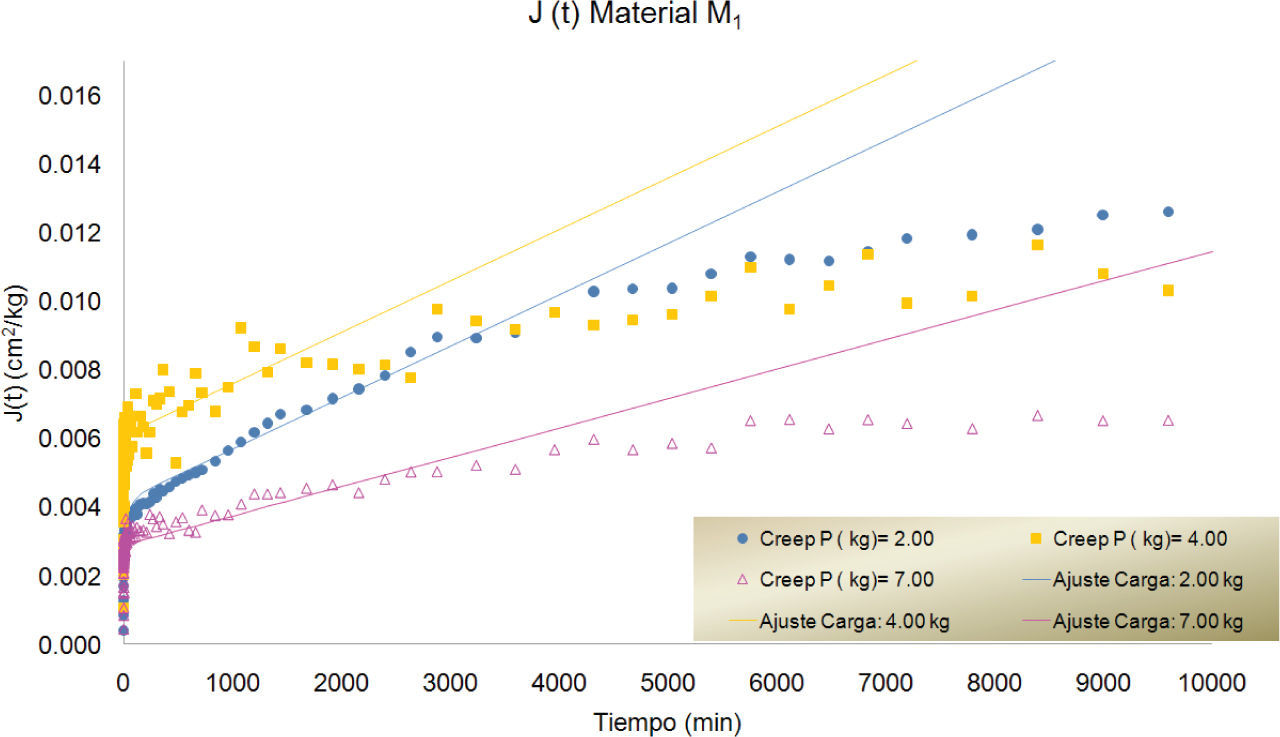
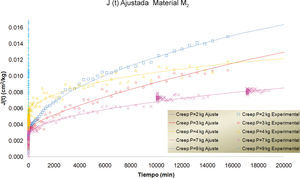
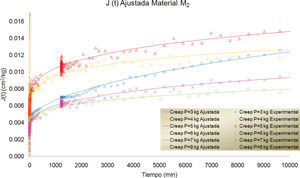
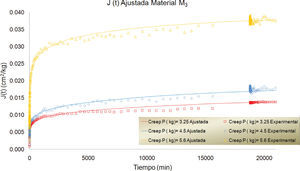
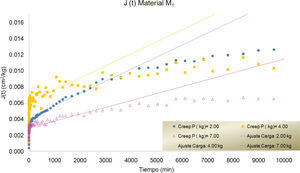
En las figuras 7, 8 y 9 se presentan las curvas correspondientes a los datos registrados durante los ensayes de creep para los materiales M₁, M₂ y M3, para diferentes magnitudes de carga. Cada una de las curvas se ajustó utilizando el modelo fraccionario ya descrito. Las curvas ajustadas se presentan superpuestas a las experimentales en las mismas gráficas.

Figura 7.

Curvas experimentales, ensayes de creep. Material M1

Figura 8.

Curvas experimentales, ensayes de creep. Material M₂

Figura 9.

Curvas ajustadas con el modelo reológico fraccionario, material M3

Como caso comparativo, en la figura 10 se presentan los ajustes de algunas curvas de creep registradas para el material M₁ utilizando la ecuación clásica del arreglo de Burgers. Puede notarse la baja capacidad para simular el fenómeno, debido a que se requiere de un arreglo mecánico más elaborado y su ecuación diferencial correspondiente. Puede apreciarse que las curvas experimentales se reproducen adecuadamente solo para tiempos cortos (menos de 3000 minutos en dichas pruebas).

Figura 10.

Curvas ajustadas con el arreglo clásico de Burgers, material M₁

En general, como se puede apreciar en los ajustes anteriores, la funcion J(t) fraccionaria resulta ser adecuada para simular el fenómeno de creep en suelos arcillosos. Por último, se presentan las conclusiones referentes al ajuste de curvas experimentales mediante modelos reológicos fraccionarios y su importancia sobre los modelos clásicos.

Conclusiones

• •

  El arreglo reológico fraccionario (FVMS) utilizado para simular el fenómeno de creep en suelos arcillosos sedimentados artificialmente resultó ser eficiente con respecto a los parámetros considerados bajo la premisa de que la ecuación de creep correspondiente (20) reproduce con bastante aproximación las curvas obtenidas experimentalmente.

• •

  Las constantes y los exponentes fraccionarios, determinados mediante los ajustes de las curvas de creep obtenidas experimentalmente, dependen de la carga aplicada. Para cargas muy grandes (cercanas a la carga de falla), la constante viscoelástica fraccionaria E₁, correspondiente al elemento resorte en el arreglo de Kelvin fraccionario, toma un valor diferente de cero. Esto indica que para diferentes niveles de carga, pueden empezar a trabajar elementos del arreglo fraccionario que para otros niveles de carga no presentaban actividad.

• •

  Por lo observado en los ajustes, en general, puede decirse que para modelar el comportamiento de los suelos analizados mediante reología fraccionaria, bastaría un arreglo en serie de tres elementos: un elemento elástico (resorte, para el caso particular de α = β) con el cual se tiene una respuesta inmediata a la deformación, más un elemento viscoso (amortiguador, β = 1) el cual tiene un efecto de retardo en el tiempo, más un elemento viscoso fraccionario (amortiguador fraccionario, 0 < g ≤ 1), que tiene una evolución en el tiempo más compleja que el amortiguador clásico; esta conclusión se debe a que, en los ajustes presentados, puede observarse que en el cuerpo de Kelvin fraccionario, que la constante E₁ sea igual a cero, implica que este cuerpo trabaja como un amortiguador fraccionario, esto para cargas menores que 70% de la carga de resistencia, porque para cargas mayores se comporta como un cuerpo de Kelvin fraccionario.

• •

  Debe considerarse que al modelar el fenómeno de creep con ecuaciones diferenciales fraccionarias se está utilizando implícitamente un arreglo fractal de varios elementos (elásticos y viscosos) en cada elemento fraccionario (Schiessel y Blumen, 1995). Esto presenta una gran ventaja sobre los modelos reológicos clásicos, ya que plantear una ecuación diferencial de un arreglo clásico equivalente a uno fraccionario se torna muy complicado. Por tanto, una gran ventaja de los modelos reológicos fraccionarios sobre los clásicos es que requieren de menos parámetros cuando se simulan ciertos fenómenos.

• •

  El empleo de modelos reológicos fraccionarios permite la simulación total de curvas de creep en el tiempo; esto significa una gran ventaja sobre los modelos clásicos como el de Kelvin, Maxwell o Burgers, ya que estos pueden utilizarse para simular solo intervalos de tiempo y no toda la historia de deformaciones presentada durante el desarrollo del fenómeno, como puede observarse en la figura 10.

• •

  La investigación realizada en este trabajo permite concluir que este tipo de modelos es adecuado para estudiar y modelar el comportamiento de los suelos arcillosos sometidos a una carga sostenida, por ejemplo cuando esta origina que se presente el fenómeno de creep.

• •

  Debe darse mayor énfasis al empleo de la reología fraccionaria y de las ecuaciones diferenciales fraccionarias en problemas y fenómenos que se presentan en ingeniería civil, ya que el comportamiento de muchos materiales que se utilizan o están presentes en obras civiles, como los suelos, pueden tratarse más adecuadamente usando estas herramientas matemáticas.

Nomenclatura

Simbología de funciones y variables:Dⁿf(t)

= derivada n-ésima de la función f(t)

Dxαf(x)

= derivada fraccionaria (con exponente fraccionario α) respecto a x de la función f(t)

L{f(t)}

= transformada de Laplace

E_a,b(z)

= función Mittag-Lefler

a, b

= constantes arbitrarias

ℜ

= conjunto de los números reales

⊄

= conjunto de los números complejos

α, β, γ

= exponentes fraccionarios de la derivada

Γ(z)

= función gamma

E_i, η_i

= módulos de elasticidad y viscosidad

ε(t)

= función de deformación en el tiempo

J(t)

= función de creep