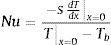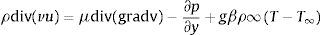Simulación numérica de la convección mixta en un canal vertical aletado

Resumen

La simulación numérica para fl de aire con transferencia de calor por convección a través de un canal vertical con cuatro aletas en estado permanente y régimen laminar en dos dimensiones se realizó mediante un código numérico desarrollado en la plataforma MATLAB® y los resultados se presentan en este trabajo. Una combinación de la técnica de discretización de los volúmenes finitos, el algoritmo SIMPLE y un esquema de ley de potencias para definir la ecuación de convección-difusión en la interface de cada volumen de control se implementaron para encontrar los campos de velocidad y presión, así como la distribución de temperatura dentro del dominio computacional propuesto. El análisis de fl y transferencia de calor se dio para números de Reynolds de 50, 100 y 150; y gradientes de temperaturas entre la pared más caliente y la temperatura del fl a la entrada de 50K y 70K. Combinaciones que permitieron tener números de Richardson de 0.46, 1.04 y 4.16 que corresponden a regímenes de convección forzada, natural y mixta, respectivamente para un Pr=0.72. Los resultados que aquí se presentan son las distribuciones de velocidad y temperatura, las estructuras de fl y la caracterización de las zonas de recirculación adyacentes a las aletas. Finalmente se muestran las gráficas del número de Nusselt local y la temperatura promedio a través del canal. El número de Nusselt y las zonas de recirculación, crecen con el incremento del número de Reynolds.

Abstract

A numerical simulation for mixed convective airflow through a vertical finned channel was carried out by means of a MATLAB® code. Steady state and two dimensional conditions are considered for solving the problem. The discretization technique used was finite volume and the SIMPLE (Semi-Implicit Pressure Linked Equations) algorithm was used to link the pressure and velocity fields inside the computational domain. The simulation was carried out for Re = 50, 100 and 150. The heat transfer problem was solved for a temperature difference between the hot wall and the fluid temperature at the entrance of 50K and 70K. These combinations resulted on Richardson of 0.46, 1.04 and 4.16 corresponding to forced, mixed and natural convection, respectively. As a result, the fluid flow structures, the flow velocity and temperature fields as well as the recirculation zones adjacent to the fines are shown. Local Nusselt number and bulk temperature through the channel are presented. The Nusselt number and the recirculation zones increase when the Reynolds number is augmented.

Introducción

En la actualidad la investigación de flujos internos convectivos es importante, principalmente por la creciente necesidad en aplicaciones tecnológicas de procurar el control térmico de los dispositivos utilizados para la disipación de calor, aunado al hecho de que los avances en la tecnología demandan un alto desempeño, compactibilidad y poco peso en los mismos. El impacto en las aplicaciones tecnológicas referidas llega, entre otras, a la industria de equipo aeroespacial, equipos utilizados en energía nuclear, procesos químicos, al desarrollo de los microcomponentes electrónicos y circuitería, etcétera. Tradicionalmente, las superficies extendidas como aletas y nervios se han utilizado para aumentar la transferencia incitando una mezcla en el fluido, en donde su diseño y optimización son una área de estudio de alto interés (Yang et al., 2010). Las aletas del tipo rectangular se usan en su mayoría para incrementar la convección, ya que son sencillas y de costo relativamente bajo para su manufactura (Sahiti, 2008). Por otra parte, Bakkas y colaboradores (2008) mencionan que la mayor parte de los trabajos en ductos con superficies aletadas o extendidas están enfocadas en convección mixta o forzada. Sin embargo, aún cuando la remoción de calor por convección natural es pequeña comparada con la convección forzada y mixta, esta puede tener un importante papel en el enfriamiento de sistemas térmicos, provocando ahorros y compactibilidad en los diseños, así como promoviendo la investigación de un mecanismo de enfriamiento eficiente que tiene mucho campo por descubrir.

El estudio de los efectos de la convección natural, forzada y mixta en canales verticales ha sido de gran interés para los investigadores. Aung et al. (1986a) desarrollaron una metodología teórica para el estudio del flujo en un canal vertical. El trabajo provee una percepción adicional a las características de dicho flujo para la región totalmente desarrollada. En su trabajo determinaron que la combinación de un caudal fijo y ascendente además de alta flotabilidad en la parte superior del canal, puede precipitar un flujo hacia abajo que emana desde la parte superior abierta del canal. El trabajo concluye que, en convección natural pura no es posible encontrar flujo de retorno, y que cuando las temperaturas de las paredes son distintas, ocurre una situación de flujo reversible, siempre y cuando la magnitud del parámetro de flotación excede un cierto valor crítico; finalmente, para un flujo de calor simétrico en las paredes puede no existir flujo reversible.

Desrayaud et al. (2009) realizaron una investigación numérica concerniente al fenómeno del flujo reversible para convección mixta laminar en un canal vertical de placas paralelas de longitud finita. Los resultados obtenidos se presentaron para un canal calentado simétricamente a temperatura constante para varios números de Grashof y de Reynolds. Los autores expusieron los efectos de las fuerzas de flotación en los patrones del flujo para velocidad y temperatura, y mostraron que la longitud del canal no tiene influencia en la presencia de flujo reversible siempre que esa longitud sea 10 veces mayor o igual que la separación de las placas.

Wang et al.(2009) llevaron a cabo una investigación sobre la convección natural en canales verticales con obstáculos por medio de la técnica numérica del elemento finito. Los obstáculos que se presentan incluyen un semicírculo y dos aletas en diferentes posiciones. Muestran los patrones de flujo y térmicos, incluidos el número de Nusselt promedio para diferentes parámetros. Los resultados que se obtienen son que la transferencia de calor local aumenta con el aumento de obstrucciones por dos razones: el incremento de la superficie de contacto con el fluido y la aceleración del flujo en las zonas cercanas al obstáculo; y que la transferencia de calor, así como el número de Nusselt se incrementan con el aumento del número de Rayleigh.

También se han elaborado investigaciones acerca de canales con diferentes inclinaciones. Fung et al. (1996) realizaron una investigación teórica de la convección mixta para flujo laminar y completamente desarrollado en un canal aletado, presentando los efectos de los números de Reynolds, Grashof y Prandtl, medidas de la aleta y el ángulo de inclinación del canal, en los patrones de flujo y el número de Nusselt. Obtuvieron entre otros resultados, que los parámetros geométricos afectan tanto la transferencia de calor como la fricción en las dos paredes del canal.

Yang et al. (2010a) estudiaron numéricamente la convección mixta en el enfriamiento de una aleta en un canal inclinado, utilizando el método de los volúmenes de control y con una malla no uniforme. El canal mantenía una placa a temperatura constante y otra se suponía adiabática, el flujo lo consideraron permanente, incompresible y adimensional. Usaron la aproximación de Boussinesq y presentaron resultados de la orientación del canal respecto a la horizontal para diferentes números de Richardson y Reynolds. Los autores concluyeron que existe una relación de aspecto óptima de la aleta para la cual hay una máxima transferencia de calor en el canal y esta aumenta cuando el número de Reynolds se incrementa.

Por otra parte, Boutina et al. (2011) estudiaron la convección mixta para el enfriamiento por aire de componentes electrónicos montados en un canal inclinado por medio del método numérico de los volúmenes finitos y utilizan el algoritmo SIMPLER para acoplar la distribución de presión y los campos de velocidad en el dominio computacional. Presentan resultados para números de Reynolds de 1, 5, 10, 50, 100 y 200 y muestran que el número de Reynolds, la inclinación respecto a la horizontal, las dimensiones de las fuentes de calor (componentes electrónicos) y el espacio entre ellas tienen efectos considerables en la mejora de la transferencia de calor dentro del canal.

La motivación del presente trabajo es simular la transferencia de calor en un canal aletado considerando diferentes regímenes de convección desde la forzada hasta la natural y la combinación de ambas para posibles aplicaciones en enfriamiento de componentes electrónicos o disipadores de calor. En el ámbito de estudios relacionados con el enfriamiento de equipo electrónico la mayoría de las aplicaciones están relacionadas con bloques rectangulares que ocupan solo una pequeña porción del canal, en el presente trabajo las aletas que se proponen ocupan prácticamente la mitad del canal con lo que los resultados que se prevén implican una mayor complejidad en las estructuras de flujo. En el presente trabajo se muestran los resultados del estudio numérico del comportamiento del flujo en un conducto vertical con cuatro aletas analizando contornos de velocidad, planos de isotermas y líneas de corriente para relacionar las zonas de recirculación y separación de flujo con zonas de alta trasferencia de calor a lo largo del dominio computacional.

Metodología

Problema a resolver

Se busca por medio de la simulación numérica resolver el fenómeno de la convección forzada, natural y mixta para un flujo laminar en dos dimensiones para un número de Reynolds Re = 50, 100 y 150, en estado permanente a través de un canal vertical que tiene 4 aletas adjuntas a las paredes laterales orientadas de tal forma que son perpendiculares al flujo principal. Las características geométricas del dominio computacional que se analiza se muestran en la figura 1.

Figura 1.

Geometría con condiciones de frontera para el canal vertical y malla generada para el dominio.

Se usa aire como fluido de trabajo con propiedades constantes, exceptuando la variación de la densidad en el término de flotación en la ecuación de conservación de la cantidad de movimiento en la dirección vertical. Las propiedades termofísicas del fluido de trabajo se definen a condiciones de temperatura ambiente. Para las aletas se considera como material el aluminio y para el análisis numérico se supone que están a una temperatura uniforme igual a la pared adyacente. Lo anterior según Young et al. (1998) tiene sustento en el hecho de que si la relación de conductividad térmica del sólido al fluido es de dos a tres órdenes de magnitud la aleta o bloque está a temperatura constante debido a que el número de Biot tendrá valores muy pequeños. Por otra parte, el suponer una elevada conductividad en la aleta causará que los gradientes de temperatura en el sólido sean mínimos pudiéndose considerar que las superficies de la aleta sean isotérmicas (Mills, 1999). En este trabajo se observa que la relación de conductividades térmicas entre el aluminio y la del aire como fluido de trabajo es del orden de 8×103, justificándose la consideración de superficie isotérmica para el estudio propuesto.

A la entrada del canal, el perfil de velocidad corresponde a uno completamente desarrollado (Leung et al., 2000; Young et al., 1999; Young et al., 1998; Yang et al., 2010), y a temperatura constante (T0 = 293K). Esta situación considera que cualquier nuevo comportamiento del flujo se debe a la presencia de las aletas y a las condiciones de calentamiento propuestas. En las paredes del canal se considera que la condición de frontera para el flujo es la de no deslizamiento, mientras que la condición impuesta para el problema de transferencia de calor es de temperatura constante y uniforme en las paredes laterales, de manera que en el canal, la pared izquierda es la de mayor temperatura mientras que la pared derecha se impone un valor de 313K para todos los casos de estudio.

A la salida del canal se considera que los gradientes de los componentes de velocidad y temperatura en la dirección axial son iguales a cero. Esta consideración se fundamentan en el hecho de que el dominio computacional se extiende lo suficientemente lejos de cualquier cambio en la geometría (área normal al flujo y por tanto el flujo alcanza condiciones de un flujo completamente desarrollado (Ferziger et al., 2002). A este respecto, Versteeg et al., (2007) proponen que una longitud de 10 veces la longitud característica del cambio en la geometría (longitud de la aleta o altura del bloque) es suficiente para asegurar numéricamente dichas condiciones. Por su parte, Patankar (1980) asegura que para un Peclet (Re × Pr) mayor a 10 se exhibe un comportamiento de influencia de las variables del flujo convectivo en la dirección del mismo y por tanto las condiciones a la salida no tienen efecto sobre el dominio físico de la solución numérica, justificándose completamente la condición de que los gradientes de las variables involucradas evaluados a la salida y en la dirección normal al fl sean igual a cero. Experimentalmente este último aspecto fue analizado y discutido ampliamente por Young et al. (1999) en su publicación. En este trabajo, tanto las condiciones de la longitud del canal necesaria así como la del número de Peclet se satisfacen según se puede inferir en la figura 1 y en las condiciones de simulación de los números de Reynolds propuestos y el Prandtl del aire.

Matemáticamente las condiciones de frontera pueden expresarse de la siguiente manera (Desrayaud et al., 2009; Aung et al., 1986a):

Entrada: (0 < x < l_x, y = 0)

Salida: (0 < x < l_x, y = l_y)

Pared izquierda: (x = 0, 0 < y < l_y)

Pared derecha: (x = l_x, 0 < y < l_y)

Para estudiar el efecto del flujo de fluidos se consideraron tres diferentes regímenes del número de Reynolds (Re = 50, 100 y 150) para flujo laminar que se determinaron con base en la longitud de la aleta (s) como longitud característica y con la velocidad media del perfil parabólico (vm) de forma que el número de Reynolds queda definido por la relación Re=ρvms/μ. Para la solución del problema de transferencia de calor en el canal, se consideraron dos condiciones de calentamiento en la pared izquierda, es decir, se supusieron dos incrementos de temperatura ΔT = 50K y 70K, considerando como la temperatura base la de la entrada del fluido al dominio computacional, es decir, que la pared izquierda se supuso a una temperatura de 343K y 363K para generar los deltas de temperatura de ΔT=50K y ΔT=70K, respectivamente. La tabla 1 presenta la matriz para los casos de estudio seleccionados. También muestra los parámetros del número de Richardson [Ri = Gr/Re²] que se producen para cada condición considerando los deltas de temperatura y los regímenes del número de Reynolds.

Tabla 1.

Matriz de casos de estudio para el canal

Re	50	100	150
ΔT [K]
50	Ri=2.97	Ri=0.74	Ri=0.33
70	Ri=4.16	Ri=1.04	Ri=0.46

La cuantificación de la transferencia de calor por convección se realiza mediante el cálculo del número de Nusselt local evaluado en la pared de mayor tempe-ratura (x = 0) considerando como longitud característica la longitud de la aleta (s = 0.421l_x) y usando un esquema de diferencias hacia adelante de dos puntos para evaluar la derivada en la pared. Asimismo, se utiliza la diferencia entre la temperatura de la pared en x = 0 y la temperatura media o de bulk en el denominador. Finalmente, la relación utilizada para el cálculo del número de Nusselt se define como:

Ecuaciones fundamentales

Las ecuaciones que gobiernan el comportamiento del flujo bidimensional e incompresible de un fluido newtoniano en estado permanente, régimen laminar y sin generación interna de calor, se expresan en su forma vectorial en las ecuaciones (1) a (4) (Versteeg et al., 2007).

Ecuación de la conservación de la masa:

Ecuación de la conservación de la cantidad de momento

Ecuación de la conservación de la energía

La ecuación (3) representa la cantidad de movimiento del fl en la dirección vertical, y el último término en el lado derecho de la misma representa los efectos de las fuerzas de flotación resumidas en la aproximación de Boussinesq (Mills, 1999). La solución de las ecuaciones (1) a (4) requiere la implementación de un proceso numérico para su solución completa en la geometría que se pretende analizar. En el apartado siguiente se encuentra la descripción de la estrategia numérica utilizada en el presente trabajo.

Procedimiento numérico

La técnica de discretización utilizada para simplificar las ecuaciones que gobiernan el fenómeno es la de los volúmenes finitos debido a que por su construcción es una técnica conservadora que se adecua perfectamente a los principios de conservación de masa, cantidad de movimiento y conservación de energía que rigen el flujo de fluidos. En particular, se desarrolló un código en Matlab^® para la solución numérica del problema citado.

La función que se usa para representar la dominancia entre el flujo difusivo y convectivo de las propiedades en la interfase de los volúmenes de control se evalúa mediante el esquema de la ley de potencias (Patankar, 1980). El algoritmo SIMPLE (Semi-Implicit Method for Pressure-Linked Equations) se utiliza para acoplar los campos de velocidades y presión (Patankar, 1980).

Para la solución del sistema de ecuaciones que se forma al establecer la ecuación de cantidad de movimiento, así como la de conservación de la energía para cada nodo, se usa el algoritmo de Thomas ó TDMA (Chapra et al., 2002). Este algoritmo se implementa en una modalidad de línea por línea en cada dirección para acelerar la razón de difusión de la información numérica durante el procedimiento numérico (Versteeg et al., 2007). Asimismo, se utiliza una relajación hacia abajo (under-relaxation) en todas las variables (α = 0.1) para evitar problemas de convergencia y obtener una estabilidad en la solución. La convergencia de la solución se declara cuando los residuos normalizados para la presión y para las componentes de la velocidad alcanzan un orden de magnitud menor que 1 × 10^–5, mientras que para la temperatura el criterio de convergencia es 1 × 10^–4.

Con el objetivo de evitar soluciones irreales asociadas con las distribuciones de presión y velocidad se utiliza una malla dislocada, considerando una malla para las velocidades y otra para los parámetros escalares, para los que se establecen valores en cada punto nodal (Versteeg et al., 2007; Patankar, 1980). Por último, para obtener mayor información en las zonas cercanas a la pared donde los gradientes son mayores se emplea una cantidad mayor de nodos, utilizando una malla no uniforme. El proceso de generación de la malla utiliza un esquema de crecimiento exponencial donde cada volumen de control es cierto porcentaje más grande que supredecesor, detalles de la implementación en el tamaño de malla se puede ver en publicaciones previas de los autores (Hernández, 2012).

Proceso de validación de la herramienta numérica

El hecho de implementar un código numérico para la solución de problemas de ingeniería conlleva una verificación de que los resultados obtenidos sean fiables. Con ello se pretende evaluar la exactitud y precisión del código desarrollado, así como explorar sus capacidades y limitaciones para reproducir diferentes condiciones de flujo de fluidos en canales comparando los resultados con los ya publicados.

Desrayaud et al. (2009) realizaron una investigación correspondiente al flujo reversible en un canal vertical. El modelo físico bajo consideración consiste en un canal bidimensional, cuyas paredes se encuentran a temperatura constante más alta que la temperatura de entrada del fluido. El fluido de trabajo es aire que se asume es incompresible en régimen laminar y la disipación viscosa es despreciable.

Los casos que se simularon se presentan para diversos valores de diámetro del canal D = 0.02, 0.025, 0.03, 0.06 m (separación entre placas planas). Las líneas de corriente se presentan en la figura 2, y en la figura 3 se muestran los perfiles de velocidad axial obtenidas por los autores para diferentes alturas (6D, 10D, 20D y 45D) a lo largo del canal, estas alturas se ilustran en la figura 2 y se comparan con los resultados del estudio actual. También se presentan las isotermas en la figura 4 y los perfiles de algunas de ellas a lo largo del canal en la figura 5, exhibiendo la comparación con los resultados entregados por el código desarrollado en el presente trabajo.

Figura 2.

Líneas de corriente para diferentes diámetros presentadas por a) Desrayaud et al., 2009 y b) estudio actual.

Figura 3.

Comparación de los perfiles de velocidad axial a través del canal para diferentes alturas.

Figura 4.

Isotermas para diferentes diámetros presentadas por Desrayaud et al., 2009 y b) estudio actual.

Figura 5.

Comparación de las isotermas a través del canal para diferentes alturas.

De las líneas de corriente e isotermas mencionadas, se observa que los patrones y tendencias son semejantes en cada caso y los errores que se presentan en los perfiles deben atribuirse al tamaño de malla utilizado, pero en el peor de los casos se tienen diferencias porcentuales relativas del orden de 3.0. Con las validaciones anteriores se infiere que los errores obtenidos con el código desarrollado son aceptables y, por lo tanto, el programa implementado es adecuado para la simulación de los estudios propuestos.

Una vez establecidas la precisión y el rango de exactitud de la herramienta numérica desarrollada validando los resultados, en el apartado siguiente se muestra el estudio de independencia de malla para definir completamente el proceso numérico implementado.

Independencia de malla

Con la finalidad de darle mayor claridad a los resultados se llevó a cabo un estudio de independencia de malla tomando como parámetro el tamaño de la zona de recirculación formada después de la primera aleta. La numeración de las aletas es en la dirección principal del flujo según van apareciendo; es decir, la aleta 1 y 3 están adjuntas a la pared izquierda, mientras que las aletas 2 y 4 están unidas a la pared derecha.

Se varió el número de nodos en la dirección x y en la dirección y para un número de Re = 150 y un delta de temperatura ΔT = 70K, dado que son los valores más críticos a los que se sometió el estudio. Se concluye que la malla que presenta un error relativo porcentual menor es la malla de 170:97 y no existe una diferencia sustancial entre una malla con mayor densidad de nodos 192:97. La malla considerada reportó errores relativos en el rango de 1% y una disminución considerable en el tiempo de cómputo, por lo que se selecciona como base para las corridas que se reportan a continuación. Para ver con mayor detalle el proceso de independencia de malla se pueden consultar publicaciones previas de los autores (Hernández, 2012). Una vez comentado el proceso numérico se procede a la sección de resultados y su discusión.

Resultados y discusión

Para la exposición de resultados y su discusión, primero se presenta el caso del delta de temperaturas de ΔT = 50K para todos los Reynolds y posteriormente el delta de temperaturas ΔT = 70K. Es importante mencionar que la tendencia del campo de velocidad y distribución de temperatura para ambos casos es similar, la mayor diferencia estriba en el hecho de que para el delta de temperaturas más elevado los efectos en el campo de velocidad tienen más influencia debido a que las fuerzas de flotación tienen mayor presencia.

Canal vertical ΔT = 50K

Inicialmente, en las figuras 6 y 7 se presenta la distribución de las componentes de velocidad v y u, respectivamente, para los diferentes números de Reynolds considerados. En cuanto a la componente de flujo en la dirección principal, se observa que al paso por las aletas se forman zonas de baja velocidad e incluso zonas de velocidades negativas, las cuales aumentan en magnitud con el número de Reynolds, presentándose una relación de velocidad de hasta 10 veces más pequeña que el flujo principal.

Figura 6.

Contornos de velocidad v para el canal vertical para ΔT = 50K.

Figura 7.

Contornos de velocidad u para el canal vertical para ΔT = 50K.

Asimismo, a la salida del canal se observa la presencia de flujo reversible o flujo invertido asociado a zonas de velocidad negativa del componente vertical de velocidad que se extienden desde la salida del canal hasta la aleta cuatro y se adjuntan a la pared derecha, se observa que la presencia de esta zona de flujo reversible ocupa más área dentro del canal a a medida que el número de Reynolds es mayor. Cuando se produce el flujo invertido, el flujo de velocidad negativa pasa en la vecindad de la pared fría y por lo tanto lleva un nivel menor de energía térmica y, adyacente a la pared caliente, se encuentra un flujo ascendente en la dirección vertical llevando de este modo una mayor cantidad de energía. La situación de flujo ascendente y descendente a la salida del canal se debe al hecho de la condición de calentamiento asimétrica que se impone en las paredes del canal. Al respecto algunos autores mencionan que con condiciones de simetría de calentamiento solo se produce flujo invertido cuando se supera un valor crítico del número de Rayleigh y que para un canal vertical con convección natural el flujo invertido no existe (Aung et al., 1986).

Al observar la figura 7, donde se presentan los contornos del componente de velocidad en la dirección horizontal u se puede determinar que no existe mucha aportación de este componente al campo de flujo, dado que el movimiento del mismo se da en la dirección vertical. Se pueden apreciar pequeñas zonas del componente diferentes de cero en la vecindad de las aletas, pero en la mayor parte del canal predominan valores de cero. La presencia de valores diferentes de cero en la componente horizontal de la velocidad en la zona aletada, se asocia al hecho de que el flujo debe sortear las aletas y por tanto existe un desplazamiento del flujo hacia izquierda o derecha dependiendo la ubicación de la aleta sólida. A la salida del canal se aprecia que los valores del componente horizontal de velocidad son imperceptibles tendiendo a valores de cero.

Las líneas de corriente se presentan en la figura 8 donde se observa la formación de zonas de recirculación en la zona aletada, las cuales aumentan de tamaño tanto en la dirección horizontal como vertical al incremento del número de Reynolds. En la tabla 2 se presenta la longitud en la dirección vertical de las zonas de recirculación formadas en las regiones adyacentes a las aletas. Los resultados de la tabla están adimensionalizados respecto a la longitud de la aleta (s = 0.01 m) y permiten confirmar lo mencionado en cuanto a que existe un crecimiento de las zonas de recirculación a medida que el número de Reynolds crece. Sin embargo, al aumentar el número de Richardson dichas zonas disminuyen su longitud.

Figura 8.

Líneas de corriente para el canal vertical para ΔT = 50K.

Tabla 2.

Longitud de las zonas de recirculación para el canal vertical con ΔT = 50K

Zona de Recirculación
ΔT= 50 [K]					(yr/s)
	Primer Aleta		Segunda Aleta		Tercer Aleta		Cuarta Aleta
	Antes	Después	Antes	Después	Antes	Después	Antes	Después
Re=50	Ri=2.97	No existe	1.0	0.2	1.7	0.2	1.5	0.5	0.2
Re=100	Ri=0.74	No existe	1.4	0.8	1.9	0.6	1.9	0.7	1
Re=150	Ri=0.33	No existe	1.7	0.9	2	0.7	2	0.8	1.3

La figura 8 indica que en la zona aletada las líneas de corriente se vuelven más densas juntándose unas a otras debido a los cambios repentinos en la geometría, produciendo una aceleración en el flujo debido al cambio repentino en el área transversal al flujo axial. De forma similar, se aprecia de una manera más clara, la presencia en la salida del canal del flujo reversible mencionado. Se observa que el flujo reversible forma una zona de recirculación que se deforma y se alarga adhiriéndose a la pared fría y que toma mayor presencia a medida que aumenta el número de Reynolds.

Las líneas de corriente muestran que el flujo reversible o invertido que desciende por la pared derecha se extiende hacia abajo hasta encontrar la cuarta aleta en donde choca y se mueve hacia la izquierda llegando hasta la zona central del canal donde se encuentra con la corriente del flujo principal que asciende. La unión de estas dos corrientes provoca que se forme una zona de recirculación que se extiende desde la cuarta aleta hasta la salida del canal y cuyo vórtice se desplaza hacia arriba a medida que el número de Richardson es mayor. Lo anterior, definitivamente se asocia con que conforme el número de Richardson crece, las fuerzas de flotación son más intensas y por tanto su aporte al flujo vertical es de mayor relevancia.

La extensión en la dirección horizontal por donde entra el flujo invertido a la salida del canal disminuye a medida que el número de Reynolds es mayor. Asimismo, se aprecia que en la zona de la aleta 4 el flujo reversible ocupa una mayor extensión en la dirección horizontal a medida que el número de Reynolds disminuye. Esta situación puede atribuirse a que para un número de Reynolds elevado se tiene una mayor cantidad de movimiento en la dirección vertical del flujo lo que causa que el flujo reversible sea desplazado hacia la pared derecha.

La distribución de temperatura se presenta en la figura 9 para los diferentes casos de estudio. Se observa que la pared de la izquierda presenta las temperaturas más elevadas según las condiciones impuestas al proceso numérico. También se encuentran zonas de temperatura media cerca de la pared derecha del orden de 323K. Si se hace una retrospectiva de la figura 8, se puede decir que es en las zonas de alta temperatura y, por tanto, de menor densidad, por donde el fluido asciende debido a las fuerzas de flotación. Asimismo, por condición de conservación de la cantidad de movimiento el fluido acelerado hacia arriba por la parte de la derecha debe descender, lo cual hace por la vecindad de la pared derecha, aún cuando no es la zona con mayor densidad o más baja temperatura.

Figura 9.

Contornos de temperatura para el canal vertical para ΔT = 50K.

La gráfica para la temperatura promedio en la dirección vertical se muestra en la figura 10. Se observa que a la salida del canal la temperatura es mayor para números de Reynolds bajos debido al tiempo de residencia del fluido en el canal y a que en la salida del canal se observa que la influencia de la temperatura en la pared derecha tiene una mayor penetración en la dirección x positiva a medida de que el número de Reynolds es menor. Se puede observar que el aumento de la temperatura a lo largo del canal muestra un crecimiento repentino en la zona de entrada y posteriormente el aumento de la misma se da de una forma gradual. Se observa en la figura que para 0 < x < 0.12 la pendiente de la curva es más pronunciada y que a partir de ese punto la curva presenta una pendiente menor. Este hecho se debe asociar con que en la zona donde la pendiente es mayor se encuentra la zona aletada y, en consecuencia, las zonas de recirculación del fluido favorecen los mecanismos de transferencia de calor.

Figura 10.

Temperatura promedio para el canal vertical con ΔT = 50K.

La distribución del número Nusselt de la pared izquierda (la de mayor temperatura) se muestra en la figura 11. Inicialmente el desarrollo de la curva muestra el comportamiento clásico del número de Nusselt para un canal vertical. Sin embargo, en la zona de recirculación previo a la aleta 1 se muestra un punto de inflexión en la curva que termina con valores de cero justo en la esquina inferior izquierda de la aleta. Este valor se asocia al hecho de que existe un flujo estancado que se forma entre la esquina de la aleta y la pared. Después de este punto, se encuentra que la curva muestra un crecimiento repentino que se debe al crecimiento brusco del componente de velocidad dado en la esquina inferior derecha de la aleta. Sobre la pared vertical de la aleta ocurre una caída de la curva para el Nusselt local y después en la esquina superior derecha de la misma hay un ligero incremento que se asocia con que en este punto, el área de transferencia de calor aumenta debido a la propia esquina. Posterior a este punto ocurre una caída súbita en la curva debido a que se tiene una recirculación y por tanto un estancamiento del flujo, de ahí la curva crece hasta un máximo que se localiza entre las aletas y que después de este punto la curva vuelve a caer hasta cero por efectos de la zona de recirculación previa a la aleta 3. Adelante de la aleta 3 se alcanza el máximo valor del Nusselt en la curva y después cae asintóticamente hacia la salida del canal. El punto donde se encuentra el máximo valor para el Nusselt local se encuentra muy próximo al valor donde cambia el crecimiento repentino y exponencial de la temperatura media y que se discutió después de la figura 10. Este punto también se encuentra muy próximo al punto que delimita la recirculación que se forma posterior a la aleta 3 y adyacente a la pared izquierda. Es de relevancia mencionar que los valores picos del Nusselt local se encuentran en la región de la zona aletada con lo que se establece que en región se ve favorecida la transferencia de calor.

Figura 11.

Número de Nusselt local para el canal vertical a través de la pared izquierda con ΔT = 50K.

Finalmente, se observa que para el número de Re = 50 se presenta un aumento conforme se aproxima a la salida del canal en la curva, esto se puede asociar con el hecho de que en la salida la zona de flujo invertido ocupa casi la mitad del canal.

La figura 12 presenta los contornos de velocidad en la dirección vertical para un delta de temperaturas ΔT = 70K. Se observa que las zonas de flujo acelerado son de mayor tamaño comparadas con las del caso anterior para ΔT = 50K (figura 6), de la misma forma las zonas de baja velocidad son más pronunciadas. Se observan zonas de velocidades en dirección ascendente en la vecindad de la pared izquierda y zonas de velocidad descendente en la pared derecha. Esta situación se atribuye a la condición de temperatura asimétrica impuesta en las paredes del canal.

Figura 12.

Contornos de velocidad v para el canal vertical para ΔT = 70K.

Para un número de Re = 150 y un número de Ri = 0.33 se aprecia una zona de alta velocidad atrapada entre la pared izquierda y la zona central del canal. Este comportamiento no se presenta en un número de Re = 100 y un número de Ri = 1.04, ni para un número de Re = 50 y un número de Ri = 4.16. Por lo tanto, este particular efecto se puede atribuir a que para números de Richardson bajos, la condición de convección forzada es predominante, mientras que para números de Richardson altos el mecanismo de movimiento del flujo se atribuye principalmente a las fuerzas de flotación.

En la figura 13 se muestran los contornos de la distribución de velocidad en la dirección x. Se observa poco contraste, es decir, que el campo de velocidad en la dirección horizontal no presenta grandes modificaciones o variaciones. Únicamente se muestran zonas de velocidad importante en la región de la zona aletada y tiene que ver con el hecho de que en esta zona, el flujo tiene que eludir las aletas y por tanto se mueve de izquierda a derecha o viceversa, siempre buscando la salida natural del canal.

Figura 13.

Contornos de velocidad u para el canal vertical para ΔT = 70K.

Las líneas de corriente para el caso de un delta de temperatura ΔT = 70K se muestran en la figura 14. Comparando con el caso anterior de ΔT = 50K (figura 8), se observa que al aumentar el delta de temperatura las líneas de corriente en el caso de un número de Re = 50 tienden a acercarse hacia la pared más caliente, mientras que el vórtice presente en la base de la última aleta disminuye considerablemente su tamaño y la zona de recirculación adyacente a esta aleta es menor. También se observa que el flujo reversible ocupa la mitad del canal para un número de Reynolds de Re = 50 y un delta de temperatura de ΔT = 70K. Este comportamiento se debe a que para un ΔT = 70K y un número de Re = 50 las fuerzas de flotación tiene mayor importancia.

Figura 14.

Líneas de corriente para el canal vertical para ΔT = 70K.

Para los otros dos casos de número de Reynolds, comparando el comportamiento para un delta de temperaturas diferente (figuras 8 y 14), se tiene que para un número de Re = 100 y un delta de temperaturas ΔT = 70K el vórtice parece segmentarse en comparación con el de la figura 8, mientras que para un número de Re = 150 la zona de fl invertido ocupa una mayor porción del canal.

Al incrementar el número de Reynolds para este delta de temperatura (ΔT = 70K) se presenta la misma tendencia del incremento en el tamaño de las zonas de recirculación como se indica en la tabla 3, dónde se presenta la longitud axial de las zonas de recirculación en las partes laterales de las aletas. Coincidiendo que para un número de Reynolds elevado los vórtices crecen y se presenta el comportamiento inverso para el parámetro del número de Richardson.

Tabla 3.

Longitud de las zonas de recirculación para el canal vertical con ΔT = 70K

Zona de Recirculación
ΔT= 70 [K]					(yr/s)
	Primer Aleta	Segunda Aleta	Tercer Aleta	Cuarta Aleta
	Antes	Después	Antes	Después	Antes	Después	Antes	Después
Re=50	Ri=4.16	No existe	0.8	0.2	1.8	0.2	1.4	0.7	0.1
Re=100	Ri=1.04	No existe	1.5	0.7	1.9	0.6	1.9	0.7	0.5
Re=150	Ri=0.46	No existe	1.7	0.9	2	0.7	2	0.8	0.9

En la figura 15 se presentan los contornos de temperatura para los diferentes Reynolds y un delta de temperatura de ΔT = 70K. Se observa que para un número de Richardson elevado la distribución de temperatura va en forma de capas, mientras que para los números de Ri = 1.04 y 0.46 se encuentran zonas de baja temperatura entre las paredes laterales. En estos dos últimos casos, se observa que para la pared izquierda el comportamiento se asemeja al crecimiento de una capa límite térmica y es en esta zona por donde el flujo asciende debido a que es la zona de mayor temperatura y más baja densidad. Se encuentran también zonas de baja temperatura en la parte central, esto se puede asociar a que para números de Richardson cercanos a cero existe dominancia de la convección forzada y para las condiciones impuestas la transferencia de calor se da de las paredes a la región central del canal.

Figura 15.

Contornos de temperatura para el canal vertical para ΔT = 70K.

En la temperatura promedio (figura 16) se observa un incremento importante de la temperatura a la salida del canal comparado con el caso vertical con ΔT = 50K. Para un número de Re = 50, se observa que la temperatura promedio se acerca al valor asintótico de la temperatura de pared. Asimismo, en la misma figura se observan pequeñas oscilaciones en el desarrollo de la curva de temperatura media. Estas oscilaciones corresponden a la presencia de las aletas y corresponden a los picos que se reportan en las curvas del número de Nusselt local. Se observa también que el crecimiento de la temperatura tiene dos tendencias. A la entrada del canal el crecimiento es más pronunciado o repentino, mientras que a la salida del canal el crecimiento de la curva ocurre de forma más gradual. Una vez más se asocia este comportamiento a la zona aletada que favorece las condiciones de mezclado y por tanto provocan una mayor transferencia de calor.

Figura 16.

Temperatura promedio para el canal vertical con ΔT = 70K.

La gráfica del número de Nusselt para la pared izquierda y un delta de temperaturas de ΔT = 70K se muestra en la figura 17. El número de Nusselt aumenta con el incremento del número de Reynolds, y muestra la presencia de las aletas y un incremento hacia la salida para un número de Re = 50 debido a la influencia de la convección natural. Se muestra que con el incremento del número de Richardson el número de Nusselt disminuye sustancialmente. Lo anterior se puede atribuir al efecto de que los mecanismos de transferencia de calor predominantes son los debidos a la convección forzada y no a la convección natural en los casos de estudio propuestos. De forma similar, menciona que entre las zonas de las aletas se encuentran picos en el valor del número de Nusselt, lo que se puede asociar al hecho de que las zonas de recirculación favorecen el mezclado y la transferencia de calor por convección.

Figura 17.

Número de Nusselt local para el canal vertical a través de la pared izquierda con ΔT = 70K.

Conclusiones

Se presentaron las distribuciones de velocidad para las componentes u y v, las estructuras de fl así como la distribución de temperatura, el número de Nusselt local y la temperatura promedio para un canal vertical con cuatro aletas por el cual circula un fl de aire para tres números de Reynolds y dos diferentes condiciones de calentamiento. El código numérico desarrollado para tal efecto fue validado previamente, obteniéndose errores menores que 3%.

Las zonas de recirculación aumentan en tamaño en la dirección axial y en la dirección normal según la dirección principal del flujo en el canal. Asimismo, al incremento del número de Reynolds todas las zonas de recirculación aumentaron su tamaño. Sin embargo, al aumento del número de Richardson las zonas de recirculación disminuyen su longitud.

El número de Nusselt en el canal aumenta al incremento del número de Reynolds y el máximo valor se encuentra en la vecindad de la zona de recirculación adyacente a la aleta 3, después la curva cae de forma asintótica hasta la salida del canal. Para el caso del número de Re = 50 se presentó un aumento hacia a la salida del canal, que se atribuye al flujo reversible presente en esta zona.

Los máximos en la distribución del Nusselt local se encuentran en la zona aletada confirmando que las zonas de recirculación favorecen la transferencia de calor.

Al aumentar la diferencia de temperaturas entre las paredes y la entrada del fluido se encontró que las zonas de flujo acelerado son de mayor tamaño, provocando la condición de flujo reversible o invertido y que entra al canal por la zona de menor energía que se en-cuentra adyacente a la pared derecha.

Este artículo se cita:

Citación estilo Chicago

Hernández-Gutiérrez, Isabel Virginia, Juan Gabriel Barbosa-Saldana, Claudia del Carmen Gutiérrez-Torres, José Alfredo JiménezBernal, Luis Alfonso Moreno-Pacheco. Simulación numérica de la convección mixta en un canal vertical aletado. Ingeniería Investigación y Tecnología, XVI, 02 (2015): 157-172.

Citación estilo ISO 690

Hernández-Gutiérrez I.V., Barbosa-Saldana J.G., Gutiérrez-Torres C. del C., Jiménez-Bernal J.A., Moreno-Pacheco L.A. Simulación numérica de la conveccion mixta en un canal vertical aletado. Ingeniería Investigación y Tecnología, volumen XVI (número 2), abriljunio 2015: 157-172.

Semblanzas de los autores

Isabel Virginia Hernández-Gutiérrez. Se graduó como ingeniero en mecatrónica en la Unidad Profesional Interdisciplinaria en Ingeniería y Tecnologías Avanzadas (UPIITA) del Instituto Politécnico Nacional en 2008. Posteriormente, obtuvo el grado de maestro en ciencias en ingeniería mecánica en el área energética de la Sección de Estudios de Posgrado e Investigación de la ESIME Unidad Profesional Adolfo López Mateos del Instituto Politécnico Nacional con los máximos honores en 2012. Actualmente cursa el doctorado en electrónica en la ESIME Unidad Profesional Adolfo López Mateos del Instituto Politécnico Nacional.

Juan Gabriel Barbosa-Saldaña. Doctor en ciencias en ingeniería mecánica por la Universidad de Texas A&M (2005). Actualmente es profesor titular de la SEPIESIME, Unidad Profesional Adolfo López Mateos en el Instituto Politécnico Nacional y es miembro activo del SNI desde 2006. Dentro de su producción académica cuenta con diversas publicaciones en journals del JCR Data Base, en revistas internacionales, así como en revistas reconocidas por el padrón de excelencia del CONACYT. Actualmente las áreas de investigación incluyen la simulación numérica de flujo de fluidos y transferencia de calor, y aplicación de energías renovables.

Claudia del Carmen Gutiérrez-Torres. Es ingeniera electromecánica por el Instituto Tecnológico de Acapulco (1997). Maestra en ciencias en ingeniería mecánica de la Sección de Estudios de Posgrado e Investigación de la ESIME-IPN (2000) y doctora en ciencias en ingeniería mecánica de la Universidad de Texas A&M (2004). Actualmente es profesora titular de la SEPI-ESIME, Unidad Zacatenco. Sus áreas de interés son termofluidos, turbulencia y sistemas de separación.

José Alfredo Jiménez-Bernal. Es ingeniero electromecánico del Instituto Tecnológico de Acapulco (1997). Maestro en ciencias en ingeniería mecánica de la Sección de Estudios de Posgrado e Investigación de la ESIME-IPN (2000) y doctor en ciencias en ingeniería mecánica de la Universidad de Texas A&M (2004). Actualmente es profesor titular de la SEPI-ESIME, Unidad Zacatenco. Sus áreas de interés son turbulencia y termodinámica endorreversible.

Luis Alfonso Moreno-Pacheco. Obtuvo el doctorado por el instituto de Turbomaquinaria y dinámica de fluidos de la universidad de Hannover Alemania, tiene especial interés en las áreas de dinámica de fluidos computacionales y de Turbomaquinaria.