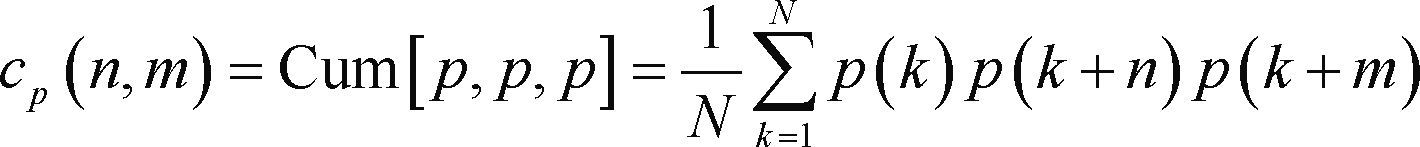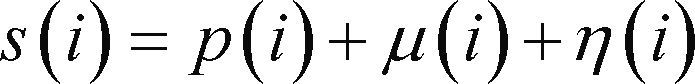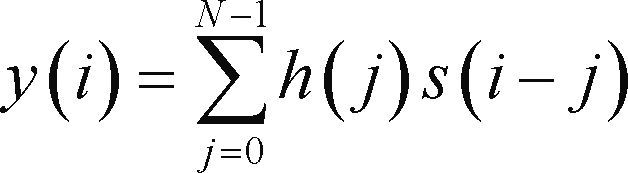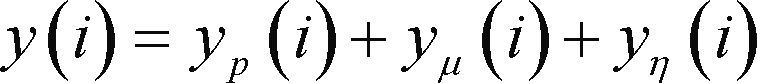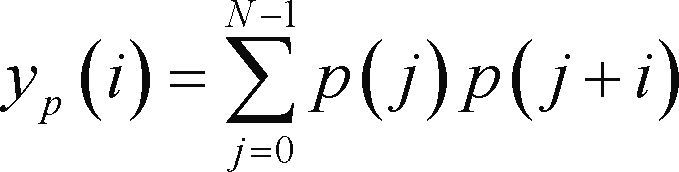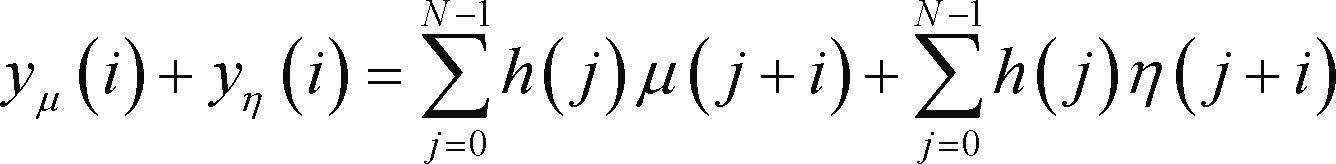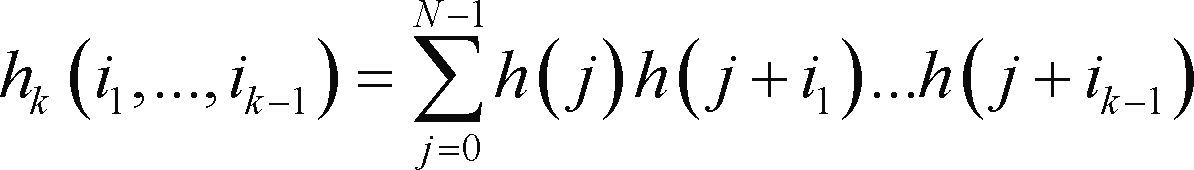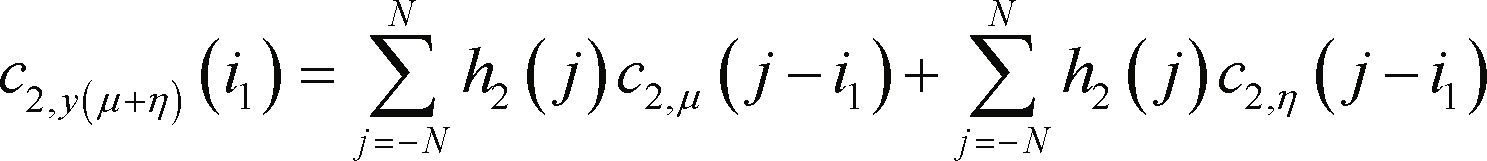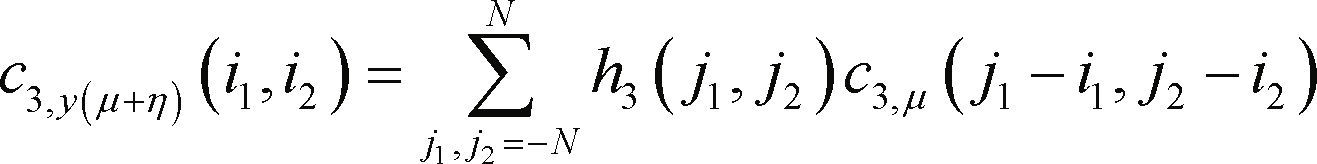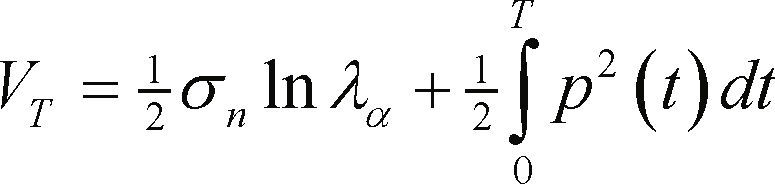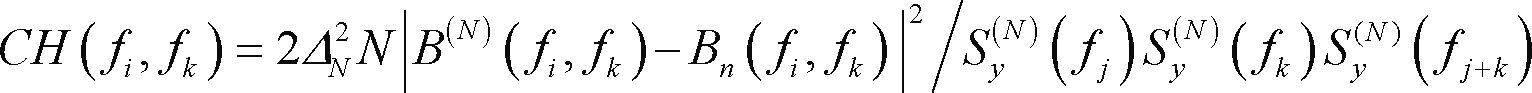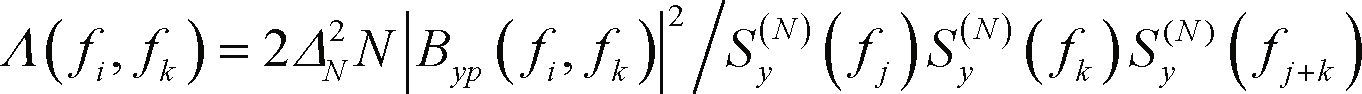Wireless Synchronization Preamble Detection Scheme Using Bispectra-Based Statistics in the Presence of Stationary Noise

Abstract

Higher-order statistical analysis has been applied in many areas of communication systems, such as blind equalization, pattern recognition and channel estimation; among others. In this paper, wireless preamble sequences in additive noise are processed to reduce the signal to noise ratio of synchronization signals thereby improving interconnectivity. For such end, detection structures using matched filtering in the form of passive implementation along with cumulant-based processing are proposed. A framework based on bispectra is used to obtain the probability of detection confirming successful synchronization in the presence of Gaussian and non-Gaussian noise. Signal bispectra and power of the tests are estimated over a number of samples within the length of standard wireless preamble signals.

Resumen

El análisis estadístico de alto orden ha sido aplicado en muchas áreas de los sistemas de comunicaciones, como igualación ciega, reconocimiento de patrones y estimación del canal; entre otros. En este artículo se procesan las secuencias del preámbulo mezcladas con muestras de ruido, con el objeto de reducir la relación señal a ruido de las señales de sincronización inalámbricas y por este medio mejorar la interconectividad. Se proponen estructuras de detección basadas en filtrado acoplado en su forma pasiva conjuntamente con el procesamiento basado en cumulantes de alto orden. Se desarrolla un esquema basado en el biespectro para obtener la probabilidad de detección confirmando sincronización en presencia de ruido Gausiano y no-Gausiano. El biespectro de la señal y la prueba de hipótesis se estiman con un número de muestras cuya longitud es menor o igual que la longitud de las secuencias de sincronización en una trama.

Introduction

Wireless systems need to satisfy simultaneously the communication and computing demands through different radio protocols. The current tendency is towards the usage of multiple-radio systems that preserve good performance through a range of synchronization techniques required for supporting coherent operation. Currently, orthogonal multicarrier frequency division multiplexing and multicarrier (code division multiple access) CDMA are considered for transmission wireless standards (Hanzo et al., 2003; Keller & Hanzo, 1996).

In a commonly found environment surrounding wireless systems interference from radio systems crowding into small areas as well as incidental radiation from electrical devices arise. These sources of interference, which are coupled to the radio receiver in the form of additive non-Gaussian noise, become a foremost impairment. Wireless systems are designed to operate most effectively against the usually assumed additive white Gaussian noise (AWGN) and therefore non-Gaussian coupled to the radio receiver degrades greatly the interconnectivity. Additionally, the non-Gaussian nature of the noise is strengthened by a large sort of near-field interferences from computing platforms that are currently integrated with wireless subsystems (Slattery, Neal, & Cui, 1999). In this article, the detection of wireless synchronization sequences using higher-order statistical analysis (HOSA) is proposed. Among other applications, HOSA is effective in developing algorithms to counteract channel distortion (Nikias & Petropulu, 1993) and also for detecting and classifying signals that features higher-order polyspectra energy (Giannakis & Tsatsanis, 1990). Here, for the first time, higher-order cumulant processing is proposed to detect the preamble of wireless 802.11 standards.

Synchronization of wireless systems is critical. Keller and Hanzo (1996) developed synchronization algorithms relying on the autocorrelation function between received and stored samples of synchronization frames. The periodicity of the synchronization pattern in consecutive frames allows frequency tracking and frame synchronization. Nonetheless, these functions are influenced by additive Gaussian noise at lower signal-to-noise ratios (SNR's) (Keller & Hanzo, 1996) and, consequently, wireless range is diminished. In dense networks preamble signals create interference that is handled in the form of Gaussian interference (Sridhara, 2007; Nagaraj, Khan, Schlegel, & Burnashev, 2009). In Nagaraj et al. (2009) differential correlation type preamble detection sets time coherence to perform statistical metric computation and flag the presence or absence of preamble at the receiver input. For our proposal, higher-order cumulant processing would be helpful in discriminating the presence of multiple wireless systems, however; latency of matched filtering proceeding by cumulant-based processing needs to be addressed carefully. This issue is beyond the scope of the present article. Here, receiver schemes that detect the presence of wireless systems are proposed and their performance is analyzed statistically considering stationary Gaussian and non-Gaussian interference. First, a receiver based on passive matched filtering for synchronization of wireless systems is introduced. Then, the correlation properties of the cumulants and the proposed detectors are analyzed. The processing of wireless preamble using a matched filter preceded by higher-order cumulant com- putation for different sample sizes and signal-to-noise ratios are investigated. Later, a hypothesis testing framework that obtains the preamble detection statistics for a given false alarm probability is developed. Finally, conclusions of the proposed matched filter strategy are outlined.

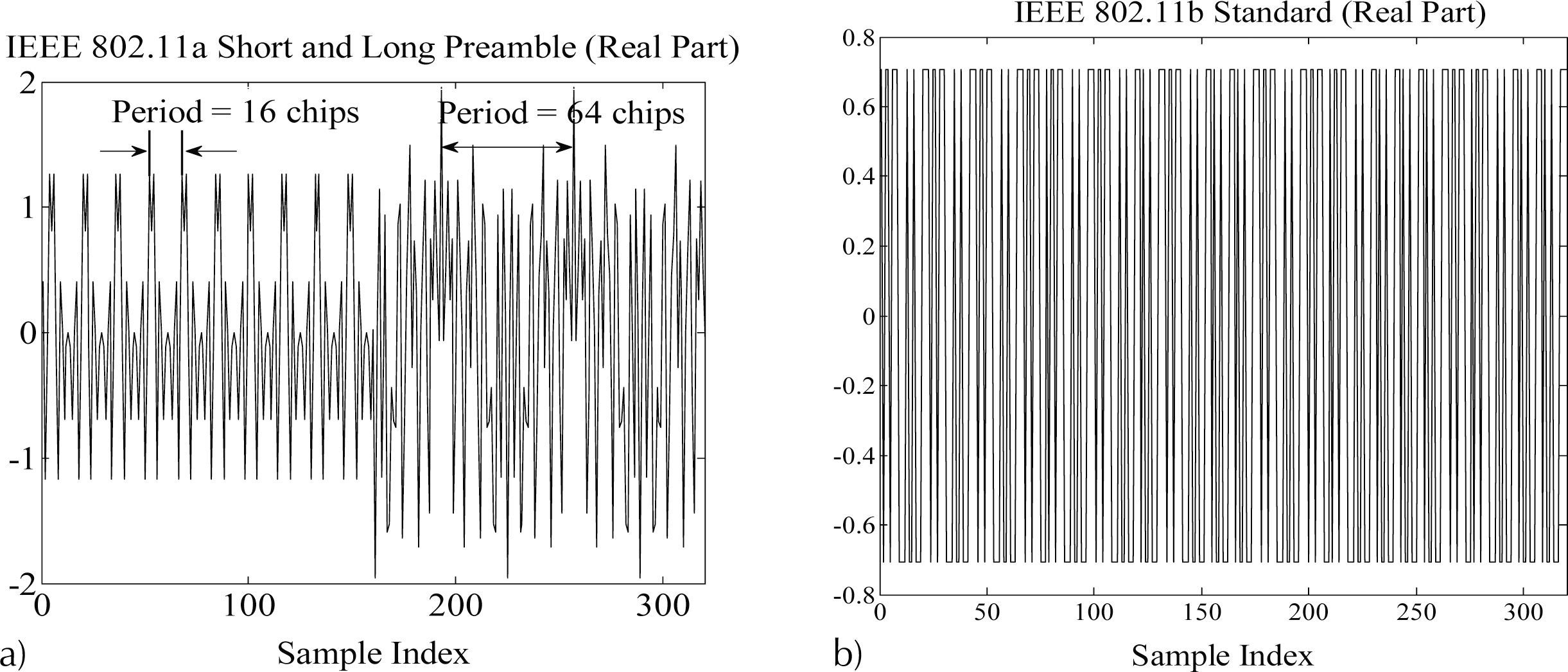
Preamble bispectra

Wireless transmission standards 802.11 specify message and synchronization frames for the Medium Access Control and Physical layers (Agere Systems Inc., 2004). Wireless standards 802.11a and 802.11b are based on the principles of Orthogonal Frequency Division Multiplexing (OFDM) and multicarrier code division multiple access (MC- CDMA) systems; respectively (Hanzo et al., 2003). The transmitted frame of the wireless system consists of copies of the prescribed synchronization sequences, also named herein preambles, and the messages are transmitted in the form of OFDM symbols or in a multi-carrier CDMA scheme. Figure 1 displays the 802.11a and 802.11b preambles as defined by the IEEE standard (Agere Systems Inc., 2004). The preamble 802.11b is effectively a pseudorandom sequence while the standard 802.11a consists of large and short periodicity terms corresponding to a set of frequency tones.

Figure 1.

Real part of the synchronization preambles, a) 802.11a preamble, b) 802.11b preamble.

The goal of the preamble processing technique is to achieve an improvement on the receiver sensitivity. Receiver sensitivity is impaired by different electromagnetic compatibility (EMC) effects, such as broadband emissions (Bronaugh & Lambdin, 1988) that produce interference of nature sufficiently non-Gaussian (Linares & Miranda, 1996). Some assumptions are as follows. First, noise prewhitening filter at the input is avoided and thus the ensuing receiver desense, and second, the preamble sequence has zero frequency and time misalignment along the frame structure which allows to achieve large processing gain by the input matched filter (MF).

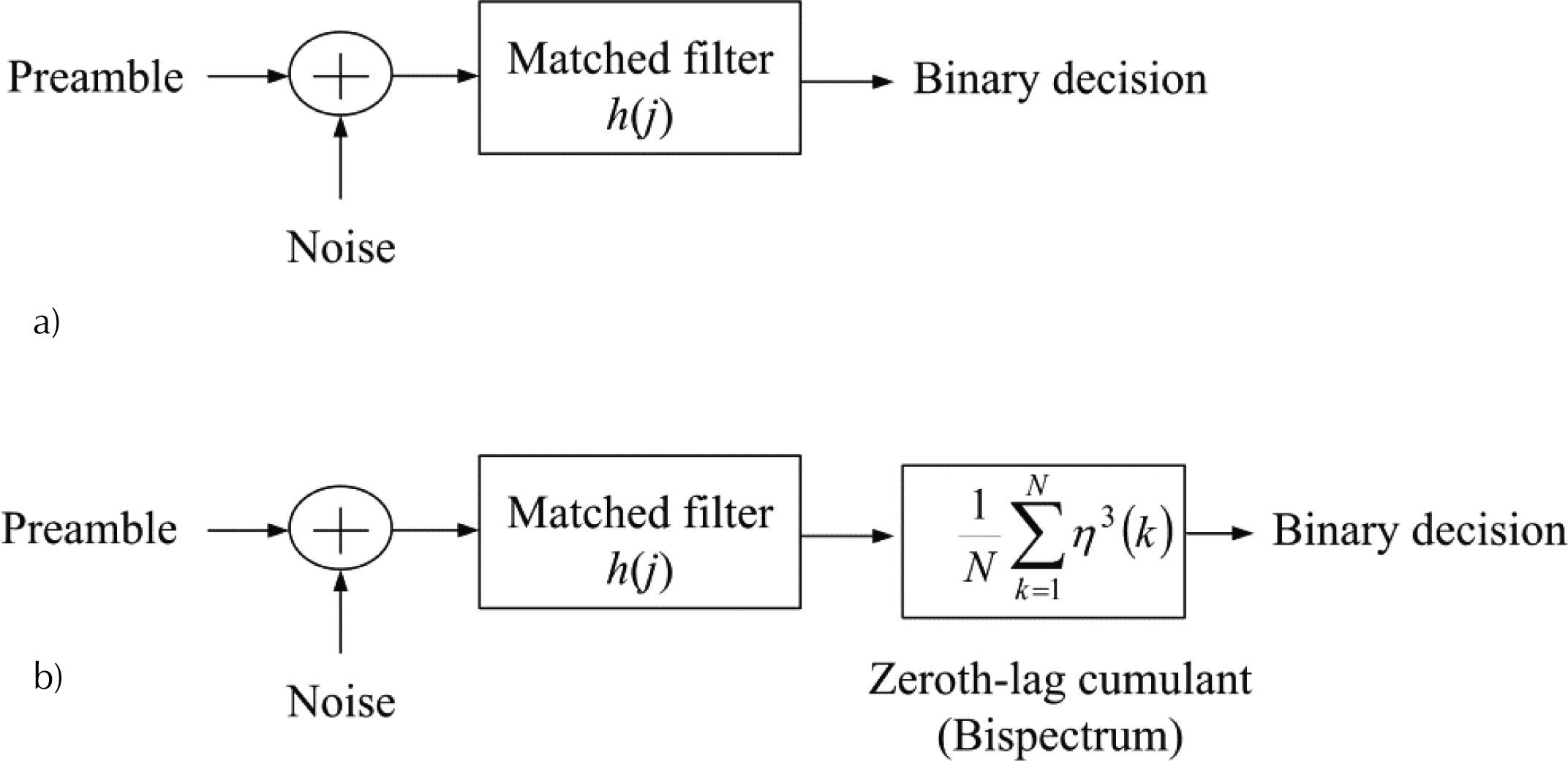
The proposed detection schemes are shown in Figure 2. Both schemes are based on passive matched filtering realizations where the matched filter function is set with the preamble sequence. If the preamble sequence is present at the input, the matched filter outputs a zeroth-lag pulse. If the channel is AWGN, the matched filter solution in Figure 2a is optimal because the output provides a signal-to-noise ratio (SNR) that minimizes the detection error probability (Whalen, 1971). The scheme in Figure 2b achieves cumulant computation using replicas of the preamble sequences stored in the processor.

Figure 2.

Schemes used for preamble detection, a) matched filtering, b) matched filter followed by third-order cumulant computation.

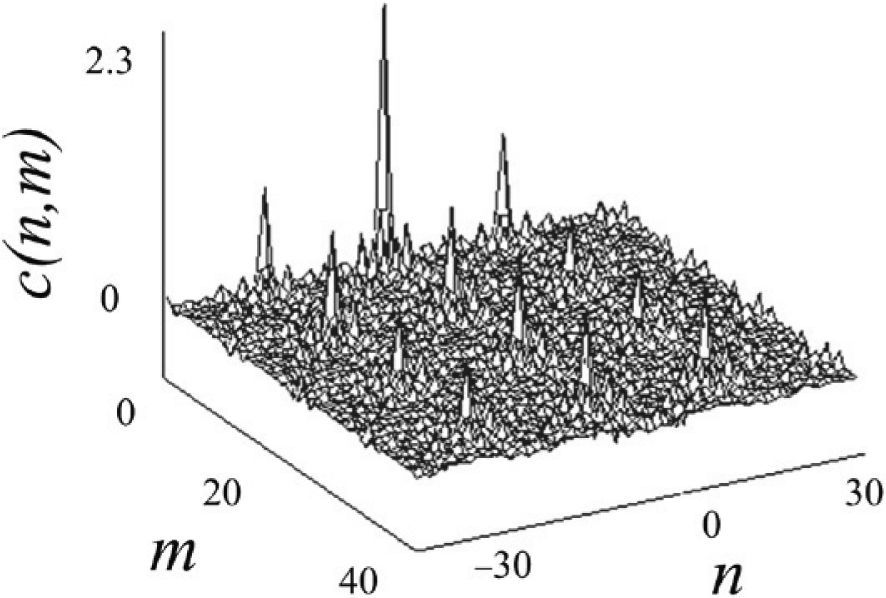
As shown later, a key advantage of the further cumulant-based processing is that the preamble detection is more insensitive to additive noise. The preambles in Figure 1 do not follow a Gaussian distribution given that their mean (which is equal to zero for both preamble sequences) and variance do not characterize completely the distributions. For the 802.11a sequence normalized with its r.m.s., the skewness; γ = 0.2197 and kurtosis, κ = 2.35, and for the normalized 802.11b sequence; γ = 0.025 and κ = 1.0. A more enlighten characteristic is the third-order cumulant function, c(n,m), of the preamble. Figure 3 displays the cumulant of the preamble 802.11a, which is approximately a two-dimensional impulse function of amplitude equal to the preamble skewness at zeroth lag, c(0,0) (Nikias & Petropulu, 1993). The large energy of the pulse is potentially useful for preamble detection.

Figure 3.

Tird-order cumulant of the 802.11a preamble showing a large pulse at zeroth-lag, c(0,0).

The preamble is a deterministic signal and its third-order cumulant is computed simply as the averaged third-order correlation

It is useful to introduce the polyspectra (sampled bispectra) which is given by the Fourier transform

The Fourier transform is evaluated over the principal domain contained in the triangle defined by {j, k: 0 ≤ j ≤ 1/2, k ≤ j, j + k ≤ 1/2} (Nikias & Raghuveer, 1987). Ideally, the polyspectra of a non-Gaussian process are spectrally flat functions.

Matched filter responses

Consider the baseband receiver input signal is a summation samples comprising the preamble, p, non-Gaussian noise, μ, and Gaussian noise, η

Given N-samples of the preamble, the finite impulse response (FIR) filter is matched to the preamble sequence; i.e. h(i) = p(N – i) and the detector output is given by

The response of the (linear) matched filter consists of the preamble correlation function and filtered noise terms

where y_p(i) is the preamble autocorrelation function

and

The cumulant analysis of the filtered random processes was achieved in (Giannakis & Tsatsanis, 1990). The ouput of the random process needs to compute the kth-order correlation of the impulse filter response, which is defined by

The second and third-order cumulant of the noise filtered by the matched filter, c_2,y(μ+η) and c_3,y(μ+η), respectively, have the equation 9.

The cumulants of the preamble autocorrelation, c_yp (which is effectively the cumulants of y_p given by Equation 6), are determined in a similar fashion to the preambles in Equation 1. Of theoretical interest is the assumption that the random variables μ(i) and η(i) are independent and identically distributed (i.d.d.) (Giannakis & Tsatsanis, 1990). Under this assumption, c_2,η (j-i₁) = σ_η²δ(j-i₁) and c_2,μ (j-i₁) = σ_μ² δ(j-i₁) where σ_η² and σ_m² are the variance of the processes and δ(j-i₁) is the 1-D delta function. On the other hand, the third-order cumulant in Equation 10 c_3,y(μ+η) depends only on the non-Gaussian noise cumulant c_3,μ (j₁− i₁,j₂-i₂) = g_mδ(j₁-i₁,j₂-i₂) where g_μ is the skewness of the non-Gaussian noise and δ(j₁-i₁,j₂-i₂) is the 2-D delta function. The third-order cumulant of the Gaussian-noise c_3,η(j₁-i₁,j₂-i₂) is equal to zero. Nonetheless, the result of the insensitivity to Gaussian noise in Equation 10 is not satisfied for a finite number of samples but in the mean of a large number of independent records (Nikias & Petropulu, 1993; Giannakis & Tsatsanis, 1990). It is woth mentioning that statistical analysis based on the bispectra shown in a following section presents asymptotic independence for lengths lower than the preamble size of interest, in agreement with results in Hinich and Wilson (1990).

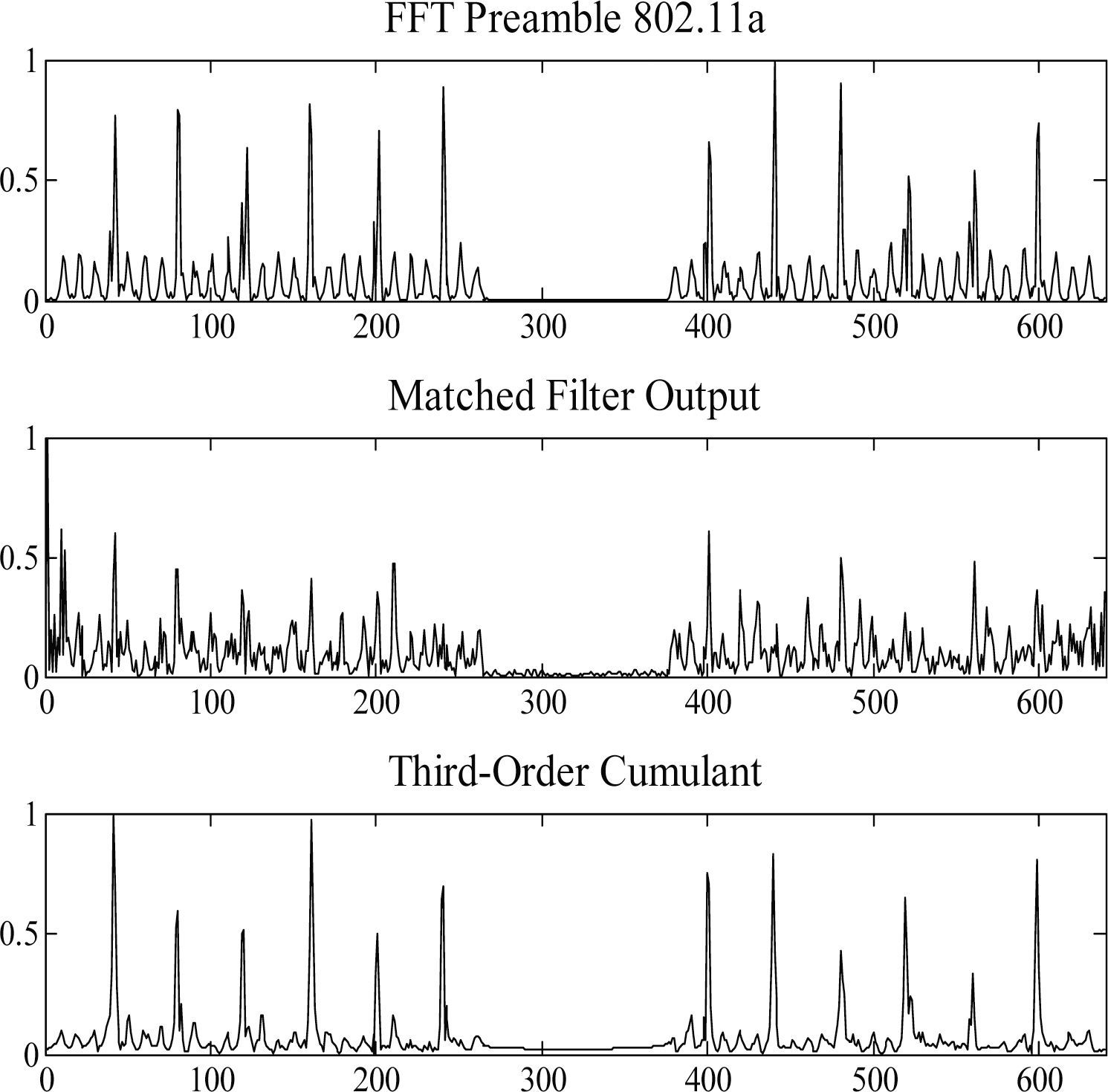
Detector performance

To test both detectors, the input sequence of the preamble is combined linearly with input noise sources of zero mean. The sample rate of the preamble sequences shown in Figure 4 is inversely proportional to the Gaussian noise bandwidth. Receiver floor noise is defined for a given SNR. Non-Gaussian interference is included by setting a signal-to-interference ratio (SIR) and the same sampling rate. In our simulations samples of non-Gaussian noise are produced by a random process characterized by a Lognormal distribution. The use of this distribution facilitates testing the detectors as it allows simulating broadband stationary non-Gaussian interference which is often characterized by a large positive skewness and a long-tail distribution (Primak et al., 2004). Figure 5 displays the reconstruction of the 802.11a preamble achieved at SNR = 0 dB and SIR= -10 dB. It is seen that the third-order cumulant processing of the matched filter output improves preamble reconstruction compared with that based on the matched filter structure. It is apparent that OFDMA tones are best reconstructed. Some noise components are filtered out which result from the high energy of the third-order cumulant. It is important to mention that at high SNR ratios (results not shown herein) the scheme based on the third-order cumulant cannot improve the preamble reconstruction to any further extent. This is due to fact that the preamble cumulant is not an ideal impulse function (Figure 3). However; the following statistical analysis of the preamble detector confirms its effectiveness.

Figure 4.

Distribution of the non-Gaussian noise used in simulations.

Figure 5.

(Upper) FFT of the matched filter output; (middle) matched filter output with noise at the input; and (bottom) matched filtering proceeded by third-order cumulant computation. The preamble retrieval was achieved at SNR = 0 dB and SIR= -10 dB.

Desense levels

The capability of detecting the preamble is analyzed statistically using the corresponding schemes in Figure 6. The matched filter output is processed to estimate both the preamble variance (energy detection) and the preamble bispectrum from which decision rules for hypothesis testing are derived.

Figure 6.

Statistical analysis of the detectors. The upper branch corresponds to the preamble processing using the matched filter output and the lower branch to the bispectra-based detector.

The Newman-Pearson criterion is used to obtain the probability of detection as it does not involve knowledge on apriori probabilities of the preamble transmission (which is periodic in the transmitted frames). By using this criterion, one has to admit errors in the hypothesis testing. An error of the first kind is the probability of false alarm which is the event to saying the preamble is present at the input when there is none. A binary decision is made by computing the likehood ratio, λ(x), which is constrained by a threshold level, l_α that satisfies certain false alarm probability, α (Whalen, 1971). If λ(x) ≥ l_α for a single observation x, the choice is to say the preamble is present. The choice between variance and bispectra depends on the nature of input noise; a decision rule based on the variance (or energy of the preamble) is suboptimal when the input noise is non-Gaussian while bispectra can deal with both types of noise, straightforwardly.

Consider the input noise is Gaussian. For the energy detector in Figure 6, the pulse obtained at the matched filter output is the variance (preamble energy) which is compared against a threshold level, V_T. The decision rule given by λ(x) ≥ l_α is established by comparing the output pulse with the threshold level given by

where σ_n is the variance of the (colored) noise at the matched filter output and T is the preamble duration.

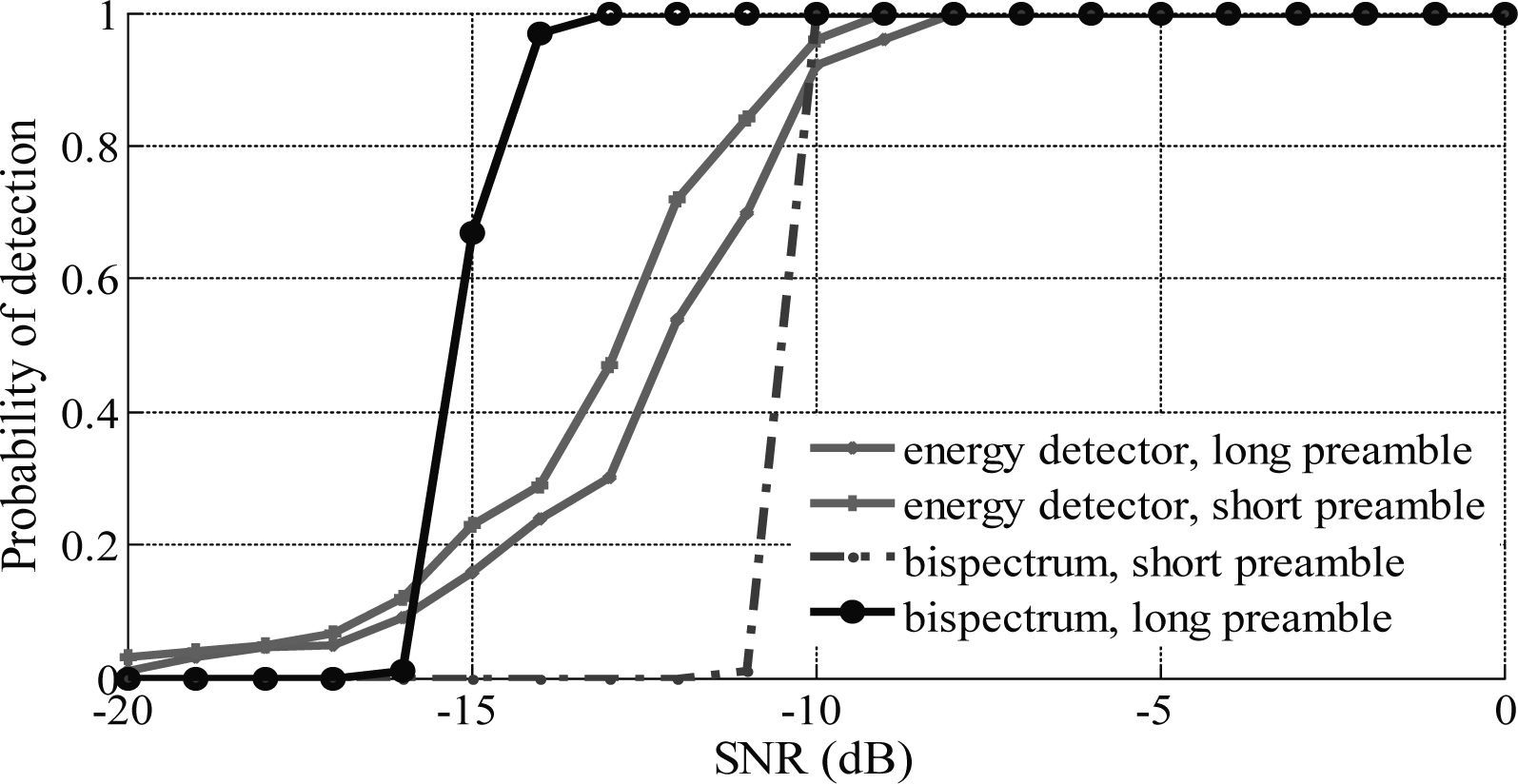
Figure 7 shows the probability of detection using 320 and 640 sample points of the preamble 802.11a. The probability of detection is obtained as an average over a number of observed signals that ensures convergence. It is seen that for a detector based on the preamble energy, the probability of detection does not change substantially with the sample size. At a SNR equal to −8 dB both preambles give approximately a probability of detection equal to 1. A thoughtful analysis of the energy detection by Hinich and Wilson (1990) shows that a 3-dB increase in the receiver sensibility involves an increase on sample size by a factor of 4. For our wireless preamble scheme, such increase is well beyond the chip length of the synchronization preamble within a frame.

Figure 7.

Effect of the sample size on the 802.11a preamble statistics, α is set to be equal to 10^-3 for both detectors.

The bispectra-based detector can deal with non-Gaussian noise. This detector presents theoretical and implementational aspects that have been thoroughly investigated in Hinich and Wilson (1990) and (Nikias & Raghuveer, 1987); among other references. In order to present the preamble detection based on third-order cumulant, some relevant results are shown herein. The probability of detection is derived by taking into account the statistical characteristics of the random variable

where B^(N)(f_j, f_k) is an estimator of the input bispectrum, B(f_j, f_k), for a sample size of N, B_n(f_j, f_k) is the bispectrum of the noise assuming that we have a noise-only sample at the matched filter output; S_y^(N) is the estimated power spectrum density comprising the samples of the preamble and additive noise at the frequencies {f_k}. D_N is the bandwidth of the bispectrum. Using the approximation D_N ≅ 1/√N Hinich and Wilson (1990) give a sampled bispectrum in the form of independent random variables defined at the bifrequency pair (f_i, f_k) and then CH(f_j, f_k) can be considered as a chi-square variable with 2 degrees of freedom.

The bispectrum of the noise B_n(f_j, f_k) is estimated in absence of the preamble. Since noise is stationary; its bispectrum can be estimated at the beginning of the simulations and out-of-line computation of the input bispectrum B(f_j, f_k). The function CH(f_j, f_k) given in Equation 12 is a random variable with a non-central parameter that is defined by the preamble bispectrum and considered as the mean value of the random variable. On the other hand, the power of the test is defined by the skewness of the distribution (Hinich & Wilson, 1990), which is obtained by replacing the difference in Equation 12, B^(N)(f_j, f_k) − B_n(f_j, f_k) by the bispectra of the preamble, B_yp(f_j, f_k)

where Λ is computed over the main dominion of the bispectra. This variable is then a summation of K chi-square variables of 2K degrees of freedom, c²_2K. A consistent estimation of the bispectrum in Equation 13 provides the decision rule for the hypothesis testing. The hypothesis testing and power of the test are computed using the Marcum's Q function (Proakis, 1990). This is established by rejecting the hypothesis that the input is noise only if Λ exceeds the threshold T_α where Pr(c²_2K > T_α) = α. The algorithm that computes the non-centrality parameter includes the signal-to-noise power ratio, ρ(f) = S_y(f)/S_n(f) at each of the three frequencies f_j, f_k and f_j+k, as obtained at the matched filter output.

The probability function is computed through the Generalized Marcum's Q function of 2K degrees of freedom as a function of the c² random variable obtained in Equation 12 as well as the skewness of the distribution in Equation 13. An algorithm was developed to compute the threshold T_α for a given false alarm α. In this algorithm, Gaussian and non-Gaussian processes are generated at each iteration (or observation). The power of the noise and interference are set by SNR and SIR parameters; accordingly. The probability of detection is then obtained as an average over a number of observed signals that ensures convergence.

Figure 7 allows contrasting the statistical analyses of the schemes shown in Figure 6. The detection curves based on cumulant processing display a rapid increase with SNR which stems from the non-linear relationship of the non-centrality parameter with SNR. This is in full agreement with the detection bispectra analysis in Hinich and Wilson (1990). Figure 7 also indicates that the short-preamble can be detected at SNR > -10 dB, which is slightly lower than the ratio at which the energy detector can detect the preamble. Figure 7 also shows that an increase on the preamble length renders an improvement of about 4 dB with respect to the energy detector. This result demonstrates that the preamble autocorrelation function is sufficiently non-Gaussian and the bispectrum can detect it at a lower SNR than the energy detector could detect it with the same sample size.

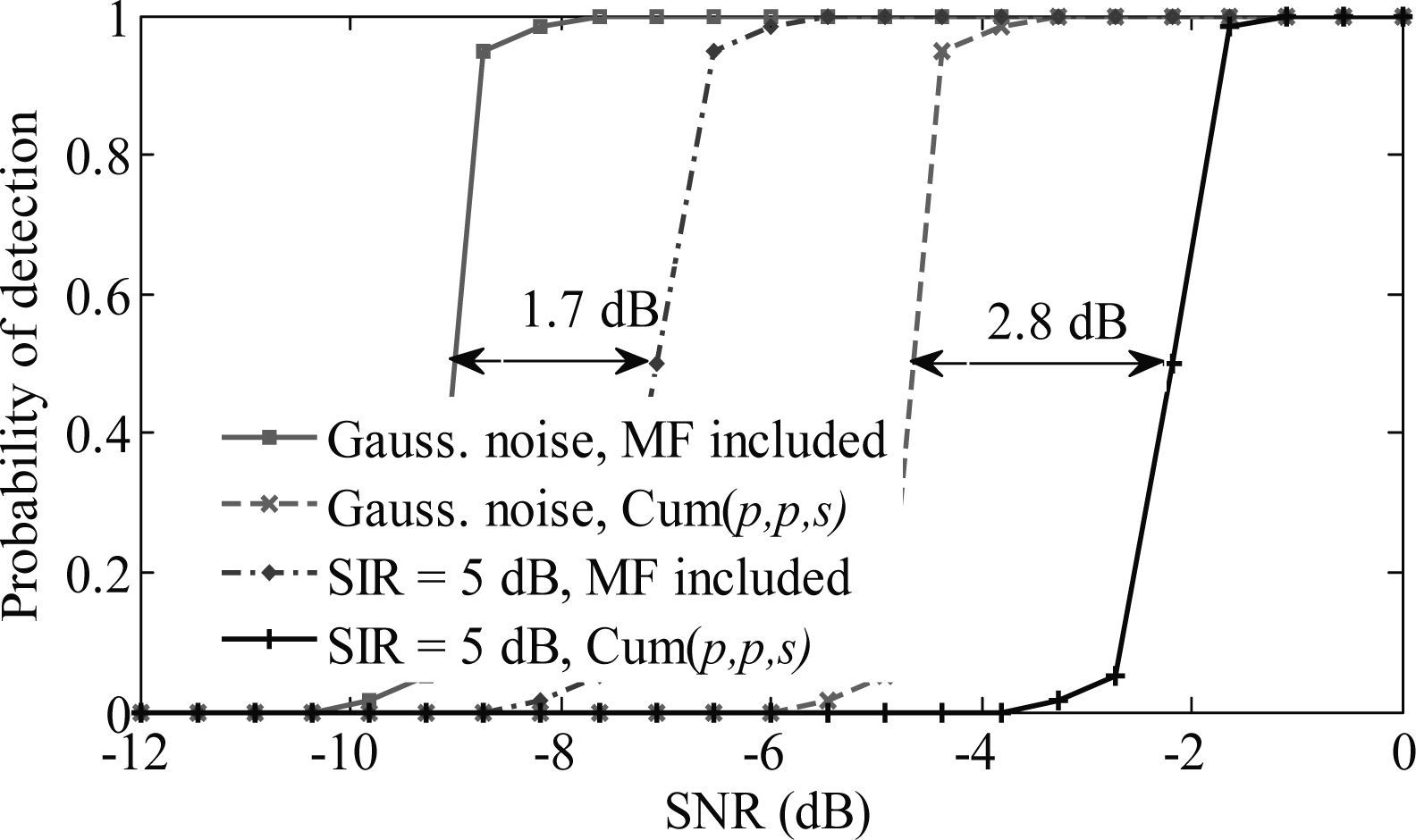
Preamble detection in non-Gaussian noise

The energy detection of the preamble sequence is not optimal when non-Gaussian noise is present at the input. On the other hand, the benefit of the preamble detection based on bispectra-based statistics is obtained when larger preamble lengths are used (for example 640 sample points, see Figure 7) and the preamble or its autocorrelation function is characterized by large a skewness. However, the preamble 802.11b and its autocorrelation function have low skewness coefficients, which results in a probability detection equal to 1 at higher SNR (> −9 dB, see Figure 8 for the detector including MF). Notice that the dense level is slightly lower to that obtained by energy detection. Figure 8 also shows changes in desense levels when non-Gaussian noise of power equal −5 dB are added at the input. The reduction in the desense is about 1.7 dB.

Figure 8.

Test statics of the preamble 802.11b (640 sample size) corrupted by Gaussian and non-Gaussian noise; scheme based on a direct third-order cumulant computation and the other is referred to the scheme in Figure 2b.

Other scheme that reduces at some extent the receiver complexity is the one based on cumulant-processing without including the MF at the input and is referred herein to as the third-order cumulant scheme. The input signal is then processed directly by the third-order cumulant processor that stores replicas of the preamble sequence. It is seen in Figure 8 that the third-order cumulant processor behaves poorly due to the low skewness of the preamble in both Gaussian and non-Gaussian noise. The detection level reduced by 2.8 dB when non-Gaussian noise of power equal to −5 dB is added at the input. The results confirm that the preamble autocorrelation function is best detected than the preamble itself, in agreement with (Giannakis & Tsatsanis, 1990).

Conclusions

The radio receivers of wireless systems that employ wideband transmission protocols are susceptible to non-Gaussian interference. In this paper, the detection of wireless preamble sequences in additive Gaussian and non-Gaussian noise is investigated. It is seen that wireless preambles and their autocorrelation functions have significant energy in their polyspectra which can efficiently be detected using the proposed structures. IEEE standard preambles have different skewness coefficients, which leads to different detection performance. Improved preamble detection for the standard 802.11a is observed in wireless synchronization regardless the nature of input noise. For instance; the structure based matched filtering and cumulant-processing improves the receiver desense by approximately 4-dB compared with that obtained by using energy detection. The statistics of the receiver show that the skewness of the preamble becomes higher than the energy of the noise as well as the energy in its third-order spectrum for non-Gaussian noise at the input. On the other hand, the preamble of the standard 802.11b and its correlation function has lower skewness coefficient which results in lower performance when Gaussian noise only is present at the input. For both preambles, an increase of the sample size leads to improve desense levels. Statistically, the bispectra estimation shows convergence within the length of standard synchronization sequences which could be beneficial in the development of algorithms with multiple wireless systems discrimination. The structures proposed in this paper form a basis for improving radio receiver immunity against stationary interference.

Citation for this article:

Chicago citation style

Aguilar-Torrentera, Jorge. Wireless synchronization preamble detection scheme using bispectra-based statistics in the presence of stationary noise. Ingeniería Investigación y Tecnología, XVI, 03 (2015): 383-390.

ISO 690 citation style

Aguilar-Torrentera J. Wireless synchronization preamble detection scheme using bispectra-based statistics in the presence of stationary noise. Ingeniería Investigación y Tecnología, volume XVI (issue 3), July-September 2015: 383-390.