This paper analyzes the literature produced on Bradford's Law from 1934 to June 2012. The study compiled 936 documents produced by 1,123 authors, working in sixteen languages to communicate the results of their research, with English the leading language, followed by Chinese, Spanish and Portuguese. The study reveals the fifteen most productive authors, all of which work in English in both academic journals and conference settings. This literature is growing exponentially (R2=0.974), at a rate of 5.4% per year and doubling in size every 13.2 years.
Se analiza la literatura producida sobre la ley de Bradford desde 1934 hasta junio del 2012. Se encontraron 936 documentos producidos por 1 123 autores diferentes. Estos autores utilizaron 16 idiomas para comunicar los resultados de sus investigaciones; el inglés fue el idioma dominante, seguido del chino, español y portugués. Se identificó también a 15 autores como los más productivos, quienes publican sus investigaciones en inglés, en la forma de artículos en revistas académicas, y las presentan en congresos del área. Esta literatura crece de forma exponencial (R2=0.974), a una tasa de 5.4% al año y duplica su tamaño cada 13.2 años.
The term “literature” refers to the subset of documents published on a given topic. Generally these documents are scientific modalities such as journal papers, book chapters, papers read at conferences, pamphlets, monographs, books, academic theses and grey literature, etc. The term can convey diverse levels of granularity; for example, it may refer to a body of general literature, as in the literature on chemistry or of the field of chemistry; and it can also be employed to specify a narrower range of documents, such as the literature on the greenhouse effect. What is held as knowledge in a given scientific field, however, extends beyond the formal literature; and even though most of this knowledge issues from this literature “we must look at knowledge of any given field as consisting of three layers. First, there is original research carried out by researchers that is subsequently published. Then there are the systematic or conceptual reviews that come in response to such research, but which do not move beyond the confines of that body of literature. Finally, there are perceptions, conclusions and interpretations made by people in informal conversations that also become part of the tradition of the field” (Kennedy, 2007: 141). The published literature is collected and indexed in specialized bibliographic data bases; but as knowledge grows so does the literature explicating it. Therefore, one must pay close attention to the annual growth rate and rate of duplication.
Bradford's Law was proposed in 1934. Since that time a vast amount of literature has been produced; but, to the best of this author's knowledge, only biographies (Quemel et al., 1980) and literature reviews (Lockett, 1989) have been published that do not attempt any analysis of the growth of literature on this particular bibliometric technique. As such, the purpose of this paper is to analyze the growth of literature on Bradford's Law published since 1934 to June 2012, a span of 79 years, during which time we expect the published literature to expand and grow. This mathematical model in conjunction with others, i.e., Lotka's Law, Zipt's Law, the 80/20 rule, literature growth and obsolescence models, citation analysis, etc., make up the organic structure of the field of Bibliometrics (Urbizagástegui, 2007).
Bradford (1934) hypothesized that most of the papers on a specialized topic are in fact published by a limited subset of specialized journals and some journals existing on the fringes of the topic area and many others with a wider, more general editorial scope. As such, the subset of journals in a given field would act as a family with successive generations of diminishing parentage, in which each succeeding generation is more numerous that the preceding one. The practical application of Bradford's Law provides mechanisms for selecting the periodicals that are not only the most productive, but also most relevant for covering a given area of knowledge. When the literature of a given field is studied through the lens of citations or internal use in libraries and information centers, it also provides mechanisms for discard of seldom used magazines and books, and for assigning low demand bibliographic materials to regional storage and depositories. The growth of this literature is the focus of this paper. The research questions to answer are as follows: What kinds of documents are published in this topic area? Who are the most productive authors writing on Bradford's Law? What types of documents do these authors produce and in what languages? Is this topic area still in a growth phase or has it reached its saturation point? If it is still growing, what is its duplication rate?
To achieve the proposed objective, this paper is organized in six sections. The first section presents an introduction to the topic, detailing the problem and posing the research questions. The second section provides the theoretical framework of studies of literature growth. The third section describes the methodology used to apply the chosen growth model, emphasizing how data is collected and measured. The fourth section reports results, and the fifth section offers conclusions and further discussion. |The sixth and final section contains the bibliography.
THEORETICAL FRAMEWORKThe foundation of knowledge in any scientific field is contained in its published literature. As such, the quantitative measure of its volume constitutes the size and structure of this literature, since any new information and contribution springs forth from earlier publications (Braun, Schubert and Kostoff, 2000). For this reason, one of the most obvious features of scientific practice has always been the growth of the published scientific literature. This literature presents new problems, new methods for approaching research problems, novel points of view or applications in diverse lines of research or knowledge sub-fields.
The growth of literature is expressed in terms of an estimated average rate, using statistical models to analyze data gathered chronologically as per year of publication. Early examinations of this area focused only on the form of growth, but did not provide estimations of growth rate. For example, Houzeau and Lancaster (1880, cited by Jaschek, 1989: 164) compiled the total number of papers written on astronomy over a period of 170 years, showing that this literature grew exponentially. Tamiya (1931) studied literature on aspergillus fungi, showing that it grew logistically. Wilson and Fred (1935) studied literature on nitrogen fixation in plants and verified that this literature grew along a logistical curve. For Crane (1944) literature in the field of chemistry grew exponentially, and the same was found to be true in the field of biochemistry by Schwartz and Powers (1963).
These early studies attained methodological consistency only after 1951, when Price (1951) launched a series of studies on the growth of science as gauged by published scientific literature. This author held that: “the number of scientific papers published each year can serve as an approximate indicator of the activity deployed in any general or specialized field of research” (Price, 1951: 86). He performed a statistical analysis of the Physics Abstracts, which cover a broad range of the general field of physics; and the theory of determinants and matrices, a specialized field of mathematics, showing that in normal times a general field such as physics exhibits nearly perfect exponential growth; while a highly specialized field such as matrices and determinants exhibits exponential growth only to a certain point, after which growth patterns become linear. The literature in both cases doubled every 10 or 11 years.
At a later time, Price (1956) asserted that a yearly count of the number of abstracts in Physical Abstracts and Chemical Abstracts would provide a gauge of the number of articles published in these fields over a given period. These data serve to posit three important conclusions: 1) almost all growth curves exhibit the same tendency; 2) growth is exponential, and 3) the constant of the exponential curve is capable of doubling in size every 10 to 15 years. It would seem that the exponential law governs the size of science. Moreover, “data sets that go back as far as the year 1700 or earlier clearly show that the ‘size’ of science has been growing in this way over the entire period of the scientific revolution and the age of Newton” (Price, 1956: 518). Conrad (1957) studied the growth of literature in the field of biology by examining the Biological Abstracts, finding the literature in this field exhibits exponential growth. In this way he projected the 348,000 papers in this field by the year 2010. Strong and Benfey (1960) performed a study of the growth of literature in the field of chemistry, examining Chemical Abstracts and the Beilstein Handbuch der Organischen Chemie, showing that this literature doubles approximately every 13 years.
In 1963, Price published a paper on the growth of literature in the field of Physics using a count of the abstracts in Physical Abstracts from 1900 to 1950. Price proved that the literature in the field of physics grows exponentially, doubling every 12 years. May (1966) studied the growth of mathematics literature on the basis of the Jahrbuch über die Fortschritte der Mathematik from 1868 to 1940, and the Mathematical Reviews from 1941 to 1965. This study showed that the number of published papers grew from 800 to 13,000, with a mean growth of 2.5% per year and doubling period of about 28 years and quadrupling approximately every one-hundred years. Stoddart (1967) studied the growth of the number of journals and associations in the field of geography, finding an exponential growth rate for journals and a doubling period of 30 years. He also found that associations also grow exponentially, doubling every 22 years.
Menard (1971) studied the literature of several sub-fields of geology, finding that the literature on vertebrate paleontology grew slowly until the end of the eighteenth century and thereafter began to grow exponentially at a doubling time of 15 years. Brookes (1973) asserted that in light of the number of articles published each year, the literature produced in most scientific fields tends to exhibit exponential growth, doubling every 10 years. After these times, it is commonly held that “in the field of science, contributions accumulate like successive rows of bricks in a wall. Each researchers adds his brick to the wall in an orderly way that at least in theory, shall remain in place as an intellectual edifice built from abilities and artifices standing upon foundational ideas and extending upwards to the edge of research knowledge” (Price, 1975: 162). To exemplify this, Price states that “[...] the number of journals has grown exponentially rather than linearly. Instead of there being an exact number of new journals each year, the number doubles over the period of several years. This doubling time is a constant of about 15 years, which is a power of 10 in 50 years and factor of one thousand over a century and a half” (Price, 1975: 169). According to Price (1975: 169), this “exponential law is the mathematical consequence of having an amount that increases in such a way that the larger the number the faster the rate of growth”; so much so that the “exponential growth law found for the number of scientific journals is also obeyed by the real number of scientific papers in those journals” (Price, 1975: 170).
Price illustrates the study of the growth of publications, and insists that “it is remarkable that since 1918 to date the total number of papers in the field of physics recorded in abstracts [...] has accurately followed an exponential growth curve without variance of more than 1% of the total. There are now nearly 180,000 papers recorded in Physics Abstracts, and the number has doubled at a rate even faster than every fifteen years” (Price, 1975: 171). In view of this type of growth, one can clearly discern the following phases: first there are the precursors; then constant exponential growth, followed by a decline to linear growth, when no new labor force enters the field. Finally, we observe the collapse of the field, a when few papers are produced, or alternatively a rebirth when the field's contents and operational modalities are redefined” (Price, 1975: 173).
Following up on the work of Price (1951, 1956, 1963, 1975), there have been many studies of the literature of diverse areas of knowledge. For example, Hall (1989) found that the literature of the field of geology doubled every eight years, but between 1945 and 1970 it had doubled every six years. Urbizagástegui and Lane-Urbizagástegui (2008) studied the literature on medicinal plants of Peru, finding that this body of literature grew exponentially, with a yearly growth rate of 6.5%, doubling every 11.3 years. Urbizagástegui (2009) studied the growth of literature on Lotka's Law and found that it has an annual growth rate of 7.5% per year, doubling every 9.6 years. Biglu (2009) studied the relationship between patents and scientific publications in the field of medicine on the basis of the Medline index. All of the publication indexed with the term “patents” in Medline between 1965 and 2005 were extracted and analyzed. The study shows exponential growth of the literature at an annual growth rate of 3.1% and doubling time of 22.5 years. Urbizagástegui and Lane-Urbizagástegui (2007) again analyzed the literature on plant dyes and found that it grew at an annual rate of 3.4%, doubling in a period of 20.7 years. Finally, Restrepo (2011) studied the literature produced by historians working in the Colegio de México, showing this output obeys an exponential growth pattern, with an annual growth rate of 7.1% and doubling time of 10.1 years.
MATERIALS AND METHODSThe data examined consists of each paper published in academic journals, chapters of books and papers read at conferences that address Bradford's Law or which employ this model in the analysis of any discipline or sub-field. Books, thesis, monographs and gray literature are not included in the data set, since such literature is not indexed in the bibliographic data bases used in this research. The period of the data set is 1934 to June of 2012. To collect the data, the following search terms were used: “Bradford's law”, “Bradford's distribution”, “Bradford Scattering law”, “Bradford type distribution”, “Bradford analysis”, “Bradford curve”, “Bradford zones” and “Bradford core journals”. These terms were entered using diverse idiomatic forms in English, French, German, Portuguese and Spanish, etc. The terms were entered into the search engines for titles, descriptors and abstracts of the following bibliographic data bases: Library Literature & Information Science Full Text, Library and Information Science Abstract (LISA), Library, Information Science & Technology Abstracts (LISA), Agrícola, Biosis, CAB Abstracts, Medline, Anthropological Literature, Anthropological Index, Anthropology Plus, WorldCat, HAPI, ArticleFirst, Science Citation Expanded Index, Web of Science, Scopus, Elsevier, JSTOR and another 120 data bases available in the University of California, Riverside, including the Spanish-language data bases ISOC, ICYT and Dialnet. The research also included searches of Latin American data bases such INFOBILA in Mexico and LICI of the Instituto Brasileiro de Informação em Ciência e Tecnologia (ibict); Chinese data bases such as China Academic Journals via EastView Online Services, and Japanese data bases via: Citation Information by National Institute of Informatics (cinii), Japanese Scholarly & Academic Information; the Russian Academy of Sciences Bibliographies, as well as German and Arabic bibliographic sources. Researchers also made visits to repositories such as Scielo Brasil, Scielo México, Scielo Venezuela, Scielo Colombia, Scielo Chile, Scielo Argentina and Scielo Bolivia, among others.
The citations identified were loaded to EndNote x5 in order to create a data base specific to this matter. Thereafter, researchers read the details of each of the documents identified in the search, paying special attention to each citation found. Any reference to Bradford's Law was run against the data base and, if not already identified, duly included. Duplicate citations were eliminated, so that each citation appeared only once. This close reading served to produce a bibliography of 936 citations produced between 1934 and June 2012, which include papers published in journals, book chapters, papers read at conferences and other venues. This body of work constitutes the universe under study. The period covered by the data gathered is sufficiently long to expect a growth pattern to be discernible.
It should be noted, however, that without knowing the shape of literature growth point cloud it is difficult to present a measure of the data collected. It is impossible to assert beforehand whether this literature will exhibit linear or exponential growth or by power law or as per a Gompertz curve, etc. Nonetheless, researchers expect to find exponential growth, because it is the most common pattern found in studies of literature production over long periods. Exponential growth represents an increase in the population in a fixed proportion within each unit of time. It is expressed in percentages, with a constant rate of growth and unlimited ceiling. The model not only provides a mean growth rate, but also a doubling time. Generally, exponential curves first exhibit a concave shape. The function is represented mathematically as follows:
C(t)=CO eat
In accord with Egghe and Ravichandra Rao (1992), the function can be written as follows:
C(t)=c gt
Where,
c>0, g>1, y t ≥ 0.
The study of the growth of literature entails a postulation of the relationship between time measured in years (the independent variable) and the accrued volume of the literature measured in units produced (the dependent variable). This bivariate relationship, it is assumed, can be modeled statistically. To assess the model's fit, a dispersion cloud is plotted on the basis of the observed data. This allows one to discern whether there is any regularity in the frequency distribution observed. When this regularity matches up with curve shown in the graph, one attempts to adjust the curve to the point cloud through nonlinear regression. In an exponential growth distribution, one attempts to show that the accrued production volume of documents in accord with the years t arises from an exponential distribution, i.e., the probability of a frequency in the sample being equally probable for all frequencies in the same situation.
The calculation of the parameters of the exponential distribution was performed by determining the nonlinear regression using the spss 17.0 statistical package for Windows. Since a high correlation between the dependent and independent variables is expected, this correlation was examined with a determination correlation (R2) and significance level of 0.01.
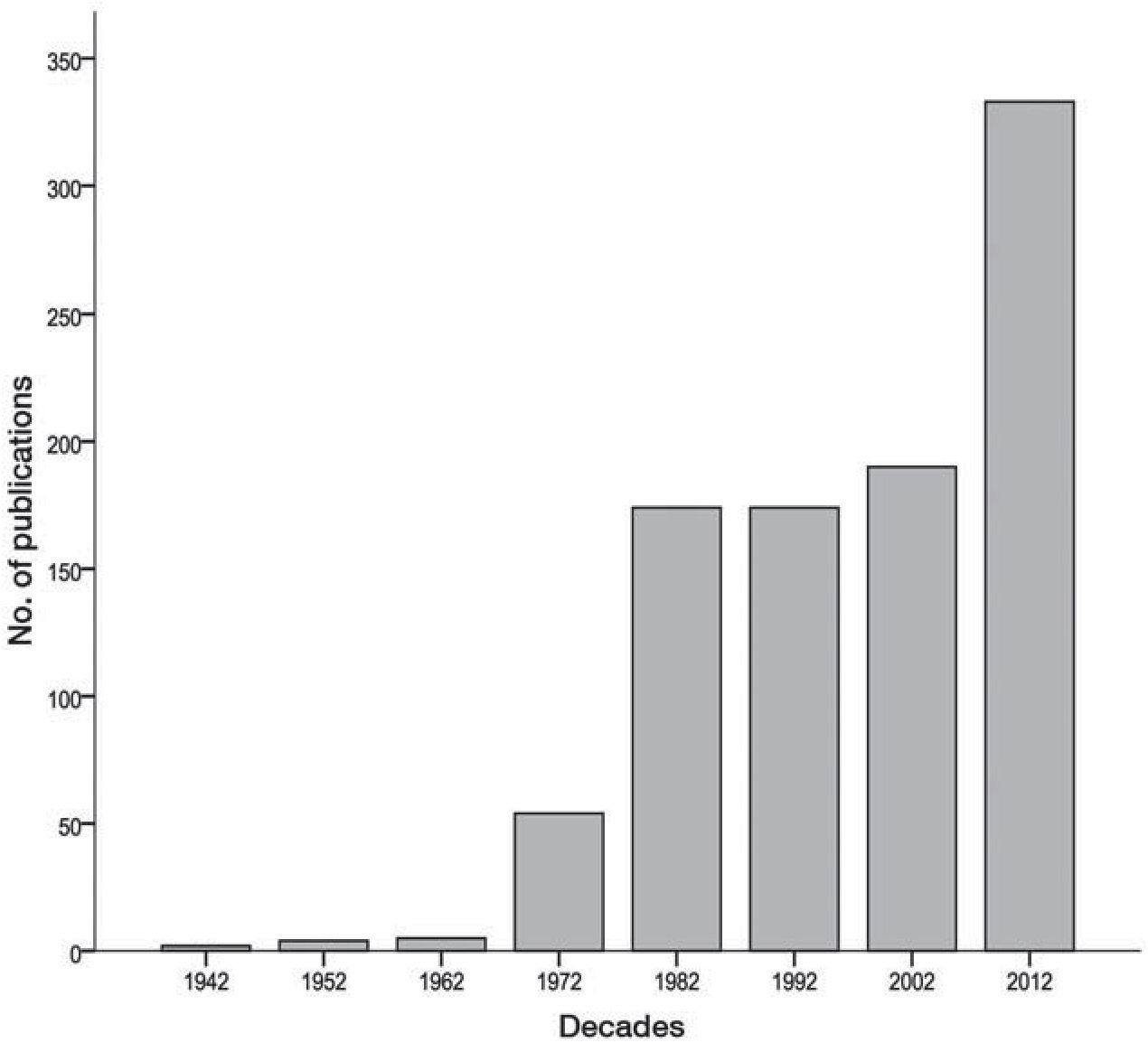
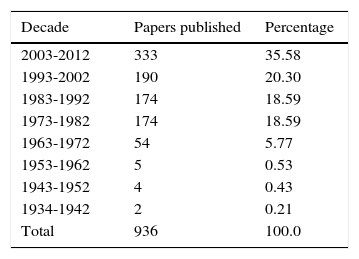
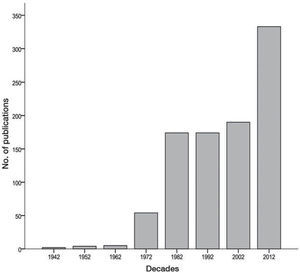
RESULTSNine-hundred and thirty six papers by 1,123 different authors were found. Table 1 shows the number of documents published on Bradford's Law since 1934, when Bradford first proposed his theory, to 2012. The volume of documents was grouped by decades.
The literature published on Bradford's Law has growth steadily decade by decade, moving from 0.2% of the total in the first decade under study (1934-1942) to 19% in the fifth decade (1973-1982), and on to 36% of the total in the last decade (2003-2012). The range of distribution moves from one paper at the lowest end to 52 publications at the highest. The mean number of papers published is 11.85±12 papers per year, with a standard deviation of 1.4 papers. The median is 13 papers with a variance of 155.6 documents published and standard deviation of 12.5 papers.
Figure 1 is a bar graph showing this growth by decade. After the decade of 1934-1942, the literature published grows gradually until it reaches its maximum volume in the decade of 2003-2012. The growth gradient is easily apparent at first glance and does not require further emphasis. The years expressed in decades span from the next consecutive year to the next year shown in the graph. For example, 1972 means the decade spans from 1963 to 1972.
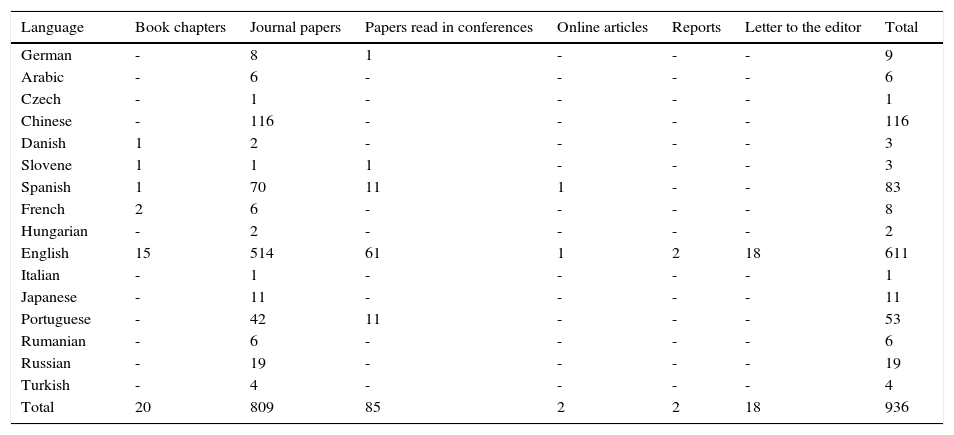
The 1,123 authors writing on Bradford's Law identified in this study published in 16 languages. Table 2 shows that publications in English constituted 65% of the output, with 35% of the output coming in other languages. Papers published in Chinese comprised 12% of the output, followed by those in Spanish at 9.0%, Portuguese at 6.0% and Russian with 2.0%. Japanese- and German-language papers each accounted for 1.0%, while French-and Arabic-language publication came in a 0.8% and 0.6%, respectfully. The remainder of the output was comprised of papers in Turkish (0.4%), Danish (0.3%), Slovene (0.3%) and Czech and Italian each with 0.1% of the total output under study. This is not a surprising finding, since Price (1971) estimated that fully half of all scientific and philosophical output in the world is published in English.
Types of documents publish by language.
| Language | Book chapters | Journal papers | Papers read in conferences | Online articles | Reports | Letter to the editor | Total |
|---|---|---|---|---|---|---|---|
| German | - | 8 | 1 | - | - | - | 9 |
| Arabic | - | 6 | - | - | - | - | 6 |
| Czech | - | 1 | - | - | - | - | 1 |
| Chinese | - | 116 | - | - | - | - | 116 |
| Danish | 1 | 2 | - | - | - | - | 3 |
| Slovene | 1 | 1 | 1 | - | - | - | 3 |
| Spanish | 1 | 70 | 11 | 1 | - | - | 83 |
| French | 2 | 6 | - | - | - | - | 8 |
| Hungarian | - | 2 | - | - | - | - | 2 |
| English | 15 | 514 | 61 | 1 | 2 | 18 | 611 |
| Italian | - | 1 | - | - | - | - | 1 |
| Japanese | - | 11 | - | - | - | - | 11 |
| Portuguese | - | 42 | 11 | - | - | - | 53 |
| Rumanian | - | 6 | - | - | - | - | 6 |
| Russian | - | 19 | - | - | - | - | 19 |
| Turkish | - | 4 | - | - | - | - | 4 |
| Total | 20 | 809 | 85 | 2 | 2 | 18 | 936 |
The most prevalent form of publication is the journal article comprising 86% of the output total across all languages. This is followed by papers read at conferences at 9.0% and book chapters at 2.0%. These three modalities represent 98% of the total output under study up to 2012. All types of works are published in English, with 84% all English-language publications in this modality, while papers read at conferences comprise 10%, and book chapters 2.5%. Spanish- and Portuguese-language publications follow a similar pattern. For all other languages the prevalent modality of publication is the journal article. Interestingly, the universe of publications contains letters to the editor only in English.
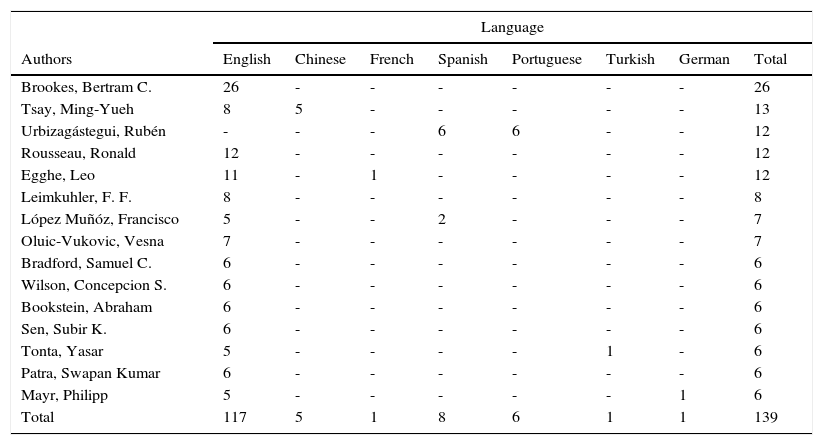
Table 3 shows the most productive authors by language of publication. Most of these authors publish in English. Of the 15 most productive authors, Ming-Yueh Tsay also publishes in his native Chinese. The Spanish researcher Francisco López Muñoz also publishes in English, most likely in the interest of gaining a broader readership (Miranda, 1982, 1998). Yasar Tonta of Turkey prefers to publish in English as does the German researcher Philipp Mayr. Resisting the English language bias in science and technology, Urbizagástegui, publishes in Portuguese and Spanish. Most of these authors publish papers in journals and present research results in specialized conferences and congresses.
Most productive authors by language.
| Language | ||||||||
|---|---|---|---|---|---|---|---|---|
| Authors | English | Chinese | French | Spanish | Portuguese | Turkish | German | Total |
| Brookes, Bertram C. | 26 | - | - | - | - | - | - | 26 |
| Tsay, Ming-Yueh | 8 | 5 | - | - | - | - | - | 13 |
| Urbizagástegui, Rubén | - | - | - | 6 | 6 | - | - | 12 |
| Rousseau, Ronald | 12 | - | - | - | - | - | - | 12 |
| Egghe, Leo | 11 | - | 1 | - | - | - | - | 12 |
| Leimkuhler, F. F. | 8 | - | - | - | - | - | - | 8 |
| López Muñóz, Francisco | 5 | - | - | 2 | - | - | - | 7 |
| Oluic-Vukovic, Vesna | 7 | - | - | - | - | - | - | 7 |
| Bradford, Samuel C. | 6 | - | - | - | - | - | - | 6 |
| Wilson, Concepcion S. | 6 | - | - | - | - | - | - | 6 |
| Bookstein, Abraham | 6 | - | - | - | - | - | - | 6 |
| Sen, Subir K. | 6 | - | - | - | - | - | - | 6 |
| Tonta, Yasar | 5 | - | - | - | - | 1 | - | 6 |
| Patra, Swapan Kumar | 6 | - | - | - | - | - | - | 6 |
| Mayr, Philipp | 5 | - | - | - | - | - | 1 | 6 |
| Total | 117 | 5 | 1 | 8 | 6 | 1 | 1 | 139 |
One author alone (Brookes) sent six letters to the editor of several academic journals in which he addressed aspects of Bradford's Law. Brookes was a great advocate of Bibliometrics and especially Bradford's Law, publishing 20 academic papers in journals on the subject as well as lecturing in congresses (see Table 4).
Types of publications of the most productive authors.
| Author | Journal paper | Presentation in congress | Book chapter | Letters to the editor | Total |
|---|---|---|---|---|---|
| Brookes, Bertram C. | 20 | 1 | - | 5 | 26 |
| Tsay, Ming-Yueh | 13 | - | - | - | 13 |
| Urbizagástegui, Rubén | 10 | 2 | - | - | 12 |
| Rousseau, Ronald | 12 | - | - | - | 12 |
| Egghe, Leo | 10 | 1 | 1 | - | 12 |
| Leimkuhler, Ferdinand F. | 8 | - | - | - | 8 |
| López Muñóz, Francisco | 6 | - | 1 | - | 7 |
| Oluic-Vukovic, Vesna | 6 | - | 1 | - | 7 |
| Bradford, Samuel Clement | 2 | 3 | 1 | - | 6 |
| Wilson, Concepcion S. | 4 | 1 | 1 | - | 6 |
| Bookstein, Abraham | 5 | 1 | - | - | 6 |
| Sen, Subir K. | 6 | - | - | - | 6 |
| Tonta, Yasar | 4 | 2 | - | - | 6 |
| Patra, Swapan Kumar | 6 | - | - | - | 6 |
| Mayr, Philipp | 5 | 1 | - | - | 6 |
| Total | 117 | 12 | 5 | 5 | 139 |
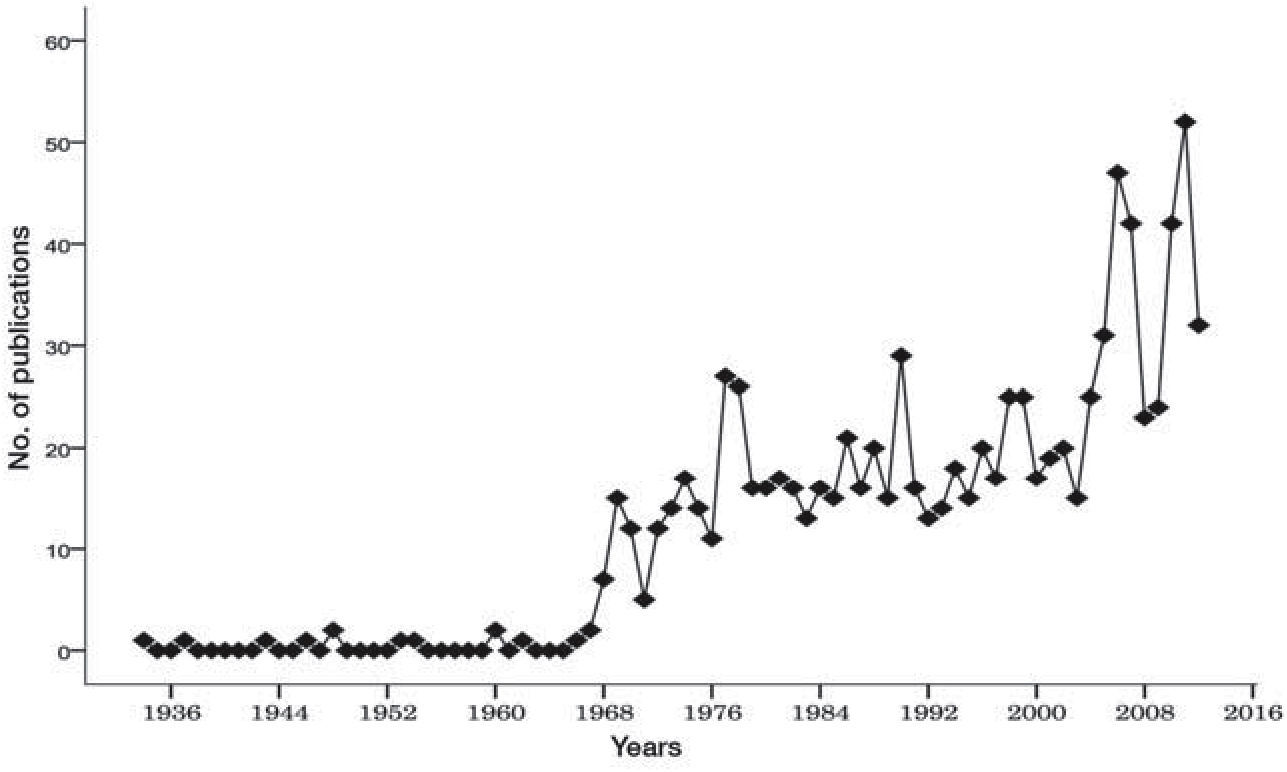
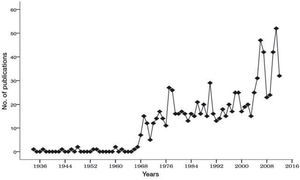
Figure 2 shows the shape of the growth of literature on Bradford's Law. Initially the curve is concave, with the point cloud increasing steadily until 2012, though there are minor oscillations between 1979-1980 and 1985-2008. One can observe that publications on Bradford's Law up are quite flat to 1968 after which steady growth begins.
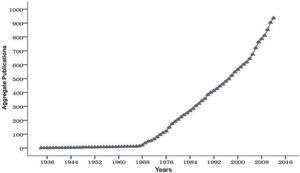
Bradford's model of dispersion of papers in academic journals postulated in 1934 and presented in the 14th aslib conference in 1937 was a unique approach to the subject. He also published articles in the Proceedings of the British Society for International Bibliography (Bradford, 1943, 1946) with only modest impact. In 1948 he includes the Chapter “Documentary Chaos” in his book Documentation (Bradford, 1948). Shortly thereafter, Vickery (1948) publishes an article that is critical of Bradford's mathematical approach. Five years later, Stevens (1953) publishes and paper citing Vickery (1948) and Bradford (1948) in which he explains the features of dispersion of specialized literature. In the early 1960s, three references to Bradford appear, i.e., Fourmont and Kervégant (1960), Kendall (1960) and Cole (1962). Every year from 1966 and until 2012 an average of 12 papers per year employing the strategies proposed by Bradford (1934, 1948) were found in the sample under study. It is important to remember that 1961 saw the publication of Science Since Babylon (Price, 1961) and in 1963 Little Science, Big Science (Price, 1963) was published. These works called attention to the possibilities opened up by analyzing the literature published in the field of science, while establishing the foundations of Bibliometrics and the systematic study of the sciences. Both books comment on the growth of literature and the universe of scientists, especially in the fields of physics and chemistry. At the end of the decade, Pritchard (1969) coins the terms “bibliometrics.” From that moment on, bibliometrics is considered a discipline within Information Science, and the literature addressing the subject begins to grow constantly. In this way, Bradford's Law becomes a key element in the practice of bibliometrics. Figure 3 shows the distribution of the data by year.
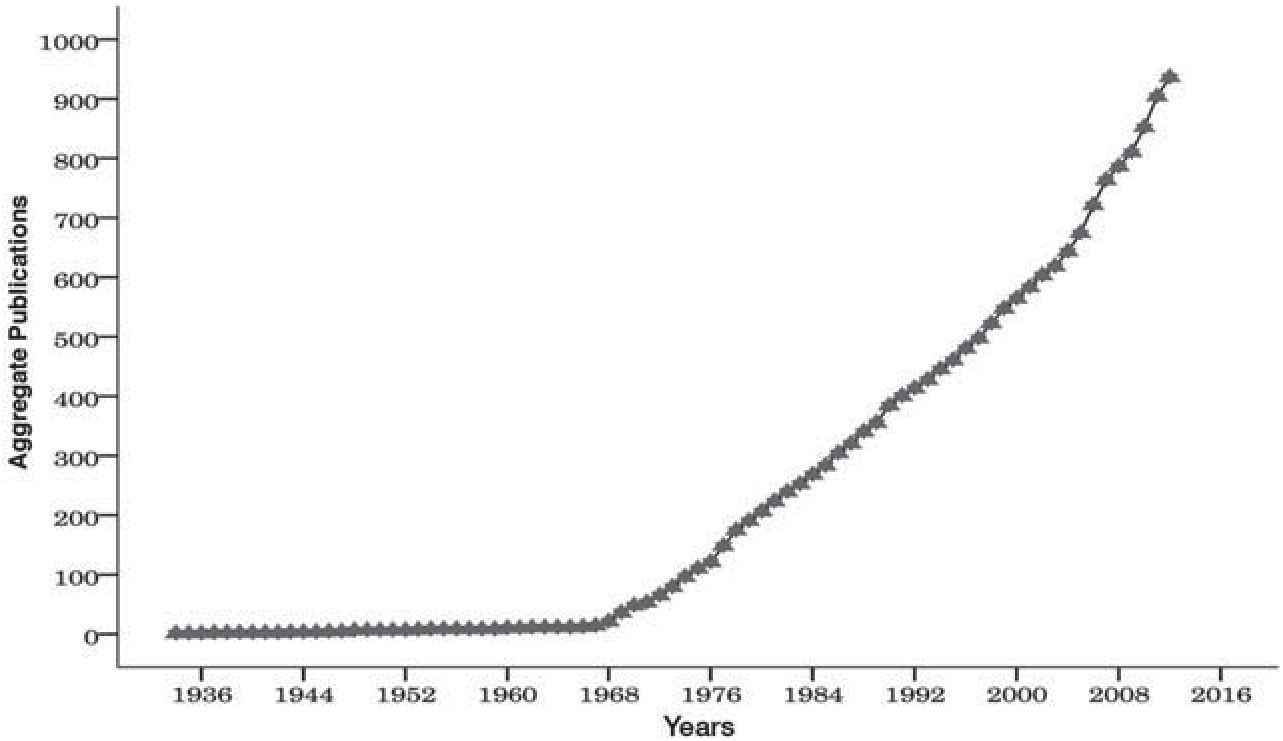
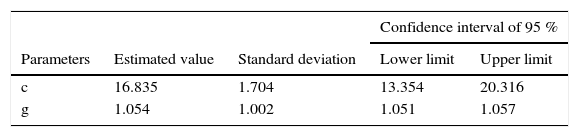
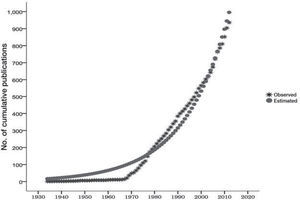
These cumulative data were used to estimate the growth and doubling rate of the literature on Bradford's Law. This body of literature stayed stable until 1968, after which its growth accelerated, tracing a nearly straight line of growth until 2012. The shape of the dispersion cloud makes it evident that we are observing exponential growth. The nearly straight line indicates that it is continuing to grow and the saturation point is still in the offing. As Price (1975) asserts, a literature may be linear, then become exponential until it reaches a saturation point with a logistical form. This does not appear to be the case for the literature on Bradford's Law, which over the course of 79 years is still growing. Table 5 shows the parameters and values obtained from applying the exponential model using the non-linear regression model.
The value of c came to 16.835, and the value of g was 1.054. Using these known values in the following equation allows one to predict the exponential growth of the literature published on Branford's Law:
C(t)=16.835x1.054t
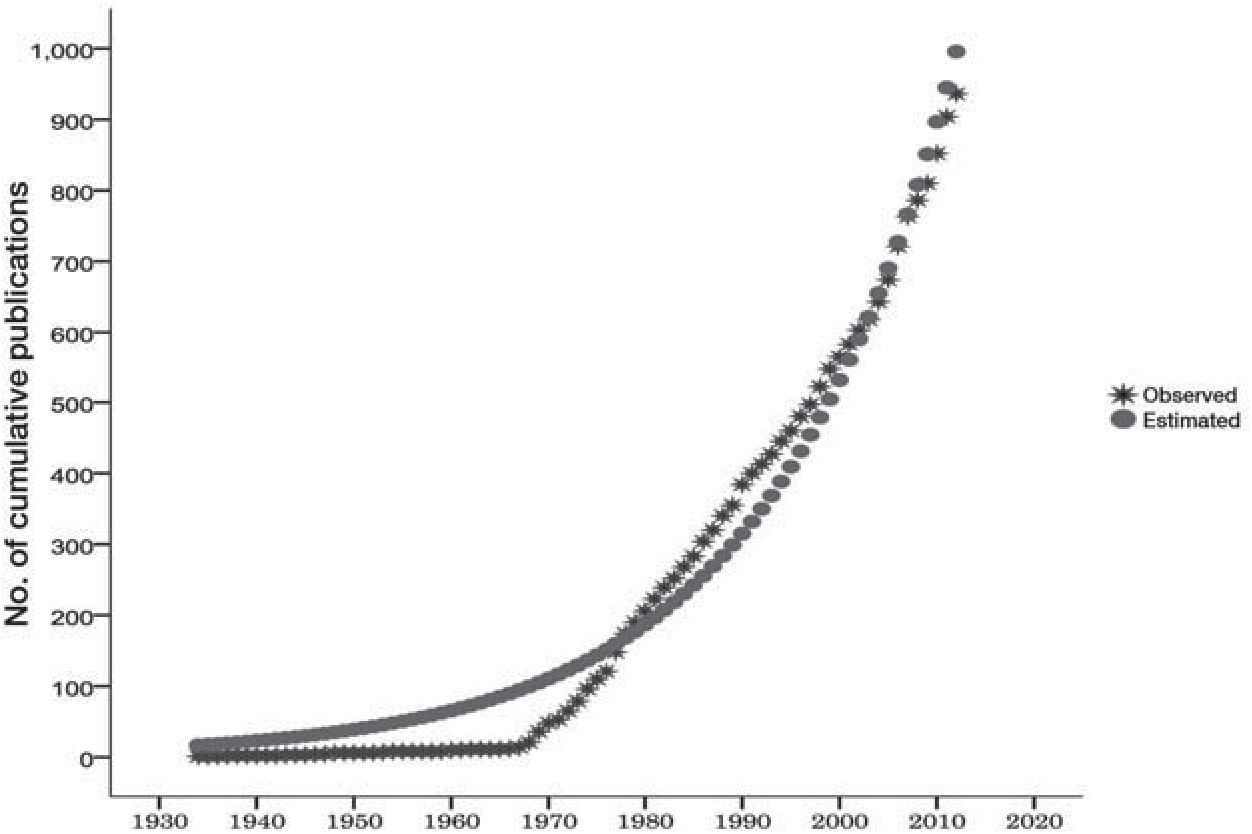
The equation demonstrates that the literature on Bradford's Law since 1934 has grown at a rate of 5.4% annually and its volume doubles every 13.2 years. A graph of these values and the estimated data is provided in Figure 4. It is important to note the proximity of the observed values and the estimate data using the non-linear regression method, where R2 came to 0.974, indicating there is only a 2.6% probability of error in the estimate of the projected values.
DISCUSSION AND CONCLUSIONSThe study of the growth of a body a literature is important because it makes claims on the several kinds of spaces in libraries, i.e., shelves, computer memory, etc. Space is synonymous, of course, with financial resources, overhead and capital investment. The growth of literature also has sociological implications regarding matters of access to information (Egghe, 1994). The study of such matters is also important because it serves to make projections. “A simple way to compare diverse exponential growth rates is to look at doubling times” (Braun, Lyon and Bujdosó, 1977: 682A) and annual growth rates. It is also common to find “the growth of an exponential function described in terms of the doubling period, the annual growth rate or the exponential index” (Gilbert and Woolgar, 1974: 280).
Over the period under study, we observed that the growth of the body of literature on Bradford's Law fits an exponential growth model, with an annual growth rate of 5.4% and doubling period of 13.2 years. This annual growth rate is very near to the 5.5% observed by Holt and Schrank (1968) in the field of economy and the 6.5% rate observed by Urbizagástegui and Lane-Urbizagástegui (2008) in the field of medicinal plants in Peru. The doubling period of this literature was slightly more than the 10-year period observed by Brookes (1973) for the general body of science literature and somewhat below the 15 year doubling period observed by Menard (1971) in the field of geology. Moreover it falls within the range of 11 to 15 years found by Price (1951, 1956) for physics and chemistry.
These results contradict Egghe and Ravichandra Rao (1992), who asserted that the doubling time in social sciences is less than that of pure and applied sciences. If this were the case, bibliometrics, specifically the Branford's Law sub-discipline, would be much closer to the bibliometrics of pure and applied sciences than to bibliometrics of social sciences and humanities. It would seems that the growth rate of a body of literature is not a function of the field, whether pure or social science, but rather a function of the intensity of research and number of researchers working in a given field. Where there are more researchers, there is a greater propensity for a larger volume of literature. The converse is also true. If a given field of research has 10,000 researchers and each one publishes one paper per year, this means 10,000 papers are added to the body of literature every year. On the other hand, if a field has only 100 researcher publishing one paper per year, only 100 papers are accrued to the body of literature. As such, the duplication period achieved by 10,000 researchers shall be much shorter than that attained by the 100 researchers in the other hypothetical field. This comportment has been observed by Menard (1971) in the field of geology, where he found that the several sub-disciplines of geology grew at different rates, and that the best growth predictors were achieved when the relations between these sub-disciplines were closely observed.
This research found 1,123 authors writing in sixteen languages. Fully 65% of the research was published in English, with the balance of 35% coming in other languages, confirming that English is the preferred language in the field of bibliometrics. It is important to keep in mind that: “the English language can slant the direction of social sciences in the same way the front page of a newspaper skews the news. Slanting in this sense can take the form of emphasizing some topics to the detriment of others” (Ortiz, 2009). The study also identifies the 15 most productive authors in the field of Bradford's Law, most of which publish only in English.