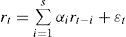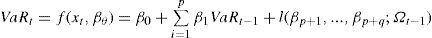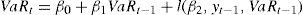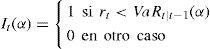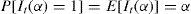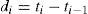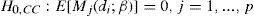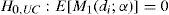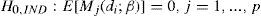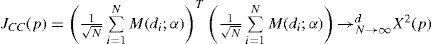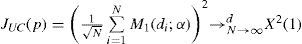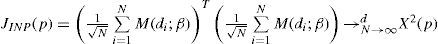En este artículo se analizan tres metodologías para el cálculo del valor en riesgo (var): modelos paramétricos, semiparamétricos y no paramétricos. Con el objetivo de evaluar su validez se eligió un método representativo para cada uno: el egarch para los paramétricos, el caviar para los semiparamétricos y el de simulación histórica para los no paramétricos. Para la validación de estas metodologías se utilizó el método propuesto por Candelon et al. (2011), un backtest basado en el método general de los momentos. Las variables a pronosticar fueron los tipos de cambio de los principales mercados latinoamericanos (Argentina, Brasil, Chile, Colombia, Perú y México) y sus principales índices accionarios. Los resultados muestran que el modelo caviar es el que mejor proyecta el var para los mercados y monedas en los periodos analizados.
El tomar decisiones bajo incertidumbre es un hecho relevante y que frecuentemente está presente en los mercados financieros. Poder tomar estas decisiones con mayor información y conocimiento es fundamental para los diversos agentes inmersos en estos mercados, más aún cuando no es sólo el riesgo la principal variable a evaluar, sino también la rentabilidad.
Por mucho tiempo el riesgo se ha cuantificado a través de una medida de dispersión (desviación estándar o varianza) que caracteriza a la volatilidad de la rentabilidad de un activo. Un defecto de esta medida es no ser capaz de proyectar los riesgos futuros con alguna incertidumbre. En la década de l970 se comienzan a publicar artículos con análisis similares a los que en los años 1980 se formalizan como valor de riesgo (Value at Risk, var). Estos estudios buscaban responder a la necesidad de poder acotar la incertidumbre en la proyección del riesgo y rentabilidad de un activo. Básicamente, esta metodología da la respuesta a las siguientes preguntas: ¿cuánto se puede esperar perder en un día, semana, mes o año dada una cierta confianza o probabilidad?, ¿cuál es el porcentaje del valor de la inversión que está en riesgo?
Se define como la cuantificación, para un determinado nivel de confianza, del monto o porcentaje de pérdida que un activo o portafolio enfrentará en un periodo predefinido de tiempo (Jorion, 1997). Por ende, se puede evaluar cuál es la rentabilidad mínima de un portafolio de inversión para el próximo mes con un grado de confianza de 75%. Así, se encontrará un valor crítico tal que, según los supuestos de entrada al modelo, existe una probabilidad de 75% que se materialice esa rentabilidad o una mayor. La aplicación del var se realiza en inversiones, operaciones bancarias, evaluaciones de proyectos, entre otras. El análisis del tiempo de proyección varía de minutos (caso de datos de alta frecuencia) a años, según sea su aplicación.
En el 2004, el acuerdo de Basilea II permitió a las instituciones financieras formular sus propias metodologías para la administración de riesgos. Por ello, muchas han usado técnicas académicas aceptadas, como la simulación histórica (HS, Historical Simulation), el valor en riesgo condicional autorregresivo (caviar, Conditional Autoregressive Value at Risk), los modelos generalizados de heterocedasticidad condicional autorregresiva (garch, Generalized Autoregressive Conditional Heteroscedasticity), entre otras. En este contexto, se hace importante saber cuál es el mejor modelo según su aplicación y el periodo de análisis, siendo ello lo que busca determinar este artículo.
Para determinar el método más apropiado se realiza un backtest compuesto de tres diferentes pruebas: de cobertura incondicional (uc, Unconditional Coverage), de independencia (ind, Independence) y de cobertura condicional (cc, Conditional Coverage), siguiendo la metodología de Candelon et al. (2011).
El análisis se realiza con el fin de verificar la validez de las distintas familias de metodologías en la valorización del var a lo largo de diversos periodos de tiempo que permitan observar los cambios en la validez de las metodologías respecto a la situación económica global de los mercados, generando evidencia para los mercados acccionarios latinoamericanos que sirva a los agentes que intervienen en la toma de decisiones.
El artículo se compone de cuatro secciones posteriores a la introducción: la revisión de la literatura, donde se han desarrollado los conceptos fundamentales del estudio; la data y las metodologías utilizadas para el análisis de los mercados latinoamericanos; el análisis de los resultados obtenidos, y la deducción de las conclusiones.
Rsevisión de la literaturaEl análisis de riesgo de una inversión es un aspecto fundamental que está presente desde que existen las inversiones. La primera cuantificación intuitiva de lo que se conoce actualmente como var se remonta al trabajo de Leavens (1945), quien desarrolló un ejemplo cuantitativo de las ventajas de la diversificación. Posteriormente, Markowitz (1952) y Roy (1952) proponen de forma independiente unas medidas del actual var asociadas a selección de carteras, optimizando la rentabilidad para un nivel dado de riesgo, con estimaciones que incorporaban covarianzas entre los factores de riesgo a fin de reflejar los efectos de cobertura y diversificación. Markowitz (1952) utilizó una variación sencilla de la rentabilidad, mientras que Roy (1952) empleó un indicador de riesgo que representaba un límite superior a la probabilidad de retorno bruto de la cartera. Posterior-mente, se desarrollan diferentes trabajos teóricos apuntando a la medición del concepto del var sin definirlo necesariamente: Tobin (1958), Treynor (1961), Sharpe (1964), Lintner (1965) y Mossin (1966). Dusak (1973) describió simples mediciones de lo que hoy se conoce como var para carteras de futuros, pero sin abordar el problema de la estacionalidad. Lietaer (1971) describió una medida práctica para los tipos de cambio. Garbade (1986) modeló las mediciones de riesgo con base en la sensibilidad de los bonos respecto a su rendimiento, suponiendo que los valores de la cartera de mercado se distribuían de forma normal. Garbade (1987) extendió su propio trabajo al introducir un esquema que le permitió reasignar una amplia cartera de bonos a una más pequeña, que sólo tuviese a los bonos más representativos, con ello logró desagregar el riesgo de una cartera.
Jorion (1997) formaliza el valor de riego y lo define como la cuantificación con determinado nivel de significancia o incertidumbre del monto o porcentaje de pérdida que un portafolio enfrentará en un periodo predefinido de tiempo; aunque el creador formal del concepto fue Till Guldimann durante su cargo como jefe de investigación global en JP Morgan a fines de la década de 1980.
De acuerdo con Acerbi y Tasche (2002), el var no satisface las propiedad de subaditividad de las medidas de riesgo coherentes para análisis de diversificación de diferentes activos que compongan una cartera de inversión, mientras que Embrechts, McNeil y Straumann (2002) demuestran que el var si cumple dicha propiedad cuando la rentabilidad de los activos cumplen con tener una distribución normal o T-student. Si bien la mayoría de las distribuciones de las rentabilidades de los activos no cumplen esta propiedad, pueden ser transformadas por medio de una expansión de Cornish-Fisher (Favre y Galeano, 2002), que mediente la curtosis y asimetría crea un Z que se asemeja mucho al Z normal.
Engle (1982) plantea los modelos de heterocedasticidad condicional auto-rregresiva (arch, Autoregressive Conditional Heteroscedasticity) originando una nueva familia de modelos que podían calcular la variabilidad de una proyección. Engel se basaba en el origen heterocedástico de los errores de los modelos de predicción e indicaba que estos eran autoregresivos entre sí, pero con el paso del tiempo Bollerslev (1986) y Engle y Bollerslev (1986) extenderían este estudio al generalizar los modelos arch y plantear, de una forma indirecta, un método para calcular el var directamente a través de los modelos garch.
En 1988 el comité de Basilea genera el Acuerdo de Basilea I. Este acuerdo establecía que el capital mínimo que los bancos podían tener era el 8% del total de los activos de riesgo (crédito, mercado y tipo de cambio sumados). Esto habría sido el primer paso para regular el tema del riesgo en los bancos. En 1989, el JP Morgan, por intermediación de su departamento de estudios, y en consideración a los requerimientos del Acuerdo de Basilea I, crea el RiskMetrics®, el cual tiene sus orígenes en el modelo garch de Engle (1982) y Bollerslev (1986), pero con unos parámetros suavizados que le dan mayor importancia de lo que ya se les daba a los datos más recientes.
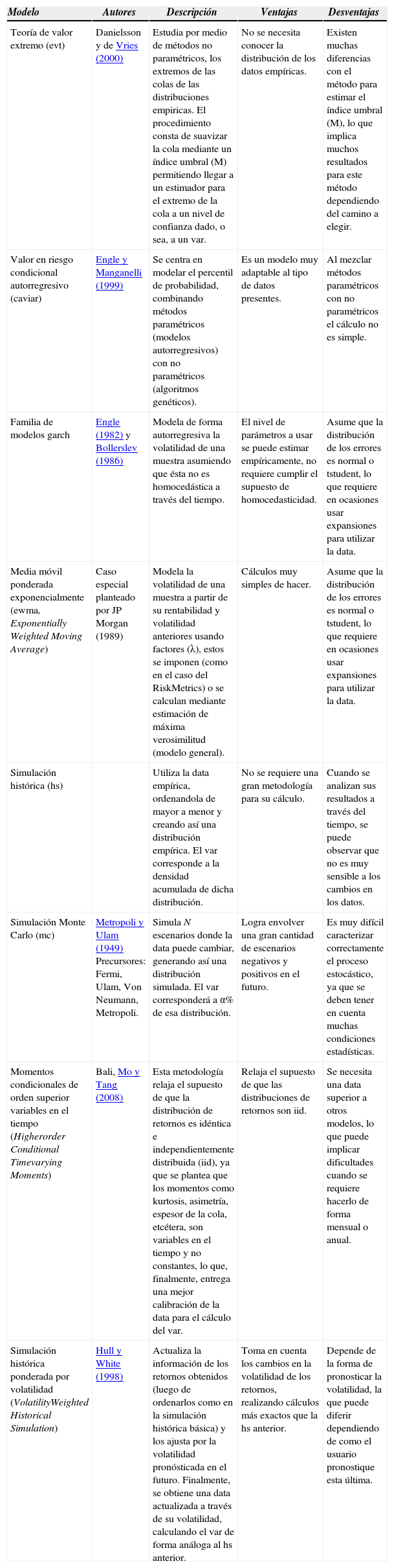
Danielsson y Vries (2000) definen los modelos semiparamétricos, donde se encuentran los modelos de la teoría de valor extremo (evt, Extreme Value Theory) y el caviar, planteado por Engle y Manganelli (1999). La ventaja del caviar es que al centrarse en modelar directamente el percentil de probabilidad en estudio, no se requiere de un conocimiento previo de la distribución de retornos. En el cuadro 1 se complementan otros modelos que se utilizan para calcular el var.
Modelos utilizados para calcular el var
| Modelo | Autores | Descripción | Ventajas | Desventajas |
|---|---|---|---|---|
| Teoría de valor extremo (evt) | Danielsson y de Vries (2000) | Estudia por medio de métodos no paramétricos, los extremos de las colas de las distribuciones empiricas. El procedimiento consta de suavizar la cola mediante un índice umbral (M) permitiendo llegar a un estimador para el extremo de la cola a un nivel de confianza dado, o sea, a un var. | No se necesita conocer la distribución de los datos empíricas. | Existen muchas diferencias con el método para estimar el índice umbral (M), lo que implica muchos resultados para este método dependiendo del camino a elegir. |
| Valor en riesgo condicional autorregresivo (caviar) | Engle y Manganelli (1999) | Se centra en modelar el percentil de probabilidad, combinando métodos paramétricos (modelos autorregresivos) con no paramétricos (algoritmos genéticos). | Es un modelo muy adaptable al tipo de datos presentes. | Al mezclar métodos paramétricos con no paramétricos el cálculo no es simple. |
| Familia de modelos garch | Engle (1982) y Bollerslev (1986) | Modela de forma autorregresiva la volatilidad de una muestra asumiendo que ésta no es homocedástica a través del tiempo. | El nivel de parámetros a usar se puede estimar empíricamente, no requiere cumplir el supuesto de homocedasticidad. | Asume que la distribución de los errores es normal o tstudent, lo que requiere en ocasiones usar expansiones para utilizar la data. |
| Media móvil ponderada exponencialmente (ewma, Exponentially Weighted Moving Average) | Caso especial planteado por JP Morgan (1989) | Modela la volatilidad de una muestra a partir de su rentabilidad y volatilidad anteriores usando factores (λ), estos se imponen (como en el caso del RiskMetrics) o se calculan mediante estimación de máxima verosimilitud (modelo general). | Cálculos muy simples de hacer. | Asume que la distribución de los errores es normal o tstudent, lo que requiere en ocasiones usar expansiones para utilizar la data. |
| Simulación histórica (hs) | Utiliza la data empírica, ordenandola de mayor a menor y creando así una distribución empírica. El var corresponde a la densidad acumulada de dicha distribución. | No se requiere una gran metodología para su cálculo. | Cuando se analizan sus resultados a través del tiempo, se puede observar que no es muy sensible a los cambios en los datos. | |
| Simulación Monte Carlo (mc) | Metropoli y Ulam (1949) Precursores: Fermi, Ulam, Von Neumann, Metropoli. | Simula N escenarios donde la data puede cambiar, generando así una distribución simulada. El var corresponderá a α% de esa distribución. | Logra envolver una gran cantidad de escenarios negativos y positivos en el futuro. | Es muy difícil caracterizar correctamente el proceso estocástico, ya que se deben tener en cuenta muchas condiciones estadísticas. |
| Momentos condicionales de orden superior variables en el tiempo (Higherorder Conditional Timevarying Moments) | Bali, Mo y Tang (2008) | Esta metodología relaja el supuesto de que la distribución de retornos es idéntica e independientemente distribuida (iid), ya que se plantea que los momentos como kurtosis, asimetría, espesor de la cola, etcétera, son variables en el tiempo y no constantes, lo que, finalmente, entrega una mejor calibración de la data para el cálculo del var. | Relaja el supuesto de que las distribuciones de retornos son iid. | Se necesita una data superior a otros modelos, lo que puede implicar dificultades cuando se requiere hacerlo de forma mensual o anual. |
| Simulación histórica ponderada por volatilidad (VolatilityWeighted Historical Simulation) | Hull y White (1998) | Actualiza la información de los retornos obtenidos (luego de ordenarlos como en la simulación histórica básica) y los ajusta por la volatilidad pronósticada en el futuro. Finalmente, se obtiene una data actualizada a través de su volatilidad, calculando el var de forma análoga al hs anterior. | Toma en cuenta los cambios en la volatilidad de los retornos, realizando cálculos más exactos que la hs anterior. | Depende de la forma de pronosticar la volatilidad, la que puede diferir dependiendo de como el usuario pronostique esta última. |
Allen y Singh (2010) aplicaron el caviar para obtener el riesgo del mercado de acciones australiano, mientras que Jeon y Taylor (2012) lo usaron junto a otros modelos para proyectar el riesgo en el S&P500 y DAX30.
So y Yu (2006) analizaron empíricamente los modelos arch en el var mediante los modelos garch, igarch (garch integrado), figarch (garch integrado fraccionariamente) y RiskMetrics® para diversos indicadores y tipos de cambio asiáticos. Angelidis, Benos y Degiannakis (2004) aplicaron los modelos garch, egarch (garch exponencial) y tgarch (garch de umbral) a los indicadores S&P500, Nikkei225, DAX30, CAC40 y FTSE100.
Christoffersen (1998) introduce la hipótesis de cobertura condicional, la cual se divide en la hipótesis de cobertura incondicional (la medida clásica de número de fallas) y la hipótesis de independencia. La hipótesis de independencia, un valor agregado, define que cada “hit” (falla o violación) es independiente de los hits anteriores; también involucra el análisis de la duración entre cada hit (hitting time).
Christoffersen y Pelletier (2004) elaboran un test que fusiona las dos hipótesis que testeaban las dos propiedades necesarias para validar una proyección, planteadas por Christoffersen (1998), en una sola hipótesis global. Berkowitz, Christoffersen y Pelletier (2009) se basan en Christoffersen y Pelletier (2004) para extender su estudio hacia su propio test, el cual está basado en la duración entre hits. Candelon et al. (2011) utilizan lo propuesto por Berkowitz, pero logran separar las hipótesis que Christoffersen y Pelletier habían unido, planteando las dos hipótesis iniciales y la hipótesis conjunta en el mismo. Candelon et al. (2011) someten su test a pruebas de poder, flexibilidad y exactitud de diversas propiedades (tipos de muestras, tamaño, etc.) logrando resultados positivos, lo que posiciona a esta prueba en la cúspide de los test del var del momento.
Data y metodologíaLos valores a analizar son las principales monedas latinoamericanas: el real brasileño, los pesos argentino, chileno, colombiano y mexicano y el nuevo sol peruano, todas expresadas como moneda local por dólar americano. Los índices bursátiles analizados son: el índice del Mercado de Valores de Buenos Aires S.A. (Merval), de la Bolsa de Valores de São Paulo (Bovespa), el Índice de Precio Selectivo de Acciones (ipsa) de Chile, el Índice General de la Bolsa de Valores de Colombia (igbc), el Índice de Precios y Cotizaciones (ipyc) de México, el Índice General de la Bolsa de Valores de Lima (igbvl) y el Dow Jones Industrial Average (djia) y el índice de la National Association of Securities Dealers Automated Quotation (Nasdaq) de Estados Unidos. La data fue obtenida de la base Economática para el periodo comprendido desde el 2 de enero de 1990 hasta el 31 de mayo de 2012. El índice igbc en su moneda nacional está disponible del 2 de enero de 1991 al 4 de enero de 1993 (en dólares). El peso argentino estuvo fijo hasta el 2002, por lo cual sólo analiza el periodo posterior a esta fecha.
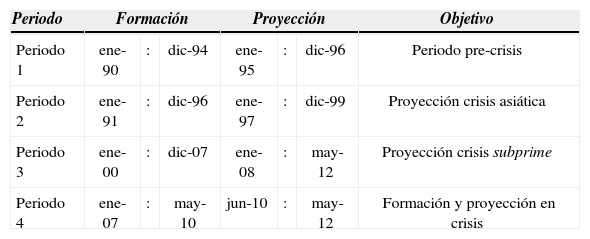
Los análisis se realizan para cuatro periodos de tiempo, cada uno de los cuales se dividen en dos subperiodos: uno de formación del modelo y el otro de proyección, siendo la relación de tiempo entre estos subperiodos de 2:1. El primer periodo (periodo 1) es el periodo de enero de 1990 a diciembre de 1996 (Ene-90 y Dic-96, respectivamente), que analiza el comportamiento del modelo en periodo precrisis; el segundo (periodo 2) de enero de 1991 a diciembre de 1999 (Ene-91 y Dic-99), que ilustra los modelos proyectado en la crisis asiática; el tercero (periodo 3) comprende desde enero de 2000 hasta mayo de 2012 (Ene-00 y May-12), tiene como objetivo proyectar en la crisis subprime con datos de formación previos a ésta. Finalmente, el cuarto periodo (periodo 4) es de enero de 2007 a mayo de 2012 (Ene-07 y May-12) e intenta probar los modelos en periodos de alta volatilidad, tanto en la formación como en la proyección. En el cuadro A1 se exponen los periodos analizados.
Las metodologías a aplicar en este estudio son el hs, el caviar y el garch. Cada una representa un tipo de cálculo del var: no paramétricos, semiparamétricos y paramétricos. La simulación histórica usará los retornos del índice observado en un periodo de tiempo con el fin de determinar la serie de cambios en su valor, siendo el var de ese periodo igual al percentil de la distribución de retornos dado un porcentaje de confianza requerido. Esto se realizará mediante ventanas móviles de 250 días, lo cual equivale aproximadamente a un año.
Para la aplicación directa del modelo garch al cálculo del var, si bien Engle y Manganelli (2001) plantean que es más recomendable utilizar un garch(1,1), se optó por utilizar un egarch, propuesto por Nelson (1991), ya que así se puede incorporar el efecto de la asimetría (veáse la ecuación [1]). Para cada periodo de formación se optimizó el mejor modelo, comparando el criterio de información de Akaike (aic, Akaike Information Criterion) para todos los modelos posibles con diferentes s, p y q, siendo 5 el máximo valor para cada rezago.
Por su parte, el modelo caviar, formulado por Engle y Manganelli (1999), se centra en la modelación del percentil de probabilidad. Para su realización, lo primero a tener en cuenta es que la rentabilidad de los instrumentos tienden a agruparse con el tiempo, es decir, presentan correlación entre ellas. Los parámetros de este modelo son estimados mediante regresiones por cuantiles, de acuerdo con Koenker y Bassett (1978). La definición general del caviar será:
donde Ωt–1 es el conjunto de información disponible en el momento t.
Cabe destacar que en la mayoría de los casos prácticos esta expresión se puede linealizar, quedando expresada de una forma más sencilla:
El término autorregresivo β1VaRt–1 asegura que los cambios del var SEAN SUAVES a través del tiempo; mientras que l(β2, yt–1,VaRt–1) muestra la relación entre el nivel de VaRt y el de yt–1, es decir, mide la cuantía en que debe cambiar el var en función de la nueva información en y. Es de señalar, que este término juega el mismo papel que la curva de impacto de los modelos garch introducidos por Engle y Ng (1993).
El backtest se divide en tres diferentes test, el uc, el ind y el cc. El test cc es el que engloba a los otros dos, pero la ventaja que tiene la ejecución de los tres es que si el cc se rechaza se puede ver si se rechazó por uc o por ind. Estos test requieren del no rechazo de la hipótesis nula, por lo tanto requieren de un valor p1 mayor al valor de seguridad especificado. Otro parámetro a considerar es el número de polinomios utilizados en el test (P). Este número es importante para determinar si las hipótesis se rechazan o no, dado que mientras más alto es hay un mayor grado de polinomios en el estadístico y éste se hace más exacto, por lo que le da mayor exactitud. Para este estudio, el valor p a utilizar es 10% y el número de polinomios es 6; valores utilizados por Candelon et al. (2011). Todos estos tests se basan en el hit o “golpe”, el cual es una variable binaria que se activa cuando el var ha sido violado:
De esta variable, Christoffersen (1998) determina que las predicciones del var son válidas sí y sólo sí la secuencia de hit [It(α)] satisface la propiedad de cobertura incondicional y la propiedad de independencia. La propiedad de cobertura incondicional se refiere a la probabilidad de que un retorno a posteriori sea superior a la previsión, el var debe ser igual a la tasa de cobertura de α%:
La propiedad de independencia se asocia con las violaciones del VaR. La variable It(α) asociada a una violación del var en el tiempo t para una tasa de α% de cobertura debe ser independiente de la variable It+k(α) para toda k no igual a cero.
Cuando las propiedades uc e ind son simultáneamente válidas se dice que las proyecciones del var tienen una correcta cobertura condicional, y el proceso de violación al var es un proceso de martingala. Los estadísticos para estas hipótesis se basan en di, la duración entre dos violaciones consecutivas:
donde ti denota la fecha de la violación i-ésima.
Se establece que el backtest cumple las condiciones de los momentos basados en polinomios ortonormales, por lo que se define una secuencia de duraciones entre N violaciones al VaR, {d1, d2,…, dN}, las cuales se calculan a través de la secuencia de variables hit It(α). Bajo el supuesto de cobertura condicionada, la duración di, i=1,…,N, es independiente e idénticamente distribuida (i.i.d.) y tiene una distribución geométrica con una probabilidad de éxito igual a la tasa de cobertura α. Por tanto, la hipótesis nula de CC se puede expresar según la ecuación [7].
donde p denota el número de momentos condicionados. Así la hipótesis nula uc se puede expresar según la ecuación [8], mientras que la hipótesis nula ind conforme a la ecuación [9]:
La ecuación [9] muestra que la duración entre dos violaciones consecutivas tiene una distribución geométrica. Cabe destacar que la hipótesis UC no es válida si β no es igual a α.
Ahora bien, de acuerdo con Bontemps y Meddahi (2006) los polinomios ortonormales presentan la ventaja de que su matriz asintótica de covarianza es conocida. La matriz de pesos óptimos bajo los criterios del método generalizado de momentos (gmm, Generalized Method of Moments) es simplemente una matriz de identidad, en la cual JCC(p) denota la prueba estadística de cc asociada a los primeros p polinomios ortonormales. Suponiendo que el proceso de duración (di=1<i) es estacionario y ergódico la hipótesis nula de la cobertura condicionada JCC(p) se describe como:
donde M(di;α) representa un vector (p,1), cuyos componentes son los polinomios ortonormales Mj(di;α) para j=1,…,p, y α indica la tasa de cobertura α%.
El estadístico de prueba para la uc, JUC, se obtiene como un caso especial del estadístico JCC, cuando sólo se considera el primer polinomio ortonormal, es decir, cuando M(di;α)=M1(di;α). Entonces JUC es equivalente a JCC(1) obteniéndose la siguiente expresión:
Por último, el estadístico de ind, JIND, se puede expresar según la ecuación [12]:
donde M(di;β) denota un vector (p,1), cuyos componentes son los polinomios ortonormales Mj(di;β) para j=1,…,p evaluada para una probabilidad de éxito igual a β.
Cabe destacar que todos los valores p que entrega este test están corregidos por medio del proceso optimizador de corrección de Dufour (Dufour, 2006).
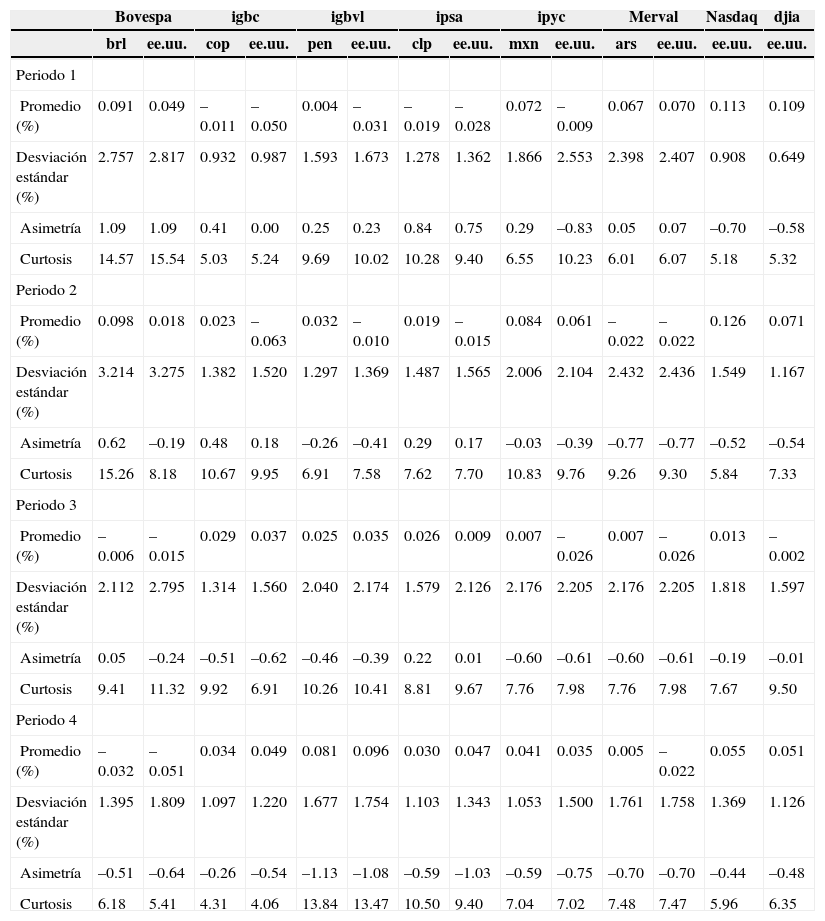
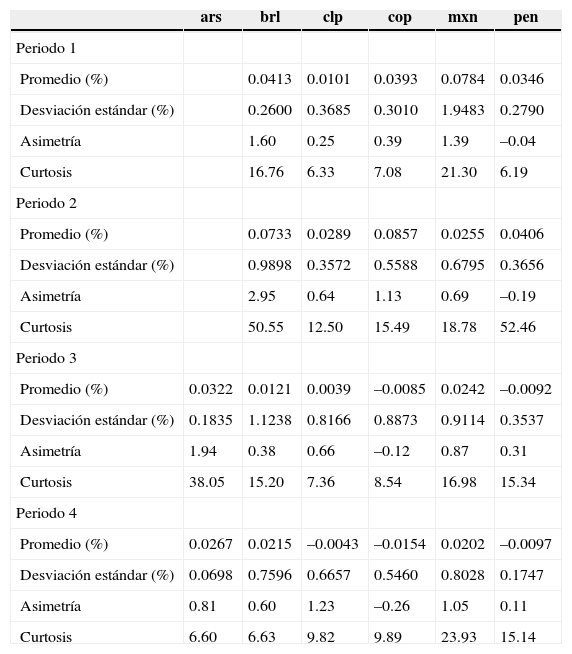
Análisis de resultadosPara el mejor análisis de los resultados se debe tener en cuenta la estadística descriptiva asociada a los periodos de proyección tanto para los índices bursátiles en moneda nacional y en dolares (véase el cuadro A2 del anexo) como de los tipos de cambio (véase el cuadro A3 del anexo). Para el primer periodo de proyección (periodo 1), se puede observar que la rentabilidad promedio no es homogéneamente positiva. La desviación estándar es menor en éste que en el de la crisis asiática (periodo 2), esto responde al hecho de que éste es de pre-crisis. Se observa una asimetría positiva en casi todos los índices salvo en el ipyc en dólares, en el Nasdaq y en el djia.
El segundo periodo, asociado a la crisis asiática, se caracteriza por una volatilidad mayor. Se observa en casi todas las series una asimetría negativa, salvo en el igbc y el ipsa, ambos en dólares. También se advierte un comportamiento leptocúrtico en todas las series, cuestión que se repite en todos los periodos. El peso mexicano es menos volátil que en el periodo pre-crisis. En general, nuevamente los tipos de cambio tienen signo contrario en la simetría al compararlos con sus índices bursátiles. En el tercer periodo, asociado a la crisis subprime, se aprecia para los índices bursátiles un comportamiento similar al de la crisis asiática, con valores de desviación estándar similares. Con respecto al tipo de cambio, su volatilidad es mayor que en el periodo de crisis anterior, salvo en el nuevo sol peruano (pen). Se observa que para tipos de cambio con volatilidades altas se tienen diferencias entre su índice en moneda nacional y en dólares, caso peso mexicano (mxn) y el ipyc.
Finalmente, en el cuarto periodo, asociado a la proyección en etapa volátil con una de formación volátil, la desviación estándar de las series de rentabilidad bursátil es inferior al periodo completo de crisis (periodo 3), lo cual está asociado a la recuperación que existió hacia el final de éste. Se observa un comportamiento asimétrico negativo y leptocúrtico en todas las series. Para el caso del tipo de cambio, se observa el mismo fenómeno, una menor volatilidad, mientras que la asimetría es positiva en todas las series, salvo en el peso colombiano (cop). Todas se comportan de forma leptocúrtica.
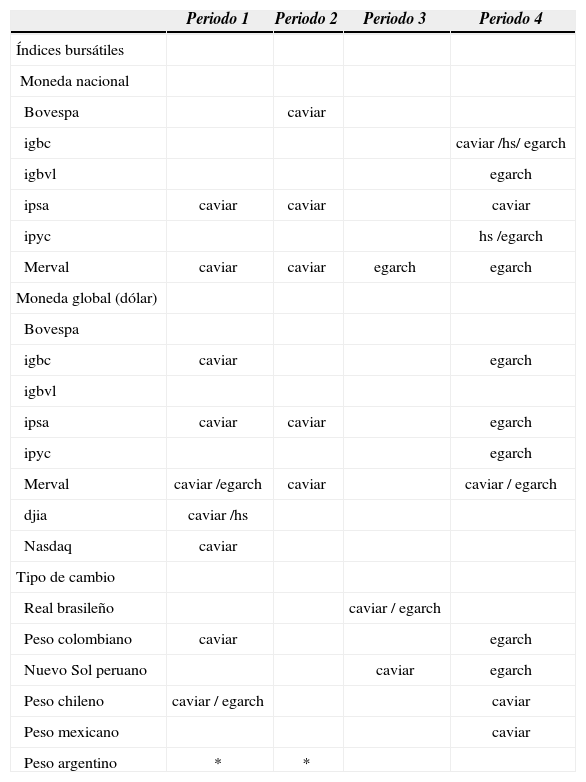
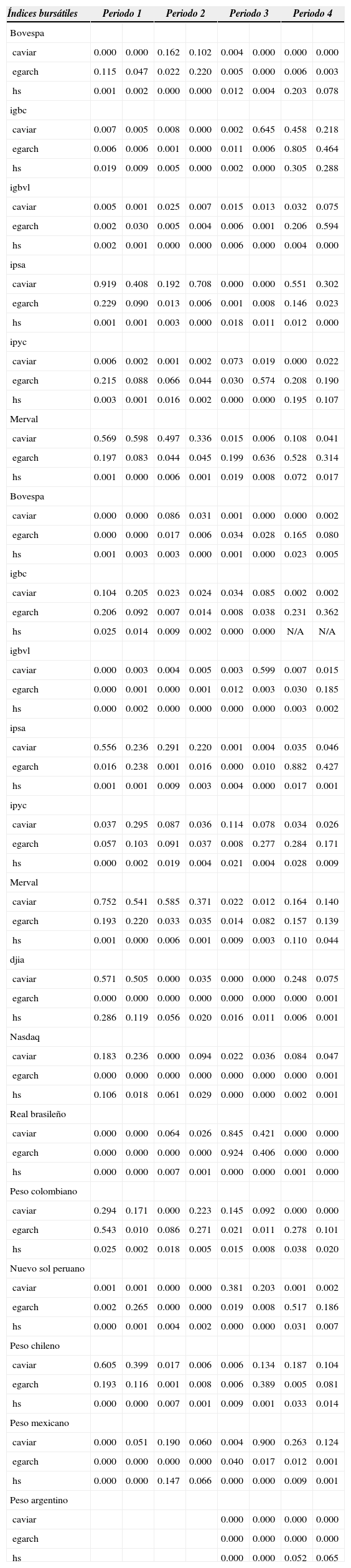
Los resultados del backtest aplicados a la proyección hecha por los diferentes modelos garch, hs y caviar, para los periodos definidos de análisis, se observan en la cuadro 2. Para el periodo 1 se puede advertir que cinco de los mercados accionarios tienen modelos válidos, predominando el caviar como el mejor modelo de ajuste. Este periodo no presenta una volatilidad muy alta de los tipos de cambio (salvo en el mxn), por lo que no es de extrañar que en los modelos válidos el Merval y el ipsa sean iguales tanto en moneda nacional como en dólar. En el caso del igbc, hay que recordar que la data proyectora no es igual en número, ya que en dólares está disponible desde 1993, por lo tanto, no es sorpresa que difieran los resultados aún con un tipo de cambio con poca desviación estándar. Se observa que el ipyc y Bovespa presentan las mayores desviaciones estándar del periodo, las cuales podrían indicar que existe un límite superior con respecto a esta característica de las series para que sus proyecciones del var sean válidas. Con respecto al tipo de cambio, se observa que el peso chileno (clp) y cop presentan modelos válidos, el peso argentino (ars) no fue analizado dado su comportamiento de tipo de cambio fijo en el periodo en cuestión. Se destaca en esta etapa que dos tipos de cambio que no poseen modelos válidos son los más y menos volátiles dentro de la misma, lo que permite enunciar que hay un límite superior e inferior con respecto a la volatilidad de las variables para poder poseer modelos válidos en la proyección de su correspondiente var. Con respecto al pen se observa que la hipótesis ind y uc en el garch fueron levemente rechazadas, lo que tendría al pen dependiente al grado de confianza que se requiera en el test estadístico.
Modelos válidos para índices bursátiles en moneda nacional y global (dólar) y tipo de cambio según periodos de análisis
| Periodo 1 | Periodo 2 | Periodo 3 | Periodo 4 | |
|---|---|---|---|---|
| Índices bursátiles | ||||
| Moneda nacional | ||||
| Bovespa | caviar | |||
| igbc | caviar /hs/ egarch | |||
| igbvl | egarch | |||
| ipsa | caviar | caviar | caviar | |
| ipyc | hs /egarch | |||
| Merval | caviar | caviar | egarch | egarch |
| Moneda global (dólar) | ||||
| Bovespa | ||||
| igbc | caviar | egarch | ||
| igbvl | ||||
| ipsa | caviar | caviar | egarch | |
| ipyc | egarch | |||
| Merval | caviar /egarch | caviar | caviar / egarch | |
| djia | caviar /hs | |||
| Nasdaq | caviar | |||
| Tipo de cambio | ||||
| Real brasileño | caviar / egarch | |||
| Peso colombiano | caviar | egarch | ||
| Nuevo Sol peruano | caviar | egarch | ||
| Peso chileno | caviar / egarch | caviar | ||
| Peso mexicano | caviar | |||
| Peso argentino | * | * |
En el segundo periodo de análisis, asociado a la crisis asiática, existe una mayor volatilidad en general, lo cual genera diferencias en los resultados entre moneda nacional y dólar para el Bovespa. Viendo la estadística descriptiva de su moneda, está dentro de las más volátiles del periodo, por lo que podría justificar esa diferencia en los resultados de sus índices; mientras que el ipsa y el Merval, al igual que en el periodo anterior, mantienen como modelo válido el caviar, tanto para moneda nacional como en dólar. En este caso, la estadística descriptiva muestra diferencias entre el djia y el Nasdaq, explicadas por el periodo de crisis, el cual impactó de diversas maneras a los distintos sectores del mercado estadounidense, de hecho durante esta etapa reventó la burbuja puntocom. Ninguno de los dos índices, djia ni Nasdaq, presentan modelo válido en este periodo. Al analizar los tests (véase el cuadro A4 del anexo) se puede ver que la gran mayoría rechaza la hipótesis ind y no la uc como en los periodos anteriores. Esto indica que los hits (o violaciones) no se distribuyen en forma independiente, lo que se puede confirmar dado el periodo en el que se está. Cabe destacar que los índices igbc e igbvl presentan cero violaciones en algunos modelos, por lo cual confirman la tendencia suave de sus rentabilidades.
Por otra parte, ninguna moneda obtuvo modelos válidos en su proyección del var, lo que se puede explicar con su estadística descriptiva, ya que si bien existe una mayor variabilidad hay una mayor asimetría de las monedas de alta variabilidad. Es por ello que se cree que el brl no logró obtener modelos válidos a pesar de su alta dispersión, ya que su coeficiente de asimetría es muy alto respecto a la media de las monedas.
El periodo asociado a la crisis subprime es más largo que el de la asiática. Se puede ver que en la primera existe un menor número de modelos válidos para los indicadores. Para el caso de las monedas, sólo el real brasileño y el nuevo sol peruano presentan modelos válidos, en ambos casos caviar; y, en particular, para el real también el egarch.
El último periodo de análisis es el completo con crisis subprime, por ende de formación en crisis, donde aparece el modelo hs como válido en dos mercados, lo que indica que al tener una data proyectora más volátil, aumenta la probabilidad de que éste sea válido. El igbc tiene dos modelos válidos, lo que demuestra que la alta desviación estándar de los datos proyectores entrega una mejor proyección del var.
Se observa una diferencia en la validez de los modelos entre los indicadores en moneda nacional y en dólar. Esto puede ser efecto de la volatilidad presentada en los datos proyectores del tipo de cambio, el cual puede traer diver-gencias entre ambos índices. Al analizar los tests de los indicadores en dólares, fallan levemente más en la hipótesis uc, lo que confirma la carencia o exceso de violaciones en el var.
ConclusionesUna vez analizados los resultados obtenidos por las proyecciones con las diferentes metodologías y los backtest se puede concluir que el caviar es el método más acertado para usar con tipo de cambio independiente del periodo. Para las proyecciones de los mercados accionarios, el caviar, junto con el modelo egarch, son los que tienen mayor cantidad de aciertos. Esto muestra que los modelos paramétricos y los semiparamétricos tienen similitudes en sus cálculos, ambos tienen una componente autorregresiva.
La simulación histórica para los mercados y los periodos analizados tiene un desempeño muy deficiente. Sólo es acertada en el último periodo para dos índices bursátiles, en donde se nota una mayor variabilidad de los datos reales que cubren el periodo proyectado. El índice bursátil peruano y el peso mexicano sólo pudieron ser modelados en el último periodo.
En el de pre-crisis asiática existe una predominancia de los modelos caviar en la proyección de los índices bursátiles, mientras que en el de pre-crisis subprime hay una homogeneidad de los garch. En este último periodo, para el caso de tipo de cambio, sólo aparece válido el caviar.
En los de pre-crisis, la gran mayoría de las metodologías rechazó sólo el testuc, lo que indica un exceso o déficit de violaciones del var para llegar al nivel de 5% de confianza requerido, esto indica que existen límites en la desviación estándar de los datos a proyectar. En cuando al testind, este se rechazó mayor-mente en los periodos de crisis, siendo explicado por las variables económicas móviles inherentes a cualquier periodo de crisis, las cuales son omitidas por estas metodologías.
Se observó la existencia de leptocurtosis en la mayoría de las series estudiadas, lo que respalda el uso de un modelo garch con una distribución t-student en sus errores.
Dado los resultados obtenidos, se observa la importancia de los datos históricos para el cálculo del riesgo futuro, tanto en crisis como en periodos normales. Este hecho puede ayudar en la estimación de la volatilidad al tomar alguna decisión de política económica, como puede ser intervenir el tipo de cambio o modificar la política monetaria (incentivo o desincentivo al ahorro), lo que agregado a las metodologías aprobadas puede entregar una estimación más certera de lo que ocurrirá en el futuro y resguardar así el riesgo al cual se pueden exponer los fondos. Con una regulación más ajustada se fortalece, entre otras, la industria bancaria y financiera, la industria de seguros y también la industria de la administración de fondos de pensiones.
La conclusión final es que, en general, la mejor de las tres metodologías para calcular el var de índices bursátiles y tipos de cambio latinoamericanos en los periodos analizados es el caviar. En la actualidad, diversas normas de regulación de riesgo de fondos exigen el cálculo del var como métrica de control, pero no en todas se define la metodología para su cálculo. Es en ese contexto que debiera aparecer el caviar como metodología propuesta, ya que es esencial al momento de normar el riesgo de la administración de fondos, ya sea por bancos o instituciones financieras.
Esta síntesis, consideramos que es importante para los legisladores medir el riesgo cuando se enfrenten a proponer leyes en las cuales existan formas de acotarlo en las inversiones o regulaciones en las operaciones bancarias. También, desde el punto de vista de los agentes del mercado accionario y del mercado cambiario en Latinoamérica, es relevante para tomar sus decisiones riesgo-retorno, exposición de riesgo y formas de cubrirse de éste. Siempre la cuantificación del riesgo es necesaria para la toma de decisiones bajo incertidumbre, por lo cual este artículo contribuye a aumentar el conocimiento de este aspecto en la región.
Periodos de formación y de proyección para las etapas analizadas
| Periodo | Formación | Proyección | Objetivo | ||||
|---|---|---|---|---|---|---|---|
| Periodo 1 | ene-90 | : | dic-94 | ene-95 | : | dic-96 | Periodo pre-crisis |
| Periodo 2 | ene-91 | : | dic-96 | ene-97 | : | dic-99 | Proyección crisis asiática |
| Periodo 3 | ene-00 | : | dic-07 | ene-08 | : | may-12 | Proyección crisis subprime |
| Periodo 4 | ene-07 | : | may-10 | jun-10 | : | may-12 | Formación y proyección en crisis |
Estadística descriptiva de índices bursátiles para periodos de proyección
| Bovespa | igbc | igbvl | ipsa | ipyc | Merval | Nasdaq | djia | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| brl | ee.uu. | cop | ee.uu. | pen | ee.uu. | clp | ee.uu. | mxn | ee.uu. | ars | ee.uu. | ee.uu. | ee.uu. | |
| Periodo 1 | ||||||||||||||
| Promedio (%) | 0.091 | 0.049 | –0.011 | –0.050 | 0.004 | –0.031 | –0.019 | –0.028 | 0.072 | –0.009 | 0.067 | 0.070 | 0.113 | 0.109 |
| Desviación estándar (%) | 2.757 | 2.817 | 0.932 | 0.987 | 1.593 | 1.673 | 1.278 | 1.362 | 1.866 | 2.553 | 2.398 | 2.407 | 0.908 | 0.649 |
| Asimetría | 1.09 | 1.09 | 0.41 | 0.00 | 0.25 | 0.23 | 0.84 | 0.75 | 0.29 | –0.83 | 0.05 | 0.07 | –0.70 | –0.58 |
| Curtosis | 14.57 | 15.54 | 5.03 | 5.24 | 9.69 | 10.02 | 10.28 | 9.40 | 6.55 | 10.23 | 6.01 | 6.07 | 5.18 | 5.32 |
| Periodo 2 | ||||||||||||||
| Promedio (%) | 0.098 | 0.018 | 0.023 | –0.063 | 0.032 | –0.010 | 0.019 | –0.015 | 0.084 | 0.061 | –0.022 | –0.022 | 0.126 | 0.071 |
| Desviación estándar (%) | 3.214 | 3.275 | 1.382 | 1.520 | 1.297 | 1.369 | 1.487 | 1.565 | 2.006 | 2.104 | 2.432 | 2.436 | 1.549 | 1.167 |
| Asimetría | 0.62 | –0.19 | 0.48 | 0.18 | –0.26 | –0.41 | 0.29 | 0.17 | –0.03 | –0.39 | –0.77 | –0.77 | –0.52 | –0.54 |
| Curtosis | 15.26 | 8.18 | 10.67 | 9.95 | 6.91 | 7.58 | 7.62 | 7.70 | 10.83 | 9.76 | 9.26 | 9.30 | 5.84 | 7.33 |
| Periodo 3 | ||||||||||||||
| Promedio (%) | –0.006 | –0.015 | 0.029 | 0.037 | 0.025 | 0.035 | 0.026 | 0.009 | 0.007 | –0.026 | 0.007 | –0.026 | 0.013 | –0.002 |
| Desviación estándar (%) | 2.112 | 2.795 | 1.314 | 1.560 | 2.040 | 2.174 | 1.579 | 2.126 | 2.176 | 2.205 | 2.176 | 2.205 | 1.818 | 1.597 |
| Asimetría | 0.05 | –0.24 | –0.51 | –0.62 | –0.46 | –0.39 | 0.22 | 0.01 | –0.60 | –0.61 | –0.60 | –0.61 | –0.19 | –0.01 |
| Curtosis | 9.41 | 11.32 | 9.92 | 6.91 | 10.26 | 10.41 | 8.81 | 9.67 | 7.76 | 7.98 | 7.76 | 7.98 | 7.67 | 9.50 |
| Periodo 4 | ||||||||||||||
| Promedio (%) | –0.032 | –0.051 | 0.034 | 0.049 | 0.081 | 0.096 | 0.030 | 0.047 | 0.041 | 0.035 | 0.005 | –0.022 | 0.055 | 0.051 |
| Desviación estándar (%) | 1.395 | 1.809 | 1.097 | 1.220 | 1.677 | 1.754 | 1.103 | 1.343 | 1.053 | 1.500 | 1.761 | 1.758 | 1.369 | 1.126 |
| Asimetría | –0.51 | –0.64 | –0.26 | –0.54 | –1.13 | –1.08 | –0.59 | –1.03 | –0.59 | –0.75 | –0.70 | –0.70 | –0.44 | –0.48 |
| Curtosis | 6.18 | 5.41 | 4.31 | 4.06 | 13.84 | 13.47 | 10.50 | 9.40 | 7.04 | 7.02 | 7.48 | 7.47 | 5.96 | 6.35 |
Estadística descriptiva de tipo de cambio para periodos de proyección
| ars | brl | clp | cop | mxn | pen | |
|---|---|---|---|---|---|---|
| Periodo 1 | ||||||
| Promedio (%) | 0.0413 | 0.0101 | 0.0393 | 0.0784 | 0.0346 | |
| Desviación estándar (%) | 0.2600 | 0.3685 | 0.3010 | 1.9483 | 0.2790 | |
| Asimetría | 1.60 | 0.25 | 0.39 | 1.39 | –0.04 | |
| Curtosis | 16.76 | 6.33 | 7.08 | 21.30 | 6.19 | |
| Periodo 2 | ||||||
| Promedio (%) | 0.0733 | 0.0289 | 0.0857 | 0.0255 | 0.0406 | |
| Desviación estándar (%) | 0.9898 | 0.3572 | 0.5588 | 0.6795 | 0.3656 | |
| Asimetría | 2.95 | 0.64 | 1.13 | 0.69 | –0.19 | |
| Curtosis | 50.55 | 12.50 | 15.49 | 18.78 | 52.46 | |
| Periodo 3 | ||||||
| Promedio (%) | 0.0322 | 0.0121 | 0.0039 | –0.0085 | 0.0242 | –0.0092 |
| Desviación estándar (%) | 0.1835 | 1.1238 | 0.8166 | 0.8873 | 0.9114 | 0.3537 |
| Asimetría | 1.94 | 0.38 | 0.66 | –0.12 | 0.87 | 0.31 |
| Curtosis | 38.05 | 15.20 | 7.36 | 8.54 | 16.98 | 15.34 |
| Periodo 4 | ||||||
| Promedio (%) | 0.0267 | 0.0215 | –0.0043 | –0.0154 | 0.0202 | –0.0097 |
| Desviación estándar (%) | 0.0698 | 0.7596 | 0.6657 | 0.5460 | 0.8028 | 0.1747 |
| Asimetría | 0.81 | 0.60 | 1.23 | –0.26 | 1.05 | 0.11 |
| Curtosis | 6.60 | 6.63 | 9.82 | 9.89 | 23.93 | 15.14 |
Mínimos p-valor para cada una de las pruebas realizadas
| Índices bursátiles | Periodo 1 | Periodo 2 | Periodo 3 | Periodo 4 | ||||
|---|---|---|---|---|---|---|---|---|
| Bovespa | ||||||||
| caviar | 0.000 | 0.000 | 0.162 | 0.102 | 0.004 | 0.000 | 0.000 | 0.000 |
| egarch | 0.115 | 0.047 | 0.022 | 0.220 | 0.005 | 0.000 | 0.006 | 0.003 |
| hs | 0.001 | 0.002 | 0.000 | 0.000 | 0.012 | 0.004 | 0.203 | 0.078 |
| igbc | ||||||||
| caviar | 0.007 | 0.005 | 0.008 | 0.000 | 0.002 | 0.645 | 0.458 | 0.218 |
| egarch | 0.006 | 0.006 | 0.001 | 0.000 | 0.011 | 0.006 | 0.805 | 0.464 |
| hs | 0.019 | 0.009 | 0.005 | 0.000 | 0.002 | 0.000 | 0.305 | 0.288 |
| igbvl | ||||||||
| caviar | 0.005 | 0.001 | 0.025 | 0.007 | 0.015 | 0.013 | 0.032 | 0.075 |
| egarch | 0.002 | 0.030 | 0.005 | 0.004 | 0.006 | 0.001 | 0.206 | 0.594 |
| hs | 0.002 | 0.001 | 0.000 | 0.000 | 0.006 | 0.000 | 0.004 | 0.000 |
| ipsa | ||||||||
| caviar | 0.919 | 0.408 | 0.192 | 0.708 | 0.000 | 0.000 | 0.551 | 0.302 |
| egarch | 0.229 | 0.090 | 0.013 | 0.006 | 0.001 | 0.008 | 0.146 | 0.023 |
| hs | 0.001 | 0.001 | 0.003 | 0.000 | 0.018 | 0.011 | 0.012 | 0.000 |
| ipyc | ||||||||
| caviar | 0.006 | 0.002 | 0.001 | 0.002 | 0.073 | 0.019 | 0.000 | 0.022 |
| egarch | 0.215 | 0.088 | 0.066 | 0.044 | 0.030 | 0.574 | 0.208 | 0.190 |
| hs | 0.003 | 0.001 | 0.016 | 0.002 | 0.000 | 0.000 | 0.195 | 0.107 |
| Merval | ||||||||
| caviar | 0.569 | 0.598 | 0.497 | 0.336 | 0.015 | 0.006 | 0.108 | 0.041 |
| egarch | 0.197 | 0.083 | 0.044 | 0.045 | 0.199 | 0.636 | 0.528 | 0.314 |
| hs | 0.001 | 0.000 | 0.006 | 0.001 | 0.019 | 0.008 | 0.072 | 0.017 |
| Bovespa | ||||||||
| caviar | 0.000 | 0.000 | 0.086 | 0.031 | 0.001 | 0.000 | 0.000 | 0.002 |
| egarch | 0.000 | 0.000 | 0.017 | 0.006 | 0.034 | 0.028 | 0.165 | 0.080 |
| hs | 0.001 | 0.003 | 0.003 | 0.000 | 0.001 | 0.000 | 0.023 | 0.005 |
| igbc | ||||||||
| caviar | 0.104 | 0.205 | 0.023 | 0.024 | 0.034 | 0.085 | 0.002 | 0.002 |
| egarch | 0.206 | 0.092 | 0.007 | 0.014 | 0.008 | 0.038 | 0.231 | 0.362 |
| hs | 0.025 | 0.014 | 0.009 | 0.002 | 0.000 | 0.000 | N/A | N/A |
| igbvl | ||||||||
| caviar | 0.000 | 0.003 | 0.004 | 0.005 | 0.003 | 0.599 | 0.007 | 0.015 |
| egarch | 0.000 | 0.001 | 0.000 | 0.001 | 0.012 | 0.003 | 0.030 | 0.185 |
| hs | 0.000 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.002 |
| ipsa | ||||||||
| caviar | 0.556 | 0.236 | 0.291 | 0.220 | 0.001 | 0.004 | 0.035 | 0.046 |
| egarch | 0.016 | 0.238 | 0.001 | 0.016 | 0.000 | 0.010 | 0.882 | 0.427 |
| hs | 0.001 | 0.001 | 0.009 | 0.003 | 0.004 | 0.000 | 0.017 | 0.001 |
| ipyc | ||||||||
| caviar | 0.037 | 0.295 | 0.087 | 0.036 | 0.114 | 0.078 | 0.034 | 0.026 |
| egarch | 0.057 | 0.103 | 0.091 | 0.037 | 0.008 | 0.277 | 0.284 | 0.171 |
| hs | 0.000 | 0.002 | 0.019 | 0.004 | 0.021 | 0.004 | 0.028 | 0.009 |
| Merval | ||||||||
| caviar | 0.752 | 0.541 | 0.585 | 0.371 | 0.022 | 0.012 | 0.164 | 0.140 |
| egarch | 0.193 | 0.220 | 0.033 | 0.035 | 0.014 | 0.082 | 0.157 | 0.139 |
| hs | 0.001 | 0.000 | 0.006 | 0.001 | 0.009 | 0.003 | 0.110 | 0.044 |
| djia | ||||||||
| caviar | 0.571 | 0.505 | 0.000 | 0.035 | 0.000 | 0.000 | 0.248 | 0.075 |
| egarch | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 |
| hs | 0.286 | 0.119 | 0.056 | 0.020 | 0.016 | 0.011 | 0.006 | 0.001 |
| Nasdaq | ||||||||
| caviar | 0.183 | 0.236 | 0.000 | 0.094 | 0.022 | 0.036 | 0.084 | 0.047 |
| egarch | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 |
| hs | 0.106 | 0.018 | 0.061 | 0.029 | 0.000 | 0.000 | 0.002 | 0.001 |
| Real brasileño | ||||||||
| caviar | 0.000 | 0.000 | 0.064 | 0.026 | 0.845 | 0.421 | 0.000 | 0.000 |
| egarch | 0.000 | 0.000 | 0.000 | 0.000 | 0.924 | 0.406 | 0.000 | 0.000 |
| hs | 0.000 | 0.000 | 0.007 | 0.001 | 0.000 | 0.000 | 0.001 | 0.000 |
| Peso colombiano | ||||||||
| caviar | 0.294 | 0.171 | 0.000 | 0.223 | 0.145 | 0.092 | 0.000 | 0.000 |
| egarch | 0.543 | 0.010 | 0.086 | 0.271 | 0.021 | 0.011 | 0.278 | 0.101 |
| hs | 0.025 | 0.002 | 0.018 | 0.005 | 0.015 | 0.008 | 0.038 | 0.020 |
| Nuevo sol peruano | ||||||||
| caviar | 0.001 | 0.001 | 0.000 | 0.000 | 0.381 | 0.203 | 0.001 | 0.002 |
| egarch | 0.002 | 0.265 | 0.000 | 0.000 | 0.019 | 0.008 | 0.517 | 0.186 |
| hs | 0.000 | 0.001 | 0.004 | 0.002 | 0.000 | 0.000 | 0.031 | 0.007 |
| Peso chileno | ||||||||
| caviar | 0.605 | 0.399 | 0.017 | 0.006 | 0.006 | 0.134 | 0.187 | 0.104 |
| egarch | 0.193 | 0.116 | 0.001 | 0.008 | 0.006 | 0.389 | 0.005 | 0.081 |
| hs | 0.000 | 0.000 | 0.007 | 0.001 | 0.009 | 0.001 | 0.033 | 0.014 |
| Peso mexicano | ||||||||
| caviar | 0.000 | 0.051 | 0.190 | 0.060 | 0.004 | 0.900 | 0.263 | 0.124 |
| egarch | 0.000 | 0.000 | 0.000 | 0.000 | 0.040 | 0.017 | 0.012 | 0.001 |
| hs | 0.000 | 0.000 | 0.147 | 0.066 | 0.000 | 0.000 | 0.009 | 0.001 |
| Peso argentino | ||||||||
| caviar | 0.000 | 0.000 | 0.000 | 0.000 | ||||
| egarch | 0.000 | 0.000 | 0.000 | 0.000 | ||||
| hs | 0.000 | 0.000 | 0.052 | 0.065 | ||||