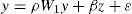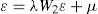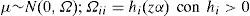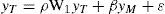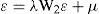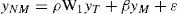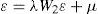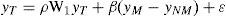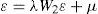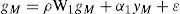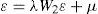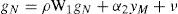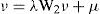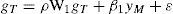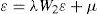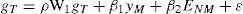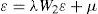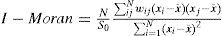El crecimiento y desarrollo económico de México y Corea del Sur han seguido trayectorias diferentes en las últimas décadas. Desde los ochenta, la economía mexicana ha mantenido un avance lento, lo que no le ha permitido entrar a una senda de crecimiento acelerado como sí le ha sucedido a Corea. La evidencia empírica muestra que en este último país el crecimiento está determinado de forma endógena; el sector manufacturero sirve de pivote para el desarrollo al encabezar el crecimiento sectorial y de la productividad del trabajo. En México, caso contrario, la evidencia empírica señala que no existe un crecimiento endógeno. No hay un liderazgo sectorial que amplíe y mantenga un mercado local robusto, lo que influye en su trayectoria de crecimiento de largo plazo. Asimismo, el crecimiento manufacturero coreano da lugar a efectos de derrama en un conjunto de regiones, lo que ocasiona externalidades espaciales positivas, mientras que en México, el lento crecimiento del sector no se ha traducido en una fuente del crecimiento regional en el período 1998-2008.
En los últimos años, el crecimiento y desarrollo de las economías mexicana y coreana han seguido trayectorias contrarias. Actualmente el primero de estos países se encuentra inmerso en lo que Myrdal (1975) denominó el círculo viciosode crecimiento, mientras que el segundo ha entrado en lo que Thirlwall (2003) llamaría círculo virtuoso de crecimiento. En la explicación de estas trayectorias ha tenido una relevante contribución el hecho de que en la economía mexicana se ha reducido significativamente el papel del Estado al darse prioridad a una economía de libre mercado. En tanto, en Corea el papel del Estado ha sido más activo en la consolidación del sector manufacturero como el motor de su crecimiento. Gracias a dicha consolidación el sector actúa como pivote para el crecimiento de esa nación, contribuyendo no sólo al fortalecimiento del mercado interno, sino además a disminuir y amortiguar la dependencia externa en ese país. Sumado a lo anterior, el espacio en el cual se desarrolla la actividad manufacturera coreana opera de manera activa al contribuir a la generación de un efecto de derramamientos o spillovers en las regiones de ese país, lo que no se puede constatar en el caso de la economía mexicana.
Como ya han señalado otros autores, sustentar en las exportaciones la generación de empleo, la producción y el crecimiento puede traer graves consecuencias. Al respecto Clavijo y Casar (1994) afirman que pequeñas perturbaciones en las exportaciones (por cambios en los gustos y preferencia de los consumidores externos) tenderá a afectar el empleo y, por ende, el crecimiento nacional. La elevada vulnerabilidad del país frente a los choques externos se asocia al alto grado de su apertura comercial (Blecker, 2010); en consecuencia el mercado interno podría operar como un amortiguador ante eventos desafortunados en el sector externo. Esto no implica que el mercado internacional no sea relevante para el crecimiento y desarrollo, sino que puede complementarse con políticas endógenas, con el desarrollo adecuado de un mercado interno, tal como muestra la evidencia del caso coreano.
El principal propósito de este trabajo consiste en utilizar las tres leyes de Kaldor (1966, 1984) para analizar la trayectoria de crecimiento de la economía mexicana y compararla con el caso de Corea durante el periodo de 1998 a 2008. El estudio del caso coreano es relevante para la economía mexicana, en la medida en que ejemplifica cómo el sector manufacturero puede ser la base del crecimiento y las exportaciones un factor complementario de su dinámica de desarrollo. En México se ha seguido una estrategia opuesta: el sector externo determina la trayectoria del crecimiento y el sector manufacturero lo complementa. Esta diferencia ha ocasionado que nuestro país sea altamente dependiente del comercio internacional y no pueda consolidar un mercado interno sólido que le permita reducir su vulnerabilidad frente a los choques externos.
El presente trabajo está dividido en tres apartados. En el primero se discute brevemente la evolución de ambas economías durante el periodo analizado. En ella se destacan las políticas económicas emprendidas a partir de los ochenta y cómo esas políticas fueron evolucionando para consolidar al sector manufacturero y las exportaciones como el motor de crecimiento de ambas economías. En la segunda sección se desarrolla el modelo de Kaldor-Thirlwall donde se enfatiza la importancia del sector manufacturero y las exportaciones totales. En la tercera parte se hace una inferencia empírica sobre los principales hechos estilizados. Por último, se proporcionan las principales conclusiones y recomendaciones de política derivadas de esta investigación y se destaca la importante necesidad de impulsar al mercado interno como el eje del crecimiento y desarrollo de largo plazo para la economía mexicana.
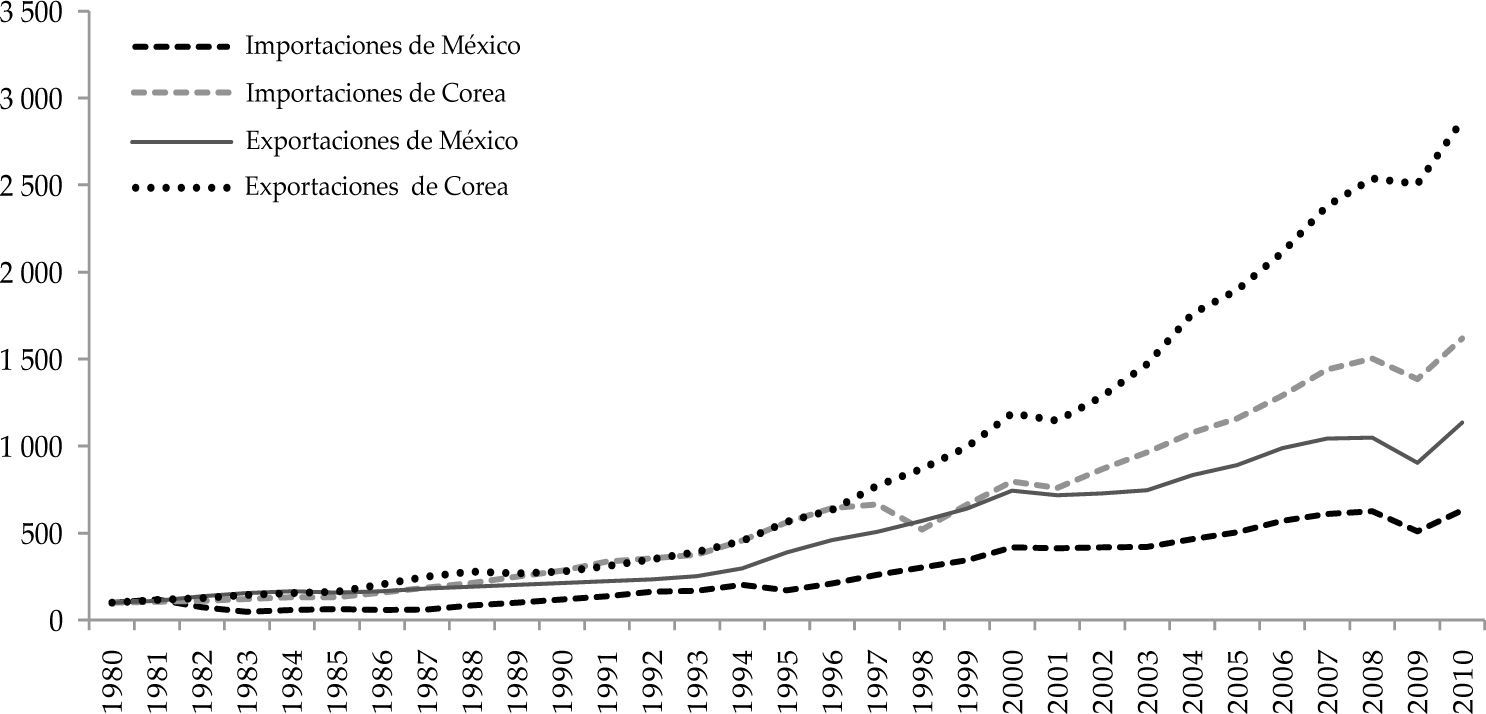
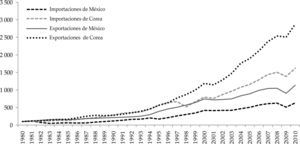
Crecimiento económico de México y Corea del SurDesde mediados de los ochenta en México se dio prioridad a una estrategia de apertura al comercio internacional, lo que ha traído beneficios y resultados favorables para el crecimiento de las exportaciones. Pese al énfasis puesto en la promoción de éstas, su aumento promedio fue de 8% entre 1980 y 2010, en tanto que para Corea del Sur esta misma cifra fue de 12%. El incremento de las importaciones para ambas economías, en el mismo periodo, fue de 6 y 10 por ciento, respectivamente.
De los datos de la gráfica 1 se observa que las exportaciones coreanas se dinamizaron desde inicios de la década de los noventa. La brecha entre las exportaciones e importaciones de ese país ha tendido a ampliarse de manera favorable al fortalecer la capacidad de generación de divisas de esa economía. Al contrario, en el caso mexicano los datos indican que a pesar del crecimiento exportador, éste ha sido más débil que el coreano, por lo que la brecha entre las exportaciones e importaciones mexicanas no es tan amplia como en la economía oriental.
Pese al rápido crecimiento de las exportaciones, el comercio internacional no ha operado como un fuerte motor de crecimiento para la economía mexicana (Ros, 2009). El hecho de que las ventas mexicanas al exterior tengan poca influencia en el crecimiento del país responde a múltiples factores, entre los cuales tienen gran relevancia la apreciación real del peso y la elevada participación de las maquiladoras en las exportaciones (Moreno-Brid y Ros, 2009; Ibarra, 2011). A medida que se incrementan las ventas al exterior de esas empresas, también tienden a hacerlo las importaciones que el sector realiza, lo cual se constata con los datos de la gráfica 1, en donde se observa que las exportaciones y las importaciones tienen dinámicas muy parecidas, situación que es el reflejo de un mercado interno débil (Ibarra, 2008). Se ha comprobado que las exportaciones sustentadas en la maquila no fomentaron las cadenas nacionales ni estimularon la producción interna y que, al contrario, contribuyeron a eliminar cadenas de proveedores locales al incrementar la importación de insumos (Stallings y Peres, 2000) y al exponerlos a la competencia externa (Moreno-Brid y Ros, 2004). De esta manera, el patrón exportador mexicano ha sido incapaz de generar un cambio estructural hacia la eficiencia dinámica, en la cual tanto la productividad como el empleo puedan crecer al mismo tiempo pero sin generar presiones insostenibles en el sector externo (cepal, 2012). En síntesis, la liberalización comercial y las reformas macroeconómicas han fallado para impulsar a México a una trayectoria de sólido crecimiento dirigido por el mercado externo (MorenoBrid y Ros, 2009). A las debilidades del modelo exportador mexicano se deben añadir problemas estructurales internos que han obstaculizado la capacidad de crecimiento del país, entre los cuales destacan el mal sistema de crédito, la creciente informalidad de la economía, el control monopólico de los mercados claves, el bajo rendimiento educativo (Hanson, 2010) y la baja tasa de inversión (Ros, 2010).
Al contrario del caso mexicano, el gobierno coreano promovió las exportaciones con base en un modelo centralista de capitalismo administrado. Un eje de esta estrategia fue la política de industrialización orientada al exterior. El reducido volumen del mercado interno y la falta de recursos naturales hicieron que ese país buscara una vía de crecimiento sustentada en la demanda expansiva del mercado exterior. En este proceso el gobierno ejerció y controló la contratación de préstamos, la inversión de empresas nacionales y hasta la ubicación de las plantas (Lee y Yoo, 1998). La estrategia industrial coreana fue, en sus inicios, altamente selectiva con el fin de impulsar las industrias pesadas y la química conforme a una orientación exportadora (Cho, 1991). En los años ochenta se buscó consolidar ese crecimiento con una base de estabilidad, lo cual se consiguió en los noventa vía el desarrollo de industrias sustentadas en nuevas tecnologías nacionales producto del apoyo estatal a las instituciones de investigación públicas y privadas. El éxito de la estrategia coreana consistió en centrarse en el crecimiento económico y en busca de esa meta impulsar las exportaciones privilegiando las inversiones que contribuyeran al incremento de la productividad (Koh, 2012).
Si comparamos la tasa de crecimiento promedio del producto interno bruto (pib) de ambas economías de 1980 a 2010, los datos del Banco Mundial (2013) permiten destacar el hecho de que México presentó un crecimiento de apenas 2% anual promedio, mientras que Corea tuvo una tasa del 6% anual en el mismo periodo. En el sector manufacturero esos diferenciales son mayores, dado que en Corea ese sector creció 8.7% anual, mientras que el mexicano apenas lo hizo en 2.4%. La experiencia coreana muestra que para lograr una senda de crecimiento de largo plazo es necesario que las exportaciones sean intensivas en conocimientos y tecnología (Hounie y Pittaluga, 1999), además de promover la creación de redes productivas y de servicios articulados en torno a su dinámica para lograr desarrollar proveedores locales competitivos (cepal, 1990; 2012). Esto significa que los productos exportados deben ser los de mayor contenido y valor agregado de carácter tecnológico y no puramente productos maquilados.
Para revertir esta situación es necesario consolidar un mercado interno fuerte con un sector exportador vinculado sólidamente a aquél. Por ello, la discusión con respecto al caso coreano sigue siendo aleccionadora, en la medida en que esa economía ha logrado establecer un sector industrial endógeno de alta tecnolo- gía sobre el que se sustenta su estrategia de desarrollo de largo plazo. Desde nuestra perspectiva, el éxito de Corea se ajusta al planteamiento de Kaldor (1966) en el sentido de que es el sector manufacturero el que causa el crecimiento económico desde el lado de la demanda.
Las leyes de Kaldor desde la perspectiva espacialKaldor (1966) argumentó que es difícil entender el proceso de crecimiento económico sin tomar en cuenta la importancia de los sectores, distinguiendo entre actividades con rendimientos crecientes y decrecientes. Los primeros se encuentran en el sector industrial, mientras que los segundos en el sector primario (McCombie y Thirlwall, 1994; Thirlwall, 1986). Un mayor dinamismo y crecimiento manufacturero se traduce en el impulso de los demás sectores, de la productividad y competitividad. Por ello, el comportamiento de ese sector define la trayectoria de crecimiento de un país o región. Este planteamiento se ha formalizado en las llamadas leyes de Kaldor, las cuales formulan tres proposiciones en las que se establece la forma en que el sector manufacturero se constituye en el motor del crecimiento económico.
Aunque el planteamiento original de Kaldor se realizó de manera agregada y no regional o espacial, se han ido generando estudios en los cuales las tres leyes se evalúan a nivel subnacional; McCombie y de Ridder (1983, 1984) y Bernat (1996) lo aplican al caso regional de los Estados Unidos; Casetti y Tanaka (1992) consideran a Japón; Dasgupta y Singh (2006) analizan países en desarrollo; PonsNovell y Villadecans-Marsall (1999) y Fingleton y López-Bazo (2006) generan evidencia sobre las regiones europeas, y Wells y Thirlwall (2003) toman en cuenta países africanos. Sin embargo, es esos trabajos, pese a contar con una dimensión regional, no consideran explícitamente el papel del espacio y la dependencia espacial que tienen los procesos de crecimiento. Sólo recientemente se han realizado estudios de las leyes de Kaldor en las que se incorporan efectos de dependencia espacial, como los de Bernat (1996), Pons-Novell y VilladecansMarsall (1999), Fingleton y López-Bazo (2006), Don (2007), Yonbock (2007), Angeriz, McCombie y Roberts (2008).
En este trabajo se aplican las leyes de Kaldor en una perspectiva subnacional, tanto para México como para Corea del Sur. Esto permite considerar la existencia de procesos de concentración espacial del crecimiento (Fujita, Krugman y Venables, 1999) y su irradiación regional por medio de externalidades espaciales (Fingleton y López-Bazo, 2006). Para considerar estos efectos se hace uso de la econometría espacial (Anselin, 1988); una técnica que se revisa en detalle en Cliff y Ord (1972), Paelinck y Klaassen (1979), Anselin (1987), Anselin y Florax (1995) y Arbia (2008).
De acuerdo con la econometría espacial, la presencia de la autocorrelación o dependencia espacial tiene consecuencias negativas en el estimador estándar de mínimos cuadrados ordinarios, los cuales son insesgados pero no eficientes (Anselin, 1988).
Para detectar la presencia de la dependencia espacial hacemos uso del índice de Moran (I-Moran), el cual utiliza una matriz de pesos espaciales (W), cuyos elementos toman el valor de 1 cuando la unidad territorial presenta vecindades y 0 en otros casos. Utilizando el I-Moran, el rechazo de la hipótesis nula de una distribución aleatoria de las variables en el espacio permite justificar el uso de modelos de la econometría espacial que se pueden generalizar en la siguiente especificación:
donde y es un vector de n observaciones de la variable dependiente, el término de perturbación aleatoria (ε)incorpora una estructura de dependencia espacial autorregresiva. A su vez se considera que ε se distribuye normalmente, con una matriz de varianzas y covarianzas Ωii diagonal pero heterocedástica, en la cual los elementos de su diagonal principal son función de las variables exógenas z, siendo α un vector asociado a los términos no constantes de z. En las ecuaciones [1] y [1a], W1 y W2 son dos matrices de pesos espaciales.1
Con base en las ecuaciones [1] y [1ª] podemos tener dos casos particulares, el primero cuando λ=0 y ρ≠0 es el modelo de rezago espacial. El segundo, cuando λ≠0 y ρ=0 es el modelo de error espacial. La selección de estos modelos se realiza utilizando las pruebas lm y sus versiones robustas propuestas por Anselin (1988).2
Bernat (1996) retoma esta ecuación espacial y la adapta al caso de las leyes de Kaldor; nosotros retomamos las especificaciones de Bernat y las aplicamos a los casos de México y Corea. En su aplicación a las leyes de Kaldor, los dos modelos particulares de rezago y de error espacial tienen una interpretación diferente. En el caso del modelo de rezago espacial el crecimiento de una región es directamente afectado por el que logren sus vecinos, en tanto que en el modelo de error espacial el crecimiento de una región afectará al de sus vecinos si se encuentra por arriba de lo que puede considerarse como “normal” (Bernat, 1996).
Las leyes de KaldorLa primera ley establece que existe una relación positiva entre la tasa de crecimiento de la producción total (yT) y la producción de los bienes manufacturados (yM) representada por la siguiente ecuación:
donde β es la propensión marginal del ingreso manufacturero; W1, la matriz de pesos espaciales; ρ, el coeficiente de autocorrelación espacial, y ε, un término de perturbación aleatoria. Sin embargo, esto no es corolario de una simple correlación espuria como resultado de que la producción manufacturera es una fracción de la producción total; para ello Kaldor también mostró que existe una profunda correlación entre la tasa de crecimiento de la producción manufacturera, por un lado, y la tasa de crecimiento de la producción no manufacturera, por otro (Kaldor, 1966; Ocegueda, 2003; McCombie y Thirlwall, 1994). Resultados que fueron confirmados por investigadores como Cripps y Tarling (1973) y Thirlwall (1983), por lo que la expresión [2] se modifica de la siguiente forma en su especificación espacial:
donde yNM es la tasa de crecimiento de la actividad no manufacturera. Utilizando esta formulación del modelo, pero sin considerar los efectos espaciales, Kaldor la aplica a una muestra de 12 países desarrollados y concluye que la industria manufactura es el motor del crecimiento (Kaldor, 1966). Thirlwall (1983) propone otra especificación (la cual retoman Pons-Novell y Villadecans-Marsall, 1999), reformulando la primera ley como sigue:
La implicación de esta tercera formulación es que hay una relación positiva entre el incremento de la producción manufacturera y la no manufacturera. Esto significa que si el sector manufacturero mantiene elevadas tasas de crecimiento, el diferencial de este último debe ser tal que influya en la producción total del país. Es decir, Kaldor argumenta que una vez que la economía desarrolla su ventaja competitiva –lo que implica endogeinizar su crecimiento– tenderá a sostenerla por medio de los rendimientos crecientes que el propio desarrollo induce y se acrecienta por el progreso de los demás.
La primera ley se valida si β es positiva y estadísticamente significativa. Es decir, para que se considere a la industria manufacturera como el eje del crecimiento se necesita mostrar que el registrado por la producción nacional yT no esté estrechamente relacionado con el de los otros sectores, como la agricultura, la minería o los servicios, porque:
[…] no existe una correlación positiva entre el crecimiento del pib y el crecimiento de la agricultura o la minería. Aunque existe una correlación entre el crecimiento del pib y el crecimiento del sector servicios, Kaldor considera que la dirección de causalidad es al menos cierta desde el crecimiento del pib al crecimiento del sector de los servicios más que de otra forma, porque la demanda de muchos servicios es derivada de la demanda de la producción manufacturera (McCombie y Thirlwall, 1994:166).
El hecho de que el crecimiento del sector manufacturero involucre el aumento del pib nacional queda justificado de la siguiente manera: cuando la producción industrial se expande genera factores productivos y de empleo que en otros sectores se subutilizan. Así, la transferencia no produce un descenso en los demás sectores sino que ayuda a incrementarla. Mientras más rápido y de largo plazo sea este crecimiento, también lo será la tasa de transferencia de trabajo de los sectores sujetos a rendimientos decrecientes, como la agricultura y la minería, al sector que posee los rendimientos crecientes (Carton, 2009). No obstante, la tasa de crecimiento del sector debe ser superior al resto de los sectores y, de esta forma, se le considerá como el líder del crecimiento nacional (Kaldor, 1966; Ocegueda, 2003).
La segunda ley establece que hay una relación positiva entre la tasa de crecimiento del producto manufacturero yM y la tasa de crecimiento de la productividad del trabajo (gM) dentro del mismo sector (Kaldor, 1966; Ocegueda, 2003; Thirlwall, 2003; McCombie y Thirlwall, 1994). Esta proposición se conoce como la ley de Verdoorn y justifica que el aumento en la tasa de crecimiento de la producción manufacturera incremente la correspondiente a la productividad del trabajo dentro del mismo sector a consecuencia de los procesos de aprendizaje y de la mayor especialización que conlleva la ampliación del mercado (Ocegueda, 2003). En ese sentido Kaldor afirmaba:
Una mayor división del trabajo es más productiva, en parte porque genera mayor habilidad y conocimientos, más experiencia, que da por resultado más innovaciones y mejoras en los diseños. No podemos aislar la influencia de las economías de la producción de gran escala debido a la indivisibilidad de varios tipos, y que son en sí mismos reversibles, de estos cambios en la tecnología asociados con un proceso de expansión que no es reversible. El aprendizaje es producto de la experiencia, [lo que significa] que la productividad tiende a crecer más rápidamente cuanto más rápidamente se expanda el producto; esto implica también que el nivel de productividad es función del producto acumulativo más que de la tasa de producción por unidad de tiempo (Kaldor, 1984: 13-14).
Formalmente tenemos una expresión para la segunda ley en su especificación espacial siguiente:
donde gM y gN son las tasas de crecimiento de la productividad3 del trabajo y del empleo en el sector manufacturero,4 ε y ν son perturbaciones aleatorias. El coeficiente α se denomina coeficiente de Verdoorn. La interpretación de las ecuaciones [3] y [4] se centra en el valor de α1 y α2; si son positivos implican economías de escala.
La tercera leyse refiere al incremento general de la productividad del trabajo en cualquiera de los sectores. Supone que el crecimiento de la industria manufacturera produce una sobredemanda de empleo, lo que reduce la oferta de empleo hacia el resto de los sectores pero no disminuye el producto. Esto promueve que la productividad del trabajo se incremente en todos los sectores (Kaldor, 1966; Ocegueda, 2003).
Esto puede formalizarse del modo siguiente en su versión espacial:
La ecuación [5] muestra que la tasa de crecimiento de la productividad de todos los sectores (gT) está en función de la tasa de crecimiento de la producción manufactura yM, donde se ha eliminado el componente autónomo. Esto implica que si la industria manufacturera presenta mayores tasas de crecimiento se elevará la productividad del trabajo en esta industria y, una vez alcanzado su desarrollo y consolidación, la productividad se elevará en el resto de los sectores debido al sistema de arrastre que genera el sector secundario.
Cripps y Tarling (1973) proponen una formulación alternativa para la tercera ley de Kaldor e incorporan el crecimiento del empleo no manufacturero (ENM) en la ecuación y se puede incorporar al modelo espacial de la siguiente forma:
“Las tres leyes de Kaldor indican de que el sector manufacturero y su productividad son factores decisivos del crecimiento económico” (Pons-Novell y Villadecans-Marsall, 1999: 445). Las variables incorporadas para modificar las ecuaciones originales de Kaldor son para enfatizar la importancia del sector manufacturero.
Análisis exploratorio de la dependencia espacial en el proceso de crecimientoCon el fin de evaluar si nuestras variables presentan una distribución espacial aleatoria o exhiben patrones de dependencia espacial –los cuales permitan identificar procesos de derrama del crecimiento–, se hace uso del I-Moran, el cual se define formalmente como:
donde xi es la variable cuantitativa x en la región i, x¯ es su media muestral, wij son los pesos de la matriz W, N es el tamaño de muestra y S0=∑i∑jwij..5
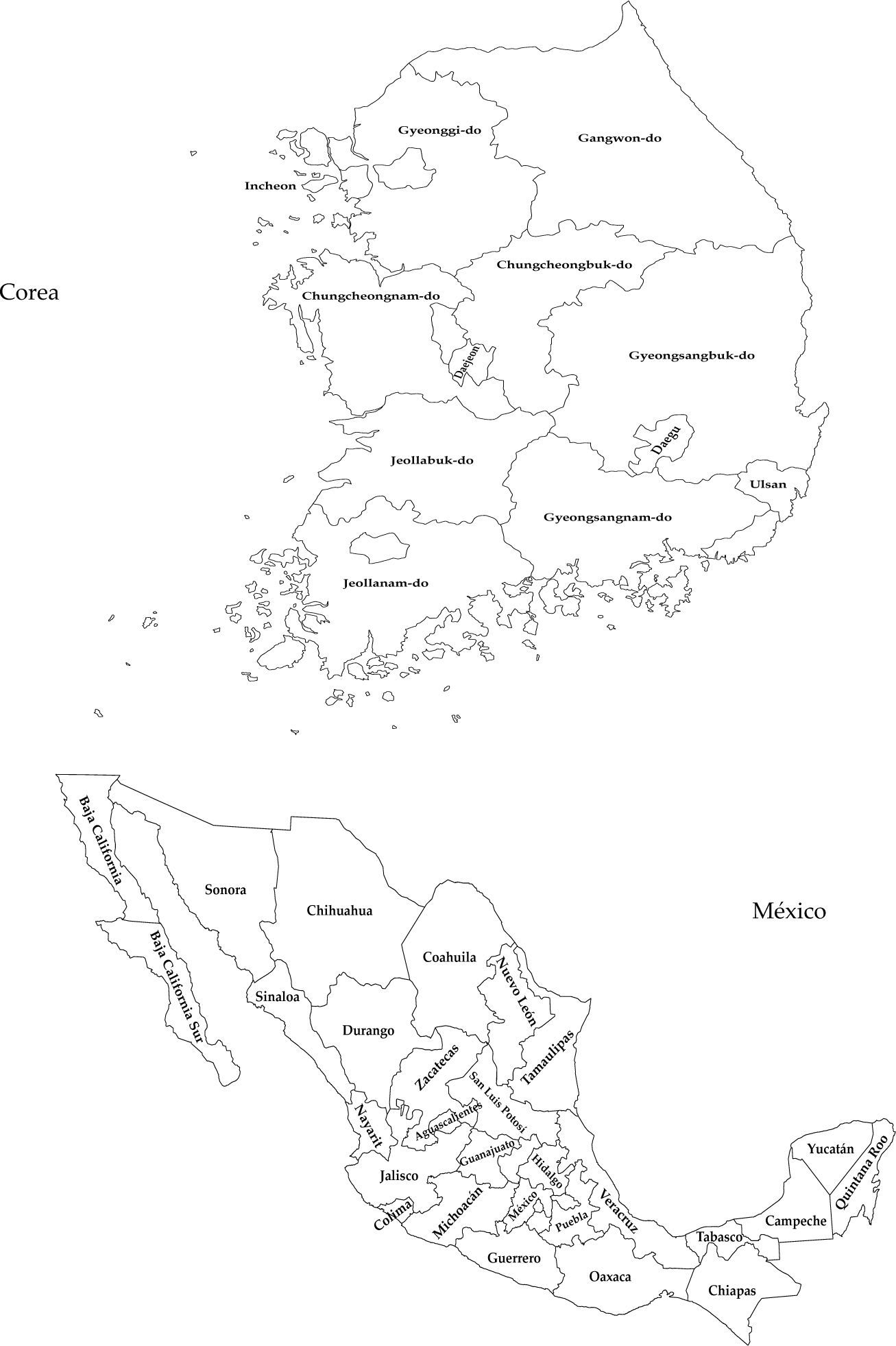
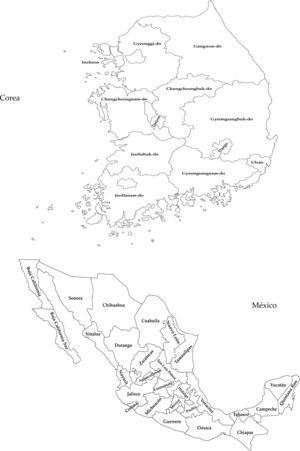
En la figura 1 se muestra la división administrativa utilizada para el análisis regional en México y Corea del Sur.
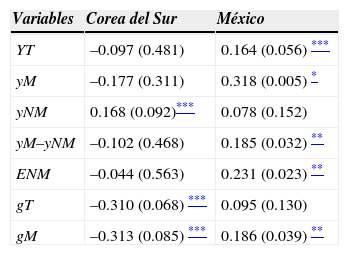
El cuadro 1 muestra los resultados del índice y su significancia estadística:6 por sus datos se constata que en Corea del Sur el pib no manufacturero yNM, la productividad global del trabajo gT y la productividad del trabajo manufacturero gM presentan dependencia espacial significativa. Para el caso mexicano, las pruebas de autocorrelación espacial fueron estadísticamente significativas en las variables del pibyT, pib manufacturero yM, diferencial del crecimiento manufacturero y no manufacturero (yM – yNM), empleo no manufacturero ENM, productividad global del trabajo gT y productividad del trabajo manufacturero gM.
Autocorrelación espacial (I Moran), 1998-200 8
| Variables | Corea del Sur | México |
|---|---|---|
| YT | –0.097 (0.481) | 0.164 (0.056) *** |
| yM | –0.177 (0.311) | 0.318 (0.005) * |
| yNM | 0.168 (0.092)*** | 0.078 (0.152) |
| yM–yNM | –0.102 (0.468) | 0.185 (0.032) ** |
| ENM | –0.044 (0.563) | 0.231 (0.023) ** |
| gT | –0.310 (0.068) *** | 0.095 (0.130) |
| gM | –0.313 (0.085) *** | 0.186 (0.039) ** |
Dado que el I-Moran es un indicador de dependencia espacial global, es necesario verificar la existencia de dependencia espacial local debido a la heterogeneidad que presentan las regiones interiores de los dos países. Por ello, en la figura 1 es posible observar los resultados del indicador local de dependencia espacial (lisa, por sus siglas en inglés), que permite evaluar la existencia de autocorrelación espacial en regiones específicas y la conformación de conglomerados o cluster con efectos de derrama positiva.7
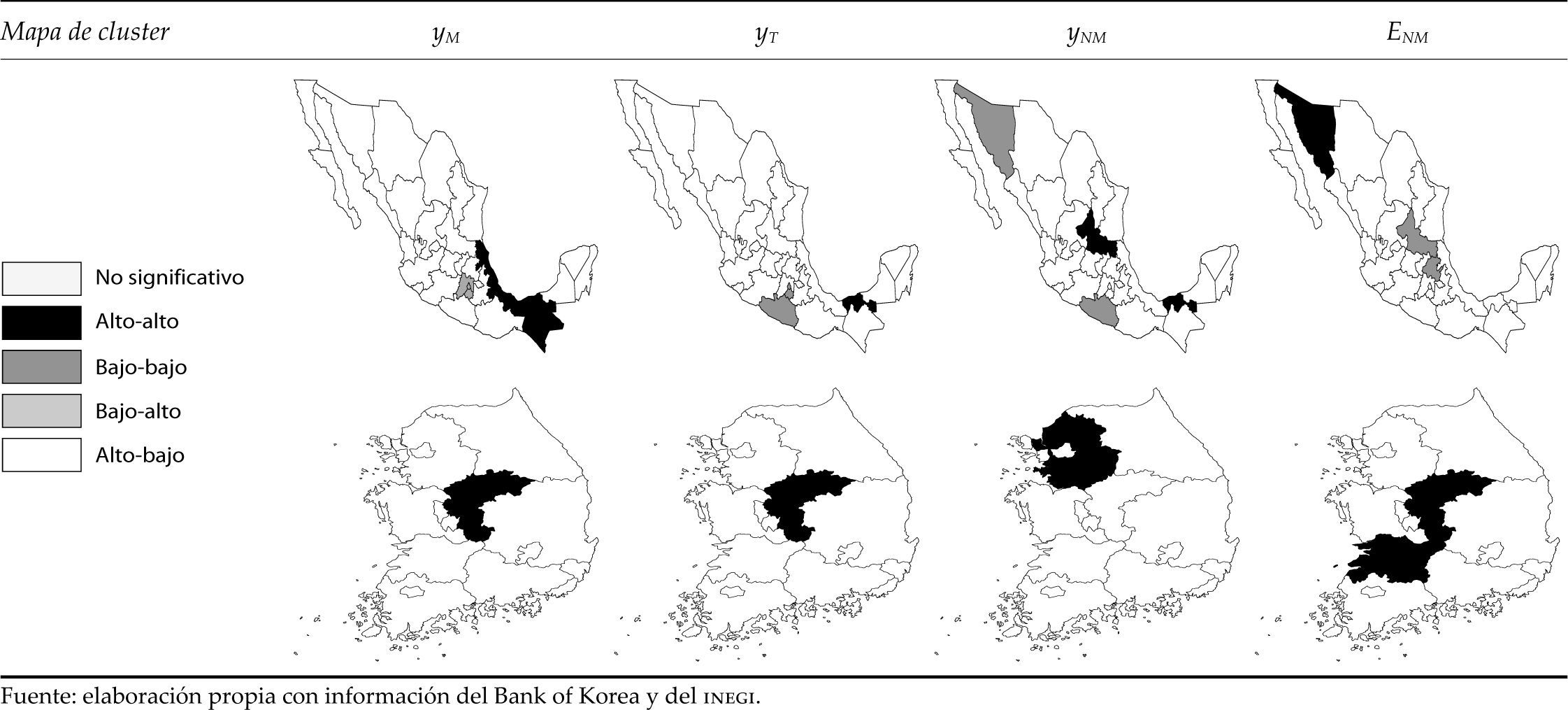
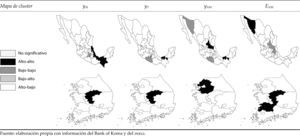
En la figura 2 se observa que, en el crecimiento promedio de la producción manufacturera mexicana, hay evidencia de la formación de agrupamientos o clusters de crecimiento (estados identificados como alto-alto) en Veracruz, Tabasco y Chiapas. En la producción total se observan estos agrupamientos en Tabasco; para la producción no manufacturera en Tabasco y San Luis Potosí, y en el diferencial del crecimiento manufacturero en Sonora. Al mismo tiempo, es posible observar valores extremos espaciales de bajo crecimiento (estados identificados como bajo-bajo) en el pib manufacturero del Estado de México, Morelos y Distrito Federal. El mismo caso se presenta en el pib para los estados de Guerrero y Morelos y el Distrito Federal; en la producción no manufacturera de Guerrero, y en el diferencial del crecimiento manufacturero y no manufacturero de San Luis Potosí e Hidalgo.
En Corea del Sur es posible constatar la formación de agrupamientos para el crecimiento promedio del sector manufacturero y el pib para Chungcheongbuk-do. Con respecto al crecimiento promedio de la producción no manufacturera, se observa este mismo patrón espacial en Gyeonggi-do y del diferencial del crecimiento promedio del sector manufacturero con respecto al no manufacturero en Jeollabuk-do.
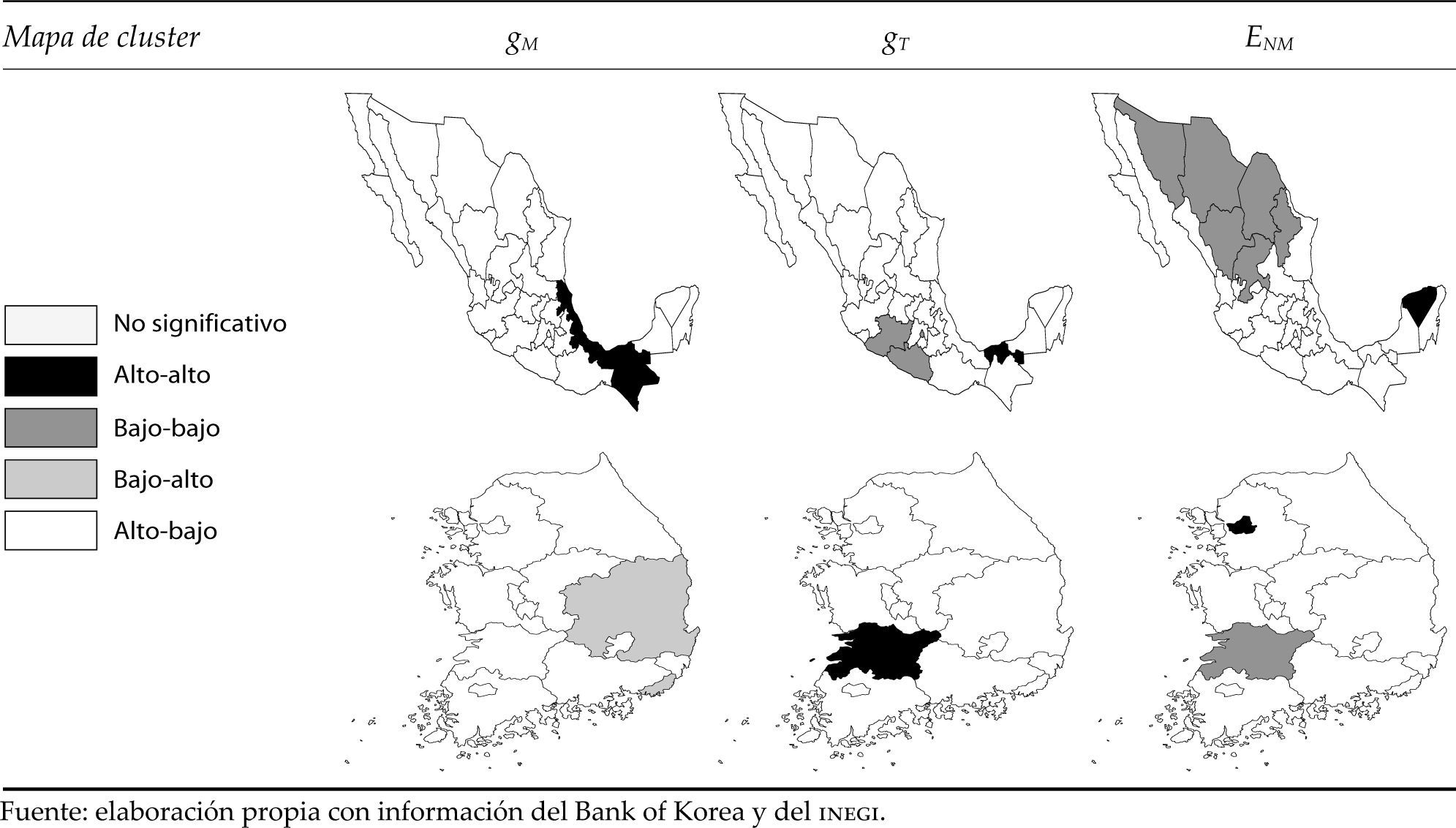
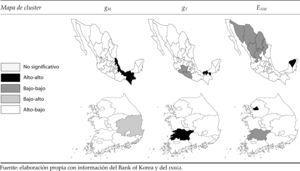
Los resultados del análisis lisa para la tasa de crecimiento promedio de la productividad del trabajo manufacturero, de la producción total y del empleo no manufacturero confirman los elementos ya referidos en el comportamiento de la producción mexicana. De acuerdo con la figura 3 se observan agrupamientos del trabajo manufacturero en Veracruz, Tabasco y Chiapas, y del no manufacturero en Yucatán. Mientras que las regiones de baja productividad global se presentan en Guerrero y Michoacán, y en el crecimiento promedio del empleo no manufacturero en Sonora, Chihuahua, Coahuila, Nuevo León, Durango y Zacatecas.
Los resultados del análisis lisa permiten establecer que tanto en México como en Corea hay concentraciones regionales específicas en las cuales el crecimiento tiende a autorreforzarse, lo cual supone la existencia de procesos de polarización.
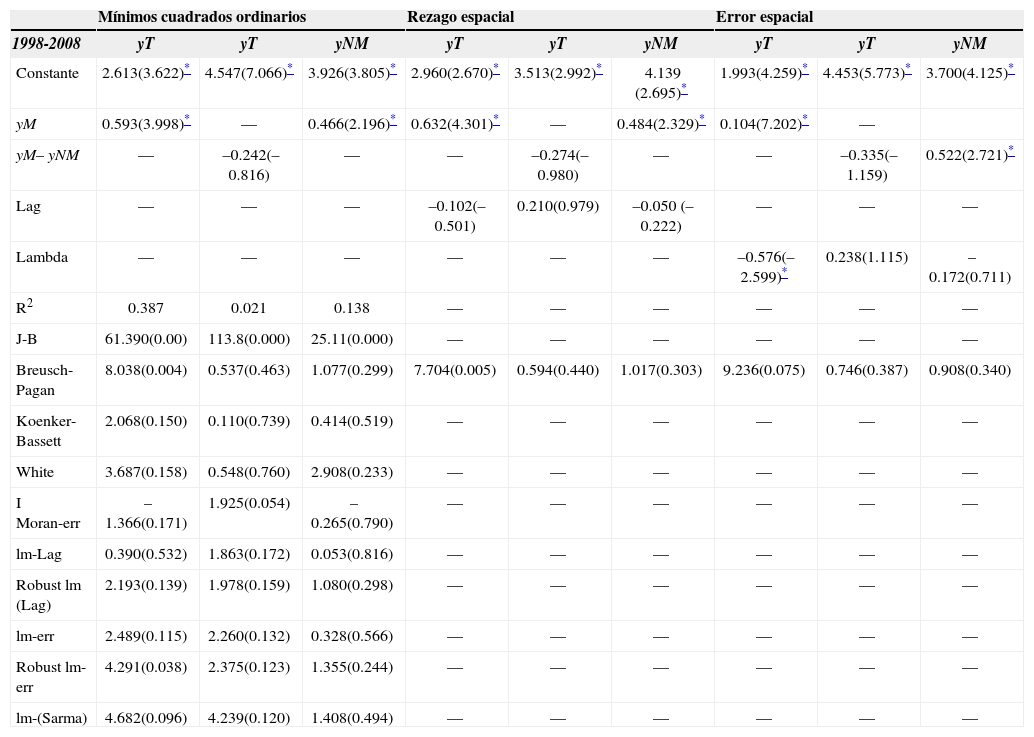
Evidencia empírica de las leyes de KaldorPara corroborar la hipótesis sobre la endogeneidad del crecimiento económico en México y Corea del Sur, en los cuadros 2 y 3 se presentan los resultados de las estimaciones de la primera ley de Kaldor. Las primeras tres columnas de los cuadros muestran los resultados de los modelos sin efectos espaciales y las siguientes contienen las estimaciones de los modelos de rezago espacial y de error espacial.
México: primera ley de de Kaldor
| Mínimos cuadrados ordinarios | Rezago espacial | Error espacial | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1998-2008 | yT | yT | yNM | yT | yT | yNM | yT | yT | yNM |
| Constante | 2.613(3.622)* | 4.547(7.066)* | 3.926(3.805)* | 2.960(2.670)* | 3.513(2.992)* | 4.139 (2.695)* | 1.993(4.259)* | 4.453(5.773)* | 3.700(4.125)* |
| yM | 0.593(3.998)* | — | 0.466(2.196)* | 0.632(4.301)* | — | 0.484(2.329)* | 0.104(7.202)* | — | |
| yM– yNM | — | –0.242(–0.816) | — | — | –0.274(–0.980) | — | — | –0.335(–1.159) | 0.522(2.721)* |
| Lag | — | — | — | –0.102(–0.501) | 0.210(0.979) | –0.050 (–0.222) | — | — | — |
| Lambda | — | — | — | — | — | — | –0.576(–2.599)* | 0.238(1.115) | –0.172(0.711) |
| R2 | 0.387 | 0.021 | 0.138 | — | — | — | — | — | — |
| J-B | 61.390(0.00) | 113.8(0.000) | 25.11(0.000) | — | — | — | — | — | — |
| Breusch-Pagan | 8.038(0.004) | 0.537(0.463) | 1.077(0.299) | 7.704(0.005) | 0.594(0.440) | 1.017(0.303) | 9.236(0.075) | 0.746(0.387) | 0.908(0.340) |
| Koenker-Bassett | 2.068(0.150) | 0.110(0.739) | 0.414(0.519) | — | — | — | — | — | — |
| White | 3.687(0.158) | 0.548(0.760) | 2.908(0.233) | — | — | — | — | — | — |
| I Moran-err | –1.366(0.171) | 1.925(0.054) | –0.265(0.790) | — | — | — | — | — | — |
| lm-Lag | 0.390(0.532) | 1.863(0.172) | 0.053(0.816) | — | — | — | — | — | — |
| Robust lm (Lag) | 2.193(0.139) | 1.978(0.159) | 1.080(0.298) | — | — | — | — | — | — |
| lm-err | 2.489(0.115) | 2.260(0.132) | 0.328(0.566) | — | — | — | — | — | — |
| Robust lm-err | 4.291(0.038) | 2.375(0.123) | 1.355(0.244) | — | — | — | — | — | — |
| lm-(Sarma) | 4.682(0.096) | 4.239(0.120) | 1.408(0.494) | — | — | — | — | — | — |
(**) estadísticamente significativo a 5%;
(***) estadísticamente significativo a 10%.
Corea: primera ley de de Kaldor
| Mínimos cuadrados ordinaries | Rezago espacial | Error espacial | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1998-2008 | yT | yT | yNM | yT | yT | yNM | yT | yT | yNM |
| Constante | 2.538(7.335)* | 4.202(13.753)* | 3.391(7.812)* | 0.811(0.903) | 2.763(2.388)* | 1.474(1.319) | 2.418(5.587)* | 4.053(7.764)* | 3.315(7.769)* |
| yM | 0.389(7.437)* | — | 0.148(2.249)** | 0.044(9.554)* | — | 0.173(3.172)* | 0.408(13.34)* | — | 0.162(3.345)* |
| yM– yNM | — | 0.372(2.218)* | — | — | 0.409(5.240)* | — | 0.439(7.242)* | — | |
| Lag | — | — | — | 0.307(1.903)** | 0.274(1.209) | 0.409(1.710)*** | — | — | — |
| Lambda | — | — | — | — | — | — | 0.691(3.958)* | 0.591(2.792)* | 0.459(1.827)** |
| R2 | 0.809 | 0.578 | 0.280 | — | — | — | — | — | — |
| J-B | 0.455(0.796) | 0.957(0.619) | 2.421(0.298) | — | — | — | — | — | — |
| Breusch-Pagan | 0.032(0.856) | 0.461(0.497) | 0.002(0.963) | 0.427(0.775) | 0.082(0.775) | 0.081(0.776) | 0.244(0.621) | 0.008(0.927) | 0.056(0.812) |
| Koenker-Bassett | 0.041(0.839) | 0.561(0.454) | 0.001(0.969) | — | — | — | — | — | — |
| White | 0.091(0.955) | 0.657(0.719) | 0.050(0.975) | — | — | — | — | — | — |
| I Moran-err | 3.170(0.001) | 2.743(0.006) | 2.543(0.011) | — | — | — | — | — | — |
| lm-Lag | 3.391(0.065) | 1.160(0.281) | 3.295(0.069) | — | — | — | — | — | — |
| Robust lm (Lag) | 0.165(0.683) | 0.876(0.349) | 0.019(0[ce].891) | — | — | — | — | — | — |
| lm-err | 5.901(0.015) | 4.036(0.044) | 3.562(0.059) | — | — | — | — | — | — |
| Robust lm-err | 2.676(0.102) | 3.752(0.053) | 0.286(0.593) | — | — | — | — | — | — |
| lm-(Sarma) | 6.068(0.048) | 4.913(0.086) | 3.580(0.167) | — | — | — | — | — | — |
Los aspectos más relevantes de los resultados de los cuadros 2 y 3 son los siguientes:
- a)
El sector manufacturero mexicano influye en el crecimiento del pib positivamente (0.593) sólo si se utiliza el modelo más simple de la ley de Kaldor (ecuación [2]) o si se relaciona a dicho sector con el no manufacturero (ecuación [2.2]), pero no cuando se usa el planteamiento modificado por Thirlwall (ecuación [2.1]). En virtud de ello, la evidencia econométrica a favor de la primera ley no es completamente robusta. Sumado a lo anterior, las pruebas lm para detectar efectos espaciales dan cuenta de que no hay evidencia de autocorrelación espacial. Estos resultados son consistentes con la evidencia encontrada por Ocegueda (2003) para las entidades federativas mexicanas. Dicho autor, con estimaciones de datos de panel para el periodo 1980-2000 concluye también que no hay soporte econométrico sólido en torno a la primera ley. En estimaciones no regionales, sino nacionales y con series de tiempo, tampoco se ha encontrado evidencia del cumplimiento de la primera ley; por ejemplo, Loría (2009) estimó para el periodo 1970-2008 un coeficiente de 0.69, pero que no puede aceptarse estadísticamente debido a problemas de especificación en el modelo.
- b)
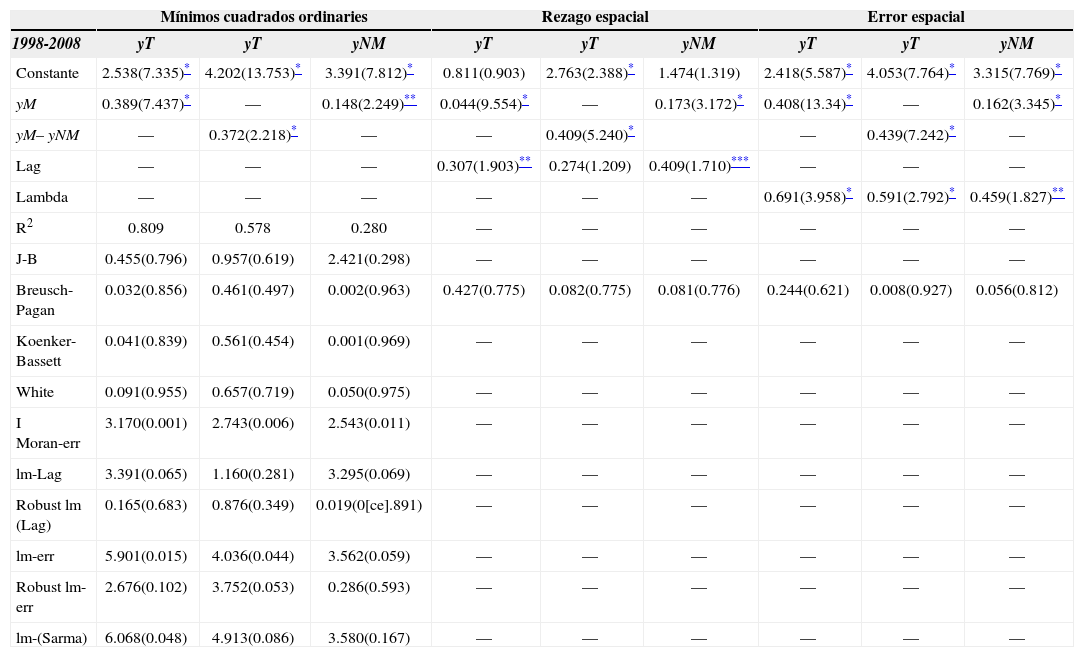
En el cuadro 3 se muestran los mismos resultados de la primera ley de Kaldor para el caso coreano. En contraste con los resultados para México, en Corea el sector manufacturero sí resulta significativo en el crecimiento del pib; tanto en el modelo simplificado de Kaldor como en las ecuaciones modificadas, el sector manufacturero impacta positiva y significativamente la tasa de crecimiento de la economía coreana con coeficientes que se encuentran entre 0.389 y 0.148. Aunque no se cuenta con otros estudios similares para las regiones coreanas, la evidencia mostrada por Felipeet al. (2007) para un grupo de países asiáticos, entre los que se encuentra Corea del Sur, confirma el cumplimiento de la primera ley en el periodo 1980-2004. Las estimaciones realizadas por Mamgain (1999) para el conjunto del país también confirman la primera ley para Corea del Sur en el periodo 1960-1988.
- c)
Las pruebas de dependencia espacial que se presentan en el cuadro 3 para Corea indican la existencia de efectos espaciales, dado que el estadístico I-Moran-Err es significativo. Al mismo tiempo, las pruebas lm-Lag y lm-Error espaciales justifican la estimación de un modelo de error espacial. Los resultados obtenidos de dicho modelo espacial permiten verificar la existencia de efectos de derrama en el crecimiento, los cuales refuerzan positivamente los efectos del sector manufacturero en el conjunto de la economía coreana; los impactos espaciales, medidos por el coeficiente lambda, son del orden de 0.459 a 0.691.
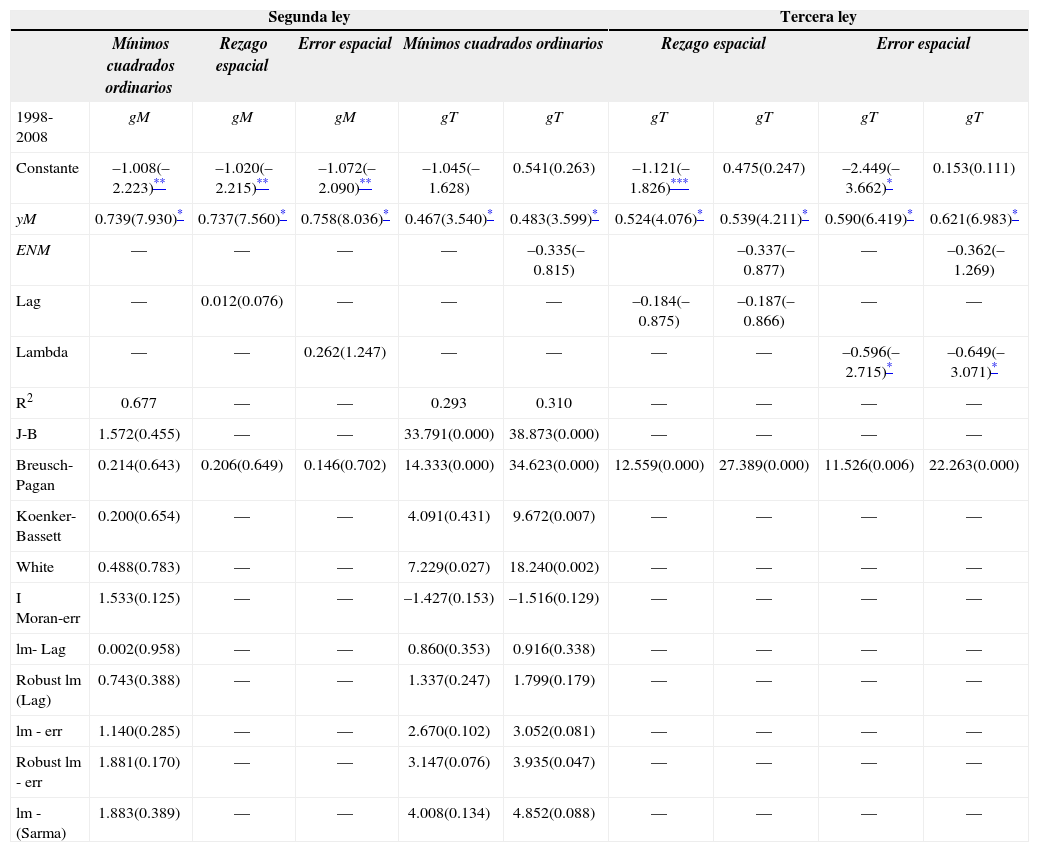
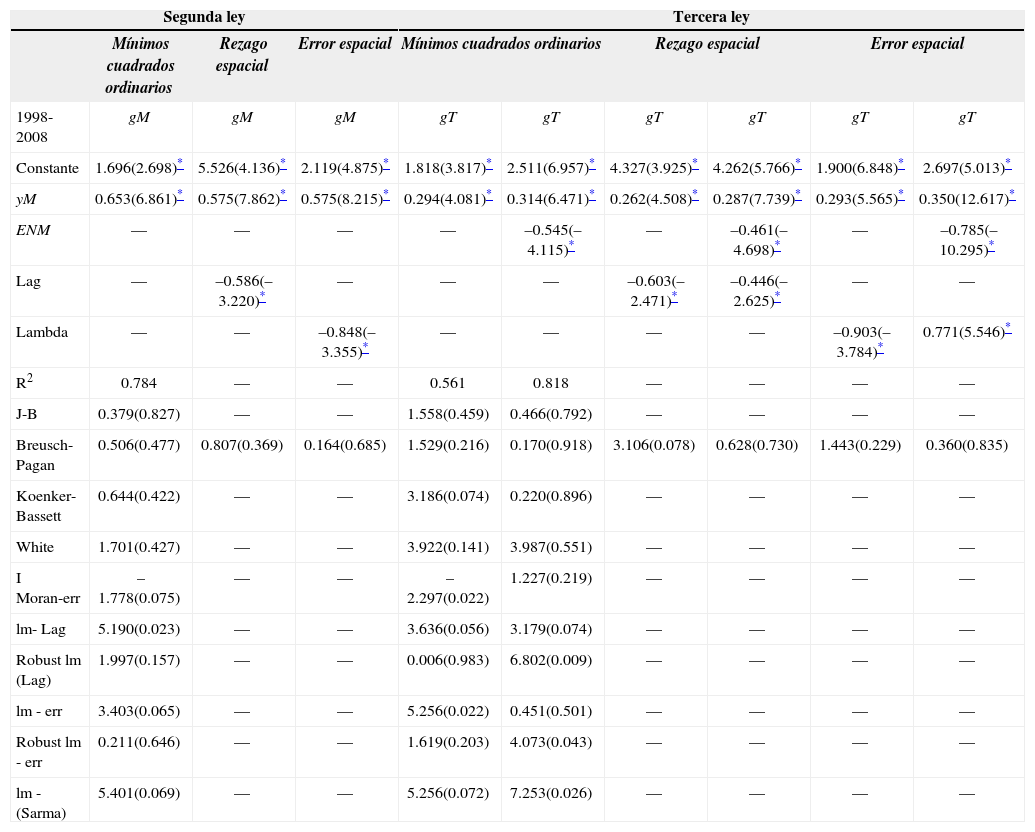
La segunda ley de Kaldor brinda elementos para considerar que el dinamismo del sector industrial, en particular del sector manufacturero, es significativo para la endogenización del crecimiento, por sus efectos positivos en la productividad del trabajo. En los cuadros 4 y 5 se presenta la evidencia empírica de esta segunda ley, de la cual destacamos los siguientes resultados:
- a)
En la economía mexicana existen economías dinámicas de escala en el sector manufacturero, lo cual se confirma al verificar que cuando crece el sector su productividad también se eleva; un punto porcentual de crecimiento manufacturero da lugar a un crecimiento de 0.73% (véanse los resultados de la primera columna del cuadro 4). Aun cuando se encontraron rendimientos crecientes en el sector, las pruebas lm de efectos espaciales no permiten confirmar la presencia de dependencia espacial en este proceso de crecimiento para el caso mexicano. En la estimación de la segunda ley de Kaldor, Ocegueda (2003) encontró coeficientes de 0.26 y 0.36, lo que valida la hipótesis de rendimientos crecientes a escala en la manufactura. Por su parte, Calderón y Martínez (2005) realizan estimaciones para los estados del país y encuentran coeficientes significativos y crecientes de 0.45 para 1965-1970 y de 0.68 para 1993-1998.
- b)
Para Corea, los resultados del cuadro 5 indican que el crecimiento del sector manufacturero tiene un efecto positivo sobre el crecimiento de la productividad del trabajo, con un coeficiente de 0.653. Es relevante señalar que, en trabajos que examinaban la evidencia de esta ley para los primeros años del proceso de industrialización coreana, el coeficiente estimado era 0.10 y se consideraba muy bajo en comparación con otros países (Woo-Sik, 1993). Para el período 1980-1997 las estimaciones de Mamgain (1999) dan cuenta de un coeficiente estimado entre 0.32 y 0.52, situación que se explica por el hecho de que en la primera fase del proceso de industrialización se promovió la absorción de mano de obra barata y, posteriormente, se creció con base en el desarrollo tecnológico. En nuestras estimaciones, las pruebas lm de efectos espaciales justifican la utilización de un modelo de error espacial (sus resultados se muestran en la tercera columna de resultados del cuadro 4). Un aspecto sobresaliente es el efecto negativo del rezago espacial, medido por el coeficiente lambda (–0.848). Esto implica que cuando se presenta un choque aleatorio en la productividad manufacturera de una región, la de las regiones vecinas tiende a decrecer, situación compatible con las relaciones tipo centroperiferia que se han discutido en los modelos de la Nueva Geografía Económica (nge) postulados por Krugman (1991).
México: segunda y tercera leyes de de Kaldor
| Segunda ley | Tercera ley | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Mínimos cuadrados ordinarios | Rezago espacial | Error espacial | Mínimos cuadrados ordinarios | Rezago espacial | Error espacial | ||||
| 1998-2008 | gM | gM | gM | gT | gT | gT | gT | gT | gT |
| Constante | –1.008(–2.223)** | –1.020(–2.215)** | –1.072(–2.090)** | –1.045(–1.628) | 0.541(0.263) | –1.121(–1.826)*** | 0.475(0.247) | –2.449(–3.662)* | 0.153(0.111) |
| yM | 0.739(7.930)* | 0.737(7.560)* | 0.758(8.036)* | 0.467(3.540)* | 0.483(3.599)* | 0.524(4.076)* | 0.539(4.211)* | 0.590(6.419)* | 0.621(6.983)* |
| ENM | — | — | — | — | –0.335(–0.815) | –0.337(–0.877) | — | –0.362(–1.269) | |
| Lag | — | 0.012(0.076) | — | — | — | –0.184(–0.875) | –0.187(–0.866) | — | — |
| Lambda | — | — | 0.262(1.247) | — | — | — | — | –0.596(–2.715)* | –0.649(–3.071)* |
| R2 | 0.677 | — | — | 0.293 | 0.310 | — | — | — | — |
| J-B | 1.572(0.455) | — | — | 33.791(0.000) | 38.873(0.000) | — | — | — | — |
| Breusch-Pagan | 0.214(0.643) | 0.206(0.649) | 0.146(0.702) | 14.333(0.000) | 34.623(0.000) | 12.559(0.000) | 27.389(0.000) | 11.526(0.006) | 22.263(0.000) |
| Koenker-Bassett | 0.200(0.654) | — | — | 4.091(0.431) | 9.672(0.007) | — | — | — | — |
| White | 0.488(0.783) | — | — | 7.229(0.027) | 18.240(0.002) | — | — | — | — |
| I Moran-err | 1.533(0.125) | — | — | –1.427(0.153) | –1.516(0.129) | — | — | — | — |
| lm- Lag | 0.002(0.958) | — | — | 0.860(0.353) | 0.916(0.338) | — | — | — | — |
| Robust lm (Lag) | 0.743(0.388) | — | — | 1.337(0.247) | 1.799(0.179) | — | — | — | — |
| lm - err | 1.140(0.285) | — | — | 2.670(0.102) | 3.052(0.081) | — | — | — | — |
| Robust lm - err | 1.881(0.170) | — | — | 3.147(0.076) | 3.935(0.047) | — | — | — | — |
| lm -(Sarma) | 1.883(0.389) | — | — | 4.008(0.134) | 4.852(0.088) | — | — | — | — |
Corea: segunda y tercera leyes de de Kaldor
| Segunda ley | Tercera ley | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Mínimos cuadrados ordinarios | Rezago espacial | Error espacial | Mínimos cuadrados ordinarios | Rezago espacial | Error espacial | ||||
| 1998-2008 | gM | gM | gM | gT | gT | gT | gT | gT | gT |
| Constante | 1.696(2.698)* | 5.526(4.136)* | 2.119(4.875)* | 1.818(3.817)* | 2.511(6.957)* | 4.327(3.925)* | 4.262(5.766)* | 1.900(6.848)* | 2.697(5.013)* |
| yM | 0.653(6.861)* | 0.575(7.862)* | 0.575(8.215)* | 0.294(4.081)* | 0.314(6.471)* | 0.262(4.508)* | 0.287(7.739)* | 0.293(5.565)* | 0.350(12.617)* |
| ENM | — | — | — | — | –0.545(–4.115)* | — | –0.461(–4.698)* | — | –0.785(–10.295)* |
| Lag | — | –0.586(–3.220)* | — | — | — | –0.603(–2.471)* | –0.446(–2.625)* | — | — |
| Lambda | — | — | –0.848(–3.355)* | — | — | — | — | –0.903(–3.784)* | 0.771(5.546)* |
| R2 | 0.784 | — | — | 0.561 | 0.818 | — | — | — | — |
| J-B | 0.379(0.827) | — | — | 1.558(0.459) | 0.466(0.792) | — | — | — | — |
| Breusch-Pagan | 0.506(0.477) | 0.807(0.369) | 0.164(0.685) | 1.529(0.216) | 0.170(0.918) | 3.106(0.078) | 0.628(0.730) | 1.443(0.229) | 0.360(0.835) |
| Koenker-Bassett | 0.644(0.422) | — | — | 3.186(0.074) | 0.220(0.896) | — | — | — | — |
| White | 1.701(0.427) | — | — | 3.922(0.141) | 3.987(0.551) | — | — | — | — |
| I Moran-err | –1.778(0.075) | — | — | –2.297(0.022) | 1.227(0.219) | — | — | — | — |
| lm- Lag | 5.190(0.023) | — | — | 3.636(0.056) | 3.179(0.074) | — | — | — | — |
| Robust lm (Lag) | 1.997(0.157) | — | — | 0.006(0.983) | 6.802(0.009) | — | — | — | — |
| lm - err | 3.403(0.065) | — | — | 5.256(0.022) | 0.451(0.501) | — | — | — | — |
| Robust lm - err | 0.211(0.646) | — | — | 1.619(0.203) | 4.073(0.043) | — | — | — | — |
| lm -(Sarma) | 5.401(0.069) | — | — | 5.256(0.072) | 7.253(0.026) | — | — | — | — |
(**) estadísticamente significativo a 5%;
(***) estadísticamente significativo a 10%.
La tercera ley de Kaldor es la vía para mostrar que el sector manufacturero contribuye a incrementar la productividad de los demás sectores, dando lugar a una economía más productiva y competitiva. En las últimas seis columnas de los cuadros 4 y 5 se presentan los resultados de las estimaciones de esta ley y sus aspectos más relevantes son los siguientes:
- a)
El crecimiento del sector manufacturero mexicano influye en el incremento de la productividad del trabajo de la economía; sus efectos van de 0.467 a 0.483 por ciento por cada punto porcentual de crecimiento manufacturero. Por su parte, el aumento del empleo no manufacturero no influye en el crecimiento de la productividad; el coeficiente obtenido en los resultados de la ecuación [5.1] indica que no es estadísticamente significativo. Resultados similares reporta Ocegueda (2003) en la comprobación de la tercera ley para las entidades federativas en la economía mexicana de 1980 al 2000. En ningún caso los modelos espaciales fueron significativos para ésta.
- b)
Para el caso coreano, el crecimiento del sector manufacturero influye positivamente en el aumento de la productividad del trabajo total de este país con un efecto del 0.294 a 0.314 por ciento por cada punto porcentual de crecimiento manufacturero. Sin embargo, en la ecuación modificada se constata que la tasa de crecimiento del empleo no manufacturero influye negativamente sobre la productividad global del trabajo (–0.545). Mamgain (1999) también confirma la tercera ley de Kaldor para Corea del Sur aunque utiliza una especificación diferente de las que aquí se emplearon. Las pruebas estadísticas lm de autocorrelación espacial indican que el modelo más adecuado es el de error espacial. De nueva cuenta se obtienen efectos espaciales de tipo centro-periferia. Un choque aleatorio sobre la productividad de una región coreana impacta negativamente en la de sus vecinos.
En suma, los resultados de la estimación de las tres leyes de Kaldor indican que existe un liderazgo del sector manufacturero en Corea, mientras que en México ese sector no es el motor del crecimiento de la economía. Sin embargo, en nuestro país se observa que la manufactura cuenta con rendimientos crecientes a escala e influye positivamente en la productividad de la economía. Para la economía mexicana no fue posible constatar efectos de derrama espacial del crecimiento, mientras que en el caso coreano dichos efectos existen para el crecimiento de la producción, lo cual refleja vinculaciones insumo-producto muy fuertes entre las regiones. Al mismo tiempo se observaron efectos espaciales tipo centro-periferia en el crecimiento de la productividad de las regiones coreanas.
ConclusionesEl crecimiento endógeno de un país es de vital importancia para afrontar y compensar los efectos de los choques económicos internacionales, reducir la desigualdad y promover un crecimiento económico más equilibrado. La industria, y en particular la manufactura, desempeñan un papel central en dicho proceso, al permitir la endogeneización del crecimiento. En el caso mexicano la industria no logra operar como motor del crecimiento y tampoco da lugar a externalidades espaciales que contribuyan a estimular procesos de causación acumulativa positiva en las regiones más dinámicas del territorio nacional. Corea es un caso contrastante, pues la industria es fundamental para explicar el crecimiento y se aprecian los efectos espaciales de este proceso de las regiones más dinámicas al resto del país.
Desde la perspectiva kaldoriana, la endogenización del crecimiento es posible si se logra liderazgo sectorial del sector manufacturero. El desarrollo del sector manufacturero mexicano, si bien contribuye a la productividad de los demás sectores no ha sido capaz de operar como fuerza de arrastre ni de generar efectos de derrama del crecimiento. El caso coreano muestra que ahí la manufactura si impulsa el crecimiento general de la economía e incide en la productividad global. Sin embargo, las concentraciones industriales coreanas operan en un marco de relaciones centro-periferia cuando se presentan choques en la economía; las concentraciones más ricas tienen procesos acumulativos en tanto que sus regiones vecinas tienden a decrecer en su productividad.
Pese a las debilidades del proceso de industrialización mexicano, la indus-tria sí tiene efectos en la productividad sectorial, los cuales podrían traducirse en tasas más elevadas de crecimiento de la economía si la política industrial se orientara a promover los clusters más dinámicos del crecimiento industrial en las regiones del país. Es decir, la utilización de una política industrial nacional, sectorial y regional podría, a mediano plazo, incidir en la conformación de un sector industrial más sólido, con mayores vinculaciones regionales e inter-sectoriales, con lo cual se podría sustentar un crecimiento más elevado de la economía. En particular, la debilidad del sector industrial como motor del crecimiento en México tiene una de sus explicaciones en el hecho de que las políticas industriales se dejaron de lado por un largo tiempo, mientras que en Corea se mantuvieron, adaptaron y reformularon en función de las experiencias obtenidas y de los desafíos de cada periodo (cepal, 2012). Asimismo, en Corea la política industrial ha contado con una fuerte base territorial que operó mediante la construcción de parques industriales regionales, apoyos para la descentralización y el desarrollo de obras de infraestructura (Joh, Young-Pyo y Koh, 2012). En México, como lo han constatado Isaac y Quintana (2012) y Pradilla (2012), las principales zonas metropolitanas han concentrado la base industrial del país y por ello una política clara de reindustrialización sustentable de esas áreas podría contribuir a darle preponderancia a la industria como motor del crecimiento del país.
Los autores agradecen los valiosos comentarios de dos dictaminadores anónimos. Este trabajo fue apoyado por el Fondo de Investigación de la Hankuk University of Foreign Studies de 2012, y la Cátedra Especial “José Vasconcelos” de la fes-Acatlán.
Los autores agradecen los valiosos comentarios de dos dictaminadores anónimos. Este trabajo fue apoyado por el Fondo de Investigación de la Hankuk University of Foreign Studies de 2012, y la Cátedra Especial “José Vasconcelos” de la fes-Acatlán.
Los autores agradecen los valiosos comentarios de dos dictaminadores anónimos. Este trabajo fue apoyado por el Fondo de Investigación de la Hankuk University of Foreign Studies de 2012, y la Cátedra Especial “José Vasconcelos” de la fes-Acatlán.
Las dos matrices de pesos espaciales W1 y W2 están asociadas respectivamente con un proceso espacial autorregresivo en la variable dependiente y en el término de error. Simplemente se sigue la notación planteada por Anselin (1988: 34).
Las pruebas de efectos espaciales utilizadas fueron las versiones Multiplicador de Lagrange (retardo) y Multiplicador de Lagrange (error). La metodología utilizada en la selección de modelos fue la propuesta por Anselin (1988) y Anselin y Griffith (1988), en la cual el no rechazo de la hipótesis nula de no significancia de los efectos espaciales lleva a mantener el modelo sin dichos efectos; el rechazo de una de las dos pruebas mencionadas lleva a la utilización del modelo espacial correspondiente (retardo espacial o error espacial) y el rechazo en las dos pruebas lleva a la utilización de las pruebas robustas correspondientes para identificar cuál de los dos modelos es el más significativo.
La productividad manufacturera se calculó como la producción interna manufacturera dividida entre el empleo del mismo sector.
Aquí se hace una diferencia respecto a los obreros y empleados. Donde los obreros son los que producen realmente los bienes y los empleados ayudan a realizarlos.
El índice de Moran sigue una distribución normal estandarizada en muestras grandes, de forma tal que un valor positivo (negativo) significativo del índice Z(I) llevará al rechazo de la hipótesis nula de no autocorrelación espacial y a la aceptación de autocorrelación espacial positiva (negativa).
El periodo analizado abarca de 1998 a 2008 y está en función de su disponibilidad y homogeneidad. Para el caso de la economía coreana, la información a nivel regional se encuentra disponible de 1989 a 2010, en tanto que para México la información homogénea es de 1998 a 2008. Los datos utilizados provienen de los Censos Económicos de 1999, 2004 y 2009 del Instituto Nacional de Estadística y Geografía (inegi), del Korea Eximbank (disponible en: http://www.koreaexim.go.kr>) y del Statistics Korea (disponible en: <http://kostat.go.kr>).
La técnica utilizada aquí es exploratoria y se sustenta en el Análisis Exploratorio de Datos Espaciales (esda, por sus siglas en inglés). El uso de esda permite identificar la existencia de regímenes espaciales en los datos, en particular los mapas lisa son un indicador local de dependencia espacial significativa y se construyen a través del índice de Moran; muestran las regiones que contribuyen significativamente al índice global de Moran y que conforman entre sí clusters significativos de dependencia espacial. Sus peculiaridades se pueden ver en Anselin (2005).