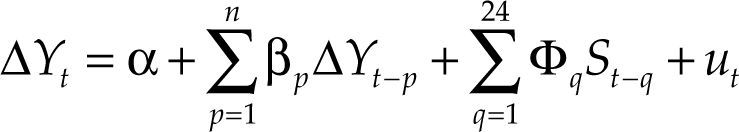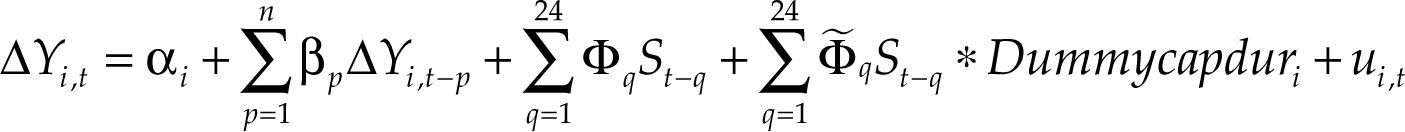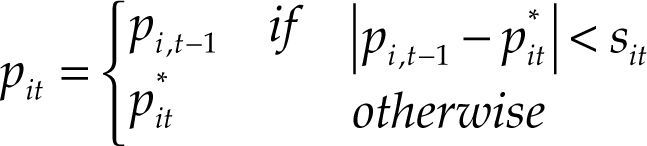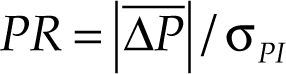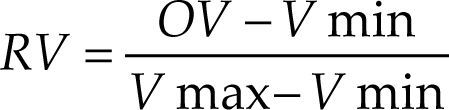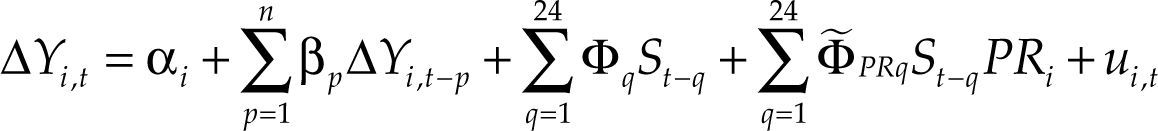Industrial structure and transmission of monetary policy in Latin American countries

Abstract

Based on data from the manufacturing industry and its subsectors, this article shows the impact of monetary policy according to the industrial structure in Brazil, Chile, Colombia, Mexico and Peru, the five Latin American countries adopting the system of inflation targeting for the longest time. Results show that the impact of monetary policy on industrial production is stronger in countries where the interest rate channel is more relevant, since the subsectors producing capital goods and durable consumer goods are more sensitive to monetary decisions. These results are closely linked to the role of price rigidities on the differential impact of monetary policy on industrial subsectors.

Resumen

Este artículo emplea información de la industria manufacturera y los subsectores que la componen con el fin de determinar la incidencia de la estructura industrial en la transmisión de la política monetaria en Brasil, Chile, Colombia, México y Perú, los cinco países de América Latina donde más tiempo lleva operando el esquema de inflación objetivo. Los resultados obtenidos muestran que el impacto de la política monetaria sobre la producción industrial es mayor en los países donde el canal de tasa de interés es más relevante, al ser los sectores productores de bienes de capital y de consumo duradero los más sensibles a las decisiones monetarias. Estos resultados están muy relacionados con el papel de las rigideces de precios en las diferencias en el impacto de la política monetaria sobre los subsectores industriales.

INTRODUCTION

The study of monetary policy impacts on productive activity and its transmission channels has been a subject of great interest in recent decades, both in developed and emerging economies. In Latin America, only a few studies in a vast literature have dedicated attention to comparative analyses of countries. An exception is Quintero (2015), who estimated both the impact of monetary policy on economic activity and the incidence of the main transmission channels in the five countries adopting inflation targeting for the longest time (Brazil, Chile, Colombia, Mexico and Peru). Based on structural vector autoregressions (svar) for each country, but employing the same variables to make results comparable, the study found that Mexico and Peru are the countries where total production is more responsive to unexpected movements in interest rates set by monetary policy. This result is mainly explained by the high relevance of the interest rate channel in monetary transmission in these countries compared to Chile and Brazil. In Colombia, the interest rate channel is also important, but due to the weak operation of the exchange rate channel and those associated with views on credit, the impacts of monetary policy on production are weaker.

Another hypothesis from Quintero (2015) is that country differences in the importance of the interest rate channel, and the resulting ones in the impact of monetary policy on total production, derive from how economic structure mediates the effect of monetary policy on production. In principle some sectors should be more sensitive to monetary policy and changes in interest rate, due to the higher elasticity of demand for produced goods. This could explain why the interest rate channel works differently depending on the country.

Testing this hypothesis requires data on disaggregated production by sector or economic activity, and corresponding estimates of the effects of monetary policy shocks. Several studies were published on this topic at global level. Since Bernanke and Gertler (1995), interest in sectoral effects of monetary policy has grown and contributed to the identification of transmission channels of monetary policy. The underlying logic is that if two sectors respond differently to the same monetary policy, they must exhibit differences affecting the operation of channels. Therefore, the usual methodology applied in such studies is to identify monetary policy shocks, measure their impact on different sectors, and attribute differences to structural characteristics affecting the transmission channels.

Notwithstanding their relevance for the identification of transmission channels, no previous study of monetary policy effects on economic sectors is known for Latin American countries. The reason may be the lack of long-time series of sectoral production or appropriate indicators of monetary policy, as a result of the changes in monetary policy in the region over the last three decades.

This study seeks to overcome this limitation by analysing the effects of monetary policy on industrial manufacture subsectors in Latin America. This approach has three advantages. First, various sectoral studies at global level have revealed that the manufacturing sector is one of the most sensitive to monetary policy. Therefore, this article focuses on a sector able to provide relevant insights about why effects of monetary policy on productive activity differ by country. Second, monthly production data are available for the selected countries both for industry in general and its subsectors, allowing for utilizing the monetary policy shocks estimated in Quintero (2015), which, in spite of being obtained for a relatively short time horizon (January 2003-June 2013), have the advantage of being estimated using only one indicator as an instrument of monetary policy (the interest rate of monetary policy), whereby controlling for changes in the monetary policy management. And thirdly, since total manufacturing output can be broken down into various subsectors, one can measure the response to monetary policy shocks manifested by economic activities with more clearly defined characteristics and associated interest rate channels.

The first aim of the article is to assess the impact of monetary policy on manufacturing production in the five countries mentioned above through autoregressive distributed lag modelling (adl), which revealed that unexpected increases in the monetary policy interest rate generate larger decreases in industrial production in Mexico, Colombia and Peru, but have no statistically significant impacts in Chile and Brazil.

Next, taking advantage of extensive information on manufacturing industry, we evaluate the importance of the interest rate channel by estimating adl models independently for four large sectors according to produced final good. If channels operate as predicted, the subsectors producing capital goods and durable consumer goods should be the most sensitive to monetary policy. Results strongly confirmed the prediction for Mexico and Colombia, while in Peru, Chile and Brazil differences between sectors were not statistically significant.

Finally, given that according to the channel theory the effect of monetary policy transmission on real activity is determined by price rigidities, we examine how they can explain differences in the impact of monetary policy shocks on different subsectors. Results revealed that subsectors with greater price rigidity are more responsive to monetary policy only in Mexico and Colombia, precisely the two countries where the interest rate channel most significantly affects transmission to industrial production.

This paper is organised as follows. Section 2 reviews the most relevant empirical literature at the global level on sectoral differential impacts of monetary policy. Section 3 estimates the effects of monetary policy shocks on manufacturing output in the five countries. Section 4 relates country differences in the effect of monetary policy to differences in industrial structure, while section 5 analyses the role of price rigidities in differential sector effects. Finally, section 6 presents the conclusions of the study.

PREVIOUS EMPIRICAL STUDIES

Studies of sectoral effects due to monetary policy have not yet addressed Latin American countries. At the global level, the major study was performed by Bernanke and Gertler (1995) who measured responses of important components of private domestic expenditure to monetary contraction in the United States. Using monthly data from 1965 to 1993 and estimating svar models for each sector, they found that residential investment exhibited the most drastic fall and explained most of the contraction in final demand, followed by durable and non-durable consumer goods. Fixed corporate investment also declines but with comparatively more lag.

Much of the literature is based on the methodology proposed by Bernanke and Gertler (1995). In a similar study in the United States for seven large sectors defined by demand type, Raddatz and Rigobon (2003) analysed quarterly data from 1955 to 2002 and found that monetary policy has a greater impact on durable and non-durable consumer goods and residential investment. Since sectors most sensitive to interest rate are in principle also the most affected by monetary policy shocks, their results confirm the importance of the interest rate channel.

Sectoral studies have mostly focused on differences in response to monetary policy among sectors according to productive activity. The influential study by Arnold and Vrugt (2002) identified significant differences in the impact of a monetary policy shock on production in 11 regions and 12 economic sectors in the Netherlands in the period 1973-1993. Construction, trade, industry, finance and agriculture were the most responsive sectors, as well as the regions where construction had a larger share in total production. Together, their results confirmed the importance of the interest rate channel in the Netherlands.

Another relevant study by Alam and Waheed (2006) based on quarterly data from 1973 to 2003 found evidence of differences in response to monetary policy shocks in seven major economic activities in Pakistan, with the strongest effects being manifested in the mining, manufacturing, wholesale, retail, and financial sectors.

Other studies have relied instead on micro data. Based on quarterly data from 1971 to 2004, Jansen, Kishan and Vacaflores (2013) showed that monetary policy had a heterogeneous impact on net sales in eight large sectors of the American economy, with a greater effect on wholesale and retail trade and the services sector.

As for the few studies focusing on the manufacturing industry, three deserve mentioning. Ganley and Salmon (1997) compiled data for 24 economic activities (14 in industry) and found that the construction sector was the most affected by monetary policy. Industry as a whole is very sensitive to monetary policy, with marked differences in response among its subsectors. The weakest effect was observed in the food, beverage and tobacco sector, and the biggest in the production of rubber and electronic equipment.

Later, the study by Hayo and Uhlenbrock (1999) for 28 subsectors of German industry and mining based on monthly data from 1978 to 1994 concluded that heavy industries react more strongly to interest rate shocks than non-durable goods sectors such as food and clothing. By relating the results to sectoral characteristics, they found that the magnitude of capital stock relative to product, export orientation and government subsidies are the main factors explaining differences among sectors, suggesting that the interest rate and exchange rate channels are the most important in Germany.

Another important study by Dedola and Lippi (2005) compiled monthly data from 1975 to 1997 disaggregated into 21 industrial subsectors in five countries (France, Germany, Italy, the United Kingdom and the United States), revealing a weaker impact on food and textiles, and a stronger response by the heavy industries (iron and machinery and equipment, and vehicles). Furthermore, the response of sectoral production to monetary policy shocks is systematically related to product durability, financial requirements, borrowing capacity and firm size, which demonstrates the operation of the interest rate and credit channels in the five countries.

Two other studies addressed the industrial sector based on a relevant methodological variant. Peersman and Smets (2005) investigated the effects of a change in monetary policy on output growth in 11 industrial subsectors in 11 Eurozone countries between 1980 and 1998. They estimated a svar to obtain a single history of monetary policy shocks in Europe, and then assessed their effect on economic growth based on country-specific regressions also distinguishing between shocks during expansion or recession periods. Results revealed both significant heterogeneity among industries in the general effects of monetary policy and a considerable asymmetry between the two phases of the economic cycle. Rodríguez and Padrón (2008) also investigated monetary policy shocks in Spain through data on aggregated variables between 1988 and 1998 and a svar model specifying a reaction function for the monetary authority. They analysed the response of different industrial sectors to the same history of monetary shocks, identifying significant differences in sectoral responses.

An alternative to the application of vector autoregressions modelling (var) of sectoral impacts of monetary policy shocks is the estimation of a dynamic stochastic general equilibrium model (dsge) for heterogeneous production sectors, as in Bouakez, Cardia, and Ruge-Murcia (2009) for the United States. dsge models relax the standard symmetry assumptions, allowing companies in different sectors to vary in degree of price rigidity, production technology and input use. Estimation is based on the Generalised Method of Moments. The authors concluded that the sectors reacting most strongly to monetary policy are services, construction, durable goods industry, non-durable goods industry, and finally the primary sector (agriculture and mining). The main advantage of this approach over svar models is that it directly identifies the mechanism behind different sectoral responses, which in this case were the price rigidities specific to some sectors but transmissible to the whole economy through its input-output structure. However, dsge models are computationally demanding due to the high number of parameters and simultaneous solution of a large system of nonlinear equations. Such drawbacks require the decomposition of production into a few large sectors, which prevents a precise identification of particular sectoral characteristics underlying the transmission of monetary policy.

IMPACT OF MONETARY POLICY ON INDUSTRIAL PRODUCTION IN LATIN AMERICAN COUNTRIES

The above review shows that the common methodology to previous studies on sectoral effects of monetary policy is the estimation of a svar model for each sector including as main variables the sectoral production, a monetary policy indicator, and a price index. However, by changing the sectoral production variable in each sectoral svar model, a different monetary policy shock is applied to each sector, a problem exemplified in Ganley and Salmon (1997), Hayo and Uhlenbrock (1999), and Dedola and Lippi (2005).

To overcome this problem, we adopt here a methodological approach similar to the one defined by Peersman and Smets (2005) and Rodríguez and Padrón (2008). They estimate different adl models for each country, first for the total manufacturing industry and then for industrial subsectors, using the same history of monetary policy shocks. However, our study is innovative by being the first on developing economies including Latin America, and by grouping industrial subsectors according to the type of final good. In addition, a measure of price rigidity is calculated for each subsector to identify its impact on the operation of the interest rate channel.

The impact of a monetary policy shock on the total manufacturing industry is measured using the regression:

Where γ is the total manufacturing production index and S are monetary policy shocks.

adl models of this type are found in the two influential studies by Romer and Romer (2004, 2010) who analysed the effects of monetary policy shocks and tax changes respectively on production in the United States. A weakness of those models is that they do not control for other factors affecting industrial production and may therefore generate biased results. However, omitted variables can generate biases only if they correlate with the monetary policy shock variable. In contrast, since our svar model includes the most relevant macroeconomic variables, the estimated shocks are not related to these variables, and therefore their omission does not generate biases. Additionally, a potential bias due to omitted variables is reduced by the inclusion of dependent variable lags, which helps to control for the normal dynamics of output. Finally, since many factors affecting production are likely to be serially correlated, our procedure also controls for other influencing factors.

The number of lags used in the industrial production index was different for each country, and their selection was always based on the optimum number suggested by at least two of three information criteria: Akaike, Schwarz and Hannan-Quinn. The number of dependent variable lags in the models for Chile and Colombia was two, for Brazil and Colombia three, and for Mexico four.

As for the number of lags in the monetary shocks variable, the base estimate included 24 lags, since the greatest impacts of monetary policy on total productive activity are usually recorded in the first two years after a shock (Quintero, 2015). Another reason to limit the number of shock lags to 24 is that each additional shock increases the number of parameters to be estimated and decreases the study period by one month. However, as shown below the results are robust in all countries up to 30 lags.

Given the regression structure, the effect of a monetary policy shock of 1% is estimated not only by the coefficients directly measuring its impact on production, but also by effects transmitted through product lags. Therefore, the estimated impact of a monetary policy shock is the dynamic multiplier taking product lags into account. Hence the estimated product growth one month after the recorded shocks is Φ₁, the coefficient for the first S lag; the estimated product growth after two months is Φ₁ + (Φ₂ + β₁Φ₁); and so on.

As for our data, the production indicator was defined as the logarithm of the industrial production index calculated monthly by the national statistical institutes. All data were seasonally adjusted using the Census X12-Arima method¹. Statistical stationarity of this variable was verified for each country through the Augmented Dickey-Fuller Fisher (adf) in both the levels and first differences of the variable. The maximum number of lags was automatically selected based on the Schwarz information criterion. The results are presented in Table 1. As all series are integrated of order one, or I(1), in all the countries equation [1] was estimated with production as a variable in first difference.

Table 1.

adf-Fisher unit root test of industrial production.

Series	Brazil		Chile		Colombia
	Level	1 difference	Level	1 difference	Level	1 difference
Log of industrial production index	–2.39	–5.54^***	–2.41	–15.9^***	–2.08	–16.0^***
Series	Mexico		Peru
	Level	1 difference	Level	1 difference
Log of industrial production index	–1.24	–3.7^***	–1.73	–6.03^***

Note: Significance levels, 1% (***), 5% (**), 10% (*).

Source: Own estimates.

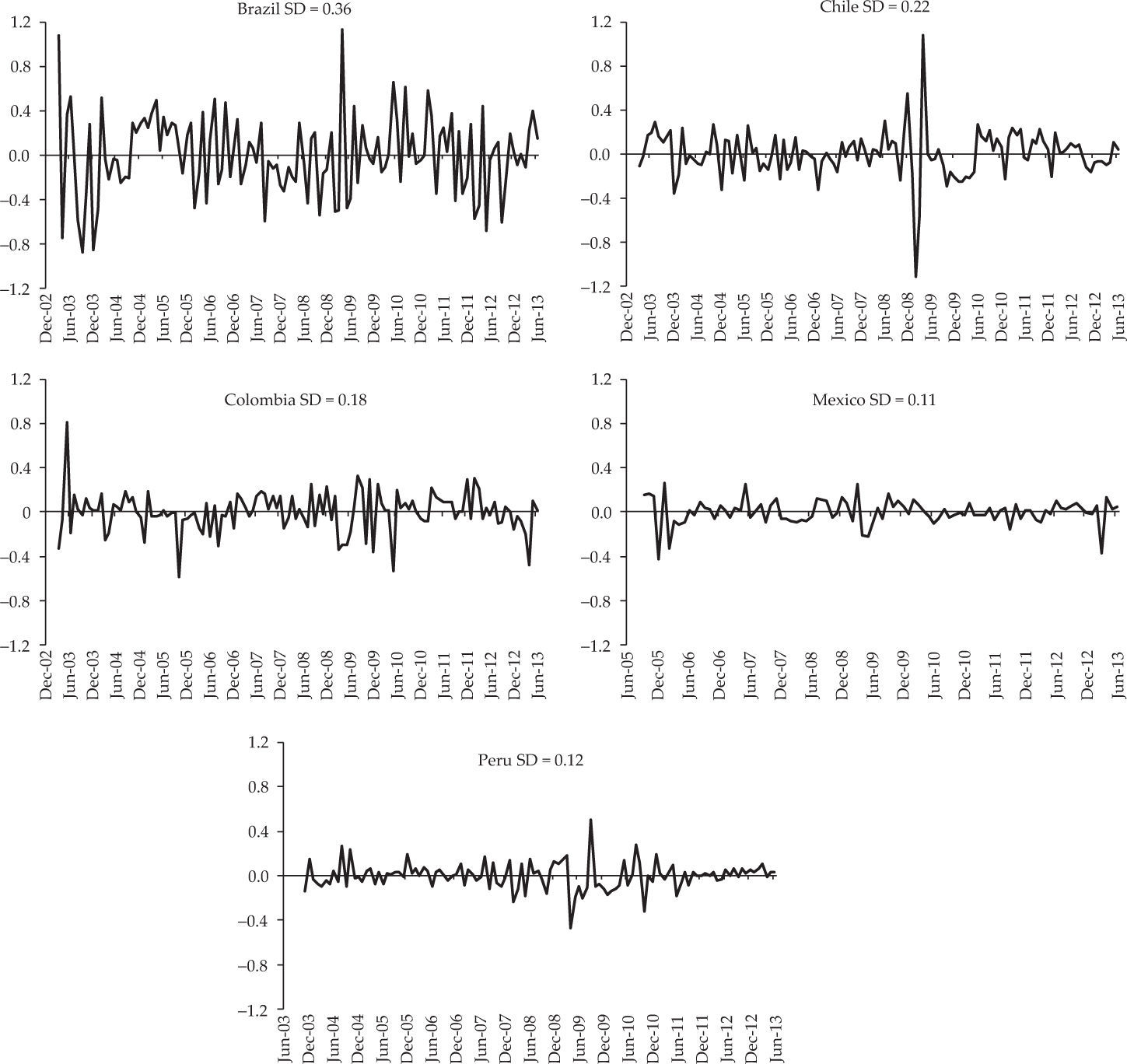
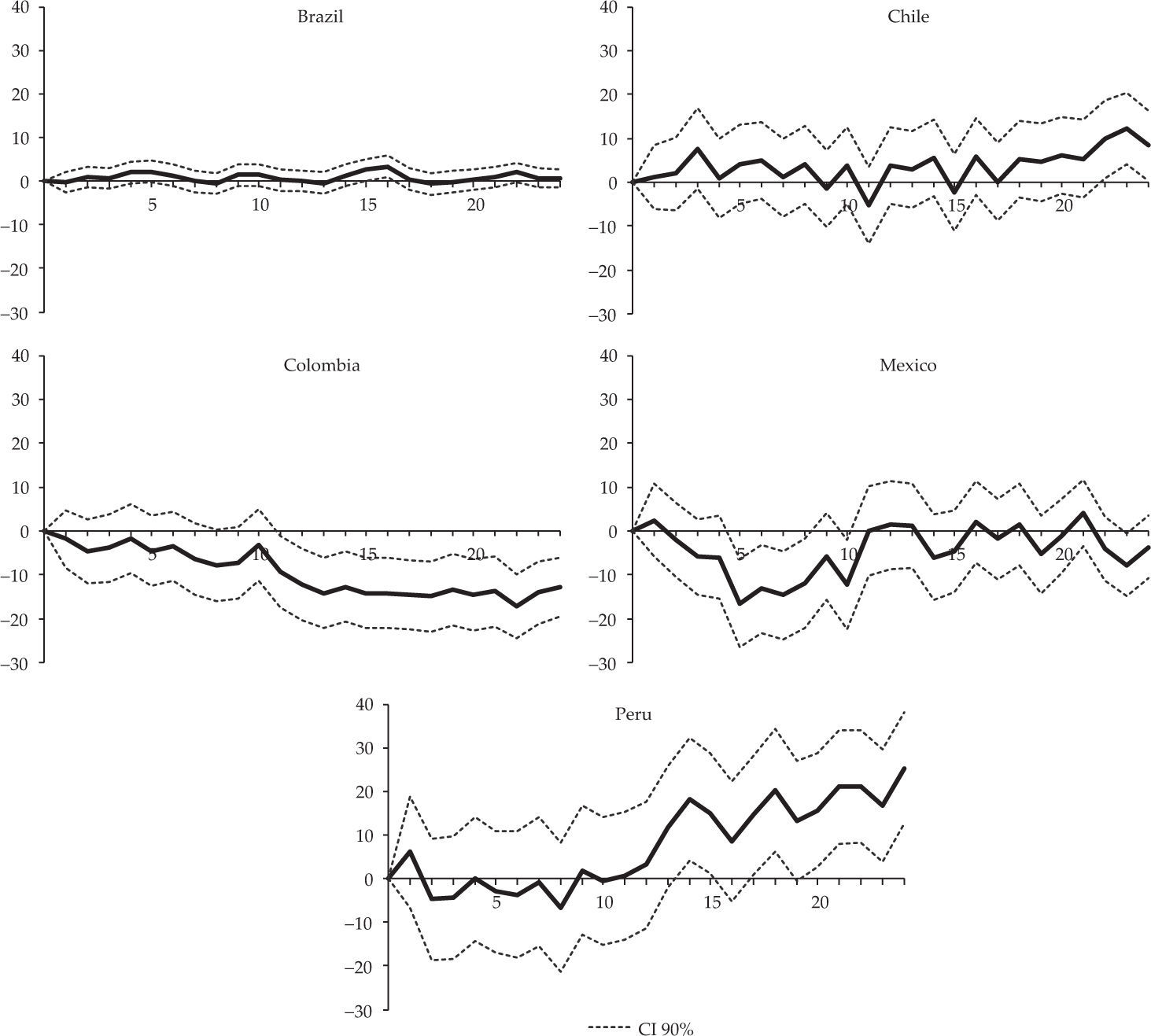
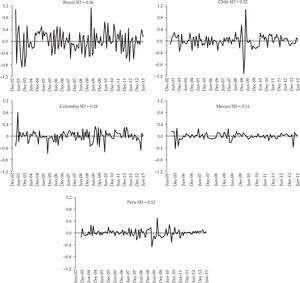
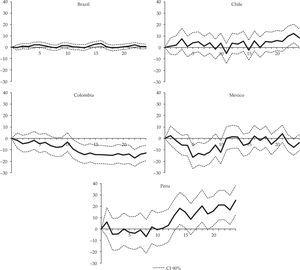
We rely on the estimates of monetary policy shocks for the five countries made by Quintero (2015) who applied svar models in levels estimated for each country using the same variables (economic activity index, consumer price index, oil prices, embi index as a country risk indicator, monetary policy interest rate, and M1 as monetary aggregate). Shocks were estimated between January 2003 and June 2013 in Brazil, Chile and Colombia, while in Peru and Mexico they had to be calculated for a slightly shorter period (November 2003-June 2013 and September 2005-June 2013 respectively) due to their use of the short-term interest rate as the monetary policy instrument. The patterns of shocks in the five countries is shown in Figure 1, which reveals less volatility in Mexico and Peru where monetary policy remained stable for most of the analysed period, especially in the last months and after the strong downward adjustments in interest rate in all five countries as a response to the global financial crisis of 2008 and 2009².

Figure 1.

Monetary policy shocks in Latin American countries, 2003-2013

Source: Quintero (2015).

The period for estimation of equation [1] was determined by the availability of monetary policy shocks. However, during the analysed period in Chile there were several methodological changes in the calculation of the industrial production index, such as changes in measurement and weights of industrial subsectors. For this reason, the index base 2002 was used, which is available until December 2011, being this the limit of the period of study for this country and not June 2013 as in the rest of the countries. And with regard to the method of estimation of the equation [1], ordinary least squares (ols) was used, assuming that monetary policy shocks obtained in Quintero (2015) are orthogonal to the behavior of the industry, considering that the indicator of economic activity used for estimating the shocks gathers in all countries the behavior of industrial production.

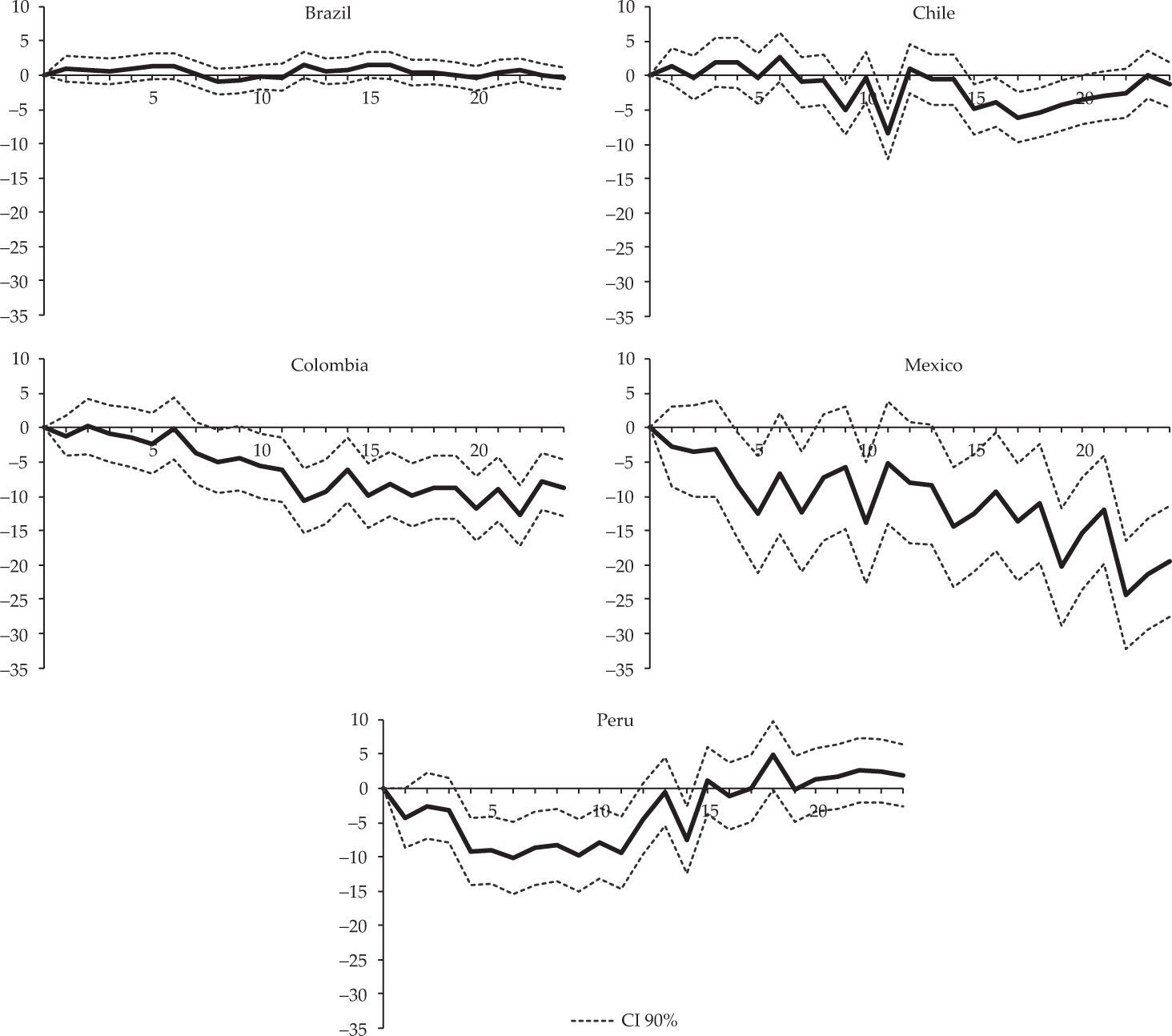
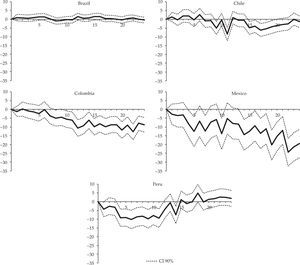
Figure 2 shows the results obtained for the five countries represented by the impulse response function with 90% confidence intervals³. Mexico, Colombia and Peru (in that order) are the countries where an unexpected increase in the interest rate of 1% leads to the most significant drops in industrial production. The impact on industrial production in Mexico is noticeable from month 5 and peaks in month 22 with a cumulative effect of 24.3 percentage points (pp). In Colombia, the response is weak during the first six months but later becomes significant and also peaks in month 22 (12.8 pp). In Peru, impacts are mostly limited to the first year, reaching the highest cumulative impact (10.2 pp) in month 6. In Chile, although the response is negative most of the time, there are significant fluctuations especially during the first year and the overall impact is not statistically significant. The maximum response was 8.5 pp in month 11. Brazil is the only country where industrial production does not respond significantly to monetary policy. The highest cumulative response was 1 pp in month 8.

Figure 2.

Impact of a positive shock of 1% in interest rate on industrial production in Latin American countries

Source: Own estimates.

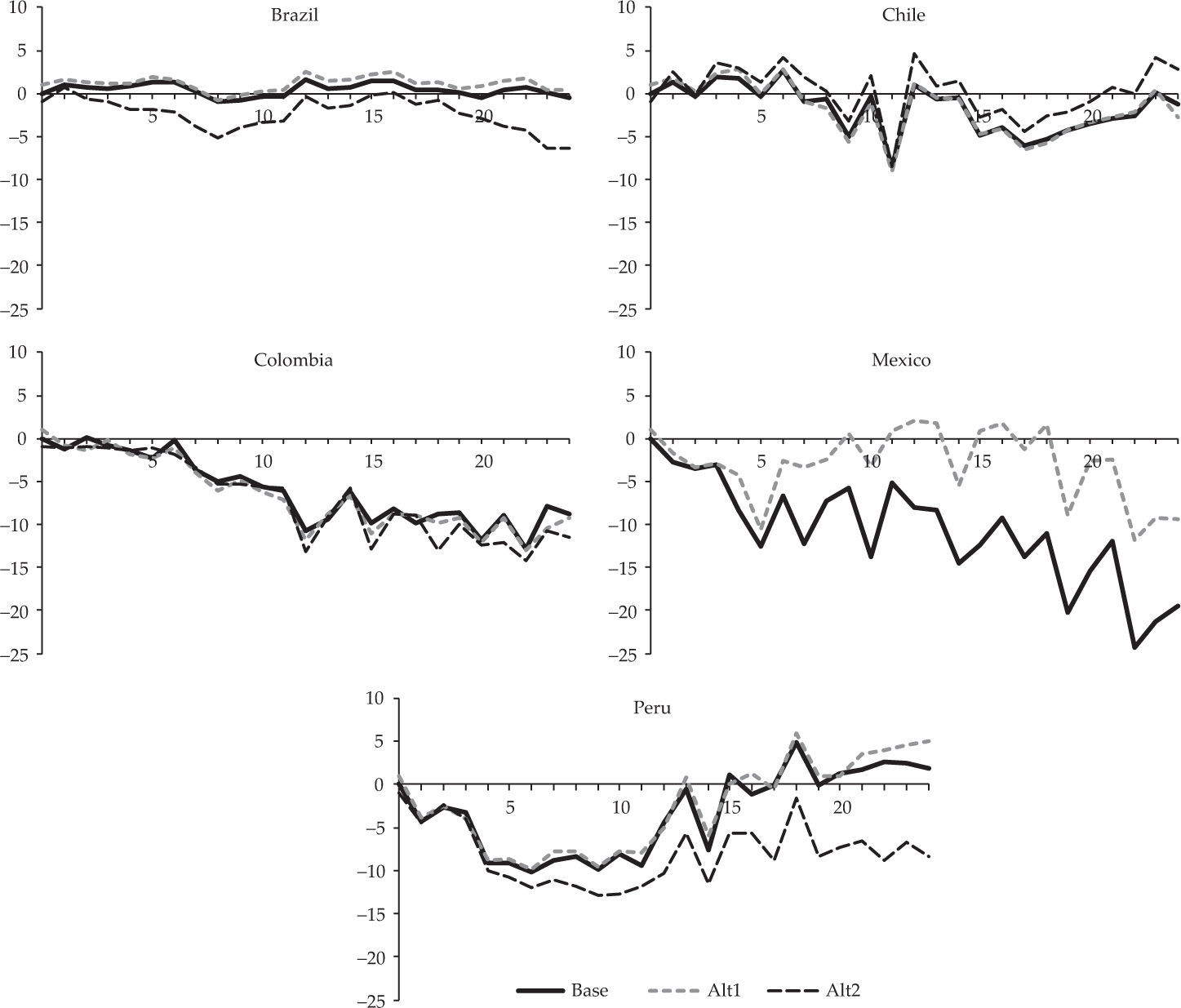
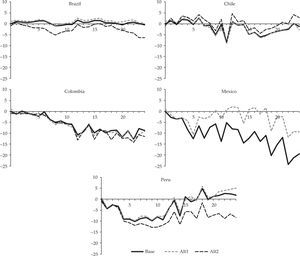
As evidence of robustness, two additional models were estimated for each country. In the first, the base model was estimated using 30 lags of monetary policy shocks, but with the same dependent variable lags. The second alternative model adopts the same base model specification but uses a common period for all countries (September 2005-June 2013), during which data on the indicator of monetary policy are available for Mexico⁴.

Figure 3 shows the responses of economic activity for each country during the same 24 months after monetary shocks from the base model and the two alternative models. The inclusion of additional lags (alternative model 1) does not alter the estimates dramatically, except for Mexico where fewer observations increase the sensitive of results. On the other hand, homogenising the study period across countries, changes the magnitude of impacts in some countries (notably Brazil and Peru) but does not modify the overall results⁵.

Figure 3.

Impact of a positive shock of 1% in interest rate on industrial production in Latin American countries (base model vs. alternative models)

Source: Own estimates.

INDUSTRIAL STRUCTURE AND THE INFLUENCE OF THE INTEREST RATE CHANNEL

Within the price vision of the financial market, the interest rate channel has been traditionally the most popular in literature, and one of the reasons is because it is the key mechanism of monetary transmission in IS-LM model, that is widely addressed in the text books on macroeconomics. The channel implies that an increase in the monetary policy interest rate increases the interest rate that the financial system charges on loans to the public. Given the rigidities of prices, the real interest rate on loans also increases, generating an increase in the cost of capital and decreasing the demand for goods, especially capital and durable consumption goods whose demand is in principle more sensitive to the interest rate (Taylor, 1995; Mishkin, 1996). Non-durable consumer goods in contrast are mainly staple goods whose demand is less elastic and should be less affected by changes in interest rate. Companies producing capital goods or durable consumer goods should therefore be more affected by a monetary contraction.

This section relies on characteristics of the manufacturing industry subsectors to establish the role of the interest rate channel in explaining differences in responses of countries to monetary policy. For this purpose, production indexes are calculated for four sectors depending on the type of final goods produced: non-durable consumer goods, durable consumer goods, intermediate goods and capital goods. We predict capital goods and durable consumer goods to be the most affected by a monetary policy shock.

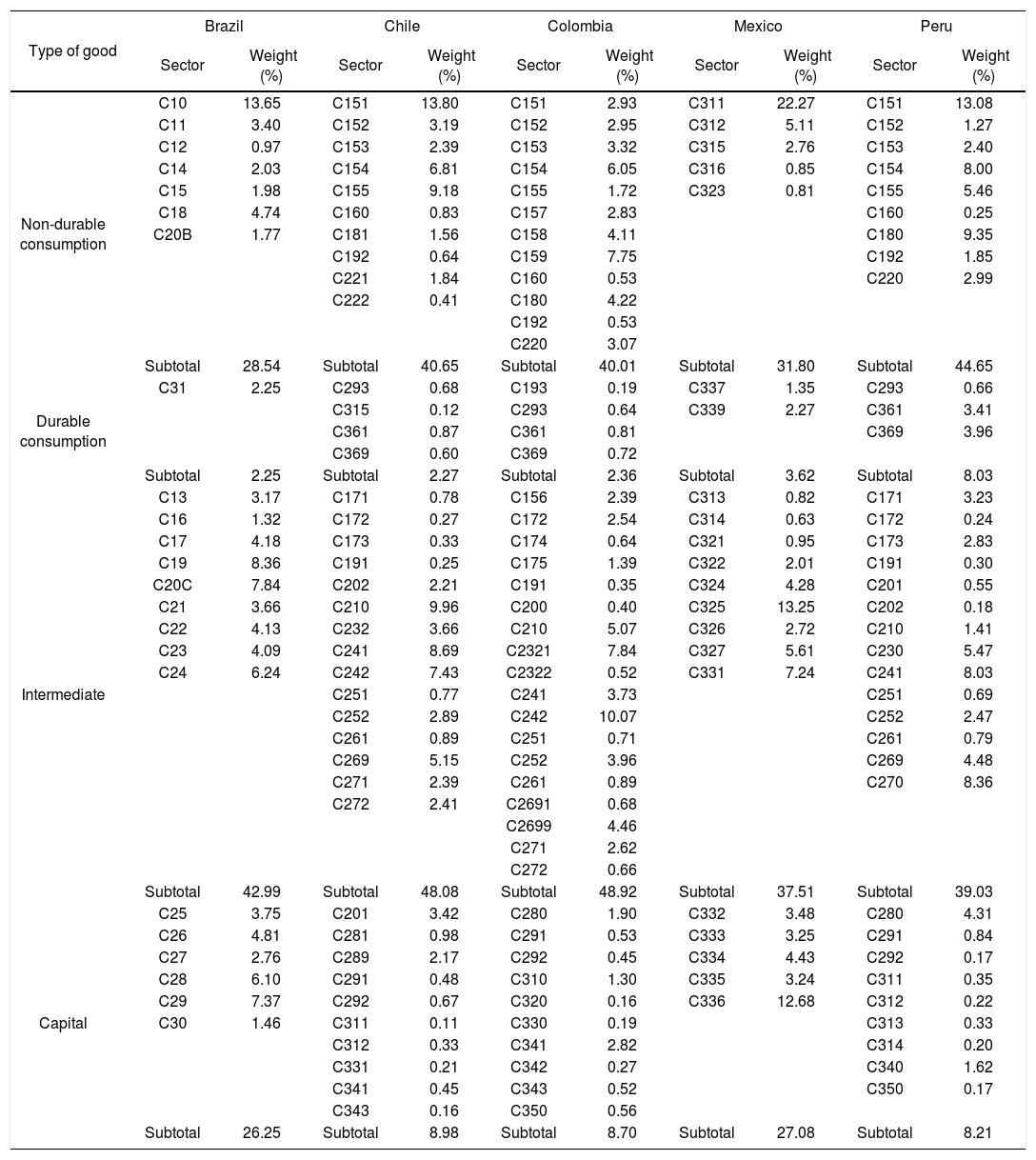
Table 2 shows the index of industrial production for subsectors defined by statistical institutes in each country, and their assigned weights. Each subsector was classified into one of four major sectors defined by the type of final good produced, according to the National Administrative Department of Statistics (dane) in Colombia and correlative tables of classification schemes used in the other countries. Significant homogeneity is observed in industrial structure across Chile, Colombia and Peru, with a high share of intermediate and non-durable goods (around 40%) and low fraction of durable consumer goods and capital goods (never exceeding 10%). In Mexico and Brazil, on the other hand, the share of consumer capital goods is much higher (around 30%) and smaller share of non-durable consumer goods.

Table 2.

Classification and weighting of industrial subsectors according to type of final goods produced.

Type of good	Brazil		Chile		Colombia		Mexico		Peru
	Sector	Weight (%)	Sector	Weight (%)	Sector	Weight (%)	Sector	Weight (%)	Sector	Weight (%)
Non-durable consumption	C10	13.65	C151	13.80	C151	2.93	C311	22.27	C151	13.08
	C11	3.40	C152	3.19	C152	2.95	C312	5.11	C152	1.27
	C12	0.97	C153	2.39	C153	3.32	C315	2.76	C153	2.40
	C14	2.03	C154	6.81	C154	6.05	C316	0.85	C154	8.00
	C15	1.98	C155	9.18	C155	1.72	C323	0.81	C155	5.46
	C18	4.74	C160	0.83	C157	2.83			C160	0.25
	C20B	1.77	C181	1.56	C158	4.11			C180	9.35
			C192	0.64	C159	7.75			C192	1.85
			C221	1.84	C160	0.53			C220	2.99
			C222	0.41	C180	4.22
					C192	0.53
					C220	3.07
	Subtotal	28.54	Subtotal	40.65	Subtotal	40.01	Subtotal	31.80	Subtotal	44.65
Durable consumption	C31	2.25	C293	0.68	C193	0.19	C337	1.35	C293	0.66
			C315	0.12	C293	0.64	C339	2.27	C361	3.41
			C361	0.87	C361	0.81			C369	3.96
			C369	0.60	C369	0.72
	Subtotal	2.25	Subtotal	2.27	Subtotal	2.36	Subtotal	3.62	Subtotal	8.03
Intermediate	C13	3.17	C171	0.78	C156	2.39	C313	0.82	C171	3.23
	C16	1.32	C172	0.27	C172	2.54	C314	0.63	C172	0.24
	C17	4.18	C173	0.33	C174	0.64	C321	0.95	C173	2.83
	C19	8.36	C191	0.25	C175	1.39	C322	2.01	C191	0.30
	C20C	7.84	C202	2.21	C191	0.35	C324	4.28	C201	0.55
	C21	3.66	C210	9.96	C200	0.40	C325	13.25	C202	0.18
	C22	4.13	C232	3.66	C210	5.07	C326	2.72	C210	1.41
	C23	4.09	C241	8.69	C2321	7.84	C327	5.61	C230	5.47
	C24	6.24	C242	7.43	C2322	0.52	C331	7.24	C241	8.03
			C251	0.77	C241	3.73			C251	0.69
			C252	2.89	C242	10.07			C252	2.47
			C261	0.89	C251	0.71			C261	0.79
			C269	5.15	C252	3.96			C269	4.48
			C271	2.39	C261	0.89			C270	8.36
			C272	2.41	C2691	0.68
					C2699	4.46
					C271	2.62
					C272	0.66
	Subtotal	42.99	Subtotal	48.08	Subtotal	48.92	Subtotal	37.51	Subtotal	39.03
Capital	C25	3.75	C201	3.42	C280	1.90	C332	3.48	C280	4.31
	C26	4.81	C281	0.98	C291	0.53	C333	3.25	C291	0.84
	C27	2.76	C289	2.17	C292	0.45	C334	4.43	C292	0.17
	C28	6.10	C291	0.48	C310	1.30	C335	3.24	C311	0.35
	C29	7.37	C292	0.67	C320	0.16	C336	12.68	C312	0.22
	C30	1.46	C311	0.11	C330	0.19			C313	0.33
			C312	0.33	C341	2.82			C314	0.20
			C331	0.21	C342	0.27			C340	1.62
			C341	0.45	C343	0.52			C350	0.17
			C343	0.16	C350	0.56
	Subtotal	26.25	Subtotal	8.98	Subtotal	8.70	Subtotal	27.08	Subtotal	8.21

Source: Own estimates based on data from national statistics institutes in Brazil, Chile, Colombia, Mexico and Peru.

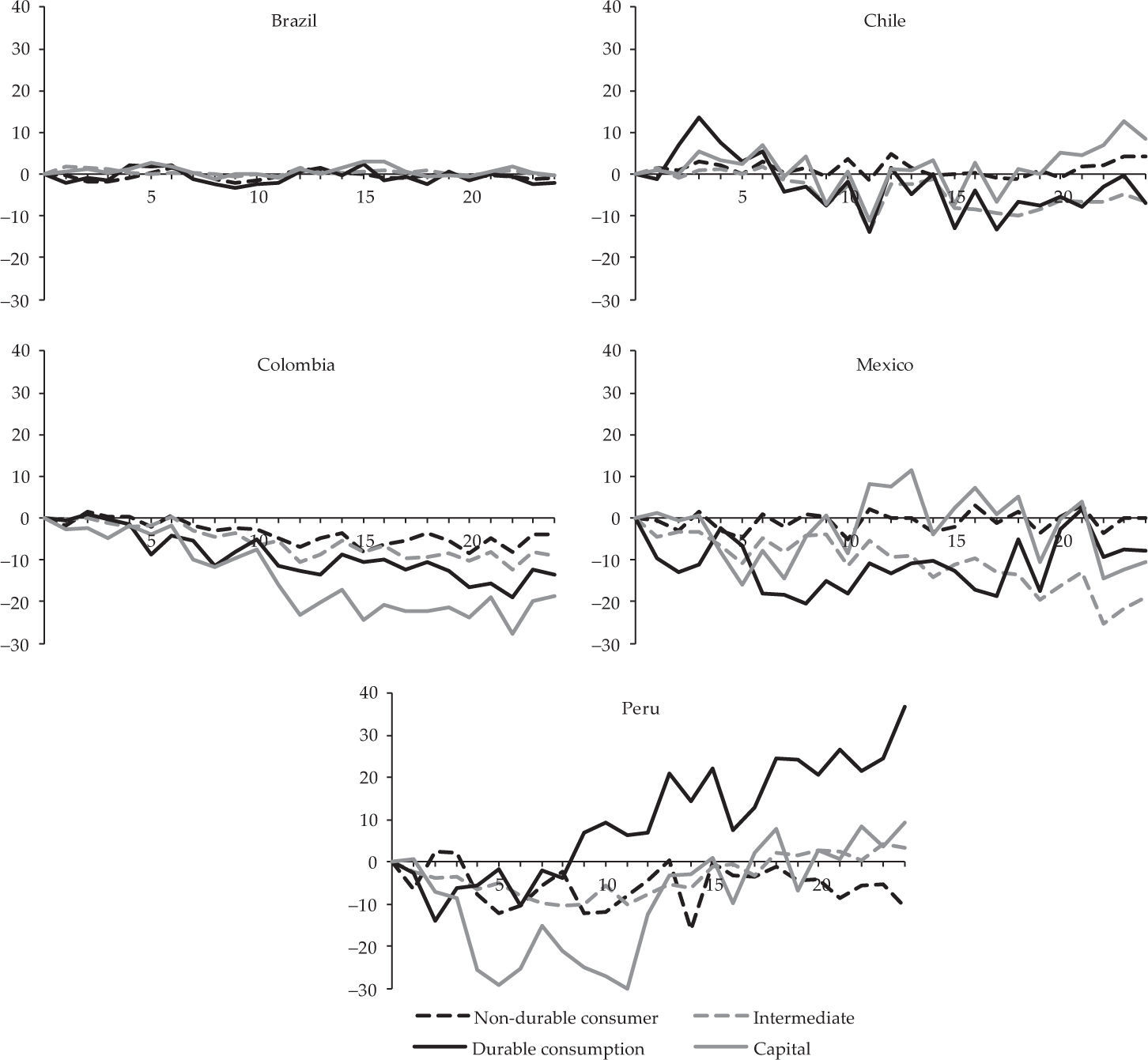
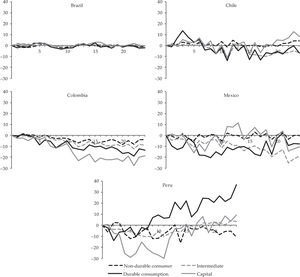
Based on Table 2 and the production indices for each subsector, production indices for the four large sectors were calculated for each country. The resulting series were seasonally adjusted and the same equation [1] model was estimated for each country, using the same monetary policy shocks employed to estimate effects on total industrial production, but separately for each of the four sectors. The obtained dynamic multipliers are shown in Figure 4.

Figure 4.

Impact of a positive shock of 1% in interest rate on industrial production in Latin American countries by sector according to final goods produce

Source: Own estimates.

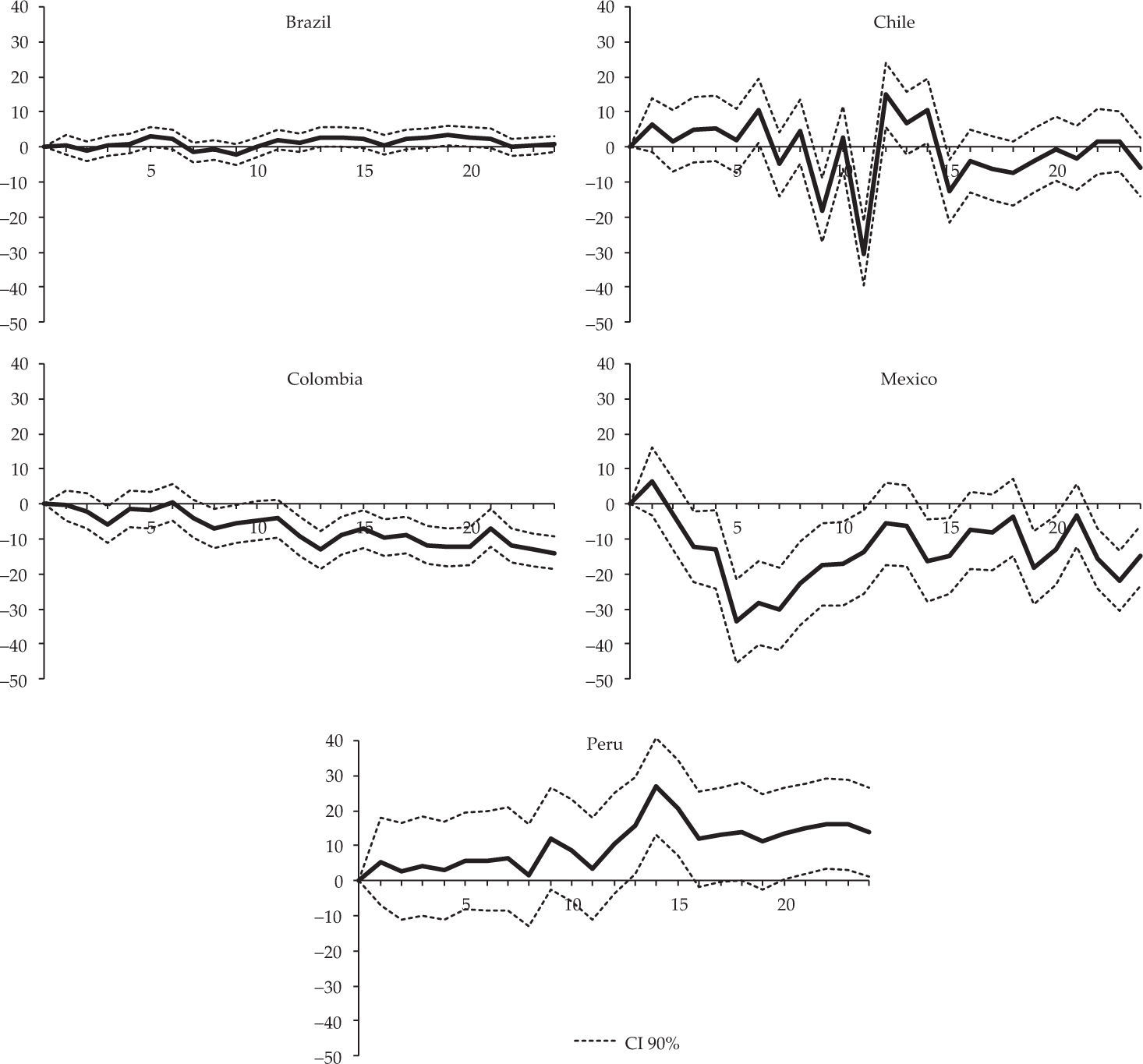
The results show that the interest rate channel seems to operate very clearly in Colombia, since the capital goods and durable consumer goods subsectors exhibit the most negative response to a positive monetary policy shock. The difference to the non-durable consumer goods and intermediate goods subsectors is greater in the second year after the shocks, when total industrial activity is most responsive in Colombia. Mexico is the country with the highest response of industrial production to monetary policy shocks, and also where the interest rate channel seems to be most relevant. The subsectors producing durable consumer goods respond for most of the period, while capital goods subsectors exhibit a strong response especially during the first year after the shocks. Figure 4 also shows that in these two countries non-durable consumer goods are weakly affected by a monetary policy shock, in agreement with the interest rate channel theory.

As for the other countries, in Peru a relatively stronger response is observed in the production of capital goods, but only in the first year. Contrary to expectations, durable consumer goods respond favourably to a positive monetary policy shock. In Brazil and Chile, no major differences in response to monetary shocks are observed across subsectors.

The results suggest that only in Colombia and Mexico monetary policy does have a stronger effect on the activity of subsectors producing capital goods and durable consumer goods compared to non-durable consumption and intermediate goods sectors, as predicted by the interest rate channel theory. However, to test for statistical significance of subsectoral differences in each country, we used production index data for all industrial subsectors simultaneously in a time series panel analysis. The model estimated for each country is:

Where γ is the manufacturing subsector production, S is the monetary policy shock estimated by Quintero (2015) and used in previous sections, and Dummycapdur is a dummy variable distinguishing capital goods or durable consumer goods subsectors (value = 1) from other subsectors (value = 0).

The number of dependent variable lags for each country is the same as in the estimation of equation [1], while the number of lags for monetary policy shocks remains as 24. The estimate was made by weighted least squares with weights reflecting the importance of sectors to total industrial production. The fixed effect model was used, considering that this provides consistent estimates in dynamic models when T > N, as in this case.

It should be noted that equation [2] does not include the variable Dummycapdur without its interaction with shocks, as it is a variable not changing over time and thus exhibiting perfect colinearity with the model fixed effects. However, as a fixed effects model, equation [2] controls for all time-invariant factors not included in this equation (Allison, 2009).

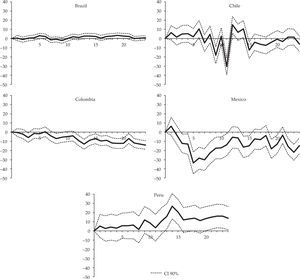
In equation [2], the parameters Φ˜q are relevant by showing the difference in average response to a positive interest rate shock in the capital or durable consumption goods subsectors compared to others. As when estimating the effect on total industrial production, due to the structure of the regression the difference in response between the two sectoral types after q months is given not only by the coefficients Φ˜q but also by the effect transmitted by β_p. Figure 5 displays the results for the five countries together with their 90% confidence intervals.

Figure 5.

Differential impact of a positive shock of 1% in interest rate on industrial production of capital and durable consumption goods relative to other subsectors

Source: Own estimates.

The previous graphs confirm that only in Colombia and Mexico the subsectors producing capital goods or consumer durables show a significantly stronger negative response to positive monetary policy shocks, as expected if the interest rate is relevant for the transmission of monetary policy. However, differences are statistically significant in Colombia in the second year after the shocks, and in Mexico during the first year.

The results of this section are consistent with Quintero (2015), who showed that in Mexico and Colombia the interest rate channel was relatively the most important to the transmission of monetary policy to total production. In other countries, the channel still operates but its importance is less clear compared to the other channels.

THE ROLE OF PRICE RIGIDITIES IN THE INCIDENCE OF INTEREST RATE CHANNEL

In a context of price rigidities, in principle the transmission of monetary policy to real activity through the interest rate channel should be stronger. When prices are fully flexible, nominal shocks should only affect prices and have no effect on quantities. But if there are obstacles for price adjustment, nominal shocks should have at least temporary effects on quantities.

According to this, industrial sectors with most rigid prices should be the most affected by a monetary policy shock. Therefore, the next section calculates an indicator of price rigidities for industrial subsectors, and evaluates its relationship to differential impacts of monetary policy.

A measure of price rigidity

In most empirical studies of price rigidities, measures of frequency and size of price changes are calculated from information on goods and services prices composing consumer price indices. These goods and services are classified by type of expenditure (food, clothing, transport, etc.) and therefore price indices are also usually calculated by type of expenditure. On the other hand, producer price indices are rarely analysed since they are seldom available for goods. Nonetheless, statistical institutes in many countries calculate a general producer price index classified by sector or economic activity.

This section estimates how sectoral differences in the degree of price rigidities relate to differences in their responses to monetary shocks, and to this purpose we use producer prices indices to calculate a measure of price rigidities originally proposed by Dhyne et al. (2009). The measure is based on the menu cost model, the most popular and widely tested theoretical approach to nominal rigidities. The model rationale is that firms must incur costs to change nominal prices, which limits continuous price changes.

Caplin and Spulber (1987) proposed the Ss rule version of this model, where the price of a product i moves towards its optimal value when its price in period t − 1, p_i,t−1 deviates from the optimal price pit* during a given range of inaction s_it, which depends on the costs incurred to adjust prices, the costs of no adjustment, and the typical magnitude of shocks:

This model generates periods of inaction when prices are held constant, depending on the evolution of the optimal price and on whether its difference to current price is greater or smaller than s_i. The current price p_it may remain unchanged if the difference between current optimal price and previous period price pi,t−1 − pit*, is small, or if the range of inaction, sit it, is large. In the former case, price adjustment does not occur because the economic environment is stable and price change is less required, which Dhyne et al. (2008)⁶ define as extrinsic rigidity. In the latter case, prices do not change due to reasons inherent to the pricing process such as high costs of price adjustments, which is known as intrinsic rigidity.

The index proposed by Dhyne et al. (2009) produces a measure of price rigidities (PR) fractioned into intrinsic and extrinsic dimensions:

Under the assumption of a constant range of inaction, the average absolute size of price adjustments, ΔP¯, is a good estimate of the inaction range s. Moreover, since the extrinsic rigidity corresponds to the variance of shocks, the standard deviation of the logarithm of monthly price indices over a period of time is a proxy for the size of the common shocks and degree of extrinsic rigidity.

A large value of PR means that for a given size of common shocks (σ_PI), companies should change prices significantly, which is a sign of high price rigidity since large changes in prices reflect either large ranges of inaction or high costs of price adjustments.

In calculations, we used the producer price indices by economic activity from national statistics institutes or central banks. Periods covered by data differed by country as a function of availability: in Brazil from January 2010 to December 2013, in Chile from April 2003 to December 2011, in Colombia from January 2003 to June 2013, in Mexico from January 2007 to June 2012, and in Peru from September 2009 to June 2013.

To facilitate comparisons between countries, the price rigidity indicator in each country was re-scaled to fluctuate between 0 (subsector with the lowest indicator value) and 100 (sector with the highest indicator) based on the equation:

Where RV is the re-scaled value, OV is the original value, and Vmin and Vmax are the lowest and highest values among all sectors.

Relationship between price rigidities and sectoral impacts of monetary policy

Using the price rigidities for each sector obtained above, a regression similar to equation [2] was estimated, with the only difference being that the dummy variable Dummycapdur (which indicates whether a subsector is a producer of capital goods or durable consumer goods or not) is replaced by the measure of price rigidities, PR. The new regression is thus: n 24 24

Where PR is the indicator of price rigidities, γ is the manufacturing subsector production, and S represents the monetary policy shock estimated by Quintero (2015) and used in the previous sections. As in equation [2], we do not include the variable PR without interactions with shocks because fixed effects control for all time-invariant variables.

Similarly to the analysis by type of final goods in section 4, dynamic multipliers were calculated based on the parameters Φ˜PRq and the β_p associated with the dependent variable lags and expressing the differences in response among sectors with distinct levels of price rigidities. As the sectors with higher price rigidity are in principle the most sensitive to monetary policy, their dynamic multiplier values are expected to be negative and statistically significant, and contractionary effects of the monetary policy should be amplified. Figure 6 presents estimates from equation [6] and their respective 90% confidence intervals.

Figure 6.

Impact of a positive shock of 1% in interest rate on industrial production of industrial subsectors as a function of levels of price rigidities

Source: Own estimates.

The results reveal that in Mexico and Colombia, where differences between subsectors are more extreme, price rigidities are mostly clearly determining monetary transmission, since the sectors with most rigid prices are clearly the most affected by a monetary policy shock. In Mexico, a stronger relative response of sectors with higher price rigidity is visible in the first year following the shocks, while in Colombia this is observed only after month 11, which is when monetary policy shocks most strongly affect production, especially of capital and durable consumption goods.

The results for the two countries can also explain the relevance of the interest rate channel in monetary transmission to total economic activity revealed by Quintero (2015). In the other countries (Brazil, Chile and Peru), the role of price rigidities in monetary transmission was almost never statistically significant.

CONCLUSIONS

This article compared the impact of monetary policy on manufacturing production in five Latin American countries: Brazil, Chile, Colombia, Peru and Mexico. By estimating an adl model it was found that in all countries an unexpected increase in the monetary policy interest rate reduces industrial production. The largest responses are observed in Mexico, Colombia and Peru in that order. In Mexico, an unexpected increase in the monetary policy rate of 1% generates a cumulative decrease of around 24 pp in industrial production 22 months after the shocks, and in Colombia a maximum contraction of approximately 13 pp also in month 22. In Peru the response also noticeably reaches a maximum of 10.2 pp in month 6. In Chile the maximum response is 8.5 pp recorded in month 11, although impacts are highly volatile and not statistically significant most of the time, while Brazil is the only country where industrial production does not respond significantly to a monetary policy shock, with a maximum cumulative response of 1 pp recorded in month 8.

To evaluate the relevance of the interest rate channel in the five countries, a new adl model was independently estimated for four large sectors defined by type of produced final goods. In Mexico and Colombia, as predicted by the channel theory, subsectors producing capital and consumer durables goods present the most negative response to a positive interest rate shock, which implies that the interest rate channel is crucial to the transmission of monetary policy to real activity. In Peru, results are not clear since a greater impact on capital goods is equally seen in the first year after the shocks, but durable consumer goods respond in the opposite way to theoretical expectations. In Brazil and Chile, there are no major differences in the response of industrial subsectors to a monetary policy shock.

Since the channel theory attributes the effectiveness of monetary transmission to the sensitivity of demand to interest rate changes as well as to price rigidities, we attempted to evaluate the role played by rigidities on effect magnitudes. Panel time series models with information on manufacturing subsectors were estimated for each country, with monetary policy shocks interacting with a measure of price rigidities calculated from information on producer price indices of industrial subsectors (Dhyne et al., 2009). The results show that price rigidities affect monetary transmission as predicted only in Mexico and Colombia, the countries where the interest rate channel has a greater impact on industrial production.

The main result from our study is thus that even within a single large production sector such as the industry, there are visible differences in the impact of the monetary policy among subsectors, demonstrating that economic structure is decisive to the transmission of monetary policy. This result has important implications for the effectiveness of monetary policy in the analysed countries. For example, the higher response of capital goods subsectors to monetary policy in some countries implies that a relative increase in the production of capital goods, in addition to their expected effects on long-term economic growth (given that they are more technology-intensive sectors), may also lead to higher effectiveness of the monetary policy on productive activity in the short-term, which is an aspect that monetary authorities should take into account when determining the magnitude of their adjustments.

Another important implication for economic policy is that given the determinant role of economic structure in the transmission of monetary policy and the differences in economic structures across countries, the putative creation of a monetary unit, and therefore the establishment of a common monetary policy, would have different consequences for each country, especially regarding the effectiveness of monetary policy decisions, a point to be considered in any future debates on this topic.

Following the same line of reasoning, regions within each country also exhibit different economic structures, and for this reason regional differential effects of the monetary policy are expected, a factor that should also be considered by national and regional economic authorities when considering the coordination of economic policies.

Therefore, the relevance of our results to public policy should stimulate a continuous effort to evaluate effects of monetary policy in different economic sectors. An aspect not considered in this study is the distinction between direct effects on each sector and effects that result from links to other subsectors affected by monetary policy. If possible, it would also be important to extend our analysis to all sectors contributing to total production, which would require alternative methodological approaches to maximise the use of limited information available at sectoral level.