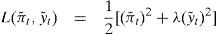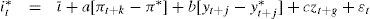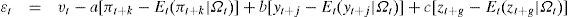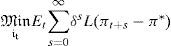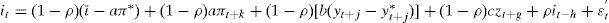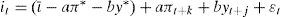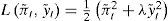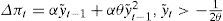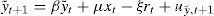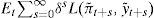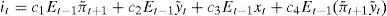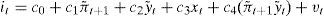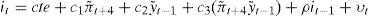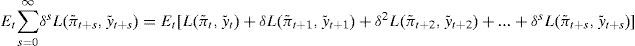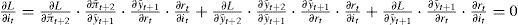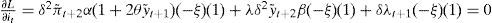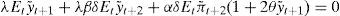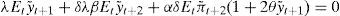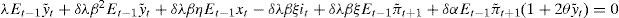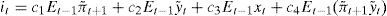¿Son asimétricas las reacciones de política monetaria de un banco central? El caso del bce

Resumen

Una gran parte de los bancos centrales adopta sus decisiones conforme a determinados objetivos, fundamentalmente de inflación y crecimiento económico. La pregunta que nos hacemos es si son igual de intensas las reacciones de esos institutos centrales cuando las desviaciones respecto a los objetivos señalados son positivas, en comparación con el caso en que sean negativas, o si, por el contrario, las reacciones son asimétricas. Para responder a esta cuestión, con base en los planteamientos taylorianos de la función de reacción de política monetaria, analizamos las posibles causas de comportamientos asimétricos y establecemos una metodología para determinar si las decisiones de un banco central han sido asimétricas, o no. Empíricamente, analizamos el caso del Banco Central Europeo (bce), para concluir que en el caso de éste no es posible afirmar que haya reaccionado asimétricamente en el periodo1999-2008.

Introducción

Este trabajo se inscribe en la línea de investigación sobre las estrategias de política monetaria seguidas por los bancos centrales. Es importante conocer con el mayor detalle posible la estrategia de decisión de política monetaria de cualquier banco central, pues es sabido que cuanto más transparente sea esa estrategia, más eficaz será la política monetaria, en la medida en que las modificaciones adoptadas en los tipos de interés por el banco central se transmitirán de forma más plena y más rápida a los tipos a diferentes plazos y, además, se conseguirá un mejor anclaje de las expectativas de inflación. De esta manera, los agentes económicos afrontarán sus decisiones en un contexto de menor incertidumbre.

El análisis de la estrategia de política monetaria de un banco central mediante la estimación de su función de reacción es una metodología plenamente consolidada. Con su aplicación en este trabajo tratamos de detectar la posible presencia de asimetrías en las decisiones de política monetaria adoptadas en el caso concreto del Banco Central Europeo (bce), es decir, si las reacciones son más o menos intensas cuando se producen desviaciones, positivas o negativas, de la inflación y de la producción respecto de sus valores objetivo. Puesto que en este trabajo no se trata de estimar las ponderaciones en la función de pérdidas, sino de detectar comportamientos asimétricos, no es necesario recurrir a un enfoque estructural (véase, por ejemplo, Aguiar y Martins, 2008).

La base lógica de este planteamiento implica que el banco central modificará el tipo de interés siguiendo el principio formulado por Taylor (1993). Pero la cuestión adicional que aquí nos ocupa consiste en averiguar si el banco central reacciona con igual o con diferente intensidad (asimétricamente en este segundo caso) ante una inflación por arriba del objetivo, en comparación con el caso de una tasa de inflación por debajo de la meta. Y otro tanto podemos decir en cuanto a las desviaciones de la producción real respecto a su tendencia. Es decir, si reacciona igual ante las desviaciones positivas que frente a las desviaciones negativas. Las causas del hipotético comportamiento asimétrico podrían localizarse en las preferencias del banco central, o en las características que la relación entre la inflación y la brecha del producto muestre en la realidad económica.

Desde el punto de vista empírico, el principal aporte de esta investigación sobre este supuesto comportamiento asimétrico será mostrar si ése ha sido el caso concreto del bce, y si este método también puede aplicarse al caso de otros bancos centrales y contribuir de forma significativa a conocer mejor la estrategia de política monetaria seguida a lo largo de estos años por este banco central que, en un principio, parece que ha intentado labrarse una reputación antiinflacionaria, lo que induciría a pensar, a priori, en la existencia de comportamientos asimétricos. La hipotética presencia de comportamientos asimétricos tendría una gran importancia para la economía real, en la medida en que la actividad estabilizadora del bce sería tanto más enérgica cuánto mayores fueran las desviaciones, sometiendo así a la actividad productiva real a un mayor estrés, con las consiguientes disfuncionalidades que ello puede conllevar para los agentes económicos.

Para llevar a cabo el análisis propuesto, en el siguiente apartado debatimos sobre la incidencia de las asimetrías en las reacciones de política monetaria y comentamos otras aportaciones publicadas. A continuación modelizamos la función de reacción con base en diversas hipótesis y estudiamos la convexidad de la curva de Phillips. En otro apartado, abordamos el análisis empírico, donde, en primer lugar, analizamos la existencia, o no, de convexidad en la curva de Phillips, para luego estudiar la naturaleza lineal o asimétrica de la función de reacción de política monetaria del bce durante su primera década de existencia. Finalmente, ofrecemos algunas conclusiones.

Asimetrías en la reacción de política monetaria del banco central

Para comenzar señalemos que, en principio, se pueden considerar dos fuentes de comportamiento asimétrico en las intervenciones de política monetaria de un banco central: las relacionadas con las preferencias de política, y las que tienen que ver con la pendiente del trade-off entre la inflación y la brecha del producto, es decir, la curva de Phillips.

En cuanto al primer tipo, al definir la función de pérdidas del banco central se suele asumir que las desviaciones tanto a la inflación objetivo como al nivel de producción natural son igual de costosas, tanto si son positivas, como si son negativas, lo cual es consistente, según Rotemberg y Woodford (1999), con una aproximación razonable a una función de bienestar subyacente con base en la utilidad. Sin embargo, a corto plazo nos podemos encontrar con que el sacrificio que suponga la desinflación, si éste le importa al banco central, lleve a que se asigne una mayor importancia a las desviaciones negativas. Esto podría suponer, por ejemplo, la alteración de la función de pérdidas habitual:

en la que π˜;t es la desviación de la inflación respecto al objetivo; y˜;t es la brecha del producto (output gap), habitualmente la desviación de la tasa de crecimiento del producto interno bruto (pib) real respecto a su tendencia. Como resultado de la transformación sugerida la tasa de inflación adecuada puede ser superior al objetivo, para así aminorar el empleo sacrificado, aunque a largo plazo no haya trade-off entre inflación y el producto.

No obstante, se puede cuestionar la comentada simetría en las preferencias si el objetivo de inflación se ubica en una banda de fluctuación respecto a un valor central (cuya anchura depende positivamente de λ), en vez de estar focalizado en un único punto. Así, según Orphanides y Wieland (2000), si el banco central se ha fijado el objetivo en forma de banda, cuando la inflación se encuentra relativamente cerca del punto central de ésta, la única preocupación de la política monetaria es fijar el tipo de interés que permita la estabilización del output. Mientras que si el banco central observa que la inflación tiende a superar los límites de la banda, el tipo de interés será reajustado para evitarlo. Con su modelo numérico, que incorpora preferencias no cuadráticas, una curva de Phillips no lineal y ningún retardo en la transmisión de la desviación de la brecha del producto a los precios, estos autores detectan que la incertidumbre respecto a choques inesperados tiene importantes efectos sobre el ancho de la banda objetivo y el tamaño relativo de las respuestas de política dentro y fuera de la banda. De forma que la regla de política óptima con incertidumbre no induce a una respuesta mecánica sólo cuando la inflación está fuera de la banda, sino a ir aumentando progresivamente la intensidad de la respuesta para hacerla más agresiva cuanto mayor sea el riesgo de salirse de los límites de la banda.

Relacionado con la aportación de Orphanides y Wieland (2000), el trabajo de Medina y Valdés (2002), con dos periodos de retardo para la política monetaria, confirma la tendencia a modificar el tipo de interés aunque la tasa de inflación se encuentre dentro de la banda objetivo. Sin embargo, estos últimos interpretan la asimetría en las preferencias considerando que las desviaciones positivas de la inflación son más costosas que las negativas, es decir, ponderando más las desviaciones positivas de la inflación en la función de pérdidas.

Surico (2007a) aborda el tema centrándose en la asimetría de las preferencias y llega a la conclusión de que en el caso de la Reserva Federal sus preferencias sólo han sido asimétricas antes de 1979, siendo comparativamente mayores las respuestas a las contracciones del output que las adoptadas ante expansiones del output de la misma magnitud. El mismo Surico (2007b) investiga la posible existencia de asimetría en la regla de política del bce. Su principal resultado muestra que las desviaciones de la inflación van seguidas por similares respuestas del tipo de interés, mientras que las reacciones a las desviaciones de la brecha del producto están asociadas con preferencias asimétricas.

En esta línea se sitúan otros trabajos de investigación teóricos y empíricos: Dolado, Maria-Dolores y Ruge-Murcia (2002) descubren preferencias asimétricas de la Reserva Federal en el periodo de Wolcker-Greenspan; Cukierman y Muscatelli (2008) encuentran evidencias de que las modificaciones en la regla de política del banco central en el Reino Unido, en el régimen de objetivo de inflación, se deben a cambios en las preferencias más bien que a cambios en la curvatura de la curva de Phillips (similares resultados obtienen para el caso de la Reserva Federal); Vasicek (2011) plantea estrategias empíricas que permiten descubrir en qué medida las asimetrías, si las hay, tienen su origen en la función de pérdidas del banco central.

Por otro lado, respecto a la pendiente del trade-off entre la inflación y la brecha del producto, varios modelos analíticos, según Dupasquier y Ricketts (1998), sugieren una relación asimétrica entre ambos. Uno de esos modelos hace hincapié en el papel de las restricciones de capacidad, es decir, en el hecho de que algunas empresas pueden tener dificultades para incrementar su capacidad de producción más allá de cierto límite en el muy corto plazo. En consecuencia, la curva de Phillips tendrá una forma convexa: cuando la demanda agregada aumenta, el impacto sobre la inflación tenderá a ser mayor que cuando aquélla tiene un nivel bajo, y esta no-linealidad, a su vez, puede implicar respuestas no simétricas de política monetaria: las modificaciones en el tipo de interés tendrán que ser mayores ante desviaciones por encima del objetivo que en el caso contrario, de forma que, según Schaling (2004), la función de reacción para el tipo de interés sería asimétrica e implicaría, en general, un mayor nivel en el tipo de interés que la función de reacción deducida por Svensson (1997).

Schaling (2004) muestra, para del caso de objetivo de inflación estricto, que las desviaciones positivas de la inflación respecto al objetivo implican mayores cambios en el tipo de interés, en valor absoluto, que las desviaciones negativas. Y, además, que los aumentos en el tipo de interés, ante una perturbación positiva en el output, son mayores que los que se darían con una función de reacción lineal, de lo que se deduce que tales funciones de reacción lineales subestiman el nivel adecuado para el tipo de interés.

Posteriormente, Dolado, Maria-Dolores y Naveira (2005) profundizan en el análisis anterior y generalizan el modelo de Schaling considerando el caso en el que la función de pérdidas del banco central también prevé la estabilización del output, es decir, el caso de objetivo de inflación no estricto. Se centran en el análisis de la presencia de convexidad en la curva de Phillips¹ y llegan a conclusiones similares a las de Schaling, en el sentido de que las desviaciones de la inflación por encima del objetivo dan lugar a incrementos crecientes en el tipo de interés real, mientras que en las desviaciones por debajo la disminución en el tipo de interés real es decreciente. Empíricamente, confirman la existencia de ese comportamiento asimétrico en el caso de los bancos centrales europeos para distintos periodos muestrales que arrancan en los años ochenta, mientras que el caso de la Reserva Federal de Estados Unidos es una excepción a este comportamiento. Este análisis lo llevan a cabo mediante dos procedimientos, el primero de ellos consistente en la estimación de una regla de Taylor con expectativas de inflación a la que añaden un término multiplicativo (término de interacción) de la inflación esperada por la brecha del producto. El segundo está basado en un modelo probit que captura la naturaleza discreta de las modificaciones en los tipos de interés y así modeliza la probabilidad de que el banco central intervenga según su percepción del estado de la economía, incluyendo de nuevo un término multiplicativo en el que interactúan la inflación y la brecha del producto.

Desde un punto de vista teórico, también pueden verse otros trabajos en los que se justifica la posible existencia de asimetrías, como son los de Kahneman y Tversky (1979), Persson y Tabellini (1999), Erosa y Ventura (2002), Nobay y Pell (2003) y Galí y Gertler (2007). Mientras que, con un carácter más empírico, aparte de los citados, pueden verse los trabajos de Cukierman y Muscatelli (2002), Martin y Milas (2004), Ruge-Murcia (2003), Cukierman y Gerlach (2003), Altavilla y Landolfo (2005), Kim, Osborn y Sensier (2005) y Klose (2011).

Modelización de las asimetrías en la functión de reacción de política monetaria

Como hemos dicho, el objetivo de este trabajo es estudiar si un banco central ha seguido un comportamiento asimétrico al adoptar sus decisiones sobre los tipos de interés. Partimos de la base de que su objetivo fundamental es lograr la estabilidad de precios, que se podría concretar en un objetivo de inflación. Además, la actividad económica también podrá influir en las decisiones de política monetaria, aunque sólo sea por su vinculación con los precios. En otros trabajos, como puede verse en García-Iglesias, Pateiro y Salcines (2011), el modelo teórico base que se ha adoptado es de naturaleza intertemporal y se inscribe en la corriente de reglas de tipo de interés. Más concretamente, se corresponde con la aportación de Clarida, Galí y Gertler (1998):

donde i* es el tipo de interés nominal a corto plazo determinado por el banco central; ι¯ es el tipo de interés nominal de equilibrio que equivale a ι¯=r¯+π*, siendo r¯ el tipo de interés real de equilibrio y π^* el objetivo de inflación; y_t es un indicador de la actividad económica real, habitualmente la tasa de crecimiento del pib real, e yt* es su tendencia; Et es el operador de expectativas; Ωt es un vector que incluye la información de que dispone el banco central en el periodo t; zt es un vector que contiene otras variables hipotéticamente explicativas de la política monetaria seguida. Los subíndices temporales k, j, g pueden adoptar valores positivos o negativos, por lo que el modelo puede ser forward-looking o backward-looking. A su vez, este modelo se podría ampliar al incorporarle la hipótesis de alisamiento en las modificaciones en el tipo de interés por parte del banco central.² No obstante, opcionalmente podremos prescindir del término de ajuste parcial, suponiendo que ρ = 0 en algunas de nuestras estimaciones. Suprimimos las variables no observadas de forma que:

donde

Dando por hecho que el banco central, al decidir sobre los tipos de interés, se comporta de manera racional en la persecución de los objetivos encomendados, formalmente la especificación anterior se corresponde con un planteamiento de minimización de una función de pérdidas, es decir que, con carácter inter-temporal, el problema del banco central es pues, en el caso en que se centre en la consecución del objetivo de inflación:

donde δ ϵ [0,1) es un factor de descuento.

En definitiva, la función de reacción de política monetaria, si se tiene en cuenta el ajuste parcial del tipo de interés, será:

Mientras que si prescindimos del ajuste parcial y de z, y suponemos que la tasa de crecimiento tendencial es constante, separando las variables de los valores objetivo, la función de reacción de política monetaria a estimar sería la siguiente:

En todo el planteamiento que acabamos de exponer subyace la hipótesis de linealidad en los comportamientos, pues, como hemos deducido, la función de reacción de política monetaria es lineal, dando lugar a decisiones simétricas sobre el tipo de interés, independientemente de que las desviaciones respecto a los objetivos de inflación y del producto sean positivas o negativas.

Pero, como se indicó arriba, la función de reacción de un banco central puede ser asimétrica, bien porque el banco central tenga preferencias asimétricas o bien por la existencia de una curva de Phillips no lineal. Nuestro trabajo empírico se centra en contrastar la posible presencia de asimetrías en las decisiones del bce que se originen en una relación no lineal entre las variaciones de la inflación y del producto, es decir, la posible existencia de una curva de Phillips no lineal, de acuerdo con Dolado, Maria-Dolores y Naveira (2005).

Así, vamos a utilizar una función de pérdidas cuadrática del tipo de la ecuación [1]:

donde, como decíamos, π˜;y˜; e son, respectivamente, las desviaciones de la inflación y la brecha del producto, y λ > 0 es una medida de la ponderación que el banco central otorga a la actividad económica. La evolución de la economía se caracteriza por una relación convexa entre la variación de la inflación y la brecha del producto descrita por la curva de Phillips (o curva de oferta agregada):

y por una curva IS que describe un ajuste lento de la brecha del producto según la ecuación:

donde r es el tipo de interés real: rt = it – Etπt₊₁. Por su parte, xt captura otras variables determinantes del tipo de interés, como podrían ser el tipo de cambio, el saldo presupuestario, etcétera.

Al igual que en Svensson (1997), las variaciones del tipo de interés afectan al producto con un periodo de retardo y éste a la inflación con otro periodo de retardo. El proceso de transmisión, que se puede describir como Δit → Δyt₊₁ → Δπt₊₂, ha de ser remarcado para obtener la ecuación de Euler resultante de minimizar el valor presente descontado de las pérdidas periodo por periodo de la función [1], es decir, hacer mínimo:

Según puede verse en el apéndice, la regla para el tipo de interés adopta la forma:

donde los coeficientes ci son función de los parámetros estructurales (δ, α, λ, μ, θ, ξ y β), como se expone en el apéndice. Si reemplazamos las expectativas sobre inflación y la brecha del producto por sus valores efectivos, resulta la regla óptima para el tipo de interés que contrastaremos en este trabajo por el método de los momentos generalizado (mmg):

La ecuación [11] es una regla de Taylor modificada. Al igual que la regla tayloriana de la ecuación [6], la función de reacción [11] es lineal respecto de las variables inflación, brecha del producto y x. Sin embargo, presenta, además, el término de interacción o componente rectangular entre la desviación de la inflación esperada y la brecha del producto [c4(π˜;t+1y˜;t)]. Si la curva de Phillips es convexa (θ > 0; c_{4 >} 0)³ el banco central reaccionará más fuertemente sobre la tasa de interés que en el caso de una curva de Phillips cóncava (θ < 0; c_{4 <} 0) debido a la futura presión inflacionaria causada por la mayor brecha del producto (recordemos que, como en Svensson [1997], Δi_t → Δy_t+1 → Δπ_t+2).⁴ Si la curva de Phillips es lineal (θ = 0), se cumplirá c_{4 =} 0 y la función de reacción de la ecuación [11] será una regla de Taylor lineal. De esta manera, el término de interacción en la ecuación de Euler nos permitirá determinar la existencia de asimetría en la función de reacción del banco central.

El trabajo empírico

Como se indicó, la asimetría en el comportamiento de un banco central puede provenir de la existencia ya sea de una curva de Phillips convexa o bien de preferencias asimétricas del banco central. Nuestro trabajo empírico en este artículo consiste en contrastar, en primer lugar, la posible existencia de convexidad de la curva de Phillips de la ecuación [7] para el periodo 1999:1 a 2007:4⁵ y, en segundo lugar, la presencia de asimetría en las decisiones adoptadas por el bce sobre el tipo de interés. La presencia de esta potencial asimetría se analizaría con base en la ecuación [11], pero sin variable exógena xt, e incorporando un comportamiento alisado del tipo de interés, es decir, como muestra la ecuación [12]. Como se explica más adelante, adoptamos el comportamiento forward-looking de cuatro trimestres para la desviación de la inflación y de backward-looking de un trimestre para la brecha del producto, por lo que la ecuación concreta a estimar por el mmg es:

¿Es convexa la curva de Phillips?

Siguiendo un planteamiento similar al de Dolado, Maria-Dolores y Naveira (2005), hemos contrastado por mínimos cuadrados (mco) la posible convexidad de la curva de Phillips para la zona euro en los periodos 1999:1 a 2007:4 y 1999:1 a 2008:4.⁶ El producto es el pib y el nivel natural del producto es el filtro de Hodrick-Prescott (hp), con un coeficiente de 1.600. La brecha del producto se calcula como la diferencia entre el logaritmo del pib y su hp tendencia. Para los precios utilizamos el deflactor del pib de la zona euro. Todas las series de datos son estacionalmente ajustadas.

La ecuación a estimar es la [7]:Δπ=αy˜;t-1+αθy˜;t-12+επ,t. Siendo α > 0, la curva de Phillips será convexa si θ > 0,⁷ y cóncava en el caso opuesto. La linealidad de la curva de Phillips se recupera si θ = 0.

Del periodo 1999:1 hasta 2007:4, θ = –0.25 es negativa y no significativa (p = 0.265). La curva de Phillips en este periodo se aproximaría más a una forma cóncava que convexa. No obstante, al ser no significativa la concavidad, consideramos más bien una relación lineal entre inflación y output.⁸ Los resultados para el periodo 1997:1 a 2008:4 no experimentan modificaciones significativas.

Si sustituimos los datos trimestrales del pib por los mensuales del índice de producción industrial (ipi) para el output⁹ y por los datos de inflación subyacente en el caso de los precios, los resultados para el periodo 1999:1 a 2007:12 nos permiten rechazar una vez más la convexidad de la curva de Phillips en la zona euro en dicho periodo. Al igual que en el caso anterior, θ toma valores negativos y es no significativa (p = 0.35). Resultados similares se obtienen para el periodo que incluye el 2008.

¿Es asimétrica la función de reacción del bce ?

Para contrastar la ecuación [12] adoptamos una frecuencia trimestral para los datos de nuestros periodos de análisis, que transcurren desde el primer trimestre de 1999 hasta el cuarto de 2007, y desde el primer trimestre de 1999 hasta el cuarto de 2008. Las fuentes son Eurostat y el bce, con datos adaptados a la sucesiva agregación de países a la euro área.

Para la variable tipo de interés utilizamos el oficial, o básico, del bce, que equivale al tipo mínimo de las Operaciones Principales de Financiación, como señalizador fundamental de su política monetaria, teniendo en cuenta el último dato trimestral observado.

En cuanto a la tasa de inflación, empleamos la correspondiente a la subyacente, es decir, excluyendo del Índice Armonizado de Precios de Consumo los precios de la energía y de los alimentos no elaborados, obtenida en Eurostat. Usaremos esta serie porque, como se muestra en García-Iglesias (2007) y en García-Iglesias y Pateiro (2009), explica adecuadamente las decisiones del bce. Al igual que en el caso anterior adoptamos una frecuencia trimestral que toma en cuenta el último dato. Para la brecha del producto utilizamos la misma definición que del mismo se expone en la subsección anterior.

En cuanto al método a seguir para llevar a cabo las estimaciones de los parámetros de la función de reacción de política monetaria, al adoptar un análisis intertemporal nos debemos centrar en el mmg, pues en éste subyace un enfoque de comportamiento racional y optimizador, con carácter intertemporal, que es el que suponemos que sigue el banco central al decidir sobre el tipo de interés para procurar controlar la inflación en relación con un valor objetivo y tratar de ayudar también a conseguir la estabilidad económica. Como es sabido,¹⁰con este método, una vez deducida la relación entre las variables, obtenemos los parámetros “profundos” que describen las preferencias del banco central en su función de reacción de política monetaria, cumpliéndose las condiciones de ortogonalidad entre los residuos del ajuste y la información de que dispone el banco central en el momento de decidir sobre el tipo de interés.

Como variables instrumentales usamos una constante y las variables que intervienen en la función de reacción retardadas desde –1 a –3 trimestres, es decir, el tipo de interés, la tasa de inflación y la brecha del producto, según el comportamiento observado a lo largo del año inmediato anterior.

Respecto al grado de estacionariedad de las series, como se argumenta en otros trabajos, ¹¹ cuando se trata de muestras cortas, como es este caso, las pruebas habituales están sesgados en contra de la hipótesis alternativa de estacionariedad en su nivel. Por ello, y teniendo en cuenta el contexto de estabilidad en el que se sitúa nuestro análisis, suponemos que se cumplen las condiciones requeridas para realizar las estimaciones por medio del mmg.

Para contrastar la validez de los instrumentos utilizados tendremos en cuenta el p-valor del estadístico J con la prueba de Sargan. El estadístico J que reporta Eviews 4.1 está dividido entre el número de observaciones, así que para poder calcular el p-valor de J, esto es, la probabilidad de cometer error tipo I al rechazar la hipótesis de validez de los instrumentos, hemos de multiplicarlo por el número de observaciones.

Al llevar a cabo los ajustes, teniendo en cuenta los resultados obtenidos en los citados trabajos de García-Iglesias (2007), García-Iglesias y Pateiro (2009) y García-Iglesias, Pateiro y Salcines (2011), adoptamos el criterio de que el bce, al decidir sobre el tipo de interés, tiene en cuenta la inflación adelantada cuatro trimestres y el crecimiento del pib retardado un trimestre, es decir, que actúa de forma forward-looking respecto a la inflación subyacente, y backward-looking en cuanto al crecimiento de la producción.

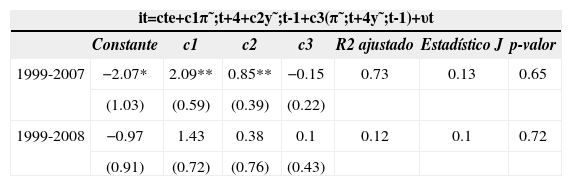
Por otra parte, dando por hecho que el bce sigue una estrategia alisada como hemos comentado más arriba,¹² inicialmente, en los ajustes que se presentan en el cuadro 1, prescindimos del término de ajuste parcial con el fin de que en los ajustes de la función de reacción de política monetaria del bce se pueda detectar mejor el grado de protagonismo que en la determinación del tipo de interés tiene cada una de las dos variables que estamos teniendo en cuenta: la inflación, vista a través de la inflación subyacente, y la brecha del producto. Dado que nuestra investigación trata de detectar comportamientos asimétricos cuando el bce modifica el tipo de interés a corto plazo, estimamos la ecuación [12], para poder contrastar si el coeficiente c₃ correspondiente al término rectangular (π˜;t+4y˜;t-1) es significativamente distinto de cero.

Cuadro 1.

Función de reacción sin ajuste parcial, con término rectangular, 1999-2007 y 1999-2008

it=cte+c1π˜;t+4+c2y˜;t-1+c3(π˜;t+4y˜;t-1)+υt
	Constante	c1	c2	c3	R2 ajustado	Estadístico J	p-valor
1999-2007	−2.07*	2.09**	0.85**	−0.15	0.73	0.13	0.65
	(1.03)	(0.59)	(0.39)	(0.22)
1999-2008	−0.97	1.43	0.38	0.1	0.12	0.1	0.72
	(0.91)	(0.72)	(0.76)	(0.43)

Notas: los errores estándar aparecen entre paréntesis. Los superíndices ** y * denotan el rechazo de la hipótesis de que el verdadero coeficiente es cero a un nivel de significación de 5 y 10 por ciento, respectivamente.

Del cuadro 1 se deduce que, para el periodo analizado, el coeficiente c₃ no es significativamente distinto de cero. En tanto que si ampliamos el análisis hasta final de 2008, de nuevo los valores de los coeficientes de reacción tienden a mantenerse, pero ahora dejan de ser significativos, y el coeficiente de deter-minación se reduce a 0.12, en línea con lo que señalábamos más arriba acerca de que el bce dejó de seguir un comportamiento regulado en el contexto de la profunda crisis financiera en 2008.

Como puede observarse, la intertemporalidad adoptada recoge adecuadamente el comportamiento seguido por el bce, y por medio del estadístico J comprobamos que no debemos rechazar la hipótesis de validez de los instrumentos utilizados en los ajustes.

Como se ha dicho, el objetivo de esta investigación es detectar la posible existencia de decisiones asimétricas a través del grado de significación del coeficiente c₃, y como puede verse no podemos rechazar la hipótesis de no significatividad de dicho coeficiente, lo que, a su vez, nos conduce a pensar que no hay suficientes evidencias de comportamiento asimétrico por parte del bce. Estos resultados son compatibles con la inexistencia de una curva de Phillips (o una curva de oferta agregada) convexa en el área euro en el periodo analizado, como se expone más arriba.

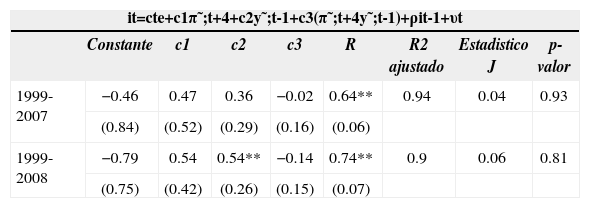
En el cuadro 2 se resumen los resultados de la contrastación de la ecuación [12], en este caso con ajuste parcial (alisamiento del tipo de interés) y término rectangular o de interacción.

Cuadro 2.

Función de reacción con ajuste parcial, con término rectangular

it=cte+c1π˜;t+4+c2y˜;t-1+c3(π˜;t+4y˜;t-1)+ρit-1+υt
	Constante	c1	c2	c3	R	R2 ajustado	Estadistico J	p-valor
1999-2007	−0.46	0.47	0.36	−0.02	0.64**	0.94	0.04	0.93
	(0.84)	(0.52)	(0.29)	(0.16)	(0.06)
1999-2008	−0.79	0.54	0.54**	−0.14	0.74**	0.9	0.06	0.81
	(0.75)	(0.42)	(0.26)	(0.15)	(0.07)

Notas: los errores estándar aparecen entre paréntesis. Los superíndices ** y * denotan el rechazo de la hipótesis de que el verdadero coeficiente es cero a un nivel de significación de 5 y 10 por ciento, respectivamente.

El resultado es menos satisfactorio en cuanto a la significatividad de los coeficientes de reacción c₁ y c₂, hecho que está relacionado con el carácter muy alisado de las decisiones del bce, y que implica un elevado protagonismo del coeficiente del término de ajuste parcial ρ. Por lo que respecta al coeficiente del término rectangular c₃ que, como decimos, debe reflejar la posible existencia de comportamientos asimétricos en las decisiones del bce, de nuevo no podemos rechazar la hipótesis de que sea distinto de cero.

Conclusiones

La asimetría de las reglas de política monetaria debe buscarse en la existencia de una función de preferencias asimétricas del banco central y en la potencial convexidad de la relación entre output y producción. Los bancos centrales no explicitan la función de preferencias, por lo que la existencia de una función de pérdidas asimétrica ha de ser detectada mediante de las acciones sobre el instrumento de política monetaria en periodos suficientemente largos. Además, dichas preferencias pueden verse modificadas con motivo de la renovación de los equipos de gobierno de la institución monetaria y por la propia evolución de la economía. En este sentido, las preferencias de un banco central son institucionalmente dependientes aun cuando el objetivo del banco central esté bien definido. Por su parte, la presencia de una curva de Phillips convexa tiene su origen en el modelo estructural de la economía, alguno de cuyos aspectos se escapan a la acción del banco central y a la política monetaria.

A lo largo de este trabajo hemos reseñado cómo la presencia de asimetrías en las preferencias del banco central o en la curva de Phillips puede derivar hacia un comportamiento asimétrico en la toma de decisiones de política monetaria por parte de esa institución. Tales comportamientos asimétricos consistirían en algún tipo de sobre o infrarreacción al modificar el tipo de interés ante desviaciones respecto al objetivo de inflación o de la tendencia de la producción, dependiendo dicho comportamiento de si las desviaciones son de signo positivo o bien negativo. Esa asimetría, si existe, deberá quedar reflejada en la función de reacción de política monetaria, en la que se resume la estrategia de decisión seguida. De esta forma, la función deberá incorporar un término no lineal, en este caso (π˜;t+4y˜;t-1), cuyo coeficiente sea significativamente distinto de cero.

Podría suponerse que en el caso del bce, un instituto relativamente joven y deseoso de ganarse credibilidad antiinflacionaria, en principio, éste hubiera desarrollado un comportamiento asimétrico, reaccionando con más intensidad ante las desviaciones positivas de la tasa de inflación respecto al objetivo de referencia que ante las desviaciones negativas. Sin embargo, tras llevar a cabo las correspondientes estimaciones, llegamos a la conclusión de que, en sus primeros diez años de ejecución de la política monetaria, las reacciones del bce no han sido asimétricas. Se comprueba una mayor bondad de las funciones de reacción lineales estimadas (los resultados no se incorporan en este trabajo), tanto con término de ajuste parcial, como sin él, en comparación con las no lineales, que incorporan el término rectangular. Además, se ha comprobado que el coeficiente correspondiente a este último término no es significativamente distinto de cero.

La explicación de este resultado no puede radicar en la compensación de asimetrías, en el sentido de que las posibles asimetrías ante las desviaciones de la inflación estuvieran compensadas por posibles asimetrías de signo opuesto ante desviaciones en el producto puesto que, dada la prioridad que el bce asigna a la estabilidad de precios, creemos que este efecto compensador no debe haber tenido mucha influencia. Por otra parte, como se ha mostrado, en la estimación de la curva de Phillips para este periodo prevalece la hipótesis de linealidad sobre la de convexidad, con lo que se puede descartar esta causa de comportamiento asimétrico.

Por último, podría haber ocurrido que el smoothing en las decisiones sobre el tipo de interés haya diluido el comportamiento asimétrico, haciéndolo más difícil de detectar. No obstante, consideramos que hemos eliminado este riesgo al adoptar una frecuencia trimestral. Además, también hemos tenido en cuenta el smoothing al realizar los ajustes incluyendo un término de ajuste parcial, comprobando de nuevo la no significatividad del coeficiente c3. Como conclusión complementaria, se puede añadir que la aceptación de la hipótesis de linealidad equivale a que el BCE opta por la sencillez, en aras de la transparencia, frente a otras estrategias de decisión más complejas.

Apéndice

it está implícito en y˜;t+1,  π˜;t+2  e  y˜;t+2. Aplicando la regla de la cadena se obtiene la condición de primer orden:

operando:

obtenemos la siguiente ecuación de Euler:

Usando [8] para remplazar Ety˜;t+2 en términos de Ety˜;t+1,Etxt+1 y Etrt+1, y despejando i_t obtenemos una regla de Taylor:

donde c1=1+αλξβ;c2=1+δβ2δξβ;c3=ηξ;c4=2θαλξβ.