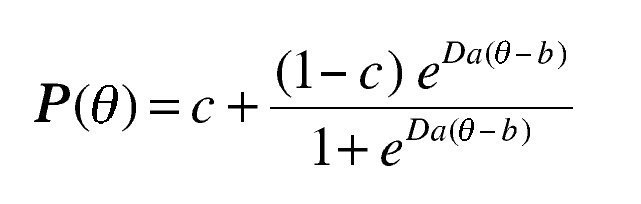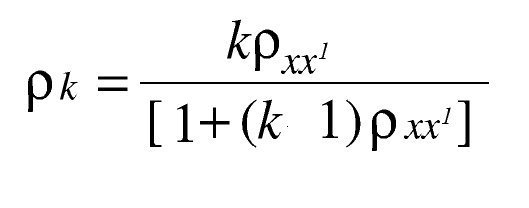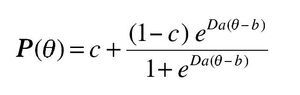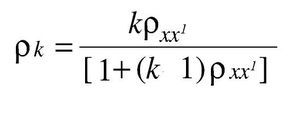Introducción: El examen profesional es la evaluación sumativa de altas consecuencias, más importante de la carrera de médico cirujano. Una fuente de evidencia de validez del examen es el análisis psicométrico de los reactivos, para el que tradicionalmente se ha utilizado la Teoría Clásica de los Test (TCT), la cual tiene algunas desventajas, que la Teoría de Respuesta al Ítem (TRI) pretende resolver. El presente estudio reporta el análisis del Examen Profesional Teórico de la Facultad de Medicina de la UNAM con la TRI.
Objetivo: Explorar los beneficios del uso de la TRI, para documentar evidencia de validez en un examen de altas consecuencias en educación médica.
Método: Se efectuó el análisis psicométrico del Examen Profesional Teórico de la Facultad de Medicina de la UNAM, aplicado en 2008. La prueba consistió en un examen de opción múltiple acerca de seis áreas de conocimiento: Medicina interna, Pediatría, Gineco-obstetricia, Urgencias médicas, Cirugía y Medicina familiar, evaluadas con 420 reactivos de opción múltiple. Se calcularon confiabilidad, dificultad y discriminación con la TCT. Se utilizó el modelo de tres parámetros de la TRI. Con las dos aproximaciones se seleccionaron los mejores ítems, y se estimó la longitud de la prueba con la fórmula de Spearman-Brown.
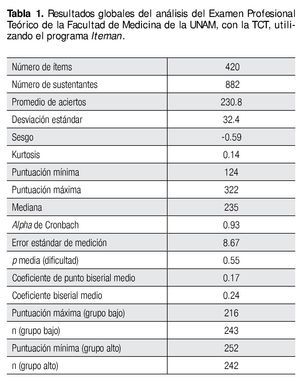
Resultados: El examen fue respondido por 882 sustentantes, tuvo un índice de dificultad de 0.55 y una confiabilidad de 0.93. Con el modelo de 3pl-TRI, el examen es informativo en niveles de habilidad cercanos al promedio en la escala theta. El parámetro de discriminación promedio (a) fue 0.67, el parámetro de dificultad (b) fue 1.21, y el parámetro de seudoadivinación (c) fue 0.18. Se encontró que es posible reducir el número de reactivos de la prueba, manteniendo una alta confiabilidad. La mayoría de los ítems en la prueba original (84%) tuvieron un buen ajuste al modelo 3pl-TRI, y en la versión acortada la gran mayoría (97%) tuvieron un ajuste similar.
Discusión y conclusiones: El Examen Profesional Teórico de la Facultad de Medicina cubre los requisitos teóricos de número de reactivos y sustentantes, para aplicar el modelo de TRI. Se obtuvo evidencia de validez de constructo y un panorama psicométrico del instrumento, útil para la planeación de versiones subsecuentes. El examen puede reducirse en longitud haciéndolo más eficiente, sin perder precisión en la estimación de los niveles de habilidad de los sujetos ni validez de contenido.
Introduction: The end-of-career Professional Exam is a high-stakes summative assessment done at UNAM's Faculty of Medicine in Mexico, to certify that undergraduate medical students have achieved the knowledge level required to enter practice as a general physician. One source of validity evidence is the exam's internal structure, studied with item analysis. Classical Measurement Theory (CMT) has traditionally been used for this purpose, but it has several disadvantages that Item Response Theory (IRT) intends to solve. This report describes the use of the IRT model in the analysis of the written Professional Exam at UNAM's Faculty of Medicine.
Objective: To explore the benefits of using the IRT model to obtain validity evidence for a high-stakes achievement test in a medical school.
Method: A psychometric analysis of the written Professional Exam at UNAM's Faculty of Medicine was performed in 2008. The test was a written 420-item multiple-choice question exam that covers Internal medicine, Pediatrics, Obstetrics and gynecology, Emergency medicine, Surgery and Family medicine. CMT elements were calculated: reliability, difficulty and discrimination. The three-parameter IRT model was used. With these calculations the best items were selected, and the length of the test was estimated with Spearman-Brown's prophecy formula.
Results: The exam was taken by 882 medical students, had mean difficulty index of 0.55 and reliability of 0.93. With the 3pl-IRT model, it was found that the test was particularly informative in ability levels close to the mean in the theta scale. The average discrimination parameter (a) was 0.67, the difficulty parameter (b) was 1.21, and the seudo-guessing parameter (c) was 0.18. A shortened version of the test (250 items) was designed using the information obtained, maintaining a high reliability. A majority of the items in the original test (84%) had a good fit to the 3pl-IRT model, and in the shortened version almost all of them (97%) had an appropriate model fit.
Discussion and conclusions: The written Professional Test at UNAM's Faculty of Medicine fulfills the conceptual requirements (item number, examinees' sample size) to apply the IRT model in its item analysis. This information augments the validity evidence of the exam's score inferences and interpretations, and provides a psychometric panorama of the instrument that is useful to plan subsequent versions of the exam. The exam can be reduced in length making it more efficient, without losing precision in the estimation of the subjects' ability level or content validity.
Introducción
La formación de médicos generales implica un largo periodo de instrucción, en el cual los estudiantes de medicina transitan por múltiples cursos, prácticas y actividades que contribuyen a la adquisición de un gran caudal de conocimientos, habilidades y destrezas necesarias para ejercer la medicina de manera independiente. Una de las principales responsabilidades de las instituciones educativas formadoras de profesionistas es el documentar, a través de una evaluación sumativa criterial, la competencia de sus graduados.1,2 En algunos países existen instancias independientes, como es el caso del National Board of Medical Examiners en EUA, las cuales se encargan de desarrollar y aplicar estas pruebas de evaluación, llamadas por algunos autores como "de altas consecuencias", por lo importante de los resultados para el sustentante y para la sociedad.2,3
En el caso de México no existe una instancia de esta naturaleza, por lo que la responsabilidad de las evaluaciones sumativas de los médicos generales al final de su entrenamiento, recae en las escuelas y facultades de medicina en donde llevan a cabo sus estudios. La Dirección General de Profesiones de la Secretaría de Educación Pública en México es la instancia responsable de registrar el título del médico y de expedir la cédula profesional correspondiente (documento legal que permite ejercer la medicina en nuestro país), de tal manera que la responsabilidad de documentar de manera objetiva y justa que un aspirante a médico general posea las competencias necesarias para ejercer dicha profesión, se descarga en las Universidades que avalan sus programas educativos.4 Por lo anterior, es aparente la importancia de los citados exámenes para los educandos y la sociedad, ya que generalmente no hay otro filtro de control de calidad para permitir que el médico graduado ejerza su profesión.
La Facultad de Medicina de la UNAM es una de las instituciones formadoras de médicos generales con mayor tradición en América Latina, y durante su historia ha tenido diferentes modalidades de exámenes de fin de la licenciatura. Desde hace muchos años, el Examen Profesional se ha constituido en la evaluación sumativa de fin de cursos para poder expedir el título de médico cirujano. Este examen se sustenta en el Reglamento General de Exámenes de la UNAM,5 y en las diversas opciones de titulación que ofrece esta casa de estudios.6 En el caso de la Facultad de Medicina, el Examen General de Conocimientos corresponde a la opción de titulación B, que comprende la aprobación de un examen escrito. Dicha prueba consiste en una exploración general de los conocimientos del estudiante, de su capacidad para aplicarlos y de su criterio profesional.5,6 El Examen Profesional tiene dos fases, una teórica y una práctica. La fase teórica consiste en un examen escrito con preguntas de opción múltiple, y la fase práctica tiene dos modalidades: examen oral tradicional ante un paciente real, y el Examen Clínico Objetivo Estructurado (ECOE) con múltiples estaciones estandarizadas.7 Ambas fases están orientadas a evaluar el nivel de conocimientos, habilidades y destrezas para ejercer la medicina general de manera independiente en nuestro país.
El concepto moderno de validez en los procesos de evaluación en educación, propone que toda la validez es de constructo, como modelo unitario, y que existen varias fuentes de la misma: contenido, proceso de respuesta, estructura interna, relación con otras variables y consecuencias.8,9 De tal manera que la validez es un concepto holístico que se alimenta de varios aspectos, el que nos ocupa en este estudio es la fuente de evidencia denominada de estructura interna, que se obtiene a través del análisis psicométrico de los resultados obtenidos con la aplicación del instrumento.8,9
Tradicionalmente se ha utilizado la Teoría Clásica de los Test (TCT) para este tipo de análisis, pero en las últimas décadas el modelo de Teoría de Respuesta al Ítem (TRI) ha surgido como una estrategia que aporta mayor información, y que subsana algunas de las limitaciones de la TCT. Debido a la importancia del Examen Profesional de la Facultad de Medicina de la UNAM, y en un afán de mejorar la calidad del instrumento y las inferencias que de sus resultados se hagan, el objetivo del presente trabajo fue determinar los elementos informativos que aporta el análisis psicométrico del instrumento considerando, además del análisis clásico de los reactivos con TCT, la aproximación con el modelo de tres parámetros de la TRI.
Se optó por el modelo de tres parámetros, debido a que es el primer acercamiento de análisis con esta aproximación teórica en nuestro medio, y se consideró relevante conocer los valores de los parámetros de dificultad, discriminación y seudoadivinación para cada reactivo. A continuación se describe el marco teórico de la TRI, para ofrecer al lector una panorámica de dicho modelo conceptual, en virtud de que los profesionales de la salud generalmente no están familiarizados con este método de análisis.
Marco teórico de la TRI
La TRI conocida inicialmente como Teoría del Rasgo Latente, intenta dar un fundamento probabilístico al problema de la medición de rasgos y constructos no observables. Esto significa que surge y se desarrolla como una necesidad de superar las limitaciones de la TCT.10,11 La TRI debe su nombre a que, a diferencia de la TCT, se centra más en las propiedades de los ítems que en las propiedades globales de una prueba, es decir, considera al ítem como la unidad de análisis del test, en lugar de las puntuaciones globales del mismo, como lo hace la TCT.11,12 Lo que permite observar los distintos modelos de la TRI como un cuerpo teórico unificado, son los supuestos que le dan estructura y solidez, que a continuación se mencionan:
• Asume de manera a priori, la existencia de un rasgo o aptitud latente del sujeto.
• Relaciona el rasgo que se está midiendo con el rendimiento del sujeto, y lo describe a partir de la Curva Característica del Ítem (CCI), en la que se señala la probabilidad de la respuesta en función de la aptitud.11,13
Seguidamente se describen los supuestos de los modelos de la TRI:11,14
Unidimensionalidad
En los modelos unidimensionales de la TRI, se asume que existe un rasgo latente el cual es el responsable de la respuesta, que emite el sujeto ante el estímulo que le demanda un reactivo. Basta con un solo rasgo para explicar los resultados de los sujetos y las relaciones entre los ítems. De lo contrario, se requeriría un valor diferente para cada rasgo (θ1, θ2, ... θn). Dicho en otras palabras, el rendimiento que un sujeto tenga en un ítem, depende del nivel que muestre en un solo rasgo o dimensión. Este principio también se aplica para la prueba en su conjunto, esto es, se espera que los ítems que conforman un test midan todos y cada uno de ellos, sólo un rasgo o dimensión.11,14
Independencia local
Es una premisa derivada de la unidimensionalidad. Plantea que la respuesta dada por el sujeto a un ítem es independiente a la que da a los subsiguientes, esto es, la respuesta a un reactivo sólo depende de sus parámetros y de la habilidad del sujeto. Matemáticamente se expresa como la probabilidad de acertar un número determinado de reactivos es igual al producto de las probabilidades, de acertar correctamente cada reactivo de manera separada. Para verificar el supuesto de independencia local, usualmente se llevan a cabo los cálculos de las probabilidades de acertar a los reactivos, considerando los patrones de respuesta del conjunto de ítems que contiene el test.11,14
Invarianza
Esta propiedad se da en dos sentidos: por una parte en el conjunto de ítems ante diferentes niveles de habilidad o rasgos de los sujetos que los contestan, y por el otro, que se puede medir el nivel de rasgo de una persona a partir de conjuntos diferentes de ítems. Ello significa que se pueden estimar los parámetros de los ítems sin que éstos dependan de la muestra o población que los respondieron, obteniéndose la misma curva para el ítem, al margen del grupo de sujetos que lo haya contestado. Respecto a la invarianza de las personas, es posible determinar la habilidad de los sujetos que contestaron sin que la medida del rasgo, dependa de las características del test que les fue aplicado.11,15
El error de medición y la función de información
En la TRI, el error de medición (error típico de estimación) es diferente al estadístico que se emplea en la TCT, y la diferencia fundamental radica en que se trata de una función del rasgo (θ) y para cada nivel de rasgo o valorθ existe un error de estimación, siendo más preciso en algunos valores de θ que en otros, dado que se calcula la función del error típico de estimación para cada valor posible θ. Además, se obtiene la función de información, la cual nos permite conocer los niveles de habilidad de los sustentantes estimados con mayor precisión y por ende, donde el error de medición es menor.11,12
El significado de los tres parámetros de la TRI
Este modelo toma en cuenta la habilidad de los sujetos y tres parámetros logísticos (a=discriminación, b=dificultad del reactivo y c=seudoadivinación), para describir la función de la respuesta al reactivo. Dicha función de respuesta, también llamada CCI indica la probabilidad que tiene el sujeto de responder correctamente al reactivo, de acuerdo con su nivel de habilidad (θ).14,15 El significado de cada uno de los parámetros se describe a continuación:
• El valor del parámetro a, representa la discriminación del ítem y es conocido como la pendiente de la curva. Es el punto fijo de inflexión de la curva cuando el sujeto tiene el 50% de probabilidad de responder correctamente al reactivo, es decir, cuando θ=b. Generalmente su valor oscila de 0 a 2.5, considerándose como discriminativos a aquellos ítems cuyo valor de a es próximo o mayor a 1.
• El índice de dificultad del reactivo o parámetro b, es el valor de θ para el cual P(θ)=0.5, esto es, cuando no hay aciertos al azar, la habilidad del sujeto y la dificultad del reactivo son iguales, por lo que la probabilidad es de 0.5. Entre mayor sea b, el reactivo será más difícil, esto es, la probabilidad de acertar el reactivo decrece cuando incrementa la dificultad del ítem. Aún cuando θ pueda estar definida en múltiples escalas, en la práctica se emplea la escala típica con media cero, varianza uno y un rango de valores que oscilan entre -3 y 3,15 considerando un valor de b=0 como la dificultad promedio que puede asumir un reactivo, valores superiores a 2.5 como reactivos muy difíciles y menores a -2.5, reactivos muy fáciles.16
• El parámetro c representa la probabilidad de que un sujeto con baja habilidad responda correctamente el reactivo, simplemente por adivinación. La probabilidad de acertar por azar en realidad se considera que es la misma para todos los sujetos, independientemente de su nivel de rasgo. Sin embargo, se considera que son los sujetos con menor habilidad quienes recurrirían al azar para tratar de tener éxito en la resolución del reactivo. Es este tercer parámetro, lo que lo distingue de los modelos logísticos de uno (que considera sólo la dificultad del reactivo), y dos (que considera tanto la dificultad como la discriminación del reactivo) parámetros de la TRI.11,14
La expresión matemática del modelo de tres parámetros es la siguiente:
En donde:
P(θ) = Probabilidad de acertar al reactivo a un nivel de rasgo θ.
θ = Habilidad o rasgo del sujeto que contesta al ítem.
e = Base de los logaritmos neperianos, cuyo valor es 2.718.
D = Constante (D=1.7 o 1).
a = Índice de discriminación del reactivo.
b = Índice de dificultad del reactivo.
c = Índice de seudoadivinación del reactivo.
En la CCI que describe la formulación anterior, la probabilidad de tener éxito en la repuesta corresponde a la asíntota inferior de la curva. A diferencia de los parámetros a y b que se tratan de parámetros libres, los valores de c van de 0-1, aunque generalmente asuman valores entre 0.0 y 0.40, considerándose como inadecuados aquellos reactivos con un valor de c superior a 0.30 y como reactivos deseables, aquellos cuyo parámetro c sea igual o inferior a 0.20, prefiriéndose los valores más bajos, dado que ello indicaría que la probabilidad de que los sujetos cuya habilidad es baja acierten al reactivo es mínima.
Método
Los sustentantes que presentaron el Examen General de Conocimientos son alumnos que finalizaron el quinto año del Plan Único de Estudios, de la carrera de Médico Cirujano, en la Facultad de Medicina de la UNAM. Los estudiantes deben aprobar la fase teórica y práctica del Examen Profesional para poder ingresar al Servicio Social, y ser candidatos a obtener el título universitario de médico cirujano. La aplicación del examen estuvo a cargo de la Secretaría de Educación Médica de la Facultad de Medicina, efectuándose en el mes de enero de 2008, en las instalaciones de la misma Facultad.
El Examen Profesional Teórico escrito ha tenido estructuras diferentes en el transcurso de los años, en el momento que se realizó el presente estudio estaba conformado por seis áreas de contenidos: Medicina interna, Pediatría, Gineco-obstetricia, Urgencias médicas, Cirugía y Medicina familiar. El instrumento se estructuró con 420 reactivos, distribuidos en las seis áreas de conocimientos anteriormente señaladas. Los reactivos tuvieron el formato de opción múltiple con cinco opciones de respuesta, de las cuales sólo una era la correcta. La prueba se aplicó en condiciones estandarizadas para todos los sustentantes, con papel y lápiz. Los resultados del examen se colectaron en hojas de lector óptico, que fueron capturadas para generar los datos utilizados en el análisis psicométrico.
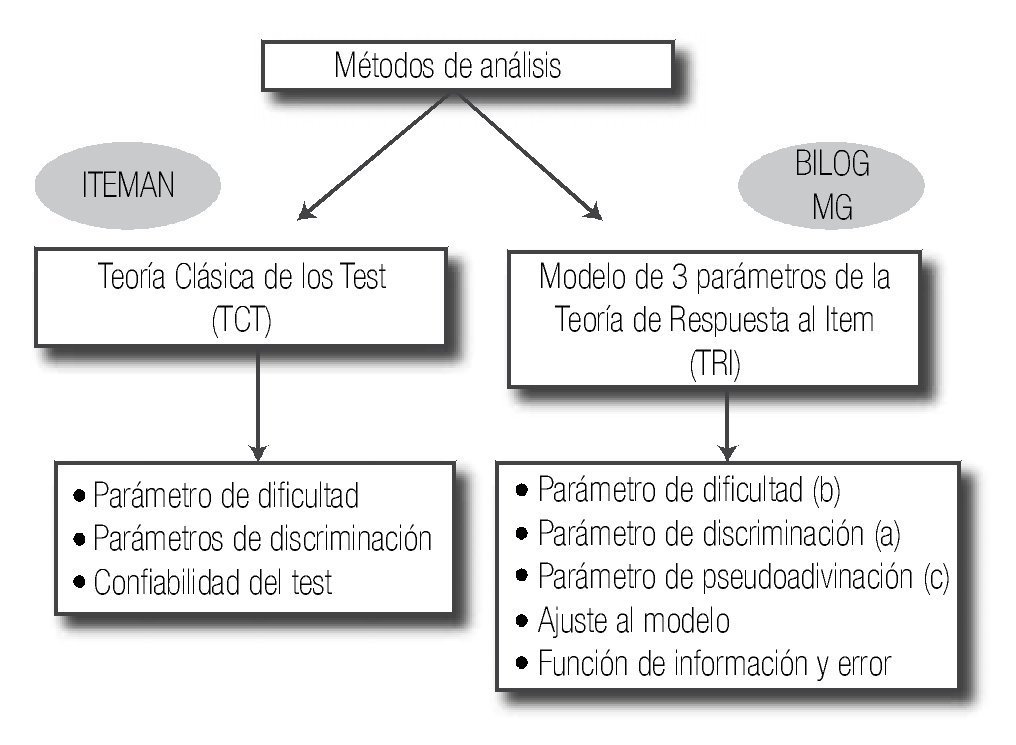
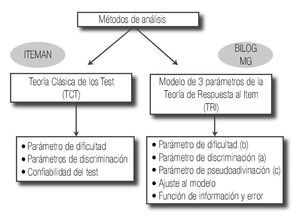
Para el análisis de los resultados obtenidos con el instrumento, se utilizaron los dos modelos: el de TCT con el programa Iteman versión 4 (Assessment Systems Corporation®, Minnesota, EUA), y el de TRI con el modelo logístico de tres parámetros, con el programa BILOG-MG 3.17 Se consideró para la estimación de la habilidad de los sustentantes, el método de estimación máxima verosimilitud. El esquema de los métodos de análisis se describe en la Figura 1.
Figura 1. Procedimientos de análisis utilizados para la evaluación del Examen Profesional Teórico, de la Facultad de Medicina de la UNAM.
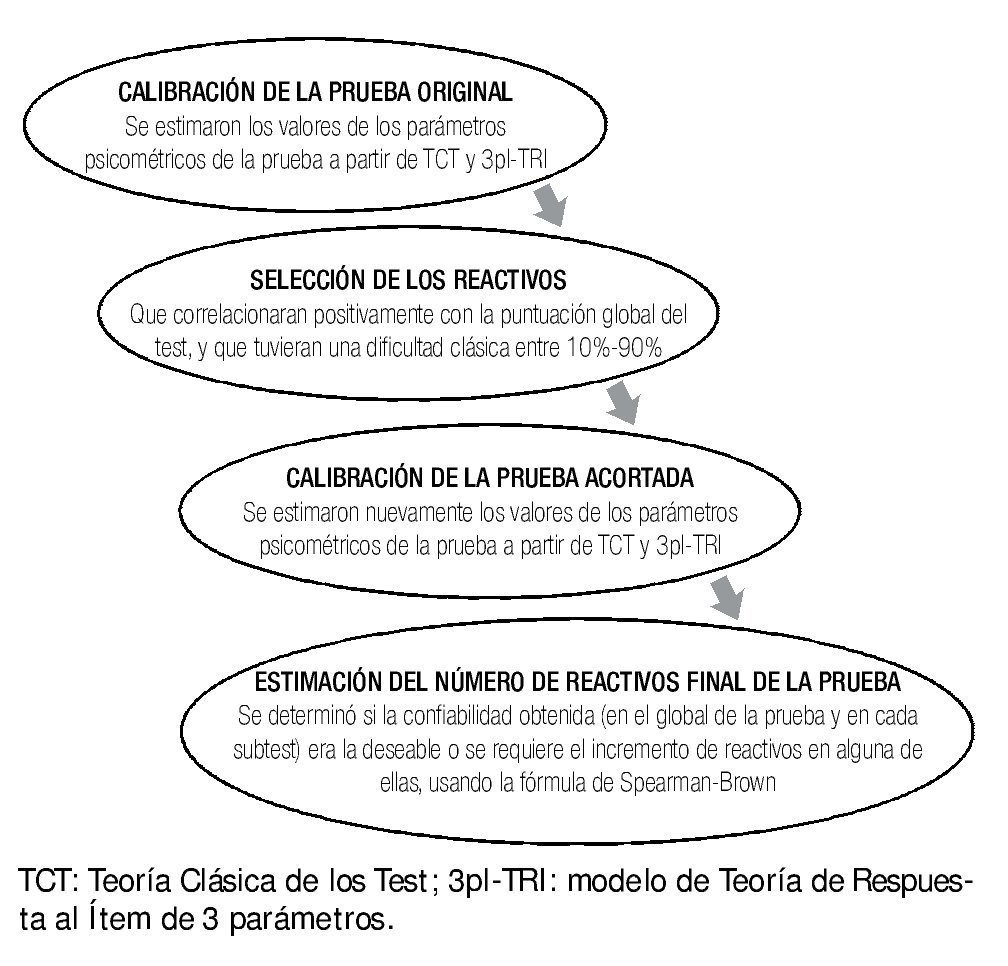
En un ejercicio de integración de la información obtenida a partir de estas dos aproximaciones, se seleccionaron los mejores reactivos en términos de sus cualidades métricas y que atendieran al constructo medido para los distintos contenidos del examen, estimándose la longitud de la prueba, a fin de conservar la misma confiabilidad del instrumento en una versión reducida del examen. La secuencia de acciones realizada se esquematiza en la Figura 2.
Figura 2. Secuencia de acciones durante el proceso de análisis del Examen Profesional Teórico de la Facultad de Medicina de la UNAM.
Para la estimación de la longitud de la prueba se utilizó la fórmula de la profecía de Spearman-Brown:18
En donde:
ρxx1 = Confiabilidad obtenida en el cálculo original.
ρk = Confiabilidad deseada.
k = Proporción o número de veces que debe ser acortado o alargado el test, para alcanzar la confiabilidad deseada.
Resultados
El examen profesional teórico de la Facultad de Medicina de la UNAM analizado tuvo lugar en las instalaciones de la institución en el mes de enero de 2008, y el número de sustentantes que contestó el examen en esa ocasión fue de 882.
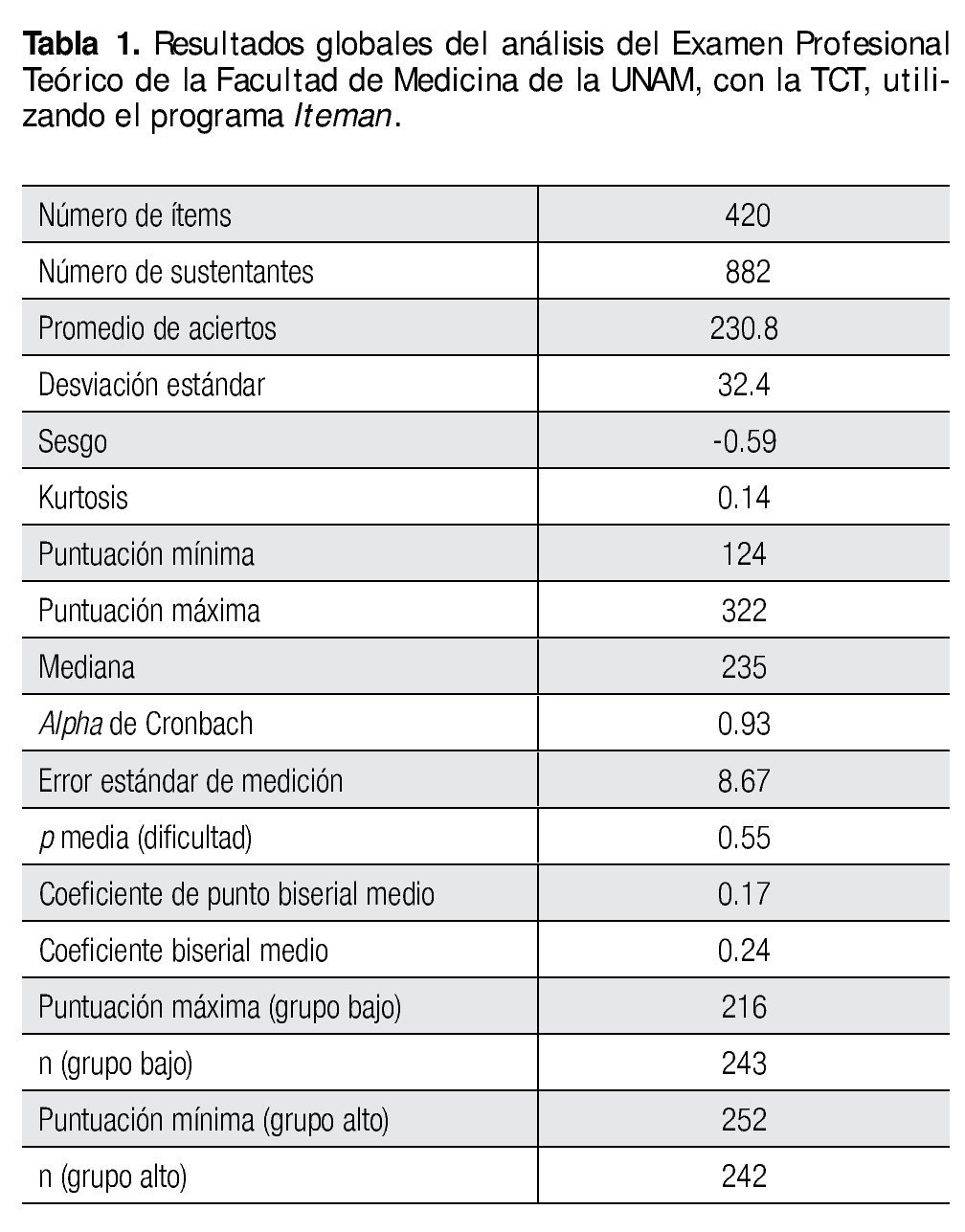
Respecto al conjunto global de la prueba, se encontró que el promedio de dificultad clásica fue de 54.95% de aciertos y su confiabilidad medida con el coeficiente de Cronbach tuvo un α=0.93. El alpha de Cronbach calculado para cada subtest de la prueba o área de conocimiento, tuvo un valor adecuado, a saber: Medicina interna (α=0.73), Pediatría (α=0.69), Gineco-obstetricia (˚=0.74), Urgencias médicas (α=0.76), Cirugía (α=0.72) y Medicina familiar (α=0.64). Los resultados globales de la prueba con la TCT, se presentan en la Tabla 1.
Parámetros obtenidos con el análisis de TRI
De acuerdo con la calibración del examen con el modelo de tres parámetros, a continuación se presentan los valores de los parámetros de discriminación, dificultad y seudoadivinación. Respecto a la distribución del parámetro a, se observó una concentración en reactivos cuyo valor se encuentra alrededor de 0.5, esto es, más del 55% de ellos tuvo un valor de discriminación igual o superior a 0.5. En lo concerniente a la distribución del parámetro b, se destaca que aun cuando se encontró una tendencia a que la distribución sea uniforme en el rango de -2.0 a 2.0, cerca del 70% de los reactivos tiene una dificultad entre -3 y 3. Respecto al parámetro de seudoadivinación, se encontró una mayor concentración en valores iguales o menores a 0.20 (aproximadamente el 70%), lo cual es de esperarse, dada la cantidad de alternativas que tiene cada reactivo (1/k=1/5=0.20). Además, sólo el 0.47% de los reactivos tuvo un valor no deseable en este parámetro (de más de 0.30).
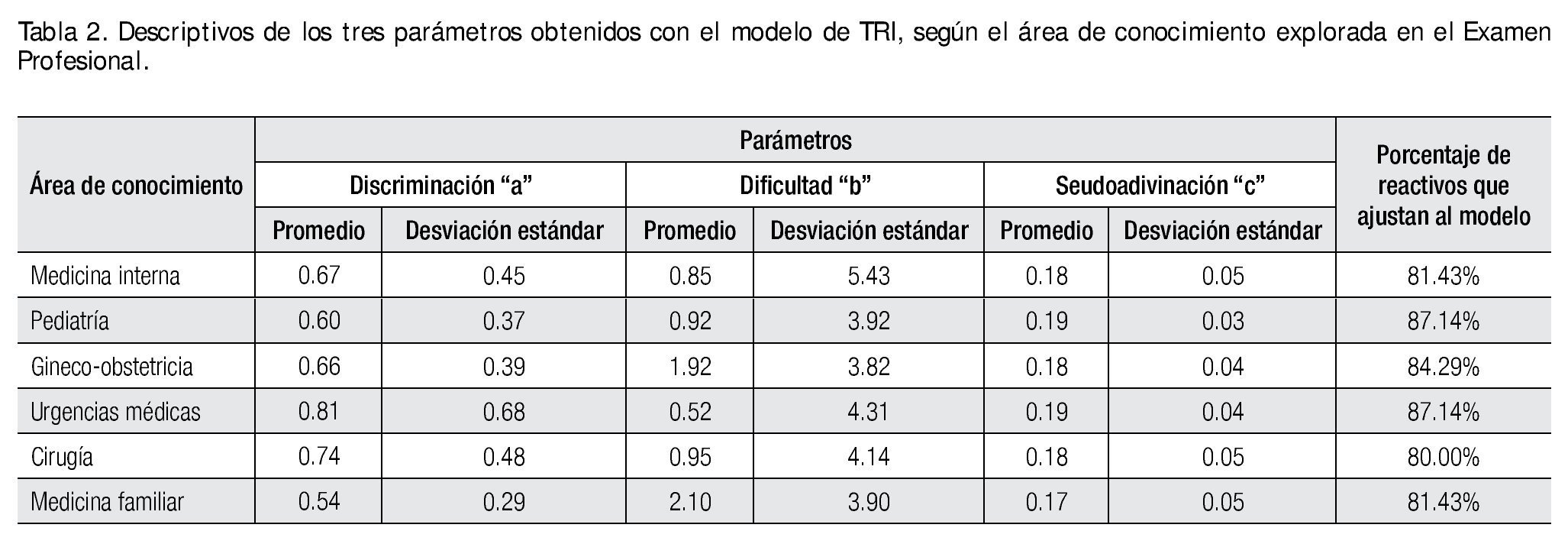
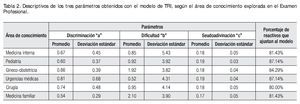
Para tener un mayor acercamiento respecto a cada una de las áreas del examen, en la Tabla 2 se aprecian los descriptivos de los tres parámetros en cada una de ellas. En dicha tabla se observa que todas las áreas tienen valores promedios de discriminación adecuados, destacando el área de Urgencias médicas, cuyo valor promedio de discriminación es el más alto, aunque también la dispersión es la mayor. Este parámetro tiene su referente en la teoría clásica, y es el coeficiente de correlación punto-biserial. Las medias de las correlaciones puntobiseriales por área de conocimiento fueron: Medicina interna (0.17), Pediatría (0.15), Gineco-obstetricia (0.17), Urgencias médicas (0.19), Cirugía (0.17) y Medicina familiar (0.13).
El parámetro de dificultad es un poco más alejado del parámetro clásico de dificultad, que básicamente lo definimos en este espacio como la proporción de sujetos que contestaron correctamente al reactivo, en tanto que para la dificultad del área, se establece como el valor promedio del porcentaje de aciertos del conjunto de reactivos que constituyen el subtest. Esta diferencia tiene implicaciones respecto al nivel de habilidad de los sustentantes, por ejemplo, dos sujetos que contestaron correctamente el mismo número de reactivos, en el parámetro clásico de dificultad el nivel de dominio sería el mismo, pero en el modelo de tres parámetros de la TRI, la habilidad estimada puede ser radicalmente diferente, dados los valores de discriminación y seudoadivinación de los reactivos. Regresando a la dificultad clásica de las áreas, se observaron los siguientes valores: Medicina interna (57.6%), Pediatría (55.0%), Gineco-obstetricia (47.9%), Urgencias médicas (60.9%), Cirugía (60.1%) y Medicina familiar (48.1%).
Finalmente, la media del valor del parámetro de seudoadivinación para las cuatro áreas es cercana a cero y con una dispersión muy baja, particularmente en el caso del área de Medicina familiar. Este parámetro no tiene referente directo con la teoría clásica, como ya se señaló anteriormente.
Función de información
Una seria desventaja de la TMC es asumir que el error de medición es el mismo para toda la población de estudiantes. Es aquí, donde la función de información obtenida con la TRI adquiere un papel trascendental en el análisis, ya que ésta nos permite conocer el grado de precisión que tienen las áreas a diferentes valores de habilidad de los sustentantes. A continuación, en el resto de la sección de "Resultados", se utilizarán los datos de la prueba acortada, ya que como se argumentó previamente no se pierde precisión en la estimación del rasgo.
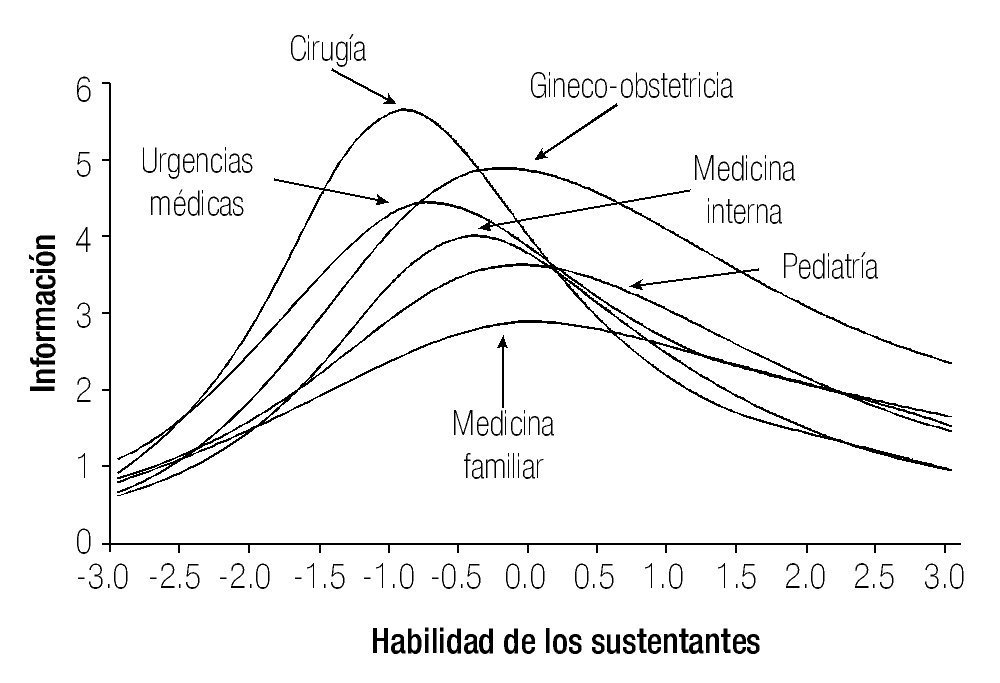
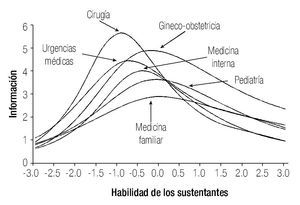
En la Figura 3 se observan las CCT o Función de Información, de cada área de conocimiento, con los datos de la prueba acortada.
Figura 3. Funciones de información de cada una de las áreas del examen, calculadas con el modelo de tres parámetros de TRI.
Las áreas cuyos reactivos tienen un promedio de discriminación mayor fueron Cirugía y Urgencias Médicas, que son particularmente informativas en niveles de habilidad próximos a -1.3, de hecho, es en este valor donde la prueba alcanza su nivel máximo de precisión. Por otra parte, se observa que el área de Medicina familiar es la menos informativa de las seis áreas de conocimiento que conforman la prueba.
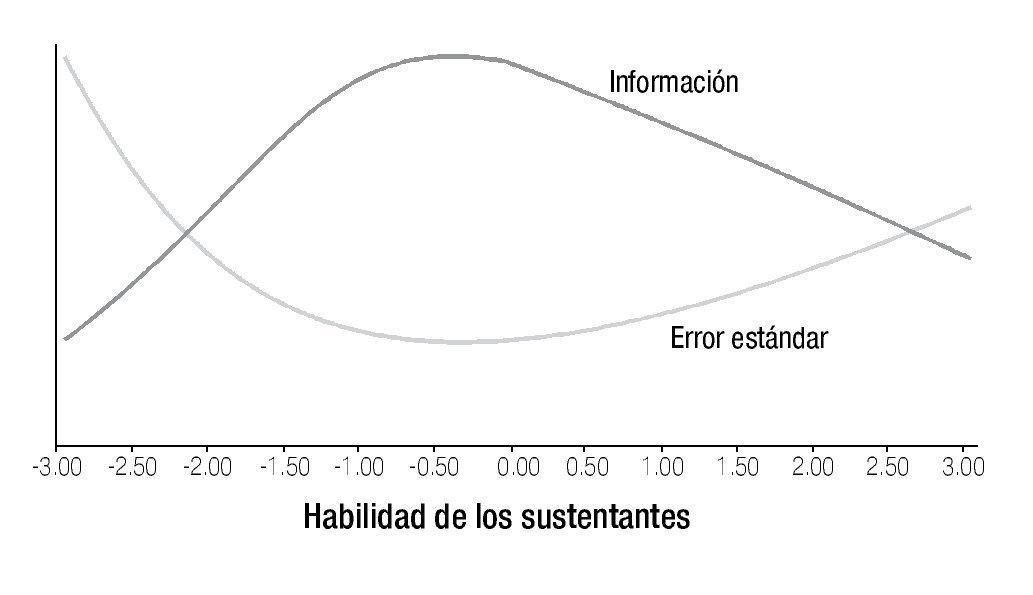
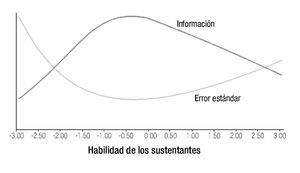
Con base en los resultados obtenidos, se observó que el examen es particularmente informativo en niveles de rasgo cercanos al promedio (cero). Ello implica, que el nivel de precisión con el cual se están estimando los valores de habilidad promedios, particularmente en el intervalo de -0.5 a 0.5 y por ende, el error de medición son los más pequeños en este intervalo (Figura 4).
Figura 4. Función de información de la prueba y error estándar de medición calculados con el modelo de TRI.
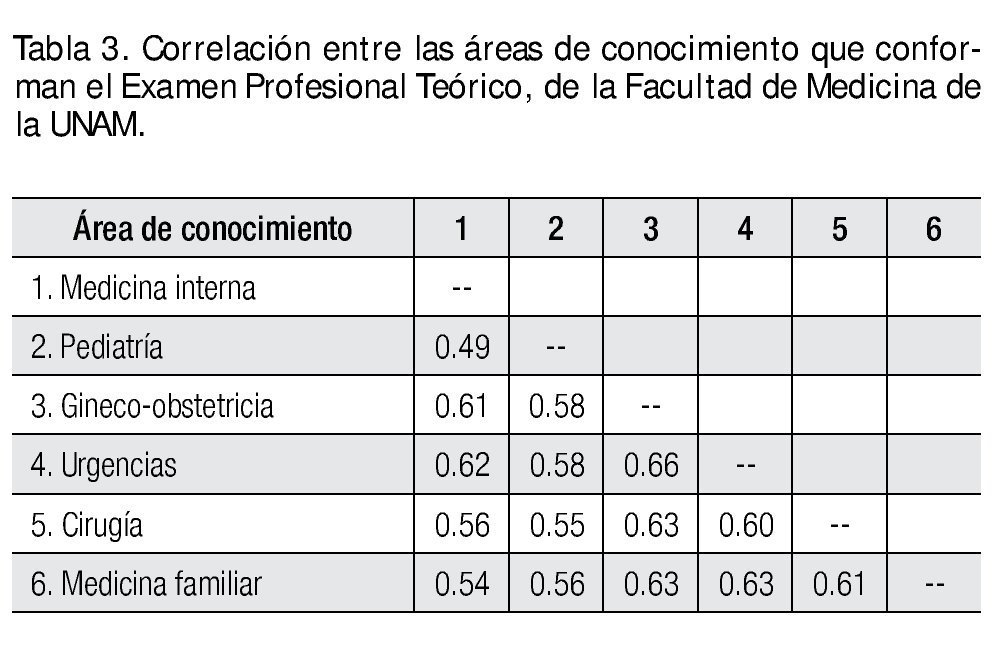
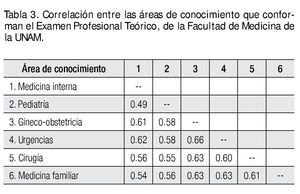
En la Tabla 3, se muestran los coeficientes de correlación de Pearson entre las distintas áreas de conocimiento que conformaron el examen acortado, observándose los valores de correlación moderados, lo cual permite vislumbrarlos como constructos relativamente independientes entre sí.
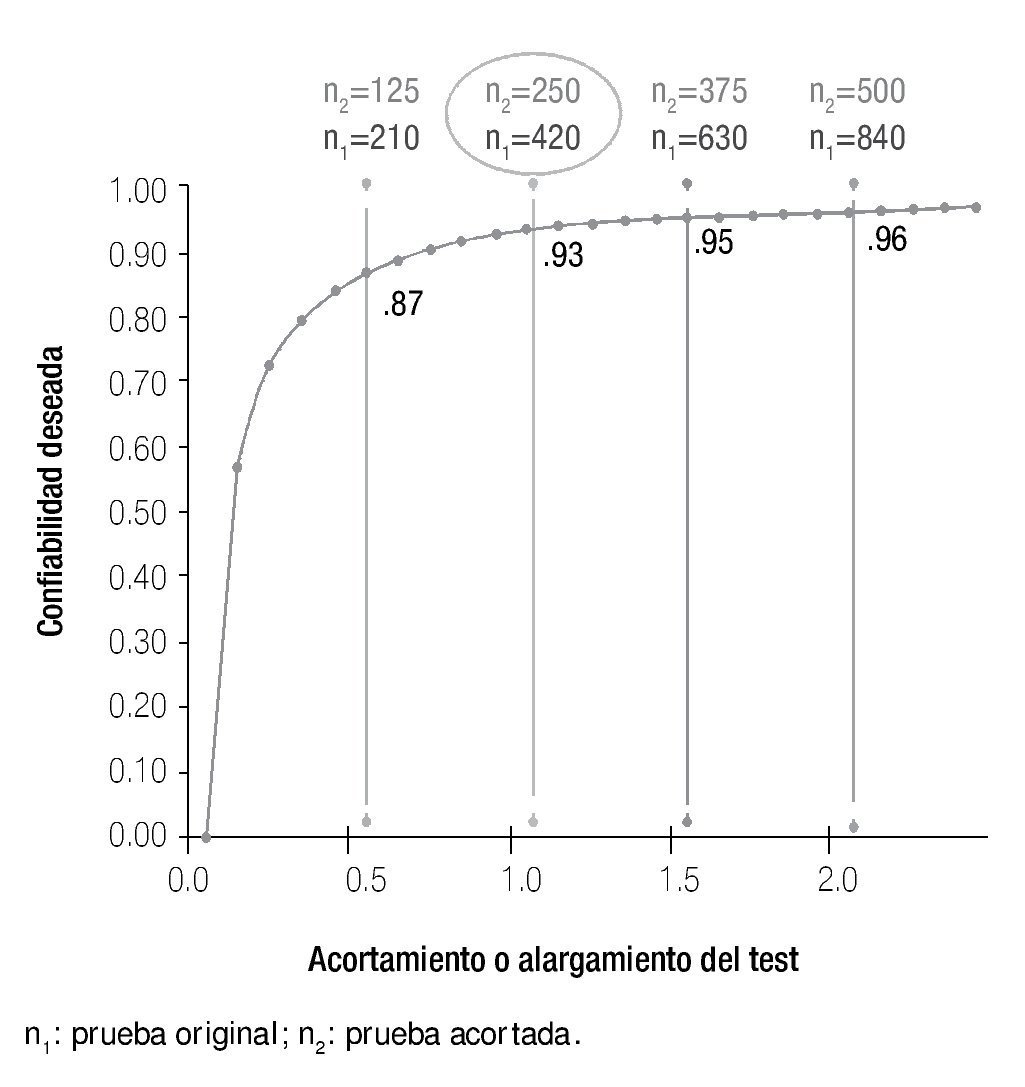
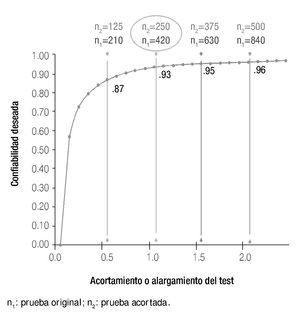
A partir de los resultados del análisis y selección de reactivos, se encontró que inicialmente era posible reducir el número de reactivos que conformaban la prueba a 250, manteniendo la misma confiabilidad global que la longitud original con α=0.93 (Figura 5), así como una confiabilidad aceptable en las áreas de conocimiento exploradas.
Figura 5. La confiabilidad de la prueba se mantiene constante después de seleccionar los reactivos y disminuir su longitud.
Asimismo, en las dos versiones de la prueba, original y acortada, el examen es particularmente informativo en niveles de habilidad bajos y cercanos al promedio (cero), para los distintos subtest que lo constituyen (lo que implica que el error de medida es menos en estos niveles de habilidad). Por otra parte, en la versión acortada del instrumento, en general, hay una mejoría en la discriminación de los reactivos que la constituyen (el promedio de este parámetro pasó de 0.67 a 0.74). Por otro lado, los valores de la dificultad mejoraron sensiblemente al excluirse ítems con valores de dificultad extremos (el promedio de dificultad pasó de 1.21 a 0.39), en tanto que los valores del parámetro c quedaron muy similares en ambas versiones de la prueba (0.18 en la versión extendida y 0.19 en la versión acortada), siendo en ambos casos adecuado. Finalmente, 244 de los 250 reactivos que conforman la prueba acortada, proporcionalmente tienen un mejor ajuste al modelo de 3pl, que los de la prueba extensa (97% y 84%, respectivamente).
Discusión y conclusiones
El presente trabajo describe una experiencia de análisis psicométrico con la TRI en el Examen Profesional Teórico de la Facultad de Medicina de la UNAM, una prueba sumativa de altas consecuencias, que se aplica al final de la carrera de médico cirujano. Hasta donde pudieron identificar los autores, se trata de uno de los primeros reportes en la literatura publicada disponible sobre el uso de la TRI en exámenes sumativos en escuelas de medicina, en nuestro medio. El análisis muestra las diversas aristas de información que pueden obtenerse con el uso de esta familia de modelos matemáticos, que no es posible definir con el modelo de TCT. El uso de la TRI en este reporte proveyó de una serie de elementos a los diseñadores y usuarios de los resultados del examen, que contribuyeron a la mejoría de calidad del instrumento e incremento de la validez de las interpretaciones de los resultados. Por otra parte, la información obtenida con esta metodología ayudó a seleccionar los reactivos con mejores características psicométricas, así como a reducir la longitud de la prueba de manera sustancial manteniendo una confiabilidad adecuada. Casi la totalidad de los reactivos del examen acortado se ajustaron al modelo propuesto.
La TRI ha sido extensamente utilizada en las últimas décadas en diversos escenarios educativos, y se han escrito múltiples libros y revisiones sobre el tema, algunos dirigidos a la evaluación en ciencias de la salud.11,19-23 A pesar de las extraordinarias propiedades de los modelos psicométricos de TRI, que pueden contribuir a resolver los profundos problemas de la TCT como son su dependencia de la muestra y la confusión de los resultados con el instrumento, por diversas razones no se han utilizado de manera más amplia en las escuelas de medicina e instituciones que realizan evaluaciones del aprendizaje en ciencias de la salud, a pesar de que están disponibles programas de cómputo capaces de realizar los cálculos requeridos.11,24 Algunas de estas razones son los orígenes y evolución histórica de dichos modelos, su complejidad matemática y lo estricto de las premisas que deben satisfacerse para que sean aplicables y produzcan resultados apropiados, como son la unidimensionalidad y lo grande de los tamaños muestrales. Se requieren aproximadamente 200 sujetos para utilizar el modelo de TRI de un parámetro, 500 sujetos para el de dos parámetros y hasta 1 000 o más para el de tres parámetros.10,11,25 La Facultad de Medicina de la UNAM es la escuela de medicina más grande de México, con aproximadamente 16 000 estudiantes, 7 000 de la licenciatura de médico cirujano y más de 9 000 residentes,26 lo que la coloca en el rango de tamaño de muestra apropiado para utilizar la TRI en sus evaluaciones de aprendizaje. En este trabajo con una muestra de 882 estudiantes se logró satisfacer los requerimientos conceptuales para el uso de la TRI, con la mayoría de los reactivos seleccionados ajustándose al modelo de tres parámetros. Es importante hacer notar que la TRI no debe aplicarse en grupos pequeños de sujetos, ya que los resultados serían cuestionables.
La información proporcionada por el análisis del examen de la Facultad de Medicina de la UNAM, considerando el conjunto global de la prueba es muy informativa a niveles de habilidad cercanas al promedio. Cuando se observan los resultados considerando las áreas de conocimiento, en algunas de ellas el nivel de precisión es mayor a niveles de dominio bajos, en particular en el área de Urgencias médicas, donde si bien su valor de confiabilidad es el más alto, su precisión es más certera en los niveles de habilidad en torno a -1. Estos niveles de precisión en la estimación de rasgos bajos o promedios de dominio se deben fundamentalmente a que los reactivos de las distintas áreas del examen tienen en promedio, valores altos de índice de dificultad y de discriminación bajos o moderados. Por otra parte, la constante de que los valores del parámetro de seudoadivinación sean bajos en las áreas de conocimiento, permite observar que la posibilidad de que sujetos con bajo nivel de dominio acrediten el examen por simple adivinación o azar sea virtualmente imposible. Es necesario señalar, la conveniencia de que esta prueba contenga reactivos que permitan estimar de una manera más precisa niveles de dominio altos, particularmente si se considera que se trata de un examen de egreso en donde se busca medir con mayor precisión a la mayor parte de la población que sustenta la prueba, con la finalidad de obtener su título profesional.10,11
Una de las ventajas de la TRI sobre la TCT es la información que se obtiene del Error Estándar de Medición (EEM), ya que en la TCT, el EEM tradicional representa una banda de error que es la misma para todos los sustentantes, y en la TRI el EEM se computa para cada valor de θ. Lo anterior hace posible, que en la TRI sea pueda evaluar qué tan confiable es la medición para cada punto en la distribución de resultados.10,11 En este trabajo se encontró que el EEM es menor en los niveles promedio de habilidad, y mayor en los extremos, lo que coadyuva a tener mayor precisión de la medición en las áreas más potencialmente cercanas al punto de corte.
Uno de los alcances del presente trabajo es mostrar la relevancia de emplear estrategias de análisis innovadoras en el campo de la educación. En nuestro país es de trascendental importancia mejorar la calidad de la educación a todos los niveles, y la evaluación con pruebas estandarizadas realizadas de manera profesional es un componente fundamental de esta estrategia.27 Encontramos pocos trabajos publicados del uso de la TRI en evaluación del aprendizaje en nuestro país.27-30 Los trabajos publicados en la literatura arbitrada en México se refieren a exámenes de ingreso a la universidad, y exámenes para evaluación del aprendizaje en educación básica y media superior.28,30 Es importante incrementar la profesionalización en medición educativa de los grupos de trabajo que laboran en las facultades y escuelas de medicina, para lograr darle a la evaluación del aprendizaje el lugar preponderante que se merece. La magnitud de la responsabilidad que las universidades, Consejos de certificación de especialistas e instituciones de atención a la salud, tienen para documentar de manera válida y confiable, que los médicos generales y especialistas que se gradúan y obtienen el certificado y cédula profesional, debe apreciarse en su justa dimensión. La sociedad espera y merece que las instancias correspondientes documenten realmente, que los profesionales de la salud poseen las competencias requeridas para una práctica efectiva y segura.
Una de las conclusiones importantes de este trabajo es que los modelos de TCT y TRI, si bien tienen diferencias substanciales, en la práctica se pueden utilizar de manera complementaria para lograr una práctica de evaluación educativa más profesional y eficaz, ya que cada uno tiene virtudes y limitaciones que debemos ponderar de acuerdo a la situación de evaluación específica.31-33 De manera particular, el modelo de TRI permite analizar de una manera más integral los ítems que componen un test, permitiendo seleccionar aquellos que muestren mejores parámetros en cuanto a los valores de dificultad, discriminación y seudoadivinación y, con un menor número de ítems, determinar la habilidad de los examinados. Además, permite identificar los reactivos que proporcionen mayor información de los niveles de rasgo en los que se tenga particular interés. Con esto, se logran seleccionar a priori los reactivos cuyo error de medición sea menor en los niveles de rasgo que se pretenden medir y así conformar la prueba más precisa a esos valores de dominio.
El Examen Profesional Teórico de la Facultad de Medicina era muy extenso, con las consecuencias que esto implica, por lo que el disminuir su longitud, con fundamentos técnicos, fue uno de los objetivos del presente trabajo. Con frecuencia el número de reactivos que conforman los exámenes en las escuelas de medicina es determinado por la tradición, por la dificultad de diseñar e implementar exámenes muy extensos, y por las limitaciones de tiempo de los estudiantes y profesores. Es deseable realizar un esfuerzo por informar este tipo de decisiones educativas con la mejor evidencia científica disponible, y no hacer exámenes más largos y difíciles de lo que es educativamente necesario, algunos autores sugieren que pruebas de más de 300 ítems pueden ser innecesariamente largas y costosas.34,35 En nuestro trabajo se encontró que el examen era susceptible de reducirse en longitud, obteniéndose o incluso mejorando la precisión en la estimación de los niveles de habilidad de los sujetos. Existen varias ventajas de realizar una prueba de menor longitud, que mejoran la eficiencia del instrumento: disminución de cansancio y desgaste por parte de los sustentantes al enfrentarse a un examen más corto, ahorro de recursos (de tiempo y económicos) en el diseño y aplicación de una prueba con menor número de ítems, ingreso a la prueba de reactivos nuevos con fines de conocer su calidad métrica, con el objetivo de crear y nutrir un banco de reactivos calibrados y con un amplio repertorio para medir distintos niveles de habilidad, particularmente en el rasgo de interés. Por lo anterior se sugiere trabajar un banco de reactivos de manera permanente, con ítems calibrados y que cubran el constructo a evaluar, para estar en condiciones de aplicar instrumentos de evaluación que identifiquen apropiadamente las habilidades necesarias en los sustentantes.
Contribución de los autores
LDM y MSM participaron en el diseño, colección de los datos, búsqueda bibliográfica y redacción del documento. LDM realizó el análisis psicométrico de los datos.
Financiamiento
Ninguno
Conflicto de intereses
Los autores declaran no tener ningún conflicto de intereses.
Presentaciones previas
Trabajo oral en las Jornadas de Educación Médica, Facultad de Medicina de la UNAM.
Recepción 22 de febrero 2012;
aceptación 28 de marzo 2012
Correspondencia:
Dr. Melchor Sánchez Mendiola.
Secretaría de Educación Médica. Edif. B, 3er Piso, Av. Universidad 3000, C.U.
C.P. 04510. México D.F., México.
Teléfono: (5255) 5623 2448. Fax: (5255) 5616 2346.
Correos electrónicos: melchorsm@gmail.com, melchors@liceaga.facmed.unam.mx