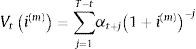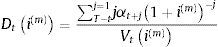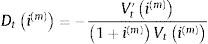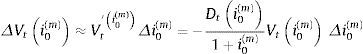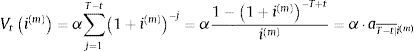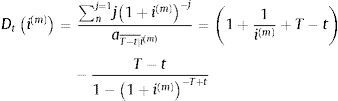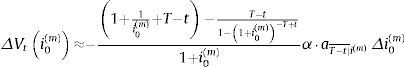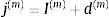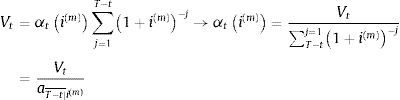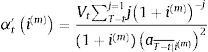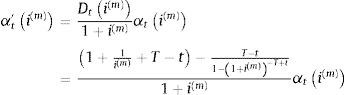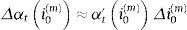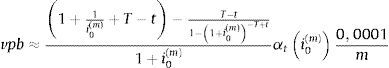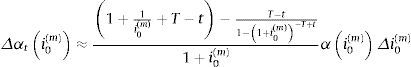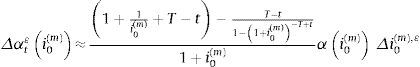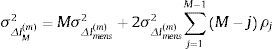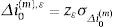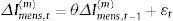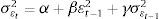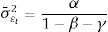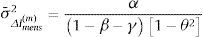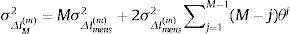En los préstamos pactados a interés revisable, el prestatario asume el riesgo de subidas del tipo de interés. Dada la importancia de este riesgo, se trata de un tema recurrente en la prensa económica-financiera. En este trabajo mostramos cómo la duración de un préstamo francés pactado a tipo de interés fijo puede ser utilizada para evaluar la sensibilidad de la cuota de un préstamo análogo, pero pactado a tipo de interés revisable, ante cambios de dicho tipo. También realizamos una aplicación empírica sobre los índices oficiales del mercado hipotecario en el mercado español para el periodo 2009-2013. En esta comprobamos que el índice que provoca menos volatilidad en las cuotas del préstamo es el EURIBOR, mientras que el que provoca una mayor volatilidad es el tipo medio de los préstamos para la adquisición de vivienda de la zona euro.
In adjustable interest loans the borrower assumes the risk of interest rate rising, which leads to the growth of loan annuities. Given the importance of this risk in both corporate and personal finance, it is a recurrent topic in economic and financial press. In this paper, we show that the duration of a loan with constant annuity and interest rate can be used to assess the sensitivity of payments of an analogous loan with adjustable interest rate. Also, we develop an empirical application on official indexes of the Spanish mortgage market during the period 2009-2013. We find that EURIBOR is the index that causes less volatility in the mortgage annuity. Likewise, we also obtain that the average rate of loans for house purchasing in the euro zone is the index that cause greater volatility in the payments of loans.
Los préstamos a tipo de interés variable se introdujeron, tal como señalan Meneu, Jordà y Barreira (1997), durante la profunda transformación que sufrió el sistema financiero español a principios de la década de los 80. De hecho, en préstamos para adquisición de vivienda residencial, el interés revisable se ha convertido en un estándar de mercado, llegando a suponer, desde el año 2002, la práctica totalidad de los saldos vivos (Alonso, del Río y Blanco, 2004). Dicho trabajo también señala que la posibilidad de pactar préstamos a medio y largo plazo a tipo de interés revisable permite adecuar, a las entidades de crédito, la frecuencia de cambio de los tipos pasivos, que vencen en su mayoría a corto plazo, con la de los tipos activos, cuyo vencimiento es más largo. Así, este tipo de operaciones permite eliminar lo que Bierwag y Kaufman (1985) denominan GAP de tipos de interés de las entidades de crédito.
El riesgo de precio en los préstamos a interés variable, si no contienen opciones tipo cap o floor, es prácticamente nulo para el prestamista. Ello es consecuencia directa de la aplicación del principio de valor financiero de un activo, que provoca que las cuotas de interés futuras se ajusten a los tipos empleados para la actualización de las mismas1. En cambio, el valor de los préstamos pactados a tipo de interés fijo disminuye si aumentan los tipos de interés de mercado, ya que los flujos de caja futuros, que están prefijados, son descontados a un tipo más elevado. Así, la contratación de préstamos a tipo variable permite a una entidad de crédito disminuir el riesgo de interés del margen financiero y del riesgo de depreciación de unos activos, los préstamos, susceptibles de ser movilizados. En cambio, el prestatario sufre el riesgo de fluctuaciones al alza en el tipo de interés2.
En el mercado español, donde se utiliza masivamente el método amortizativo de carácter pospagable francés (Fuentes, 2010), la revisión del tipo de interés supone, bien la variación de la cuota del préstamo, reemplazándose por otra nueva, bien el mantenimiento de la cuota, cambiándose la duración residual del préstamo. Este trabajo se centra en la primera modalidad de revisión, que es la más usual.
Propondremos una medida del riesgo del incremento en la cuota del préstamo ante aumentos del índice de referencia que se basará en el concepto de duración de un préstamo análogo pactado a tipo fijo. Esta medida cuantificará la incertidumbre de los desembolsos que el prestatario, con independencia de que sea persona física o jurídica, deberá realizar en el futuro, cuestión que entendemos muy relevante en la gestión de su tesorería. Resaltamos que excede de los límites del trabajo la contabilidad que, según el nuevo Plan General Contable, las sociedades deben realizar de este tipo de préstamos en su balance y cuenta de resultados.
También desarrollamos una aplicación empírica para el periodo 2009-2013 sobre los índices aceptados como referencia en el mercado hipotecario español según el artículo 27 de la Orden EHA/2899/2011, de 28 de octubre, y que se definen en la norma 14 y anexo 8 de la Circular del Banco de España 5/2012. Este análisis empírico nos permitirá sopesar, a la luz de la evolución real de dichos índices, la fluctuación que puede llegar a tener la cuota de un préstamo en función de diferentes parámetros como la duración residual, la frecuencia de revisión del tipo de interés, etc.
El resto del trabajo está organizado de la siguiente manera. En el siguiente apartado describimos la valoración del riesgo de precio con el concepto de duración, haciéndose especial hincapié en el préstamo francés pactado a tipo fijo. Posteriormente, proponemos una medida de sensibilidad de la cuota de un préstamo francés a interés variable ante variaciones del índice de referencia. En el tercer apartado, desarrollamos una aplicación empírica en los índices hipotecarios del mercado español en la que estimamos las variaciones esperadas máximas de la cuota con 2 aproximaciones. Con la primera, utilizamos la estructura de varianzas y autocorrelaciones de los índices asumiéndose su normalidad. Con la segunda, modelizamos la evolución de los índices como un proceso autorregresivo con varianza heterocedástica condicional.
2Aproximación de la sensibilidad de la cuota de un préstamo indexado con el concepto de duración2.1Evaluación del riesgo de precio de un préstamo francés pactado a tipo de interés fijoExponemos a continuación los conceptos básicos de valoración del riesgo de interés en los activos de renta fija. Sea un activo que proporciona flujos de caja inmediatos, periódicos y pospagables en el momento de emisión: {αj}j=1,2,…,t,…,T y que presentan una frecuencia de pago de m (veces al año). El valor del activo en un periodo t, según un tanto periodal de la misma frecuencia, i(m), es:
La duración del activo en t al tanto periodal i(m), Dti(m) es, según Macaulay (1938):
Tal como remarca Bierwag (1987), (2a) cuantifica periodos, de tal manera que si, por ejemplo, los flujos de caja son mensuales, Dti(m) está expresado en meses. Por otra parte, según Hicks (1939), también podemos entender la duración como la derivada elástica del valor del activo respecto a cambios en el tipo de interés:
La duración permite estimar linealmente la fluctuación de su valor ante una variación dada del tipo de interés. Con un desarrollo en serie de Taylor hasta un orden 1, podemos aproximar la fluctuación del valor del activo, ΔVi0(m) desde una situación inicial donde el tipo de interés es i0(m), Vi0(m), debido a una fluctuación del interés Δi0(m), como:
donde Vi0(m) y Di0(m) se evalúan con (1) y (2a), respectivamente. Partiendo de (3), es muy usual medir la sensibilidad del valor de un activo ante fluctuaciones del tipo de interés con la duración modificadaDi0(m)1+i0(m), que cuantifica la modificación porcentual del valor del título, ΔVti0mVti0(m) ante una variación determinada del tipo de valoración.Otro indicador de riesgo muy utilizado es el valor del punto básico (vpb), que indica cómo varía el precio del activo ante variaciones de un punto básico en el tanto anual de valoración. Con (3), y si la estructura temporal de los tipos de interés es plana, circunstancia que se da en el mercado de préstamos hipotecarios, también podemos estimar con facilidad el valor en riesgo (VeR) del activo siguiendo la metodología de J. P. Morgan y Reuters (1996). Este puede definirse como la pérdida límite que puede sufrir dicho activo para un horizonte temporal predefinido y un nivel de probabilidad dado. Así, por ejemplo, para hallar el VeR del activo con un nivel de probabilidad del 99%, deberíamos tomar en (3) para Δi0(m) su percentil 99.
En el sistema de amortización francés –que supone amortización pospagable–, cuando el tipo de interés es fijo, el término amortizativo constante α queda predeterminado desde el origen de la operación financiera. Su valor en el periodo t-ésimo, Vti(m), es, según (1):
El valor Vti(m) es el capital pendiente del préstamo en ese momento si evaluamos (4) con el tanto de interés fijado para el préstamo, y será mayor (menor) que el capital pendiente, si (4) se evalúa con un tanto de interés menor (mayor) que el pactado para el préstamo.
La duración del préstamo se hallará con (2a), y siguiendo a Lacey y Nawalkha (1990), podemos expresarla como:
Como cualquier activo de renta fija con flujos de caja predefinidos, la posesión de un préstamo francés supone asumir el riesgo de su depreciación derivado de aumentos en el tipo de interés de mercado. Por supuesto, este puede sopesarse con (3) y sus indicadores derivados. Bastará con considerar como valor de partida (4), y como duración, (5):
En este contexto, entendemos interesante resaltar que Ott (1986) deriva una expresión para la duración de un préstamo pactado a interés mixto que generaliza (5).
2.2Utilización de la duración para la medición de la sensibilidad de la cuota de un préstamo pactado a interés revisableEn los préstamos a interés variable, el valor del préstamo y su deuda pendiente están prácticamente alineados a lo largo de su vida. Así, para la entidad de crédito poseedora del préstamo, supone mantener en su cartera un activo con riesgo de precio prácticamente nulo; pero para el prestatario, implica la asunción del riesgo de fluctuación en el tipo de interés. Así, el momento de finalización del préstamo y/o sus términos amortizativos son desconocidos y, por tanto, la evolución de sus magnitudes y su incertidumbre debe ser modelizada estocásticamente tal como plantean, por ejemplo, Alegre y Mayoral (1997).
En el momento de una revisión del tipo de interés, t, el valor del préstamo, Vt, es conocido desde la revisión anterior e idéntico al capital pendiente en dicho momento. En cambio, el término amortizativo dependerá del tipo periodal que se aplique en el momento de la revisión. Lo más habitual es que el tanto anual con la periodicidad de amortización del préstamo (m), j(m), se obtenga como la agregación del valor de índice, que es también un tanto anual de dicha periodicidad, I(m), y del diferencial aplicable para hallar el tanto anual, d(m). Así:
siendo el tanto periodal aplicable i(m)=j(m)m. Notaremos al término amortizativo que surge aplicando i(m) en una ecuación análoga a (4) como αti(m):Podemos obtener la primera derivada del término amortizativo αt'i(m) como:
En (5) se observa que DtimaT−t|¯im=∑j=1T−tj1+im−j, mientras que en (8), αti(m)=VtaT−t|¯i(m). Así, αt'i(m) queda reescrito como:
Aproximaremos la fluctuación del término amortizativo tras la revisión, Δαti0(m), a partir del término amortizativo existente antes de la revisión, αti0(m), que fue calculado con el tanto periodal i0(m), con un desarrollo en serie de Taylor de orden 1:
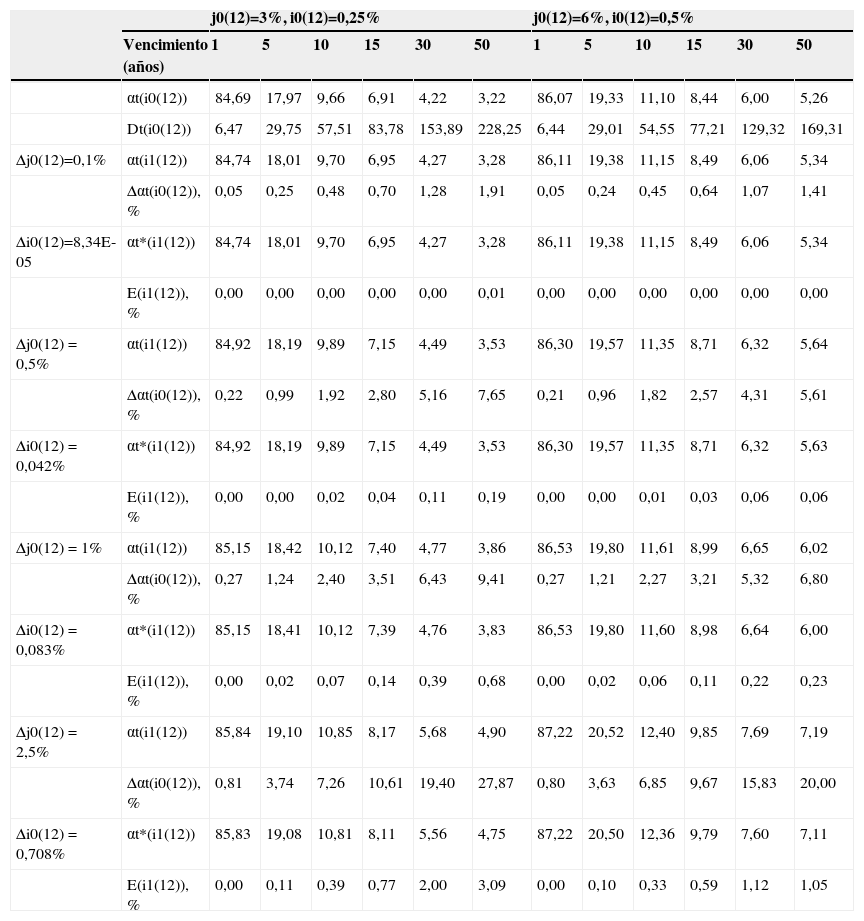
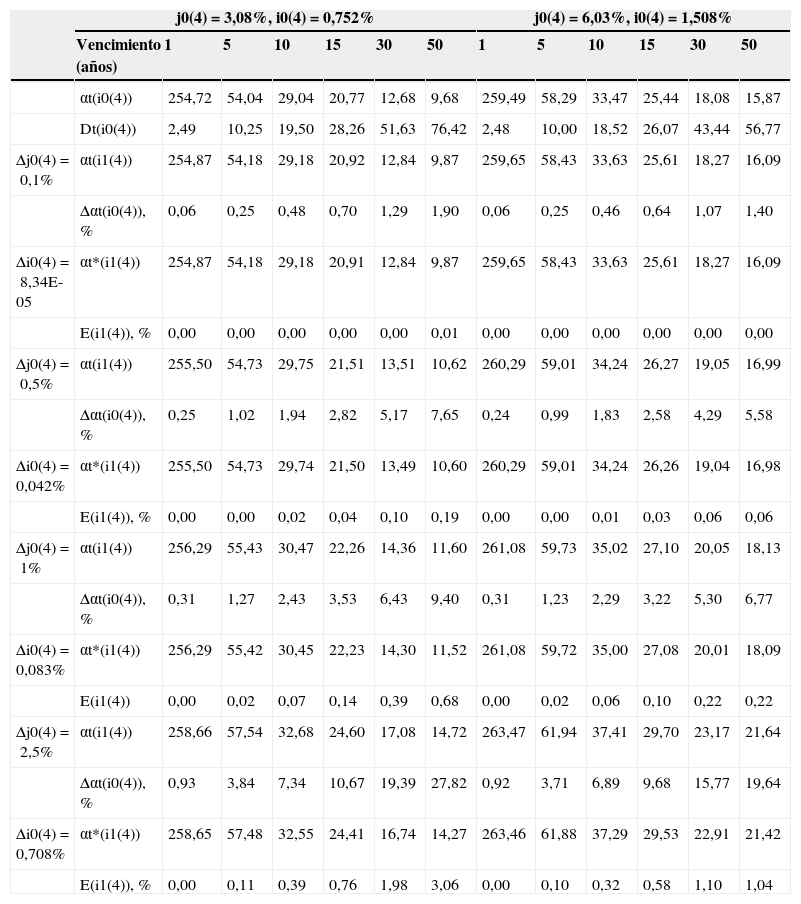
y así, sustituyendo (10) en (11), obtenemos:En las tablas 1 y 2 cuantificamos la sensibilidad de la cuota del préstamo revisable con 2 posibles periodicidades de amortización (mensual y trimestral), diversos vencimientos residuales (desde un año hasta 50 años) y 2 escenarios iniciales de tipos de interés (j(12)=3% y j(12)=6% en el caso de amortización mensual; y sus equivalentes trimestrales, j(4)=3,08% y un j(4)=6,03% en el caso de que la amortización tenga dicha periodicidad). Asimismo, partimos de un capital pendiente de 1.000€. En dichas tablas observamos:
- a)
La sensibilidad de la cuota del préstamo medida como variación porcentual crece con la duración del préstamo análogo a tipo de interés fijo y con la magnitud de la variación del tipo de interés. En cambio, decrece a medida que el tipo de interés de partida aumenta. Asimismo, una mayor frecuencia en la amortización redunda en una mayor sensibilidad de la cuota del préstamo; si bien, en este caso, dicha diferencia parece poco relevante.
- b)
La calidad de la aproximación empeora a medida que aumenta la fluctuación del tipo de interés y/o la duración residual del préstamo. No obstante, en todos los casos es muy buena. Así, en el peor de los escenarios, muy improbable en la práctica real, donde la fluctuación del índice de referencia es el 2,5% y el vencimiento residual del préstamo es 50 años, los errores registrados apenas llegan al 3%. También observamos que la aproximación es ligeramente mejor cuando la frecuencia amortizativa es menor (en nuestro caso, trimestral).
- c)
Observamos que la aproximación propuesta es optimista; es decir, los incrementos de la cuota producidos por aumentos en el tipo de interés quedan minusvalorados, ya que el error toma siempre un valor positivo. En cambio, debemos recordar que la duración como medida de sensibilidad de las fluctuaciones del precio es pesimista, ya que sobrevalora las disminuciones del precio ante aumentos en el tipo de interés y minusvalora los aumentos.
Evaluación de la sensibilidad del término amortizativo de un préstamo francés con periodicidad de amortización mensual ante diferentes fluctuaciones del tipo de interés y determinación del error que produce la aproximación (12) en el cálculo del incremento de la cuota
| j0(12)=3%, i0(12)=0,25% | j0(12)=6%, i0(12)=0,5% | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vencimiento (años) | 1 | 5 | 10 | 15 | 30 | 50 | 1 | 5 | 10 | 15 | 30 | 50 | |
| αt(i0(12)) | 84,69 | 17,97 | 9,66 | 6,91 | 4,22 | 3,22 | 86,07 | 19,33 | 11,10 | 8,44 | 6,00 | 5,26 | |
| Dt(i0(12)) | 6,47 | 29,75 | 57,51 | 83,78 | 153,89 | 228,25 | 6,44 | 29,01 | 54,55 | 77,21 | 129,32 | 169,31 | |
| Δj0(12)=0,1% | αt(i1(12)) | 84,74 | 18,01 | 9,70 | 6,95 | 4,27 | 3,28 | 86,11 | 19,38 | 11,15 | 8,49 | 6,06 | 5,34 |
| Δαt(i0(12)), % | 0,05 | 0,25 | 0,48 | 0,70 | 1,28 | 1,91 | 0,05 | 0,24 | 0,45 | 0,64 | 1,07 | 1,41 | |
| Δi0(12)=8,34E-05 | αt*(i1(12)) | 84,74 | 18,01 | 9,70 | 6,95 | 4,27 | 3,28 | 86,11 | 19,38 | 11,15 | 8,49 | 6,06 | 5,34 |
| E(i1(12)), % | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | |
| Δj0(12)=0,5% | αt(i1(12)) | 84,92 | 18,19 | 9,89 | 7,15 | 4,49 | 3,53 | 86,30 | 19,57 | 11,35 | 8,71 | 6,32 | 5,64 |
| Δαt(i0(12)), % | 0,22 | 0,99 | 1,92 | 2,80 | 5,16 | 7,65 | 0,21 | 0,96 | 1,82 | 2,57 | 4,31 | 5,61 | |
| Δi0(12)=0,042% | αt*(i1(12)) | 84,92 | 18,19 | 9,89 | 7,15 | 4,49 | 3,53 | 86,30 | 19,57 | 11,35 | 8,71 | 6,32 | 5,63 |
| E(i1(12)), % | 0,00 | 0,00 | 0,02 | 0,04 | 0,11 | 0,19 | 0,00 | 0,00 | 0,01 | 0,03 | 0,06 | 0,06 | |
| Δj0(12)=1% | αt(i1(12)) | 85,15 | 18,42 | 10,12 | 7,40 | 4,77 | 3,86 | 86,53 | 19,80 | 11,61 | 8,99 | 6,65 | 6,02 |
| Δαt(i0(12)), % | 0,27 | 1,24 | 2,40 | 3,51 | 6,43 | 9,41 | 0,27 | 1,21 | 2,27 | 3,21 | 5,32 | 6,80 | |
| Δi0(12)=0,083% | αt*(i1(12)) | 85,15 | 18,41 | 10,12 | 7,39 | 4,76 | 3,83 | 86,53 | 19,80 | 11,60 | 8,98 | 6,64 | 6,00 |
| E(i1(12)), % | 0,00 | 0,02 | 0,07 | 0,14 | 0,39 | 0,68 | 0,00 | 0,02 | 0,06 | 0,11 | 0,22 | 0,23 | |
| Δj0(12)=2,5% | αt(i1(12)) | 85,84 | 19,10 | 10,85 | 8,17 | 5,68 | 4,90 | 87,22 | 20,52 | 12,40 | 9,85 | 7,69 | 7,19 |
| Δαt(i0(12)), % | 0,81 | 3,74 | 7,26 | 10,61 | 19,40 | 27,87 | 0,80 | 3,63 | 6,85 | 9,67 | 15,83 | 20,00 | |
| Δi0(12)=0,708% | αt*(i1(12)) | 85,83 | 19,08 | 10,81 | 8,11 | 5,56 | 4,75 | 87,22 | 20,50 | 12,36 | 9,79 | 7,60 | 7,11 |
| E(i1(12)), % | 0,00 | 0,11 | 0,39 | 0,77 | 2,00 | 3,09 | 0,00 | 0,10 | 0,33 | 0,59 | 1,12 | 1,05 | |
Fuente: Elaboración propia.
El valor de los términos amortizativos está calculado sobre un nominal de 1.000€.
La duración viene expresada en meses.
Como αt*(i1(12)) denotamos al valor del término amortizativo tras la revisión si utilizamos la aproximación (12).
El error cometido por la aproximación (12) es medido como E(i1(m))=αt(i1(m))−αt*(i1(m))αt(i1(m))×100
Evaluación de la sensibilidad del término amortizativo de un préstamo francés con periodicidad de amortización trimestral ante diferentes fluctuaciones del tipo de interés y determinación del error que produce la aproximación (12) en el cálculo de la variación de la cuota
| j0(4)=3,08%, i0(4)=0,752% | j0(4)=6,03%, i0(4)=1,508% | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vencimiento (años) | 1 | 5 | 10 | 15 | 30 | 50 | 1 | 5 | 10 | 15 | 30 | 50 | |
| αt(i0(4)) | 254,72 | 54,04 | 29,04 | 20,77 | 12,68 | 9,68 | 259,49 | 58,29 | 33,47 | 25,44 | 18,08 | 15,87 | |
| Dt(i0(4)) | 2,49 | 10,25 | 19,50 | 28,26 | 51,63 | 76,42 | 2,48 | 10,00 | 18,52 | 26,07 | 43,44 | 56,77 | |
| Δj0(4)=0,1% | αt(i1(4)) | 254,87 | 54,18 | 29,18 | 20,92 | 12,84 | 9,87 | 259,65 | 58,43 | 33,63 | 25,61 | 18,27 | 16,09 |
| Δαt(i0(4)), % | 0,06 | 0,25 | 0,48 | 0,70 | 1,29 | 1,90 | 0,06 | 0,25 | 0,46 | 0,64 | 1,07 | 1,40 | |
| Δi0(4)=8,34E-05 | αt*(i1(4)) | 254,87 | 54,18 | 29,18 | 20,91 | 12,84 | 9,87 | 259,65 | 58,43 | 33,63 | 25,61 | 18,27 | 16,09 |
| E(i1(4)), % | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | |
| Δj0(4)=0,5% | αt(i1(4)) | 255,50 | 54,73 | 29,75 | 21,51 | 13,51 | 10,62 | 260,29 | 59,01 | 34,24 | 26,27 | 19,05 | 16,99 |
| Δαt(i0(4)), % | 0,25 | 1,02 | 1,94 | 2,82 | 5,17 | 7,65 | 0,24 | 0,99 | 1,83 | 2,58 | 4,29 | 5,58 | |
| Δi0(4)=0,042% | αt*(i1(4)) | 255,50 | 54,73 | 29,74 | 21,50 | 13,49 | 10,60 | 260,29 | 59,01 | 34,24 | 26,26 | 19,04 | 16,98 |
| E(i1(4)), % | 0,00 | 0,00 | 0,02 | 0,04 | 0,10 | 0,19 | 0,00 | 0,00 | 0,01 | 0,03 | 0,06 | 0,06 | |
| Δj0(4)=1% | αt(i1(4)) | 256,29 | 55,43 | 30,47 | 22,26 | 14,36 | 11,60 | 261,08 | 59,73 | 35,02 | 27,10 | 20,05 | 18,13 |
| Δαt(i0(4)), % | 0,31 | 1,27 | 2,43 | 3,53 | 6,43 | 9,40 | 0,31 | 1,23 | 2,29 | 3,22 | 5,30 | 6,77 | |
| Δi0(4)=0,083% | αt*(i1(4)) | 256,29 | 55,42 | 30,45 | 22,23 | 14,30 | 11,52 | 261,08 | 59,72 | 35,00 | 27,08 | 20,01 | 18,09 |
| E(i1(4)) | 0,00 | 0,02 | 0,07 | 0,14 | 0,39 | 0,68 | 0,00 | 0,02 | 0,06 | 0,10 | 0,22 | 0,22 | |
| Δj0(4)=2,5% | αt(i1(4)) | 258,66 | 57,54 | 32,68 | 24,60 | 17,08 | 14,72 | 263,47 | 61,94 | 37,41 | 29,70 | 23,17 | 21,64 |
| Δαt(i0(4)), % | 0,93 | 3,84 | 7,34 | 10,67 | 19,39 | 27,82 | 0,92 | 3,71 | 6,89 | 9,68 | 15,77 | 19,64 | |
| Δi0(4)=0,708% | αt*(i1(4)) | 258,65 | 57,48 | 32,55 | 24,41 | 16,74 | 14,27 | 263,46 | 61,88 | 37,29 | 29,53 | 22,91 | 21,42 |
| E(i1(4)), % | 0,00 | 0,11 | 0,39 | 0,76 | 1,98 | 3,06 | 0,00 | 0,10 | 0,32 | 0,58 | 1,10 | 1,04 | |
Fuente: Elaboración propia.
El valor de los términos amortizativos está calculado sobre un nominal de 1.000€.
La duración viene expresada en trimestres.
Como αt*(i1(4)) denotamos al valor del término amortizativo tras la revisión si utilizamos la aproximación (12).
El error cometido por la aproximación (12) es medido como E(i1(m))=αt(i1(m))−αt*(i1(m))αt(i1(m))×100
La analogía de (3) y (12) nos permite utilizar los indicadores de riesgo de precio derivados de la duración en la valoración del riesgo de incremento del término amortizativo. Así, en nuestro contexto, podemos interpretar la duración modificada como la variación relativa del término amortizativo, Δαti0mαti0(m), ante una variación del tipo de interés determinada.
También podemos construir un indicador análogo al vpb. Debemos resaltar que la variación de un punto básico debe entenderse que se produce sobre el índice y, tal como sugiere la relación (7), se traslada íntegramente en el tanto anual j(m), a partir del que se determina el tanto periodal i(m). Así, una variación desde las condiciones iniciales de un punto básico en el índice, ΔI0(m)=0,0001, implica una variación idéntica en el tanto anual aplicable al préstamo Δj0(m). Entonces, la variación del tanto periodal a considerar sería Δi0(m)=0,0001m, siendo el vpb:
También podemos definir un indicador similar al VeR que cuantifique el máximo incremento esperado del término amortizativo para un nivel de probabilidad dado. En primer lugar, deberemos modelizar la fluctuación del tipo nominal como una variable aleatoria, dado que la variación del índice de revisión a lo largo del tiempo lo es. Dado que en (7) es inmediato observar que Δj(m)=ΔI(m), la variable aleatoria incremento del tipo nominal Δj0(m) y la fluctuación del valor del índice, ΔI0(m) son idénticas. Por tanto, la variación del tanto periodal también es una variable aleatoria, donde: Δi0(m)=Δj0(m)m.
A partir de la variable aleatoria «fluctuación del tanto periodal» podemos aproximar la variable aleatoria «fluctuación del término amortizativo en t», Δαti0m, como:
Cuantificaremos el máximo incremento esperado del término amortizativo con una probabilidad ¿, Δαtεi0m, a través al percentil de orden ¿ de Δαti0m. Así, la probabilidad de que la fluctuación de la cuota supere Δαtεi0m en la próxima revisión será 1−¿. Si denotamos como Δi0m,ε al ¿-percentil de la fluctuación del tanto periodal, obtenemos:
3Fluctuaciones esperadas de la cuota de un préstamo indexado con los índices de referencia en el mercado hipotecario español durante 2009-20133.1Base de datosEn este apartado estimamos, utilizando (15), el incremento de la cuota que como máximo puede esperarse para un préstamo con interés variable, si éste se revisara con los índices de referencia oficiales en España para préstamos hipotecarios3. Dichos índices son el EURIBOR; el MIBOR (para contratos anteriores al 1 de enero de 2000); el tipo de rendimiento interno en el mercado secundario de la deuda pública entre 2 y 6 años; el tipo de los préstamos hipotecarios a más de 3 años concedidos por el conjunto de las entidades de crédito (IRPH3), que sustituye a los conocidos como IRPH de Cajas, IRPH de Bancos y al índice de la CECA; el tipo medio de los préstamos hipotecarios entre uno y 5 años para adquisición de vivienda libre concedidos por las entidades de crédito en la zona del euro (PHZE1_5) y la TIR de los swaps sobre tipos de interés al plazo de 5 años (IRS).
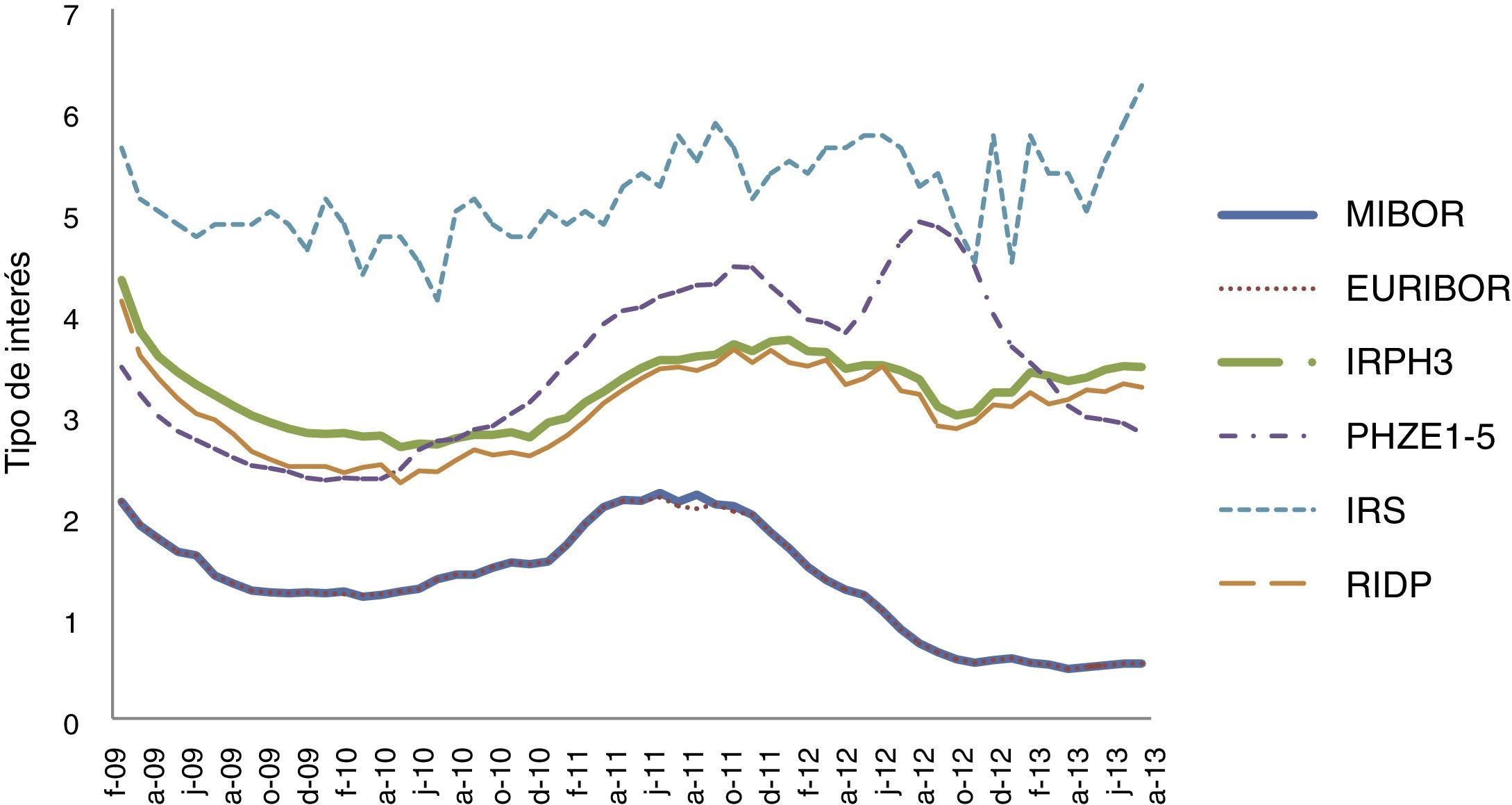
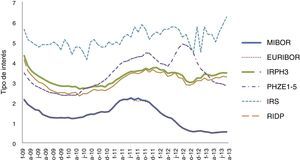
Los datos que utilizamos provienen de las series temporales del Banco de España, abarcan el periodo que va desde enero de 2009 hasta diciembre de 2013, y presentan una periodicidad mensual. Hemos optado por no utilizar datos anteriores por el cambio que supuso en la dinámica de los mercados financieros la crisis subprime iniciada en agosto de 2007, y cuyo momento culminante se produjo con la declaración de quiebra de Lehman Brothers en septiembre de 2008. Esta generó un cambio profundo tanto en las actuaciones del Banco Central Europeo (Taylor, 2009) como en el comportamiento de los mercados crediticios (Fernández y García, 2008), de los de renta fija soberana (Von Hagen, Schuknecht y Wolswijk, 2011) y de los de deuda corporativa (Del Pino, 2012). La figura 1 muestra la evolución de los índices en el periodo de análisis. El índice con valores más elevados es el de los IRS, que a principios de 2014 estaba situado por encima del 6%. Le siguen los derivados del mercado de créditos hipotecarios (IRPH3 y PHZE1_5) y el de la deuda pública española. Los tipos de interés más reducidos son el EURIBOR y el MIBOR, que a principios de 2014 se situaban en el 0,5%.
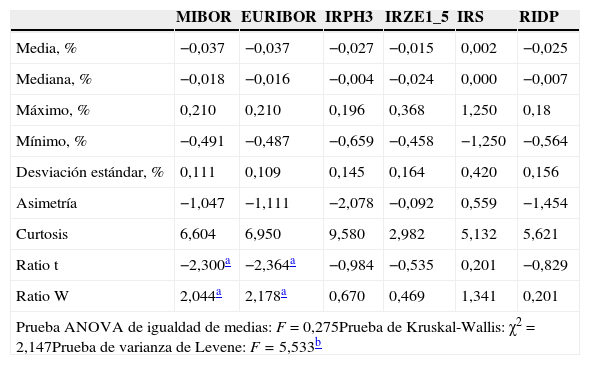
La tabla 3 y la figura 1 muestran que, excepto en el índice de swaps, la tendencia de los tipos de interés ha sido descendente. Este aspecto es más claro en los tipos de interés provenientes del mercado interbancario, para los que se rechaza la hipótesis de que por término medio no fluctúan. En cambio, en el resto de los índices no rechazamos la nulidad ni de la fluctuación media ni de la variación mediana. No obstante, tampoco rechazamos que las variaciones medias de los índices sean iguales ni con la prueba ANOVA ni con la de Kruskal-Wallis. Observamos que los índices menos volátiles son los interbancarios y, con mucha diferencia, el más volátil es el de los IRS, situándose en un nivel intermedio los vinculados a préstamos hipotecarios y a la deuda pública. También comprobamos que la prueba de Levene nos lleva a aceptar la heterogeneidad de las varianzas de los índices.
Estadísticos de la variación mensual de los índices de referencia del mercado desde enero de 2009 hasta diciembre de 2013
| MIBOR | EURIBOR | IRPH3 | IRZE1_5 | IRS | RIDP | |
|---|---|---|---|---|---|---|
| Media, % | −0,037 | −0,037 | −0,027 | −0,015 | 0,002 | −0,025 |
| Mediana, % | −0,018 | −0,016 | −0,004 | −0,024 | 0,000 | −0,007 |
| Máximo, % | 0,210 | 0,210 | 0,196 | 0,368 | 1,250 | 0,18 |
| Mínimo, % | −0,491 | −0,487 | −0,659 | −0,458 | −1,250 | −0,564 |
| Desviación estándar, % | 0,111 | 0,109 | 0,145 | 0,164 | 0,420 | 0,156 |
| Asimetría | −1,047 | −1,111 | −2,078 | −0,092 | 0,559 | −1,454 |
| Curtosis | 6,604 | 6,950 | 9,580 | 2,982 | 5,132 | 5,621 |
| Ratio t | −2,300a | −2,364a | −0,984 | −0,535 | 0,201 | −0,829 |
| Ratio W | 2,044a | 2,178a | 0,670 | 0,469 | 1,341 | 0,201 |
| Prueba ANOVA de igualdad de medias: F=0,275Prueba de Kruskal-Wallis: χ2=2,147Prueba de varianza de Levene: F=5,533b | ||||||
Fuente: Elaboración propia a partir de las Series Temporales del Banco de España.
Con la ratio t (ratio W) contrastamos la nulidad de la media (mediana) de la muestra. Asimismo, con las pruebas ANOVA y de Kruskal-Wallis contrastamos la homogeneidad de momentos centrales de las fluctuaciones de los índices, y con la de Levene, la heterogeneidad de la varianza. Con el estadístico de Jarque y Bera (1987) comprobamos que las fluctuaciones de los índices siguen una distribución normal.
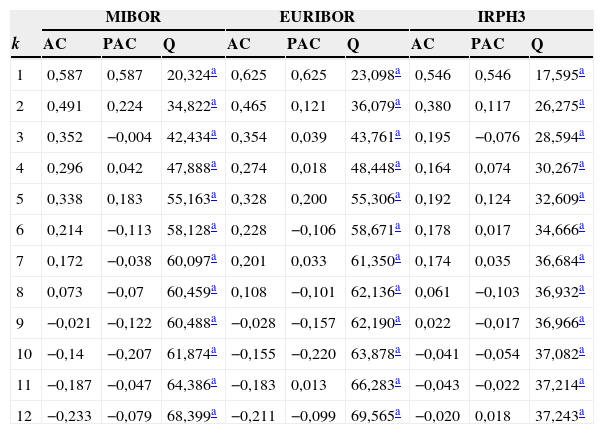
En la tabla 4 podemos observar que la dinámica autorregresiva es común en todos los índices excepto en el de los swaps. Son series con una fuerte autocorrelación positiva, especialmente la de orden 1, que decrece con bastante rapidez, lo que es congruente con el hecho de que son series no integradas. En cambio, el índice de swaps presenta una autocorrelación negativa de orden 1 significativa. En todos los casos, el comportamiento de los índices se aleja de un camino aleatorio y de la eficiencia informativa en sentido débil, lo que es congruente con los resultados de Terceño, de Andrés y Barberà (2002).
Autocorrelaciones de las fluctuación de los índices y significación
| MIBOR | EURIBOR | IRPH3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| k | AC | PAC | Q | AC | PAC | Q | AC | PAC | Q |
| 1 | 0,587 | 0,587 | 20,324a | 0,625 | 0,625 | 23,098a | 0,546 | 0,546 | 17,595a |
| 2 | 0,491 | 0,224 | 34,822a | 0,465 | 0,121 | 36,079a | 0,380 | 0,117 | 26,275a |
| 3 | 0,352 | −0,004 | 42,434a | 0,354 | 0,039 | 43,761a | 0,195 | −0,076 | 28,594a |
| 4 | 0,296 | 0,042 | 47,888a | 0,274 | 0,018 | 48,448a | 0,164 | 0,074 | 30,267a |
| 5 | 0,338 | 0,183 | 55,163a | 0,328 | 0,200 | 55,306a | 0,192 | 0,124 | 32,609a |
| 6 | 0,214 | −0,113 | 58,128a | 0,228 | −0,106 | 58,671a | 0,178 | 0,017 | 34,666a |
| 7 | 0,172 | −0,038 | 60,097a | 0,201 | 0,033 | 61,350a | 0,174 | 0,035 | 36,684a |
| 8 | 0,073 | −0,07 | 60,459a | 0,108 | −0,101 | 62,136a | 0,061 | −0,103 | 36,932a |
| 9 | −0,021 | −0,122 | 60,488a | −0,028 | −0,157 | 62,190a | 0,022 | −0,017 | 36,966a |
| 10 | −0,14 | −0,207 | 61,874a | −0,155 | −0,220 | 63,878a | −0,041 | −0,054 | 37,082a |
| 11 | −0,187 | −0,047 | 64,386a | −0,183 | 0,013 | 66,283a | −0,043 | −0,022 | 37,214a |
| 12 | −0,233 | −0,079 | 68,399a | −0,211 | −0,099 | 69,565a | −0,020 | 0,018 | 37,243a |
| PHZE1_5 | IRS | RIDP | |||||||
|---|---|---|---|---|---|---|---|---|---|
| k | AC | PAC | Q | AC | PAC | Q | AC | PAC | Q |
| 1 | 0,793 | 0,793 | 37,151a | −0,449 | −0,449 | 11,924a | 0,399 | 0,399 | 9,3800a |
| 2 | 0,535 | −0,255 | 54,341a | 0,143 | −0,074 | 13,158a | 0,343 | 0,218 | 16,439a |
| 3 | 0,307 | −0,067 | 60,100a | −0,014 | 0,027 | 13,171a | 0,274 | 0,101 | 21,052a |
| 4 | 0,105 | −0,119 | 60,788a | 0,016 | 0,038 | 13,187b | 0,066 | −0,148 | 21,325a |
| 5 | −0,066 | −0,104 | 61,067a | −0,034 | −0,021 | 13,260b | 0,243 | 0,225 | 25,093a |
| 6 | −0,158 | 0,031 | 62,697a | −0,039 | −0,085 | 13,358b | 0,224 | 0,12 | 28,359a |
| 7 | −0,04 | 0,435 | 62,804a | 0,031 | −0,025 | 13,421c | 0,096 | −0,103 | 28,977a |
| 8 | 0,046 | −0,216 | 62,949a | −0,008 | 0,009 | 13,425c | 0,161 | 0,017 | 30,728a |
| 9 | 0,071 | −0,089 | 63,298a | 0,102 | 0,138 | 14,138 | 0,003 | −0,072 | 30,729a |
| 10 | 0,077 | −0,021 | 63,719a | −0,122 | −0,031 | 15,196 | −0,076 | −0,121 | 31,132a |
| 11 | 0,072 | −0,012 | 64,095a | 0,026 | −0,084 | 15,243 | −0,006 | −0,007 | 31,135a |
| 12 | 0,066 | 0,113 | 64,414a | 0,08 | 0,068 | 15,721 | −0,049 | 0,029 | 31,310a |
Fuente: Elaboración propia a partir de las Series Temporales del Banco de España.
k denota orden; AC, autocorrelación; PAC, autocorrelación parcial, y Q, el estadístico de Box-Jenkins.
A continuación realizamos una aproximación a las máximas variaciones que pueden esperarse en la cuota de un préstamo hipotecario con amortización mensual y para el que la revisión del tipo de interés presente una periodicidad, bien semestral, bien anual, que son las más usuales (Fuentes, 2010). El nivel de probabilidad considerado es el 99%. Utilizaremos 2 métodos de cálculo y en ambos supondremos que es igualmente probable que el índice aumente o disminuya desde una fecha de revisión hasta la siguiente. Hemos observado que en casi todos los índices no rechazábamos que su media y su mediana fueran nulas, y viendo los resultados de las pruebas ANOVA y Kruskal-Wallis, tampoco podemos rechazar que el valor central de las variaciones de los índices sea nulo. Así, estaríamos alineándonos dentro de la filosofía de cálculo del VeR de RiskMetrics™, que se desarrolla en J. P. Morgan y Reuters (1996).
3.2Aproximación de las fluctuaciones esperadas de la cuota de un préstamo con la varianza y las autocorrelaciones de las fluctuaciones de los índicesLa primera aproximación a las variaciones esperadas de la cuota es similar al método del cálculo del VeR basado en la normalidad de las variables involucradas y en su matriz de correlaciones. Utilizamos los resultados de las tablas 3 y 4 y seguiremos los siguientes pasos:
Paso 1: Estimamos la varianza de la variación del índice en términos mensuales, σΔImens(m)2, que en nuestro caso podemos obtener directamente de la tabla 3.
Paso 2: Hallamos la varianza de la variación del índice para un periodo de M meses σΔIM(m)2 teniendo en cuenta su estructura de autocorrelaciones (ver tabla 4). Así:
donde ρj es la autocorrelación de orden j.Paso 3: Asumimos que Δj0(m)∼N0,σΔj0(m), siendo σΔj0(m)=σΔIM(m).
Paso 4: Así, la variación del tanto periodal se aproxima con la variable aleatoria Δi0(m)∼N0,σΔi0(m), donde σΔi0(m)=σΔj0(m)m. Para evaluar (15) tomaremos, por tanto:
Siendo z¿ el ¿-percentil de una variable aleatoria normal estándar.
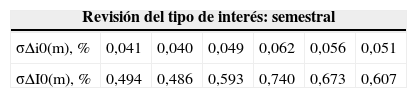
En las tablas 5.1 y 5.2 puede observarse que los índices del mercado interbancario son los que generan una menor variabilidad de la cuota. Así, en el EURIBOR, los incrementos de la cuota máximos que podemos esperar si el tipo de interés se revisa anualmente se sitúan en torno al 1% si el vencimiento residual es un año, aumentan hasta el 5% si la vida residual del préstamo es 5 años, y no llegan al 25% si el vencimiento residual es 30 años, que es la duración de largo plazo más usual en la práctica. Aunque el IRPH3 no provoca una volatilidad mucho mayor en la cuota, los resultados son contradictorios con la extendida creencia de que el índice bancario doméstico es menos volátil que los interbancarios. Incluso podemos observar que el índice de préstamos hipotecarios de la zona euro (PHZE1_5) es el más volátil. Por otra parte, la significativa autocorrelación negativa de las fluctuaciones del IRS provoca que, aunque su volatilidad mensual sea la más elevada de todos los índices, al considerar periodos de revisión que engloban varios meses, genere una volatilidad en las cuotas muy similar a los interbancarios.
Fluctuación porcentual máxima (sobre la cuota vigente) que puede esperarse a un nivel de confianza del 99% para la cuota de un préstamo francés con un tanto nominal vigente del j0(12)=3%, revisión del tipo de interés semestral y periodicidad de amortización mensual
| Revisión del tipo de interés: semestral | ||||||
|---|---|---|---|---|---|---|
| σΔi0(m), % | 0,041 | 0,040 | 0,049 | 0,062 | 0,056 | 0,051 |
| σΔI0(m), % | 0,494 | 0,486 | 0,593 | 0,740 | 0,673 | 0,607 |
| Vencimiento (años) | Duración (meses) | MIBOR, % | EURIBOR, % | IRPH3, % | PHZE1_5, % | IRS, % | RIDP, % |
|---|---|---|---|---|---|---|---|
| 1 | 6,47 | 0,62 | 0,61 | 0,74 | 0,93 | 0,84 | 0,76 |
| 5 | 29,75 | 2,84 | 2,80 | 3,42 | 4,26 | 3,88 | 3,50 |
| 10 | 57,51 | 5,50 | 5,41 | 6,60 | 8,24 | 7,49 | 6,76 |
| 15 | 83,78 | 8,01 | 7,88 | 9,62 | 12,00 | 10,92 | 9,85 |
| 30 | 153,89 | 14,71 | 14,47 | 17,67 | 22,05 | 20,05 | 18,08 |
| 50 | 228,25 | 21,82 | 21,47 | 26,20 | 32,70 | 29,74 | 26,82 |
Fuente: Elaboración propia a partir de las Series Temporales del Banco de España
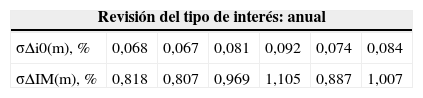
Fluctuación porcentual máxima (sobre la cuota vigente) que puede esperarse a un nivel de confianza del 99% para la cuota de un préstamo francés con un tanto nominal vigente del j0(12)=3%, revisión del tipo de interés anual y periodicidad de amortización mensual
| Revisión del tipo de interés: anual | ||||||
|---|---|---|---|---|---|---|
| σΔi0(m), % | 0,068 | 0,067 | 0,081 | 0,092 | 0,074 | 0,084 |
| σΔIM(m), % | 0,818 | 0,807 | 0,969 | 1,105 | 0,887 | 1,007 |
| Vencimiento (años) | Duración (meses) | MIBOR, % | EURIBOR, % | IRPH3, % | PHZE1_5, % | IRS, % | RIDP, % |
|---|---|---|---|---|---|---|---|
| 1 | 6,47 | 1,03 | 1,01 | 1,21 | 1,38 | 1,11 | 1,26 |
| 5 | 29,75 | 4,72 | 4,65 | 5,58 | 6,37 | 5,11 | 5,80 |
| 10 | 57,51 | 9,11 | 8,99 | 10,80 | 12,31 | 9,88 | 11,22 |
| 15 | 83,78 | 13,28 | 13,10 | 15,73 | 17,93 | 14,40 | 16,34 |
| 30 | 153,89 | 24,39 | 24,06 | 28,89 | 32,93 | 26,45 | 30,01 |
| 50 | 228,25 | 36,18 | 35,69 | 42,85 | 48,84 | 39,23 | 44,52 |
Fuente: Elaboración propia a partir de las Series Temporales del Banco de España.
En el segundo enfoque, ajustamos a los índices un modelo autorregresivo con varianza condicional del tipo GARCH(1,1), de Bollerslev (1986). No empleamos modelos más complejos ya que, por una parte, la base de datos de la que partimos no tiene un gran número de observaciones, y por otra, en la práctica el modelo GARCH(1,1) ajusta suficientemente bien las series financieras, tal como señalan Hansen y Lunde (2001).
Las autocorrelaciones de la tabla 4 evidencian que las fluctuaciones mensuales de los índices pueden ser ajustadas razonablemente bien con un modelo autorregresivo de orden 1:
donde θ es la estimación del coeficiente de autocorrelación del proceso AR(1) y ¿t el término de error, que es una variable aleatoria normal de media 0 y varianza σεt2, donde:Podemos observar que con la segunda aproximación necesitaremos estimar menos parámetros que con el procedimiento propuesto en 3.2. Basta con ajustar 4 parámetros (o menos, si alguno no es significativo) para caracterizar la dinámica de los índices.
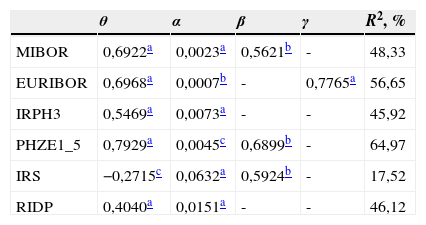
Tras una primera estimación del modelo autorregresivo con mínimos cuadrados ordinarios, hemos examinado la heterocedasticidad de los errores con el test ARCH. En el caso de que se acepte que los errores son heterocedásticos, reestimamos el modelo con el error (19). Asimismo, si los parámetros β y γ no presentan una significación estadística de, al menos, el 90%, se reestima el modelo sin incluir el coeficiente no significativo. En la tabla 6 observamos que la volatilidad del MIBOR, el PHZE1_5 y el índice de swaps queda bien ajustada con un modelo ARCH(1), mientras que el EURIBOR queda mejor caracterizado por un modelo GARCH(1,0). Tanto en el IRPH3 como en el rendimiento interno en el mercado secundario de la deuda pública entre 2 y 6 años no rechazamos que el error tenga una varianza constante.
Resultados del ajuste de los parámetros en (18) y (19)
| θ | α | β | γ | R2, % | |
|---|---|---|---|---|---|
| MIBOR | 0,6922a | 0,0023a | 0,5621b | - | 48,33 |
| EURIBOR | 0,6968a | 0,0007b | - | 0,7765a | 56,65 |
| IRPH3 | 0,5469a | 0,0073a | - | - | 45,92 |
| PHZE1_5 | 0,7929a | 0,0045c | 0,6899b | - | 64,97 |
| IRS | −0,2715c | 0,0632a | 0,5924b | - | 17,52 |
| RIDP | 0,4040a | 0,0151a | - | - | 46,12 |
Fuente: Elaboración propia a partir de las Series Temporales del Banco de España.
La ecuación (19) nos permite obtener la varianza asintótica del error, σ¯εt2:
Así, la varianza asintótica de ΔImens(m), que simbolizamos como σ¯ΔImens(m)2, será:
Los siguientes pasos a seguir son el 2, 3 y 4 del método anterior, con la salvedad de que en este caso la correlación de orden j es ρj=θj. Así, la varianza de la fluctuación del índice en M meses, (16), queda reescrita como:
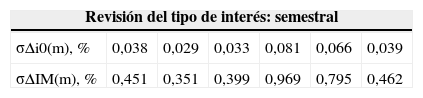
Las tablas 7.1 y 7.2 arrojan resultados que difieren de los de las tablas 5.1 y 5.2 en algunos aspectos. Aunque el EURIBOR sigue siendo el índice que provoca menor volatilidad en la cuota, el siguiente menos volátil es el IRPH3 y no el MIBOR. Asimismo, el IRS se sitúa como el que provoca mayor variabilidad en las cuotas después del PHZE1_5. También comprobamos que los aumentos de cuota esperados para el EURIBOR, el IRPH3 y el rendimiento interno en el mercado secundario de la deuda pública entre 2 y 6 años son menores con este método que con el del subepígrafe anterior. En cambio, en el PHZE1_5 y en el IRS los incrementos de la cuota son superiores. También podemos comprobar que las diferencias de volatilidad que provocan en la cuota los diferentes índices son más acusadas.
Fluctuación porcentual máxima (sobre la cuota vigente) que puede esperarse a un nivel de confianza del 99% para la cuota de un préstamo francés con un tanto nominal vigente del j0(12)=3%, revisión del tipo de interés semestral y periodicidad de amortización mensual
| Revisión del tipo de interés: semestral | ||||||
|---|---|---|---|---|---|---|
| σΔi0(m), % | 0,038 | 0,029 | 0,033 | 0,081 | 0,066 | 0,039 |
| σΔIM(m), % | 0,451 | 0,351 | 0,399 | 0,969 | 0,795 | 0,462 |
| Vencimiento (años) | Duración (meses) | MIBOR, % | EURIBOR, % | IRPH3, % | PHZE1_5, % | IRS, % | RIDP, % |
|---|---|---|---|---|---|---|---|
| 1 | 6,47 | 0,57 | 0,44 | 0,50 | 1,21 | 1,00 | 0,58 |
| 5 | 29,75 | 2,60 | 2,02 | 2,30 | 5,58 | 4,58 | 2,66 |
| 10 | 57,51 | 5,03 | 3,91 | 4,44 | 10,79 | 8,85 | 5,15 |
| 15 | 83,78 | 7,33 | 5,69 | 6,47 | 15,72 | 12,89 | 7,50 |
| 30 | 153,89 | 13,46 | 10,46 | 11,89 | 28,87 | 23,69 | 13,78 |
| 50 | 228,25 | 19,96 | 15,51 | 17,64 | 42,82 | 35,13 | 20,44 |
Fuente: Elaboración propia a partir de las Series Temporales del Banco de España.
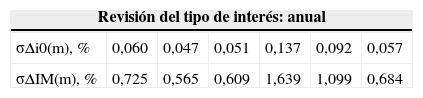
Fluctuación porcentual máxima (sobre la cuota vigente) que puede esperarse a un nivel de confianza del 99% para la cuota de un préstamo francés con un tanto nominal vigente del j0(12)=3%, revisión del tipo de interés anual y periodicidad de amortización mensual
| Revisión del tipo de interés: anual | ||||||
|---|---|---|---|---|---|---|
| σΔi0(m), % | 0,060 | 0,047 | 0,051 | 0,137 | 0,092 | 0,057 |
| σΔIM(m), % | 0,725 | 0,565 | 0,609 | 1,639 | 1,099 | 0,684 |
| Vencimiento (años) | Duración (meses) | MIBOR, % | EURIBOR, % | IRPH3, % | PHZE1_5, % | IRS, % | RIDP, % |
|---|---|---|---|---|---|---|---|
| 1 | 6,47 | 0,91 | 0,71 | 0,76 | 2,05 | 1,38 | 0,86 |
| 5 | 29,75 | 4,18 | 3,25 | 3,51 | 9,45 | 6,33 | 3,94 |
| 10 | 57,51 | 8,08 | 6,29 | 6,78 | 18,26 | 12,24 | 7,62 |
| 15 | 83,78 | 11,77 | 9,16 | 9,88 | 26,60 | 17,83 | 11,10 |
| 30 | 153,89 | 21,61 | 16,83 | 18,15 | 48,86 | 32,74 | 20,40 |
| 50 | 228,25 | 32,05 | 24,96 | 26,92 | 72,47 | 48,56 | 30,25 |
Fuente: Elaboración propia a partir de las Series Temporales del Banco de España.
En este trabajo derivamos una relación lineal que permite aproximar la variación de la cuota de un préstamo a interés variable y de carácter pospagable, concretamente amortizable por el sistema francés, ante cambios del tipo de interés. Esta se basa en la duración de un préstamo idéntico pactado a tipo de interés fijo. Así, podemos aplicar de manera inmediata los conceptos de duración modificada, vpb y valor en riesgo, habituales en la gestión del riesgo de precio en los activos de renta fija, a la cuantificación del riesgo de incremento de la cuota en un préstamo con tipo de interés variable.
Asimismo, inferimos la variación máxima de la cuota cuando la revisión del tipo de interés se realiza con los índices de referencia del mercado hipotecario españoles. Según la primera metodología propuesta, los más utilizados, el MIBOR (para contratos anteriores a 2000) y el EURIBOR (en los posteriores), son los menos volátiles. El índice swaps genera una variabilidad de las cuotas ligeramente superior, mientras que los más volátiles son el IRPH3, el índice de la deuda pública y el de préstamos hipotecarios de la zona euro.
La segunda metodología propuesta se basa en la consideración de las fluctuaciones de los tipos de interés como una serie AR(1), lo que permite estimar menos parámetros para describir la dinámica de los índices, y algunas de las conclusiones que extraemos no son coincidentes con el primer método. En algunos índices, como el EURIBOR, la volatilidad que estimamos es inferior, mientras que en otros, como el PHZE1_5, es sensiblemente superior. Por otra parte, el IRPH3 pasa de ser uno de los 3 más volátiles al segundo menos volátil. En cambio, el IRS realiza el recorrido inverso, pues de ser uno de los 3 menos volátiles pasa a generar el segundo mayor incremento esperado en la cuota.
También debe resaltarse que estamos comparando volatilidades entre índices y no entre periodos de revisión, ya que, obviamente, aunque la variación esperada para un nivel de probabilidad dado es mayor cuando el préstamo se revisa anualmente que cuando se revisa semestralmente, también es cierto que para una duración residual dada, la cuota será revisada el doble de veces si la revisión tiene carácter semestral.
Entendemos que los resultados obtenidos son relevantes para la gestión financiera, tanto de las economías familiares como empresarial, especialmente para la previsión de pagos futuros. Por una parte, proponemos expresiones analíticas que permiten sopesar el riesgo de incremento de las cuotas de un préstamo pactado a tipo de interés variable, y posteriormente, cuantificamos dicho riesgo para los índices oficiales del mercado hipotecario español.
Somos conscientes de que hemos circunscrito nuestro análisis de variación del término amortizativo a un caso concreto de amortización con cuotas pospagables: la amortización francesa. En trabajos futuros puede ser de interés extender este análisis a otro tipo de amortizaciones, tanto de carácter pospagable, como puede ser la italiana, como prepagable, como la alemana, que si bien no son tan comunes, también se observan en la práctica.
AgradecimientosEl autor agradece los comentarios de los evaluadores anónimos, que han permitido mejorar notablemente la versión preliminar del trabajo.
Una demostración en tiempo continuo puede consultarse en Cox, Ingersoll y Ross (1980).
Los préstamos a tipo fijo no están exentos de riesgos para el prestatario. En este caso el riesgo proviene de que en escenarios futuros de inflación baja (y previsiblemente, de tipos de interés bajos) la carga que supone la devolución del préstamo reduzca la renta disponible del prestatario. En cambio, con el tipo variable, el riesgo inflacionario es muy bajo, siempre que los tipos de interés nominales y la renta del prestatario se muevan en la dirección de la inflación (Alonso et al., 2004).
Estos se establecen en el artículo 27 de la Orden EHA/2899/2011, de 28 de octubre, y se definen en la norma 14 y anexo 8 de la Circular del Banco de España 5/2012.