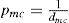Los modelos digitales de elevación (mde) son la forma más común y eficaz de representar la superficie terrestre. Desafortunadamente, al igual que la mayoría de la información geográfica en formato digital, los mde contienen errores de forma inherente, por lo que es necesario evaluar la magnitud de dichos errores e informar de su existencia a los usuarios de mde. Uno de los factores que introduce errores en los mde es el método de interpolación y diferentes estudios previos han presentado conclusiones que discrepan entre sí en cuanto a la idoneidad de diferentes métodos de interpolación para la generación de mde. Con el objetivo de contribuir a dicha discusión y de mejorar el entendimiento del error introducido por métodos de interpolación en los mde, en este trabajo se evalúa y compara la precisión de mde generados utilizando métodos de interpolación determinísticos (ide, anudem) y probabilísticos (ok, kt). Los resultados sugieren que KT genera mde más precisos que el resto de los métodos de interpolación aquí evaluados y sin la presencia de errores sistemáticos, como ocurre en los mde generados usando ide, anudem y ok. Dichos resultados concuerdan con algunos estudios previos, pero discrepan al mismo tiempo con otros estudios similares.
Digital elevation models (dem) are the most common and effective representation of the land surface. Unfortunately, similarly to most digital geographic information, dem inherently contain errors, which magnitude should be assessed and informed to dem users. One factor that introduces errors in dem is the interpolation method and several previous studies have presented findings that disagree among them regarding the suitability of several interpolation methods for dem generation. With the aim of contributing to this discussion and of improving the understanding of errors introduced in dem by interpolation methods, in this paper we evaluate and compare the accuracy of dem generated using both deterministic (idw, anudem) and probabilistic (ok, kt) interpolation methods. Our results suggest that kt produces more accurate dem than the other interpolation methods evaluated in this paper and that it produces dem without systematic errors, which occur in dem generated using idw, anudem and ok. These results are consistent with some previous studies, but at the same time disagree with other similar studies.
La superficie terrestre es un fenómeno continuo que puede ser medido y descrito en cualquier punto sobre la misma con base en un conjunto de variables (Longley et al., 2005). Entre dichas variables, la elevación es una de las variables más estudiadas, ya que es utilizada en un amplio rango de aplicaciones científicas y civiles (inegi, 2002; Fisher y Tate, 2006), y se define como la distancia vertical desde un punto sobre la superficie terrestre hasta un nivel de referencia arbitrario, como puede ser el nivel medio del mar (definido como datum vertical), (Anderson y Mikhail, 1998).
Debido a la naturaleza de la superficie terrestre, la elevación es continua y debe ser representada digitalmente como tal. Desafortunadamente, debido a limitantes técnicas y económicas, no es factible medir y almacenar la elevación de cada punto sobre la superficie terrestre (Kumler, 1994). Aun considerando nuevas tecnologías como Lidar (Light Detection and Ranging), que brinda la posibilidad de medir la elevación de un considerable número de puntos sobre el terreno en un corto periodo de tiempo, no es viable representar la superficie terrestre utilizando todas las muestras de elevación (puntos sobre el terreno) disponibles y es necesario reducir el volumen de datos (Anderson et al., 2006). Por tanto, la elevación del terreno se representa digitalmente como una superficie continua mediante Modelos Digitales de Elevación (mde) generados con base en un número finito de muestras de elevación (Li et al., 2005).
Modelos digitales de elevación (mde)Las muestras de elevación o puntos sobre el terreno no representan la superficie terrestre de manera continua por sí mismas, sin importar si su distribución espacial es regular o irregular (Kumler, 1994), y, en consecuencia, es necesario utilizar un formato que permita modelar la elevación como una superfi cie continua (Burrough y McDonell, 1998). De los diferentes formatos disponibles (curvas de nivel, redes irregulares de triángulos (TIN), celdas (Li et al., 2005)), el formato de celdas, o raster, es el más común entre los usuarios y es normalmente conocido como Modelo Digital de Elevación (mde), (Fisher y Tate, 2006). Sin embargo, las curvas de nivel y las redes irregulares de triángulos pueden ser también consideradas como mde si se utiliza la definición tradicional de mde de Miller y Laflamme (1958): “representación numérica digital de la superficie terrestre”. En este artículo se utiliza el término mde para referirse únicamente al formato de celdas, como es común en la literatura científica.
Los mde en formato de celdas representan el terreno como una superficie continua mediante la definición de una cuadrícula o malla regular sobre el área en estudio y el almacenamiento de un valor de elevación para cada celda de la cuadrícula (Burrough y McDonell, 1998). La definición de la cuadrícula depende directamente de la distribución espacial de las muestras de elevación. Si los puntos sobre el terreno disponibles se distribuyen espacialmente en forma de matriz, entonces es recomendable definir la malla con base en las muestras de elevación disponibles y almacenar la elevación directamente en cada celda. En este caso el tamaño de celda o resolución espacial está determinado por la distancia entre cada muestra de elevación (Li et al., 2005).
En caso contrario, si las muestras de elevación se distribuyen irregularmente sobre el área de estudio, es necesario definir el tamaño de celda de manera arbitraria, empírica (Hutchinson, 1996) o estadística (Hengl, 2006), y seleccionar un método de interpolación para generar un valor de elevación para cada celda de la malla tomando como entrada los puntos sobre el terreno disponibles (Li et al., 2005). Desafortunadamente, diferentes métodos de interpolación calculan diferentes valores para una misma celda aun utilizando las mismas muestras de elevación como entrada (Lloyd y Atkinson, 2002), por lo que la selección del algoritmo de interpolación puede ser considerada como un factor que introduce errores en los mde.
Errores por interpolación en los mdeLos errores introducidos por el método de interpolación seleccionado pueden ser aleatorios, debido por ejemplo al redondeo numérico (USGS, 1997); sistemáticos, manifestados como patrones en los mde (Wise, 2000); o inclusive garrafales (blunders), causados por alta variabilidad del terreno y la aplicación de métodos de interpolación sin restricciones (Smith et al., 2005). Los errores sistemáticos y garrafales pueden ser eliminados o reducidos mediante la aplicación de filtros estadísticos apropiados (López, 2000), por lo cual no es común observarlos en mde comerciales u oficiales (Fisher y Tate, 2006). Sin embargo, los errores aleatorios no pueden ser filtrados, debido al poco entendimiento de su naturaleza y localización (Li et al., 2005; Pérez y Mas, 2009), y en algunos casos la aplicación de filtros para la reducción/eliminación de errores sistemáticos y garrafales resulta en la adición de nuevos errores aleatorios en los mde (Wise, 2000).
Estudios previos han sugerido que los principales factores que influyen en la naturaleza y magnitud de los errores introducidos en los mde por el método de interpolación son: a] la cantidad de información (ej. número de muestras, correlación espacial) empleada por el método de interpolación para calcular la elevación en cada celda de la malla (Lloyd y Atkinson, 2006) y b) los rasgos topográ ficos del área geográfica representada por el mde (Fisher y Tate, 2006). No obstante, no existe un consenso en cuanto a ninguno de estos dos factores. Por ejemplo, para la generación de mde en áreas con relieve moderado, Lloyd y Atkinson (2002), Reuter et al. (2007) y Erdogan (2009) concluyeron que métodos probabilísticos que emplean gran cantidad de información para calcular la elevación de cada celda son más convenientes que métodos determinísticos. Sin embargo, Bishop y McBratney (2002), Su y Bork (2006) y Bater y Coops (2009) sugieren que métodos determinísticos producen mde más precisos en áreas de relieve similar cuando una gran cantidad de muestras de elevación es utilizada.
En áreas con relieve predominantemente montañoso, los resultados de Reuter et al. (2007) sugieren un mejor desempeño de métodos deter minísticos en este tipo de terreno. En contraste, Morillo et al. (2002) no encontraron diferencias significativas en la aplicación de métodos deter minísticos y probabilísticos para la generación de mde y lo atribuyeron a la alta densidad de datos disponibles para su área en estudio. De forma similar, Guo et al. (2010) sugieren que diferentes métodos de interpolación generan resultados similares, aunque establecen que métodos probabilísticos son más confiables en la generación de mde en áreas con relieve montañoso. Por lo tanto, es difícil establecer la superioridad de ciertos métodos de interpolación sobre otros y es necesario ampliar el nivel de entendimiento de los mismos con base en nuevos estudios (Fisher y Tate, 2006; Wise, 2011).
ObjetivoCon el objetivo de contribuir a un mejor entendimiento de los errores introducidos por diferentes métodos de interpolación en la generación de mde, en este estudio se presenta la evaluación y comparación de la precisión de mde generados utilizando métodos de interpolación determinísticos y proba bilísticos. La descripción de los métodos utilizados en este estudio se presenta a continuación; seguida de un caso de estudio que permite comparar la idoneidad de cada método para la generación de mde y alcanzar una serie de conclusiones, presentadas al final de este estudio.
Métodos de interpolaciónMétodos determinísticosLa interpolación espacial es “un procedimiento que permite calcular el valor de una variable en una posición del espacio, conociendo los valores de esa variable en otras posiciones del espacio” (Bosque, 2000:375). Los diferentes métodos de interpo lación espacial se clasifican en dos grandes categorías: determinísticos y probabilísticos (Maune et al., 2001). Los métodos de interpolación de terminísticos calculan un valor para celda de la cuadrícula usando únicamente las propiedades físicas de las muestras de elevación (Goovaerts, 1997). El método de interpolación determinístico más comúnmente empleado es la ponderación en función inversa de la distancia o idw (Inverse Distance Weighting; Wise, 2000). idw se encuentra disponible en la mayoría de los programas de sistemas de información geográfica (SIG; Pérez y Mas, 2009) y su definición formal es (O’Sullivan y Unwin, 2003:228):
donde êc es la elevación calculada para la celda c utilizando n muestras de elevación; em es el valor de las muestras de elevación; y pmc es el peso (o influencia) entre 0 y 1 asignado a cada muestra de elevación, calculado como:
donde dmc es la distancia euclidiana entre la muestra de elevación m y el centro de la celda c de la malla. Opcionalmente, con el fin de mejorar resultados, es común utilizar un exponente a para disminuir la influencia de las muestras conforme se incrementa la distancia (Bosque, 2000:378):
Otro método de interpolación determinístico ampliamente utilizado es el método anudem, desarrollado por Hutchinson (1988) específicamente para la generación de mde usando curvas adaptivas (splines) locales. anudem define un modelo estadístico en el que las muestras de elevación zi en las coordenadas xi, yi son el resultado de (Hutchinson, 2008:151):
donde f es una función bivariada desconocida potencialmente suave de ubicación horizontal representada como una malla de diferencia finita; n el número de muestras de elevación; y εi es el error aleatorio con media 0 y desviación estándar dada por:
donde h es el tamaño de celda de la malla y si es la pendiente de la celda asociada con la muestra. La función f es estimada resolviendo la aproximación de la malla de diferencia finita a la función bivariada que minimiza:
donde J(f) es la rugosidad del terreno en función de la primera y segunda derivada de f; y Λ es el parámetro positivo que suaviza dicha rugosidad. El parámetro Λ es elegido de forma que la suma de cuadrados de los residuales en la ecuación 6 sea igual a n, lo cual solo puede ser logrado mediante un método de interpolación iterativa para el cual la pendiente de cada celda se encuentre disponible. Es decir, el método anudem genera un mde de baja resolución e interpola de forma iterativa incrementando la resolución del mismo hasta alcanzar la solución de la ecuación 6 y el tamaño de celda especificado por el usuario (Ibid.).
Métodos probabilísticosLos métodos de interpolación probabilísticos, en contraste con los métodos determinísticos, inferen una gran cantidad de información utilizando las muestras disponibles (Maune et al., 2001). Los métodos de interpolación probabilísticos más comunes son los métodos geoestadísticos derivados de la forma genérica de Kriging (Goovaerts, 1997:126):
donde Z*(u) es el valor estimado para cada ubicación u utilizando n(u) muestras; λα es el peso, o ponderación, que cada muestra Z(uα) toma; y m(uα) y m(u) son los valores esperados o medias aritméticas de las muestras disponibles y de la elevación en el área cubierta por el método de interpolación. Las diferentes variables de Kriging tienen como objetivo minimizar la varianza del error de estimación mediante la restricción
alcanzada a través de la asignación de pesos λα con base en la disimilaridad de los valores de las muestras Z(uα). La disimilaridad γ(h) entre las muestras de elevación es establecida a través del semivariograma experimental definido como (Goovaerts, 1997:28):
donde h es la distancia entre las muestras z(uα) y z(uα + h) y n es el número de muestras separadas por la distancia h.
Las variantes de Kriging empleadas en este estudio son Kriging Ordinario (ok, Ordinary Kriging) y Kriging con un modelo de tendencia (KT, Kriging with a trend model). Kriging Ordinario (ok) asume que la media m(u) varía a través del área en estudio, pero es constante dentro de un área (o vecindad) local cubierta por el método de interpolación y, lo más importante, desconocida; por lo que es filtrada del método de interpolación estableciendo la suma total de los pesos de las muestras igual a 1 (Ibid. :133):
Kriging con un modelo de tendencia (KT) asume que m(u) varía ligeramente en la vecindad local W(u) del método de interpolación pero es desconocida. Dicha tendencia m(u′) es modelada como una combinación linear de funciones fk(u) de las coordenadas geográficas K disponibles (Goovaerts, 1997: 140):
donde los coeficientes ak(u′) se consideran desconocidos y constantes para cada vecindad local. Dichos coeficientes son filtrados del algoritmo de interpolación estableciendo la suma total de los pesos igual a la tendencia fk(u′), (Ibid.)
Caso de estudioÁrea en estudioLa zona en estudio (Figura 1) se encuentra ubicada en el municipio de Yecapixtla, Morelos, México, y forma parte de un corredor para el cual se elaboró un estudio topográfico para la construcción de infraestructura por encargo de una empresa paraestatal mexicana; y se delimita por las coordenadas 18°50’50.36” N, 98°53’04.28” W; UTM WGS84 Zona 14 Norte: 512165 E, 2083938 N en la esquina superior izquierda, y 18°50’09.66” N, 98°52’21.60” W; UTM WGS84 Zona 14 Norte: 513415 E, 2082688 N en la esquina inferior derecha, formando un cuadrado de 1 250 x 1 250 m. El área cuenta con variada topografía (Figura 2) con un rango de elevaciones entre 1 492 y 1 586 m snmm. Es predominantemente plana al norte y montañosa al sur, y por lo tanto presenta las características apropiadas para evaluar el desempeño de diferentes métodos de interpolación en diferentes tipos de terreno.
DatosDebido al estudio topográfico realizado previamente, se cuenta con una gran cantidad de datos para el área en estudio, incluyendo datos Lidar, fotografía aérea (Figura 2) y puntos de control recolectados con gps cinemático de precisión. Para la realización de este estudio, se simuló la realización de un levantamiento topográfico para la generación de un mde con tamaño de celda de 1 m (requerimiento de la paraestatal), para lo cual se solicitó a topógrafos con más de veinte años de experiencia en campo diseñaran dicho levantamiento. El diseño se basó en una combinación de muestras regulares y muestras representativas (Li et al., 2005); e incluye una malla regular de puntos sobre el terreno cada 10 m y secciones cada 20 m en los rasgos hidrográficos (escurrimientos) más importantes y en la infraestructura carretera presente (Figura 2). En total, el levantamiento topográfico simulado se compone de 16 042 muestras de elevación tomadas de los datos Lidar disponibles.
ProcesamientoLas 16 042 muestras de elevación tomadas de los datos Lidar disponibles, fueron importadas en el paquete estadístico R (R Development Core Team, 2012) para ser procesadas con la librería gstat (Pe besma, 2004) y generar mde con un tamaño de cel da de 1 m usando los métodos de interpolación idw (ecuación 1), ok (ecuación 10) y kt (ecuación 12). El mde idw fue generado usando 2 como exponente (ecuación 3) para ponderar la distancia de las doce muestras más cercanas al centro de cada celda de la cuadrícula y disminuir la presencia de patrones artificiales en el mde. Los mde ok y kt se generaron utilizando solo las 24 muestras más cercanas para permitir el cálculo variable de la media en la vecindad local de cada celda. El mde correspondiente al método anudem fue generado usando la versión del mismo implementada en ArcMap 10, sin forzar la definición de una red de drenaje, ya que dicha opción introdujo rasgos hidrográficos y topográficos artificiales debido a la alta densidad de datos (ESRI, 2011). Los cuatro mde generados se muestran en la Figura 3
Una vez generados los mde, la precisión de los mismos fue evaluada utilizando como referencia el mde Lidar disponible para el área en estudio. El mde Lidar tiene una precisión de 15cm por lo que puede ser considerado como un mde válido para evaluar la precisión de los mde generados mediante interpolación (Fisher y Tate, 2006). La precisión o error de los mde generados fue evaluada sustrayendo en cada celda la elevación reportada por el mde Lidar de la elevación calculada utilizando interpolación. El resultado de esta operación fueron cuatro superficies de error (Figura 4) en las cuales valores positivos y negativos indican, respectivamente, sobreestimación y subestimación de la elevación por parte de los diferentes métodos de interpolación. Dichas superficies de error fueron utilizadas para generar estadísticas descriptivas de error, incluyendo el error medio cuadrático (emc), de la zona en estudio completa (Tabla 1) y de las zonas norte (Tabla 2) y sur (Tabla 3). El emc es la estadística comúnmente utilizada para reportar la precisión de mde y definida como (Ibid.:470):
Superficies de error de los mde mostrados en la Figura 3. a. Error mde idw. b. Error mde anudem. c. Error mde ok. d. Error mde KT.
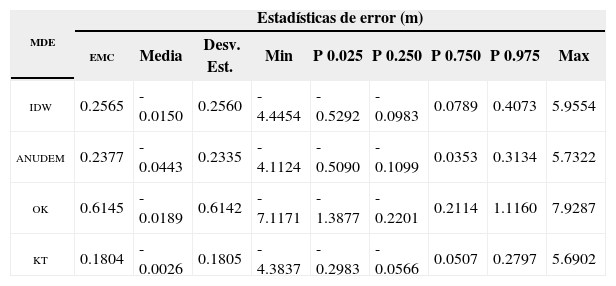
Estadísticas descriptivas del error en los mde generados mediante interpolación
| mde | Estadísticas de error (m) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| emc | Media | Desv. Est. | Min | P 0.025 | P 0.250 | P 0.750 | P 0.975 | Max | |
| idw | 0.2565 | -0.0150 | 0.2560 | -4.4454 | -0.5292 | -0.0983 | 0.0789 | 0.4073 | 5.9554 |
| anudem | 0.2377 | -0.0443 | 0.2335 | -4.1124 | -0.5090 | -0.1099 | 0.0353 | 0.3134 | 5.7322 |
| ok | 0.6145 | -0.0189 | 0.6142 | -7.1171 | -1.3877 | -0.2201 | 0.2114 | 1.1160 | 7.9287 |
| kt | 0.1804 | -0.0026 | 0.1805 | -4.3837 | -0.2983 | -0.0566 | 0.0507 | 0.2797 | 5.6902 |
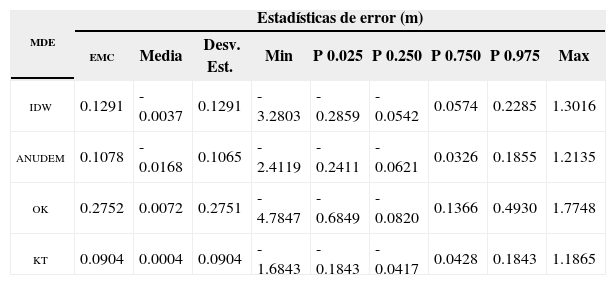
Estadísticas descriptivas del error en la zona norte (plana) de los mde generados
| mde | Estadísticas de error (m) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| emc | Media | Desv. Est. | Min | P 0.025 | P 0.250 | P 0.750 | P 0.975 | Max | |
| idw | 0.1291 | -0.0037 | 0.1291 | -3.2803 | -0.2859 | -0.0542 | 0.0574 | 0.2285 | 1.3016 |
| anudem | 0.1078 | -0.0168 | 0.1065 | -2.4119 | -0.2411 | -0.0621 | 0.0326 | 0.1855 | 1.2135 |
| ok | 0.2752 | 0.0072 | 0.2751 | -4.7847 | -0.6849 | -0.0820 | 0.1366 | 0.4930 | 1.7748 |
| kt | 0.0904 | 0.0004 | 0.0904 | -1.6843 | -0.1843 | -0.0417 | 0.0428 | 0.1843 | 1.1865 |
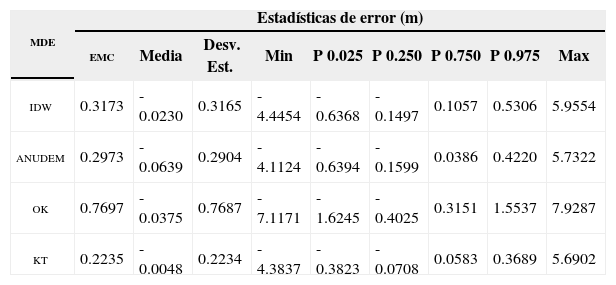
Estadísticas descriptivas del error en la zona sur (montañosa) de los mde generados
| mde | Estadísticas de error (m) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| emc | Media | Desv. Est. | Min | P 0.025 | P 0.250 | P 0.750 | P 0.975 | Max | |
| idw | 0.3173 | -0.0230 | 0.3165 | -4.4454 | -0.6368 | -0.1497 | 0.1057 | 0.5306 | 5.9554 |
| anudem | 0.2973 | -0.0639 | 0.2904 | -4.1124 | -0.6394 | -0.1599 | 0.0386 | 0.4220 | 5.7322 |
| ok | 0.7697 | -0.0375 | 0.7687 | -7.1171 | -1.6245 | -0.4025 | 0.3151 | 1.5537 | 7.9287 |
| kt | 0.2235 | -0.0048 | 0.2234 | -4.3837 | -0.3823 | -0.0708 | 0.0583 | 0.3689 | 5.6902 |
donde edem es la elevación de cada celda del mde, eref es la elevación del mde utilizado como referencia para evaluar la precisión y n el número de celdas evaluadas.
ResultadosLos diferentes métodos de interpolación deter minísticos (idw y anudem) y geoestadísticos (ok y KT) usados en este estudio generaron mde que gráficamente representan la mayoría de las características topográficas presentes en el área en estudio. No obstante, los mde idw (Figura 3a) y anudem (Figura 3b) muestran patrones arti ficiales, que pueden ser clasificados como errores sistemáticos, en las celdas cercanas a las muestras de elevación. Dichos patrones se pueden apreciar fácilmente en la zona sur de las superficies de error correspondientes a los métodos de interpolación determinísticos (Figura 4a y b). En contraste, los mde ok (Figura 3c) y kt (Figura 3d) no presentan patrones artificiales. Sin embargo, el mde ok representa los rasgos topográficos del área de manera demasiado suave, lo cual también puede ser considerado como error sistemático; e inclusive elimina algunos rasgos secundarios del área, dando como resultado la presencia de errores importantes aun en la parte plana del área en estudio (Figura 4c). El mde kt (Figura 3d) no presenta patrones visibles como se puede confirmar en la superficie de error correspondiente (Figura 4d), donde se muestra que los errores del mde kt se distribuyen de forma uniforme en el área de estudio.
La evaluación estadística del error en los mde generados (Tabla 1) confirma la evaluación visual de los mde. Todos los mde generados representan satisfactoriamente la superficie terrestre y, en consecuencia, tienen un emc bajo, con medias de error cercanas a 0 y, por lo tanto, desviaciones estándar muy cercanas al emc (Li et al., 2005). La presencia de errores sistemáticos en los mde idw, anudem y ok no es evidente en las estadísticas presentadas en la Tabla 1, por lo que es necesario recurrir a las estadísticas de error generadas para los diferentes tipos de terreno presentes en el área en estudio. En la zona norte del área, donde el terreno es predominantemente plano, las estadísticas de error (Tabla 2), de igual forma, indican que los cuatro métodos de interpolación son apropiados para generar mde. En esta zona, la diferencia entre la magnitud de los errores mínimos y máximos indica la existencia de errores sistemáticos (subestimación) en los mde idw, anudem y ok. En la zona montañosa (sur) del área en estudio, la presencia de errores sistemáticos es más evidente con errores medios más alejados del 0 (Tabla 3), con excepción de la media de error en el mde KT.
En términos de precisión absoluta, las estadísticas de error indican que kt es el método de interpolación más preciso de los cuatro métodos evaluados en este estudio, tanto en zonas con topografía variada (Tabla 1) como en zonas predominantemente planas (Tabla 2) y montañosas (Tabla 3). En el área en estudio completa el emc de kt es cercano al de idw y anudem, no obstante, la distribución de los errores en el mde kt (con un 75% de los errores entre -5.66 y 5.07cm y un 95% de los mismos entre -29.83 y 27.97cm) permite establecer que kt es más confiable que el resto de los métodos de interpolación, en los cuales la distribución de errores no es uniforme (Tabla 1). En la misma zona, ok generó el mde con el emc más alto debido principalmente al efecto suavizante del método. En la zona norte del área en estudio la precisión del mde kt es similar a la de los mde idw y anudem, no así a la del mde ok debido al efecto mencionado anteriormente. En la zona sur las estadísticas de error (Tabla 3) muestran de igual forma que el mde kt tiene una mejor precisión que la del resto de los mde; con un emc más bajo y una distribución uniforme de los errores, en contraste con el resto de los mde donde la influencia de errores sistemáticos es evidente.
ConclusionesLos mde contienen errores de forma inherente debido a diferentes factores. En este trabajo se evaluó y comparó la precisión de mde generados utilizando métodos de interpolación determinísticos (idw y anudem) y probabilísticos (ok y KT), ya que existe cierta discrepancia entre la comunidad científica acerca de la idoneidad de diferentes métodos de interpolación para la generación de mde. Los resultados del caso de estudio aquí presentado sugieren que kt genera mde más precisos que idw, anu-dem y ok. No obstante, no es posible establecer qué métodos probabilísticos de interpolación generan mde más precisos que métodos determinísticos, ya que el mde con el emc más alto fue generando usando ok (uno de los métodos probabilísticos).
Asimismo, aun cuando kt generó el mde más representativo gráficamente (sin errores sistemá ticos) y con la mejor precisión estadística en los diferentes tipos de terreno evaluados y cuando estos resultados concuerdan con aquellos de Lloyd y Atkinson (2002; 2006), Erdogan (2009) y Guo et al. (2010), es necesaria la elaboración de otros estudios que confirmen la superioridad de kt sobre otros métodos de interpolación. Lo anterior debido a que los resultados del caso de estudio, al igual que los de los otros estudios citados anteriormente, discrepan con los resultados de Bishop y McBratney (2002), Su y Bork (2006) y Bater y Coops (2009).
Es importante observar que tanto el caso de estudio aquí presentado, como aquéllos con los que se contrastan los resultados del mismo, fueron elaborados utilizando una gran densidad de muestras de elevación para la generación de mde de alta resolución con tamaños de celda menores a 5 m. Por lo tanto, para la generalización de los resultados aquí presentados se requiere de la elaboración de otros estudios que consideren combinaciones de bajas densidades de datos y bajas resoluciones.
Finalmente, es también importante mencionar que aun cuando el mde kt tiene un emc muy cercano al del mde Lidar, 18 y 15cm, respectivamente, el mde Lidar representa una mayor cantidad de características sobre el terreno en comparación con los mde generados mediante interpolación. Esto se puede observar gráficamente en las superficies de error (Figura 4) descritas anteriormente, donde se pueden observar en las cuatro superficies de error los rasgos no representadas por los mde generados.