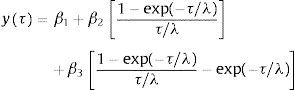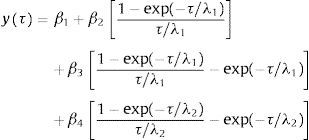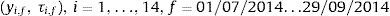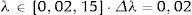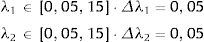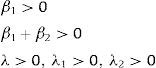La calibración del modelo Nelson-Siegel para ajustarse a curvas de rendimientos soberanas se ha encontrado problemática, pues presenta correlación entre sus factores y genera funciones objetivas con múltiples óptimos locales. Estos problemas no han sido profundizados en el contexto colombiano, dándole poca importancia al proceso de calibración. En el presente trabajo se evalúan dos métodos diferentes del gradiente para resolver el problema de ajuste por mínimos cuadrados no lineales: el metaheurístico de evolución diferencial y el método de búsquedas incrementales sobre los parámetros no lineales. Se realizan comparaciones entre los resultados en términos del ajuste logrado, consistencia en los resultados (para el metaheurístico) y formas obtenidas para la curva. El mismo procedimiento es realizado para el modelo Nelson-Siegel-Svensson, evaluando la pertinencia de su uso dentro del mercado local.
Calibration of the Nelson-Siegel (NS) model to adjust to sovereign yield curves has been found to be problematic since the model exhibits a correlation between its factors, and generates objective functions with local multiple optima. These problems are often disregarded in the Colombian market, enough importance is not being given to the calibration process. This study aims to evaluate two non-gradient based methods for solving the non-linear least squares problem: the differential evolution metaheuristic and an incremental search procedure on the non-linear parameters. Comparisons of the results are made in terms of the achieved fit, consistency (for the metaheuristic) and the shapes obtained for the curves. The same procedure is carried out on the Nelson-Siegel-Svensson (NSS) model, evaluating the advisability of its use in the local market.
La estructura temporal de tasas de interés (ETTI) de un país es la relación entre tasas de interés y plazos de inversión que se presenta en su economía en un momento en particular. El conocimiento de dicha relación no solo permite aproximar tasas de interés relevantes para valorar activos financieros; sino que contiene también información sobre el estado actual, las perspectivas de inflación y el crecimiento futuro de la economía. Por lo anterior, la ETTI resulta de gran importancia para el desarrollo de estrategias financieras en las entidades, tanto públicas como corporativas.
La ETTI soberana de un país es la curva que relaciona los rendimientos esperados de los títulos emitidos por el Estado con sus plazos de vencimiento. Esta curva es vista como una referencia para la emisión y valoración de activos financieros, ya que sus rendimientos se consideran de riesgo mínimo dentro de un país. Los instrumentos más susceptibles de ser valorados utilizando la estructura de plazos son los pertenecientes al mercado de deuda, tanto pública como privada.
El mercado de deuda pública es de vital importancia en el contexto colombiano. Esto puede verse en el saldo total de la deuda del Estado, en el cual la representación de bonos soberanos TES ha tenido un comportamiento histórico creciente, con una participación de 71,13% en junio de 2014 (Ministerio de Hacienda y Crédito Público, 2014). Sin embargo, el mercado de deuda corporativa no se ha desarrollado a la par y se encuentra rezagado, no solo frente a países desarrollados, sino también frente al resto de Latinoamérica (Leiton, Rassa y Rojas, 2014).
Dos de los modelos más frecuentemente usados a nivel internacional para aproximar la ETTI soberana en un país son: Nelson-Siegel (NS), una función de cuatro parámetros que aproxima el rendimiento esperado según el plazo al vencimiento; y Nelson-Siegel-Svensson (NSS), que introduce dos parámetros adicionales buscando una mayor flexibilidad.
El modelo NS Nelson y Siegel (1987) es introducido como una función simple y capaz de ajustarse a las diferentes formas que puede tomar una ETTI. El modelo es concebido partiendo de una solución a una ecuación diferencial de segundo orden y validado ajustándolo satisfactoriamente a las curvas de rendimiento de bonos del tesoro estadounidense en el período 1981-1983. Desde entonces, este modelo ha sido utilizado por diversas entidades bancarias y gubernamentales para estimar ETTI, partiendo de rendimientos históricos de activos de renta fija. El modelo se presenta a continuación:
Donde y es el rendimiento del título, τ su plazo al vencimiento y β1, β2, β3yλ son parámetros que pueden cambiar a través del tiempo.
Svensson (1994) implementa un término adicional de joroba en el modelo NS con el propósito de aumentar su flexibilidad. Posteriormente, utiliza este modelo para estimar curvas de tasas forward en Suecia en el período 1992-1994, obteniendo buenos resultados. Esta variación del modelo original es conocida como NSS y está dada por la siguiente ecuación:
En Colombia, se puede considerar el trabajo de Arango, Melo y Vásquez (2002) como una primera aproximación de la ETTI de bonos soberanos usando el modelo NS. Los autores realizan el ajuste utilizando el criterio de mínimos cuadrados y hacen comparaciones con la estimación CETES, reportada por la Bolsa de Valores de Colombia de la época. Se encuentra que el modelo NS obtiene mejores estimadores que la curva oficial. Sin embargo, no se describe el método utilizado para solucionar el problema de calibración de los parámetros.
Desde entonces, el modelo NS ha adquirido gran popularidad y es ampliamente usado por las entidades financieras colombianas. No obstante, no se le ha dado suficiente importancia a la metodología usada en la calibración del modelo y en la mayoría de ocasiones se reporta simplemente que se utiliza el criterio de mínimos cuadrados.
El proveedor de precios de mercado en Colombia, INFOVALMER, reporta que utiliza el modelo NS y obtiene sus parámetros mediante mínimos cuadrados, sin discutir el método usado para resolver el problema de minimización Infovalmer (2014). Se cuenta únicamente con una resolución de la Superintendencia Financiera de Colombia (2008) en la que se instaura el uso del modelo NS, calibrado por el método del descenso por gradiente, por parte del Sistema Proveedor de Información para Valoración de Inversiones.
Partiendo de dificultades numéricas reportadas en diversos estudios al calibrar modelos NS y NSS, Gilli et al. (2010) estudian las funciones objetivo de la estimación por mínimos cuadrados. Se encuentran múltiples mínimos locales, lo cual hace que los métodos basados en el gradiente presenten problemas y dependan altamente del punto de partida. Se notan también altas correlaciones entre los factores de los modelos que causan que los parámetros estimados por algunas metodologías pierdan identificabilidad.
Gilli et al. (2010) implementan un método heurístico para resolver el problema de minimización de errores en la obtención de los parámetros. El heurístico empleado se conoce como «differential evolution» (DE) y es aplicado a la estimación de ETTI en notas del tesoro estadounidense en el período 1985-2000. Se encuentra que DE brinda una posible solución al problema de calibración, obteniendo parámetros con mejor ajuste y de manera más consistente que los métodos basados en el gradiente.
En este sentido, el presente artículo pretende explorar alternativas a los métodos usados en Colombia para calibrar el modelo NS. Se implementan dos métodos: DE y mínimos cuadrados lineales con búsquedas incrementales en los parámetros no lineales (BI). Se pretende evaluar la consistencia del primero de ellos y usar el segundo como referencia para los errores, analizando también su viabilidad.
Adicionalmente, ambas metodologías de estimación se aplican al modelo NSS, el cual no presenta un uso tan amplio en Colombia como NS. Se busca analizar su pertinencia dentro del mercado local, sopesando su capacidad superior de ajuste con la mayor variabilidad en la estimación causada por los parámetros adicionales.
Se analizan entonces los errores obtenidos por ambos métodos de estimación y ambos modelos. Se evalúa también la dispersión de los parámetros obtenidos en ambos casos en la estimación por el método DE. Estas características se acompañan de una revisión de las curvas ajustadas y con ellas se formulan ventajas y desventajas observadas para cada modelo y método de estimación.
Lo que resta de este reporte se estructura de la siguiente forma: en la sección 2 se discuten los datos, fuentes, parámetros usados en la estimación y se describen las pruebas realizadas. En la sección 3 se presentan y analizan los resultados de las estimaciones y pruebas formuladas en la sección 3. En la sección 4 se presentan las conclusiones del trabajo y se identifican oportunidades de mejora para trabajos futuros. Se presenta, finalmente, un apéndice en el que se explican detalladamente los métodos de estimación por BI y DE.
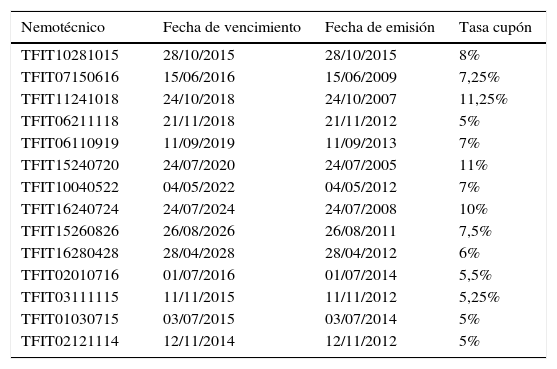
2MetodologíaLa base de datos utilizada para la realización de todas las estimaciones está conformada por las tasas de cierre diarias de los 14 bonos TES tasa fija en pesos presentados en la tabla 1. Se toman dichas tasas del sitio oficial de la Bolsa de Valores de Colombia en el período de tiempo comprendido entre 01/07/2014 y 29/09/2014 (BVC, 2014).
Estructura de pagos de los bonos seleccionados para derivar la curva de rendimientos
| Nemotécnico | Fecha de vencimiento | Fecha de emisión | Tasa cupón |
|---|---|---|---|
| TFIT10281015 | 28/10/2015 | 28/10/2015 | 8% |
| TFIT07150616 | 15/06/2016 | 15/06/2009 | 7,25% |
| TFIT11241018 | 24/10/2018 | 24/10/2007 | 11,25% |
| TFIT06211118 | 21/11/2018 | 21/11/2012 | 5% |
| TFIT06110919 | 11/09/2019 | 11/09/2013 | 7% |
| TFIT15240720 | 24/07/2020 | 24/07/2005 | 11% |
| TFIT10040522 | 04/05/2022 | 04/05/2012 | 7% |
| TFIT16240724 | 24/07/2024 | 24/07/2008 | 10% |
| TFIT15260826 | 26/08/2026 | 26/08/2011 | 7,5% |
| TFIT16280428 | 28/04/2028 | 28/04/2012 | 6% |
| TFIT02010716 | 01/07/2016 | 01/07/2014 | 5,5% |
| TFIT03111115 | 11/11/2015 | 11/11/2012 | 5,25% |
| TFIT01030715 | 03/07/2015 | 03/07/2014 | 5% |
| TFIT02121114 | 12/11/2014 | 12/11/2012 | 5% |
Todas las tasas se encuentran expresadas como nominal anual año vencido.
Fuente: Bolsa de Valores de Colombia.
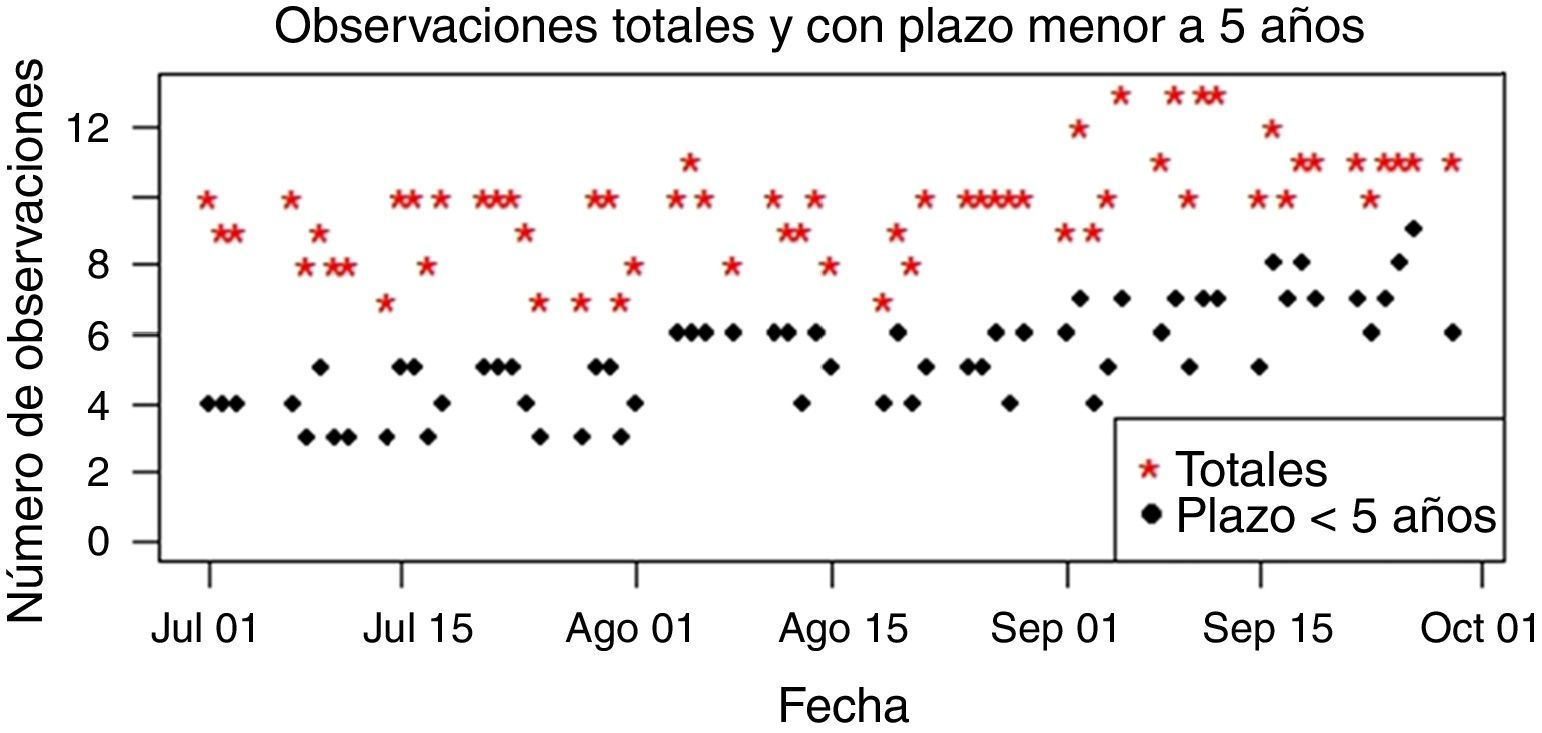
Dado que no todos los bonos se negocian diariamente, se tienen en cuenta solo los días en los que más de cinco títulos son transados. Se cuenta cada día con un número variable de observaciones de distintos bonos, para los cuales el plazo al vencimiento en años desde la fecha de observación es calculado. Adicionalmente, los modelos NS y NSS trabajan con rendimientos continuos y por lo tanto las tasas de cierre obtenidas de la BVC son llevadas a estos términos antes de realizar el ajuste.
Las observaciones tienen, finalmente, la siguiente forma:
Se realiza el ajuste de los modelos NS y NSS a estas observaciones utilizando los métodos BI y DE, explicados en el Apéndice 1. En ambos casos, el objetivo es minimizar el error cuadrático medio (ECM) entre las observaciones y el modelo ajustado. Esto da idea no solo de la bondad de ajuste alcanzada por ambos métodos, sino también de la consistencia obtenida. Se realizan también comparaciones entre los ECM de NS y NSS, se compara para cada fecha y modelo el ECM obtenido por el método BI con el ECM mínimo, máximo y promedio obtenido por el método DE en sus diez ejecuciones.
El rango de búsqueda y tamaño de paso usados para la calibración de NS por BI se presentan en (4).
Para NSS se utilizan los siguientes rangos:
Por ser un método heurístico, los parámetros del método DE son definidos mediante experimentación1. Para encontrar un buen conjunto de parámetros, se obtienen de la literatura varios conjuntos de referencia que reportan buenos resultados para problemas de dimensiones similares a este, incluyendo también el set utilizado en (4). Se selecciona una muestra de 6 días con distintos números de observaciones y se realizan estimaciones repetidas de ambos modelos para todos los días usando los diferentes parámetros.
Se encuentra que los parámetros utilizados por Gilli et al. (2011) tienen un desempeño mejor que los otros probados, obteniendo ECM menores y menos dispersos que los otros para ambos modelos. Se utilizan entonces estos parámetros para las estimaciones por DE. Sus valores se presentan en la tabla 2.
Se incluyen las siguientes restricciones en la estimación por DE para ambos modelos mediante penalización de la función objetivo.
Adicionalmente, teniendo en cuenta que DE es un método con componentes estocásticos, es necesario realizar sus estimaciones varias veces para obtener una mejor idea de su comportamiento. Así, cada estimación por DE para cada modelo y día es ejecutada diez veces partiendo desde soluciones iniciales aleatorias. Estas muestras permiten obtener información sobre la consistencia del método en términos de error y convergencia de parámetros.
Dado que el método BI da óptimos para cada conjunto de parámetros no lineales de su búsqueda, el valor del ECM obtenido para cada fecha es cercano al óptimo en los dominios discretizados definidos en (4) y (5). Entre más pequeños se hacen los cambios, se aproxima con mayor fidelidad el óptimo; sin embargo, el costo computacional crece rápidamente. Los valores de error obtenidos por este método son entonces usados como referencia (cota) para evaluar la bondad del ajuste obtenido por el método DE. Es importante, no obstante, resaltar como se expondrá en la siguiente sección, que no en todos los casos lo más conveniente es tomar la curva con el menor ECM, pues esta puede tomar formas no convencionales para ajustarse más fielmente a los datos.
La identificabilidad de los parámetros es analizada observando la dispersión de cada uno en las diez ejecuciones de DE para cada modelo y comparando sus valores con los obtenidos por BI. Se grafícan para cada fecha y modelo los valores de cada parámetro obtenidos en las 11 estimaciones realizadas (10 de DE y una de BI). Lo anterior, sumado al análisis de los ECM, permite indentificar cuándo es posible obtener ajustes similares con múltiples conjuntos de parámetros.
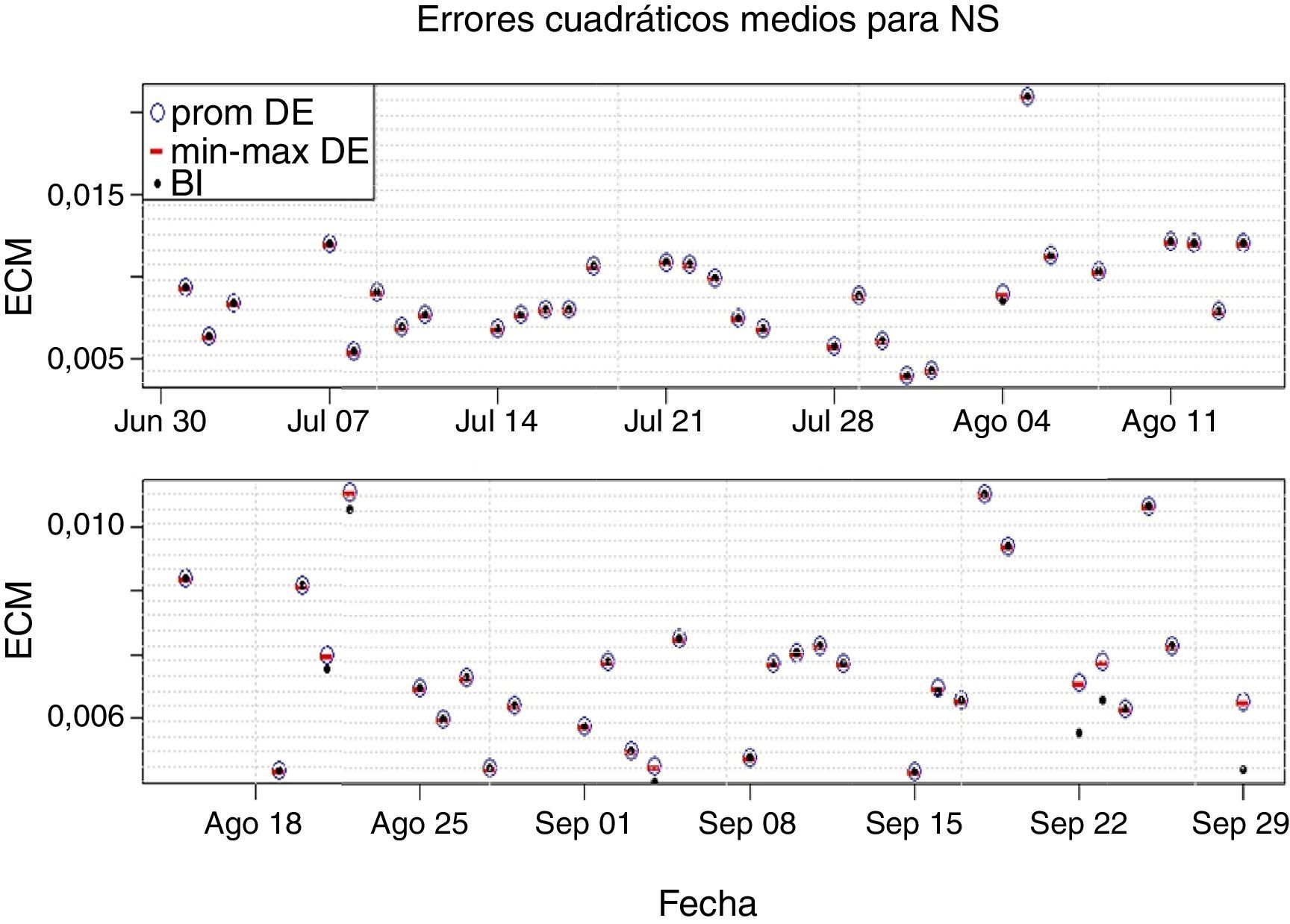
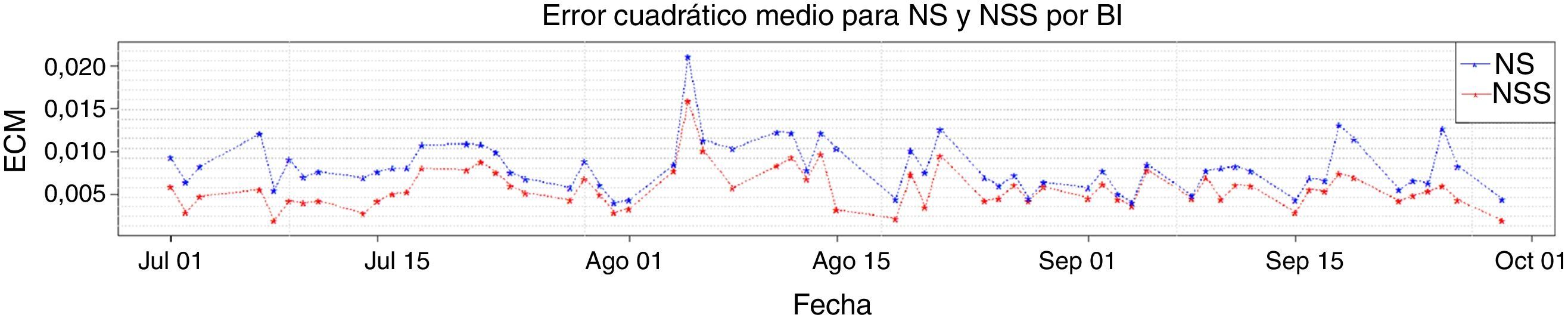
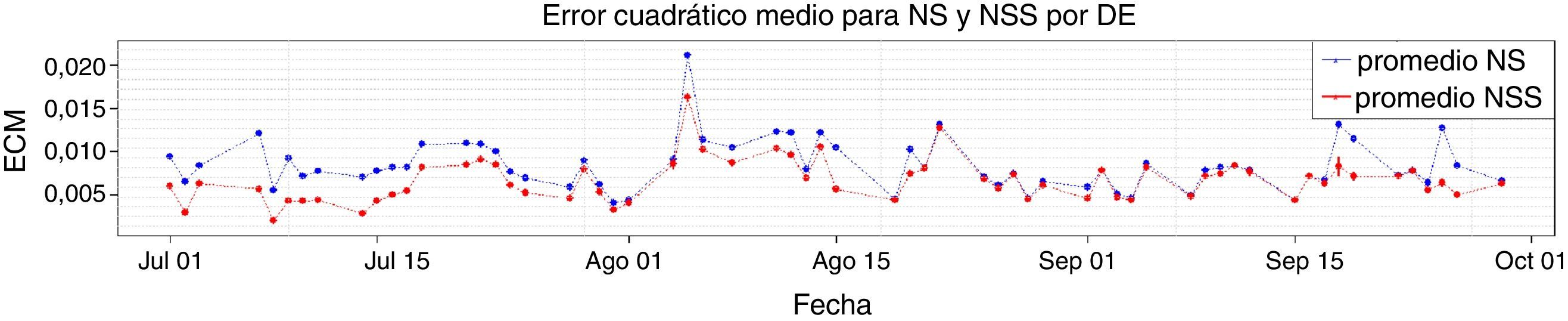
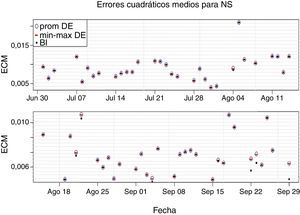
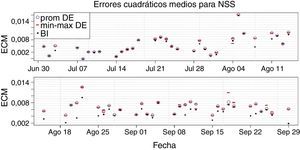
3ResultadosEn la figura 1 se presentan los ECM obtenidos para el modelo NS, comparando el mínimo, promedio y máximo obtenido en la muestra del método DE con el obtenido por el método BI.
Se puede observar que en todas las fechas los valores mínimo, promedio y máximo del método DE se encuentran aproximadamente sobre el mismo valor. Lo anterior indica que sin importar la fecha, las diez estimaciones del modelo NS por el método DE obtienen ECM indiscernibles. Este método es entonces robusto en términos de ajuste para calibrar el modelo NS.
Adicionalmente, los ECM encontrados por el método DE coinciden en la mayoría de las fechas con los obtenidos por el método BI. Lo anterior es un buen indicio dada la capacidad del método BI para aproximar ECM óptimos discutida en la sección 2. Esto indica que los ajustes obtenidos por el método DE son, generalmente, de buena calidad.
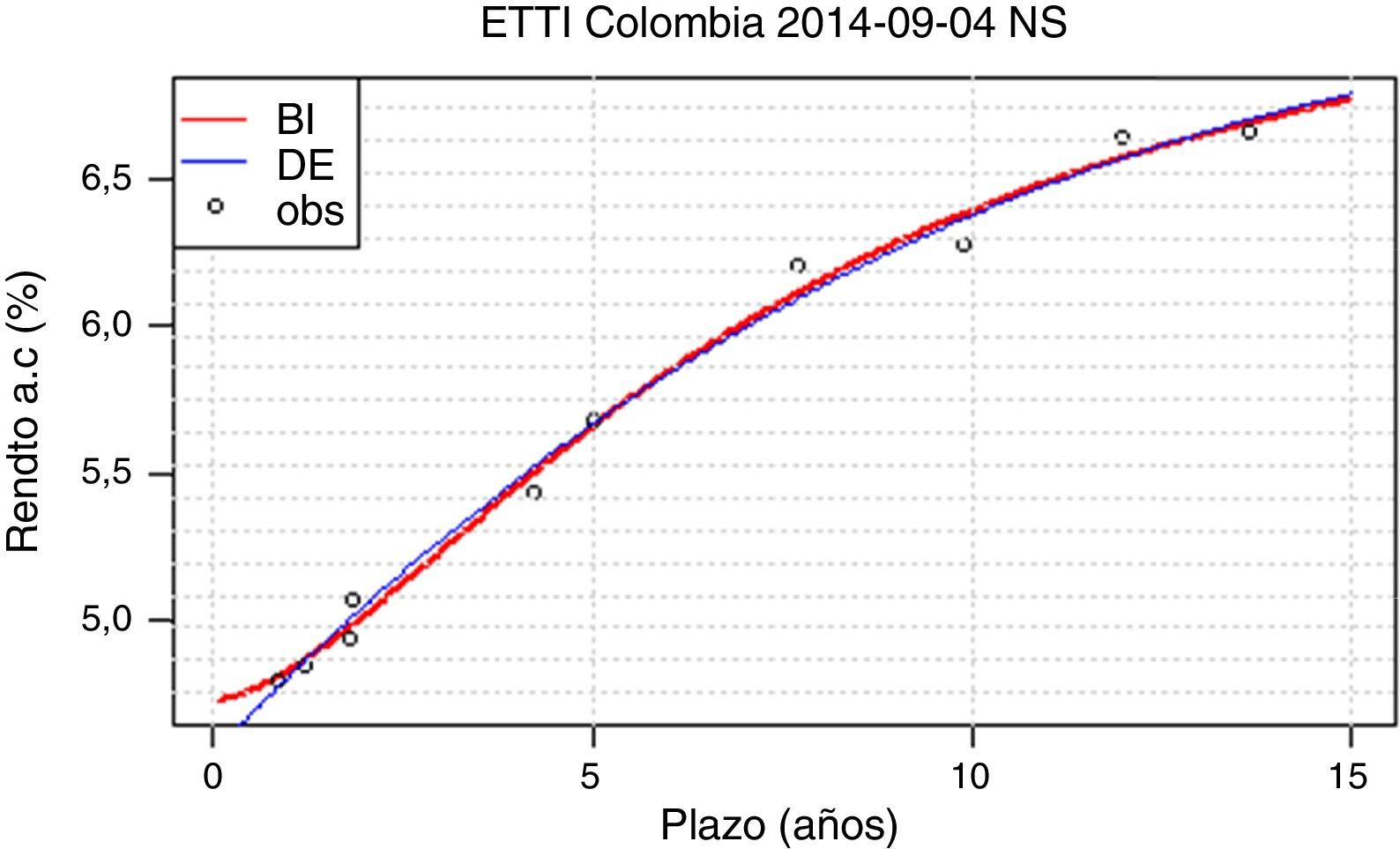
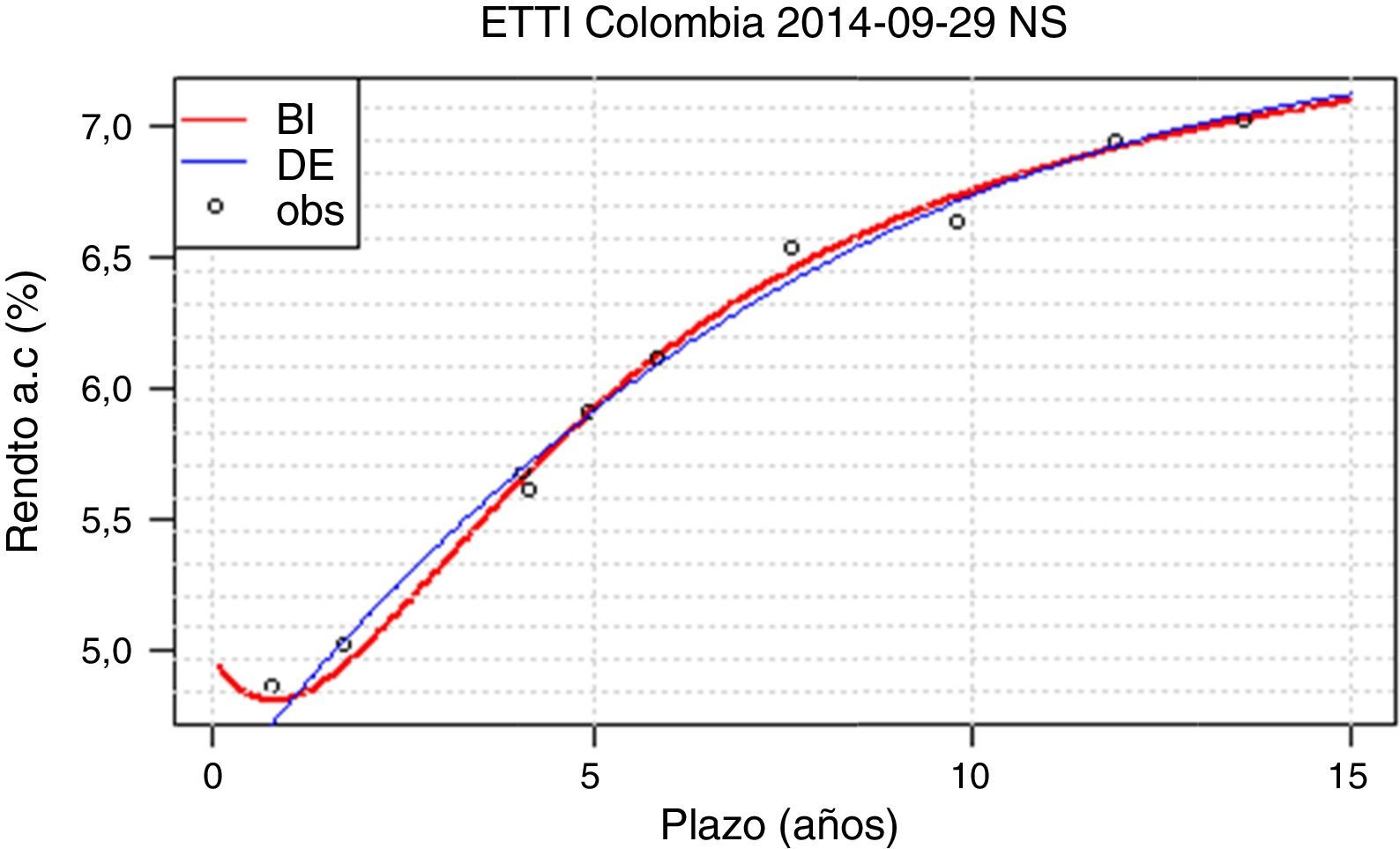
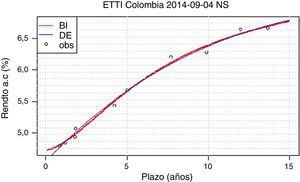
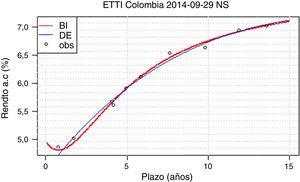
Sin embargo, se encuentra que para unas pocas fechas (sept. 4 y sept. 29, por ejemplo) el ajuste obtenido por el método BI es considerablemente mejor al obtenido por método DE. Se revisan las curvas ajustadas en las fechas con discrepancias en el ECM (para las fechas con ECM iguales las curvas obtenidas por los métodos DE y BI no presentan diferencias observables). La mayor diferencia entre las curvas ajustadas por ambos métodos es que aquellas ajustadas por el método BI son convexas en plazos cortos, mientras que el método DE genera curvas totalmente cóncavas.
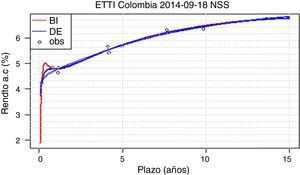
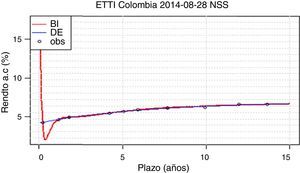
Dos ejemplos de este fenómeno se presentan en las figuras 2 y 3. En la figura 2, la convexidad de la curva del método BI en el corto plazo es leve y acorde a la realidad. En la figura 3, por el contrario, se presenta una convexidad alta y un segmento decreciente que no se presenta en condiciones de mercado normales.
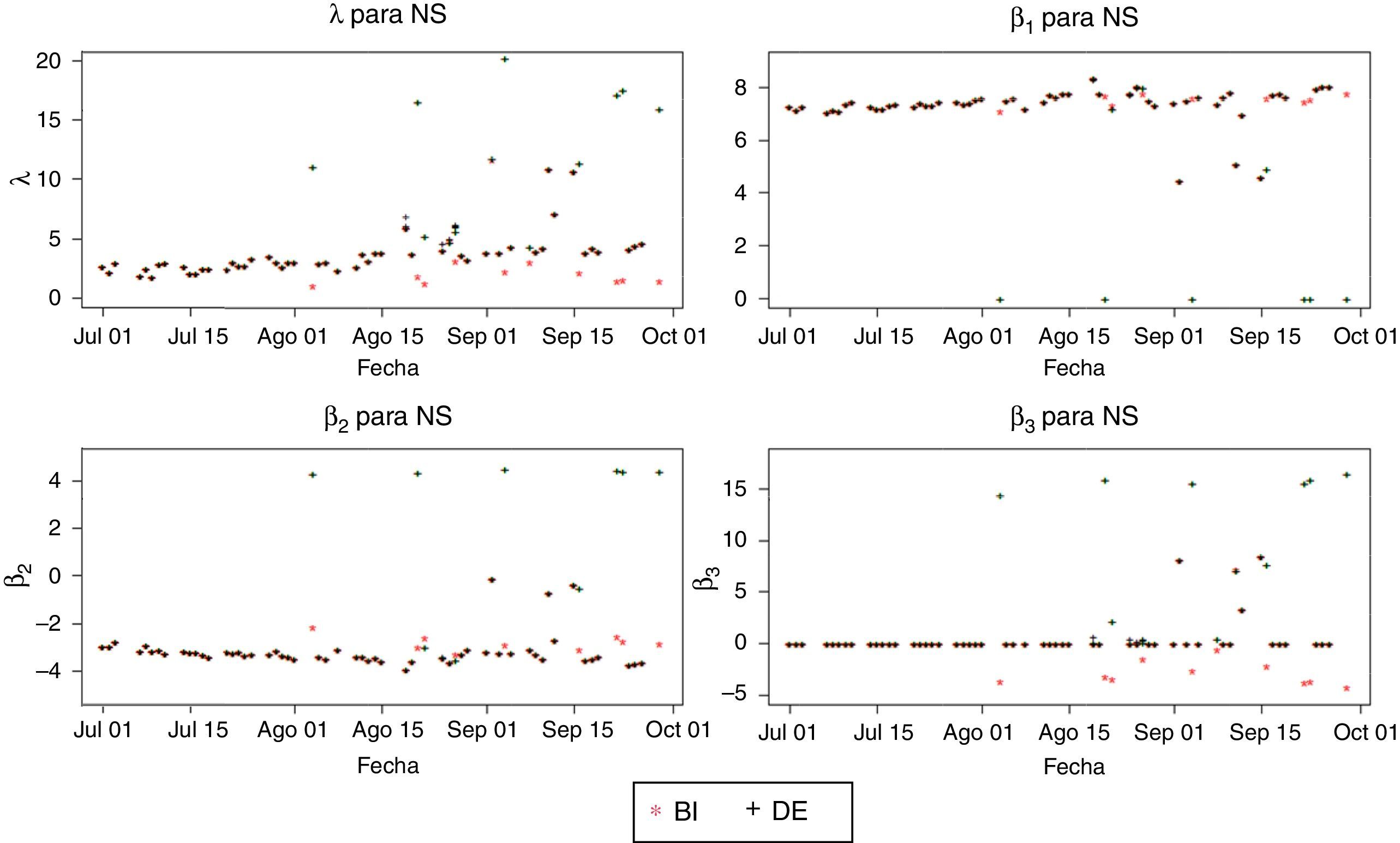
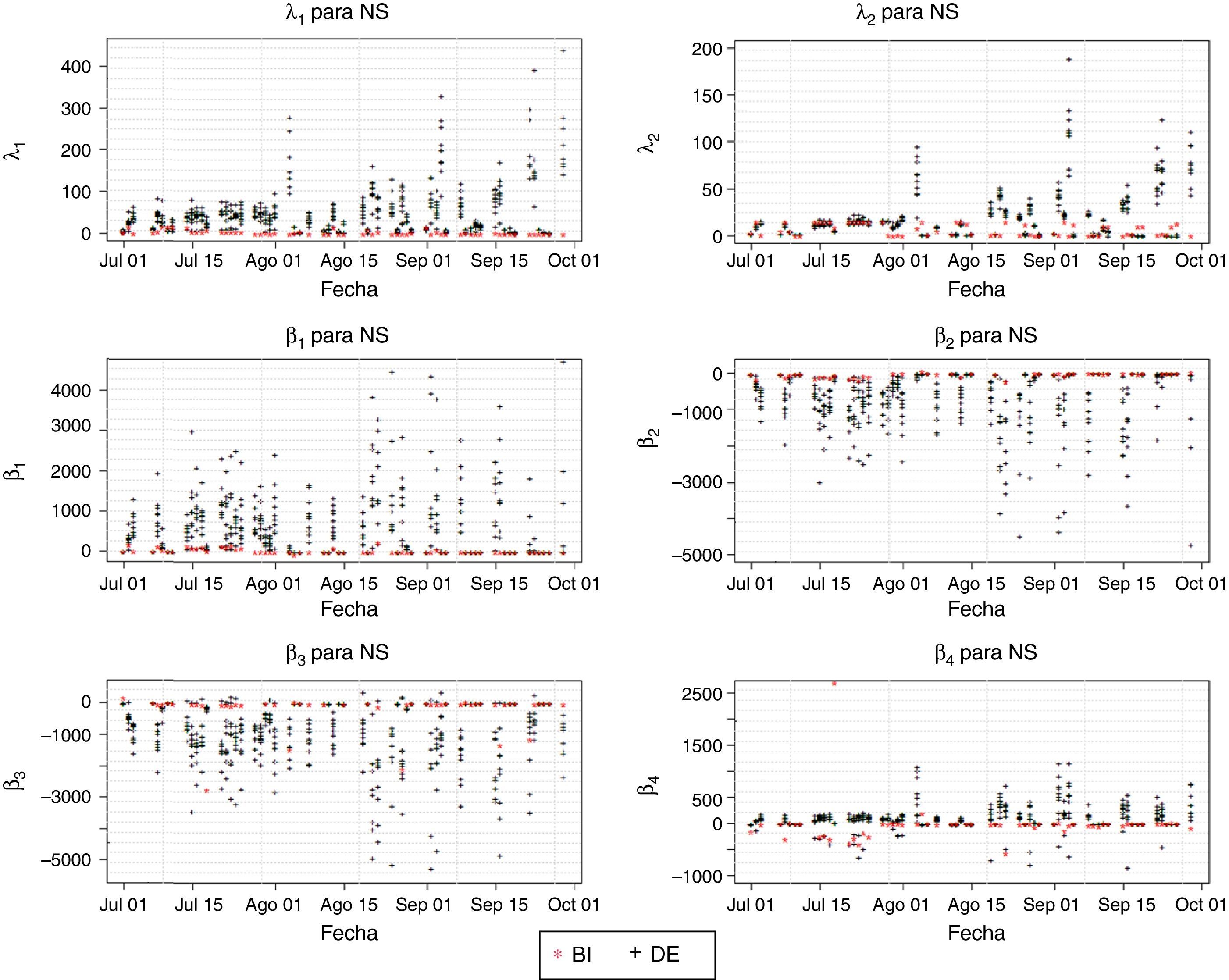
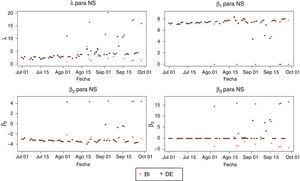
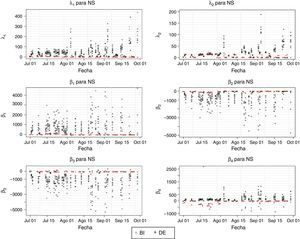
Desde el punto de vista de la robustez, se presentaron argumentos a favor del ajuste de NS por el método DE. Sin embargo, como se discute en la sección 1, puede ocurrir que diferentes conjuntos de parámetros produzcan ajustes igualmente buenos. Para evaluar la dispersión de los parámetros y comparar sus valores con los obtenidos por el método BI, se grafican para cada fecha y parámetro los diez valores obtenidos con DE y el de BI (figura 4).
En la figura 4 no se presentan variabilidades evidentes en la mayoría de los sets de diez parámetros estimados por el método DE. La mayor dispersión encontrada se da para los parámetros λ y β3 en la segunda mitad de agosto. Sin embargo, esta dispersión es pequeña.
Se puede ver también en la figura 4 que los valores obtenidos por ambos métodos para todos los parámetros son muy similares en el mes de julio. En los meses de agosto y septiembre se encuentra un gran número de días en los cuales los parámetros de los métodos DE y BI son completamente diferentes. Los días con diferencias de ajuste perceptible (figura 1) se encuentran dentro de los que presentan parámetros diferentes.
años en la muestra para todas las fechas.
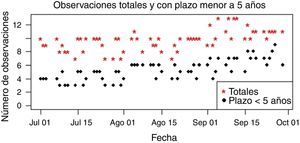
Lo anterior está relacionado con el aumento de observaciones de corto-mediano plazo que se presenta en los datos de agosto en adelante (figura 5). Las estimaciones por el método DE tienden a suavizar el comportamiento de corto plazo de la curva de rendimientos, sin capturar la inflexión presente en las curvas de BI como se veía en las figuras 2 y 3. Esta diferencia entre ambos métodos puede verse también en las discrepancias entre los valores asignados a β3 (figura 4), parámetro que acompaña el factor encargado de generar jorobas en la curva.
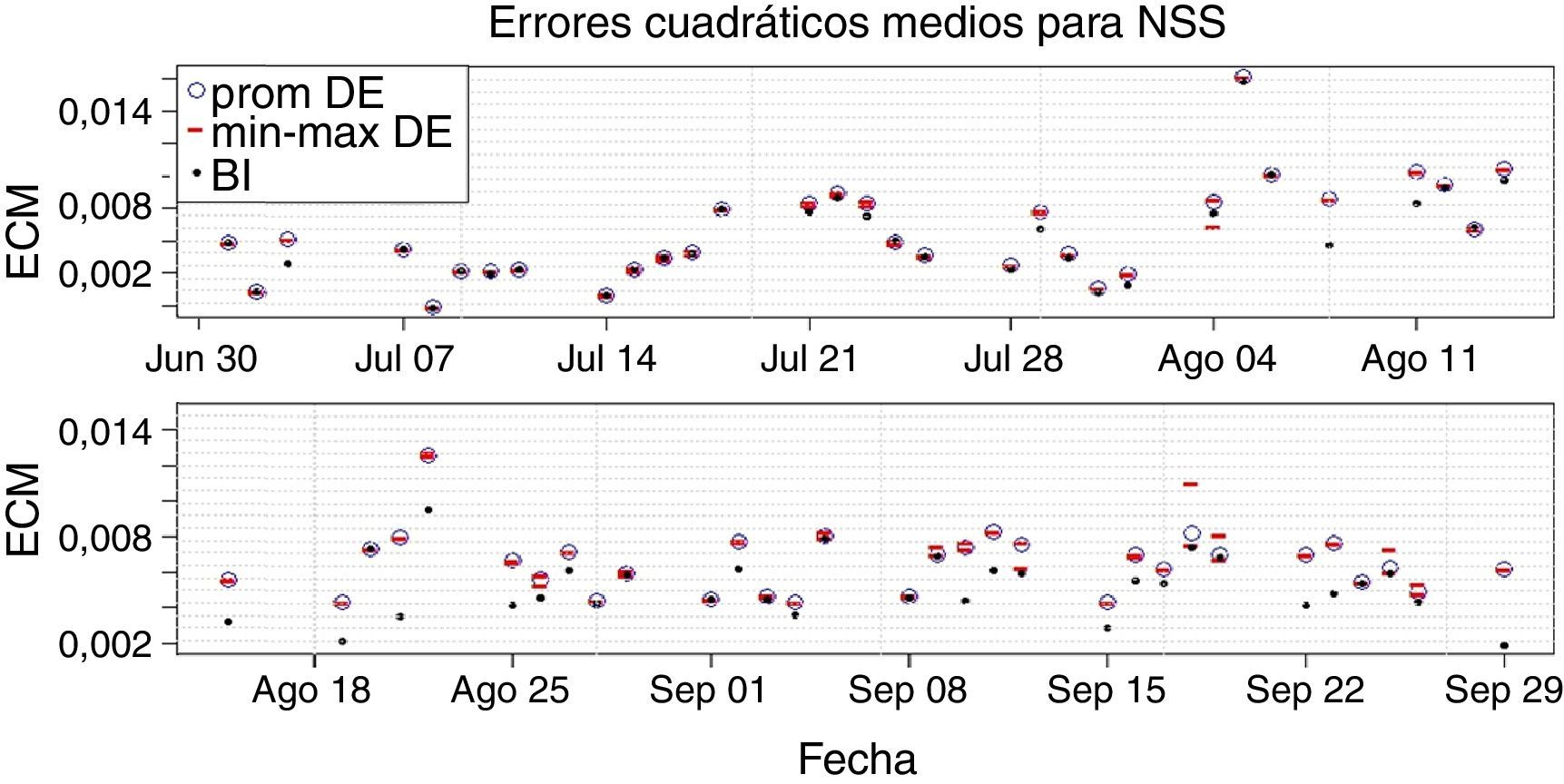
Con respecto al modelo NSS, puede verse (figura 6) que en general se obtienen ECM distintos por los métodos BI y DE. Adicionalmente, los ECM obtenidos por el método DE son más variables que en NS, presentando en algunas fechas separaciones perceptibles entre el mínimo, promedio y máximo. Las dos características anteriores se presentan con mayor intensidad en los meses de agosto y septiembre.
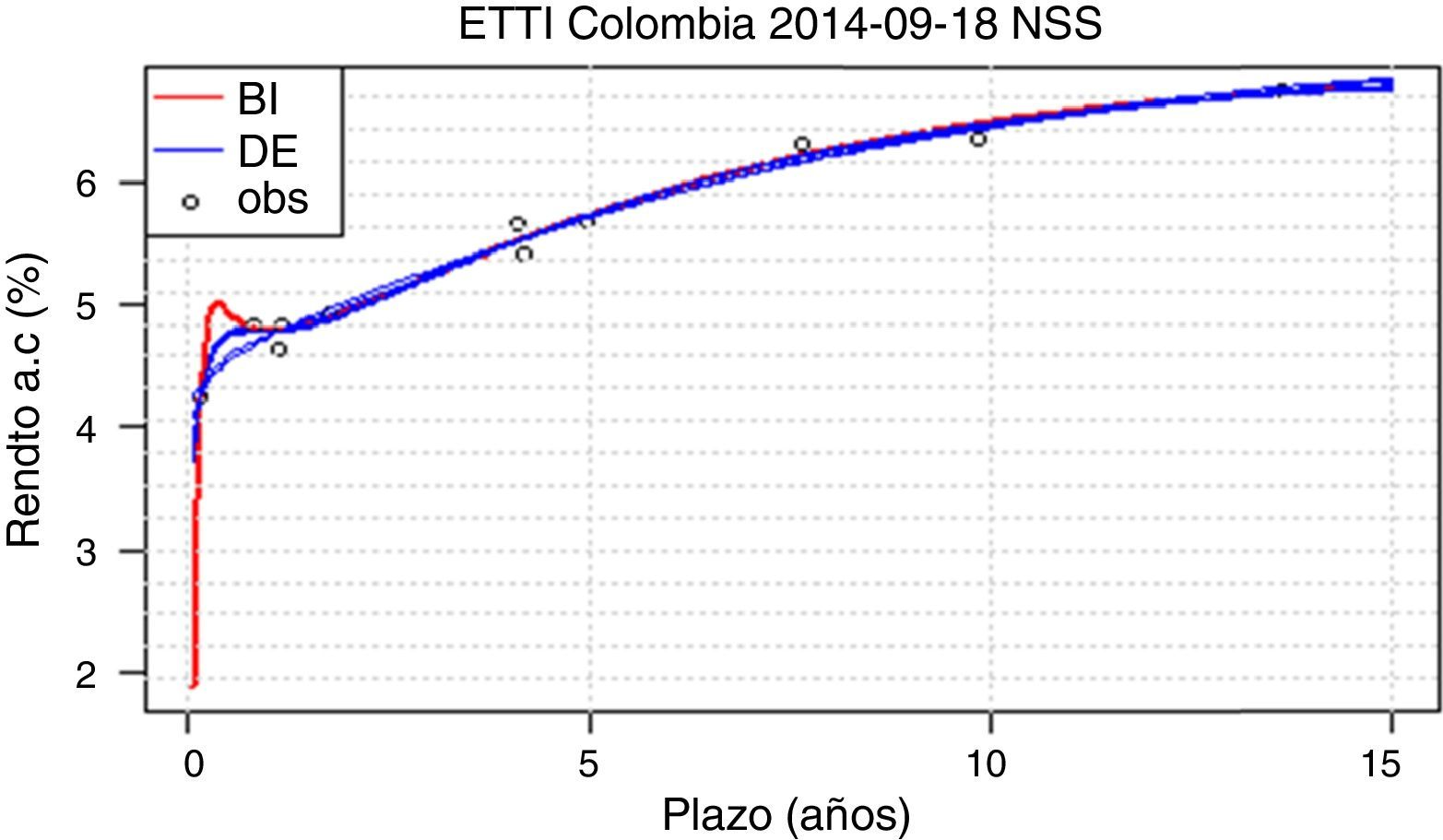
Contrario al caso visto en NS, el método DE presenta problemas de consistencia en bondad de ajuste para la calibración de NSS. Se presentan días como el 18/09/2014 con intervalos grandes para el ECM, causados por curvas de formas diferentes obtenidas en la muestra de diez calibraciones (figura 7). No se obtienen entonces resultados robustos en la calibración de NSS mediante el método DE.
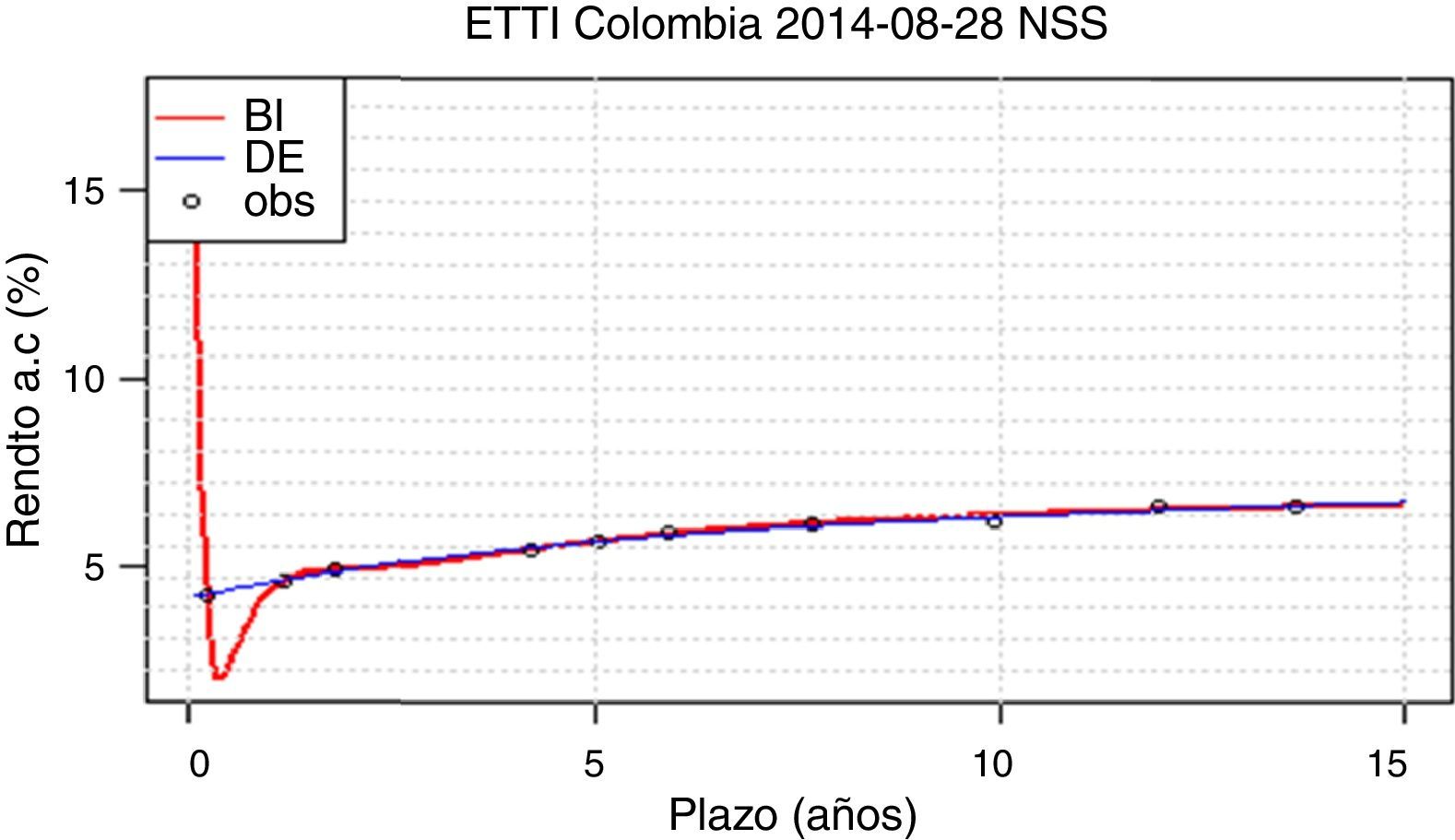
Por otra parte, el método BI presenta también problemas. Dada la ausencia de restricciones sobre los parámetros β en la estimación y la flexibilidad adicionada por los parámetros extra del modelo, se presentan casos con valores fuera de los rangos usuales, que generan un buen ajuste dentro de la muestra pero hacen que las curvas tomen formas no convencionales para plazos fuera de ella. Este es el caso en la figura 7, donde las tasas de interés para BI caen rápidamente en el corto plazo; y en la figura 8, donde las tasas toman valores equivocadamente altos.
En la figura 9 puede observarse la altísima variabilidad que se obtiene en los parámetros estimados por el método DE. Se presentan, en la mayoría de las fechas, valores que oscilan en rangos muy amplios, lo cual no se ve reflejado en el ECM. Como ejemplo, para el 29/09/2014 los valores mínimo y máximo para β2 son [−4.72×103, −1.09×10], mientras que el ECM del ajuste se encuentra en el intervalo [6.2107×10−3, 6.2268×10−3].
La anterior situación, repetida a lo largo de la mayoría las de fechas, indica que el modelo NSS es mucho más flexible que lo necesario para representar las ETTI tenidas en cuenta en el presente trabajo. Aunque se obtienen ECM ligeramente menores por ambos métodos de estimación (figuras 10 y 11), los dos términos de joroba del modelo resultan excesivos para las curvas de la muestra, haciendo que el método DE sea inestable y el BI genere formas no deseables por fuera de la muestra. Este resultado encuentra respaldo adicional en el análisis para NS, donde se encontró que para muchas fechas el término de joroba es descartado (β3≈0, figura 4).
En el presente artículo se evaluó la pertinencia de los métodos BI y DE para la calibración de los modelos NS y NSS a la ETTI soberana en Colombia en los meses de julio, agosto y septiembre de 2014. Lo anterior se hizo con el propósito de explorar alternativas a los métodos basados en el gradiente, con el fin de mejorar la calidad de estimación de los parámetros, teniendo en cuenta su amplio uso por parte de los agentes del mercado. Se analizó también la aptitud del modelo NSS para ser ajustado a la muestra tomada.
En este estudio se encontró que tanto el método BI como el DE producen buenos ajustes para el modelo NS. Los ECM encontrados por ambos métodos son bajos y coinciden en la mayoría de las fechas observadas. Se mostró también que el método DE es robusto en la calibración de este modelo, obteniendo parámetros y ECM con muy poca dispersión en ejecuciones repetidas.
En este sentido, pudo notarse que ambos métodos presentan comportamientos diferentes al complicar las formas de la curva de rendimientos con más observaciones de corto plazo. El método DE tiende a generar curvas suaves y siempre cóncavas. Por su parte, el método BI logra generar curvas con inflexión para ajustarse mejor a los datos pero en ocasiones exagera la convexidad de estas en el corto plazo.
Se considera importante resaltar que el factor de joroba adicional incorporado en el modelo NSS se encontró innecesario para los títulos y fechas considerados. Este modelo obtiene ECM ligeramente menores que NS pero presenta grandes complicaciones para ambos métodos de estimación. El método DE deja de ser robusto, obteniendo parámetros muy dispersos en sus diferentes ejecuciones lo cual hace que se generen frecuentemente curvas con formas variadas. Por no incorporar restricciones, BI permite comúnmente que β1, β2, β3, y β4 tomen valores que generan ECM muy bajos pero causan formas no deseadas para la curva por fuera de la muestra.
Adicionalmente, un resultado interesante con respecto a NSS es que el ajuste obtenido por el método DE es generalmente cercano al del método BI en términos de ECM (figura 6). Esto indica que a pesar del problema de identificabilidad que se presenta de manera particular para el mercado colombiano en el período de la muestra, el metaheurístico logra obtener curvas que se ajustan bien a las observaciones. Lo anterior, sumado a su posibilidad de incorporar restricciones sobre los parámetros para evitar formas indeseables lo hace un método más adecuado que el BI para ajustar el modelo NSS.
Desde el punto de vista de futuras investigaciones, resultaría interesante realizar pruebas de calibración del modelo NSS mediante el método DE en mercados que cuenten con más observaciones y curvas con formas más complejas. Es posible que estas dos características restrinjan más estrictamente los valores de los parámetros necesarios para un buen ajuste, reduciendo el problema de identificabilidad. Estados Unidos, por su gran número de títulos en circulación para corto, mediano y largo plazo; y su eficiencia como mercado, podría verse como un buen candidato para la realización de las pruebas.
En dichos trabajos, se debería también analizar a fondo la causa de las discrepancias de corto plazo obtenidas entre el modelo NS calibrado por los métodos DE y BI. Deben realizarse pruebas adicionales sobre las fechas con discrepancias utilizando parámetros y rangos iniciales diferentes, así como muestras más grandes. La influencia de las restricciones utilizadas para DE en este fenómeno debe ser también evaluada (tabla 3).
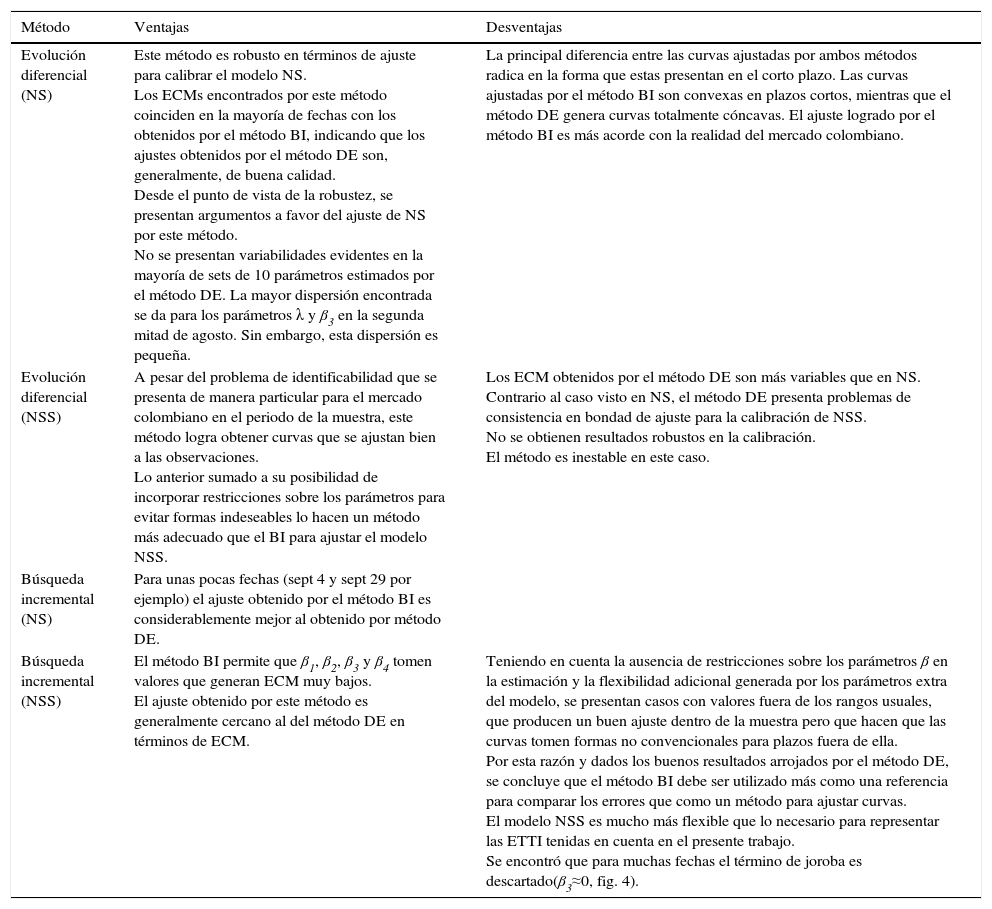
Ventajas y desventajas de cada uno de los métodos en función de los modelos NS y NSS
| Método | Ventajas | Desventajas |
|---|---|---|
| Evolución diferencial (NS) | Este método es robusto en términos de ajuste para calibrar el modelo NS. Los ECMs encontrados por este método coinciden en la mayoría de fechas con los obtenidos por el método BI, indicando que los ajustes obtenidos por el método DE son, generalmente, de buena calidad. Desde el punto de vista de la robustez, se presentan argumentos a favor del ajuste de NS por este método. No se presentan variabilidades evidentes en la mayoría de sets de 10 parámetros estimados por el método DE. La mayor dispersión encontrada se da para los parámetros λ y β3 en la segunda mitad de agosto. Sin embargo, esta dispersión es pequeña. | La principal diferencia entre las curvas ajustadas por ambos métodos radica en la forma que estas presentan en el corto plazo. Las curvas ajustadas por el método BI son convexas en plazos cortos, mientras que el método DE genera curvas totalmente cóncavas. El ajuste logrado por el método BI es más acorde con la realidad del mercado colombiano. |
| Evolución diferencial (NSS) | A pesar del problema de identificabilidad que se presenta de manera particular para el mercado colombiano en el periodo de la muestra, este método logra obtener curvas que se ajustan bien a las observaciones. Lo anterior sumado a su posibilidad de incorporar restricciones sobre los parámetros para evitar formas indeseables lo hacen un método más adecuado que el BI para ajustar el modelo NSS. | Los ECM obtenidos por el método DE son más variables que en NS. Contrario al caso visto en NS, el método DE presenta problemas de consistencia en bondad de ajuste para la calibración de NSS. No se obtienen resultados robustos en la calibración. El método es inestable en este caso. |
| Búsqueda incremental (NS) | Para unas pocas fechas (sept 4 y sept 29 por ejemplo) el ajuste obtenido por el método BI es considerablemente mejor al obtenido por método DE. | |
| Búsqueda incremental (NSS) | El método BI permite que β1, β2, β3 y β4 tomen valores que generan ECM muy bajos. El ajuste obtenido por este método es generalmente cercano al del método DE en términos de ECM. | Teniendo en cuenta la ausencia de restricciones sobre los parámetros β en la estimación y la flexibilidad adicional generada por los parámetros extra del modelo, se presentan casos con valores fuera de los rangos usuales, que producen un buen ajuste dentro de la muestra pero que hacen que las curvas tomen formas no convencionales para plazos fuera de ella. Por esta razón y dados los buenos resultados arrojados por el método DE, se concluye que el método BI debe ser utilizado más como una referencia para comparar los errores que como un método para ajustar curvas. El modelo NSS es mucho más flexible que lo necesario para representar las ETTI tenidas en cuenta en el presente trabajo. Se encontró que para muchas fechas el término de joroba es descartado(β3≈0, fig. 4). |
Elaboración propia.
Se seleccionaron los parámetros correspondientes al método DE debido a que este permite garantizar los siguientes aspectos:
• El cubrimiento de buena parte del espacio de posibles soluciones, ya que se dispone de un tamaño de población grande.
• Un paso diferencial “f” pequeño con lo cual no se dan saltos muy grandes entre individuos y por tanto la búsqueda es más exhaustiva.
• Un número de generaciones grande, que proporciona un tiempo prudente de convergencia al método.