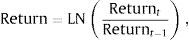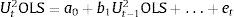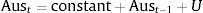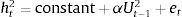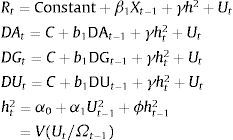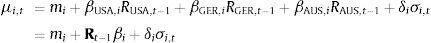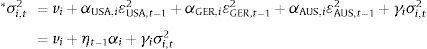The study of the stock market in a country and the understanding of the influence of stock market crashes within and across the markets has been the subject matter of many researches, academicians and analysts during recent times. In this study we investigate the mean-volatility spillover effects that happen across international stock markets. The study, by taking into consideration the stock market returns based on various indices, investigates the mean-volatility spillover effects using the GARCH in Mean model for the period January 2002 to December 2011. The GARCH-M model seeks to provide useful insights into how information is transmitted and disseminated across stock markets. In particular, the model examines the precise and separate measures of return spillovers and volatility spillovers. The analysis provides the evidence of strong mean and volatility spillover across some stock exchanges.
El estudio del mercado de valores de un país y la comprensión de la influencia de los desplomes de la bolsa en y a través de los mercados ha sido el objeto de muchas investigaciones de académicos y analistas en los últimos tiempos. En este estudio se investigan los efectos de derrame de media volatilidad que se producen en los mercados de valores internacionales. El estudio, teniendo en cuenta la rentabilidad del mercado de valores basada en varios índices, investiga los efectos de derrame promedio de volatilidad utilizando el modelo GARCH en el período comprendido entre enero de 2002 y diciembre de 2011. El modelo GARCH-M pretende proporcionar ideas útiles sobre cómo se transmite y difunde la información a través de los mercados de valores. En particular, el modelo examina las medidas precisas y separadas de los efectos de excedentes de retorno y de volatilidad. El análisis proporciona la evidencia de una media y volatilidad fuertes a través de algunas bolsas de valores.
On October 19th, 1987 the Dow Jones Industrial Average (DJIA) stood at 1738 points. It fell 508.32 points, which constituted 22.6% of the value of the entire stock exchange. Over 600 million shares had been traded and the value of the stocks on the New York Stock Exchange had fallen by over $750 million. This event trigged stock market crashes all over the world. By October end the stock markets indices like Hang Seng had fallen by 45.5%, Standard and Poor ASX 200 fell by 41.8%, and the FTSE 100 fell by 26.45%.
Academicians and economists warned that it will be many years before the world economies bounce back. But by the end of 1987 the DJIA was moving slightly upwards contrary to what many renowned economists of the world collectively predicted. By February 2, 1994 the DJIA had reached an all time high post the 1987 crash. By March 29, 1999 it has for the first time closed above 10,000 points.
On October 9, 2007, the Dow Jones Industrial Average index reached an all time high of 14,164 points. By January 2, 2009 it was 13,332 and by March 9, 2009, the Dow Jones average had reached a bottom of 6547. The Dow Jones had declined by 7,617 points, which constituted 53.8% below its October 2007 high. It has since recovered much of the decline, exceeding 12,000 during most of 2011, and occasionally reaching 13,000 in 2012. Below are given some important high and low points of various national stock market indices during the same period (Table 1).
High and low of major index between October 2007 and March 2009.
| Indices | Highest points during 2007 | Date | Lowest points during 2009 | Date |
| BSE Sensex | 20,238.16 | 30-Oct-2007 | 8047.17 | 6-Mar-2009 |
| Hang Seng | 31,958.40 | 30-Oct-2007 | 11,344.604 | 9-Mar-2009 |
| FTSE 100 | 6754.10 | 13-Jul-2007 | 3460.714 | 9-Mar-2009 |
| NIKKIE | 18,300.40 | 26-Feb-2007 | 7021.284 | 10-Mar-2009 |
| BOVESPA | 64,609.00 | 12-Nov-2007 | 37,105.00 | 2-Mar-2009 |
| DAX | 8151.57 | 13-Jul-2007 | 3588.894 | 9-Mar-2009 |
It is seen that during the same time period stock market indices all over the world also decreased. The above two instances clearly states that there exists a substantial degree of interdependence among national stock markets. Especially, after the stock market crash of 1987, the interdependence between international stock markets has increased (Eun & Shim, 1989). Unexpected developments in international stock markets have become important news events that influence domestic stock markets as news revealed in one country is perceived as informative to fundamentals of stock prices in another country. This is attributed to real productive and financial linkage of economies and also suggests that overreaction and noise trading are transmissible across borders. Moreover with the development in the liberalization of capital movements and the securitization of stock markets, international financial markets have become increasingly interdependent. Advanced computer technology and improved world-wide networking have improved and quickened the processing of “News”. This has led to domestic markets to react promptly to new information from international markets. Perhaps as a result of this, volatility has been closely synchronized across national stock markets.
Several times during the past few years the markets have taken investors on a roller coaster ride. During these volatile times many investors get spooked and begin to question their investment strategy. This is especially true for beginner investors who often can be tempted to pull out of the market altogether and wait on the sidelines until it seems safe to dive back in. If there is one safe and wise prediction about investing, it is that the future will bring both frightening drops and gratifying rises.
The extent to which stock price indices in developed and emerging countries move together is important to the individual investor, the policy maker and the forecaster, the researcher and more recently by investment banks that are specializing in new financial innovations to minimize risk. Studies have revealed that more than half of the movement in the typical developed country's stock price index is unique to the country, but this percentage varies widely between them. Also, the more open the stock market is to capital flows, the higher will be the covariance between that market and the markets in other countries. Special linkages brought about by financial ties, free capital movements and trade strengthens the common movement of stock prices (Ripley, 1973).
The thing to realize is that market volatility is inevitable. It's the nature of the markets to move up and down over the short term. The ups and downs of the financial markets are closely watched by the society with great interest. Public interest in market movements has intensified in the last decades more so after the global financial crisis of 2007. When there is a sharp decline in the stock prices it rings alarming bells all over the world and may confuse a layman who is new to the world of financial markets. He may not even be aware how this may affect him.
Trying to time the market over the short term is extremely difficult, some would say impossible. One solution is to maintain a long-term horizon and ignore the short-term fluctuations. For many investors this is a solid strategy. But even for long term investors there are still things you should know about volatile markets and steps you can take to help weather market volatility. Ideally, what traders would like to know is what the future volatility is going to be. If we knew what the future volatility would be, we could make a fortune quite easily. The fact is that volatility exists and investors must develop ways to deal with it.
The last two-decade or so have witnesses an unprecedented explosion in the number and variety of financial instruments. Although these financial innovations have been widely accepted by the markets, as the users clearly feel that they will benefit from using these instruments. In recent years the benefits of these innovations have raised a lot of questions. The feeling is widespread, becoming stronger by almost daily horror stories in the financial pages of the world. It can be stated that financial innovations are a major cause for stock market volatility. As a consequence, in recent year's innovative financial diversification and cross-market returns correlation have been the subject of much debate and research and the main focus has been in minimizing volatility spillover effects from one market to another.
The degree of interdependence among major national stock markets can be noticed by examining the nature and magnitude of mean and volatility spillovers in these markets. As the equity markets trade on different time zones, it is possible to examine whether volatility is transmitted across markets. Mean return in security analysis can be defined as the average expected return of a given investment or portfolio, when all possible outcomes are considered. The transmission of volatility has been commonly termed as “Volatility Spillover”. The transmission of mean returns has been commonly termed as “Mean Spillover”. Volatility spillovers can be viewed from two angles. Own volatility spillovers are used to indicate a one way causal relationship between past volatility shocks and current volatility in the same market. Cross volatility spillovers is used to indicate a one-way causal relation between past volatility in one market and current volatility in another market.
An international asset-pricing model can incorporate correlation between stock returns in different countries. Another possible reason for international correlation of price changes is market contagion. Under market contagion scenario, speculative trading and noise trading may occur in the international context; price movements driven by fads and a herd instinct may be transferable across borders. This study can further help in understanding and providing information in building good asset-pricing models.
The objective of this paper is to study the inter-market volatility and whether there is an association between volatility in one market and volatility in another market. In other words the study aims to show the extent to which security price changes in one market influence the opening prices in the next market to trade; and whether changes in price volatility in one market are positively related to changes in price volatility in the next market to trade. Also the influences of volatility surprises in one-market over the volatility returns in other markets are examined. This is because spillovers of returns across markets have important implications for portfolio choice and risk management.
This study assumes much significance due to the fact that, markets tend to move together at exactly at those times when investors do not want them to (i.e., when volatility is high) thus reducing the benefits of international portfolio diversification. Thus analyzing volatility spillover among markets would help investors to seek appropriate strategy to make limit his risk from international diversification portfolio.
2Previous researchOne of the important issues in stock market investments have been the all-inclusive concept of inter-market information spillovers. A collection of important empirical studies related to the interdependence among national stock markets has been brought out.
Agmon (1972) studied the lead lag relationship between four major stock markets. He stated that the one market hypothesis implies that all potential gains international as well as internal, diversification are already reflected in the current prices of capital assets traded on the world market. His findings proved that there was substantial amount of relationship among the stock markets of UK, US, Germany and Japan.
Panton, Lessig, and Joy (1976) investigated the structure of twelve of the major international equity markets co-movements. Their analysis stated that markets that are well-developed and open to international capital flows have high degree of similarity than other markets.
Hilliard (1979) focused on the degree of interdependence and causality among national stock markets. His study was mainly related in examining the structure of international equity market indices during a world-wide crisis. His findings stated that intra-continental prices move simultaneously, even in the context of hourly fluctuations, with respect to inter-continental prices, most do not seem to be closely related and he therefore dismissed the question of lead and lags.
Eun and Shim (1989) investigated the international transmission mechanism of stock market movements by estimating a nine-market vector auto regression (VAR) system. His emphasis was on understanding the mechanism by which innovations in one stock market are transmitted to other markets over time. His evidence indicated that a substantial amount of interdependence exists among national stock markets. Moreover, the US stock market was found to be the most influential in terms of its capability of accounting for the error variances of other markets. His analysis supported the view of informational efficient international stock markets.
Hamao, Masulis, and Ng (1990) studied the short-run interdependence of prices and price volatility across three major international stock markets, i.e., New York, Tokyo, and London. They used the ARCH family of statistical models in their analysis. They examined the transmission mechanism of the conditional first and second moment's in common stock prices across international stock markets and allowed for changing conditional variance as well as conditional mean returns. They found that spillover effects from foreign markets on the conditional means of the close-to-open return (which reflect effects on the opening prices in the domestic market) are predicted by international asset pricing models, while spillover effects on conditional means of the open-to-close return (which reflect effects on prices in the domestic market after the opening of trading) are predicted not to occur. Their evidence stated that price volatility spillovers from New York to Tokyo, London to Tokyo, and New York to London was observed.
King and Wadhwani (1990) article provides an excellent understanding of the subject of price volatility. Their study investigated why, in October 1987, almost all stock markets fell together despite widely differing economic circumstances. They constructed a model in which “contagion” between markets occurred as a result of attempts by rational agents to infer information from price changes in other markets. This provides a channel through which a “mistake” in one market can be transmitted to other markets. Their conclusion was based on the following principle, which is “A world in which investors infer information from price changes in other countries is also one in which a ‘mistake’ in one market can be transmitted to other markets”. Moreover, they suggested that an increase in volatility lead in turn to an increase in the size of the contagion effects which was depicted by the rise in the correlation between markets just after the crash. Basing on their evidence, they categorically stated that it would have the important implication that volatility can, in part, be self-sustaining.
Liu and Pan (1997) studied the mean return and volatility spillover effects from the US and Japan to four Asian stock markets, including Hong Kong, Singapore, Taiwan, and Thailand. They used a GARCH model in their study. Their conclusions indicated that there was instability in the international mean return and volatility transmissions, and the spillover effects increase substantially after the October 1987 stock market crash.
Engle and Patton (2001) harped on the theme that a volatility model must be able to forecast volatility, which this is the central requirement in almost all-financial applications. Their conclusion was that pronounced persistence and mean-reversion, asymmetry such that the sign of an innovation also affects volatility and the possibility of exogenous or pre-determined variables influencing volatility. Chan, Lien, and Weng (2008) studied causal relationship between Hong Kong and US financial markets, using band spectrum regression techniques to examine the dynamic properties of the interactions between capital markets. They found that before the Asian financial crisis there is a feedback relationship between the two markets which is driven by long cycles (with low frequencies), while post-911 periods, there is a one-way causality from the US market to the Hong Kong market.
Li (2007) examines the linkages between the two emerging stock exchanges in mainland China and the established markets in Hong Kong and in the US by a multivariate GARCH approach. The results indicated no evidence of a direct linkage between the stock exchanges in mainland China and the US market, but found evidence of uni-directional volatility spillovers from the stock exchange in Hong Kong to those in Shanghai and Shenzhen. The implication of the weak integration is that by investing in Chinese market overseas investors will benefit from the reduction of diversifiable risk.
Several empirical regularities can be spotted from the research undertaken in this field. It can be said that the volatility of stock price is time varying and when volatility is high, the price changes in major markets tend to become highly correlated. Moreover correlation in volatility and prices appear to be causal from the United States to other countries; and lagged spillovers of price changes and price volatility are found between major markets.
It is with setting, this paper proceeds to examine the direction and extend of mean spillovers and volatility spillovers across five stock markets. The rest of the paper is organized as follows: Section 3 explains the research method and describes the data used in the study, Section 4 describes the model and discusses the results, Section 5 concludes.
3Research method and data descriptionIn this study, we adopt one model GARCH-M to analyze a financial time series data to see for volatility spillover effects. This paper aims at investigating the issue of volatility spillovers across national stock markets for the period 2001 to 2011. This study is mainly based on secondary data that have been collected from the database on Indian economy maintained by Reserve Bank of India. To test for the presence of volatility spillovers a return series is required which can be sampled. The study undertaken uses the Weighted Average Stock Price Index as a measure of stock market return. Consequently the return series for each market is chosen on the basis of the market index which provides an historical daily time-series.
Five globally-traded stock market indices were selected to test the versatility and robustness of the approach for mean and volatility spillover. The S&P ASX 200 for Australia, S&P 500 composite for the US, BOVESPA for Brazil, DAX 30 performance for Germany and HANG SENG for Hong Kong are examined in our empirical experiment. The stock indices data used in this paper are daily and are obtained from DataStream respectively. The methodology requires matched observations between all the markets. Consequently, the sample period commences from January 1st, 2002 to December 30th, 2011. For brevity, the original data are not listed in the paper, and detailed data can be obtained from the sources. For the sake of facilitating forecast and portfolio optimization, we choose the daily excess returns of these indices and exchange rates as forecast variables.
In any time series data the volatility or changes in some periods may be due to some event. To neutralize the impact of this event on the time series we include dummy variables. A dummy variable can take the value of either 0 or 1. The transformation of indices to change in logarithms has the advantage that it eliminates most first-order serial correlation and produces series that are of greater theoretical interest. Also the data are transformed into elasticity, which are better suited in analyzing and interpretations.
The volatility of returns in stock market has a significant influence on the volatility of returns in other stock markets and there exists a causal relationship. This is because volatility in one market induces volatility in another market, through a lead-lag relationship. This happens as the trading hours between the markets are not common when measured in Greenwich Mean Time (GMT). When measured in GMT the various markets open and close at different times on a 24hour time horizon.
When measured in GMT, the US market is 5 and ½ hours ahead of the Hong Kong market, 7 and ½ hours ahead of Australia and the other time lag between markets can be seen from the figure above. The problem between measuring volatility spillovers between different time zones as well as use of the closing price of the indices any common influence from the one market will first reveal itself in the next opening market and then in the next succeeding market. However this effect can happen through an association between concurrent day volatility between the two markets when they are open at the same time. Therefore a common stock market factor will induce an association between current day markets of two stock exchanges. Therefore it is advisable to use intra-day data sampled at the open and close of each market. This would help in accurately distinguishing between effects. But as these data were not available for the study we did not use them. The advantage of using closing data as stated earlier is that spillover effects may be the strongest at the opening prices. As closing prices incorporate noise generated during the trading period, the use of closing prices provides a stronger test for spillover effects.
4Model description and empirical results4.1Model descriptionThe empirical results found while running the GARCH (1,1) M-model for estimating the volatility spillovers from the stock markets are presented below. First a preliminary statistics of the data are analyzed. Secondly, a detailed analysis of the results obtained in the model is undertaken. Finally we see whether the concluded tests present any serious evidence against the estimated GARCH (1,1) M-model.
All indices are based on local currencies and do not include dividends. The returns for each market are calculated by the following formula.
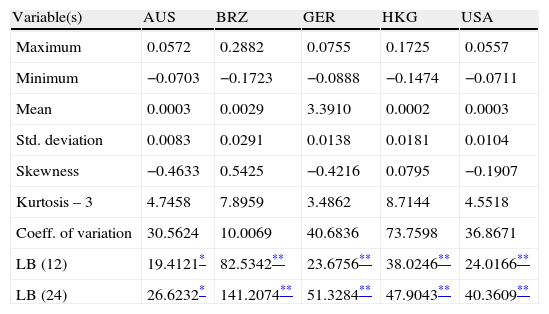
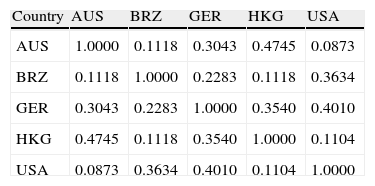
where LN=natural log to the base e.The summary statistics for the daily returns of the five national stock markets are reported in Table 2. The means of returns are positive and range between 0.0002 (Hong Kong) and 0.0029 (Brazil). The standard deviation of returns ranges between 0.0083 for (Australia) and 0.0291 for (Brazil). This indicates that the Brazilian stock market is the most volatile and the Australian market is the least volatile. The high excess kurtosis in these markets suggests that their daily return series have a fat-tailed distribution. The Ljung–Box (LB) Q statistic for the returns are highly significant at the five percent level for all markets except Australian, which indicates the presence of serial correlations and suggesting the presence of time-varying volatility. Thus the preliminary analysis of the data suggests the use of a GARCH model in capturing the fat-tails and time-varying volatility found in these stock return series. The correlations of returns range from a high of 0.4745 between Hong Kong and Australia, to a low of 0.0872 between the USA and Australia. Since all values are less than 0.8 the problem of multicollinearity will not be encountered (Tables 3 and 4).
Actual exchange trading hours.
| Country | Trading hours (eastern standard time) | Major index |
| Australia | 09:15a.m. to 16:12p.m. | S&P/ASX 200 |
| Brazil | 10:00a.m. to 17:00p.m. | BOVESPA |
| Germany | 09:00a.m. to 17:30p.m. | DAX |
| Hong Kong | 09:20a.m. to 16:00p.m. | HANG SENG |
| US | 09:30a.m. to 16:00p.m. | S&P 500 |
Preliminary statistics on the stock market returns.
| Variable(s) | AUS | BRZ | GER | HKG | USA |
| Maximum | 0.0572 | 0.2882 | 0.0755 | 0.1725 | 0.0557 |
| Minimum | −0.0703 | −0.1723 | −0.0888 | −0.1474 | −0.0711 |
| Mean | 0.0003 | 0.0029 | 3.3910 | 0.0002 | 0.0003 |
| Std. deviation | 0.0083 | 0.0291 | 0.0138 | 0.0181 | 0.0104 |
| Skewness | −0.4633 | 0.5425 | −0.4216 | 0.0795 | −0.1907 |
| Kurtosis – 3 | 4.7458 | 7.8959 | 3.4862 | 8.7144 | 4.5518 |
| Coeff. of variation | 30.5624 | 10.0069 | 40.6836 | 73.7598 | 36.8671 |
| LB (12) | 19.4121* | 82.5342** | 23.6756** | 38.0246** | 24.0166** |
| LB (24) | 26.6232* | 141.2074** | 51.3284** | 47.9043** | 40.3609** |
Estimated cross correlation matrix of market returns.
| Country | AUS | BRZ | GER | HKG | USA |
| AUS | 1.0000 | 0.1118 | 0.3043 | 0.4745 | 0.0873 |
| BRZ | 0.1118 | 1.0000 | 0.2283 | 0.1118 | 0.3634 |
| GER | 0.3043 | 0.2283 | 1.0000 | 0.3540 | 0.4010 |
| HKG | 0.4745 | 0.1118 | 0.3540 | 1.0000 | 0.1104 |
| USA | 0.0873 | 0.3634 | 0.4010 | 0.1104 | 1.0000 |
In the next step the stationarity of the data has been tested by the unit root test. The augmented Dickey–Fuller statistic was used to test for a unit root in the five stock market return series. Here we assume:
H0=non-stationary.
H1=stationary.
The ADF test result for the variables using a maximum lag of 4 was used. The results are shown below.
Tables 5 and 6 show the unit root tests. The tests indicate the existence of two logged indexed stationary series and three first orders differenced logged indexed stationary series. Thus, the two logged indexed series for Brazil and Hong Kong are excluded in our analysis and first order differenced logged indexed series for Australia, Germany and USA are included in our analysis to test for ARCH effects and volatility.
Unit root tests for variables.
| Countries | Test statistic: SBC (Schwarz Bayesian criterion) | 95% Critical value for the augmented Dickey–Fuller statistic |
| Australia | −1.9821 [ADF(1)] | −2.8632 |
| Brazil | −8.8300 [ADF(1)] | −2.8632 |
| Germany | −1.8057 [ADF(1)] | −2.8632 |
| Hong Kong | −2.8842 [ADF(3)] | −2.8632 |
| USA | −1.5732 [ADF(1)] | −2.8632 |
Unit root tests for variables after first order difference.
| Countries | Test statistic: SBC (Schwarz Bayesian criterion) | 95% Critical value for the augmented Dickey–Fuller statistic |
| Australia | −37.1496 [ADF(4)] | −2.8632 |
| Germany | −37.3953 [ADF(4)] | −2.8632 |
| USA | −38.2591 [ADF(4)] | −2.8632 |
The next step is to test for ARCH effects. This is done to see whether there is variance in the forecast errors or the presence of some kind of autocorrelation in the variance of forecast errors. The Lagrange multiplier procedure proposed by Engle (1982) is used to test for ARCH (P) effect. First, the OLS residuals of the regression are obtained. Then, the square of the residuals is regressed on a constant and P of its own lagged values. Mathematically it can be seen as:
The ARCH effects for the three stock markets were estimated from the OLS regressions stated below.
whereThe null hypothesis (H0): α=0 (there is no ARCH effects) is tested for statistical significance. The table below states the results of the ARCH effect test from order 1 to 4 for each of the three variables which are found to be of the order I (1).
Probability values of both statistic tests, i.e., LM version and F version are less than 0.05 using the 95% confidence level of significance test is reported in Table 7. This implies that we can reject the null hypothesis of no ARCH effects, i.e., α=0 for all orders from 1 to 4 for all the three variables and hence accept the existence of ARCH effects.
Autoregressive conditional heteroscedasticity test of residuals (OLS case).
| ORDER | LM-statistic | F-statistic |
| Australia | ||
| 1 | CHSQ(1)=270.3689[.000] | F(1,2495)=302.8196[.000] |
| 2 | CHSQ(2)=270.7294[.000] | F(1,2494)=151.5755[.000] |
| 3 | CHSQ(3)=303.6546[.000] | F(1,2493)=114.9942[.000] |
| 4 | CHSQ(4)=304.5221[.000] | F(1,2492)=86.4915[.000] |
| Germany | ||
| 1 | CHSQ(1)=105.4285[.000] | F(1,2495)=109.9420[.000] |
| 2 | CHSQ(2)=204.4210[.000] | F(2,2494)=111.1420[.000] |
| 3 | CHSQ(3)=307.3997[.000] | F(3,2493)=116.6115[.000] |
| 4 | CHSQ(4)=341.5369[.000] | F(4,2492)=98.6697[.000] |
| USA | ||
| 1 | CHSQ(1)=101.9001[.000] | F(1,2495)=106.1061[.000] |
| 2 | CHSQ(2)=142.8360[.000] | F(2,2494)=75.6281[.000] |
| 3 | CHSQ(3)=174.9501[.000] | F(3,2493)=62.5831[.000] |
| 4 | CHSQ(4)=175.9181[.000] | F(4,2492)=47.1977[.000] |
After having tested for multicollinearity, stationarity and for ARCH effects the study uses the GARCH (p,q) process, which allows lagged conditional variances to enter the equation above as opposed to the ARCH (q) process where the conditional variance is specified as a linear function of past sample variances only. In the GARCH-Mean model the conditional variance of Ut is used as one of the regressor explaining the conditional mean of the return of the variable. Below a basic model based on the data is specified.
where Xt−1 can be taken as the vector of ex ante dated variables and is assumed to include DAt−1, DGt−1 and DUt−1. DA=the difference logaramatic values of S&P ASX 200 price index; DG=the difference logaramatic values of DAX 30 performance price index; DU=the difference logaramatic values of S&P 500 composite price.The U2 past squared innovations (i.e., εj,t−12≡(Rj,t−1−μj,t−1)2) which are used as proxies for past volatility shocks during day t−1; are taken as the residuals from running the regression of a variable on its one period lagged variable (e.g. DA=constant+DA (−1)+Ut).
The actual model employed in the study is stated in the equation below which analyses the mean spillovers.
Here ¿i,t=Ri,t−μi,t is an innovation or the conditional forecast error and ¿2 is a proxy for a volatility shock during day t in market i.The above equation helps in analyzing the volatility spillovers. The conditional variance of returns in market i is specified as a linear function of its own past conditional variance and past volatility shocks from all five markets.
4.2Results of mean spillovers and volatility spillovers testingThe empirical model was run based on the equations above along with the lagged variable of the other variables, choosing an order of 1;1 GARCH M-model. The distribution used was the student T distribution. The initial estimates for γ, α1, and ϕ1 (“in Mean”) was 0.3, 0.1 (MA lag 1), and 0.3 (AR lag 1) respectively (a dumping factor of (0.010) was used) (Table 8).
GARCH (1,1)-M; Mean model estimates.
| Conditional mean parameters | Countries | ||
| AUS | GER | USA | |
| Constant | .0001515(.723) | .00003855(.904) | .00000006032(.998) |
| BDA | −.42817(.000) | −.012963(.588) | −.083503(.000) |
| BDG | .065719(.000) | −.53065(.000) | −.024707(.050) |
| BDU | .25081(.000) | .37431(.000) | −.49243(.000) |
| H-squared | −2.2416(.717) | .20493(.906) | −2.20583(.921) |
| E–SQ(−1) | .16517(6.1856) | .10035(3.3795) | .11917(2.638) |
| δi(H–SQ(−1)) | .64330(26.6101) | .89746(35.5274) | .87970(23.66) |
The results for the conditional mean equations show statistically significant positive mean spillovers from the markets of the USA to Australia, Germany to Australia and negative mean spillovers from Australia to Germany and USA, from USA to Germany and Germany to USA. The cross mean spillovers from the markets of USA to the Australia and Germany .25081 (.000), .37431 (.000) respectively. Past USA returns have a greater effect on current returns in Germany relative to Australia. The coefficients .64330 (26.6101), .89746 (35.5274), .87970 (23.66) for the volatility components of all conditional mean equations are statistically significant and very large, since the (t-ratios) are >1.96. This indicates high relation between conditional market volatility and expected returns.
To assess the extent to which the mean spillovers relations can predict future stock market returns, we can use a univariate R2 measure for each of the conditional mean equations. The R2 equals 1−[variance of error/variance of returns] which measures the percentage of variation in the returns of market i explained by the conditional mean equation. If the conditional mean equations could be used by investors to predict the future course of prices, the weak form of efficient market hypothesis would be violated.
4.2.2Volatility spilloversThe coefficients for the one lag conditional variances (γI) for the markets of Australia and Germany are .79071 (35.08), .88796 (4.3277), respectively. The coefficient for the Australian market as compared to the German market is quite large and highly significant at 5% level, indicating the presence of structure in the data. Here by structure we mean high volatility persistence. Since both t-ratio are greater than 1.96 we conclude the presence of volatility in these markets. Persistence of stock market volatility is higher in Australia than Germany. Negative own-spillovers are present in all the stock markets. Since own-spillovers coefficients −.65148 (.000), −.75323 (.000), −.13966 (.000) are very high and are statistically significant, we can say that past market volatility shocks in all these markets have a great effect on future volatility in these markets. If the own-spillovers coefficients are statistically insignificant we can conclude that conditional volatility in these markets are imported only from abroad.
Past-market volatility shocks in the USA influence current volatility in both, the Australian and German market, with varying degrees of intensity. That is, the USA volatility coefficients to Australia and Germany are .27555 (.000), .43946 (.000) respectively. Therefore majority of the volatility spillovers on the German stocks is from the USA markets. This may be due to the fact that the Australian market opens only after the German market and US markets have opened. According to the results, the volatility spillover from Germany to Australia is not present as the coefficient (.014631 (659)) is insignificant. Since the coefficient (.27555 (.000)) of volatility spillover from USA to Australia is significant, we can tell that majority of the volatility spillovers on the Australian stocks is from USA stock market. The presence of cross volatility spillover is seen between the Australian and German market. Since the volatility spillover coefficient (−. 058683 (.000)) of Australia market to German market is less than the volatility spillover coefficient (.43946 (.000)) of German market to Australian market, the Australian market is influenced more by the German market. This may be due to the fact that the Australian market is the last to open its market according to the time horizon. Therefore, the Australian market may be exposed to volatility spillovers from both, the USA and German market (Table 9).
GARCH (1,1) M-variance equation results.
| Conditional mean parameters | Countries | ||
| AUS | GER | USA | |
| Constant | −.0001414(.761) | −.00003612(.864) | |
| BEDA | −.65148(.000) | −.014631(.659) | −.13149(.000) |
| BEDG | .058683(.000) | −.75323(.000) | −.088727(.000) |
| BEDU | .27555(.000) | .43946(.000) | −.13966(.000) |
| γi | .79071(35.08) | .90713(4.3277) | |
Taking the US market separately we analyze the results. From the (Table 10) we can see that there is presence of volatility spillover to the US market from both the German and Australian Market. Since the coefficients are small we can conclude that this volatility spillover is not very large. We can also see the presence of negative own-spillover in the US market. The coefficients for the one lag conditional variances (γI) is quite high for the US market on its previous period. This shows that the US market is influenced to a great extends by its previous period volatility than from abroad. Although we can see that the coefficient of the Australian market is also high.
5Summary and concluding remarksThis study attempted to provide the usefulness of using a time series generalized auto regressive conditional heteroscedasticity in the Mean GARCH (1,1)-Mean model, to get additional insight into the degree of interdependence among five major national stock markets (Australia, Brazil, Germany, Hong Kong and US) by examining the nature and magnitude of mean and volatility spillovers in these markets. The transmission of volatility shocks across Australia, Brazil, Germany, Hong Kong and USA was studied and it shows that the analysis of volatility inter-dependence provides useful insights into how information is transmitted and disseminated across markets. Also spillovers of returns across markets have important implications for portfolio choice and risk management.
First, we tested for the presence of stationarity in the each of the return series. Then, we tested for the presence of ARCH effects. Due to the presence of stationarity and ARCH effects in the return series of Brazil and Hong Kong, we had excluded these countries from our final analysis for volatility spillover across different markets. Therefore, in our final analysis only three markets were analyzed, i.e., Australia, Germany and USA.
The conditional mean equations showed statistically significant mean spillovers from one market to another market. We found cross-mean spillovers from the markets of USA to the Australia and Germany, also past USA returns have a greater effect on current returns in Germany relative to Australia. Besides, the study showed the presence of high relation between conditional market volatility and expected returns, which may not be against the theory of weak form of efficient market hypothesis. This may to some extend show that investors can be able to predict the future course of prices. Regarding volatility spillover we found the presence of high volatility persistence. Also significant negative own-spillovers are present in all stock markets. Past-market volatility shocks in the USA influence current volatility in both the Australian and German market with varying degrees of intensity. Cross volatility spillover exists in all the three markets. Based on the results, we can tell that the US market is the most influential market among the markets under study. Any news occurring in US has a great impact on other markets.
The study shows that regulations and rules enacted and put forward to control the effects are not working or more need to be done to curb this inter market negative effects. But this may not be possible as with each day the world markets are becoming more and more correlated. Secondly, there may be other variables apart from these that affect stock return volatility. However, despite many regulatory measures, volatility in stock prices exists. In general, an increase in price volatility may be due to an increase in the variability of economic information that affects stock market prices or failure to observe an increase in price volatility may be due to a decrease in the variability of economic information, making any increase in price volatility. Finally, we can conclude that the test has given some results which prove that the financial markets are integrated in these countries. Any news arising in one country has an impact on the other country to some extent. Also, previous news of a country influences the future price of another country. Although we found the presence high relation between conditional market volatility and expected returns, our results are not conclusive enough as we must control for other factors that affect stock price mean and volatility spillovers, before inferring a direct casual effect obtained from the above study.
Future research in this field can be undertaken for the most stock markets and for longer time period, and the results can be compared for different sample periods as well. It is further advisable to use intra-day (open and close) of each market (as it helps to accurately distinguish between results) or to decompose daily price changes (returns and volatility) into daytime (open to close) and overnight (close to open) returns, where the daytime segment in one market is a subset of the overnight segment of the other market. This decomposition of daily price changes is essential for clean tests of how information is transmitted from one market to the other.