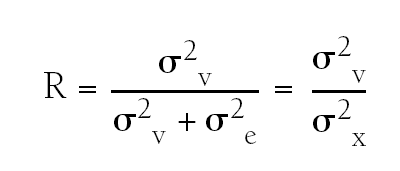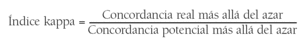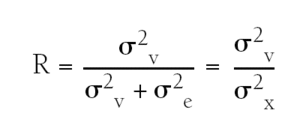INTRODUCCIÓN
Las pruebas diagnósticas, exámenes diagnósticos o test, forman parte de la práctica habitual del médico clínico. Su manejo no es siempre fácil y la solicitud de las mismas e interpretación en el contexto de sospecha o confirmación diagnósticas es un reto diario que forma parte de la incertidumbre y que nos lleva a aceptar y asumir que el error diagnóstico es un hecho posible1,2.
Bajo la denominación de pruebas diagnósticas se engloban las pruebas utilizadas para la detección precoz de enfermedades y las pruebas confirmatorias, que deben cumplir requisitos distintos en función de su utilidad.
El abordaje inicial de un paciente es realizado a través de una buena anamnesis, inspección y examen físico. En cada uno de estos pasos aplicamos criterios que nos van orientando hacia una sospecha diagnóstica, que puede derivar de forma inicial en una actividad terapéutica si el grado de certeza es alto o hacer necesaria la realización de pruebas complementarias si el grado de certeza diagnóstica es insuficiente. Si dispusiéramos de pruebas perfectas no habría incertidumbre, pero la realidad es que todas llevan algún grado de error que debemos conocer y asumir.
En un término amplio estamos hablando de pruebas clínicas porque todas ellas tienen un objetivo común, realizar un diagnóstico, y engloban no solamente pruebas de laboratorio, radiológicas, sino también los pasos del examen clínico. El diagnóstico se enmarca dentro de un proceso general de toma de decisiones y es un proceso dinámico que nos permite manejarnos en términos de probabilidades hacia la confirmación de una enfermedad o hacia su descarte.
CARACTERISTICAS DE LAS PRUEBAS DIAGNÓSTICAS
Una buena prueba diagnóstica es aquélla que resulte normal en los individuos sanos y anormal en los individuos enfermos.
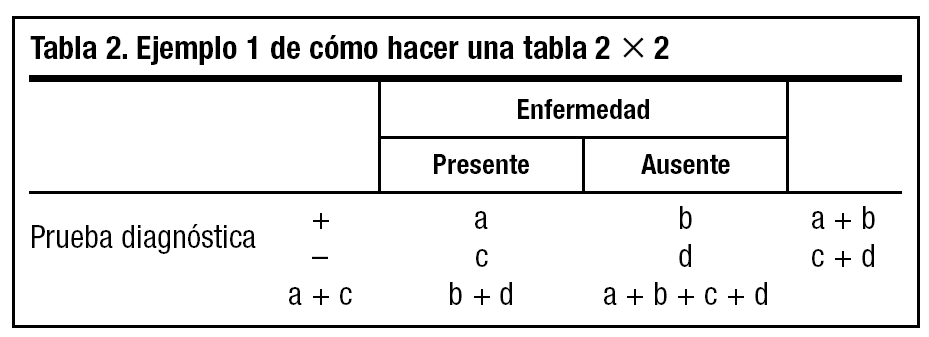
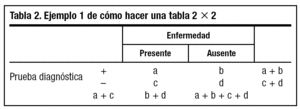
La expresión real de los resultados de la aplicación de una prueba permite clasificar a un individuo sano o enfermo, con resultados correctos o incorrectos de la prueba, y constituir de esta manera las tablas 2x2 (tabla 1).
Hemos de manejar conceptos como la sensibilidad y la especificidad, que son características de la prueba, mientras que los valores predictivos positivo (VPP) y negativo (VPN) son el resultado de aplicar una prueba a la población con una prevalencia determinada de enfermedad.
Como clínicos, cuando aplicamos una prueba diagnóstica tenemos que valorar:
1. Tipo de enfermedad:
a) Prevalencia (factores de riesgo aumentan la prevalencia).
b) Gravedad.
c) Curable o no. ¿Tiene tratamiento?
d) ¿Podemos perder casos? ¿Podemos asumir los falsos negativos?
e) ¿Qué consecuencias tienen los falsos positivos?
f) Interés en diagnosticarla o en excluirla.
2. Tipo de prueba aplicada. Qué sensibilidad y especificidad tiene la prueba en estudios previos validados.
3. Contexto y tipo de población donde se aplica la prueba.
Validez, fiabilidad y seguridad
Las características que debe tener una prueba son validez, fiabilidad y seguridad, es decir, que mida lo que realmente pretende, que sea reproducible produciendo resultados semejantes y que pueda predecir la presencia o ausencia de enfermedad3-8.
Validez
Es la capacidad de la prueba para medir lo que pretende medir. Es el grado de coincidencia entre los resultados de la prueba y los exámenes diagnósticos más complejos y rigurosos subsiguientes que se constituyen como patrón de referencia o estándar, aunque éstos no siempre son perfectos o están disponibles. Las medidas de la validez son la sensibilidad y la especificidad, que realizan el análisis de la tabla por columnas. Ambas son características inherentes a la prueba (tabla 1).
1. Sensibilidad. Probabilidad de que un enfermo sea identificado correctamente por la prueba, es decir, que tenga una prueba positiva. Son los enfermos con prueba positiva de entre todos los enfermos.
2. Especificidad. Probabilidad de que un individuo sin la enfermedad sea identificado correctamente por la prueba, es decir, que tenga una prueba negativa. Son los sanos con prueba negativa de entre todos los sanos.
3. Proporción de falsos negativos (c/[a + c]). Probabilidad de que un enfermo sea identificado incorrectamente por la prueba y obtenga una prueba negativa. Son los enfermos con prueba negativa de entre todos los enfermos.
4. Proporción de falsos positivos (b/[b + d]). Probabilidad de que un individuo sin la enfermedad sea identificado incorrectamente por la prueba, es decir, que tenga una prueba positiva. Son los sanos con prueba positiva de entre todos los sanos.
Sensibilidad y especificidad son conceptos que expresan la capacidad intrínseca de la prueba y resultan valores estables para cada una. Una prueba puede presentar distintos valores de sensibilidad y especificidad, según las condiciones de su realización.
Se pueden utilizar en todas las poblaciones y no varían con la prevalencia, siendo ésta la probabilidad de que el sujeto esté enfermo antes de realizar la prueba, que se conoce como probabilidad pre-prueba. Si no tenemos ninguna información adicional sobre el sujeto, dicha probabilidad será la prevalencia de la patología en la población, aplicable sólo en el caso de programas de cribado o screening sobre la población general, ya que en la práctica habitual los sujetos candidatos a una prueba diagnóstica lo son por las sospechas deducidas de la anamnesis o por una sintomatología, exploraciones o pruebas previas y, por tanto, la probabilidad de que padezcan la enfermedad bajo sospecha será superior a la prevalencia de ésta en la población general.
Seguridad
Capacidad de una prueba para predecir la ausencia o la presencia de enfermedad.
Los valores predictivos o probabilidad posprueba representan la probabilidad de que el paciente tenga la enfermedad una vez que conocemos el resultado de la prueba.
1. Valor predictivo positivo (VPP). Probabilidad de que un individuo con prueba positiva tenga la enfermedad. Corresponde a los enfermos con pruebas positivas de entre todas las pruebas positivas.
2. Valor predictivo negativo (VPN). Probabilidad de que un individuo con prueba negativa no tenga la enfermedad, es decir, que esté realmente sano. Corresponde a los pacientes sanos con prueba negativa de entre todas las pruebas negativas.
COMO HACER UNA TABLA DE 2x2
Ya sabemos cómo son las tablas de 2x2, lo que es la sensibilidad, la especificidad, el VPP y el VPN. Ahora vamos a tratar de ver la utilidad que puede tener todo esto para un clínico. Imaginemos que estamos en la consulta y que queremos hacer el diagnóstico a un paciente. Lo primero que hacemos es buscar una prueba diagnóstica con una sensibilidad y una especificidad apropiadas para el tipo de diagnóstico que queremos hacer (confirmar un diagnóstico, la gravedad de la enfermedad, etc.). Nosotros habitualmente para diagnosticar una enfermedad nos apoyamos en una serie de pruebas diagnósticas clínicas y/o complementarias de más o menos probada utilidad y con una sensibilidad y una especificidad determinadas que nos vienen ya dadas y sobre las que nosotros no podemos influir, sólo decidir si la utilizamos o no. Pero ¿cómo sabremos qué capacidad predictora tiene esta prueba al ser aplicada sobre nuestra población de referencia? ¿Qué le decimos al paciente en el caso de que dé positivo? ¿Y si da negativo?
Él nos preguntará si este diagnóstico es definitivo, si la predicción es real o si puede existir alguna duda en el diagnóstico y cómo de grande es esa duda.
Para ello construiremos1 una tabla de 2x2 con los datos de que disponemos:
1. Dibujamos una tabla de 2x2 en blanco (tabla 2).
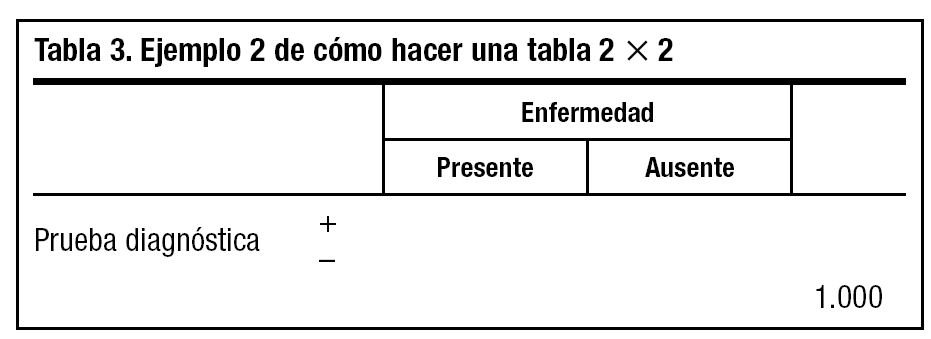
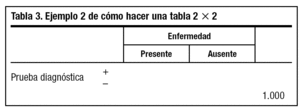
2. Añadimos un número total (a + b + c + d) ficticio que nos resulte cómodo para hacer operaciones matemáticas, por ejemplo el 1.000 (tabla 3).
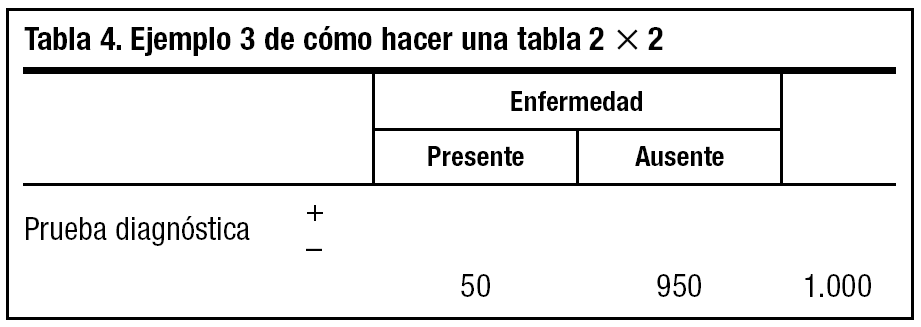
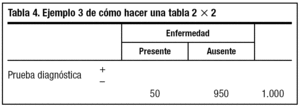
3. Multiplicamos 1.000 por la prevalencia de la enfermedad existente en nuestra población. Supongamos que en este caso es del 5% (0,05) y ponemos el resultado 1.000 * 0,05 = 50 en la celda de a + c. Ahora podemos obtener la celda del número de enfermos b + d restando al total (a + b + c + d) (1.000) el n.o de enfermos (a + c) (50), con lo que nos da 950, y lo ponemos en su celda (tabla 4).
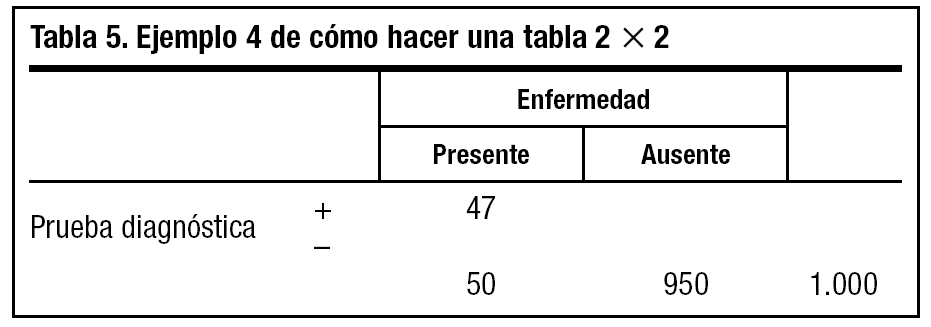
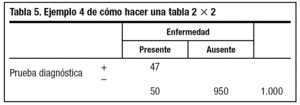
4. Multiplicamos a + c (50) por la sensibilidad de la prueba que nos ha indicado el fabricante, que es del 94% (0,94), y ponemos la cifra (47) en la casilla a (tabla 5).
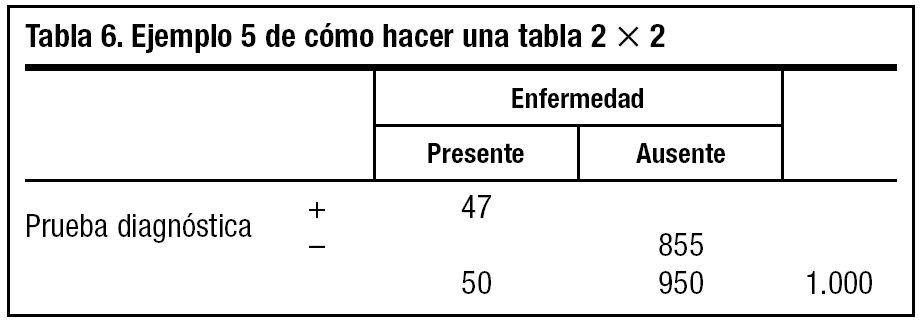
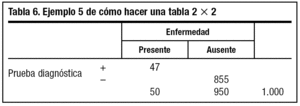
5. Multiplicamos b + d (950) por la especificidad que nos ha indicado el fabricante, que es del 90% (0,90), y la cifra (855) la ponemos en d (tabla 6).
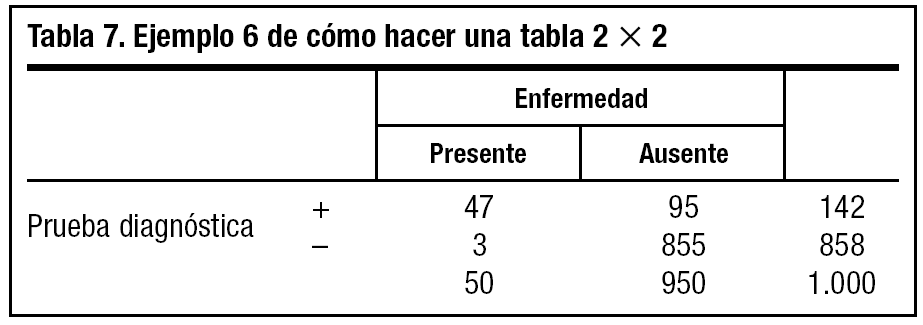
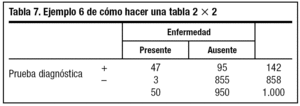
6. A partir de ahí iremos rellenando, sumando y restando, el resto de las casillas vacías (tabla 7).
Ya podemos calcular el VPP, el VPN y la exactitud de la prueba e informar al paciente sobre el valor real que tienen esos resultados.
VPP = a/(a + b) = 47/142 = 0,33. Si su prueba dio positivo, hay un 33% de probabilidad de que tenga realmente la enfermedad.
VPN = d/(c + d) = 855/858 = 0,99. Si su prueba dio negativo, podemos descartar la enfermedad en un 99%.
UTILIZACION DE PRUEBAS DIAGNÓSTICAS
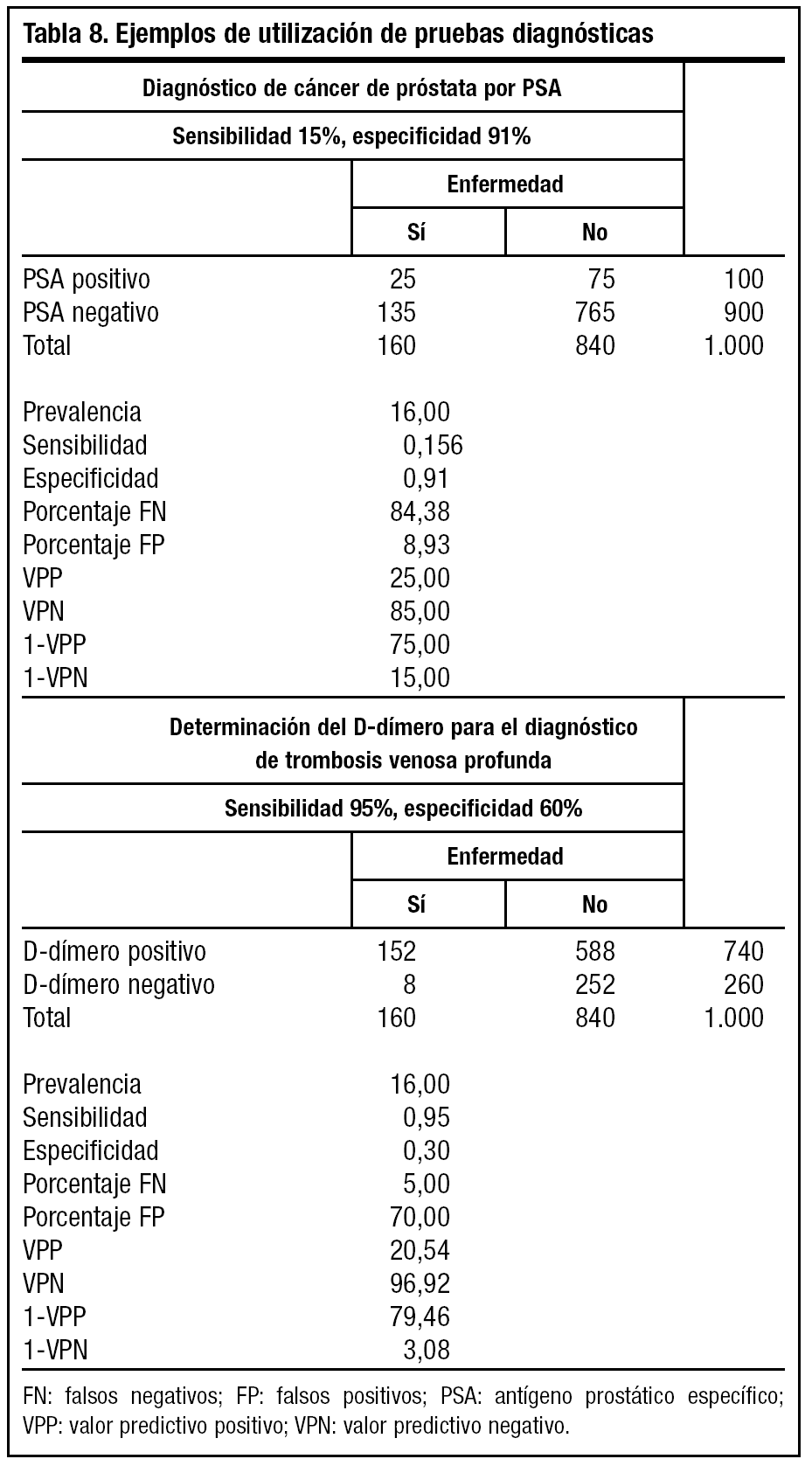
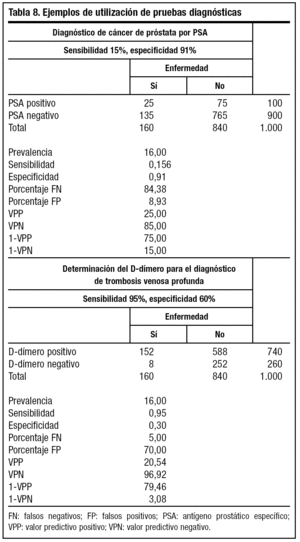
La sensibilidad y la especificidad nos permiten valorar una prueba diagnóstica, pero carecen de utilidad en la práctica clínica. Nos hablan de la "bondad" de una prueba según el objetivo diagnóstico y el tipo de patología que queramos detectar, pero no podemos saber con certeza quién está enfermo o no lo está tras su aplicación (tabla 8).
Elegiremos una prueba sensible
1. Cuando hagamos un screening o cribado para captar a todos los enfermos.
2. Ante enfermedades graves, donde no podemos perder casos (cáncer de mama, prueba de otoemisiones para la sordera infantil, etc.).
3. Ante enfermedades tratables.
4. Cuando se necesita detectar el máximo número de casos de la enfermedad en la población general (debido a que el diagnóstico tardío puede conllevar pronóstico fatal).
5. Cuando los falsos positivos no supongan un trauma psicológico o económico para los individuos.
6. Si los falsos negativos producen un trastorno importante (dejamos la enfermedad sin tratar).
Las pruebas muy sensibles implican que cuando se aplican a un individuo determinado y es negativa podemos descartar con confianza que tenga la enfermedad, porque si la tuviera hubiera dado positivo. Sin embargo, cuando es positiva no podemos asegurar que sea enfermo, y algunos de los individuos que hemos considerado inicialmente enfermos no tendrán la enfermedad (falsos positivos).
Elegiremos una prueba específica
1. Cuando la enfermedad sea importante pero difícil de curar o incurable.
2. Cuando exista gran interés por conocer la ausencia de enfermedad.
3. Cuando los falsos positivos puedan suponer un trauma psicológico o económico a los individuos.
4. Cuando necesitemos pruebas de confirmación diagnóstica (VIH, esclerosis en placas, etc.).
Las pruebas muy específicas identificarán a todos los individuos sanos, de tal manera que cuando se aplican a un individuo determinado y es positiva se puede asumir con confianza que el individuo está enfermo. Pero si la prueba es negativa, no podríamos asegurar que fuese un individuo sano, ya que puede haber falsos negativos.
En las pruebas poco específicas hay un número elevado de falsos positivos, lo que provoca un sobrediagnóstico con realización posterior de pruebas confirmatorias.
El interés clínico en el procedimiento diagnóstico es saber la probabilidad con que la prueba nos proporciona un diagnóstico correcto. La respuesta a esto la encontramos en el análisis horizontal de la tabla.
Elegiremos una prueba con alto valor predictivo positivo
1. Cuando el tratamiento de los falsos positivos pudiera tener graves consecuencias (quimioterapia).
2. Cuando queramos hacer una prueba de cribado.
El VPP depende de la prevalencia, de la especificidad y, en menor grado, de la sensibilidad.
Elegiremos una prueba con alto valor predictivo negativo
La elegiremos cuando un falso negativo tenga consecuencias indeseables.
Los valores predictivos de los signos, los síntomas y las pruebas de laboratorio cambian con la prevalencia de la enfermedad en la población donde se aplica la prueba y también con la sensibilidad y la especificidad.
Al aumentar la prevalencia aumenta el VPP para una misma sensibilidad y especificidad, ya que disminuye el número de falsos positivos.
Es importante que la enfermedad sea frecuente en la población elegida cuando se va a realizar un cribado, y ello se consigue aplicando la prueba a la población de riesgo.
El VPP es el parámetro de mayor relevancia para los programas de screening, pues un bajo valor significa que la prevalencia es baja, que la prueba es poco específica o ambas cosas.
En el ejemplo podemos observar la aplicación de la prueba del antígeno prostático específico (PSA) en el diagnóstico del cáncer de próstata y dímero-D para la trombosis venosa profunda (tabla 8).
Observamos que un resultado negativo de la prueba, el D-dímero es más concluyente, ya que existe un 3% de probabilidad de estar enfermo frente a un 15% en el PSA.
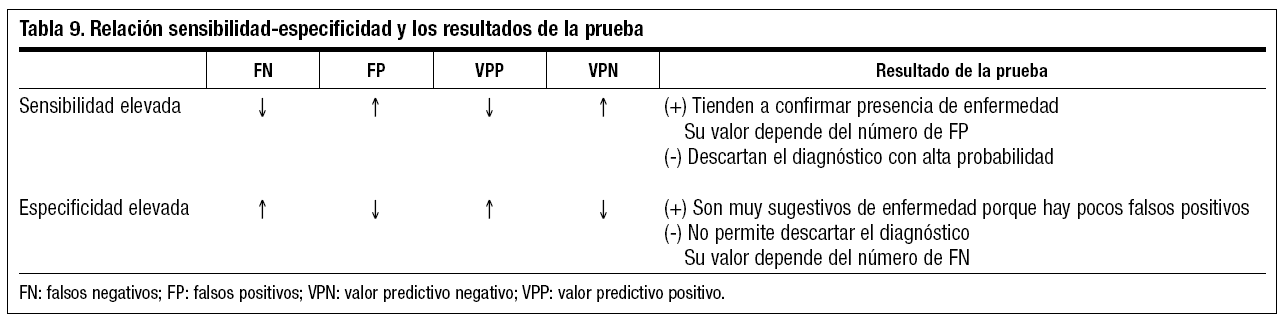
Podemos ver en la tabla 9 la relación entre la sensibilidad, la especificidad y la valoración de los resultados de la prueba.
Pongamos otro ejemplo, se hizo un estudio sobre las otoemisiones acústicas para el cribado universal de hipoacusia congénita9-11. Se utiliza como prueba de screening las otoemisiones evocadas acústicas (OEA), que es una prueba rápida, económica y sencilla, combinada con los potenciales evocados (PEATC) para la confirmación diagnóstica.
En estudios previos los valores de sensibilidad oscilan entre el 85 y el 94%. Las hipoacusias que escapan a la detección neonatal son generalmente de aparición tardía o posnatales o por interpretación incorrecta de la prueba.
Se realiza una primera prueba de OEA a los niños a las 48 horas del nacimiento y una reprueba a los 7 días a los niños que habían dado "no normal" en la primera. Tras esta segunda prueba, a todos los niños con OEA "no normales" se les aplica el PEATC de confirmación.
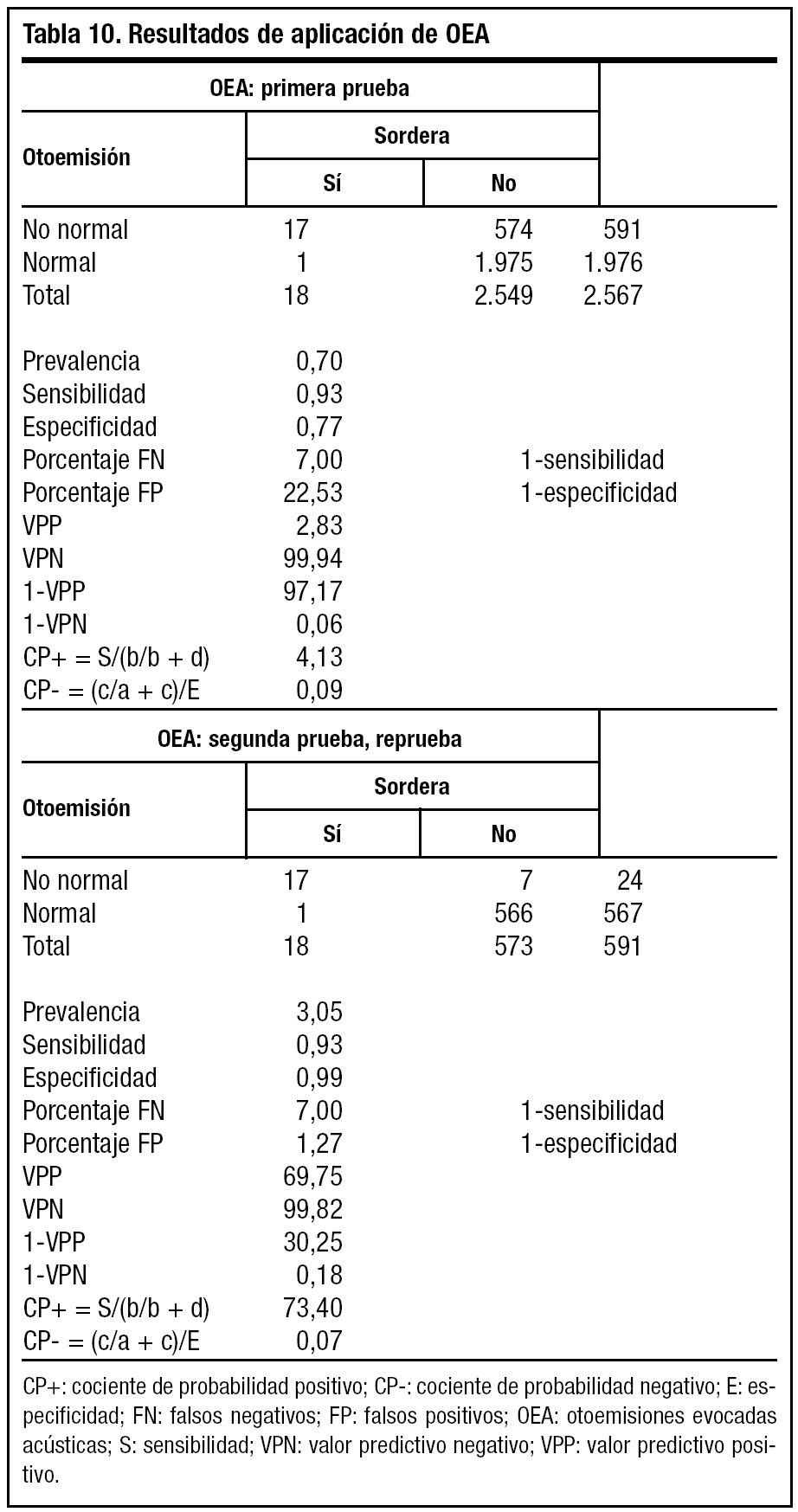
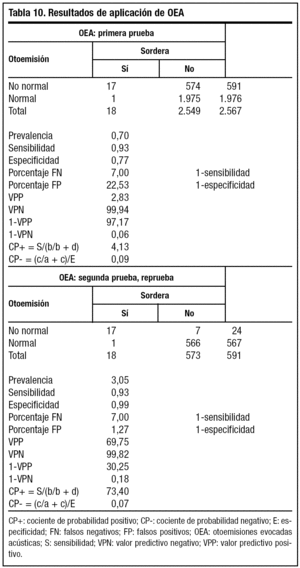
Aplicamos la OEA a 2.567 niños con una sensibilidad del 93% y una especificidad del 89%. En la tabla 10 podemos observar los resultados.
Al aplicar la prueba por primera vez vemos que 591 niños tienen otoemisiones patológicas y 1.976 presentan otoemisiones normales. La sensibilidad de la prueba es del 93% y la prueba detecta a 17 de los 18 individuos con sordera. Hay 574 pruebas "no normales" en niños sanos. El VPP es bajo debido a la baja prevalencia de la enfermedad en la población general y nos dice que ante un niño con resultado de OEA "no normal", tengo muy poca probabilidad de que sea sordo. Pero un resultado negativo en esta primera prueba del cribado me dice con certeza que es realmente sano, así, un 99% de niños con prueba negativa son realmente sanos.
La segunda prueba de cribado se realiza a la semana sobre los 591 niños que tuvieron una primera prueba no normal. Aquí la población ha cambiado, pues la prevalencia de la enfermedad ha aumentado hasta el 3%, con lo cual el VPP de la prueba ha aumentado muchísimo y nos orienta algo más, aunque no nos permite confirmar la presencia de enfermedad, de tal manera que cuando la prueba de OEA nos da "no normal" hay un 69% de probabilidad de ser sordos. El VPN nos hace descartar prácticamente la enfermedad ante un resultado normal.
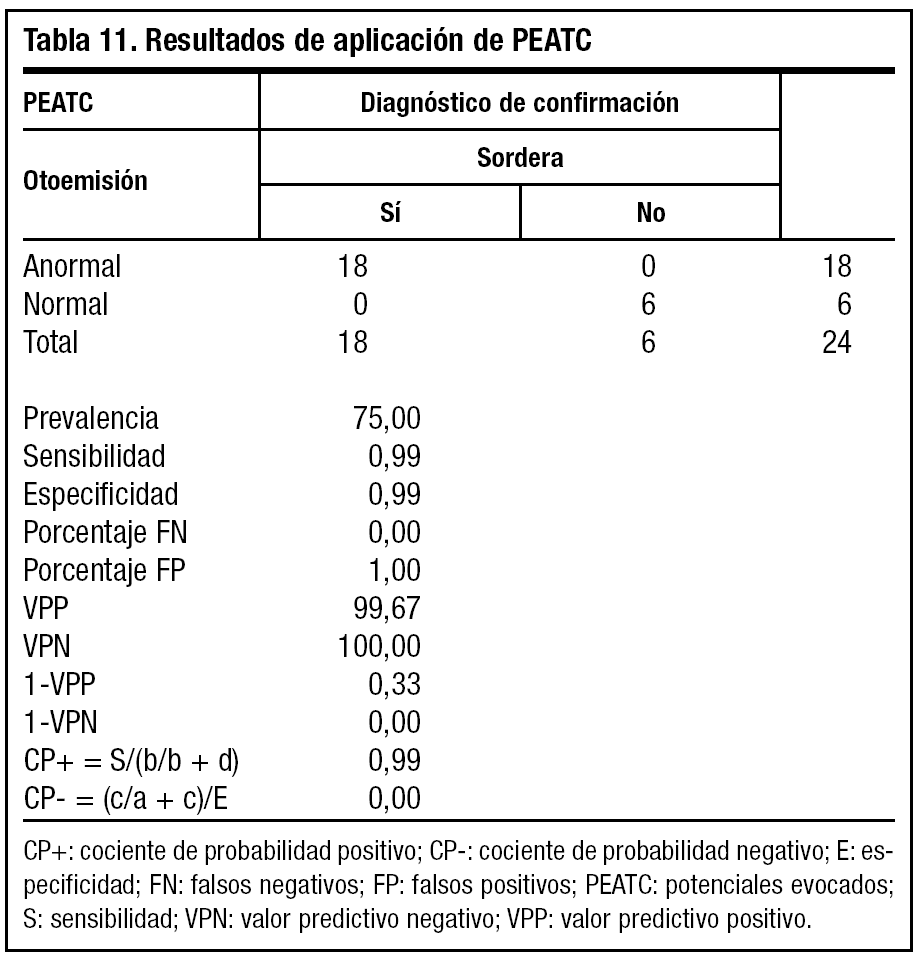
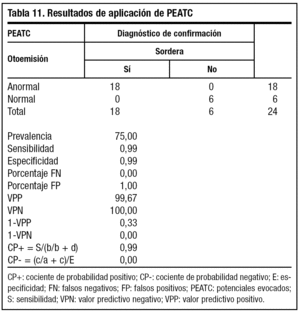
Al aplicar la prueba de confirmación diagnóstica de PEATC (tabla 11), con alta sensibilidad y especificidad a una población muy seleccionada, la prevalencia de enfermedad aumenta hasta el 75%, con lo cual un resultado positivo o negativo es concluyente de sano o enfermo.
Supongamos que una prueba diagnóstica la aplicamos en poblaciones donde la enfermedad estudiada tiene diferentes probabilidades a priori, por ejemplo en población general o en colectivos de riesgo intermedio o alto. Obtendríamos la tabla 12 empleando una prueba de sensibilidad y especificidad del 90%.
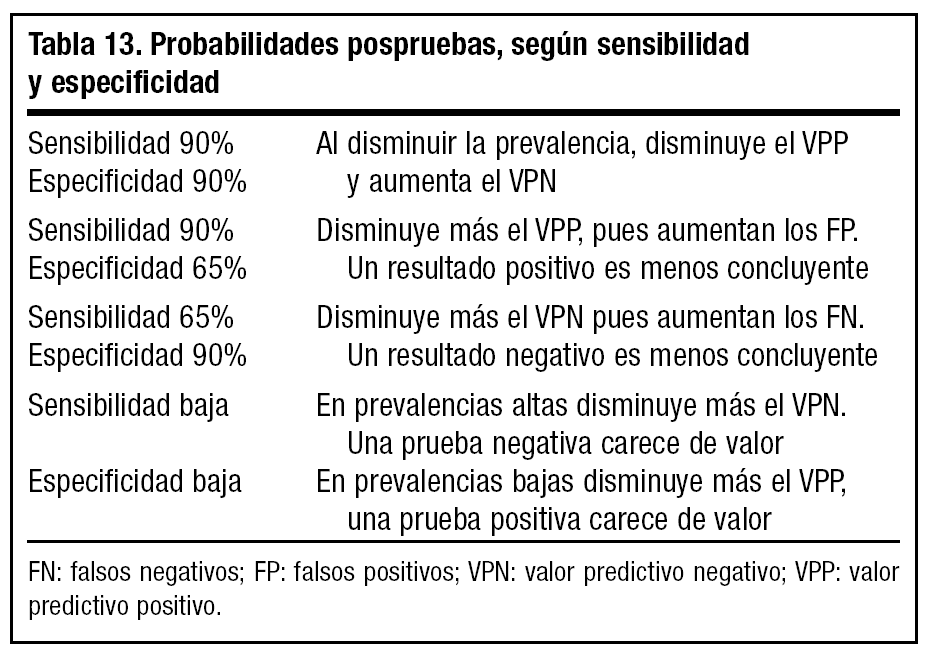
Podríamos construir de esta manera las diferentes tablas aplicando los valores de sensibilidad y especificidad de nuestras pruebas y ver las probabilidades aportadas por cada una (tabla 13).
EFECTO DE LA PREVALENCIA EN LOS VALORES PREDICTIVOS
Observamos que al disminuir la prevalencia, es decir, la probabilidad de tener la enfermedad antes de la prueba, disminuye la probabilidad de tener la enfermedad tras un resultado positivo de la misma (VPP), con lo que aumenta el VPN, de forma que la probabilidad de tener la enfermedad tras la prueba negativa es muy pequeña, por lo cual la prueba negativa la descarta prácticamente1,3,4.
La rentabilidad de la prueba medida en máxima información aportada, por modificar al máximo (aumentar o disminuir) la probabilidad pre-prueba, se obtiene con prevalencias del 40 al 60% (máximo en el 50%), de forma que los resultados positivos son indicativos de enfermedad y los negativos son indicativos de ausencia de la misma con una alta probabilidad.
En prevalencias muy altas de la enfermedad (alto índice de sospecha, con signos o síntomas o pruebas previas o colectivo de riesgo), los resultados positivos son indicativos de enfermedad y los negativos no la excluyen, pues la probabilidad de estar enfermo es alta cuando la prueba es negativa, con lo cual nos ayuda poco y habría que valorar si realizamos o no la prueba.
En prevalencias muy bajas, como nuestro ejemplo anterior, los resultados positivos no nos aportan información, pues la probabilidad de estar enfermo es pequeña y los resultados negativos sí nos confirman su ausencia.
Realmente tenemos que valorar a la hora de realizar una prueba lo que nos aporta si nos da un resultado positivo o negativo en el contexto de las características de la misma (sensibilidad y especificidad), valorando lo que aporta la prueba en términos de ayuda diagnóstica, es decir, ver la diferencia entre probabilidad pre-prueba y probabilidad posprueba.
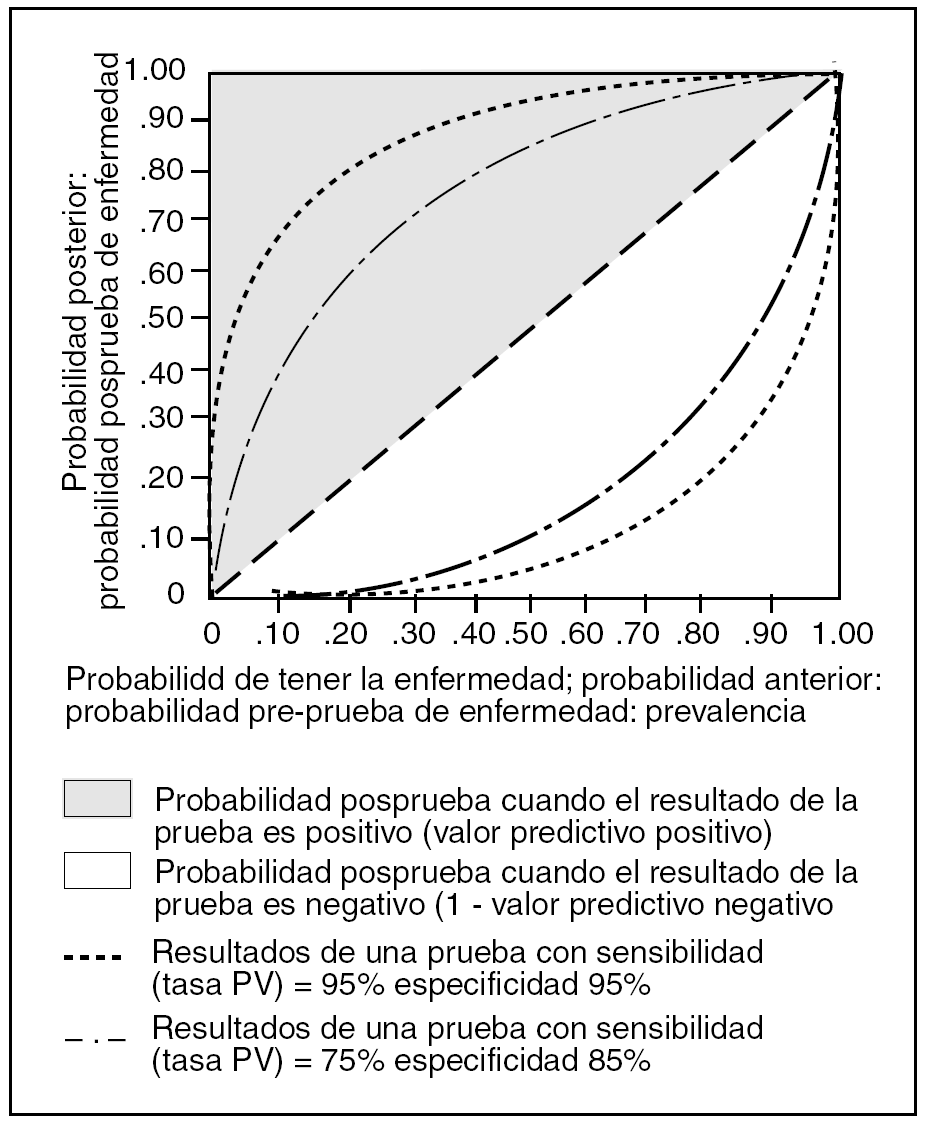
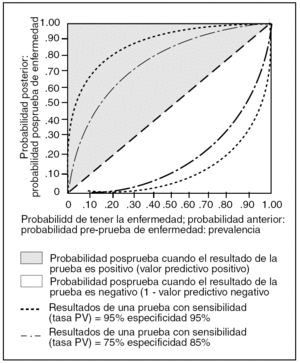
La influencia de la sensibilidad y la especificidad en todo lo anterior se refleja en la figura 1, donde vemos que una reducción de ellas disminuye el rendimiento de la prueba1.
Figura 1. Fuente: Sackett et al1.
RAZONES DE PROBABILIDAD
A veces nos interesa expresar los resultados comparando la probabilidad de obtener un resultado en un individuo con enfermedad y sin enfermedad. Ese índice llamado cociente de probabilidad nos permite evaluar dos métodos diagnósticos diferentes2,3.
Por ello, estos índices no dependen de esa proporción de enfermos en la muestra.
1. Cociente de probabilidad positivo (CP+), también conocido como cociente de verosimilitud (likelihood ratio of positive test). Se calcula dividiendo la proporción de enfermos con prueba positiva entre la proporción de no enfermos con prueba positiva.
Valores mayores de CP+ indican mejor capacidad para diagnosticar la presencia de enfermedad.
CP+ = sensibilidad/1-especificidad.
2. Cociente de probabilidad negativo (CP-). Se calcula dividiendo la proporción de enfermos con prueba negativa entre la proporción de no enfermos con prueba negativa.
Vemos que valores de CP- menores indican una mejor capacidad diagnóstica de la prueba.
CP+ = 1-sensibilidad/especificidad.
En el ejemplo tenemos un CP+ de 4, lo que quiere decir que es 4 veces más probable que la prueba sea anormal en los enfermos que en sanos para la primera prueba y 73 veces más probable para la segunda prueba.
En el mismo ejemplo, el CP- es 0,09, es decir, un resultado negativo se encontró 11 veces más frecuente entre los que no tienen la enfermedad que entre los que la tienen (1/CP- = 1/0,09 = 11,1).
La ventaja de ese índice frente a los VPP y VPN de la prueba radica en que, a diferencia de éstos, no depende de la proporción de enfermos en la muestra, sino tan sólo de la sensibilidad y la especificidad de ésta, de ahí su utilidad a la hora de comparar pruebas diagnósticas.
Además, si conocemos o podemos hacer una estimación de la probabilidad pre-prueba de que un sujeto padezca la enfermedad, utilizando los cocientes de probabilidad, al realizar la prueba podemos "corregir" ese valor de acuerdo con el resultado, de tal manera que la probabilidad aumenta o disminuye según sea el resultado positivo o negativo, aplicando la siguiente fórmula.
P Post = P * CP/1 + P(CP-1)
donde P es la probabilidad pre-prueba, CP el correspondiente cociente de probabilidad (positivo si deseamos calcular la probabilidad de que padezca la enfermedad, negativo en caso contrario) y Ppost es la probabilidad posprueba.
CURVAS ROC
Cuando los valores de la prueba diagnóstica son cuantitativos podemos elegir los puntos de corte de nuestra prueba, con lo cual la sensibilidad y la especificidad variarán.
Al usar una variable continua debe decidirse qué valor se utilizará para clasificar a los individuos como sanos o enfermos.
La curva ROC nos permite relacionar la proporción de verdaderos positivos (sensibilidad) con la proporción de falsos positivos (1-especificidad), o cociente de probabilidad positivo, de tal manera que vamos dando diferentes valores para ver en qué punto es mayor la probabilidad de clasificar correctamente a un individuo al aplicarle la prueba, es decir, la exactitud diagnóstica12,13.
Un valor del 60% significa que un individuo enfermo tiene un 60% más de probabilidad de tener la prueba positiva que uno sano.
Interpretación de la curva ROC
1. La curva ROC es creciente si se modifica el valor de corte para obtener mayor sensibilidad; sólo puede hacer-se a expensas de disminuir al mismo tiempo la especificidad.
2. La diagonal que une los vértices inferior izquierdo y superior derecho, representa el momento en que la curva no sería discriminatoria, es decir, se observan los mismos resultados en enfermos que en sanos.
3. La exactitud de la prueba aumenta a medida que la curva se desplaza desde la diagonal hacia el vértice superior izquierdo. Si la discriminación fuera perfecta (100% de sensibilidad y 100% de especificidad) pasaría por dicho punto.
PRUEBAS MULTIPLES
El uso de pruebas múltiples es muy frecuente en la práctica médica. Generalmente ante una sospecha diagnóstica se suele disponer de varias posibilidades de pruebas que nos ayuden a confirmar el diagnóstico o a descartarlo. Hay dos formas de indicar varias pruebas:
En paralelo
1. Todas las pruebas se aplican simultáneamente a la misma muestra de individuos.
2. Se consideran negativos aquellos sujetos que obtienen resultados negativos en todas las pruebas.
3. Se consideran positivos si obtienen resultados positivos en alguna de ellas.
En serie
1. Se aplica una prueba en primer lugar y después se indica la otra prueba sólo si el individuo resulta positivo en la anterior.
2. Se considera positivo al sujeto que haya tenido resultados positivos en todas las pruebas.
3. Se consideran negativos todos los demás (una o ambas pruebas negativas).
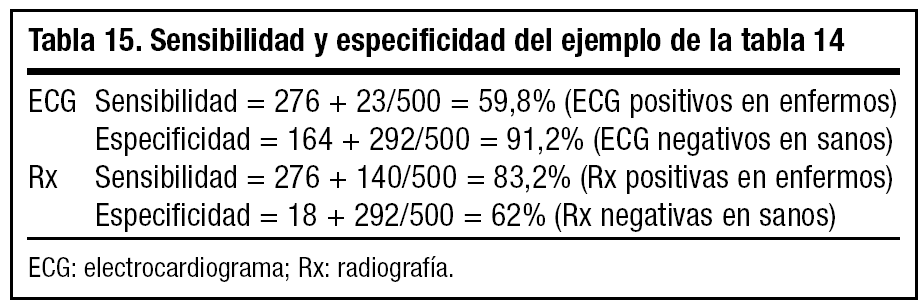
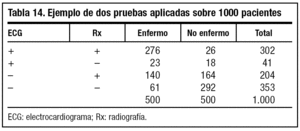
Pongamos un ejemplo: se utilizan dos pruebas para el diagnóstico de una patología cardiaca (electrocardiograma [ECG] y radiografía [Rx]), en 1.000 pacientes, y se obtienen todos los posibles resultados de las dos pruebas, que están reflejados en la tabla 14.
Calculamos la sensibilidad y la especificidad de cada prueba (tabla 15).
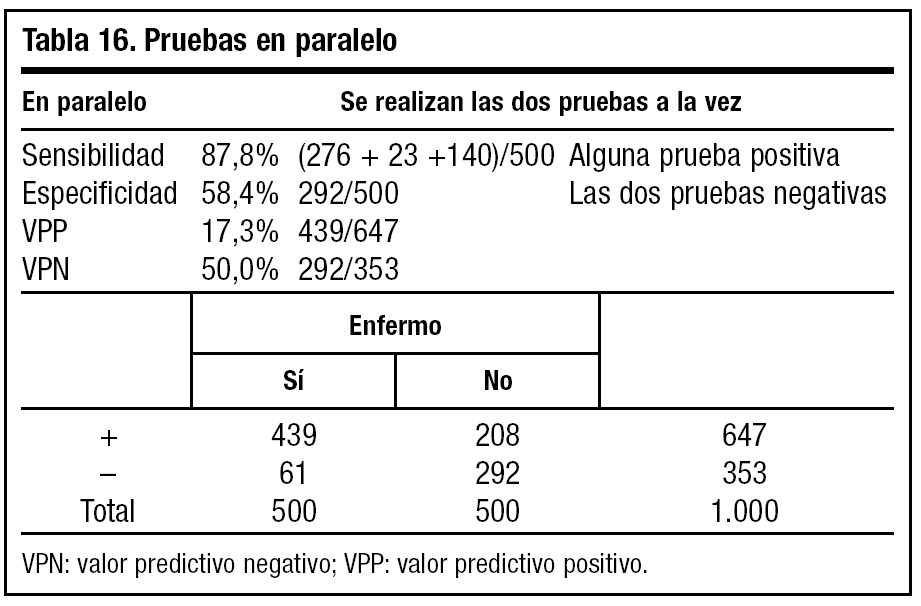
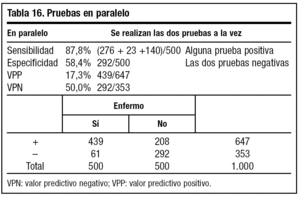
Calculamos la sensibilidad, la especificidad, el VPP y el VPN para las dos pruebas de forma conjunta.
Al realizar las pruebas en paralelo o a la vez, observamos un aumento de sensibilidad y una disminución de especificidad (tabla 16). Por ello debemos utilizar estas pruebas cuando nos interese identificar enfermos (infarto de miocardio).
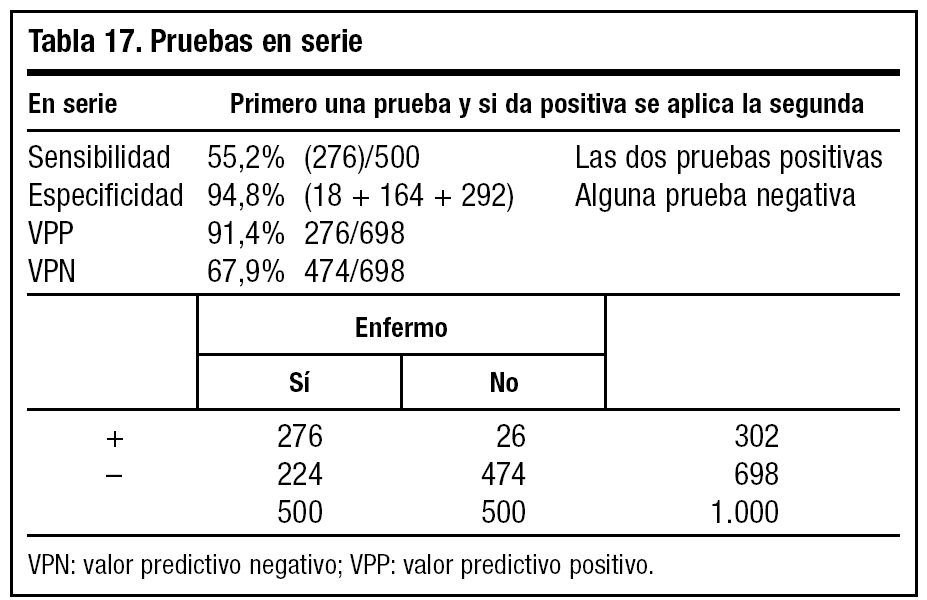
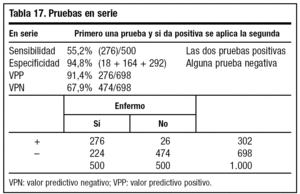
Al realizar las pruebas en serie (tabla 17) exigimos que ambas pruebas diagnósticas sean positivas y observamos un aumento de la especificidad y una disminución de la sensibilidad. Por ello, estas pruebas nos interesan cuando queramos identificar a individuos sanos (prueba del VIH).
ANÁLISIS DE CONCORDANCIA
La precisión de una prueba depende tanto del instrumento de medida como del proceso de medición. Para su control, necesitamos comparar entre sí medidas repetidas de la misma variable y evaluar el grado de acuerdo entre ellas. Ese grado de acuerdo se denomina concordancia, y el análisis de la concordancia entre dos variables nos va a permitir evaluar la reproducibilidad o variabilidad de la medición.
En el caso de que se trate de comparar dos mediciones realizadas en distinto momento por un mismo observador o un mismo instrumento de medida hablamos de concordancia intraobservador o consistencia interna. Si hablamos de comparar las mediciones de dos observadores o dos instrumentos sobre una misma variable, hablamos de concordancia interobservador o consistencia externa.
Existen varios procedimientos para evaluar la concordancia en función del tipo de variable de que se trate.
Variables cualitativas
En el caso de las variables cualitativas hablaremos del índice kappa y dentro de éste lo más sencillo se refleja cuando esta variable es dicotómica, como las que veremos a continuación2.
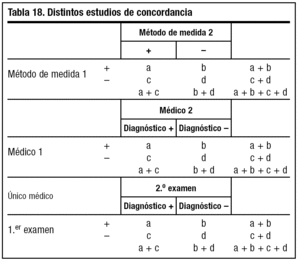
Podemos estudiar la concordancia entre dos métodos de medida distintos o entre dos observaciones distintas por un mismo observador o por dos observadores (tabla 18).
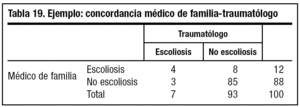
La mejor manera para entenderlo es ir haciendo paralelamente un ejemplo; en este caso veremos la valoración realizada por un médico de familia y por un traumatólogo sobre la presencia de escoliosis entre los alumnos de una clase durante el reconocimiento escolar (tabla 19).
Lo primero que se nos ocurriría para ver el grado de concordancia entre ambos médicos sería calcular la proporción del número de observaciones coincidentes (que sería la suma de los diagnósticos de escoliosis en que ha existido acuerdo y de los casos de acuerdo en la no existencia de escoliosis) con respecto al total de niños examinados, (a + d)/n = (4 + 85)/100 = 0,89, que nos indicaría una concordancia de un 89% (P0). Pero esto no es así, porque parte de este acuerdo en los diagnósticos puede deberse tan sólo al azar. Supongamos por ejemplo que el traumatólogo no explora a los pacientes y decide a cara o cruz quién tiene o no escoliosis, los resu ltados que obtendría serían aproximadamente un 50% de alumnos con escoliosis, lo que nos daría una concordancia de aproximadamente un 61%, que estaría claramente influenciada por el azar. Por tanto, este valor no nos sirve y hay que utilizar otro índice que tenga en cuenta el azar, como es el índice kappa.
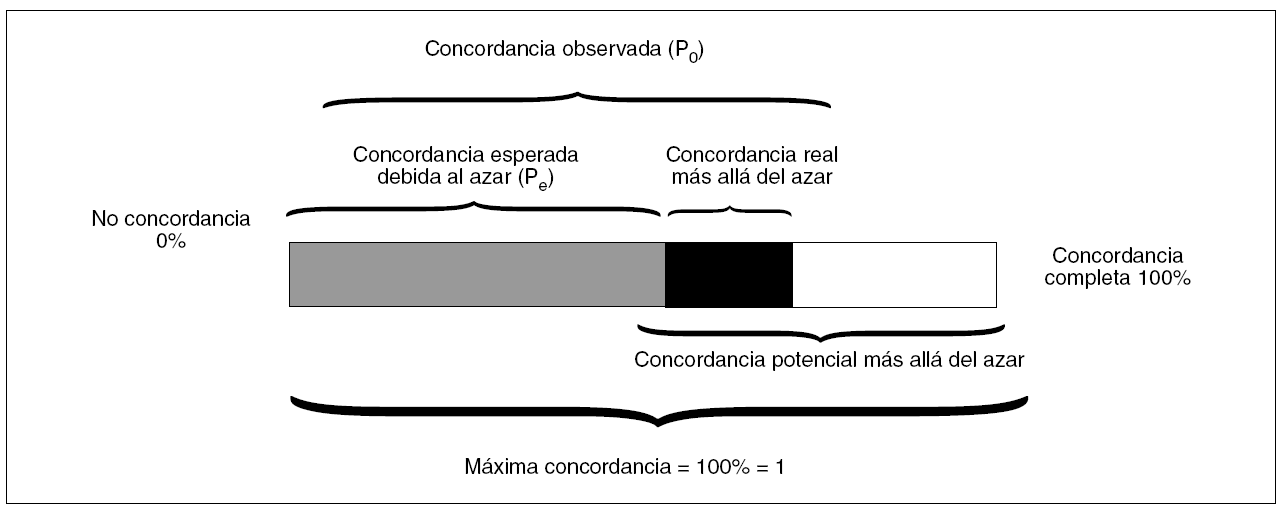
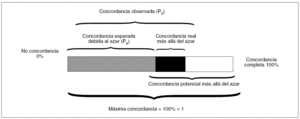
El índice de concordancia kappa se define como la proporción de la concordancia real más allá del azar con respecto a la concordancia potencial más allá del azar. Para entenderlo mejor fijémonos en la figura 21.
Figura 2. Concordancia. Modificada de Sackett et al1.
Índice kappa = P0 - Pe/1 - Pe
De donde P0 = proporción de concordancia observada.
Pe = proporción de concordancia esperada debida al azar.
P0 = (a + d)/N = 89/100 = 0,89; concordancia observada del 89%.
La proporción de concordancia esperada debida al azar (Pe) la calcularíamos a partir de las celdas marginales. Así, el número de ocasiones en que ambos médicos concuerdan debido al azar en el diagnóstico de escoliosis sería igual a (a + b)(a + c)/N = 12 * 7/100 = 0,84, y el número de ocasiones en que los dos médicos coincidirían debido al azar en la no existencia de escoliosis sería igual a (c + d)(b + d)/N = 88 * 93/100 = 81,8.
La proporción de concordancia esperada debida al azar sería la suma de ambas dividida entre el número de alumnos Pe = (0,84 + 81,8)/100 = 0,83.
Índice kappa = (0,89 - 0,83)/1 - 0,83 = 0,35.
En el caso de máxima concordancia, el índice kappa tendría un valor de 1; si la concordancia observada es igual a la esperada tendría un valor de 0; y si la concordancia observada fuese inferior a la esperada tendría un valor inferior a 0.
Para valorar el grado de concordancia en función del índice kappa se utilizan los márgenes expresados en la tabla 20.
Por tanto, en nuestro ejemplo 0,35 se trataría de un grado de concordancia bajo.
En lugar de dar un valor puntual podemos calcular su intervalo de confianza (IC) de manera sencilla con la siguiente fórmula2:
Para un IC del 95%; índice Kappa ± 1,96
En el caso de que no fuera dicotómico y presentara varias categorías se puede hacer el índice de concordancia global o transformar los resultados en dos únicas respuestas convirtiéndolo en tablas de 2x2 como si fuera dicotómica, calculando el índice kappa igual que antes.
Variables cuantitativas
Si se trata de variables cuantitativas, se han utilizado de manera inadecuada algunas pruebas estadísticas como el coeficiente de correlación de Pearson (que mide el grado de relación entre dos variables y no su concordancia), la regresión lineal (que permite predecir el valor de una variable en función de otra, pero no su concordancia) o la comparación de medias (que mide la ausencia de significación estadística dando resultados opuestos a la concordancia)2.
Mencionaremos los procedimientos utilizados con la finalidad de saber interpretarlos, pero sin ahondar en ellos para no complicar en exceso este tema.
Se utiliza el coeficiente de correlación interclase (R), que sería la proporción entre la variabilidad verdadera entre sujetos (σ2v) y la variabilidad total de las mediciones (σ2x), siendo esta última la suma de la variabilidad residual de los errores de medida (σ2e) y la variabilidad verdadera de los sujetos (σ2v) (tabla 21)2.
Otro método que se puede utilizar en caso de variables cuantitativas es el análisis de las diferencias individuales, que puede complementar al anterior.
Se basa en la determinación de la magnitud de las diferencias entre métodos de medida y se representa en un gráfico, de tal manera que hace muy asequible su interpretación.
Por último, debemos indicar que existen en Internet distintos programas de distribución gratuita con los que se pueden calcular de manera interactiva gran parte de los parámetros e índices de los que hemos hablado, por ejemplo SISA (http://home.clara.net/sisa).
Correspondencia: J.L.R. Martín.
Jefe del Área de Investigación Clínica. Fundación para la Investigación
Sanitaria en Castilla La Mancha (FISCAM). Edificio Bulevar.
C/ Berna, n.o 2, local 0-2. 45003 Toledo.
Correo electrónico: jlrmartin@jccm.es
Recibido el 01-10-07; aceptado para su publicación el 01-10-07.