Cognitive neuropsychology focuses on the concepts of dissociation and double dissociation. The performance of number processing and calculation tasks by patients with acquired brain injury can be used to characterise the way in which the healthy cognitive system manipulates numerical symbols and quantities. The objective of this study is to determine the components of the number processing and calculation system.
MethodsParticipants consisted of 6 patients with acquired brain injuries in different cerebral localisations. We used Batería de evaluación del procesamiento numérico y el cálculo, a battery assessing number processing and calculation. Data were analysed using the difference in proportions test.
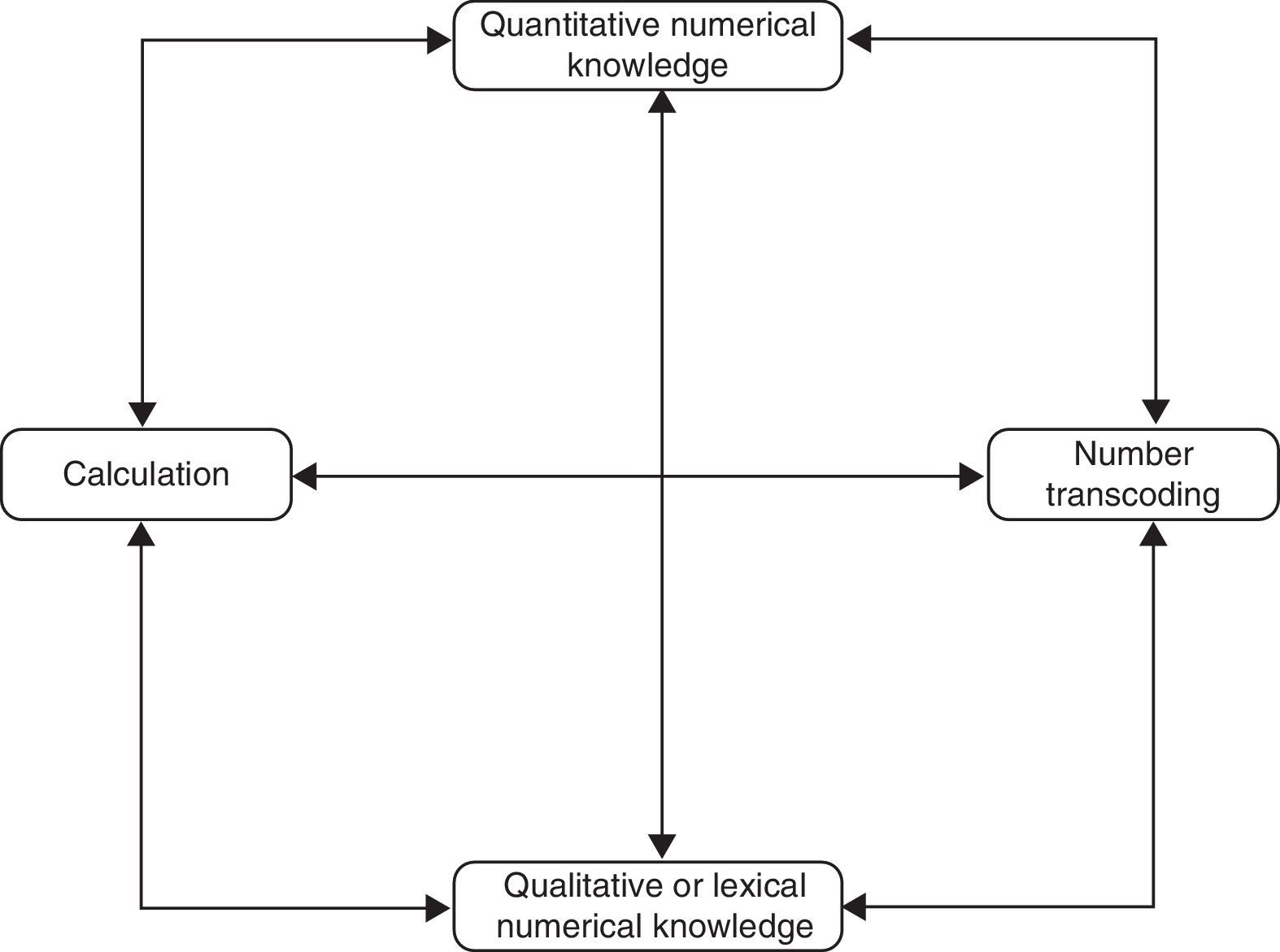
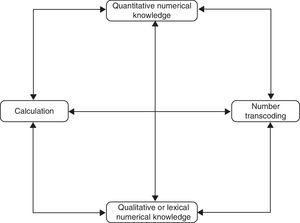
ResultsQuantitative numerical knowledge is independent from number transcoding, qualitative numerical knowledge, and calculation. Recodification is independent from qualitative numerical knowledge and calculation. Quantitative numerical knowledge and calculation are also independent functions.
ConclusionsThe number processing and calculation system comprises at least 4 components that operate independently: quantitative numerical knowledge, number transcoding, qualitative numerical knowledge, and calculation. Therefore, each one may be damaged selectively without affecting the functioning of another. According to the main models of number processing and calculation, each component has different characteristics and cerebral localisations.
La neuropsicología cognitiva se centra en los conceptos de disociación y doble disociación. Mediante la descripción de las ejecuciones de pacientes con daño cerebral adquirido en tareas de procesamiento numérico y cálculo podemos caracterizar cómo el sistema cognitivo sano manipula los símbolos numéricos y/o las cantidades. Así, el objetivo de este trabajo es conocer y caracterizar los distintos componentes que forman el sistema de procesamiento numérico y cálculo.
MétodosLos participantes en este trabajo son 6 pacientes con daño cerebral adquirido en diferentes localizaciones cerebrales. Como instrumento se ha empleado la Batería de Evaluación del Procesamiento Numérico y el Cálculo. Para el análisis de los datos se ha realizado una diferencia de proporciones.
ResultadosEl conocimiento numérico cuantitativo es independiente de la recodificación numérica, el conocimiento numérico cualitativo y el cálculo. La recodificación es independiente del conocimiento numérico cualitativo y del cálculo. El conocimiento numérico cualitativo y el cálculo funcionan de manera independiente.
ConclusionesEl sistema de procesamiento numérico y cálculo parece estar formado por al menos 4 componentes que funcionarían de manera independiente, y estos son: conocimiento numérico cuantitativo, recodificación numérica, conocimiento numérico cualitativo y cálculo. De ahí que cada uno de ellos pueda dañarse de forma selectiva sin afectar al funcionamiento de los otros. Según los principales modelos de procesamiento numérico y cálculo, cada uno de ellos tiene características y localizaciones cerebrales diferentes.
Research in the field of cognitive neuropsychology is based on the concepts of dissociation and double dissociation. When a patient who is not able to perform task A effectively can perform task B without difficulties, we say that dissociation exists between the 2 tasks. However, this finding could simply be due to one of the tasks being easier to perform than the other.1,2 Therefore, double dissociation is a more conclusive finding. Double dissociation is demonstrated by the presence of another patient who is able to complete task A but unable to perform task B. This illustrates the functional specialisation of the cognitive system by providing proof of its modularity. Double dissociation can be used to demonstrate the functional independence of certain processing modules.3
Cognitive neuropsychology research includes recent descriptions of cases that contribute key information about the processes involved in number processing and calculation.4 Major dissociations described in the literature include those of word and number processing,5,6 number production and comprehension,7,8 number processing and calculation,8 rote verbal and quantitative knowledge,7 number retrieval and calculation processes,4,6 oral and written calculation,9 and lastly, independence between different arithmetic operations.7,10
Different number processing-calculation models have been used to attempt to explain these dissociations. Each of these models presents a list of what processes, following which sequence and internal organisation scheme, occur during number processing and calculation. One of the most influential models, proposed by McCloskey et al.,6,11 includes both number processing and calculation and is fundamentally semantic. This model has given rise to others including non-semantic processing, such as the Cipolotti,12 Cipolotti and Butterworth,8 and Cuetos and Miera13 models. The latter does not include calculation processes. We should also highlight the anatomical and functional model7,14 developed after the triple-code model.15
Our study, which draws from the dissociations described in the literature and considers the contributions from various theoretical models, aims to understand the relationships between elements of the number processing and calculation system. The study used evidence obtained from the research on patients with acquired brain injury.
Patients and methodsThis research was conducted at the University of Huelva over a 6-month period. Study participants consisted of 6 patients with acquired brain injury occurring in adulthood and at different cortex localisations.
Inclusion criteriaThe study included consenting patients aged 38 to 65 years with a minimum of 8 years of basic education completed prior to injury. The disorder had to originate in the CNS and the injury had to have occurred at least 6 months before date of inclusion. Level of consciousness was optimal in all patients; intact language comprehension following injury was required to ensure that subjects understood instructions.
Appendix 1 includes a summary of each participants’ medical history.
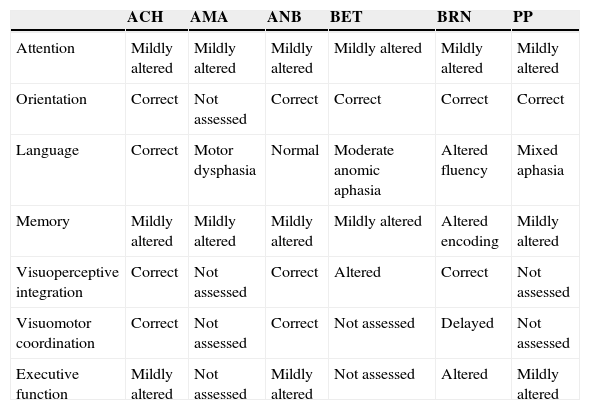
All participants in this study underwent a neuropsychological examination that tested attention, orientation, memory, visuoperceptual integration, visuomotor coordination, and executive function. Table 1 presents the most pertinent results from the neuropsychological evaluation.
Main neuropsychological features in patients.
| ACH | AMA | ANB | BET | BRN | PP | |
|---|---|---|---|---|---|---|
| Attention | Mildly altered | Mildly altered | Mildly altered | Mildly altered | Mildly altered | Mildly altered |
| Orientation | Correct | Not assessed | Correct | Correct | Correct | Correct |
| Language | Correct | Motor dysphasia | Normal | Moderate anomic aphasia | Altered fluency | Mixed aphasia |
| Memory | Mildly altered | Mildly altered | Mildly altered | Mildly altered | Altered encoding | Mildly altered |
| Visuoperceptive integration | Correct | Not assessed | Correct | Altered | Correct | Not assessed |
| Visuomotor coordination | Correct | Not assessed | Correct | Not assessed | Delayed | Not assessed |
| Executive function | Mildly altered | Not assessed | Mildly altered | Not assessed | Altered | Mildly altered |
We have used the Batería de Evaluación del Procesamiento Numérico y el Cálculo,16 a battery that assesses number processing and calculation. This battery includes 6 sections: number comprehension, number transcoding, arithmetic symbols, calculation, qualitative or lexical numerical knowledge, and number sequencing.
Data analysisWe calculated the difference of proportions,17,18 an operation that lets us compare a patient's performance to control group results, even where the total number of items used is not the same.
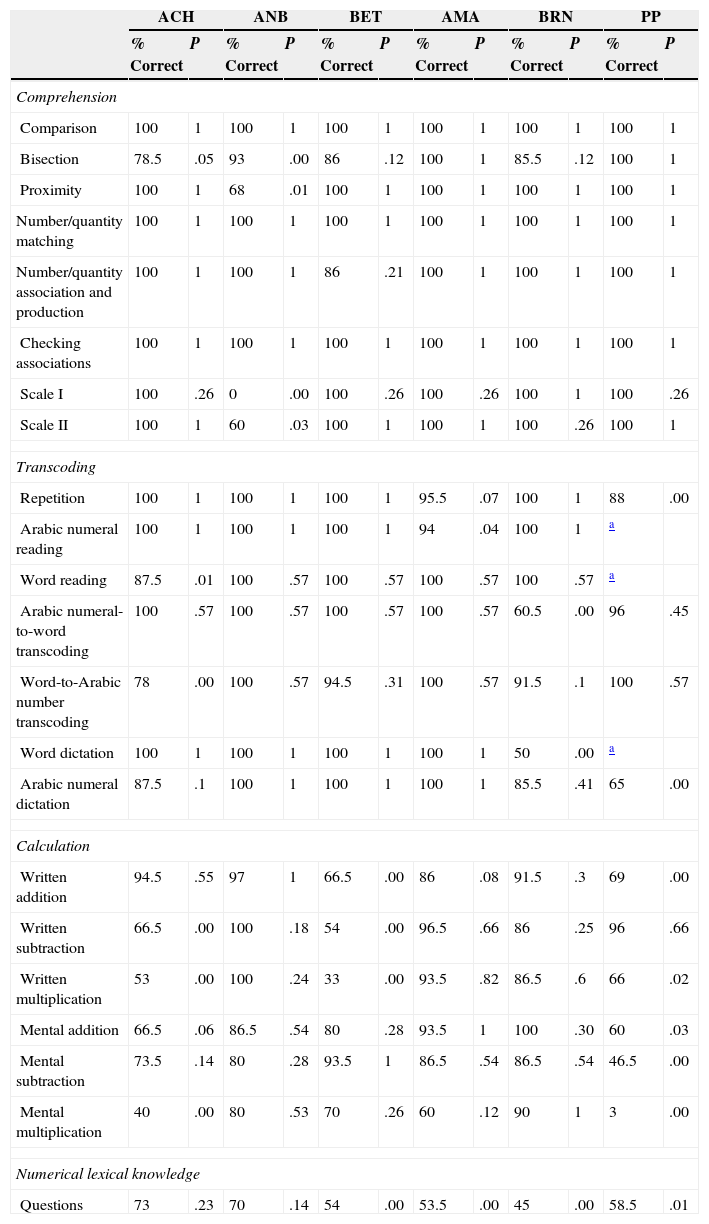
ResultsResults for each patient and each test are summarised in Table 2.
Patient results on tests assessing number processing and calculation.
| ACH | ANB | BET | AMA | BRN | PP | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| % Correct | P | % Correct | P | % Correct | P | % Correct | P | % Correct | P | % Correct | P | |
| Comprehension | ||||||||||||
| Comparison | 100 | 1 | 100 | 1 | 100 | 1 | 100 | 1 | 100 | 1 | 100 | 1 |
| Bisection | 78.5 | .05 | 93 | .00 | 86 | .12 | 100 | 1 | 85.5 | .12 | 100 | 1 |
| Proximity | 100 | 1 | 68 | .01 | 100 | 1 | 100 | 1 | 100 | 1 | 100 | 1 |
| Number/quantity matching | 100 | 1 | 100 | 1 | 100 | 1 | 100 | 1 | 100 | 1 | 100 | 1 |
| Number/quantity association and production | 100 | 1 | 100 | 1 | 86 | .21 | 100 | 1 | 100 | 1 | 100 | 1 |
| Checking associations | 100 | 1 | 100 | 1 | 100 | 1 | 100 | 1 | 100 | 1 | 100 | 1 |
| Scale I | 100 | .26 | 0 | .00 | 100 | .26 | 100 | .26 | 100 | 1 | 100 | .26 |
| Scale II | 100 | 1 | 60 | .03 | 100 | 1 | 100 | 1 | 100 | .26 | 100 | 1 |
| Transcoding | ||||||||||||
| Repetition | 100 | 1 | 100 | 1 | 100 | 1 | 95.5 | .07 | 100 | 1 | 88 | .00 |
| Arabic numeral reading | 100 | 1 | 100 | 1 | 100 | 1 | 94 | .04 | 100 | 1 | a | |
| Word reading | 87.5 | .01 | 100 | .57 | 100 | .57 | 100 | .57 | 100 | .57 | a | |
| Arabic numeral-to-word transcoding | 100 | .57 | 100 | .57 | 100 | .57 | 100 | .57 | 60.5 | .00 | 96 | .45 |
| Word-to-Arabic number transcoding | 78 | .00 | 100 | .57 | 94.5 | .31 | 100 | .57 | 91.5 | .1 | 100 | .57 |
| Word dictation | 100 | 1 | 100 | 1 | 100 | 1 | 100 | 1 | 50 | .00 | a | |
| Arabic numeral dictation | 87.5 | .1 | 100 | 1 | 100 | 1 | 100 | 1 | 85.5 | .41 | 65 | .00 |
| Calculation | ||||||||||||
| Written addition | 94.5 | .55 | 97 | 1 | 66.5 | .00 | 86 | .08 | 91.5 | .3 | 69 | .00 |
| Written subtraction | 66.5 | .00 | 100 | .18 | 54 | .00 | 96.5 | .66 | 86 | .25 | 96 | .66 |
| Written multiplication | 53 | .00 | 100 | .24 | 33 | .00 | 93.5 | .82 | 86.5 | .6 | 66 | .02 |
| Mental addition | 66.5 | .06 | 86.5 | .54 | 80 | .28 | 93.5 | 1 | 100 | .30 | 60 | .03 |
| Mental subtraction | 73.5 | .14 | 80 | .28 | 93.5 | 1 | 86.5 | .54 | 86.5 | .54 | 46.5 | .00 |
| Mental multiplication | 40 | .00 | 80 | .53 | 70 | .26 | 60 | .12 | 90 | 1 | 3 | .00 |
| Numerical lexical knowledge | ||||||||||||
| Questions | 73 | .23 | 70 | .14 | 54 | .00 | 53.5 | .00 | 45 | .00 | 58.5 | .01 |
Firstly, we observe that quantitative numerical knowledge is doubly dissociated from other elements of the number processing and calculation system. On the one hand, our patient sample illustrated a double dissociation between quantitative and qualitative (lexical) numerical knowledge. Patients BET, AMA, BRN, and PP preserve quantitative numerical knowledge but their qualitative knowledge seems altered; in patient ANB, the opposite pattern was observed.
Quantitative numerical knowledge, on the other hand, was shown to be doubly dissociated from transcoding ability. Patients ACH, AMA, BRN, and PP display preserved quantitative numerical knowledge but experience difficulties with multiple number transcoding tasks. Evidence of double dissociation was provided by patient ANB, who presents alterations in quantitative numerical knowledge but preserves the skills involved in number transcoding, as mentioned before.
Lastly, quantitative numerical knowledge was shown to be doubly dissociated from calculation. Patients ACH and PP preserved quantitative numerical knowledge while presenting calculation difficulties. Patient ANB, however, presented altered quantitative numerical knowledge with preserved calculation abilities.
Number transcoding does not depend on quantitative numerical knowledge, as mentioned before, and it is also doubly dissociated from calculation. For example, patient BET demonstrates intact number transcoding skills while showing impaired calculation (statistically significant differences are present in 3 out of 6 tasks). This double dissociation is confirmed by patient BRN who presents the opposite pattern; he performs all 6 calculation tasks correctly but his results from several number transcoding tasks display significant abnormalities.
Lastly, number transcoding is doubly dissociated from lexical or qualitative numerical knowledge as evidenced by two patients: BET, with preserved number transcoding and altered numerical-lexical knowledge; and ACH, with preserved numerical-lexical knowledge and difficulties with multiple number transcoding tasks.
Calculation, which is doubly dissociated from quantitative numerical understanding and number transcoding, as mentioned before, is also doubly dissociated from qualitative or lexical numerical knowledge. On the one hand, patient ACH, who displays altered calculation skills, shows an intact numerical-lexical knowledge. In contrast, patients AMA and BRN present the opposite pattern: altered qualitative numerical-lexical understanding and preserved number transcoding skills.
In summary, performance patterns in our patients show a series of double dissociations that support the independence of at least 4 elements of the number processing and calculation system.
DiscussionResults from our patients are consistent with the evidence reported in the literature.
Our results show that quantitative numerical knowledge is doubly dissociated from qualitative numerical and lexical knowledge, and these findings support results from prior studies, such as the cases of patient HBA15 and patient MAR.19 The latter case was particularly illustrative; even though the patient stated that 5 is greater than 6, he was still able to associate the number 5 with a religious reference: the 5 pillars of Islam (p. 192).
Therefore, our findings confirm those from other similar studies that have pointed to an independent relationship between quantitative and qualitative numerical knowledge20,21; this independence is also in line with the postulates of the functional-anatomical model.14 According to this model, the system called analogue magnitude representation, which is responsible for quantity processing, also includes non-quantitative semantic information: concepts such as ‘power of 2’, ‘prime number’, or ‘famous date’ (p. 86).
However, quantitative numerical knowledge, or numerical comprehension, is doubly dissociated from transcoding skills, which is in line with the results described in the literature.6–8,11 This independence is coherent with the functional-anatomical model,7,14 which postulates that analogue magnitude representation, which is responsible for numerical comprehension, is located in the lower parietal area of both hemispheres. It also suggests that it is independent from number production processes, which are located in the classic perisylvian language areas of the left hemisphere. Therefore, number transcoding skills would depend on the areas of the left hemisphere responsible for language, while number comprehension would be localised in both parietal lobes.
Thirdly, quantitative numerical knowledge was shown to be doubly dissociated from calculation. Evidence of this independence was recently delivered by a study on patients with focal lesions in different localisations.22 Different models provide distinct explanations for these results.
According to the model by McCloskey et al.,6 numerical inputs must reach the abstract semantic representation system and, from there, the calculation system, which may be selectively affected. Understanding a number is therefore a preliminary step in the process of performing a calculation. This provides a simple explanation for the cases of patients ACH and PP, since they had preserved the route from numerical input to semantic representation. These patients’ numerical comprehension remained intact, but they could not perform arithmetic because their calculation systems (a later stage) were altered. However, this model does not fit the results of patient ANB, since it postulates that access to the internal abstract representation of quantities –altered in this patient– is a prerequisite for performing arithmetic operations correctly (and yet patient ANB demonstrated that capacity).
Furthermore, the functional-anatomical model7,14 also postulates that both quantitative numerical knowledge (numerical comprehension), and the operations involved in subtraction, depend on the analogue magnitude representation (responsible for the semantic production processes). Therefore, if one area is altered, the other will be as well. However, results from our patient ANB are not compatible with this hypothesis; despite her difficulties with numerical comprehension, she is able to subtract correctly, using both oral and written methods. Incompatibility is confirmed by the cases of patients ACH and PP, who show preserved quantitative numerical knowledge but present altered subtraction skills.
Our results also show that number transcoding is doubly dissociated from calculation; this independent relationship has been widely described in the literature,7,8,23–26 and it concurs with the model by McCloskey et al.6 The model explains this dissociation as a result of damage to the route leading from internal abstract representation to the calculation system, or to the calculation system itself. According to the model, calculation is independent from number production. Nevertheless, our results are not compatible with the postulates of the functional-anatomical model,7,14 which would be unable to explain the results of patient BRN, who presents altered transcoding skills but is able to perform simple addition and multiplication. Therefore, these 2 tasks cannot depend on the same process.
Furthermore, number transcoding is doubly dissociated from qualitative or lexical numerical knowledge, which is compatible with postulates of the functional-anatomical model. According to this model, as previously stated, transcoding skills are located in the classic perisylvian language areas that are exclusive to the left hemisphere, whereas qualitative or lexical numerical knowledge is part of the analogue magnitude representation area, located in both parietal lobes.7,14
Lastly, our results confirm that calculation is doubly dissociated from qualitative or lexical numerical knowledge. The functional-anatomical model can only provide a partial explanation for this dissociation,7,14 since the notion of independence between the operations of addition and multiplication with regard to qualitative numerical knowledge is compatible with the model. These operations depend on different representations (semantic production and verbal word frame, respectively). However, the independence between qualitative numerical knowledge and subtraction observed in AMA and BRM does not follow the model's postulates, since it claims that both types of tasks depend on analogue magnitude representation.
To summarise, we can state that quantitative numerical knowledge is functionally independent from number transcoding skills, calculation, and from qualitative or lexical numerical knowledge. The skills involved in number transcoding also work independently from both calculation and qualitative numerical knowledge. Furthermore, calculation is independent from qualitative or lexical numerical knowledge.
If this is true, the number processing and calculation system would include at least 4 subsystems: quantitative numerical knowledge, qualitative numerical knowledge, calculation, and number processing. Since these subsystems seem to be susceptible to selective damage, they must be independent from one another. This also means that they would be dependent on different cognitive processes and be found in different brain localisations. Fig. 1 shows a schematic representation of these independent relationships.
Our most interesting finding is that the number processing and calculation system is not a single mechanism, but rather a series of different elements that are susceptible to selective damage. This being the case, rehabilitation of these processes should be carried out in the same independent way. A comprehensive diagnosis is necessary to precisely identify the damaged component of number processing and calculation so as to design the most efficient intervention targeting that component.
Lastly, regarding the methodology we have used, we would like to point out that injuries are never exactly the same among all patients, and the cortical areas they occupy can be difficult to delimit. We must therefore continue working in this line of research so as to confirm our results in future projects, while emphasising that our present results are coherent with findings from other studies.
Conflicts of interestThe authors have no conflicts of interest to declare.
ACH. Man aged 40 with a primary education. Diffuse axonal lesion secondary to head trauma in a traffic accident. Small temporal lesion in the right hemisphere. Subarachnoid haemorrhage (no area specified), predominantly right-sided frontal hygroma (cystic lymphangioma).
AMA. Woman aged 40 with a secondary education. Presurgical cranial MRI showed 6-cm-diameter mass at midline infiltrating the interventricular septum. Associated with mild dilation of the vestibular area of the lateral ventricles. She underwent surgery for a central neurocytoma; the tumour was partially resected by craniotomy, and the patient presented severe right hemiparesis and motor aphasia in the postoperative period. Following left posterior parietal craniotomy, a loculus developed at the surgical bed and its mass effect caused retraction of left lateral ventricle. A mass measuring 3.5cm×2cm was observed on the posterior half of the interventricular septum and protruding on either side of the midline. The tumour presented moderate contrast enhancement. There is also a nodular shape with a similar signal intensity in the left foramen of Monro and the wall of the left ventricular body. Findings described here are compatible with a tumour remnant on the midline. We cannot rule out a neoplastic or post-surgical origin of the lesions in the foramen of Monro and the lateral wall of the left ventricle. Postsurgical changes in the left parietal bone shows a wide area of encephalomalacia in the underlying parenchyma that communicates with the left ventricular atrium. Asymmetrical dilatation in the form of an enlarged left lateral ventricle suggests obstruction of the foramen of Monro. Imaging showed heterogeneous hyperenhancing mass (3cm at its widest point) at the base of the septum pellucidum corresponding to tumour remnants from the central neurocytoma. Anatomical pathology results showed a benign tumour.
ANB. Woman aged 38, university graduate. Admitted on emergency basis due to a 1-month history of frontotemporal headache. She was diagnosed with a colloid cyst in the third ventricle with reactive hydrocephalus; surgery was performed 3 days later. The procedure was a left frontal craniotomy with a circular corticotomy used to penetrate the left lateral ventricle. According to her family, she was completely disoriented in the early postoperative period but then recovered little by little. She experienced a period of retrograde and anterograde amnesia (the latter for a longer time period lasting about a year). The family also reported memory problems, obsessive ideation, and changes in personality. The psychological report highlights cognitive deficits related to memory failure and inappropriate adaptation to new situations. The patient presented extrapyramidal syndrome 3 years later. During that time, she experienced depressed mood with feelings of sadness, worthlessness, and lack of motivation, combined with symptoms of anxiety. Four years after onset of extrapyramidal syndrome, the neurology department confirmed ‘cognitive and behaviour sequelae following surgical removal of colloid cyst’.
BET. Woman aged 42 with primary studies, presenting with head trauma and SAH. She underwent surgery to embolise an aneurysm of the anterior communicating artery 4 months later. Hydrocephalus was treated with ventriculoperitoneal shunting. Areas of residual encephalomalacia were identified in the anterior end of both frontal lobes (anterobasal localisation in the left lobe and predominantly in the superior frontal gyrus in the right lobe). These areas were associated with a more marked retraction effect on frontal horns in the left hemisphere. The catheter for ventricular shunt passed through the right frontal lobe.
BRN. Man aged 40 with primary studies. He was admitted with a score of 3 on the GCS following a traffic accident. Results from the head CT showed contusion of the soft tissues of the left frontoparietal region. Left-sided sylvian fissure SAH showing occasional punctiform contusion foci in left centrum semiovale and left cortex, and possibly also in right frontal parasagittal region. Results from EEG 2 years later show discrete bioelectric alterations in the parietotemporal region of the left hemisphere.
PP. Man aged 54 with primary studies. Admitted to the emergency department for symptoms of sensorimotor loss in right limbs. EEG revealed high-voltage theta-delta waves in the left parietal-temporal areas. Head CT showed an ischaemic infarct in the left parietal region. Cranial MRI: left temporo-parieto-occipital infarct, small pontine infarct, ischaemic foci in the right corona radiata and right cerebral peduncle. Echo Doppler detected occlusion at the origin of the left internal carotid artery with no pathological findings in the right carotid. EEG performed 48 hours later reported slow cerebral bioelectrical activity at the level of both left parieto-temporal regions. He was diagnosed with internal carotid artery thrombosis at the origin of the internal carotid and a cerebral infarct in the territory of the same artery. Cerebral lacunar infarcts were identified in other vascular territories. Arteriography taken one month later confirmed occlusion of the origin of the left carotid artery. A CT taken 2 months later showed hypodensity in the left parietal region.
Please cite this article as: Salguero-Alcañiz MP, Alameda-Bailén JR. Sistema de procesamiento numérico y cálculo: evidencias desde la neuropsicología cognitiva. Neurología. 2015;30:169–175.