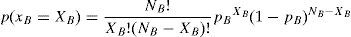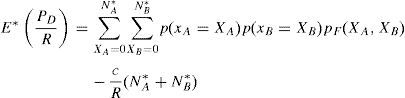New product development is an essential competence to organizations. Launching success products requires elaborate and precise knowledge about the technological platforms, like the most important market needs and characteristics, and the project team have to employ information systems to support the project decisions, which must be rapid and accurate. However, when the market characteristics are much dynamic and change rapidly or the development project aims at a really new product, the levels of uncertainties are greater, and the project team must employ more robust strategies of risk management. Option thinking is useful to develop several concept alternatives of some crucial subsystems of the new product in order to achieve new technical and market knowledge by repeating cycles of design, built and tested by several and different prototypes in parallel. These different prototypes develop, test and can accumulate knowledge about each one, different technologies, architectures and quality attributes or the usability for potential customers.
This study achieves the optimal number of concept options to develop in parallel in order to maximize the economic performance of the development project of a new product constituted of two important subsystems. Mathematical models simulating the sequential decision process are developed to determine the economic result and risk of a two-subsystem product innovation project. Our results point the parallel development of concept options as a robust strategy to manage new product development mostly in adverse conditions, that is, with greater levels of uncertainties.
The management process for new product development (NPD) is rapidly becoming the most important competence that a company must have, especially if its business environment is dynamic and competitive. To meet increasingly diversified demand, organizations from all industry sectors have had to develop competences both in the production planning and control and in the innovation of products and manufacturing processes. For Clark and Wheelwright (1993), there is a growing concern among companies in improving their management of new product and process development because of the huge pressures on them in the international business environment. For the above authors, management of the innovation process is no longer just a concern of high technology companies, but is a fundamentally necessary competence for each and every company.
Time-to-market for the whole process, from mapping out the technological and marketing strategies to the development and subsequent launch of the product in the market, has undergone a drastic reduction in companies, mostly in competitive business environment. A well-known strategy on NPD that aims at reducing time-to-market is the Integrated Project (IP), which has been cited (Clark & Fujimoto, 1991; Clark & Wheelwright, 1993; Ettlie & Stoll, 1990; Kessler & Chakrabarti, 1996; Takeuchi & Nonaka, 1986; Tidd, Bessant, & Pavitt, 1997) as the development approach that better addresses the problem for reducing time-to-market. This is a methodology that seeks to deal with the development process by integrating the functions and decisions in a multidisciplinary way and by team collocation. The main objective is to anticipate problems and conflicts earlier so that they can be solved earlier, thereby considerably reducing the amount of resources and time spent on subsequent analyses and tasks that would need to be redone. IP seeks that all tasks of the project and all elements of the life cycle of the product, from conception to sales, including quality attributes, costs and customer requirements, should be considered by all in the NPD multidisciplinary team (Brown & Eisenhardt, 1995; Clark & Wheelwright, 1993; Takeuchi & Nonaka, 1986).
The Integrated Project has been considered responsible for constantly reducing not only the time-to-market but also for new product development and reduced production costs and certainly also for gathering products with greater levels of quality and functionality, mostly for new products with lower levels of innovativeness (e.g., Brown & Eisenhardt, 1995; Clark & Fujimoto, 1991; Clark & Wheelwright, 1993; Kessler & Chakrabarti, 1996; Smith & Reinertsen, 1998; Takeuchi & Nonaka, 1986; Vesey, 1991).
However, when the market characteristics are so dynamic and unknown, where its needs change much rapidly or the development project aims at a radically or really new product, the levels of uncertainties are greater and the project team must employ more robust strategies of risk management in order to increase the chances of hitting the target quickly. Option thinking is much useful to develop several concept alternatives of some crucial subsystems of the new product in order to achieve new technical and market knowledge by also employing and considering the integrated project philosophy, repeat cycles of design, and building and testing of several and different prototypes of concepts in parallel. These different prototypes of concepts develop, test and accumulate knowledge about each one, different technologies, architectures and quality attributes or the usability for potential customers.
In these conditions, the team cannot develop only one concept because the risk is very high and a failure could compromise the project. Few concept options lead to a less costly but successfully low NPD project. On the other hand, greater quantities of concept options can improve the potentiality of obtaining success in launching the product, but incurring higher costs. In this context, the most important question is how many concept options the project team should develop in parallel in order to maximize the expected economic performance of the new product project?
This research presents a methodology to achieve the expected economic performance and the risk of the parallel development of several concept options. We apply a mathematical modeling in order to represent the sequential decision process methodology that parameterizes some of the main characteristics of product development projects (e.g., performance uncertainty, complexity, development costs and potential revenue from the market). We also consider the economic result and risks of the strategy of only one concept development in order to be used as a simple reference for comparison with the results from the parallel development strategy.
The results show that parallel development of several concept options is a strategy that presents a hedge for economic performance mostly to the projects where there are higher levels of uncertainty. Risk is considered as the probability that the project does not achieve success in the development process.
The paper is structured in four sections. The second section gives the literature review on the subject. The third section presents the mathematical modeling and main assumptions, as well as computational results and analyses. The fourth section presents the main conclusions, and contributions to literature besides the suggestions for future researches.
Literature backgroundThis section presents a brief discussion of the literature on innovation management, new products development projects and also on option thinking and parallel development, important for the conduction of this study.
The competence of innovation managementChanges in the businesses environments in the past three decades have imposed organizations to seek new strategies to produce, buy, sell, distribute and develop new products. From the 70s, organizations that have had to adapt to the new environment quickly began to form and Innovation has become the most desired competence.
For Clark and Wheelwright (1993), it is not that some companies simply increased the percentage of revenues yielded from research and development (R&D), but the process has been driven by large forces, as increase in international competition in segmentation and fragmentation of markets and also due to the diversification of new technologies.
Bolwijn and Kumpe (1990) created a phase model to understand and explain the relationships between criticism and diversification of the markets in the business environments with cycles of competences creation cycles by companies after surveying several organizations in Europe. For them, the companies were developing and accumulating competences along the past few decades. The companies that survive will be accumulating all the previous competences. The authors relate the market requisites with the competences and the performances that the companies had to develop as an answer and as evolution along time, as presented in Table 1.
Market requisites and competences evolution of organizations.
| Decades | Market requisites | Performances or strategies |
|---|---|---|
| 1960 | Price | Efficiency |
| 1970 | Price, Quality | Efficiency+Quality |
| 1980 | Price, Quality, Products Lines | Efficiency+Quality+Flexibility |
| 1990 | Price, Quality on Products Lines, Novelty | Efficiency+Quality+Flexibility+Innovation |
Source: Bolwijn and Kumpe (1990).
The new product development projects usually involve various successive stages of activities, sometimes overlapping, to reach its objectives. These activities can be classified in different forms, depending on the perspective adopted. The classification presented by Ulrich and Eppinger (2000), starting with a perspective of management of predominantly technical activities of the development project, incorporate the following generic tasks: (1) Development of concepts – identification of the needs of the target market, generation and evaluation of alternative concepts for the new product, and the selection of some concepts for the next stage of the project; (2) Project of the System – definition of the architecture of the product and its subsystems and subsystems; (3) Detailed Project – detailed specifications of each subsystem and subsystem, and respective productive processes; (4) Tests and improvements – prototypes of subsystems, subsystems and systems are constructed and tested, and the results of the tests are used to improve the project; and (5) Preparation for the launch – pilot production to identify and correct problems and train the operators.
Clark and Wheelwright (1993) point that the development project activities can be basically reduced to three important stages: design, build and test. In the design stage, the project team defines the methods and generates the alternatives of the project. The build stage has the objective of transforming the alternatives of the projects into forms/objects, that is, into prototypes, in order to permit the implementation of the tests of concepts.
The specific forms or objects can be created using Computer Aided Design (CAD) software in an initial stage of development or constructed with more easily handled materials, like plastic or less hard metals. They may also be created using materials and production processes that are similar to the commercial process in a final stage of development. In the test phase, depending on the specific objects of the design–build–test cycle in question, the test can be geared toward a particular dimension or attribute (for example, to measure the level of noise created by the mechanism) using a focused prototype or can involve an evaluation of the system in real conditions using a comprehensive prototype (Ulrich & Eppinger, 2000).
New product development requires the planning and execution of a project that combines knowledge and consistencies of various functional areas of the organization. Roughly three large areas of the project evolve: marketing to map the needs of the consumers and to position the new product in the market; engineering of the product to pursue a product project that will satisfy the needs of the consumers in an efficient form; manufacturing, that will seek the most economic and efficient forms of producing the product, and finally, the beginning of production (ramp-up) and the commercialization of the product. The paradigm was, until some decades ago, to conduct in separate and sequentially the main stages or tasks of the project. The relative certainties about demand and consumer preference for a product and about the technology employed in the product and process created an extremely comfortable situation for the project engineers who could work in a sequential form (Baldwin & Clark, 2000; Clark & Fujimoto, 1991; Clark & Wheelwright, 1993; Kessler & Chakrabarti, 1996; Liker, Collins, & Hull, 1999; Shigley & Mitchell, 1983; Smith & Reinertsen, 1998; Vesey, 1991).
Since the seminal study of contingency theory, where Lawrence and Lorsch (1969) identified different needs of integration in organizational structure for innovation as response for surviving in different business environments, several researches associate the success in innovation activities, as developing better products, the achievement of greater outcomes and decrease of projects time-to-market, to a higher degree of overlapping and integration of important tasks in NPD that could be achieved by multidisciplinary teams in a more integrated project (IP) (e.g., Brown & Eisenhardt, 1995; Clark & Fujimoto, 1991; Clark & Wheelwright, 1993; Cooper & Kleinschimdt, 1994; Gupta, Raj, & Wilemon, 1986; Utterback, 1971; Vesey, 1991).
Some studies (e.g., Clark & Fujimoto, 1991; Clark & Wheelwright, 1993; Cooper & Kleinschimdt, 1994, 1987; Kessler & Chakrabarti, 1996; Smith & Reinertsen, 1998; Takeuchi & Nonaka, 1986) have found very favorable results for IP regarding its efficiency in increasing product quality and productivity in the development and production costs and decreasing the time-to-market mostly, for incremental projects.
However, when the development project aims at a more radically or really new product, the levels of technological uncertainties are greater and the project team must employ robust strategies of risk management. Option thinking is much useful to develop several concept alternatives of some crucial subsystems of the new product. These different prototypes develop, test and accumulate knowledge about each one, different technologies, architectures and quality attributes or the usability for potential customers.
Option thinking and parallel developmentOption thinking or real option is the term employed to denominate some strategies that endow a decision process with greater flexibility of action and reaction. We can face them as very useful instruments to create business opportunities. The name appears from the term options or financial options that are strategies of risk management for financial decisions. The real options give support to the manager for the decision making, because they allow the managers mitigate the risks in future scenarios of the business environment. Such instruments enable the manager have more alternatives to choose in the future, that is, more flexibility in the decision making facing the occurrence of certain prejudicial scenarios (e.g., Adner & Levinthal, 2004; Barnett, 2008; Bowman & Hurry, 1993; Faulkner, 1996; Kogut & Kulatilaka, 2004; McGrath, 1997, 1999; McGrath, Ferrier, & Mendelow, 2004).
This effect is also found in the real options in new product development projects because they can increase the value of such projects, as more is the uncertainty level. Faulkner (1996) points the two important evaluation and philosophy approaches of investment analysis in new product projects: one is based on the discounted cash flow analysis (like NPV) and the other on options; Faulkner (1996) alerts for the fact that the option thinking presents a strategic approach and flexible character and that it carries opportunities, being much employed mostly by Japanese organizations.
In innovation management, we will only have these opportunities or flexibility of waiting, of growing or the substitution options when launching products if the organization presents the ability to build strategies during the initial development tasks in order to better deal with future technical or marketing uncertainties. The project team can mitigate the innovation risks by developing concept options until the uncertainties resolution gathers more technical information and information from the market needs and preferences that reduce the uncertainties levels, with the objective to hedge the innovation project dealing with the dynamics of the technical or marketing uncertainties. This way, the innovation team can later better decide among the concepts open to conduct to the final development stages and launch the product with best concept (see e.g., Dixit & Pindyck, 1994; Faulkner, 1996; Huchzermeier & Loch, 2001; MacMillan, Putten, McGrath, & Thompson, 2006; McGrath, 1997; Morris, Teisberg, & Kolbe, 1991).
Such flexibility protects the company against technological uncertainties. According to Bacon, Beckman, Mowery, and Wilson (1994), at the early stages of development process, investments are small, and thus changes in market requirement or product attributes do not imply large costs. On the other hand, those early stages have deep implications over the late and much more costly ones, like manufacturing and launching. Researching the product development processes of six large corporations, Bacon et al. (1994) found out that early specification freezing resulted in much larger costs with changes in the new product design due to late changes in the market.
Ward, Liker, Cristiano, and Sobek (1995) named the development approach employed by Toyota as set-based strategy, which consists of allowing parallel development of a set of alternatives as a way of decreasing the time-to-market and the development of uncertainty level. According to them, the use of a great many prototypes allows the early mapping of performance and responses to various technologies and alternatives. For Shenhar (1998, p. 39), “these intermediate programs were instituted to prove the validity of the systems concept and test the unknown technologies being developed concurrently during the project-execution period”.
Models and resultsThe objective of our research is the achievement of the optimal expected economic performance and the respective risk level of the parallel development of several concept options in a NPD project, considering a very dynamic market. The window of opportunity for the launching of new product is very small and the company must launch rapidly the right product in accordance with or, as a perfect response to the true requisites of the market (Abell, 1978; Christensen, Suárez, & Utterback, 1998; Meyer & Utterback, 1993). In this business environment, there is much uncertainty and a great risk for the company if it conducts the development of only one product concept and the project team must consider the parallel development of several concept options in order to reduce the risk of launching an unsatisfactory product into the market.
The new product in question is supposed to be constituted by two subsystems. We consider the successes of each technological option on development process as represented by probabilities and also a variable (the fitting probability) that represents the level of complexity in the architecture of the product between the two subsystems representing their interrelations when working jointly. The Section “Problem presentation and assumptions for mathematical modeling” presents the problem and the assumptions for mathematical modeling that are presented thereafter in Section “Mathematical modeling”. The Section “Results analysis and discussion” presents the results and analyses.
Problem presentation and assumptions for mathematical modelingWe developed a mathematical model (Babbie, 1998; Dane, 1990; Davis, Eisenhardt, & Bingham, 2007) to obtain the economic performance and risk of a parallel development of several option concepts, where the product is considered as constituted by two subsystems. The technical performance and the attributes of the quality that the product will present at the end of the development process will depend not only on the individual performances of each of the subsystems but also on its integrity in architecture, that is, the way in which one subsystem interacts with other when they are combined and working together. Thus, the technical performance and minimum quality attributes demanded by the market and the consequent success in launching depend not only on the individual success of each of the two subsystems but also on the success of the architecture functioning, that is, an excellent working of the two subsystems together.
The “two subsystems” of the product can be considered like two simple elements that, integrated, will form a system, or we can still consider them like two subsystems that should work together like an electronic element and another mechanism in the case of a new fuel injection system in a new car or two mechanical elements that, together, should perform a determined function like compressor and heat exchangers. Another example for the two subsystems could be a metal plate that should have been manufactured with die-casting. We could consider that the metal plate would be faced with a better or worse result of the action of the die using a certain material. Then, in this example, plate and die should be adjusted perfectly in a way to produce the part with all the required characteristics, geometric, physical, or of resistance.
The objective of developing several concept options in parallel is to accelerate the process of product development and knowledge searching. We assume that there exist several alternatives of product concepts to be developed and also that the company has sufficient resources available to develop these several concept alternatives of the subsystems in parallel. We show, in sequence, the principal assumptions for the elaboration of the model, an extension of the model developed and presented on Camargo Jr. & Yu (2005; 2006; 2007).Assumption 1 The potential revenue of the market R will be earned by the company if and only if the development process achieves any success in launching, i.e., the new product presents at least the minimum level of performance and quality required by the consumers. In other way, no revenue will be earned. To facilitate the modeling, the probabilities of success (pA and pB) are considered the same for each and every alternatives of two subsystems, respectively A and B, of the project, beyond which the success of each one of them is considered statistically independent of the success of each of the others. We consider that the probability of success represents the level of technological uncertainty related for each alternative (of the two subsystems) individually in the development project. We consider a probability of fitting (p) between two alternatives, one of each subsystem, that have already got the success in the individual development. The probability of fitting (p) is also considered the same for each and every alternative of the two subsystems of the project, beyond which the success of each pair is considered statistically independent of the success of others. We consider that the probability of fitting (p) represents the success on architecture working, that is, a well integration and functionality between the two considered subsystems. Each and every alternative has the same cost c to be developed in any cycle. In this initial model, costs and length of cycle do not vary, and learning effects and difficulty increases are not considered. The relation c/R is parameterized in the model to facilitate the modeling and analysis of results.
Table 2 shows the values for the potential total market revenue (R) and the relation cT/R, with cT representing the development total cost for some projects found in literature. Such values were obtained from Ulrich and Eppinger (2000). These numbers are employed in our study just for helping to get a definition of the range of possible variation for each parameter in our models. Thus, we use the parameterization for the values of c/R as being 0.001, 0.005 and 0.01 in order to cover an interval that is relevant enough to the projects shown in Table 2.
Potential revenue of market (R) and the relation cT/R for different projects.
| Stanley Tools | Rollerblade Skate | HP Deskjet | New Beetle | Boeing-777 | |
|---|---|---|---|---|---|
| R (million US$) | 12 | 60 | 2400 | 10,200 | 195,000 |
| cT/R | 0.0125 | 0.0125 | 0.021 | 0.039 | 0.015 |
Source: Adapted from Ulrich and Eppinger (2000).
If the project team chose quantities of alternatives NA and NB relating to the subsystems A and B to be developed in the development process, then, at the end of the development, alternatives XA and XB relative to the subsystems respectively, A and B, could be revealed as satisfactory from the point of view of individual performance. Thus, facing XA and XB individual successes, there is a probability of the occurrence of success in the architecture integration or fitting a pair of them (one alternative of each subsystem). The potential revenue of the market (R) will be earned only if a good fitting occurs. We call it the total fitting probability and it will be larger when more individual success occurs at the end of the development cycle. The expected value of the economic result of the parallel development (E[PD/R]), already considered in relation to the potential revenue from the market (R), is presented in expression (1):
where p(xA=XA) is the probability of XA individual successes occurring (alternatives within the total of NA) with the subsystem A at the end of the development cycle and is shown in the expression (2); p(xB=XB) is the probability of XB individual success occurring (alternatives within the total of NB) with the subsystem B at the end of the development cycle and is shown in expression (3); pF(XA, XB) is the total fitting probability or integrated architecture functioning satisfactorily with at least a pair of alternatives of the subsystems A and B, facing XA and XB individual successes. Expression (4) shows this probability; NA and NB are the numbers of alternatives, respectively, of subsystems A and B, developed.The expressions (2) and (3) present the probabilities of the numbers of occurrences of individual successes, which at the end of the development cycle will be, respectively XA and XB, within the totals alternatives NA and NB of the subsystems A and B that were developed:
where pA and pB are the probabilities of individual success of each alternative of subsystems A and B respectively.The expression (4) shows us the total fitting probability or perfect integration (pF), that is, the probability of finding at least one pair of alternatives, within the XA and XB individual success, that show functionality together or satisfactory quality so that the product can be launched in the market:
where p is the probability of successful architecture fitting of any pair of project alternatives, of subsystems A and B, that obtained individual success in the development process, showing satisfactory working together.As long as the probabilities of individual success (pA and pB) represent the level of technological uncertainty in the individual development of each of the subsystems, the fitting probability (p) can be considered even in a simplified form, one measure of the level of complexity on architecture functioning, that is, the interrelations between the subsystems. The NPD project with two subsystems that present higher levels of impacts or interdependence between them, or a lot of restrictions to the architecture functioning together, shows higher complexity for the development team and will be represented in our models by a low probability of fitting (p) and vice versa.
The numbers NA* and NB* of alternatives of the subsystems A and B that maximize the expected value of the economic result can be found through a numeric search based on the mapping of the expected value on a great interval of values for NA and NB in a way known as the maximum point. A routine, using Matlab language, was developed to achieve these optimal results. Thus, expression (5) shows us the maximized expected values (E*(PD/R)) for the economic result of the parallel development:
So, we define “sumprob*” as the total probability of success of product launch when NA* and NB* alternatives were developed, that is shown in expression (6). Thus, the Risk* of finishing the development process without any success is shown in expression (7):
The economic result (E(OCD/R)) and also the risk of the strategy of conducting only One Concept to the Development is obtained in order to be used as a simple reference for comparison to the results of the strategy of parallel development, and they are presented, respectively, in expressions (8) and (9):
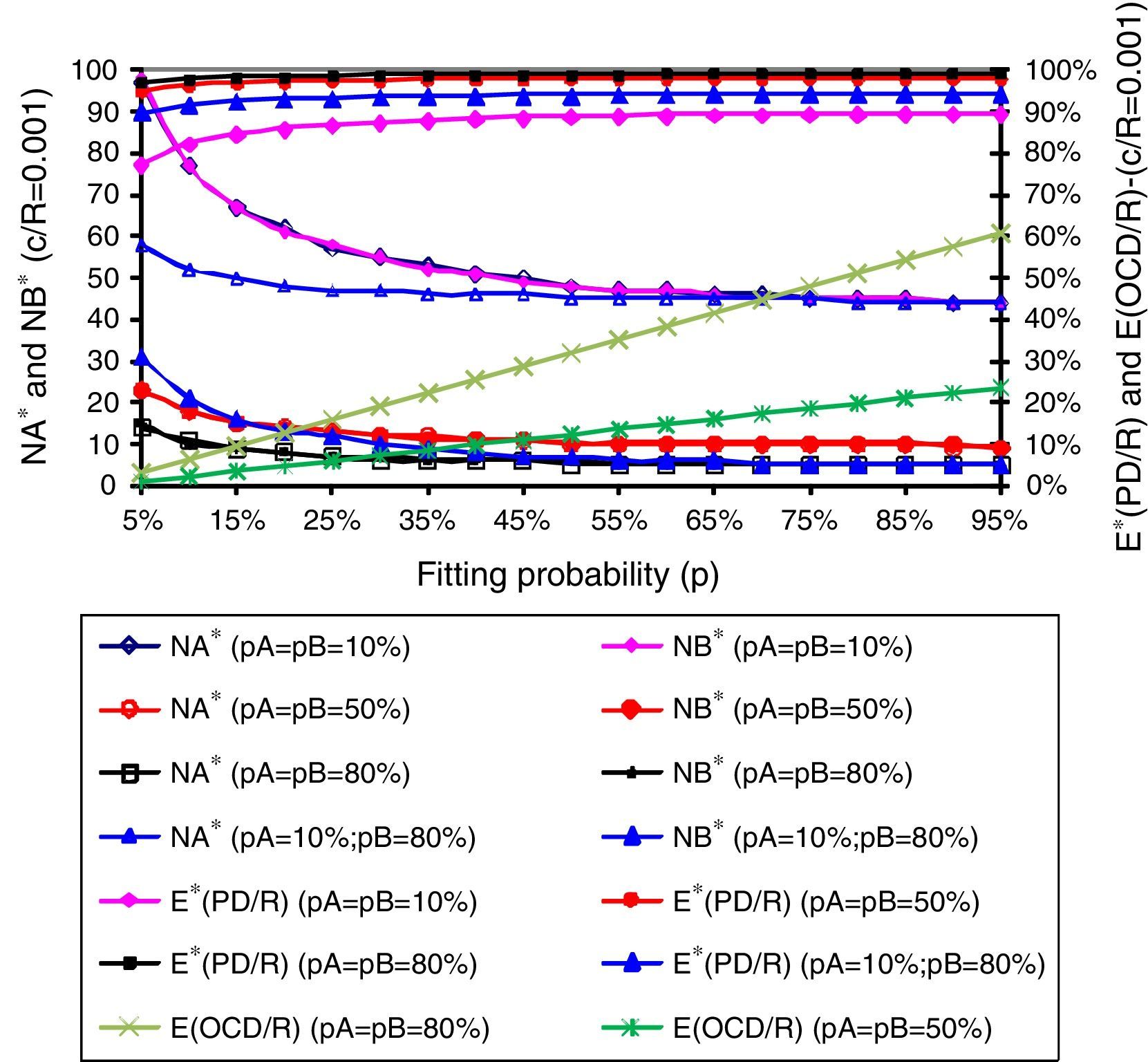
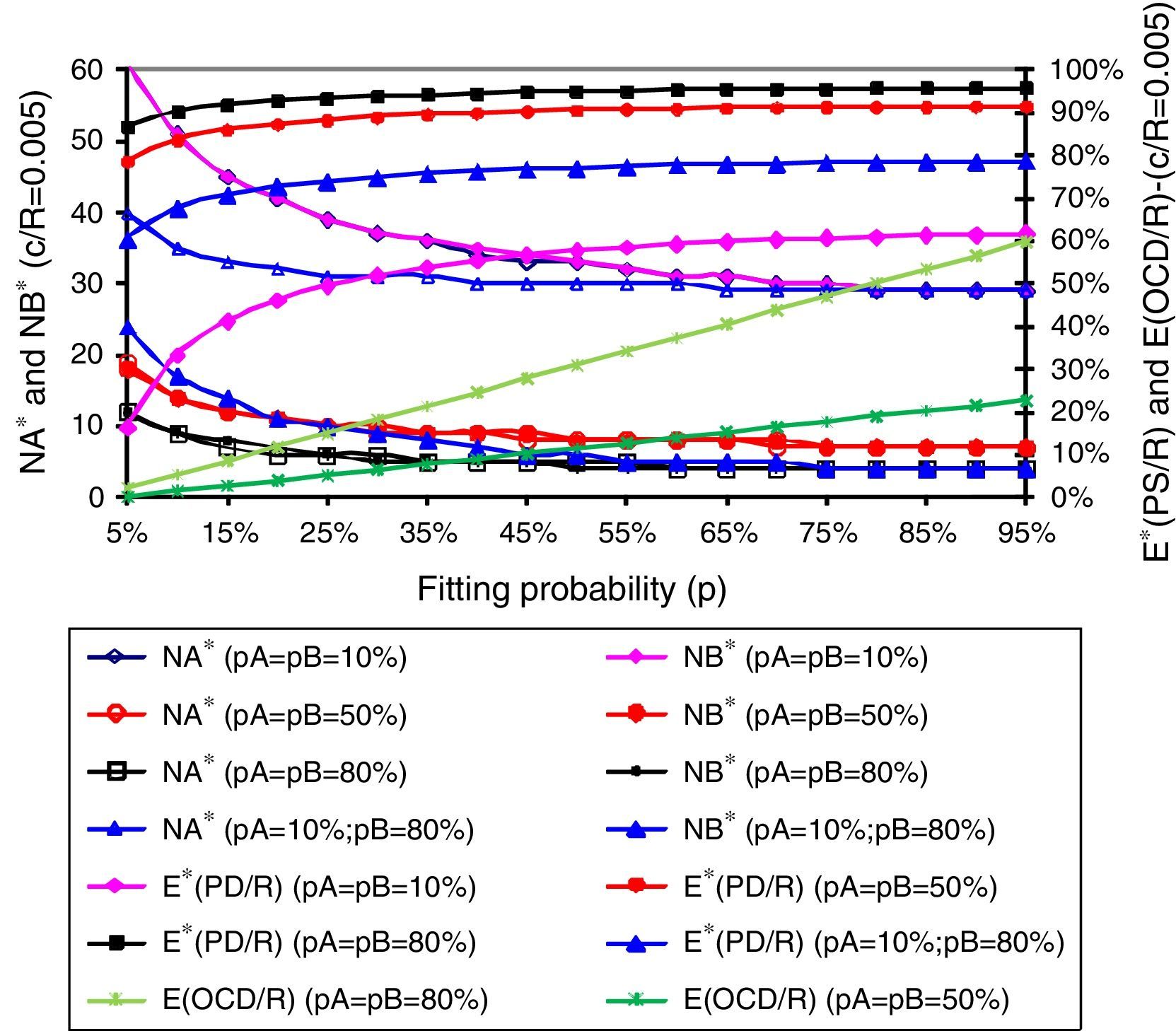
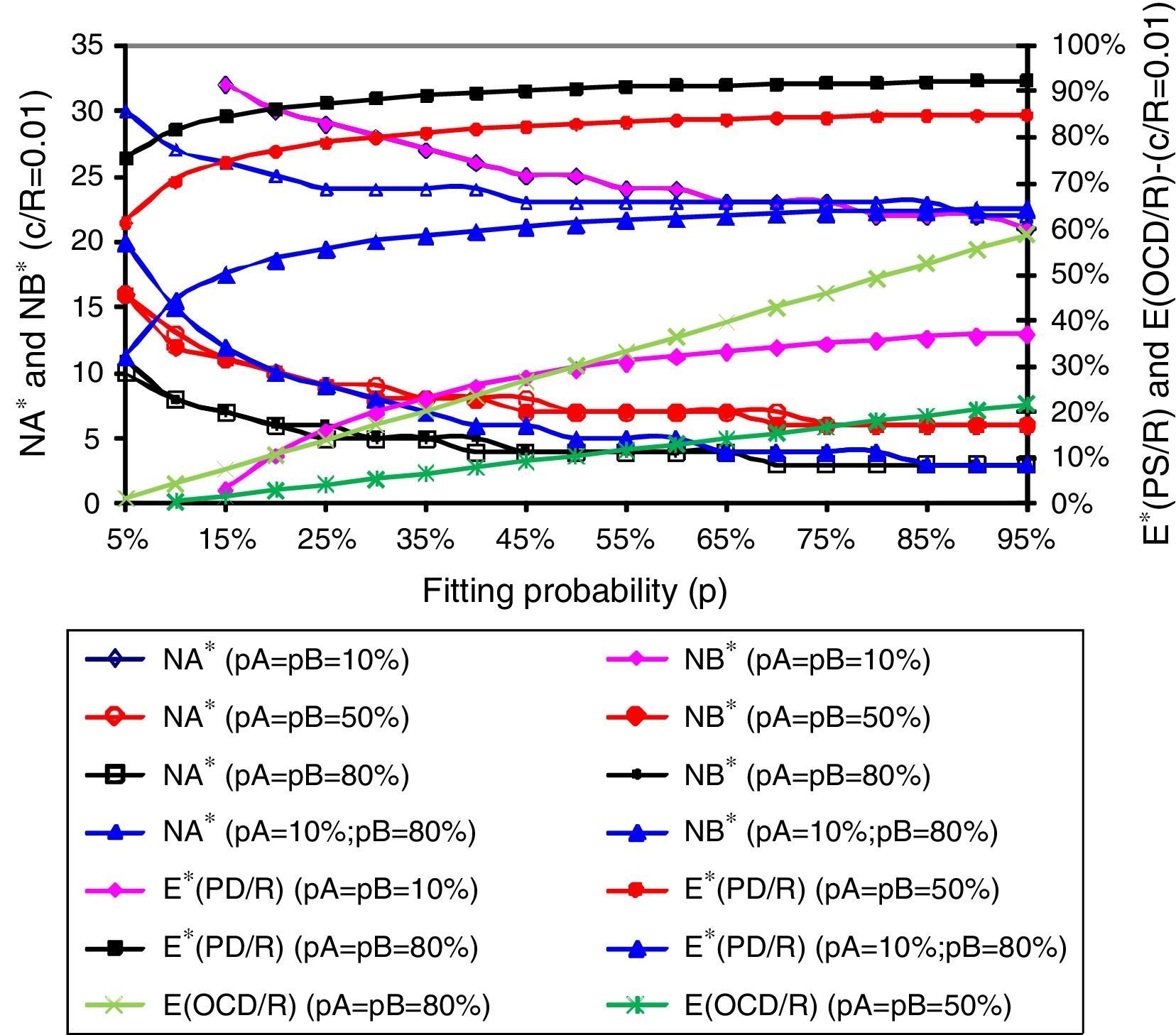
Results analysis and discussionFigs. 1–3 present us the optimal numbers (NA* and NB*) of concept options of each one of subsystems A and B, the already maximized expected values (E*(PD/R), (as expression (5)) for the economic result for parallel development of several concept options and also the expected value for the strategy of only one concept development (E(OCD/R) for each value parameterized of the c/R relation (c/R=0.001, 0.005 and 0.01).
We can see by Figs. 1–3 that the benefits of developing in parallel several concept options are much greater for projects with relation c/R relatively low (as c/R=0.001 in Fig. 1), compared with more expensive ones, like in Figs. 2 and 3. The benefits, that is, the expected economic results in relation to cost (E*(PD/R)), are so high (near 100%) mostly to costless projects (like c/R=0.001 in Fig. 1) but these benefits also exist in more expensive projects despite their decrease as the relation c/R increases (like Figs. 2 and 3), making smaller the differences to the economic results from the reference strategy of one concept development (E(OCD/R)).
However, our most important result is that the behavior of all expected economic performance in parallel development are greatly sustained in projects with higher levels of uncertainties (low levels of probabilities) in comparison to the reference strategy of OCD. These results show that parallel development of several concept options is a strategy that presents a strong hedge for economic performance mostly to the projects where there are higher levels of uncertainty.
This effect can be observed in figures above when we see that the high values of the expected economic result of parallel development, for high fitting probability (e.g., p=90% or 95% with almost none problem on architecture fitting), keeping constant for all its range with only a little loss for projects with a much complex architecture fitting (low levels of fitting probability, i.e., p=5% or 10%). This hedge potential, achieved with the parallel development of several options, is maintained even for more expensive projects, as we can see in Fig. 3 (for relation c/R=0.01). This hedge effect loses power only for projects in very unfavorable, extreme conditions, that is, very expensive projects and also those in which all concept options present very low individual probabilities, as we can see in Fig. 3.
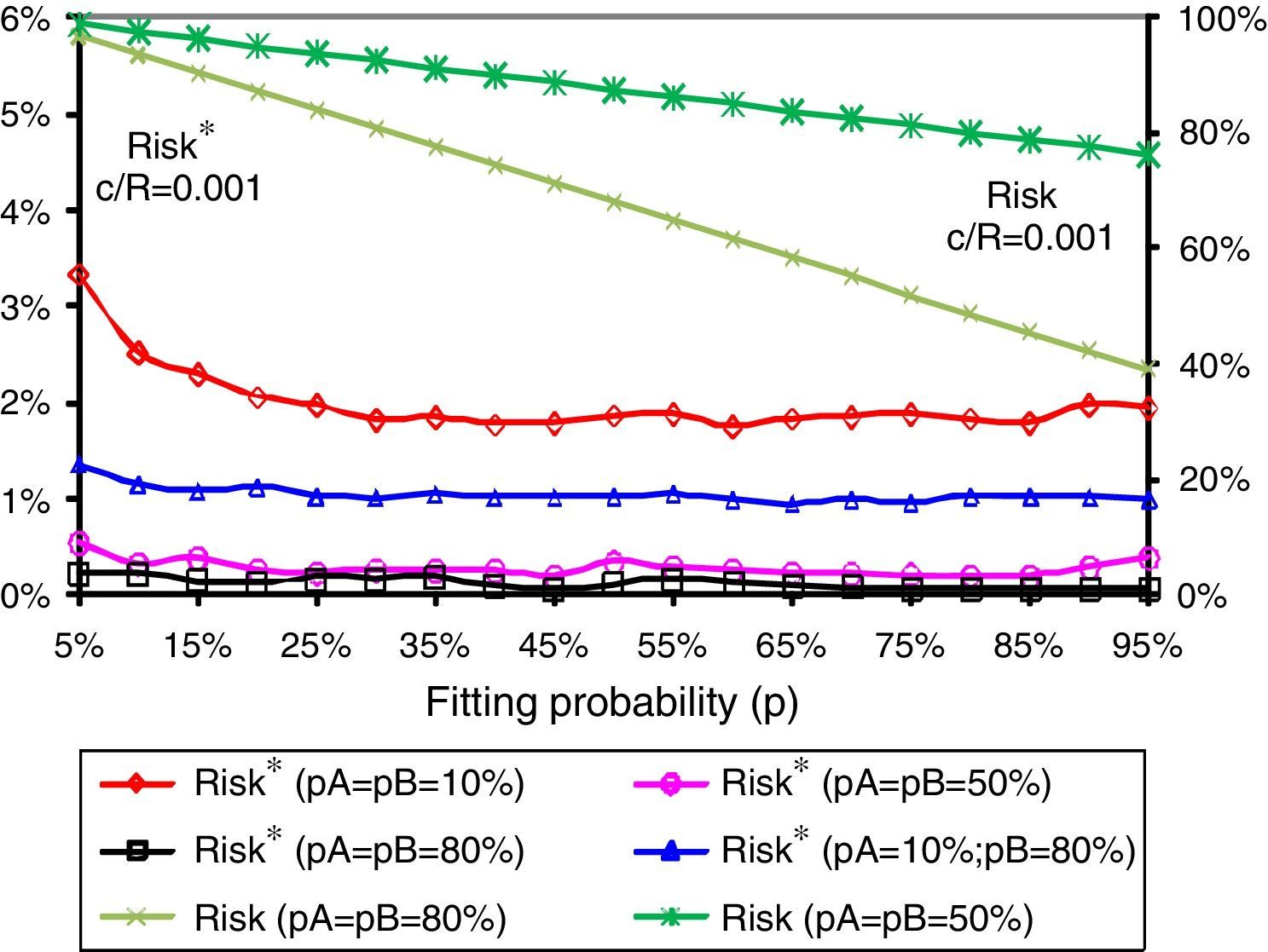
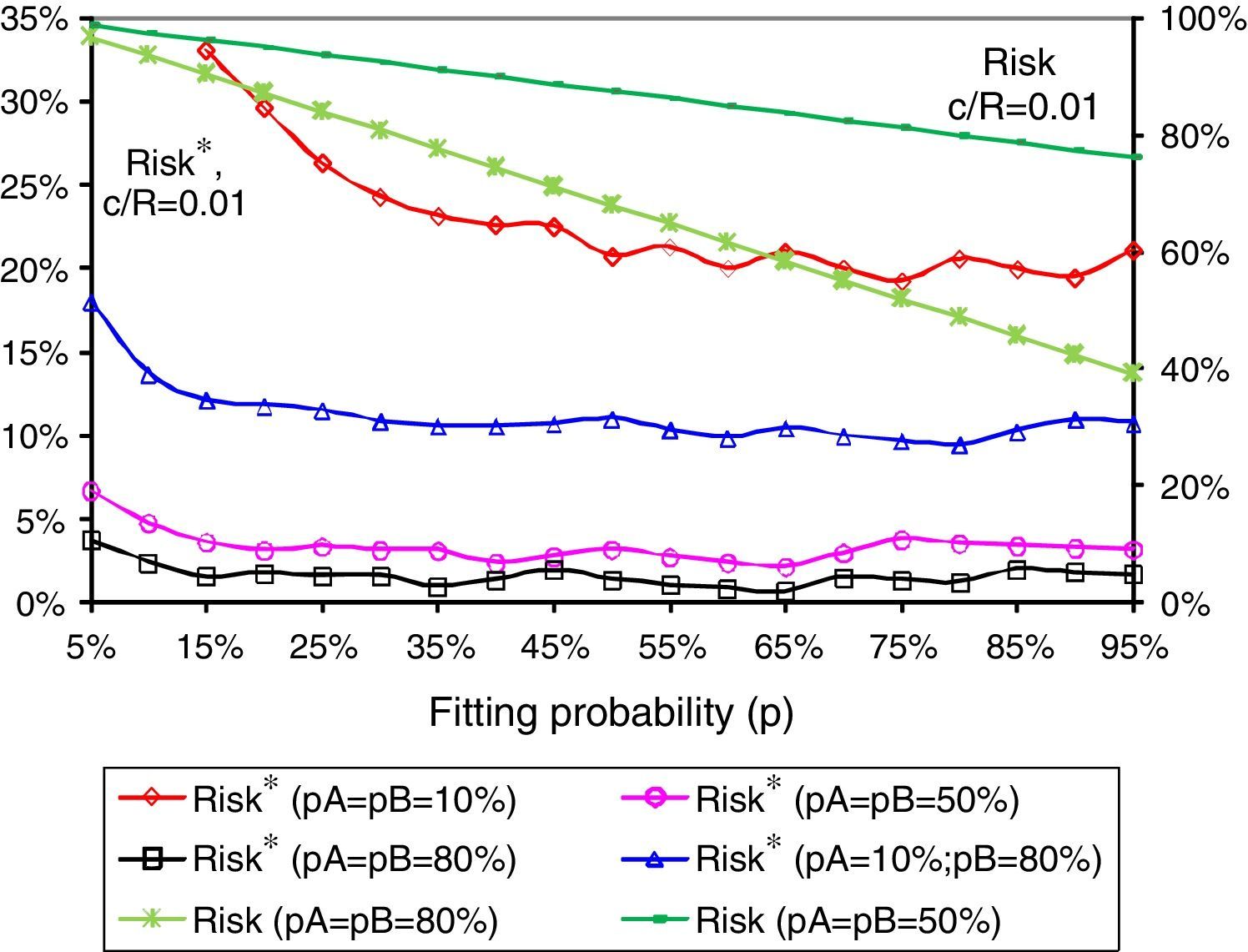
In sequence, Figs. 4 and 5 present the risks of development process ends up without any success considering projects with relations c/R of, respectively, 0.001 and 0.01, that is the risk of parallel development of several concept options (Risk*) and the risk of the strategy of one concept development (Risk).
We can observe, by Figs. 4 and 5, the robustness of the strategy of parallel development of several concept options in relation to the stability of the level of Risk* along the range of the fitting probability (p), with higher values only for extremely lower fitting probabilities (p). Such hedging effects are achieved due the just mentioned huge number of concept alternatives that are developed in parallel. These effects are intuitively greater for projects with alternatives that present lower development costs and/or greater individual probabilities of success (pA and pB).
ConclusionsThis study analyses the performance regarding the economic result and also the risk levels of the strategy of parallel development of many concept options when designing a new product in a much dynamic market with a small window of opportunity. When there is huge uncertainty about the true requisites of the attributes needed by a dynamic market or the main technologies able to better respond to fix these requisites, the development process must consider the parallel development of many concepts in order to reduce the risk of failure and finish the process with no satisfactory product to launch into the market.
We developed a mathematical modeling that was able to achieve the optimal economic performance and risk level of parallel development of several concept options as a strategy of rapidly introducing a satisfactory product in a dynamic market. The new product in question is supposed to be constituted by two subsystems. We consider the successes of each technological option on development process as represented by probabilities and also a variable (the fitting probability) that represents the level of complexity in the architecture of the product between the two subsystems representing their interrelations when jointly working.
Our results show that there are great benefits of developing in parallel several concept options when compared with economic results from the strategy of only one concept development, mostly for projects with relation c/R relatively low, compared with more expensive ones. The benefits, that is, the increase in the expected economic results, also occur for more expensive projects but they decrease as the relation c/R increases.
Another important result shows that the strategy of developing several concept options in parallel works like a hedge or a mechanism of risk management, because this approach presents a huge reduction in risk of finishing the development process without being satisfactory to launch into the market. The reduction of the risk is greater mostly for more complex and uncertain development projects, that is, for more radically and really new products.
Future researches should investigate the subject deeply regarding a more holistic approach, considering, for example, the effects of different sizes of the window of opportunities, the possibilities of new cycles of development, different levels of criticism of the customers about the product quality, different potential revenue values from the market or considering new products constituted of more than two subsystems among other important aspects.
Conflicts of interestThe authors declare no conflicts of interest.
Peer Review under the responsibility of Departamento de Administração, Faculdade de Economia, Administração e Contabilidade da Universidade de São Paulo – FEA/USP.