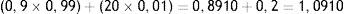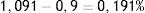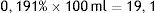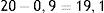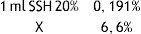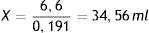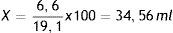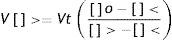Suero salino hipertónico: un método sencillo, práctico y seguro para su preparación

En el contexto de la hipertensión endocraneal, la terapia hiperosmolar con solución salina hipertónica (SSH) se utiliza con frecuencia en los servicios de urgencias y en los quirófanos, cuando las medidas de primer nivel para el control de la presión intracraneal (PIC) han fracasado¹. En la actualidad, varios estudios demuestran que la SSH podría ser más eficaz en la reducción de la PIC que el manitol al 20%, siendo su efecto más duradero^1,2.

No obstante, el suero salino está disponible en España únicamente en 2 presentaciones: al 0,9% y al 20%³. Con alguna frecuencia, he observado que mis colegas tienen dificultades para preparar una solución hipertónica a partir de estas 2 presentaciones. Por esta razón, propongo un método sencillo para su cálculo, a partir del siguiente ejemplo:

Supongamos que debemos preparar una solución de 100 ml de SSH al 7,5%, y para ello disponemos de una bolsa de 100 ml de solución salina normal (SSN) al 0,9% y un vial de 20 ml de SSH al 20%.

Es posible predecir la variación porcentual que producirá el remplazo de 1 ml de SSN al 0,9% por 1 ml de SSH al 20%, a través del siguiente razonamiento:

Es decir, si el 99% de la solución estuviera compuesta por SSN al 0,9% y el 1% de la solución por SSH al 20%, obtendríamos una nueva solución de suero salino al 1,091%. En otras palabras, el porcentaje de suero salino en esta nueva solución habrá aumentado en un 0,191%:

Al multiplicar la ecuación (2) por el volumen total de la solución, obtendríamos:

Nótese que esta variación se corresponde exactamente con la diferencia porcentual entre las 2 soluciones:

Ahora bien, si al remplazar 1 ml de SSH al 20% en una bolsa de 100 ml de SSN al 0,9% se produce un aumento de concentración del 0,191% en la nueva solución, para producir un aumento porcentual de 6,6 (i.e., 7,5-0,9%) ¿cuantos mililitros de SSH al 20% se requieren?

En donde:

O lo que es lo mismo:

Es decir, para preparar una solución de 100 ml de SSH al 7,5%, es preciso añadir 35 ml de SSH al 20% a 65 ml de SSN al 0,9%.

Desde luego, en el contexto de un servicio de urgencias estos cálculos son confusos y difíciles de recordar. Por esta razón, propongo una sencilla ecuación basada en los mismos conceptos, la cual resulta mucho más fácil de memorizar por su sencillez y versatilidad.

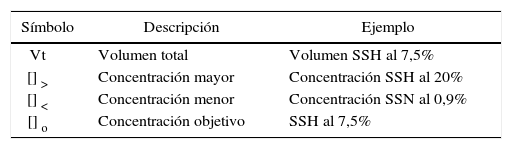
Basándonos en el mismo ejemplo, para calcular el volumen de concentración mayor (V [] _>, variable respuesta), podemos definir 4 variables explicativas que son aplicables a cualquier problema de este tipo:

Símbolo	Descripción	Ejemplo
Vt	Volumen total	Volumen SSH al 7,5%
[] >	Concentración mayor	Concentración SSH al 20%
[] <	Concentración menor	Concentración SSN al 0,9%
[] o	Concentración objetivo	SSH al 7,5%

Así, al remplazar la ecuación (6), tendríamos:

El modelo de la ecuación (7) resuelve de forma práctica y versátil el problema de preparar cualquier sustancia a una determinada concentración ([] _o), a partir de 2 concentraciones diferentes ([] _>, [] _<) para un volumen total determinado (Vt).

El mismo razonamiento es aplicable a cualquier concentración objetivo, y puede demostrarse con los siguientes ejemplos prácticos:

[] o	[] >	[] <	Vt	V [] >	V [] <
SSN al 3%	20%	0,9%	100 ml	11 ml	89 ml
Dextrosa al 10%	50%	5%	500 ml	56 ml	444 ml
Ropivacaína al 0,2%	0,75%	0,1%	10 ml	1,54 ml	8,46 ml
HCO3^− al 1,4% (1/6 M)	8,4% (1 M)	0% (agua destilada)	250 ml	42 ml	208 ml
Oxígeno al 40%	100%	21% (aire)	50 l/min	12 l/min	38 l/min

El modelo es además útil para estimar el déficit de sodio en hiponatremia⁴ o el déficit de agua en hipernatremia⁵.