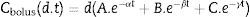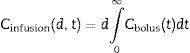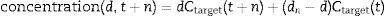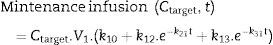Remifentanil and propofol infusion using TCI pumps has proven to be beneficial for the practice of anesthesia but the availability of these systems is limited.
ObjectiveDesigning a pharmacokinetic model-based algorithm for calculating manual infusion regimens to achieve plasma and effect-site concentrations that may be used in volume infusion pumps, and to compare the difference between the desired and the predicted concentrations via pharmacokinetic simulation.
MethodsUsing the Minto & Schnider models for remifentanil and propofol respectively, the algorithm was implemented on an iTIVA application (interactive TIVA) for iOS and Android operating systems. The performance of the algorithm was evaluated estimating the infusion regimens for achieving different effect-site concentrations for induction and maintenance in 34 theoretical patients for 240min.
ResultsThe infusion regimens obtained for remifentanil and propofol resulted in less than 5% average systemic deviation versus the target effect-site concentrations during induction and maintenance. Only one induction infusion was required for remifentanil and propofol. Just one infusion rate was required for remifentanil during maintenance, and between 2 and 5 infusion rate changes for propofol to maintain a stable concentration. The iTIVA-based algorithm estimates concentrations similar to the TivaTrainer® software.
ConclusionsThe performance of the algorithm to achieve effect-site concentrations during induction and maintenance for remifentanil and propofol was excellent, with a low systemic deviation versus the desired target concentrations.
La administración de remifentanil y propofol con el uso de perfusores TCI ha mostrado beneficios en la practica anestésica, sin embargo, su disponibilidad es limitada.
ObjetivoBasados en modelos farmacocineticos, diseñar un algoritmo capaz de calcular esquemas de infusión manual para alcanzar concentraciones en plasma y sitio efecto que puedan ser utilizados en bombas de infusión volumétricas. Adicionalmente, comparar la diferencia entre concentraciones deseadas y predichas mediante simulación farmacocinética.
MétodosSiguiendo modelos de Minto y Schnider para remifentanil y propofol respectivamente, el algoritmo se implementó en una aplicación llamada iTIVA (interactive TIVA) para los sistemas operativos iOS y Android. El desempeño del algoritmo se evaluó calculando esquemas de infusión para obtener distintas concentraciones en sitio efecto en la inducción y mantenimiento en 34 pacientes teóricos durante 240 minutos.
ResultadosLos esquemas de infusión obtenidos para remifentanil y propofol presentaron un desviación sistemática promedio menor al 5% respecto a las concentraciones en sitio efecto objetivo en la inducción y mantenimiento. En la inducción una única infusión fue requerida para el remifentanil y propofol. Durante el mantenimiento una única tasa de infusión fue requerida para el remifentanil y entre 2 y 5 cambios de tasa de infusión para el propofol para mantener una concentración estable. El algoritmo implementado en iTIVA calcula concentraciones similares que el software TivaTrainer®.
ConclusionesEl desempeño del algoritmo para alcanzar concentraciones en sitio efecto durante la inducción y mantenimiento para remifentanil y propofol fue excelente con una desviación sistemática baja con respecto a las concentraciones objetivo deseadas.
The current practice in anesthesiology is the administration of intravenous agents using standard doses that are empirically adjusted. Such approximation fails to consider the inter-individual variability of pharmacokinetics, and the variable dose-plasma concentration relationship that sometimes leads to adverse events.1
Mathematical models have been developed in the last two decades based on studying the plasma concentrations of various drugs. These models describe the process of drug distribution and clearance so as to predict the effect of administering multiple boluses, intravenous infusions, or a combination of both. The use of these models facilitates the teaching and learning process of pharmacokinetics applied to anesthesia.2,3
Computer technology has enabled the adoption of theoretical models for the pharmacokinetic simulation of drugs like propofol (Schnider's model)4 and remifentanil (Minto's model).5 These systems allow for controlling the infusions by adjusting to specific target concentrations of the particular drug.6–9 This technology is commonly referred to as TCI (Target control infusion) and has facilitated the administration of intravenous drugs including remifentanil and propofol, allowing for rapid titration to achieve different therapeutic goals with enhanced hemodynamic stability.3,10
TCI pumps are not widely available in our daily practice and few hospitals actually have the devices so the use of total intravenous anesthesia is limited. However, even in countries where the TCI technology is widely available, only 15–40% use this approach for TIVA11–13; furthermore, restrictions to access in the United States or economic limitations as in most developing countries,14,15 are an obstacle to its wide dissemination and use. Thus, the manual administration of anesthetic agents with volume infusion pumps (VIP) is a current practice.
Passive TCI systems have been developed for a real-time pharmacokinetic simulation of the drugs administered, which have proven to achieve stable plasma and effect-site concentrations, reducing the mental effort for the anesthetist.16–18 These systems are only available for some anesthesia machines (for example, Navigator Applications Suite-GE Healthcare and SmartPilot View-Drager Medical), demand careful titration, but do not suggest an infusion rate so that the anesthetist achieves the desired concentration.19
In contrast to the passive TCI systems, the TCI pumps are able to achieve plasma and effect-site concentrations swiftly and accurately, using complex infusion regimens that change every 10s under the control of a microprocessor based on a pharmacokinetic model that maintains stable concentrations throughout.20 It is currently impossible to mimic the performance of TCI pumps with a manual approach, due to the mathematical complexity and narrow variation of infusion rates.
Using the models described by Minto5 and Schnider4 for remifentanil and propofol respectively, it is possible to achieve and maintain plasma and effect-site concentrations using a mathematical algorithm that allows for minor and tolerable variations of such concentrations. According to this hypothesis, the purpose of this study was to design an algorithm able to calculate manual infusion regimens to reach plasma and effect-site concentrations, and to contrast the difference between the desired concentrations and the concentrations predicted using pharmacokinetic simulation.
MethodologyThis study was divided into two phases: first the technical information about the pharmacokinetic performance of intravenous anesthetic agents that was used to develop an algorithm to simulate plasma and effect-site concentrations, and to calculate infusion systems to accomplish specific plasma and effect-site concentrations. This algorithm was implemented on a mobile application called “iTIVA” (interactive TIVA), for the iOS and android operating systems.
The second phase used the simulation of the infusion regimens calculated based on the algorithm developed as an evaluation method, as previously described in other papers.21
Developing the algorithmMost intravenous anesthesia models including remifentanil and propofol are based on three-compartment models,2,3 described in equation 1, that predicts the plasma concentration following a “d” bolus over time “t”21:
The plasma concentration of a continuous infusion at a “d” dose equals the infinitesimal repetition of “di” boluses equivalent to “d” over time “t”, as described by the integral of Eq. (1):
By clearing “d” from Eq. (2), a “d” infusion dose is obtained to achieve a plasma concentration over time “t”.
When the infusions vary over time, the difference between the new infusion dn” over time “t+n” is added to the first infusion as described in Eq. (4):The effect-site concentrations are obtained from the plasma concentrations through a non-analytical solution described in the codes section under http://www.opentci.org/.Eq. (3) gives a “d” infusion rate to achieve “Cp” plasma concentrations over time “t” and based on that “d” infusion rate, “d” is iteratively increased by 0.1 until dose “d” is obtained to achieve the target effect-site concentration.
The next step is to calculate a maintenance infusion to offset the distribution and clearance losses for maintaining a pseudo-stable condition for a desired concentration. So Eq. (5) calculates a “d” infusion rate over time “t”, to make up for the distribution and clearance losses and is maintained over a “t+n” time, until the simulated plasma concentration exceeds the target concentration “C”+0.1. At this point, using Eq. (5) the new maintenance infusion is recalculated over a time “t+n” and this goes on successively for as long as we want to maintain the concentration.
During maintenance there is no difference if the target is plasma or effect-site since both compartments tend to rapidly balance out during this stage of the process.
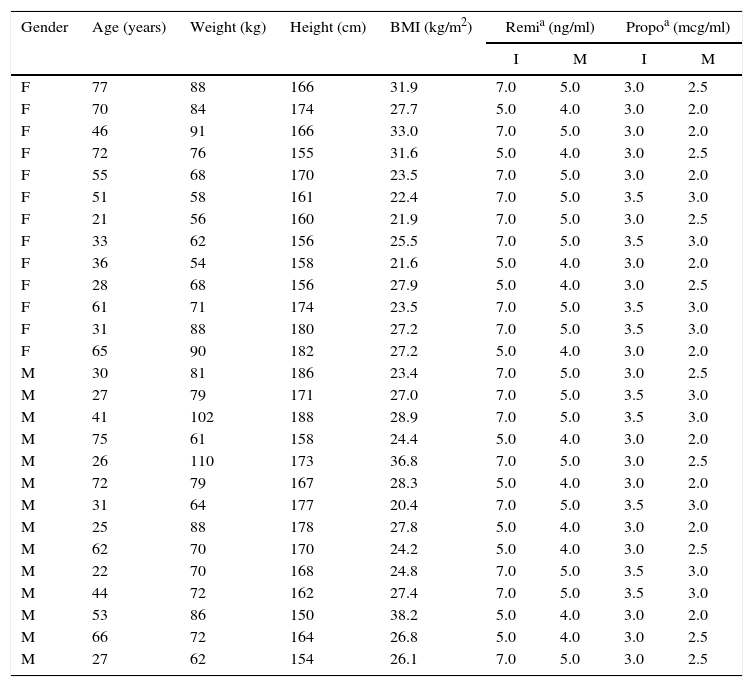
Performance of the algorithmThe data from 34 theoretical patients was used to evaluate iTIVA's performance in obtaining effect-site concentrations based on a manual infusion regimen. This was the basis to calculate infusion regimens for 240min in order to achieve different effect-site concentrations, randomly assigned for remifentanil and propofol. The data used are shown in Table 1.
Anthropometric data from patients in the simulation (n=34). Source: Authors.
| Gender | Age (years) | Weight (kg) | Height (cm) | BMI (kg/m2) | Remia (ng/ml) | Propoa (mcg/ml) | ||
|---|---|---|---|---|---|---|---|---|
| I | M | I | M | |||||
| F | 77 | 88 | 166 | 31.9 | 7.0 | 5.0 | 3.0 | 2.5 |
| F | 70 | 84 | 174 | 27.7 | 5.0 | 4.0 | 3.0 | 2.0 |
| F | 46 | 91 | 166 | 33.0 | 7.0 | 5.0 | 3.0 | 2.0 |
| F | 72 | 76 | 155 | 31.6 | 5.0 | 4.0 | 3.0 | 2.5 |
| F | 55 | 68 | 170 | 23.5 | 7.0 | 5.0 | 3.0 | 2.0 |
| F | 51 | 58 | 161 | 22.4 | 7.0 | 5.0 | 3.5 | 3.0 |
| F | 21 | 56 | 160 | 21.9 | 7.0 | 5.0 | 3.0 | 2.5 |
| F | 33 | 62 | 156 | 25.5 | 7.0 | 5.0 | 3.5 | 3.0 |
| F | 36 | 54 | 158 | 21.6 | 5.0 | 4.0 | 3.0 | 2.0 |
| F | 28 | 68 | 156 | 27.9 | 5.0 | 4.0 | 3.0 | 2.5 |
| F | 61 | 71 | 174 | 23.5 | 7.0 | 5.0 | 3.5 | 3.0 |
| F | 31 | 88 | 180 | 27.2 | 7.0 | 5.0 | 3.5 | 3.0 |
| F | 65 | 90 | 182 | 27.2 | 5.0 | 4.0 | 3.0 | 2.0 |
| M | 30 | 81 | 186 | 23.4 | 7.0 | 5.0 | 3.0 | 2.5 |
| M | 27 | 79 | 171 | 27.0 | 7.0 | 5.0 | 3.5 | 3.0 |
| M | 41 | 102 | 188 | 28.9 | 7.0 | 5.0 | 3.5 | 3.0 |
| M | 75 | 61 | 158 | 24.4 | 5.0 | 4.0 | 3.0 | 2.0 |
| M | 26 | 110 | 173 | 36.8 | 7.0 | 5.0 | 3.0 | 2.5 |
| M | 72 | 79 | 167 | 28.3 | 5.0 | 4.0 | 3.0 | 2.0 |
| M | 31 | 64 | 177 | 20.4 | 7.0 | 5.0 | 3.5 | 3.0 |
| M | 25 | 88 | 178 | 27.8 | 5.0 | 4.0 | 3.0 | 2.0 |
| M | 62 | 70 | 170 | 24.2 | 5.0 | 4.0 | 3.0 | 2.5 |
| M | 22 | 70 | 168 | 24.8 | 7.0 | 5.0 | 3.5 | 3.0 |
| M | 44 | 72 | 162 | 27.4 | 7.0 | 5.0 | 3.5 | 3.0 |
| M | 53 | 86 | 150 | 38.2 | 5.0 | 4.0 | 3.0 | 2.0 |
| M | 66 | 72 | 164 | 26.8 | 5.0 | 4.0 | 3.0 | 2.5 |
| M | 27 | 62 | 154 | 26.1 | 7.0 | 5.0 | 3.0 | 2.5 |
The data were tabulated using Microsoft Excel 2011 (Redmond, WA, USA) and exported to the statistical package R for analysis and plotting.22 The measurements and standard deviations of the simulated concentrations were calculated for each minute and the date were pooled based on the target site-effect concentrations.
To accurately evaluate the iTIVA concentrations anticipated, the predictive error, the predictive error rate, and the systematic error (bias) were estimated versus the desired concentration (Table 2). This methodology was previously described by Lerou.23 These results are presented on a graph using summary statistics and scatterplots. The performance of the algorithm was independently analyzed to accomplish target concentrations during induction and maintenance. By definition, induction was considered as the period of time between minute 5 and minute 6, and maintenance as the period of time between minute 7 and the end of the simulation (minute 240).
Definition of variables for estimating performance.
| Variable | Unit | Mathematical definitiona | Definition |
|---|---|---|---|
| Predicted error (fe) | n/a | fe=Cf−Cd | Difference between the predicted and desired concentrations |
| Percentage of predicted error (%fe) | % | %fe=Cp−CdCd×100 | Percentage of error between the predicted and desired concentrations |
| Systematic error (SE) | % | SE=1n∑i=1n%fe | Systematic deviation from the total error with direction (sign) and quantity |
Finally, the concentrations obtained in plasma and site-effect using iTIVA were compared against the concentrations estimated using TivaTrainer® software (version 8; European Society for Intravenous Anaesthesia, Glasgow, UK) (Table 3). In view of the post-hoc results, no hypotheses comparisons were done.
Plasma and effect-site concentrations for propofol and remifentanil when simulating different infusion regimens with iTIVA and TivaTariner®.
| iTIVA | TivaTrainer® | |||
|---|---|---|---|---|
| Time (min) | Plasma | Effect-site | Plasma | Effect-site |
| Propofol | ||||
|---|---|---|---|---|
| Minute 5 | 3,0±0,7 | 2,4±0,5 | 3,0±0,7 | 2,4±0,5 |
| Minute 10 | 2,2±0,6 | 2,2±0,6 | 2,2±0,6 | 2,2±0,6 |
| Minute 30 | 2,3±0,5 | 2,4±0,5 | 2,3±0,5 | 2,4±0,5 |
| Minute 60 | 2,4±0,5 | 2,4±0,5 | 2,4±0,5 | 2,4±0,5 |
| Minute 120 | 2,3±0,5 | 2,4±0,5 | 2,3±0,5 | 2,4±0,5 |
| Minute 180 | 2,4±0,5 | 2,4±0,5 | 2,4±0,5 | 2,4±0,5 |
| Minute 240 | 2,3±0,5 | 2,4±0,5 | 2,3±0,5 | 2,4±0,5 |
| Remifentanil | ||||
|---|---|---|---|---|
| Minute 5 | 6,5±2,9 | 5,2±2,3 | 6,5±2,9 | 5,2±2,3 |
| Minute 10 | 4,0±1,7 | 4,3±1,8 | 4,0±1,7 | 4,3±1,8 |
| Minute 30 | 4,1±1,8 | 4,1±1,7 | 4,1±1,8 | 4,1±1,7 |
| Minute 60 | 4,1±1,8 | 4,1±1,8 | 4,1±1,8 | 4,1±1,8 |
| Minute 120 | 4,2±1,8 | 4,2±1,8 | 4,2±1,8 | 4,2±1,8 |
| Minute 180 | 4,2±1,8 | 4,2±1,8 | 4,2±1,8 | 4,2±1,8 |
| Minute 240 | 4,2±1,8 | 4,2±1,8 | 4,2±1,8 | 4,2±1,8 |
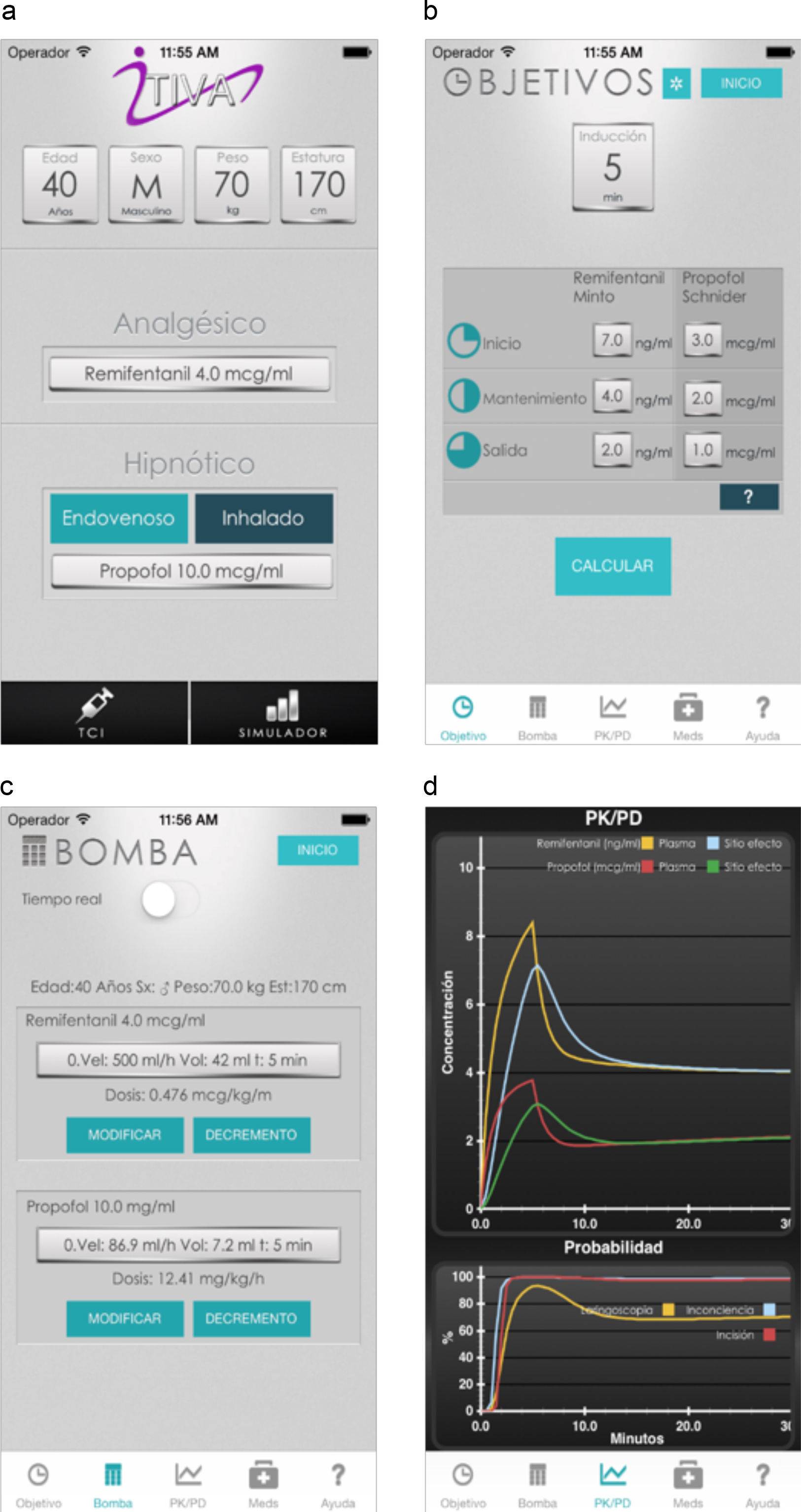
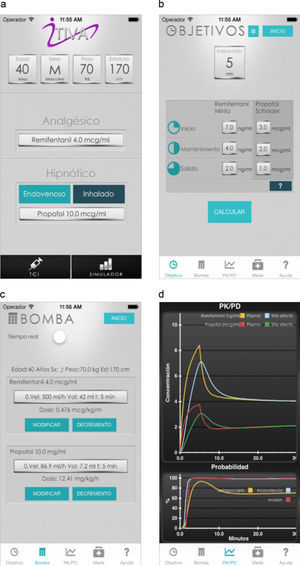
The algorithm was successfully implemented in both iOS and Android applications that are available at no cost from AppStore and Google Play. Fig. 1 shows the App screens for iPhone, including uploading of anthropometric data, target concentrations, the calculated infusion regimen and the graphical representation of the pharmacokinetic pharmacodynamic24 behavior as time progresses.
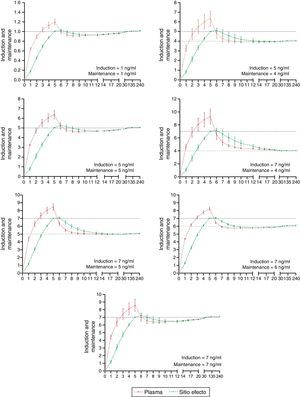
In order to maintain a stable concentration during induction, a single infusion rate for remifentanil and propofol was required. However, to maintain a stable concentration throughout the 235min of maintenance, a single infusion rate for remifentanil was required, and between 2 and 5 changes in the infusion rate for propofol (mode=4).
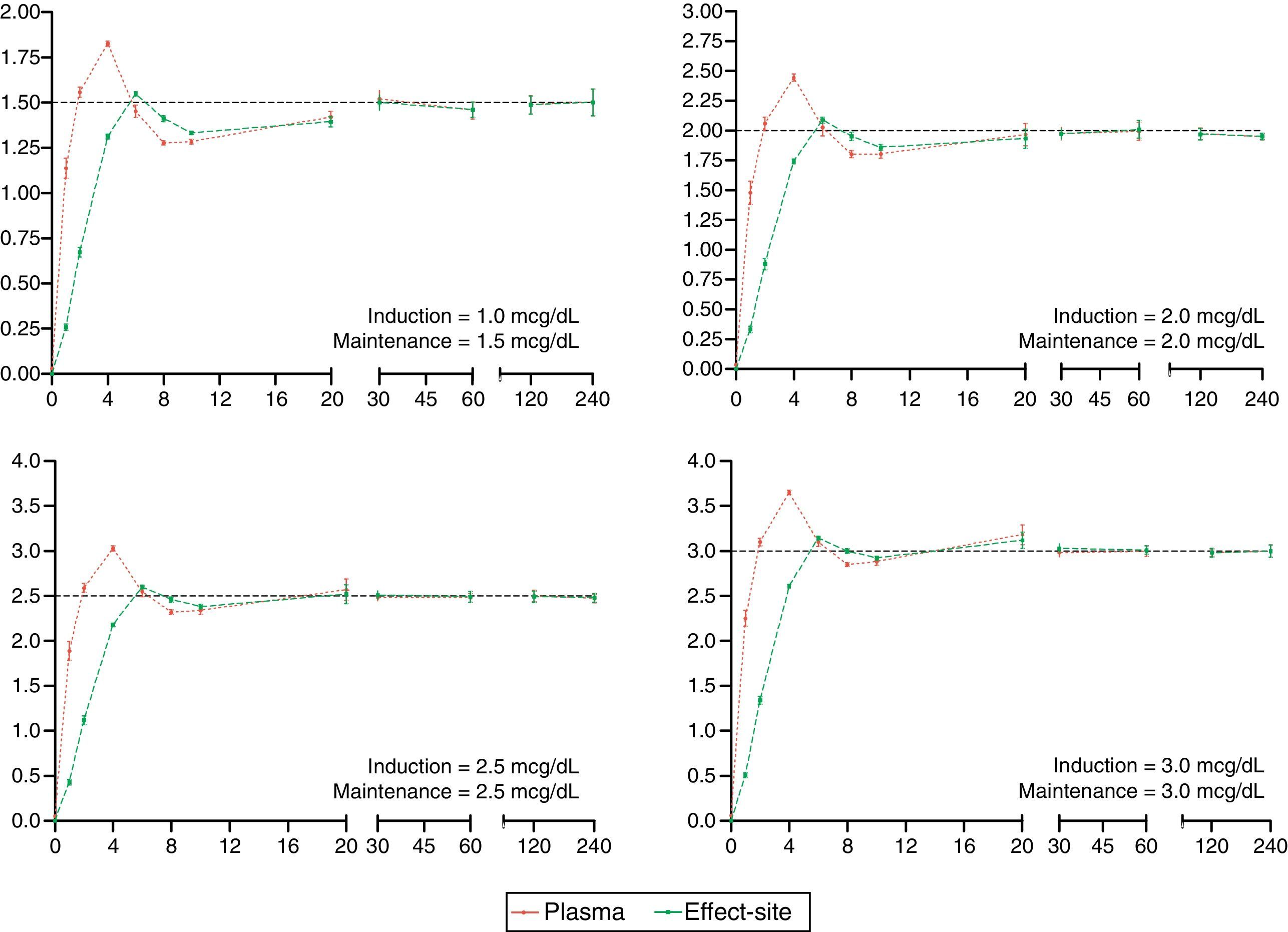
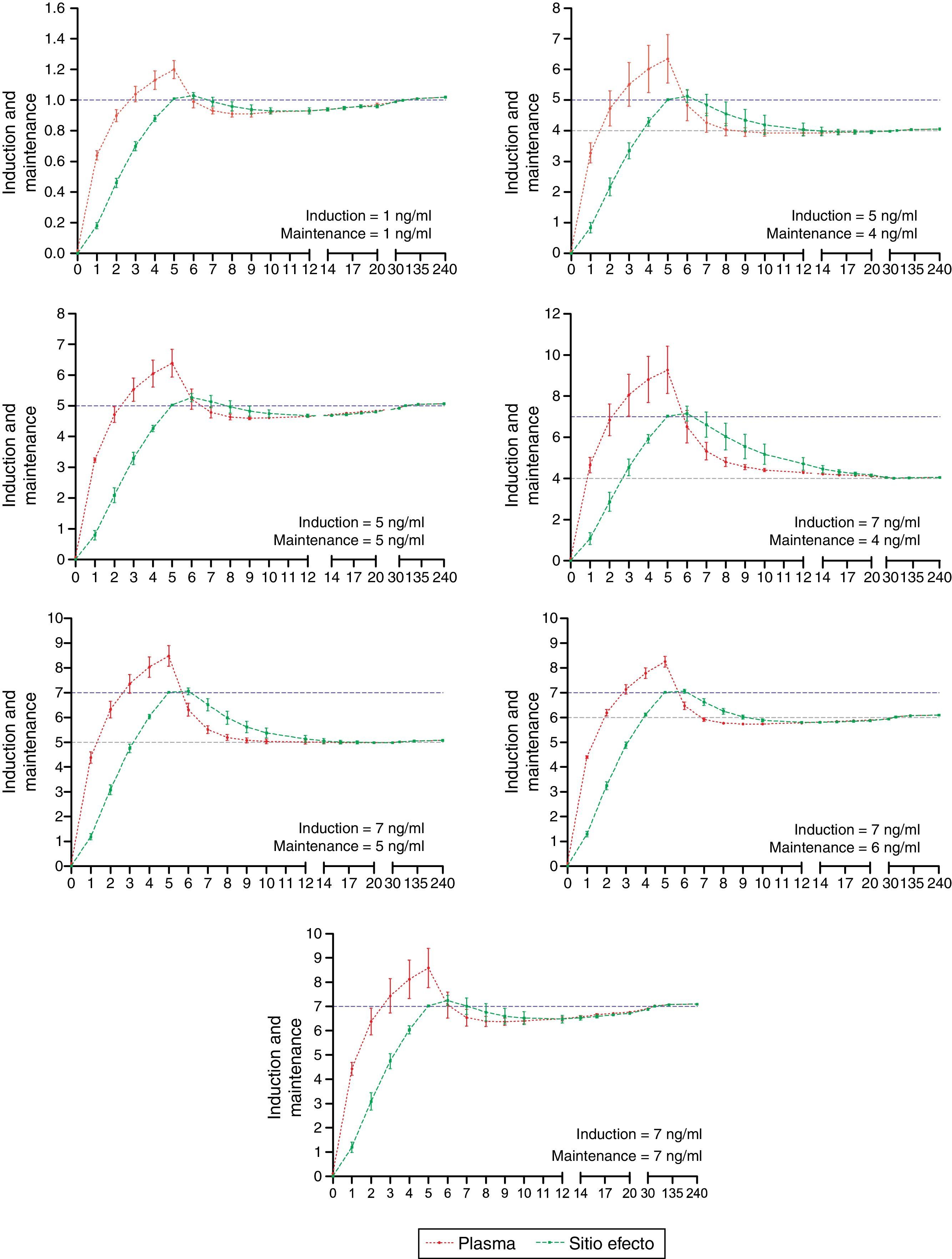
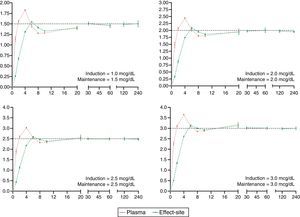
The desired and predicted plasma and effect-site concentrations obtained from the simulation and organized according to the desired targets for propofol and remifentanil are shown in Figs. 2 and 3, respectively. The time axis (X axis) emphasize the initial few minutes corresponding to the induction of anesthesia.
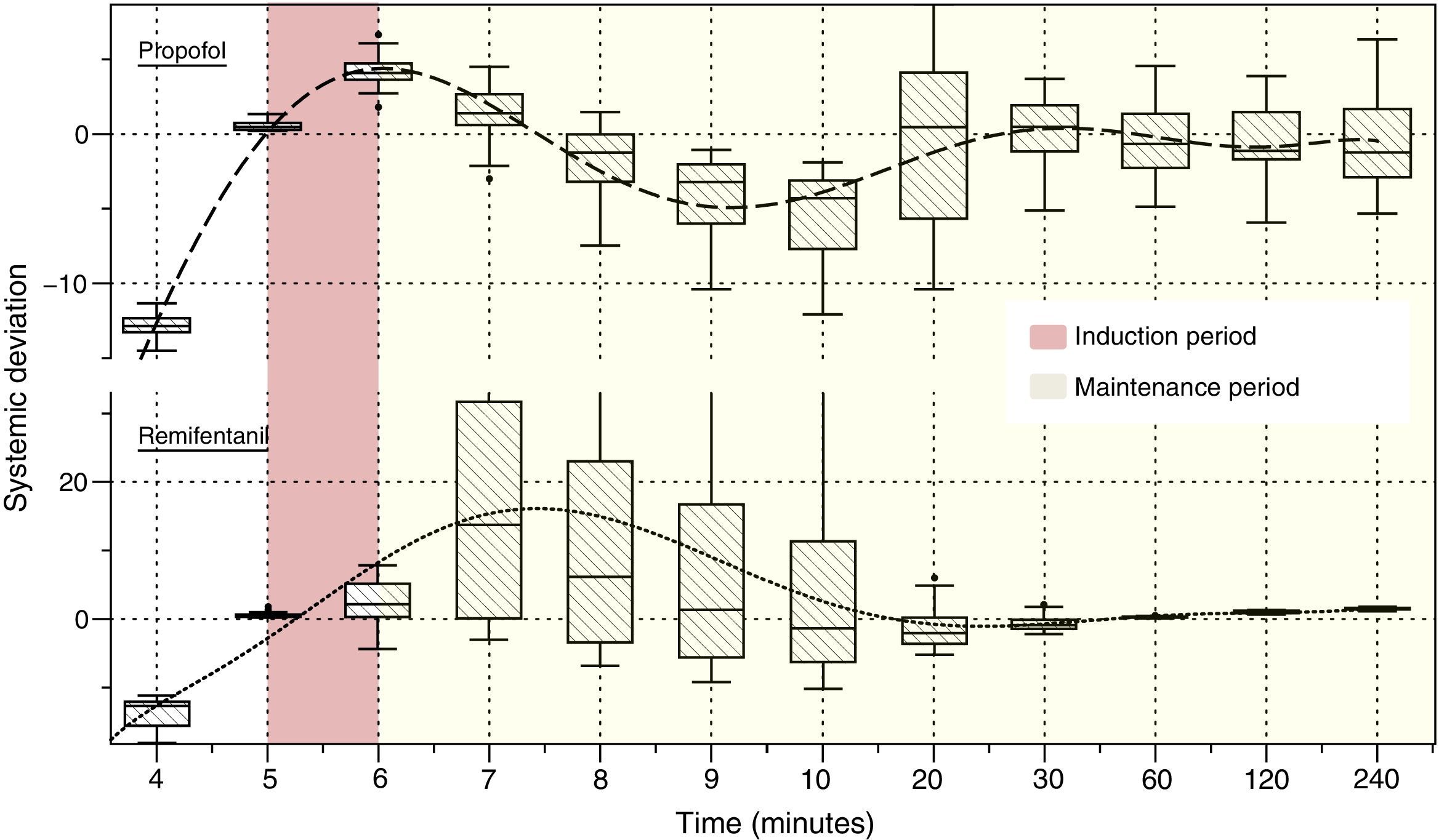
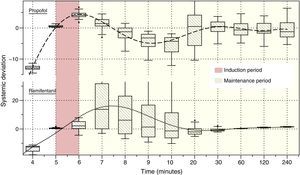
Fig. 4 illustrates the systematic error versus time of the predicted concentrations for propofol and remifentanil according to the algorithm, against the operator-desired concentrations.
Plasma and effect-site concentrations and their variability when simulating different infusion regimens using the algorithm implemented with iTIVA versus the concentrations estimated using the TivaTrainer® software were similar for different evaluation time points (Table 3).
DiscussionThe primary results from this study are: (1) the algorithm described was successfully implemented; (2) the performance of the proposed algorithm to reach effect-site concentrations during induction and maintenance for remifentanil and propofol was excellent; (3) the algorithm has a tolerable variability regarding the desired concentrations and such variability decreases during the maintenance period; and (4) the iTIVA implemented algorithm to simulate plasma and effect-site concentrations according to an infusion regimen behaves similarly to the TivaTrainer® software.
Algorithm development and implementationThe algorithm developed was smoothly implemented assisted by Apple and Google development tools for their iOS (Xcode) and Android (Eclipse) systems, respectively. Initially the algorithm was implemented for Android because it has fewer limitations for publication in the Android App store (this fact facilitated the debugging of the programming code). Then it was adapted to the iOS operating system making use of the similar syntax of both programming languages (Java and C++).
For optimal performance (during 240min of simulation) this algorithm the algorithm requires from 200,000 to 250,000 mathematical calculations but nowadays this is not a major limitation for the microprocessors available even inside the simplest mobile devices.
Algorithm performance and variabilityDuring the induction of anesthesia (minute 5 and 6) the systematic error of the desired concentrations of the two drugs was <5%. Such low variability translates into a very small difference between the desired concentration and the concentration achieved with the algorithm.
During maintenance (minute 7–240), the infusion regimens showed changes in the systematic error that was less than 5% overall for propofol and 15% for remifentanil. Such variability drops significantly at 20min for remifentanil and at 30min for propofol. The divergence observed in the first few minutes may be related to the change from one larger target concentration to a smaller one. During this time – and to maintain a stable concentration with less than 5% variation – a single infusion rate was required for remifentanil and from 2 to 5 progressive changes in the infusion rate for propofol. This difference may be accounted for by the pharmacokinetic characteristics of remifentanil that makes it unresponsive to the environment.25
In contrast to the infusion regimens used in TCI pumps that require approximately 1400 changes in the infusion rate over 240min, this algorithm provides simple, easy to implement regimens with VIP. It delivers very accurate information to achieve and maintain the desired effect-site concentrations, with one advantage versus the standard-dose based administration of medications. Several authors26–31 have reported these concentrations (based on therapeutic targets).
It should be stressed however, that the inter-individual variation and the large number of variables affecting the pharmacokinetics and pharmacodynamics of drugs hinder most pharmacological simulation processes. This fact curtails the accuracy of the pharmacokinetic models as well as the performance of this and several other algorithms. It is then essential to evaluate any individual effects. There are various types of systems available to measure the depth of anesthesia and using these systems in the right context may improve certain outcomes for the patient and lower the risk of adverse events such as intraoperative awareness.32
This research project does not validate a pharmacological forecast versus an actual blood concentration measurement. We chose Lerou's et al.,23 strategy now used by other authors, to simply compare our mathematical forecast as estimated with the algorithm, versus an operator-desired concentration. In the future, tt would be interesting to take a direct measurement of blood concentrations and to contrast those values against the forecasts of the proposed model.
Simulation of concentrations: iTIVA versus TivaTrainer®The iTIVA algorithm gives plasma and effect-site concentrations of the estimated regimens in real time (in accordance with Eqs. (1) & (2)). The concentrations obtained using iTIVA are identical to those obtained with TivaTrainer®. This latter software is widely used for pharmacological research and simulation.2 This was an expected finding since both applications are based on the same mathematical algorithm and confirms its proper implementation in iTIVA.
ConclusionUsing pharmacokinetic models, the iTIVA App quantifies the infusion rates required to manually achieve effect-site concentrations for remifentanil and propofol and this facilitates its use in VIPs. Currently this application is just designed to guide the administration of manual infusions. It is not approved for use as a single strategy for managing patients and its use should be the anesthetist's responsibility. This article presents a theoretical approach based on a simulation process and its widespread use in clinical practice should be subject to a process of validation and comparison against other infusion regimens.33
DisclosuresThere are no conflicts of interest.
FundingThis paper was sponsored by the Colombian Society of Anesthesiology and Resuscitation – SCARE.
Conflicts of interestThe authors have no conflicts of interest to declare.
Please cite this article as: Ramírez DE, Calvache JA. Diseño y evaluacion del desempeño del algoritmo “iTIVA” para la administración manual de anestesicos intravenosos según objetivo en sitio efecto. Rev Colomb Anestesiol. 2016;44:105–113.