Quisiéramos agradecer al profesor Ramos-Vera que haya leído nuestro artículo «Use of benzodiazepines and antidepressants in patients who attend a Rheumatology clinic»1.
Estamos de acuerdo con la necesidad de replicar las investigaciones clínicas, pero debemos señalar que si bien la práctica clínica basada en la evidencia2 lleva bastantes años arraigada, la revisión de artículos publicados cuando la ética y la transparencia en el proceso de tratamiento de datos no eran una práctica que las revistas obligaran a cumplir, puede devolver resultados contradictorios como muchos metaanálisis han encontrado3.
En tal sentido, cabe citar el ejemplo de los dos enfoques, el frecuentista y el bayesiano, para que el lector pueda entender a lo que nos referimos: la interpretación de una odds ratio (OR) y su significación.
Tras un ajuste multivariante se obtienen dos OR asociadas con el riesgo de desarrollar osteoporosis si previamente se tiene osteopenia, y como variables predictoras: grupo de edad y menopausia precoz.
Inicialmente, las estimaciones puntuales obtenidas son similares o prácticamente iguales, tanto con un enfoque como con el otro OREDAD=1,5 y el ORMP=2,5.
Desde un punto de vista frecuentista, los OR mencionados arriba irían acompañados en la tabla correspondiente, en el apartado de resultados del artículo, de un p-valor y posiblemente un intervalo de confianza al 95%. Si el p-valor es menor de 0,05 (nivel de significación o error de tipo I de un contraste), entonces se reconocerá a esa variable como un modificador de efecto y pasará a engrosar la lista de factores de riesgo asociados con la osteoporosis, y no se considerarán para nada los valores del intervalo de confianza; y he ahí el error, pues se debe interpretar ese intervalo. ¿Qué ocurriría si el p-valor asociado con el OR de edad fuese de 0,051? Pues sería rechazado como modificador de efecto, lo que no es del todo correcto, pues el intervalo de confianza podría recoger valores como 0,98-2,1. Como puede observarse, la mayoría de los valores del intervalo son superiores a la unidad, por tanto, más cerca de ser un riesgo que un factor protector.
Desde un punto de vista bayesiano, en la tabla solo aparecería el OR y una región de credibilidad al 95%. En estadística bayesiana, la interpretación se realiza mediante la pregunta por cuál es la probabilidad de que nuestra OR esté entre estos dos valores. Si respondemos diciendo que con una probabilidad del 95% el valor de la OR estará entre 0,98 y 2,1, ¿se diría que la edad es factor de riesgo? Es como si nos dicen que la probabilidad de llover hoy es del 75%, ¿llevaremos paraguas para ir al trabajo?
Debido a esa forma de interpretar los resultados, más subjetiva que con el p-valor de la estadística frecuentista, nace el factor Bayes (FB)4 para tener una medida menos subjetiva y dejar al amparo del facultativo la interpretación de los resultados.
De lo que se trata es de hacer un contraste sobre ese OR de edad y ver si, efectivamente, es o no un factor de riesgo, pero la diferencia es que desde el punto de vista frecuentista se es muy estricto con la regla del p-valor, sin tomar en consideración la potencia del test realizado (error de tipo II de un contraste frecuentista), y muchas investigaciones no hablan de la magnitud del efecto, sino de su significación. Mientras tanto, por otro lado, el FB hace un contraste y muestra la información que aporta aquello que estamos contrastando. Existen tablas con valores que interpretan los resultados de un FB como medida para el estudio de factores de riesgo5.
¿Qué pueden hacer los investigadores para utilizar la estadística bayesiana y su interpretación? Como lo señala Ramos-Vera5, utilizar el FB como medida alternativa al p-valor y emplear la región de credibilidad para explicar cuán plausible es el valor del OR, es decir, interpretarlo en términos de probabilidades; incluso se podría incluir una región de credibilidad al 80%. ¿Por qué? Porque la interpretación es que con una probabilidad al 80% el valor del OR estará en esa región.
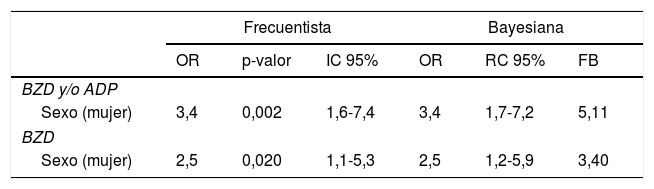
Veamos ahora un ejemplo real en el que se comparan el enfoque frecuentista y el bayesiano. En la tabla 1 se muestran los valores obtenidos en el artículo de Álvarez-Cienfuegos et al.1, junto con los cálculos equivalentes en estadística bayesiana. Como puede observarse, no hay diferencias, y esto ahonda en no abrir frentes entre metodologías, sino pedagogía de ventajas e inconvenientes de cada una de ellas.
Resultados desde la estadística frecuentista y la bayesiana
| Frecuentista | Bayesiana | |||||
|---|---|---|---|---|---|---|
| OR | p-valor | IC 95% | OR | RC 95% | FB | |
| BZD y/o ADP | ||||||
| Sexo (mujer) | 3,4 | 0,002 | 1,6-7,4 | 3,4 | 1,7-7,2 | 5,11 |
| BZD | ||||||
| Sexo (mujer) | 2,5 | 0,020 | 1,1-5,3 | 2,5 | 1,2-5,9 | 3,40 |
ADP: antidepresivo; BZD: benzodiacepina; FB: factor Bayes; IC: intervalo de confianza; OR: odds ratio; RC: región de credibilidad.
¿Cómo interpretar correctamente el intervalo de confianza y la región de credibilidad? Esta es la clave para poder utilizar un método u otro, la interpretación. Se dice que desde la estadística bayesiana se habla en términos de incertidumbre y de forma probabilística, mientras que la frecuentista se basa en eso, en los datos y la información que reportan.
Intervalo de confianza al 95%: si se repitiese 100 veces el experimento, al menos en 95 de ellas el valor obtenido de la OR estaría entre esos dos valores.
Región de credibilidad al 95%: la probabilidad de que la OR esté entre esos dos valores es del 95%.
Después de observar los resultados de la tabla 1, y a pesar de que la forma de interpretar es distinta, las conclusiones se orientan en el mismo sentido: el hecho de ser mujer es un factor de riesgo para el consumo de benzodiacepinas (BZD) o antidepresivos (ADP). Ambas magnitudes del efecto del hecho de ser mujer pueden hasta quintuplicar el riesgo comparado con los hombres en las BZP y hasta septuplicar en BZD o ADP.
Como conclusión, consideramos que tanto el enfoque frecuentista como el bayesiano son muy válidos, pero que en el frecuentista se debe acompañar siempre el p-valor del intervalo de confianza, pero no como un valor para poner al lado, sino para interpretarlo y hablar más de la magnitud del efecto y no tanto de su significación. Por otro lado, el enfoque bayesiano debe empezar a expandirse en las revistas de práctica clínica, pero para ello se necesita más pedagogía como la comunicada por autores como el profesor Ramos-Vera, para poder expresar los resultados en términos probabilísticos e indicar la probabilidad de que un cierto OR tome ese valor o se encuentre entre dos valores (región de credibilidad). Si se consigue que los frecuentistas hablen de la magnitud del efecto y su intervalo, y no tanto de su significación, y que los artículos con estadística bayesiana sean aceptados por las revistas científicas, al final quien gane será la medicina basada en la evidencia, pues habrá más hallazgos que hagan entender el comportamiento de las enfermedades.