We would like to thank Professor Ramos-Vera for reading our article «Use of benzodiazepines and antidepressants in patients who attend a Rheumatology clinic».1
We agree that there is a need to replicate clinical research, but we must point out that even though the evidence-based clinical practice2 has been rooted for many years, the review of articles published when the ethics and transparence in the process of data handling were not a practice that the journals forced to comply, can return contradictory results, as it was found in many meta-analyses.3
In this sense, it is worth mentioning the example of the two approaches, the frequentist and the Bayesian, so that the reader can understand what we mean: the interpretation of an odds ratio (OR) and its significance.
After a multivariate adjustment, two ORs associated with the risk of developing osteoporosis if the patient previously had osteopenia were obtained, and as predictor variables: age group and early menopause.
Initially, the point estimates obtained are similar or practically the same, either with one and the other approach ORAGE = 1.5 and the OREM = 2.5.
From a frequentist point of view, the ORs mentioned above would be accompanied in the corresponding table, in the results section of the article, by a p-value and possibly by a 95% confidence interval. If the p-value is less than 0.05 (significance level or type I contrast error), then this variable will be recognized as an effect modifier and will join the list of risk factors associated with osteoporosis, and the values of the confidence interval will not be considered at all; hence the error, since that interval must be interpreted. What would happen if the p-value associated with the OR of age were 0.051? In that case, it would be rejected as an effect modifier, which is not entirely correct, since the confidence interval could collect values such as 0.98−2.1. As can be observed, most of the values of the interval are higher than the unit, and therefore, they are closer to being a risk rather than a protective factor.
From a Bayesian point of view, only the OR and a 95% credibility region would appear in the table. In Bayesian statistics, the interpretation is made by the question of what is the probability that our OR is between these two values. If we answer by saying that with a probability of 95% the OR value would be between 0.98 and 2.1, the age is a risk factor? It is as if somebody tells us that the probability of rain today is 75%, will we take an umbrella to go to work?
Due to this way of interpreting the results, more subjective than with the p-value of the frequentist statistics, the Bayes factor (BF)4 was born to have a less subjective measure and leave the interpretation of the results at the judgment of the physician.
The point is to make a contrast on that OR of age and see whether, indeed, it is a risk factor or not, but the difference is that from the frequentist point of view, we are very strict with the rule of the p-value, without taking into consideration the power of the test carried out (type II error of a frequentist contrast), and many investigations do not speak of the magnitude of the effect, but rather of its significance. Meanwhile, on the other hand, the BF makes a contrast and shows the information provided by what we are contrasting. There are tables with values that interpret the results of a BF as a measure for the study of risk factors.5
What can researchers do to use Bayesian statistics and its interpretation? As noted by Ramos-Vera,5 they should use the BF as a measure alternative to the p-value and use the credibility region to explain how plausible is the OR value, that is, interpret it in terms of probabilities; even an 80% credibility region could be included. Why? Because the interpretation is that with a probability of 80% the OR value will be in that region.
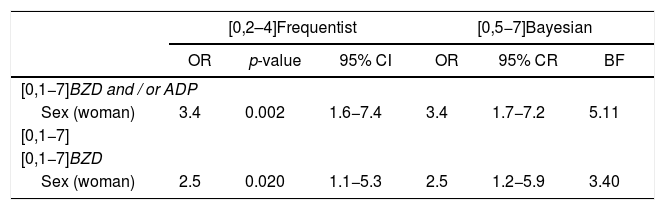
Let us see now a real example in which the frequentist and the Bayesian approaches are compared. Table 1 shows the values obtained in the article by Álvarez-Cienfuegos et al.,1 along with the equivalent calculation in Bayesian statistics. As it can be observed, there are no differences, and this deepens in not opening frontlines between methodologies, but rather pedagogy of advantages and drawbacks of each of them.
Results from the frequentist and the Bayesian statistics.
| [0,2–4]Frequentist | [0,5−7]Bayesian | |||||
|---|---|---|---|---|---|---|
| OR | p-value | 95% CI | OR | 95% CR | BF | |
| [0,1−7]BZD and / or ADP | ||||||
| Sex (woman) | 3.4 | 0.002 | 1.6−7.4 | 3.4 | 1.7−7.2 | 5.11 |
| [0,1−7] | ||||||
| [0,1−7]BZD | ||||||
| Sex (woman) | 2.5 | 0.020 | 1.1−5.3 | 2.5 | 1.2−5.9 | 3.40 |
ADP: antidepressant; BZD: benzodiazepine; BF: Bayes factor; CI: confidence interval; OR: odds ratio; CR: credibility region.
How to interpret correctly the confidence interval and the credibility region? This is the key to be able to use one method or another, the interpretation. It is said that from Bayesian statistics we speak in terms of uncertainty and in a probabilistic way, while the frequentist statistics is based on the data and the information that they report.
95% confidence interval: If the experiment were repeated 100 times, at least in 95 of them the value obtained from the OR would be between these two values.
95% credibility region: The probability of the OR to be between these two values is 95%.
After observing the results in Table 1, and although the way of interpreting is different, the conclusions are oriented in the same direction: the fact of being a woman is a risk factor for the consumption of benzodiazepines (BZD) or antidepressants (ADP). Both magnitudes of the effect of being a woman can increase up to five-fold the risk compared to men in BZP and up to seven-fold in BZD or ADP.
In conclusion, we consider that both the frequentist and the Bayesian approaches are very valid, but that in the frequentist the p-value must always be accompanied by the confidence interval, not as a value to put aside, but to interpret it and speak more of the magnitude of the effect and not so much of its significance. On the other hand, the Bayesian approach should begin to expand in clinical practice journals, but for this, more pedagogy is needed, such as that communicated by authors such as Professor Ramos-Vera, to be able to express the results in probabilistic terms and indicate the probability of that a certain OR takes that value or that it is between two values (credibility region). If we get that the frequentists speak on the magnitude of the effect and its interval, and not so much about its significance, and that the articles with Bayesian statistics would be accepted by scientific journals, in the end the one who wins will be evidence-based medicine, as there will be more findings that make us understand the behavior of the diseases.
Please cite this article as: Barber X, García-Gómez JA, Martínez-Vidal MP, Álvarez-Cienfuegos A. Carta de réplica: beneficios del factor Bayes en la investigación de reumatología. Rev Colomb Reumatol. 2021;28:232–233.