On February 2, 2021, an important article that evaluated the statistically significant association (P < .05) by means of the odds ratio (OR) was published in this Journal. The study estimated a correlation between the use of benzodiazepines and the female gender (OR = 2.5) in 350 patients who attended a Rheumatology clinic.1
To generate more credible evidence in the area of rheumatology, the replication of clinical research based on tests of significance is recommended.
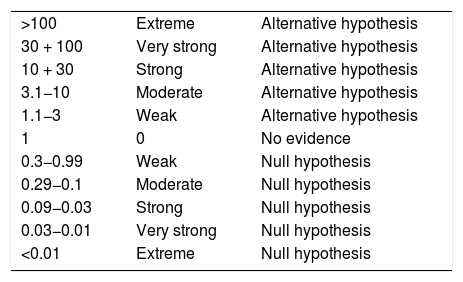
The Bayes factor is the suitable method to assess beyond the dichotomous interpretation of rejection of acceptance of the null hypothesis, since it quantifies the value of evidence or certainty with which the data support the alternative hypothesis with respect to the null hypothesis (alternative hypothesis vs. null hypothesis).2,3 The statistical replication of significant findings using the Bayes factor allows to reinforce the practical credibility of future articles in the area of rheumatology (clinical trials, interventions and treatments, among others), which is required when the Bayesian inference reports a conclusive (strong) or superior (BF10 > 10) evidence, based on the Jeffreys’ classification scheme4: weak, moderate, strong, very strong and extreme (Table 1).
Quantifiable interpretation values of the Bayes factor.
| >100 | Extreme | Alternative hypothesis |
| 30 + 100 | Very strong | Alternative hypothesis |
| 10 + 30 | Strong | Alternative hypothesis |
| 3.1−10 | Moderate | Alternative hypothesis |
| 1.1−3 | Weak | Alternative hypothesis |
| 1 | 0 | No evidence |
| 0.3−0.99 | Weak | Null hypothesis |
| 0.29−0.1 | Moderate | Null hypothesis |
| 0.09−0.03 | Strong | Null hypothesis |
| 0.03−0.01 | Very strong | Null hypothesis |
| <0.01 | Extreme | Null hypothesis |
Own elaboration according to the Jeffreys’ classification scale.4
This letter aims to report 2 examples of Bayesian reanalysis based on the sample size and the statistical value of the OR, which was converted into correlation coefficient (r) using an online calculator5 that reported an r-value = 0.245.
The Bayes factor consists of 2 interpretations: BF10 (in favor of the alternative hypothesis) and BF01 (in favor of the null hypothesis) and the credible interval from the data.6
The results obtained by the Bayes factor are BF10 = 3000 and BF01 = 0.0003, with a confidence interval (CI) of 0.143−0.340 and a very strong evidence, which supported the significant result. Likewise, the parameters of the maximum Bayes factor (maxBF10 = 48.61; maxBF10 = 6133) were estimated to determine the stability of the results, whose values of higher magnitude strengthen the estimation of the Bayesian reevaluation.
The conversion of the effect size and other statistical measures which are based on the hypotheses of significance (AUC, d, f, η2, OR, x2, Z) into the correlation effect (r) of greater universal use in health sciences, allows to strengthen future Bayesian analyses and reanalyses. These estimations are easy to carry out using the Lenhard and Lenhard calculator.5 The Bayes factor is useful in other tests of statistical significance7,8 (linear regression, ANOVA, among others), whose measures of effect size are also convertible. The Goss-Sampson manual6 is recommended for the Bayesian inference of the analyses most commonly used in rheumatology research.
The inclusive use of different magnitudes of convertible effect strengthens the increase in research with diverse statistical methods for future meta-analyses. In turn, the application of the Bayes factor is beneficial to select those effect sizes with greater evidence soundness (BF10 > 10) for the quantitative systematic studies, which reinforces the credibility of the meta-analytical conclusions.
In conclusion, the inclusive use of the conversion of the effect size or other statistical measures and the Bayes factor is a great methodological contribution that presents a practical implication in essential clinical decision-making based on the confirmation of results that are effectively conclusive, of greater importance in the context of COVID-19.
FundingThis research has not received any specific grant from agencies of the public, commercial or non-profit sectors.
Conflicts of interestNone.
Please cite this article as: Ramos-Vera CA. Beneficios del factor Bayes en la investigación de reumatología. Rev Colomb Reumatol. 2021;28:230–231.