Aproximación matemática para la corrección de la influencia de la hemólisis en pruebas frecuentes del laboratorio clínico

Resumen

Introducción

La hemólisis constituye una de las incidencias más frecuentes en el laboratorio clínico, y se erige como una de las principales causas del rechazo de muestras. El presente estudio tiene como objetivo el diseño de una ecuación matemática que permita estimar y corregir las posibles interferencias producidas por la hemólisis en 6 analitos de uso frecuente en el laboratorio clínico.

Material y métodos

Se emplearon sueros procedentes de 100 pacientes sanos, que se hemolizaron y se procesaron de acuerdo con las recomendaciones de la Comisión de Interferencias y Efectos de los Medicamentos de la Sociedad Española de Química Clínica. Las determinaciones se realizaron en el autoanalizador Modular Analytics D/P/ISE (Roche Diagnostics) y los datos obtenidos se trataron estadísticamente con la aplicación SPSS versión 15.0 (SPSS Inc., Chicago, IL, EE. UU.).

Resultados

La hemólisis induce una sobreestimación en la determinación de potasio (K), aspartato aminotransferasa (AST), alanina aminotransferasa y lactato deshidrogenasa (LDH), mientras que se traduce en una infravaloración de gamma-glutamiltransferasa y bilirrubina total. La existencia de una correlación estadísticamente significativa entre el grado de hemólisis y el porcentaje de variación en la concentración de los analitos sólo se ha observado en el caso del K, el AST y la LDH. La ecuación de corrección surge del establecimiento de una igualdad entre el porcentaje de variación empírico que muestran los analitos en sueros hemolizados y el porcentaje de variación teórico obtenido a partir de análisis de regresión. Las estimaciones se enmarcaron dentro de un intervalo de confianza del 95% definido por el error analíticamente permisible.

Conclusiones

Proponemos que la ecuación matemática puede ser de utilidad para la corrección de los valores de K, AST y LDH en el laboratorio clínico, y el rango de hemólisis susceptible de corrección es dependiente del analito analizado.

Abstract

Introduction

Haemolysis is the most common and undesirable occurrence in clinical laboratories and represents the main reason for specimen rejection. The aim of this study is to propose a mathematical equation to estimate and correct for the haemolysis interference in six common laboratory tests.

Materials and methods

A toat of 100 fresh samples from healthy people were used. They were haemolysed and analysed following the instructions from the Interferences and Drug effects Commission (SEQC). Every analysis was carried out using an Modular analytics D/P/ISE (Roche Diagnostics) autoanalyser and SPSS (V15.0; SPSS Inc., Chicago, IL) statistical analysis software was used.

Results

Haemolysis effect leads to overestimation of K, AST, ALT and LDH. On the other hand, haemolysis leads to an underestimation of GGT and BT. A statistically significant and positive linear correlation between the increase in free serum haemoglobin and the increase of the analyte were only observed in K, AST and LDH. When the real % variation of each analyte obtained in the experimental step of this study was equal to the previously calculated % variation using the regression equation, the correction equation shown was obtained. A 95% confidence interval was used to obtain the calculated results.

Conclusions

The proposed mathematical equation is useful to the correction of K, AST and LDH in clinical laboratories. The haemolysis range depends on the tests analysed.

Introducción

La eliminación completa de los errores propios del laboratorio clínico constituye una de las principales metas de los servicios de bioquímica y análisis clínicos. Los avances tecnológicos y la automatización del laboratorio han contribuido de forma decisiva a una disminución de la incidencia de errores analíticos, y existe, sin embargo, aun hoy en día múltiples circunstancias preanalíticas que influyen en la validez de los resultados^1–7.

La hemólisis se define como la rotura de los eritrocitos y la subsiguiente liberación de hemoglobina y otros componentes intracelulares al plasma circundante. Es posible diferenciar entre la hemólisis in vitro e in vivo. Así, mientras que la hemólisis in vivo es propia de enfermedades sanguíneas, como la anemia hemolítica, la hemólisis in vitro sucede durante la recogida, la manipulación y el procesado de la muestra. Si bien es posible distinguir múltiples mecanismos causantes de la interferencia por hemólisis^3–7, muchos de los cuales son fácilmente identificables, existen otros menos obvios. Este hecho, unido a la frecuente interacción de diferentes mecanismos hemolizantes, puede dar lugar a resultados analíticos incorrectos. Así, aquellos analitos de elevada concentración intracelular pueden mostrar un sesgo positivo como resultado de la liberación de éstos desde el compartimento intracelular hasta el plasma sanguíneo. Este mecanismo se ha descrito para el potasio (K), la alanina aminotransferasa (ALT), la aspartato aminotransferasa (AST) y la lactato deshidrogenasa (LDH). Por otra parte, otros analitos pueden ser susceptibles de sesgo negativo debido a la presencia de solapamientos parciales con los picos de absorción espectrofotométricos de la hemoglobina, comprendidos entre los 400 y los 600 nm, como se ha demostrado previamente en el caso de la bilirrubina total (BT) y la gamma-glutamiltransferasa (GGT)^8–13.

El objetivo del presente estudio es el de proporcionar una ecuación matemática que permita estimar y corregir el error inducido por la hemólisis en estos analitos.

Material y métodos

Diseño experimental

Se elaboró una solución concentrada de hemoglobina mediante disrupción osmótica, según el procedimiento de Meites¹⁵ recomendado por la Comisión de Interferencias y Efectos de los Medicamentos en Química Clínica de la Sociedad Española de Química Clínica (SEQC)¹⁶. A partir de este concentrado se obtuvieron diluciones seriadas con agua destilada que se utilizaron para inducir diferentes grados de hemólisis a un total de 100 sueros procedentes de voluntarios sin enfermedades conocidas, según el protocolo para la valoración in vitro de las interferencias por medicamentos¹⁷ propuesto por la anteriormente citada comisión, y se corrigieron las concentraciones de hemoglobina de partida y se respetó el grado de dilución para conservar el efecto matriz. La concentración de hemoglobina de la solución de partida fue de 10,4 g/dl y las concentraciones finales de los sueros tras la mezcla oscilaron entre 0,4 y 8,3 g/l.

Cada uno de los sueros se analizó de forma independiente, previa y posteriormente a la inducción de la hemólisis, y pudo determinarse de esta forma el porcentaje de variación en la concentración de cada analito ensayado en función del incremento en el grado de hemólisis de las muestras. La relación existente entre ambas variables se puso de manifiesto mediante la regresión lineal y el coeficiente de correlación calculados bajo la aplicación informática SPSS versión 15.0 (SPSS Inc., Chicago, IL, EE. UU.).

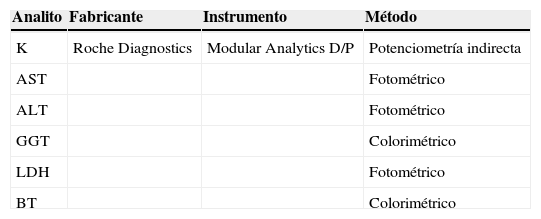
Instrumentación y pruebas de laboratorio

Se ensayaron un total de 6 pruebas frecuentes del laboratorio clínico (tabla 1), y se realizaron las medidas por triplicado en un autoanalizador Modular Analytics D/P/ISE (Roche Diagnostics). Las muestras se procesaron de forma aleatorizada en una única serie analítica y se realizaron controles internos habituales propios del laboratorio al comienzo y al final de la experimentación. Estos controles se encontraron en todos los casos dentro de los márgenes previstos. La estimación del grado de hemólisis de las muestras se llevó a cabo mediante el índice proporcionado por el autoanalizador (índice de hemólisis [IH] – unidades arbitrarias), y pudo calcularse a partir de éste la concentración de hemoglobina libre ([Hb]) presente en el suero según la siguiente ecuación: [Hb] (g/l)=0,009 IH-0,046 (coeficiente de correlación al cuadrado o coeficiente de determinación [r²]=0,999) (recta patrón elaborada a partir de sueros tipo de composición conocida).

Tabla 1.

Relación de métodos para la medida de los analitos

Analito	Fabricante	Instrumento	Método
K	Roche Diagnostics	Modular Analytics D/P	Potenciometría indirecta
AST			Fotométrico
ALT			Fotométrico
GGT			Colorimétrico
LDH			Fotométrico
BT			Colorimétrico

ALT: alanina aminotransferasa; AST: aspartato aminotransferasa; BT: bilirrubina total; GGT: gamma-glutamiltransferasa; K: potasio; LDH: lactato deshidrogenasa.

Resultados

Efecto de la hemólisis en las pruebas de laboratorio

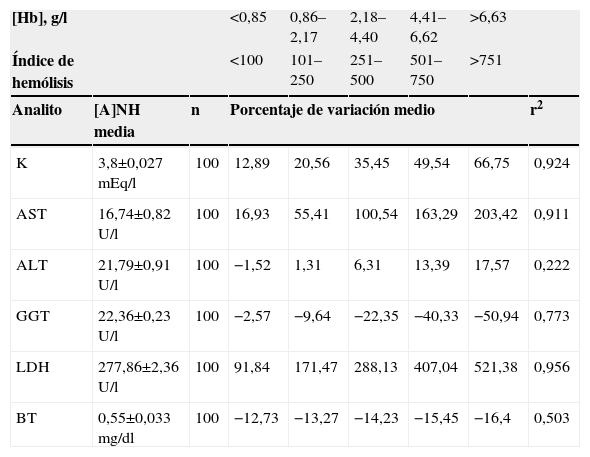
Como se ha descrito ampliamente en estudios previos^{7–14,18–23}, nuestros resultados mostraron que la interferencia hemolítica se traduce en una sobreestimación en las concentraciones de K (percentil [P]₁₀: 11%: P₅₀: 20,21%, y P₉₀: 59,06%), AST (P₁₀: 24,48%; P₅₀: 68,32%, y P₉₀: 164,91%), ALT (P₂₀: 1,01%; P₅₀: 11,69%, y P₉₀: 105,97%) y LDH (P₁₀: 77,48%; P₅₀: 171,45%, y P₉₀: 518,35%), mientras que supone una infravaloración en las medidas de GGT (P₁₀: −40,67%; P₅₀: −11,87%, y P₉₀: −1,99%) y BT (P₁₀: −20,28%, P₅₀: −14,9%, y P₉₀: −6,89%). En la tabla 2 se representa el porcentaje de variación medio de estos analitos por intervalos de hemólisis. El análisis de regresión lineal indicó la existencia de una correlación estadísticamente significativa (r²>0,9) entre porcentaje de variación e interferencia hemolítica únicamente para K, AST y LDH, por lo que el resto de las pruebas se consideraron excluidas del estudio.

Tabla 2.

Influencia de la hemólisis en el Modular Analytics D/P/ISE

[Hb], g/l			<0,85	0,86–2,17	2,18–4,40	4,41–6,62	>6,63
Índice de hemólisis			<100	101–250	251–500	501–750	>751
Analito	[A]NH media	n	Porcentaje de variación medio					r^2
K	3,8±0,027 mEq/l	100	12,89	20,56	35,45	49,54	66,75	0,924
AST	16,74±0,82 U/l	100	16,93	55,41	100,54	163,29	203,42	0,911
ALT	21,79±0,91 U/l	100	−1,52	1,31	6,31	13,39	17,57	0,222
GGT	22,36±0,23 U/l	100	−2,57	−9,64	−22,35	−40,33	−50,94	0,773
LDH	277,86±2,36 U/l	100	91,84	171,47	288,13	407,04	521,38	0,956
BT	0,55±0,033 mg/dl	100	−12,73	−13,27	−14,23	−15,45	−16,4	0,503

[A]NH: concentración inicial del analito en un suero no hemolizado; [Hb]: hemoglobina libre; AST: aspartato aminotransferasa; ALT: alanina aminotransferasa; BT: bilirrubina total; GGT: gamma-glutamiltransferasa; K: potasio; LDH: lactato deshidrogenasa; n: número de muestras; r²: coeficiente de correlación al cuadrado o coeficiente de determinación.

Diseño de una ecuación de corrección matemática

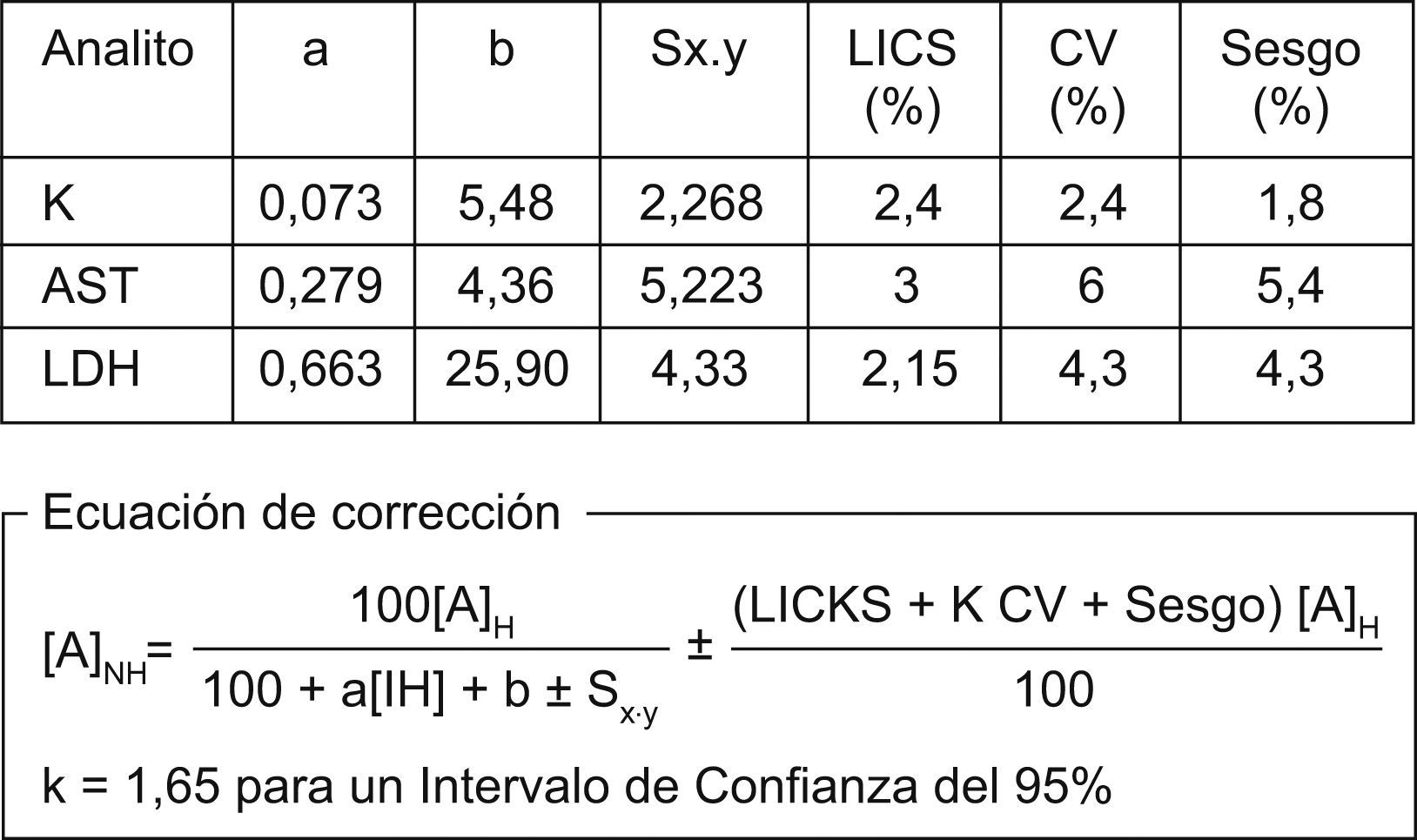
La ecuación de corrección presentada en la figura 1 surgió como resultado de establecer una igualdad entre el porcentaje de variación real (medido empíricamente) que experimenta un determinado analito cuando una muestra está hemolizada (porcentaje de variación real=100([A]_H−[A]_NH)/[A]_NH) y el porcentaje de variación estimado por una recta de regresión obtenida mediante métodos estadísticos (porcentaje de variación estimado=aIH+b±S_x.y) [a: pendiente de la recta de regresión; A: analito; b: punto de corte en ordenadas], donde [A]_H es la concentración del analito A en una muestra hemolizada, [A]_NH es la concentración inicial del analito en un suero no hemolizado y S_x.y es el error típico del análisis de regresión. La utilización de porcentaje de variación en lugar de valores absolutos relativiza desde un punto de vista matemático la importancia de la concentración inicial del analito, y amplía el rango de validez de la ecuación. Los valores de [A]_NH estimados por la ecuación de corrección se enmarcaron dentro de un intervalo de confianza del 95% definido analíticamente por el error permisible (EP), considerado como la suma del error sistemático (ES), el error aleatorizado (EA) y el error debido a interferencia (EI). Los ES y EA se cuantificaron como el porcentaje del sesgo y el porcentaje del coeficiente de variación deseable, calculados en función de los coeficientes de variabilidad biológica intraindividual e interindividual²⁴ según las recomendaciones propuestas por la Conferencia de Consenso sobre Especificaciones de la Calidad en el Laboratorio Clínico²⁵ y respaldadas por la Comisión de Calidad Analítica de la SEQC²⁶ (tablas disponibles en: URL: www.seqc.es). La determinación del EI se realizó sobre la base de los límites para las interferencias clínicamente significativas, calculado según propone la Comisión de Efectos de los Medicamentos en Química Clínica²⁷.

Figura 1.

Ecuación de corrección de la interferencia hemolítica.

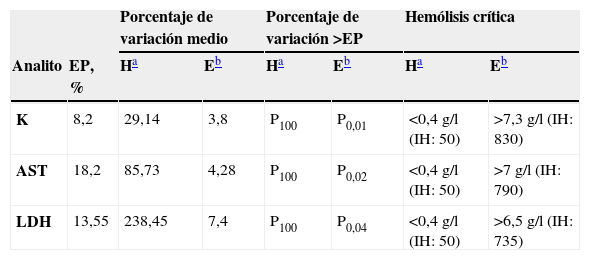
Como queda reflejado en la tabla 3, el porcentaje de variación experimentado por las concentraciones de los analitos en sueros hemolizados fue superior al EP en todos los casos. La aplicación de la ecuación de corrección tiene como consecuencia que este porcentaje de variación excede los límites marcados por el EP en un 1, un 2 y un 4% para el K, la AST y la LDH, respectivamente. Hemos considerado como hemólisis crítica aquella concentración de [Hb] en la que el EP se sobrepasa por primera vez, y fue para el K de 7,3 g/l, para el AST de 7 g/l y para la LDH de 6,5 g/l.

Tabla 3.

Percentiles y concentraciones de hemólisis críticas que implican un porcentaje de variación superior al error analíticamente permisible

		Porcentaje de variación medio		Porcentaje de variación >EP		Hemólisis crítica
Analito	EP, %	H^a	E^b	H^a	E^b	H^a	E^b
K	8,2	29,14	3,8	P100	P0,01	<0,4 g/l (IH: 50)	>7,3 g/l (IH: 830)
AST	18,2	85,73	4,28	P100	P0,02	<0,4 g/l (IH: 50)	>7 g/l (IH: 790)
LDH	13,55	238,45	7,4	P100	P0,04	<0,4 g/l (IH: 50)	>6,5 g/l (IH: 735)

AST: aspartato aminotransferasa; EP: error permisible; IH: índice de hemólisis; K: potasio; LDH: lactato deshidrogenasa; P: percentil.

a

H: valores obtenidos a partir de sueros hemolizados.

b

E: valores obtenidos tras la aplicación de la ecuación de corrección.

Discusión

Los facultativos especialistas de los laboratorios clínicos tienen la responsabilidad de proporcionar datos analíticos con la mayor fiabilidad y rapidez que sea posible. Esto sólo es factible si se posee un profundo conocimiento de la metodología empleada en cada prueba y de las posibles interferencias que pueden afectar a los resultados emitidos¹⁴.

La decisión de considerar como fiable un resultado implica, además, la elección previa de una especificación de calidad adecuada, que puede estar basada en cualquiera de los criterios que de forma jerárquica se propusieron en la Conferencia de Consenso sobre Especificaciones de la Calidad en el Laboratorio Clínico²⁵, tales como: 1) la tecnología de avanzada; 2) las recomendaciones propuestas por ley o los programas de evaluación externa de la calidad; 3) las recomendaciones de grupos profesionales; 4) los derivados de la variabilidad biológica intraindividual e interindividual, y 5) los criterios de decisión médica. Las especificaciones basadas en los niveles inferiores definen EP elevados, mientras que las especificaciones basadas en los niveles superiores son más exigentes²⁶. La aceptación de un resultado por parte del laboratorio implica en cualquier caso que el error analítico total, derivado de la imprecisión, el sesgo y las interferencias, ha de ser inferior al EP definido por las especificaciones de calidad²⁷.

La interferencia hemolítica induce en determinadas magnitudes un error que en numerosas ocasiones es superior al EP, aun cuando éste se ha definido en función de especificaciones de calidad poco exigentes, lo que se traduce en una pérdida de fiabilidad en los resultados obtenidos y en la necesidad de descartar el ensayo y solicitar una nueva muestra¹³. La aplicación de la ecuación de corrección propuesta en el presente trabajo puede estimar y corregir el efecto ejercido por la hemólisis en el K, la AST y la LDH, lo que supone una disminución en el error analítico total presente en estos ensayos. Esta disminución sitúa a los valores corregidos dentro de los límites aceptables definidos por las especificaciones de calidad deseables derivadas de los coeficientes de variabilidad biológica (criterio de cuarto nivel) y de los límites para interferencias clínicamente significativas, con un intervalo de confianza del 95%. Cabe destacar, sin embargo, que el análisis de la interferencia aquí realizado no puede generalizarse para otros reactivos, métodos o instrumentos²⁰, por lo que el uso de la ecuación no puede en ningún caso extrapolarse a sistemas analíticos diferentes a los descritos en este estudio. Además, recomendamos que la aplicación de la corrección debe tomarse con precaución a partir de 7,3, 7 y 6,5 g/l de [Hb] para K, AST y LDH, respectivamente, ya que los casos aislados en los que se ha superado el EP en la determinación de estos analitos tuvieron lugar por encima de estas concentraciones. Este hecho, sin embargo, no ha de suponer un problema real en la clínica diaria, ya que, como han descrito Caballero et al²⁸, tales grados de hemólisis son excepcionales en la práctica.

La implantación de la ecuación de corrección propuesta en un servicio de análisis puede suponer una mejora global de éste, tanto a nivel económico como a nivel asistencial. Así, por una parte, la disminución de rechazos de sueros hemolizados supone un ahorro de reactivos, un menor desgaste del instrumental y una mejor gestión del tiempo del personal técnico y facultativo. Por otra parte, desde un punto de vista asistencial, la aproximación matemática reduce la espera en el informe de resultados en aquellos casos críticos en los que el retraso puede derivar en diagnósticos precipitados y tratamientos incorrectos que causen agravamiento en el estado del paciente, y es además factible la emisión de un resultado cuando la repetición de la prueba no es posible por motivos ajenos al laboratorio.

Si bien el sistema informático puede programarse para realizar una corrección automática de los sueros hemolizados, es el facultativo especialista el que posee la responsabilidad de sopesar la conveniencia de su aplicación. Nuestra opinión es que la primera opción ante la recepción de un suero hemolizado ha de ser la solicitud de envío de una nueva muestra, con lo que se limita el uso de la ecuación de corrección a aquellos casos en los que sea logísticamente inviable la remisión, así como en aquellas situaciones en las que el tiempo de respuesta constituya un factor crítico. Recomendamos, además, que el resultado estimado por la ecuación debe ir acompañado de un comentario en el que se especifique la naturaleza estadística del valor informado, así como el EP, el intervalo de confianza y el grado de hemólisis presente en la muestra.

Agradecimientos

Agradecemos las sugerencias realizadas por Guadalupe Ruíz Martín y David Lamuño Sánchez al presente trabajo, así como la asistencia técnica de Laura Contreras Navarro y María Carola López Díaz.