Es generalmente aceptado el hecho de que el ambiente mecánico presente en el foco de fractura influye de forma determinante en el proceso de reparación ósea. Diversos autores2,6,21-23 han desarrollado los conceptos generales que explican la evolución del tejido indiferenciado inicial hacia tejido cartilaginoso, fibroso o hueso, en función de la naturaleza de las cargas y la magnitud de las deformaciones presentes en el foco de fractura. Otros estudios plantean los efectos de la aplicación de cargas o movimientos de tipo cíclico sobre el callo.13,14,19
El nivel de cargas presente en el foco de fractura depende fundamentalmente de factores relacionados con su naturaleza (estabilidad, conminución, orientación de los fragmentos, etc.) y con el sistema de fijación empleado en su tratamiento. De entre los distintos sistemas de fijación, la fijación externa ha tenido un gran auge por las ventajas que ofrece: deambulación precoz, reducción del tiempo de hospitalización, simplicidad y rapidez de aplicación, mínima invasividad de la técnica quirúrgica y posibilidad de reducción de la fractura de forma controlada.24 Además, la fijación externa permite modificar el ambiente mecánico al que está sometido el foco de fractura, en función de la evolución de la reparación.
Diversos estudios han analizado diferentes configuraciones de sistemas de fijación externa comerciales, estudiando los efectos que sobre la rigidez y estabilidad de la fractura tienen, entre otros, el número y diámetro de los tornillos, los materiales utilizados, la proximidad de las barras al hueso fracturado y la disposición espacial de tornillos y barras.4 Juan y cols.12 consideraron, además, la evolución de las características mecánicas del callo durante la reparación, relacionando la configuración del fijador y el estado de evolución de la fractura con la rigidez del conjunto.
Sin embargo, en el ambiente mecánico del callo de fractura influyen no sólo los parámetros de diseño del sistema de fijación externa, sino también variables propias de la configuración que se adopte y, lo que es más importante, las características de la reducción de la fractura que se consiga, factor particularmente crítico si se tiene en cuenta la dificultad de obtener una buena reducción durante el acto quirúrgico. La reducción de la fractura, entendida como la restauración de la alineación anatómica del hueso, incluye variables como la orientación angular y el desplazamiento relativo entre los fragmentos óseos en el espacio. En este último aspecto son muy escasos los estudios realizados y, por tanto, el diseño de los sistemas de fijación existentes no contempla, en su gran mayoría, la posibilidad de actuar de forma controlada y precisa sobre la reducción.
Con el fin de aclarar esta cuestión, se planteó como objeto del presente trabajo el análisis de las cargas presentes en el foco de fractura en función de parámetros que dependen de la naturaleza de la propia fractura y de la reducción conseguida. Para poder relacionar las cargas que actúan sobre el sistema hueso fracturado-fijador externo con los niveles de carga y estado tensional transmitido al foco de fractura, es necesario utilizar técnicas que permitan estimar dichos valores a partir de las propiedades mecánicas de los materiales y las características geométricas de dichos elementos. Hoy en día, la técnica de análisis más utilizada para tratar este tipo de problemas es el método de los elementos finitos (MEF).
El análisis mediante el MEF ha sido utilizado de forma frecuente en investigaciones relacionadas con la traumatología y, más concretamente, en el estudio de la fijación externa. Vera y cols.29 y Nishimura17 mediante esta técnica, concluían que el callo asume una gran parte de las cargas a las que se ve sometido el sistema fijador externo-hueso, incluso desde sus primeros estados. Juan y cols.12 y Chao y cols.5 en sendos estudios comparativos, modelaron mediante elementos unidimensionales (vigas) varios sistemas de fijación externa de amplio uso clínico. Meroi y Natali15 desarrollaron un modelo mixto, en el que combinaron la utilización de elementos unidimensionales y tridimensionales. Este último tipo de elementos ha sido también utilizado, más recientemente, por Richards y cols.27
Sin embargo, aunque existe un gran número de estudios que caracterizan el comportamiento de los sistemas de fijación externa, aún no ha sido determinada la importancia que tienen los factores relacionados con la fractura y la reducción conseguida durante el acto quirúrgico sobre la estabilidad global y, por tanto, sobre el proceso de reparación. Con el fin de aclarar esta cuestión, se estructuró el presente estudio en cuatro partes. La primera parte consistió en el desarrollo de un modelo de elementos finitos simplificado del sistema hueso-fijador mediante elementos unidimensionales. La segunda parte se centró en la caracterización biomecánica de un sistema de fijación externa comercial en una configuración clínica habitual mediante ensayos en laboratorio. En tercer lugar, se validó el modelo mediante la modificación de diversos parámetros del mismo hasta conseguir que su comportamiento fuese análogo al observado experimentalmente en el fijador comercial. Por último, del modelo final obtenido se extrajeron los datos referentes al estado tensional y a la magnitud y naturaleza de las cargas actuantes en el foco de fractura durante el proceso de consolidación, lo cual ha permitido conocer cómo influyen los parámetros relativos a la reducción de la fractura y a establecer cuáles de ellos pueden resultar más críticos al inducir mayores niveles de cargas y tensiones en el callo.
Material y método
Modelo de elementos finitos
Se desarrolló un modelo de elementos finitos del conjunto fijador externo-tibia fracturada, empleando las características físicas y geométricas de un fijador externo unilateral comercial (STRONGER®, IQL, S. L.). Dicho fijador de configuración unilateral comprende un cuerpo central que permite controlar el alargamiento y el giro, y dos bridas laterales a las que se fijan los tornillos de cortical. La unión entre las bridas y el cuerpo central se lleva a cabo mediante cuatro rótulas que permiten la reducción de la fractura en planos independientes.
A su vez, en el modelo se consideraron las características correspondientes a una tibia humana con una fractura de tercio medio y con un callo de fractura de características mecánicas variables con el tiempo. El modelo desarrollado permitía modificar la configuración del sistema de fijación y la orientación espacial de los fragmentos óseos, así como las propiedades mecánicas del callo de fractura, con el fin de analizar su influencia en el ambiente mecánico del montaje.
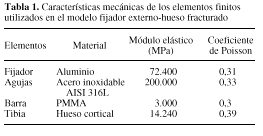
Dadas las características geométricas del conjunto, se utilizaron elementos finitos unidimensionales tipo viga, que consideran las características mecánicas más relevantes para el estudio del comportamiento mecánico del sistema. Esta aproximación permitió simplificar el tratamiento y análisis de los resultados obtenidos sin perder validez de forma significativa.4,12 Los elementos que componían el modelo fueron dotados de las características mecánicas correspondientes a los materiales de los elementos reales (tabla 1), cuyos datos fueron obtenidos de la bibliografía.8,20,30
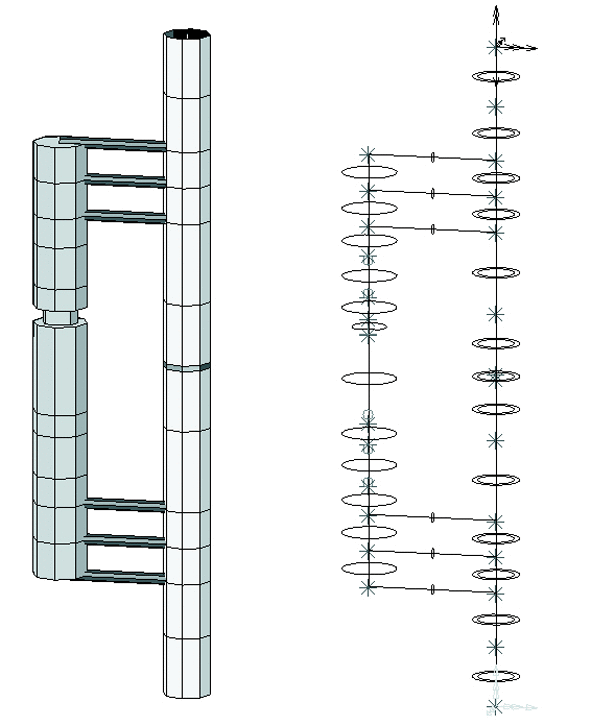
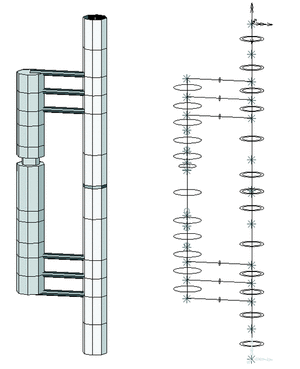
Se emplearon en el modelo del conjunto (fijador, fragmentos óseos y callo) un total de 31 elementos, conectados entre sí por 27 nodos (Fig. 1). Para el desarrollo y análisis del modelo fue utilizado el programa I-DEAS Master Series 6 (SDRC, Milford, Ohio). Como hipótesis se consideraron materiales elásticos lineales con propiedades homogéneas.
Figura 1. Modelo de elementos finitos del conjunto fijador externo-tibia fracturada.
Caracterización biomecánica de un fijador unilateral tipo
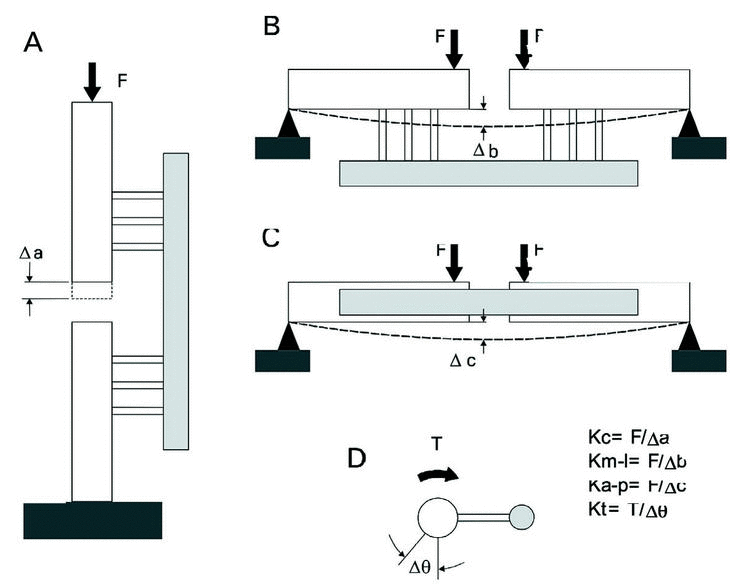
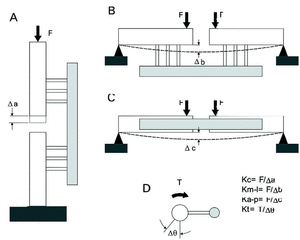
El parámetro utilizado para la caracterización del fijador fue su rigidez, es decir, la resistencia que ofrece a la deformación al ser sometido a carga. Las cargas que soporta un fijador externo durante su uso clínico normal son el resultado de una combinación de diferentes modos de carga: compresión axial, flexión en los planos anatómicos y torsión.25 Dadas las características del fijador, éste presenta una respuesta mecánica distinta respecto a los distintos modos de carga que actúan sobre él, por lo que fue necesario obtener en el laboratorio la rigidez del fijador respecto a cada uno de los modos de carga de forma independiente. Puesto que la rigidez de un sistema de fijación externa depende, entre otros parámetros, de la configuración adoptada, se estableció una configuración estándar con tres tornillos por segmento óseo. Para la realización de los ensayos se montó el fijador externo sobre dos barras de metacrilato de sección cuadrada y 25 mm de ancho, empleadas en trabajos previos como modelo sintético de hueso,4,12 quedando los fragmentos alineados entre sí longitudinalmente, simulando el foco de fractura mediante una separación entre ellos de 25 mm. La distancia entre el eje de las barras de metacrilato y el eje de la barra de estabilización del fijador se fijó en 70 mm, y la separación entre los tornillos de cortical centrales de ambos fragmentos se estableció en 200 mm. A su vez, la separación entre tornillos de un mismo fragmento se fijó en 20 mm, siendo utilizados tornillos de cortical de acero inoxidable de 6 mm de diámetro. La evaluación de la rigidez del fijador en la configuración descrita se realizó mediante una máquina universal de ensayos SERVOSIS en los modos de carga de compresión, flexión en el plano antero-posterior, flexión en el plano medio-lateral y torsión (Fig. 2), obteniéndose los resultados que se presentan en la tabla 2.
Figura 2. Esquema de los montajes utilizados para la obtención de la rigidez ante los distintos modos de carga: A: Compresión. B: Flexión en el plano frontal. C: Flexión en el plano sagital. D: Torsión.
Validación del modelo
Para poder considerar fiables los resultados obtenidos del modelo de elementos finitos fue necesario validar éste previamente, mediante el ajuste de determinados parámetros del modelo, de forma que los valores de rigidez estimados en cada modo de carga reprodujeran lo mejor posible los obtenidos en laboratorio.
Las simplificaciones introducidas en el modelo de elementos finitos (elementos tipo viga con uniones rígidas) con respecto a la estructura real que intenta reproducir, implican que ciertas características propias de las uniones entre los diversos componentes, como holguras, la deformación de elementos de conexión, de las rótulas, etc., no sean consideradas inicialmente. Sin embargo, estas características influyen notablemente en el comportamiento mecánico del fijador real, por lo que es necesario que el modelo las contemple. Por tanto, se consideran como parámetros de ajuste del modelo la rigidez a flexión de las rótulas del fijador, la rigidez a torsión del cuerpo central del fijador y la rigidez a compresión de este mismo elemento, requiriendo en cada caso para su ajuste la variación del módulo elástico de los elementos que simulan dichos componentes en el modelo.
En la unión tornillo-hueso se ha considerado empotramiento perfecto pues aunque la osteolisis alrededor de los tornillos podría aumentar la flexibilidad de dicha unión, ésta afectaría principalmente en los estados más avanzados de la consolidación10,17 y es difícil de cuantificar su efecto.
La fase de validación comprende un proceso iterativo, en el cual con unos valores iniciales de los parámetros de ajuste se estima mediante el modelo la rigidez del fijador bajo los modos de carga considerados. Con el fin de simular las condiciones de laboratorio, en el modelo se consideran las propiedades de las barras de metacrilato y un callo inexistente simulado mediante una separación entre fragmentos. A continuación se valora la desviación entre los valores estimados por el modelo y los obtenidos en laboratorio y se modifican los módulos elásticos de los elementos de ajuste. Con estos nuevos parámetros del modelo se vuelven a estimar las rigideces del fijador y la desviación respecto a los valores experimentales, y así sucesivamente hasta que se obtiene unos valores máximos de error inferiores al 5% en todos los modos de carga. Los resultados de rigidez en cada modo de carga obtenidos a partir del modelo validado se expresan en la tabla 2, así como el grado de ajuste respecto a los obtenidos experimentalmente.
Análisis de sensibilidad de los parámetros relativos al grado de reducción de la fractura
Una vez validado, el modelo se ha utilizado para simular diversos grados de reducción de la fractura y estudiar cómo afectan al ambiente mecánico y al estado tensional del callo.
Para ello se consideró el modelo de fijador y tibia facturada sometido a una combinación de cargas equivalente a los valores máximos de fuerzas y momentos que se producen durante la marcha sobre el extremo proximal del hueso18 (tabla 3).
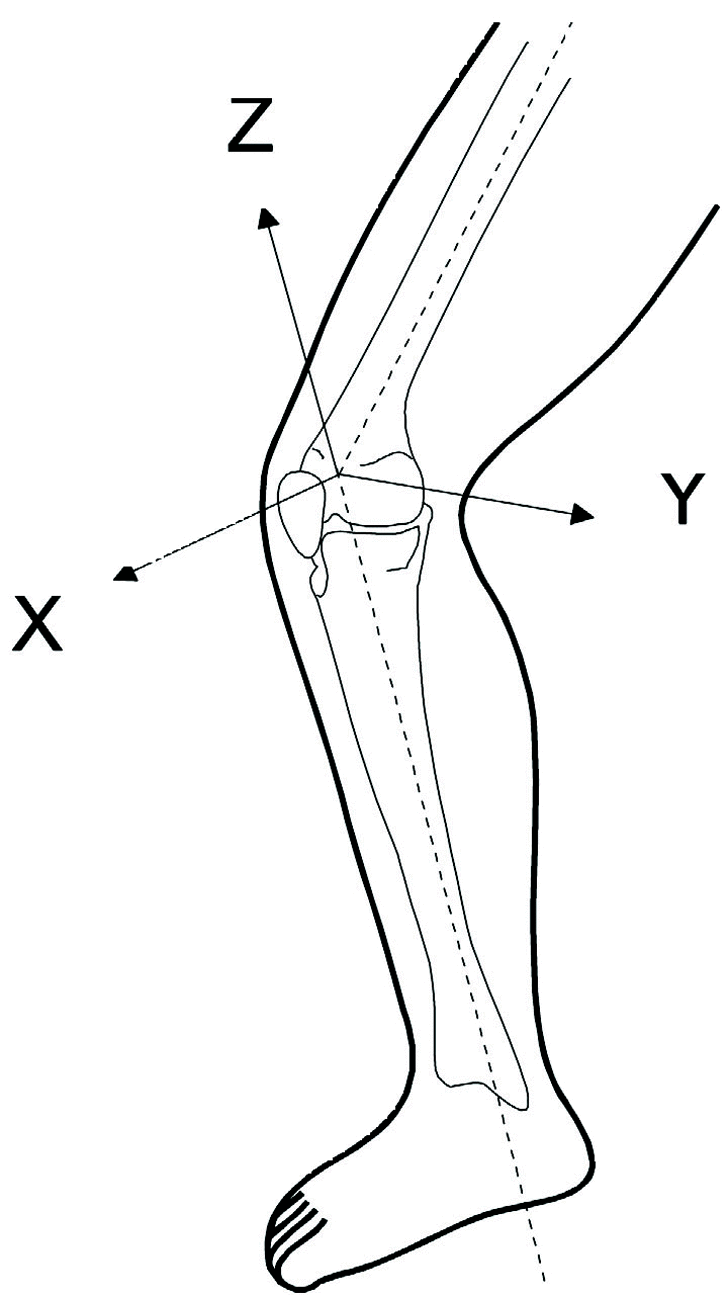
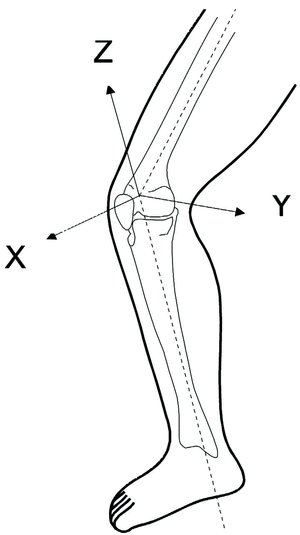
El sistema de coordenadas de referencia empleado se representa en la figura 3, siendo el plano YZ el que contiene al fijador externo.
Figura 3. Sistema de coordenadas de referencia. Pierna derecha.
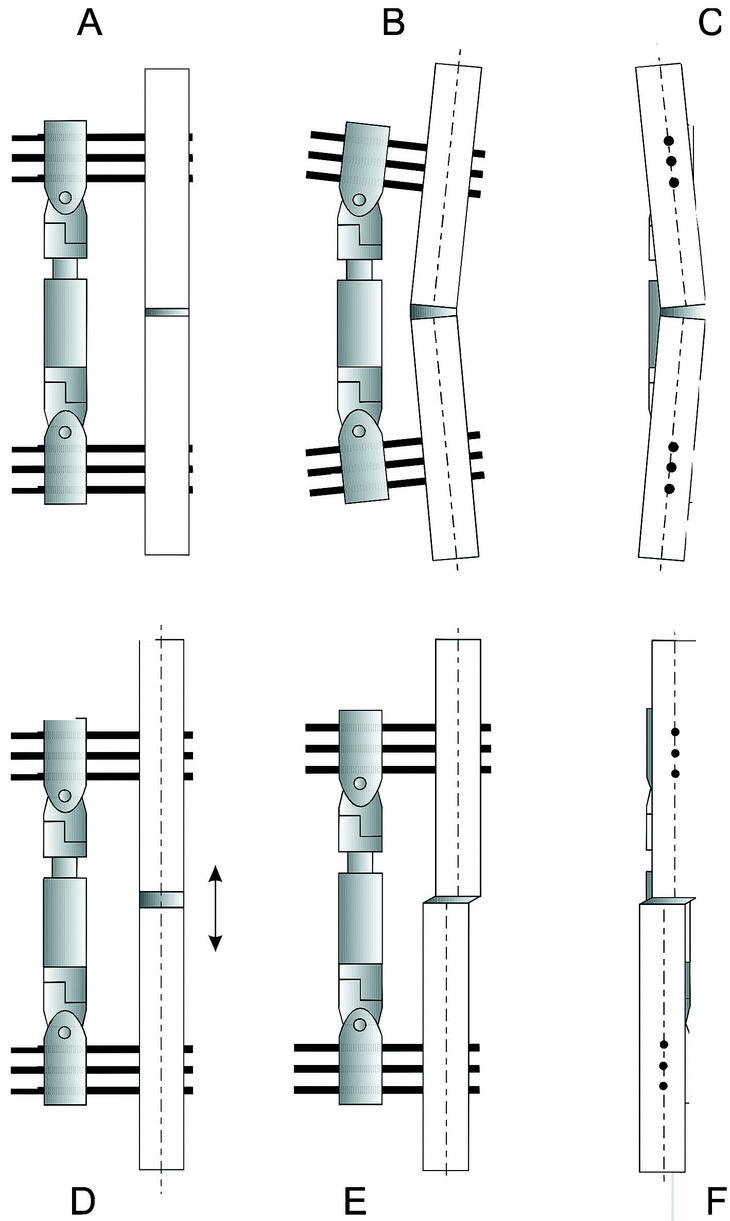
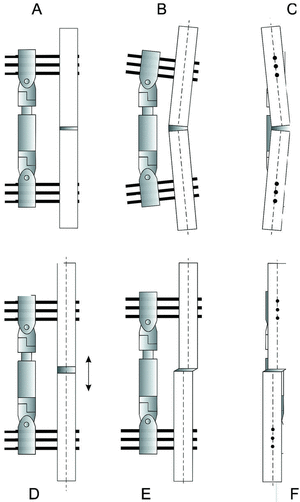
El grado de reducción de la fractura se analizó, estudiándose las siguientes variables: tamaño del defecto óseo, ángulo entre fragmentos en los planos sagital y frontal y desalineamiento de los fragmentos en los planos sagital y frontal (Fig. 4). En cada una de estas posibles configuraciones se estudiaron tres posiciones distintas, que quedan establecidas en la tabla 4.
Figura 4. Casos estudiados: A: Reducción anatómica. B: Angulación en el plano A-P o frontal. C: Angulación en el plano M-L o sagital. D: Defecto óseo. E: Desalineamiento en el plano A-P. F: Desalineamiento en el plano M-L.
Todos los casos fueron analizados teniendo en cuenta la evolución de las propiedades elásticas del callo de fractura, desde un callo con características elásticas incipientes hasta su total madurez, en que adquiere las características del hueso cortical sano. Se supuso que la evolución de los módulos elásticos (E y G) del callo sigue una escala logarítmica creciente,9,10,16 tal como se representa en la tabla 5. La evolución del callo se simplificó en cuatro estados, correspondiendo el estado 1 a un callo inmaduro, formado a los pocos días de la fractura, y el estado 4 al hueso cortical sano.
De la combinación de todos los parámetros considerados se estimaron mediante el modelo los valores de las cargas mecánicas presentes en el callo de fractura y el nivel tensional representado por el valor máximo alcanzado de la tensión equivalente de von Mises. Los valores de cargas (fuerzas y momentos) calculados fueron:
Axil: Fuerza de compresión en la dirección longitudinal de la diáfisis; Cx: Esfuerzo cortante en dirección antero-posterior; Cy: Esfuerzo cortante en dirección medio-lateral; Mz: Momento torsor; Mx: Momento flector en el plano antero-posterior; My: Momento flector en el plano medio-lateral.
Los datos obtenidos permitieron conocer cuáles de los parámetros considerados tenían mayor influencia sobre el ambiente mecánico del callo de fractura y de qué forma influían en él.
Resultados
Se presentan a continuación los valores obtenidos de fuerzas, momentos y tensiones de von Mises presentes en el foco de fractura en cada tipo de reducción no anatómica considerada, teniendo en cuenta, además, la evolución de las características mecánicas del callo desde su estado más incipiente hasta que adquiere las propiedades del hueso cortical.
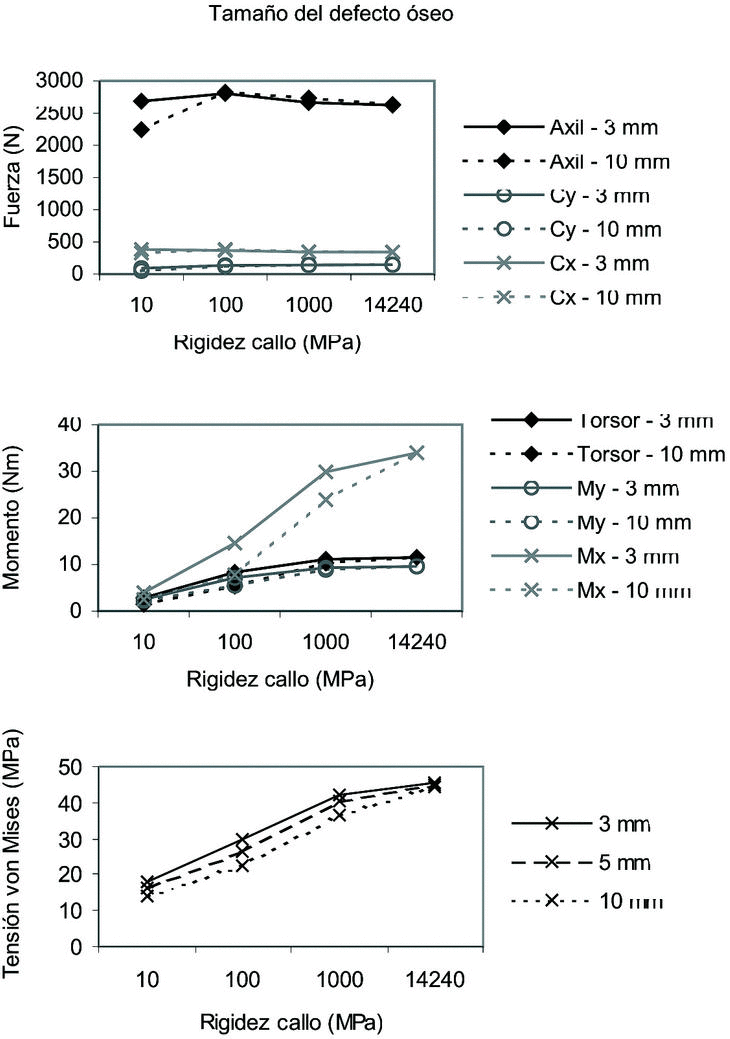
Tamaño del defecto óseo
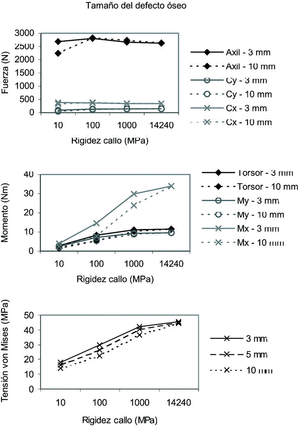
Los resultados obtenidos en función del tamaño del defecto óseo se muestran en la figura 5. Destaca la invariabilidad del nivel de fuerzas en el callo, independientemente del tamaño del defecto óseo durante toda su evolución. El momento flector Mx crece con la evolución del callo de forma pronunciada, mostrándose levemente sensible al tamaño del callo. La tensión también incrementa de forma importante su valor en los estados más maduros del callo, siendo algo mayor cuanto más pequeño es su tamaño.
Figura 5. Fuerzas, momentos y tensión de von Mises máxima en el callo en función del tamaño del defecto óseo.
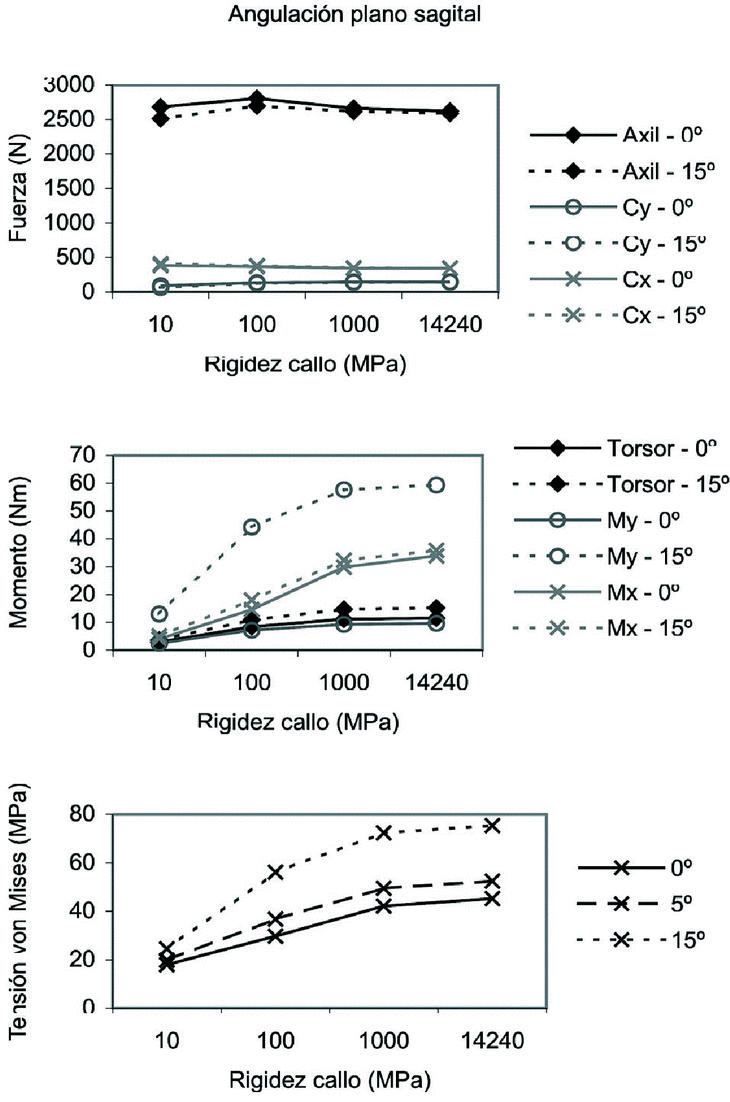
Angulación entre fragmentos en el plano sagital
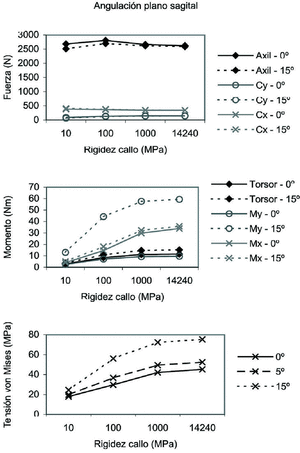
Los resultados obtenidos para este caso se presentan en la figura 6. Es destacable el fuerte incremento del momento My en los casos en que el ángulo entre fragmentos es mayor, tendencia que se acentúa en los estados más maduros del callo. El momento Mx también experimenta un incremento a medida que evoluciona el callo, pero se muestra insensible al ángulo entre fragmentos en el plano sagital. La tensión de von Mises, a su vez, también aumenta de forma importante en los casos de mayor ángulo entre fragmentos (reducción menos anatómica).
Figura 6. Fuerzas, momentos y tensión de von Mises máxima en el callo en función de la angulación entre fragmentos en el plano sagital.
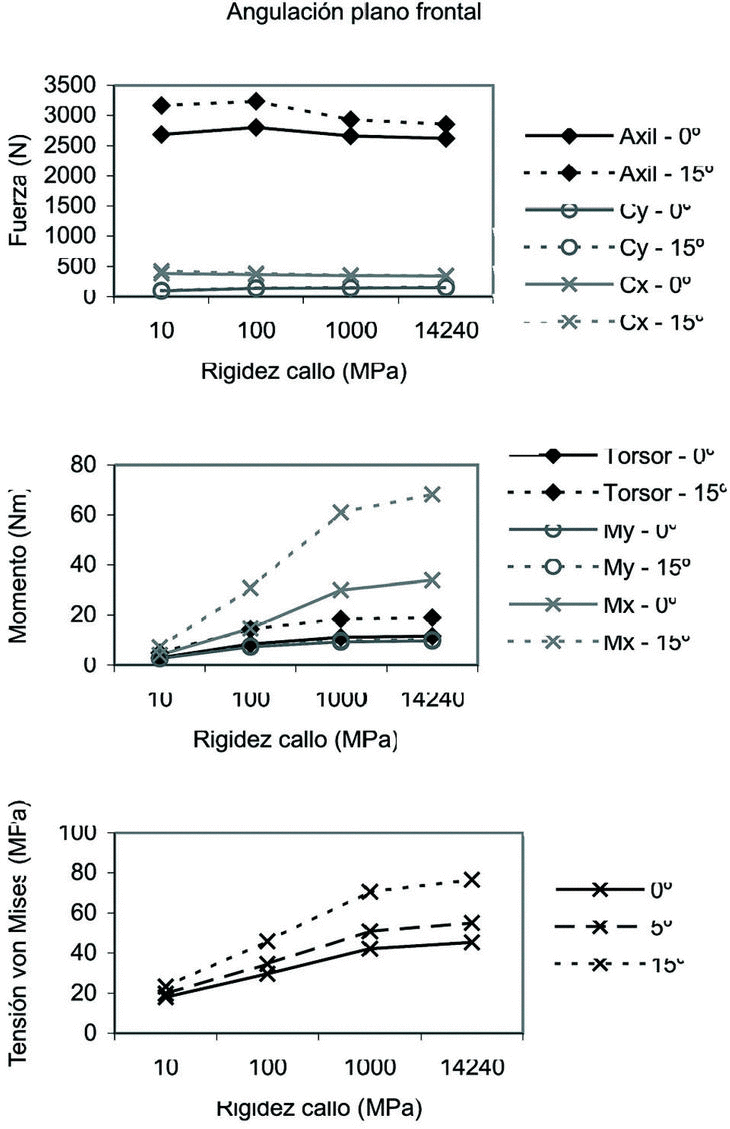
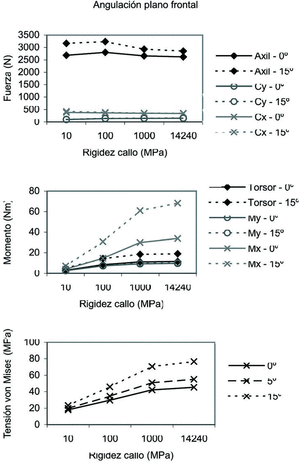
Angulación entre fragmentos en el plano frontal
Los resultados obtenidos para este caso se presentan en la figura 7. Se observa un aumento muy pronunciado del momento Mx en los casos en que existe mayor ángulo entre fragmentos. Además, este incremento se hace mayor cuanto más evolucionado se encuentra el callo en su consolidación. La tensión sigue una tendencia similar, incrementándose de forma notable cuanto mayor es el ángulo entre los fragmentos. Asimismo, también se produce un aumento significativo de tensión a medida que va madurando el callo.
Figura 7. Fuerzas, momentos y tensión de von Mises máxima en el callo en función de la angulación en el plano frontal.
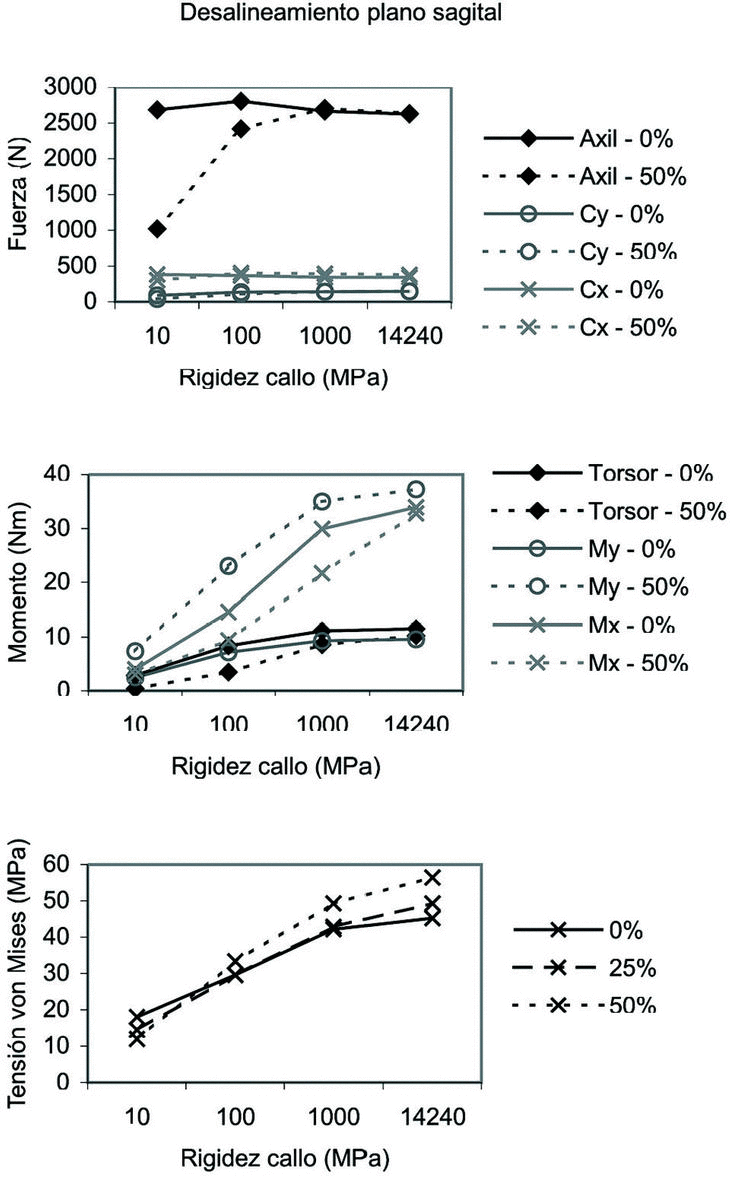
Desalineamiento entre fragmentos en el plano sagital
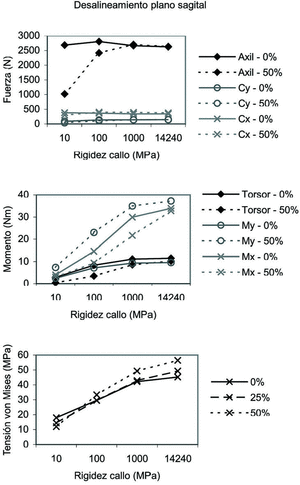
En la figura 8 se representan los resultados obtenidos para este caso. Al igual que ocurre en el resto de casos, las fuerzas tienden a permanecer estables. Es destacable en cambio la excepción de la fuerza de compresión (Axil), que es de menor magnitud en los casos de mayor desalineamiento, fundamentalmente en callos poco desarrollados. Los momentos tienden a ser mayores a medida que evoluciona el callo, aunque el efecto es mucho más pronunciado en los momentos Mx y My. A su vez, My es el único que se ve claramente influido por el grado de desalineamiento de los fragmentos en este plano, incrementando de forma muy pronunciada su valor cuanto mayor es éste. La tensión en el callo aumenta básicamente con su nivel de madurez.
Figura 8. Fuerzas, momentos y tensión de von Mises máxima en el callo en función del desalineamiento en el plano sagital.
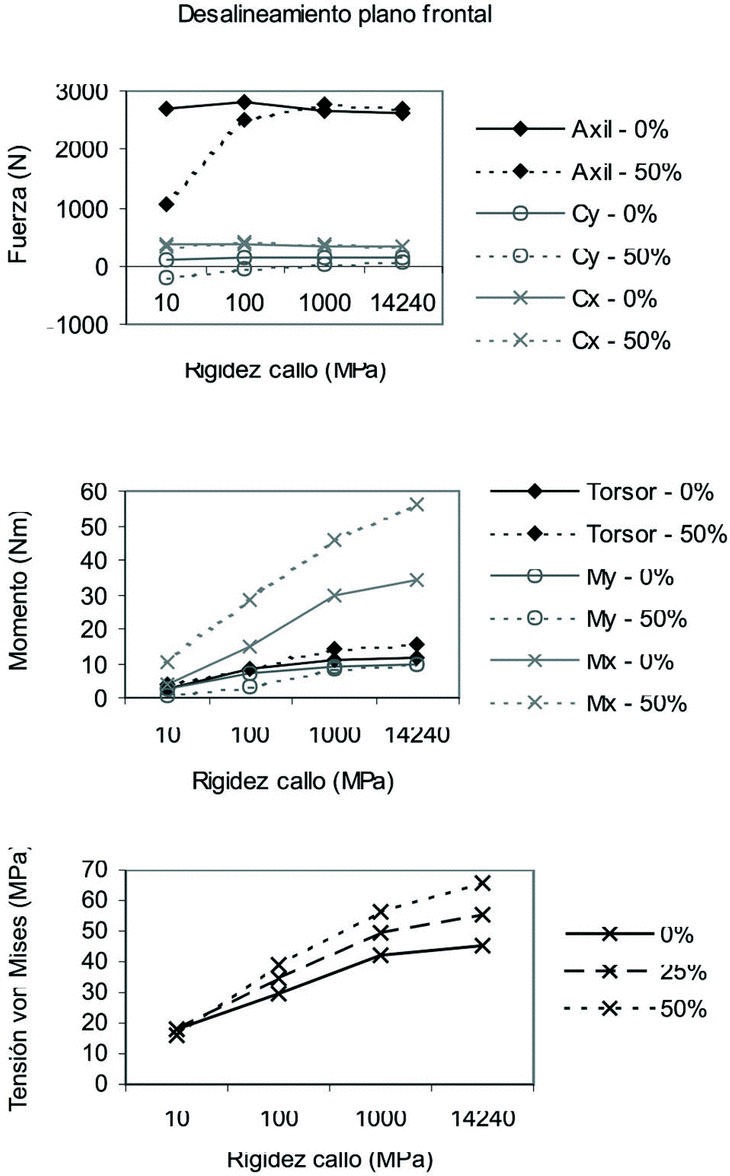
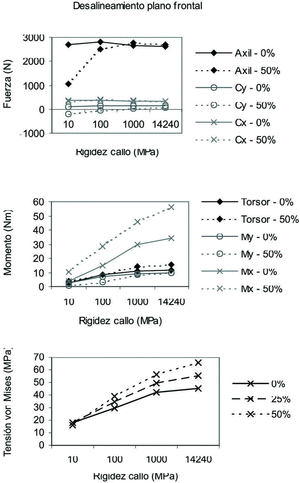
Desalineamiento entre fragmentos en el plano frontal
Se representan los resultados correspondientes en la figura 9. Destaca el hecho de que un mayor desalineamiento entre fragmentos produce una disminución intensa de la fuerza de compresión en el callo, aunque sólo en los primeros estados de evolución. El momento Mx se hace también mayor a medida que evoluciona el callo, tendencia que se hace más pronunciada en caso de que el desalineamiento sea mayor. Asimismo, la tensión en el callo aumenta tanto por un mayor desalineamiento entre fragmentos como por una mayor rigidez del callo.
Figura 9. Fuerzas, momentos y tensión de von Mises máxima en el callo en función del desalineamiento en el plano frontal.
Discusión
Los resultados obtenidos en el presente trabajo muestran que los esfuerzos cortantes que actúan sobre el callo de una fractura tratada por fijación externa unilateral no experimentan variaciones sustanciales durante su evolución hasta la consolidación final. De hecho, tampoco se muestran influidos de forma notable por el grado de reducción de la fractura conseguido, al menos, dentro de los límites establecidos en este estudio para cada tipo de reducción. Este hecho es de importancia si se considera que ciertos autores21 han relacionado las cargas de cizalladura en el callo con un mayor riesgo de refractura y con un mayor impedimento para la osteogénesis, sobre todo en su estado de evolución más incipiente. Es necesario recordar, sin embargo, que la carga a la que se ha sometido a los sistemas para su análisis corresponde a una actividad (marcha) que transmite bajos niveles de esfuerzos cortantes a la diáfisis de la tibia, en comparación con otras actividades habituales.18
Las cargas de compresión en la diáfisis de la tibia son debidas al peso corporal del paciente durante el apoyo del pie en la marcha humana. Según los resultados obtenidos, el tipo de fijación externa utilizado en este estudio transmite al callo un nivel de cargas de compresión elevado, incluso desde su estado más incipiente. Cuando el callo alcanza un módulo elástico del 1% del correspondiente al hueso intacto (Callo 2), el sistema transmite al callo la práctica totalidad de las cargas de compresión. Puede sorprender el hecho de que, en etapas tan tempranas, sea el callo el que transmita la mayor parte de la carga de compresión del sistema, y no el fijador externo, pero hay que considerar que la escasa longitud del callo y su elevada sección, combinados con un sistema de fijación con baja rigidez a compresión, provoca que la transmisión de cargas se produzca por el elemento más rígido, que en estas condiciones es el propio callo. Los resultados obtenidos se corresponden con los trabajos desarrollados por diversos autores.3,28,29 Prat y cols.26 coinciden plenamente en los resultados obtenidos en este sentido, señalando además que a los pocos días de la intervención quirúrgica, el callo ya adquiere las características mecánicas correspondientes al estado 2 considerado. Estos resultados se repiten para todos los tipos y grados de reducción estudiados, por lo que no presentan una influencia clara sobre la presencia de este tipo de cargas en el foco de fractura. Únicamente cabe destacar que el desalineamiento de los fragmentos, en cualquiera de los planos, hace que el reparto de las cargas de compresión sea más equilibrado entre fijador y callo en las fases iniciales, debido a la disminución de la sección resistente de éste. Este reparto de cargas se mantiene hasta que el callo adquiere un módulo elástico cercano al 10% del que posee el hueso intacto.
Los momentos que soporta el callo son crecientes a lo largo de su maduración. En un principio, es el fijador el que absorbe la mayor parte de los momentos presentes en el sistema, situación que traslada gradualmente al callo de fractura a medida que éste se hace más rígido. El momento torsor es el que experimenta esta tendencia de forma más atenuada, tanto por ser de menor magnitud como por el hecho de que la inercia que ofrecen dos elementos en paralelo, separados entre sí, impide que los momentos torsores presentes en éstos sean elevados, hasta el punto de que las reducciones no anatómicas, en cualquiera de los modos estudiados, tampoco les afectan de forma apreciable. Teniendo en cuenta que el momento torsor produce, principalmente, esfuerzos de cizalladura en el callo, se pueden extrapolar las mismas conclusiones que las expuestas en la discusión previa relativa a los esfuerzos cortantes.
Los momentos flectores My y Mx en el callo, además de ser progresivamente mayores a medida que el callo se hace más rígido, se ven afectados tanto por el tipo como por el grado de reducción de la fractura. Cualquier ángulo o desalineación entre los fragmentos óseos provoca un aumento importante del momento flector característico del plano en que se produce dicha reducción no anatómica; es decir, cuanto mayor es el ángulo o desalineación entre fragmentos en el plano sagital, mayor es el momento My resultante, mientras el momento Mx permanece más o menos estable. El mismo razonamiento cabe para ángulos o desalineaciones en el plano frontal, aunque en este caso es el momento Mx el que experimenta aumentos importantes, permaneciendo el momento My estable. En caso de reducción anatómica, el fijador absorbe la mayor parte del momento My del sistema, incluso en el estado más evolucionado del callo (Callo 4), transmitiéndole a éste entre el 7 y el 13% (en función del estado de madurez del callo) del momento My que actuaría sobre el hueso sin fijador. En cambio, una desalineación entre fragmentos en el plano sagital del 50% del diámetro de la tibia multiplica por 4 ese valor, y un ángulo entre fragmentos de 15° en dicho plano hace que el momento My transmitido al callo sea hasta seis veces superior. El caso del momento Mx es algo distinto, ya que en el caso de reducción anatómica, el sistema transmite al callo la mayor parte de Mx de manera gradual durante su evolución, de forma que en el estado más evolucionado (Callo 4) el callo soporta hasta el 70% del momento Mx que actuaría en el hueso sin fijador. Así, una desalineación en el plano frontal del 50% del diámetro de la tibia provoca aumentos en Mx del 70% respecto al que actuaría en el hueso sin fijador, y un ángulo entre fragmentos en ese mismo plano de 15° provoca aumentos de hasta el 100%.
Los niveles de tensión de von Mises también presentan una clara tendencia a aumentar a medida que el callo ofrece características mecánicas más consistentes. Es importante hacer notar que ya desde los primeros estadios de evolución existe un nivel de tensiones en el callo considerable, lo que puede proporcionar el ambiente mecánico que se estima necesario para promover la consolidación.1,5,7,14 Sin embargo, este efecto se intensifica de forma importante en los casos en que la reducción es no anatómica. Si en el caso de reducción anatómica se producen incrementos de tensión desde 20 MPa hasta 45 MPa durante el desarrollo del callo, con una desalineación del 50% en cualquier plano se alcanzan valores máximos de hasta 60-65 MPa, y con ángulos entre fragmentos de 15° estos valores llegan a los 75 MPa. Si bien un umbral mínimo de tensión parece necesario para conseguir la consolidación, también parece claro que existe un umbral máximo a partir del cual se impide la formación del puente óseo entre los fragmentos, umbral que podría ser traspasado por el hecho de no conseguir una reducción lo suficientemente depurada.
Por último, es necesario tener en cuenta las limitaciones del modelo simplificado presentado que se centran principalmente en la consideración del callo como un elemento unidimensional con propiedades elásticas lineales homogéneas. Dichas hipótesis, aunque permiten estimar los valores de fuerzas y momentos a nivel del callo, únicamente proporcionan una estimación global del nivel tensional, mediante el valor máximo de la tensión de von Mises. Para conocer de forma más detallada el estado tenso-deformacional a nivel de los diferentes tejidos del callo debería emplearse un modelo más complejo en el que se considerara éste mediante elementos tridimensionales.27
Aunque el estudio se ha llevado a cabo en una configuración estándar determinada, las conclusiones generales pueden ser extrapoladas a configuraciones semejantes. Sin embargo, para sacar conclusiones de configuraciones sustancialmente distintas debería adaptarse el modelo para dichas nuevas consideraciones.
La hipótesis de comportamiento lineal del modelo (que considera que las cargas sobre el callo son proporcionales a las cargas aplicadas) es una buena aproximación al problema, aunque modelos posteriores deberían considerar no linealidades, principalmente relacionadas con las características mecánicas del callo en sus etapas más iniciales.
Conclusiones
Parece claro que la función primordial del fijador externo durante la mayor parte de la evolución del callo es absorber los momentos flectores que tienden a desalinear los fragmentos y desestabilizar la fractura, pues las fuerzas de compresión son absorbidas por el callo desde etapas muy tempranas. Los datos obtenidos muestran, además, que ciertos grados de reducción no anatómica, especialmente la angulación entre fragmentos de fractura, trasladan también gran parte de los momentos flectores al callo, con lo que la función primordial del sistema de fijación externa de absorber la carga que el hueso fracturado no puede asumir quedaría muy limitada, provocando un incremento elevado de las cargas en el callo que podría desembocar en una falta de consolidación o una pseudoartrosis.
Agradecimientos
Este trabajo ha sido financiado parcialmente por el Ministerio de Industria y Energía a través de la iniciativa ATYCA (Apoyo a la Tecnología, la Seguridad y la Calidad Industrial), en un proyecto de título: «Definición de las características biomecánicas de un nuevo sistema de fijación externa de fracturas mediante alineación controlada», realizado durante los años 1998 y 1999. Los fijadores han sido suministrados por la empresa Industrias Quirúrgicas de Levante (IQL, S.L.).