Los canales y colaterales, así como los puntos de acupuntura, constituyen bases teóricas fundamentales de la Medicina Tradicional China. Su estudio ha atraído la atención de diferentes disciplinas tanto en el área de las biociencias como en el área de las matemáticas. La presente investigación tuvo como objetivo generar una matriz de cuadrados con proporciones de 1 × 1 cun para sobreponerla sobre la región anterior del abdomen, y determinar la relación entre los nodos de la matriz con los puntos de acupuntura. Asimismo, para obtener diferentes figuras geométricas a partir de puntos de acupuntura y no acupuntos que coincidan con los nodos de la matriz, para determinar la dimensión fractal de estos. Los resultados mostraron que es viable utilizar matrices con determinadas proporciones que al sobreponerse sobre la región anterior del cuerpo permiten obtener figuras geométricas formadas por puntos de acupuntura y no acupuntos. El análisis de la dimensión fractal muestra interconexión entre los puntos y forma grupos con un 97% de precisión. El prefactor “a” mostró fractalidad en algunos patrones geométricos, mientras que en otros se niega. Es necesario realizar estudios adicionales para corroborar la fractalidad en la patrones geométricos generados por la matriz.
The channels and collaterals as well as the acupuncture points constitute fundamental theoretical bases of Traditional Chinese Medicine. Their study has attracted the attention of different disciplines as biosciences and mathematics. The present investigation aimed to generate a matrix of squares with proportions of 1 × 1 cun to superimpose it on the anterior region of the abdomen, and to determine the relationship between the nodes of the matrix with the acupuncture points. Likewise, generated different geometric figures from acupuncture points and non-acupoints that coincide with the nodes of the matrix to determine their fractal dimension. The results showed that it is feasible to use matrices with certain proportions that, when superimposed on the anterior region of the body, allow obtaining geometric figures formed by acupuncture points and not acupoints. The analysis of the fractal dimension shows interconnection between the points and they form groups with 97% precision. The prefactor “a” showed fractality in some geometric patterns while in others it was absent. It is necessary for additional studies to corroborate the fractality in the geometric patterns generated by the matrix.
En términos de la Medicina Tradicional China, en el organismo existe un sistema de comunicación conformado por canales, colaterales y puntos de acupuntura, a través de los cuales fluye la sangre y la energía1,2. Este sistema mantiene una comunicación entre las diferentes estructuras periféricas con los órganos internos2. El correcto flujo de la energía y la sangre a través de este favorece el funcionamiento y protección del organismo, manteniendo de esta manera el balance entre el Yin-Yang3.
Actualmente existen evidencias de que los canales y colaterales tienen una relación con los paquetes vasculares y nerviosos en el organismo4–8, incluso ha tenido un especial interés el concepto de campo receptivo de neuronas como equivalente al punto de acupuntura9. Según este enfoque, la convergencia de entradas sensoriales en las neuronas tanto espinales como supraespinales de índole multirreceptivas, es decir, neuronas sobre las cuales convergen diferentes modalidades sensoriales que provienen de la piel, el músculo, la fascia y las vísceras, podrían explicar las relaciones entre los órganos internos y los puntos de acupuntura9. Incluso, la expansión del campo receptivo explica la sensibilización de áreas aledañas al punto de acupuntura, las cuales se encuentran asociadas a las respuestas inespecíficas obtenidas en la práctica clínica cuando se punza un no acupunto10.
La teoría de redes también se ha considerado para el estudio de los canales y puntos de acupuntura, señalando que constituyen una red compleja formada por nodos y conectores, siguiendo un orden ajeno a una distribución al azar11,12. Otros estudios han propuesto con base en la teoría de onda caótica fractal continuo, que el sistema de canales y acupuntos es una red de paquetes neurovasculares con ramificaciones que conectan a los órganos internos, extremidades periféricas y órganos sensoriales3.
Desde la perspectiva de las matemáticas, una matriz corresponde a un arreglo bidimensional de números (elementos de la matriz) ordenados en filas o renglones y columnas13. Las filas corresponden a las líneas horizontales de la matriz y las columnas a las líneas verticales. En computación, las matrices han tenido un gran auge por su facilidad y accesibilidad para manipular información, por ejemplo, cálculo numérico, animación de objetos, así como la representación de grafos14,15. Se denomina grafos al conjunto de objetos que presentan vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto. La representación de caracteres, símbolos o imágenes en la matriz de 2 dimensiones se la conoce como matriz de puntos13.
Si se sobrepone sobre el cuerpo una matriz de 2 dimensiones con cuadrados de “n” renglones y “n” columnas de determinadas proporciones, se podría extraer de sus nodos y conectores diferentes puntos, distribuidos en los cuadros que integran la matriz, lo cual aumentaría la posibilidad de considerar otros puntos sobre la superficie del cuerpo, y no solamente los señalados dentro de la teoría de canales y colaterales. Los puntos adicionales podrían incluso tener una relación geométrica entre estos, así como con los puntos de acupuntura.
Por consiguiente, la presente investigación tuvo como objetivo generar una matriz de cuadrados con proporciones de 1 × 1 cun para sobreponerla sobre la región anterior del abdomen, y determinar la relación entre los nodos de la matriz con los puntos de acupuntura. Así como obtener diferentes figuras geométricas a partir de puntos de acupuntura y no acupuntos que coincidan con los nodos de la matriz, para determinar la dimensión fractal de estos.
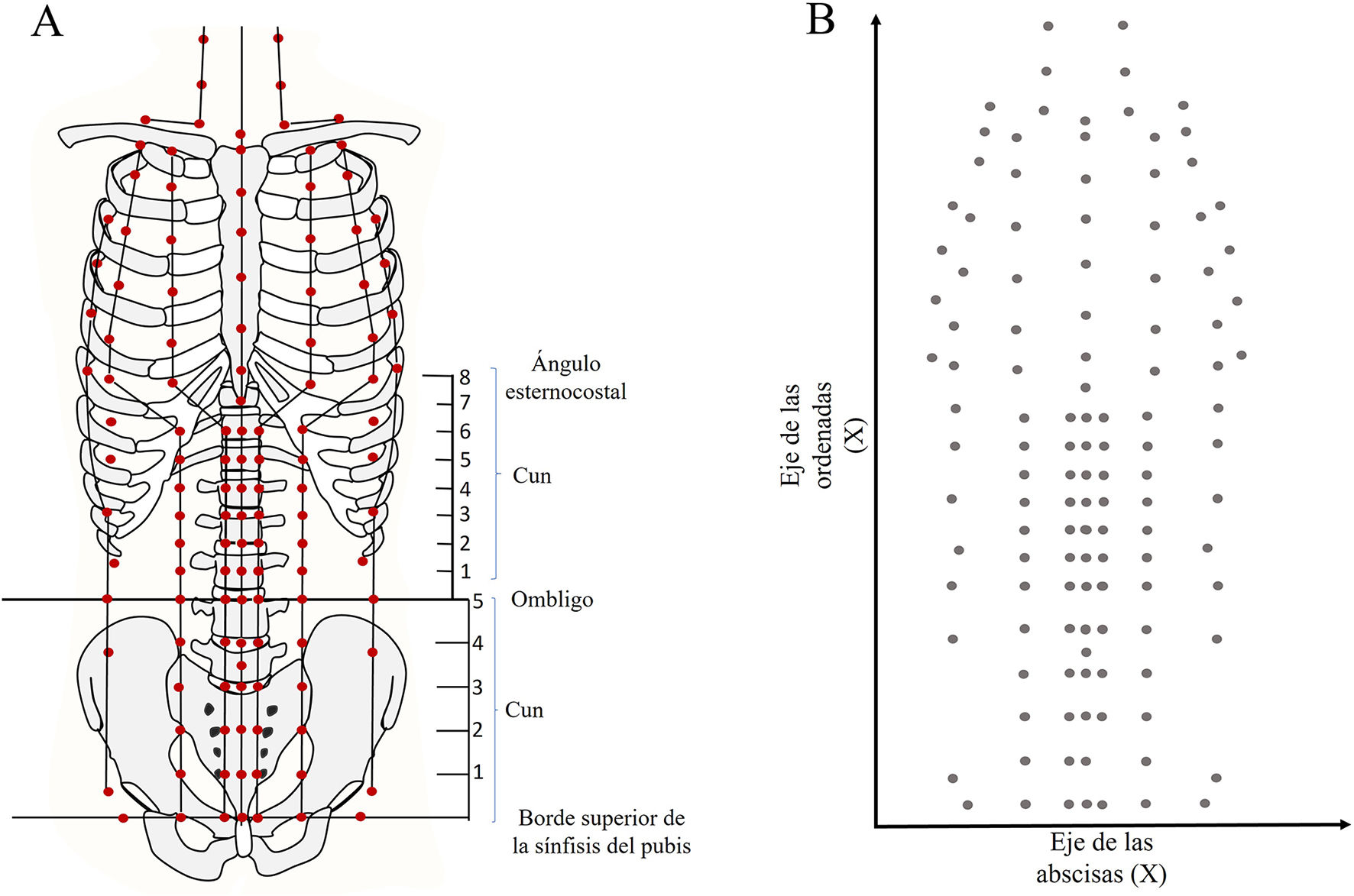
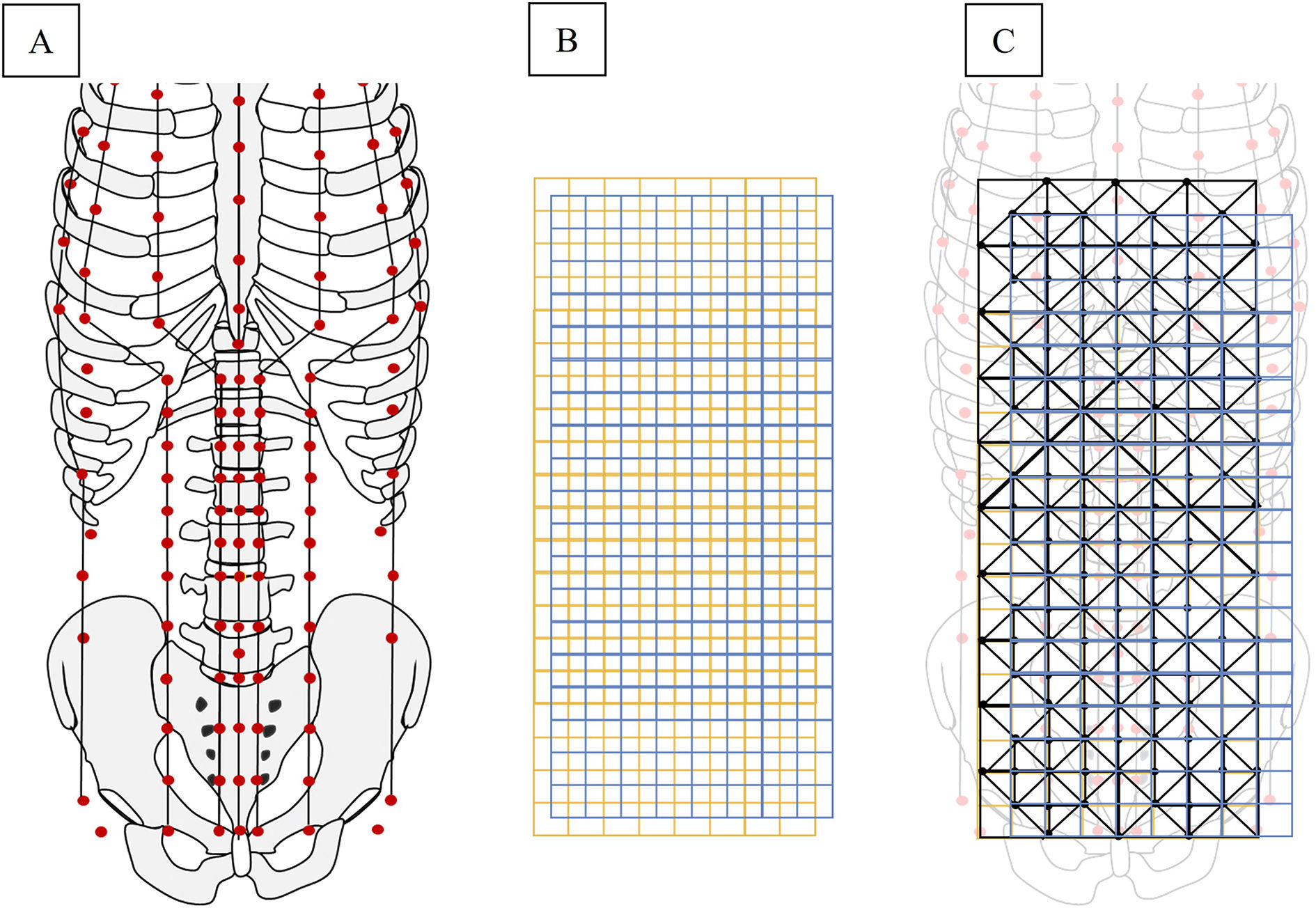
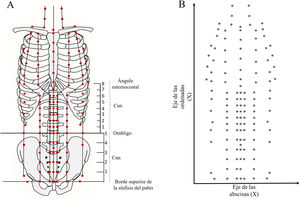
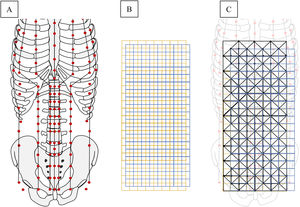
Materiales y métodosPara el presente estudio, en primer lugar se identificó la localización de los puntos de acupuntura del sistema de canales de la región anterior del abdomen y tórax en un plano bidimensional y en un sistema de coordenadas X e Y (Fig. 1), posteriormente se reconstruyó la imagen para representarse como una matriz de puntos. Seguido de ello, se construyó la matriz de 6 × 18 cuadrados tomando como referencia cuadrados de proporción 1 × 1 cun (Fig. 2A). El cun o pulgada anatómica china es la unidad de medida estándar, y se basa en las medidas mencionadas por primera vez en el texto clásico16,17. Varias áreas del cuerpo tienen medidas lineales de cun que se les atribuyen17.
Esquema de puntos de acupuntura de la regiones abdominal y torácica anteriores del cuerpo. A) Se muestran los puntos con las proporciones “cun” y algunas líneas de referencia de relevancia anatómica. B) Reconstrucción de los puntos de acupuntura a partir de un sistema de coordenadas X e Y.
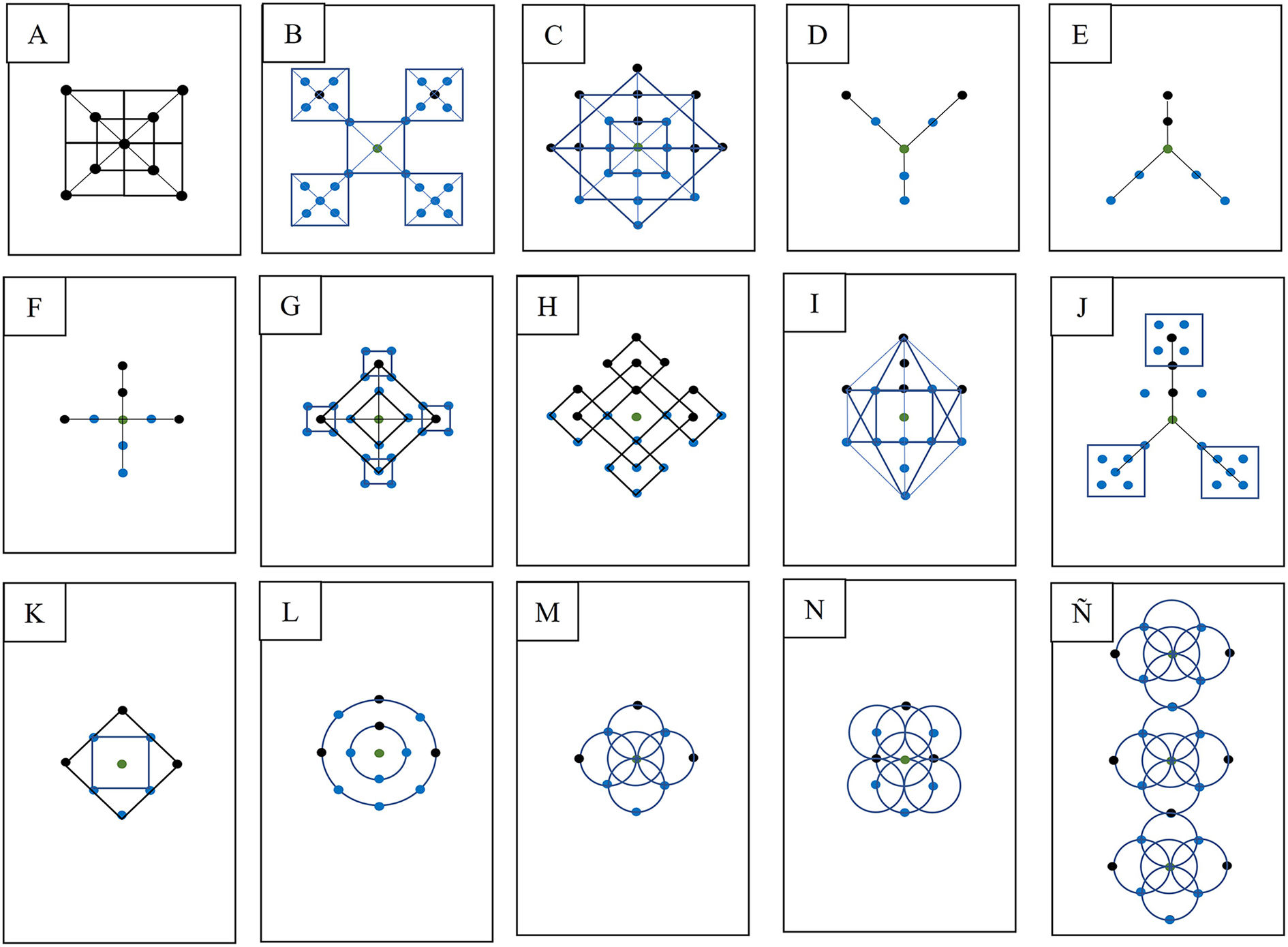
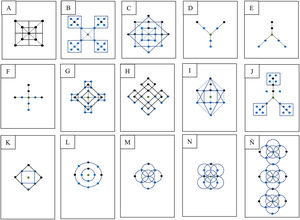
Patrones geométricos generados entre puntos de acupuntura y no acupuntos sobrepuestos sobre una matriz de 6 × 18 cuadrados de proporciones 1 × 1 cun. En color negro se muestran los puntos de acupuntura, en verde el punto central o nodo central que corresponde al punto de acupuntura Shenque (RM 8), a partir del cual se generan los patrones geométricos; en naranja, los puntos de acupuntura tradicionales que se encuentran sobre los canales de acupuntura, los cuales se omiten en las figuras B-O, y en azul, los puntos extra o no acupuntos que surgen de conectores de la matriz.
A continuación, se realizó la sobreposición de la matriz cuadrada con proporciones de 1 cun sobre el arreglo de puntos de acupuntura, para proceder a obtener figuras geométricas en función de los nodos y conectores que surgen dentro de la matriz. Una vez obtenidas las imágenes geométricas, se procedió a determinar su estructura y dimensión fractal.
Método integral de correlación fractalPara determinar la estructura fractal de las imágenes geométricas obtenidas por puntos de acupuntura y no acupuntos en la matriz, se utilizó el software fractalyse18. El análisis de correlación resultó ser el método más confiable, ya que introduce menos artefactos en comparación con otros, como el análisis de rejilla y dilatación. En el “análisis de correlación” fractal, cada píxel de la figura geométrica, conformada por un punto de acupuntura y por puntos extra o no acupuntos, está rodeado por una pequeña ventana cuadrada de tamaño ε. A continuación, se cuenta el número de píxeles de puntos de la matriz dentro de cada ventana. Esto permite calcular el número medio de correlaciones de pares por ventana N (ε). Esto se repite para ventanas de tamaño creciente. Lo que da como resultado una serie de puntos que se pueden representar en un gráfico cartesiano donde el eje X se refiere al tamaño de la ventana ε = (2i + 1) (siendo “i” el paso de iteración), y el eje Y se refiere al número medio de puntos por ventana. El siguiente paso consiste en ajustar esta curva empírica a una curva teórica que corresponde a una ley fractal, es decir, una ley de potencia que vincula el número de correlaciones N (ε) al tamaño de la ventana ε:
N = εD[1]
El exponente D es la dimensión fractal o, en este caso, la dimensión de correlación. Sin embargo, los patrones del mundo real no pueden seguir estrictamente una ley fractal. Por tanto, es útil introducir una ley fractal generalizada, que contiene un parámetro adicional:
N = aεD[2]
El parámetro “a” se denomina “factor de preforma”. Da una indicación sintética de las desviaciones locales de la ley fractal estimada19,20; que, según Frankhauser (1998), para una estructura matemática fractal debe ser igual a 119. La experiencia muestra que cuando se generan rangos de más de 4 o menos de 0,1, no se confirma un patrón fractal21. En los patrones del mundo real, el comportamiento fractal puede cambiar a través de escalas. A menudo, los cambios ocurren dentro de valores bastante pequeños de ε, es decir, para distancias pequeñas. Para estimar los parámetros mencionados anteriormente se utilizó el programa de software Fractalyse18, que en este artículo se dedica principalmente al análisis de las figuras geométricas obtenidas de la matriz sobrepuesta sobre el cuerpo y algunos puntos de acupuntura, y se escala de tal manera que el tamaño de píxel es realmente la unidad de conteo para ε. Esto asegura que los números N (ε) se cuenten correctamente en estructuras espaciales, como la que se ilustra más adelante en este documento. Los resultados se compararon con una versión simplificada de la ley generalizada Eq. 2, donde “a” se fuerza a uno:
N = εD[3]
D a menudo se estima utilizando una representación logarítmica doble de la ley de potencia. Se utilizó una regresión no lineal para estimar los parámetros que mejor se ajustan a la curva empírica, ya que esto evita supuestos implícitos sobre las desviaciones locales de la ley fractal. Se supone que el ruido es un efecto adicional independiente. La dimensión fractal D de los grupos de puntos puede tomar cualquier valor entre 0 y 2. Cuando D = 2, la figura geométrica es uniforme, siguiendo una lógica de una escala. D = 0 corresponde a un patrón compuesto por un solo punto. Cuanto más cerca está D de 2, más uniformemente se distribuyen los elementos en el espacio. La dimensión D > 1 corresponde a una mezcla de elementos conectados que forman grandes grupos, elementos conectados que forman pequeños grupos y elementos aislados. Los valores de dimensión fractal entre 1,5 < D < 2 indican que la agrupación de puntos esta interconectada.
La dimensión fractal se puede considerar como una medida de la capacidad de un objeto para llenar el espacio en el que reside20.
La calidad de la estimación se mide calculando la relación:
Donde N(est) corresponde al conjunto de valores estimados y N(obs) a los valores observados. Aquí llamamos a esta relación R2* por analogía con el coeficiente de determinación. Para valores cercanos a 1, las curvas N(est)(ε) y N(obs)(ε) tienden a ser iguales, lo que significa que el modelo fractal se ajusta bien a los datos observados. Si el ajuste entre las dos curvas (empírica y estimada) es pobre, podemos concluir que el patrón no es fractal o que es multifractal22. En nuestro caso, todos los patrones analizados dan lugar a valores de R2* > 92%.
ResultadosEn la figura 2A-Ñ se observa la reconstrucción de diversas figuras geométricas conformadas por puntos de acupuntura y no acupuntos dentro de la matriz de 6 × 18 cuadrados, con proporciones de 1 × 1 cun a nivel del abdomen y tomando como punto central el punto de acupuntura Shenque o RM 8 (este punto se localiza en el centro del ombligo). Estas figuras geométricas también resultan de la identificación de nodos entre los conectores de la matriz de líneas que forman círculos (Fig. 3L-Ñ). Incluso en algunas figuras pueden formarse patrones similares que se repiten a la misma escala (figs. 3Ñ y 4).
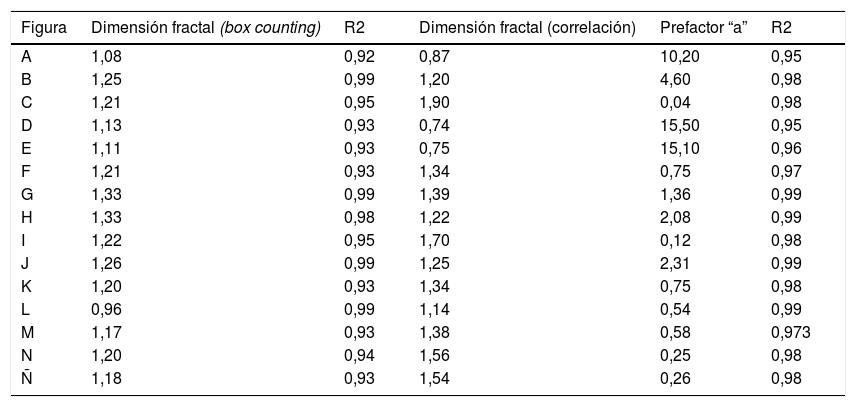
En la tabla 1 se muestran los resultados del análisis de la dimensión fractal de los patrones geométricos obtenidos de la matriz. Los métodos box counting y correlación integral determinaron que la armonía de la distribución geométrica de puntos revela un patrón de autosimilitud.
Dimensión fractal por los métodos box counting y de correlación de las figuras geométricas obtenidas de la matriz.
| Figura | Dimensión fractal (box counting) | R2 | Dimensión fractal (correlación) | Prefactor “a” | R2 |
|---|---|---|---|---|---|
| A | 1,08 | 0,92 | 0,87 | 10,20 | 0,95 |
| B | 1,25 | 0,99 | 1,20 | 4,60 | 0,98 |
| C | 1,21 | 0,95 | 1,90 | 0,04 | 0,98 |
| D | 1,13 | 0,93 | 0,74 | 15,50 | 0,95 |
| E | 1,11 | 0,93 | 0,75 | 15,10 | 0,96 |
| F | 1,21 | 0,93 | 1,34 | 0,75 | 0,97 |
| G | 1,33 | 0,99 | 1,39 | 1,36 | 0,99 |
| H | 1,33 | 0,98 | 1,22 | 2,08 | 0,99 |
| I | 1,22 | 0,95 | 1,70 | 0,12 | 0,98 |
| J | 1,26 | 0,99 | 1,25 | 2,31 | 0,99 |
| K | 1,20 | 0,93 | 1,34 | 0,75 | 0,98 |
| L | 0,96 | 0,99 | 1,14 | 0,54 | 0,99 |
| M | 1,17 | 0,93 | 1,38 | 0,58 | 0,973 |
| N | 1,20 | 0,94 | 1,56 | 0,25 | 0,98 |
| Ñ | 1,18 | 0,93 | 1,54 | 0,26 | 0,98 |
La dimensión (D > 1) corresponde a una mezcla de elementos conectados que forman grandes grupos, o de elementos conectados que forman pequeños grupos. Excluyendo el valor de la dimensión fractal de la figura 2D (D = 0,96), obtenida por el método box counting, mediante este mismo método, el promedio de la dimensión fractal de las figuras geométricas fue de 1,20, lo que indica la interconexión entre los puntos y que se forman grupos con un 97% de precisión (ajuste de la regresión lineal con determinada precisión). Mediante el método de correlación, el promedio de la dimensión, a excepción de las figuras 2A, 2D y 2E (cuyos valores fueron <1 [tabla 1]), fue de 1,4, lo que indicó interconexión entre los puntos con una precisión del 0,98%.
El método de correlación para el cálculo de la dimensión fractal mostró resultados parecidos al método box counting para las figuras 2B, 2F, 2G, 2H, 2 J, 2 K, 2 L y 2 M. Los resultados con relación al prefactor “a” se resumen en la tabla 1.
DiscusiónNuestro estudio es una primera aproximación al uso de matrices para extraer figuras geométricas formadas por puntos y no puntos de acupuntura localizados en la región anterior del cuerpo, particularmente en la región del abdomen. El empleo de tales matrices constituye un novedoso abordaje que aumenta la posibilidad de obtener diferentes patrones a partir de los nodos y conectores que se generan dentro de la matriz, y considerando la proporción 1 cun de amplio uso en la práctica clínica de la acupuntura16,17.
El análisis de la dimensión fractal mostró que algunas figuras geométricas que se obtienen de la matriz muestran valores >1, que indica interconectividad entre los puntos; sin embargo, es importante señalar que los 2 métodos utilizados para determinar la dimensión fractal mostraron resultados diferentes para algunas figuras, lo que siguiere un método adicional para corroborar los resultados en lo referente a la dimensión fractal.
Por otra parte, el factor de preforma “a” de las figuras 2A, 2E y 2D, fue > 4, lo que niega la estructura fractal (probabilidad de la estructura fractal). Sin embargo, en las figuras 2G a 2Ñ este es > 0,1, lo que confirma la estructura fractal.
No obstante, es importante considerar que un fractal implica varias escalas y repeticiones del patrón a todas esas escalas, por lo que estos primeros patrones podrían estar más en relación con la geometría clásica. Por consiguiente, se requiere un estudio adicional que incluya un rango de escalas, incluso matrices, superpuestas para determinar la posible geometría fractal en los patrones geométricos que se obtienen por medio de matrices.
En términos de la Medicina Tradicional China, los puntos de acupuntura constituyen elementos indispensables para el diagnóstico y tratamiento de patologías2,9,23. Algunas evidencias señalan que para los beneficios terapéuticos de la acupuntura se requieren la localización y estimulación precisas de los puntos de acupuntura24, haciendo énfasis en la especificidad de estos25. Por el contrario, otros estudios difieren de tal afirmación y contradicen la especificidad del punto de acupuntura26–28. Asimismo, ha tenido especial interés la considerable variación que existen en la localización de los puntos de acupuntura observado entre acupunturistas calificados25,29. Además de sus efectos en la práctica clínica, la inexactitud y la imprecisión pueden ser una causa potencial de errores de tipo II en la investigación de la acupuntura, particularmente cuando se pinchan puntos “falsos” cercanos30. Incluso la similitud de los resultados en algunos tratamientos con acupuntura “simulada” frente a “verdadera”, plantea la cuestión acerca del tamaño de los puntos de acupuntura31.
Particularmente respecto al alto grado de variación en la localización de los puntos de acupuntura, se ha sugerido el término “campo de acupuntura”, más apropiado que “punto de acupuntura”, para describir la realidad clínica y ser una explicación alternativa de los efectos aparentemente inespecíficos de la acupuntura31.
Desde la perspectiva neurofisiológica, nuestro grupo de trabajo ha propuesto el concepto de campo multirreceptivo neuronal para considerar las respuestas fisiológicas que se obtienen cuando se estimula un punto de acupuntura, así como un no acupunto previamente sensibilizado9. Desde este enfoque, cualquier parte del cuerpo se puede estimular para obtener una determinada respuesta neuronal32. La diferencia estriba en determinar el sitio eficiente para generar un efecto terapéutico asociado a una respuesta fisiológica específica. Trabajos previos ya han demostrado que el punto de acupuntura puede cambiar y no necesariamente estar restringido al lugar donde lo señala el mapa de acupuntura tradicional9,33. Es decir, asume un papel dinámico más que estático9. Por consiguiente, existen múltiples posibilidades de la presencia de puntos, tanto sensibles como no sensibles, en el cuerpo, y el empleo de matrices podría ser una forma de identificar estos puntos, así como de determinar patrones geométricos en su distribución. A pesar de que nuestro estudio no permite concluir la fractalidad en los patrones geométricos, no podemos excluir que el uso de matrices permita obtener algún patrón geométrico de orden fractal, pues las posibilidades de utilizar matrices y formas geométricas aumenta la posibilidad de mayores patrones tal y como lo podemos apreciar en la figura 4, donde se utilizan 2 matrices sobrepuestas.
La fractalidad ya se ha demostrado en numerosas estructuras anatómicas como las arborizaciones neuronales, la ramificación traqueobronquial, la mucosa intestinal, las fibras del músculo estriado, así como el sistema vascular34,35. La piel, el músculo, la fascia y los tendones están ampliamente inervados y tienen múltiples campos receptivos, los cuales a su vez presentan múltiples ramificaciones nerviosas que se ha demostrado tienen una estructura fractal36. Al considerar que un campo de acupuntura se encuentra formado por varias ramas nerviosas, que a su vez se dividen en otras más pequeñas y así sucesivamente a distintas escalas con patrones de autosimilitud, es factible proponer que el campo receptivo de acupuntura, incluyendo otras regiones que estén bajo la misma inervación, presentarán también una estructura fractal. Por consiguiente, la geometría fractal podría ser otra forma de estudiar las agrupaciones de puntos de acupuntura incluyendo no acupuntos asociados a campos multirreceptivos de neuronas multimodales que responden a diferentes modalidades sensoriales.
No obstante, es necesario continuar con estudios adicionales para corroborar la presente hipótesis y, sobre todo, la posible implicación clínica, así como la seguridad y eficacia que tendría la estimulación de puntos que se obtienen al sobreponer una matriz en el cuerpo tomando en consideración puntos centrales, tal y como se hizo en el presente estudio con Shenque (RM 8), lo cual constituiría un nuevo enfoque en el momento de prescribir un tratamiento acupuntural desde una perspectiva neurofisiológica, geométrica y fractal. Para ello, la forma geométrica constituiría un conjunto de puntos que, en función de su ubicación, podría tener una función de red ordenada y tener un efecto de sumación espacial (ya demostrada en circuitos neuronales)37–39, y en consecuencia activar mecanismos psiconeuromoduladores40 que favorezcan la homeostasis en el organismo y, por consiguiente, el tratamiento de diversas condiciones de salud.
ConclusionesEs factible el uso de matrices con proporciones de 1 × 1 cun que al sobreponerse sobre la región anterior del cuerpo permiten obtener figuras geométricas constituidas por puntos de acupuntura y no acupuntos. Tales figuras presentan una dimensión fractal >1. Al diferir los valores por los 2 métodos empleados, no podemos concluir la fractalidad en los patrones geométricos. Sin embargo, es posible que a través de matrices sobrepuestas se obtengan patrones geométricos que cumplan la fractalidad a múltiples escalas.
AgradecimientosDamos nuestro agradecimiento al Dr. Ruben Fossion por las observaciones y recomendaciones realizadas para la elaboración del presente manuscrito.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.