O presente artigo aborda a otimização topológica em problemas de elasticidade plana linear considerando a influência do peso próprio nos esforços em elementos estruturais. Utiliza‐se para este fim uma técnica numérica denominada Smooth ESO (SESO) que se baseia no procedimento de diminuição progressiva da contribuição de rigidez de elementos ineficientes com menores tensões até que ele não tenha mais influência. As aplicações do SESO são feitas com o método dos elementos finitos e considera‐se um elemento finito triangular e de alta ordem. Neste trabalho estende‐se a técnica SESO para a aplicação do peso próprio onde o programa, no cômputo de seu volume e peso específico, gera automaticamente uma força concentrada equivalente para cada nó do elemento. A avaliação é finalizada com a definição de um modelo de bielas e tirantes resultante das regiões de concentração de tensões. Nos exemplos de aplicação são apresentadas topologias ótimas de uma estrutura suspensa, de viga baixa e de viga parede considerando o peso próprio e obtendo‐se ótimas configurações e demonstrando que a consideração do peso próprio leva a maior robustez ao processo de otimização.
This paper deals with topology optimization in plane elastic‐linear problems considering the influence of the self weight in efforts in structural elements. For this purpose it is used a numerical technique called SESO (Smooth ESO), which is based on the procedure for progressive decrease of the inefficient stiffness element contribution at lower stresses until he has no more influence. The SESO is applied with the finite element method and is utilized a triangular finite element and high order. This paper extends the technique SESO for application its self weight where the program, in computing the volume and specific weight, automatically generates a concentrated equivalent force to each node of the element. The evaluation is finalized with the definition of a model of strut‐and‐tie resulting in regions of stress concentration. Examples are presented with optimum topology structures obtaining optimal settings.
Atualmente na engenharia estrutural os métodos numéricos de aplicação são ferramentas imprescindíveis e já nas 2 últimas décadas as técnicas de otimização vêm sendo empregadas no auxílio da modelagem estrutural. Dentre os métodos tradicionais de otimização, a otimização de forma e a paramétrica não são capazes de alterar a configuração da estrutura original e, desta maneira, não são possíveis de determinar os fluxos de tensões. A grande vantagem da otimização topológica (OT) é tornar possíveis estas alterações.
Os conceitos básicos da técnica OT foram estabelecidos há mais de um século, conforme descrevem Rozvany et al. [1]. Na análise topológica, 2 metodologias vêm se destacando, a abordagem micro e abordagem macro. A filosofia da técnica baseia‐se na remoção da parte do elemento que não for realmente necessário à estrutura. Esta remoção pode ser realizada de forma suave, atenuando os valores da matriz constitutiva do elemento.
Na abordagem microestrutural, o processo de otimização topológica baseado no estabelecimento de um relação entre a rigidez e a densidade associada ao domínio, que pode assumir qualquer valor entre 0 (vazio) e 1 (material sólido), sendo os valores intermediários correspondentes a um material poroso. A partir daí os algoritmos baseados em microestruturas propõem encontrar a melhor disposição do material, de modo a minimizar ou maximizar a função custo, Stump [2]. Como exemplo pode‐se citar: o método Simple Isotropic Material with Penalization (SIMP), utilizado por Bendsøe [3], Rozvany et al. [4] e [1].
Na abordagem macro, a topologia da estrutura é modificada mediante a inserção de furos no domínio. Como exemplo deste grupo de OT pode‐se citar o Evolutionary Structural Optimization (ESO), baseado no cálculo da função objetivo quando um elemento é removido da malha de elementos finitos, e Topological Sensitivity Analysis (TSA), que avalia a sensibilidade de uma função quando um furo é criado no corpo analisado, Labanowski et al. [5].
Na análise estrutural de elementos em concreto armado a analogia apresentada por Ritter e Morsch no início do século XX, que associa uma viga a uma estrutura treliçada equivalente, ainda é utilizada para representar o comportamento estrutural deste elemento fletido. A denominada teoria de treliça clássica define barras representando os fluxos de tensão procurando criar o menor e o mais lógico caminho das cargas. Os elementos discretos (barras) representam os campos de tensão de tração (denominados tirantes) e de compressão (denominados bielas comprimidas) que surgem internamente ao elemento estrutural no efeito de flexão. Este analogia foi melhorada e é ainda utilizada pelas normas técnicas no dimensionamento de vigas em concreto armado à flexão e à força cortante e que estabelecem critérios diversos para a determinação dos limites de segurança nos seus procedimentos.
O trabalho de Schlaich et al. [6] descreve o modelo de bielas e tirantes de maneira mais generalizada, abrangendo o modelo de treliça de flexão e englobando regiões com descontinuidades e elementos estruturais especiais. Estas regiões, denominadas «Regiões de Descontinuidade D», onde as tensões de cisalhamento são significativas e a distribuição das deformações na seção transversal não é linear. Mesmo tratando de um modelo de idealização simples, é bastante utilizado na prática e eficiente para o conhecimento das regiões de concentração de tensões.
A utilização de ferramentas computacionais pode trazer maior confiabilidade e rapidez na definição de configurações geométricas e do fluxo de tensões dos elementos discretos no interior do elemento estrutural, de modo que a aplicação da OT no campo da análise estrutural em concreto armado nos modelos de bielas e tirantes vem sendo amplamente desenvolvido, destacando os trabalhos de Ali [7], Liang et al. [8], Liang et al. [9], Liang et al. [10], Liang e Steven [11], Liang [12] e Brugge [13].
Visando o desenvolvimento dos modelos de bielas e tirantes, faz‐se uma aplicação da técnica de otimização topológica Smooth ESO (SESO), seguindo os trabalhos de Simonetti et al. [14], Simonetti et al. [15] na análise de elementos estruturais em concreto armado, realizando uma comparação das configurações ótimas considerando‐se a influência do peso próprio, o que muitas vezes pode levar a uma configuração final bem distinta quando da sua não consideração.
Trata‐se de uma variante do método ESO, cuja filosofia baseia‐se na observação de que se o elemento não for realmente necessário à estrutura, naturalmente sua contribuição de rigidez vai diminuindo progressivamente, até que ele não tenha mais influência. Isto é, sua heurística de remoção é feita de forma suave, atenuando os valores da matriz constitutiva do elemento, como se este estivesse em processo de danificação, sendo capaz de gerar os membros ideais de bielas e tirantes de forma mais natural. São apresentados 3 exemplos clássicos obtidos na literatura, que demonstram que o procedimento desenvolvido para o peso próprio é eficiente.
2Otimização estrutural evolucionáriaXie e Steven [16] desenvolveram uma maneira bem simples de impor modificações na topologia da estrutura, feita mediante heurística de remoção gradual e sistemática de elementos finitos da malha, correspondentes a regiões que não contribuem efetivamente para o bom desempenho da estrutura.
Define‐se inicialmente uma malha de elementos finitos que circunscreva toda a estrutura, ou domínio estendido do projeto, de forma a incluir as condições de contorno em forças e deslocamentos, cavidades e demais condições iniciais. Em um processo iterativo, avaliam‐se os parâmetros de interesse de otimização, neste artigo em especial é a diminuição da massa mediante um critério de tensão máxima da estrutura. Assim, avaliam‐se as tensões de cada elemento, conforme o uso da inequação:
com σevme σi,maxvm sendo, respectivamente, as tensões principais de Von Mises do elemento «e» e máximas da estrutura na iteração efetiva «k», RRk é raio de rejeição (RR) do k‐ésimo estado de equilíbrio.
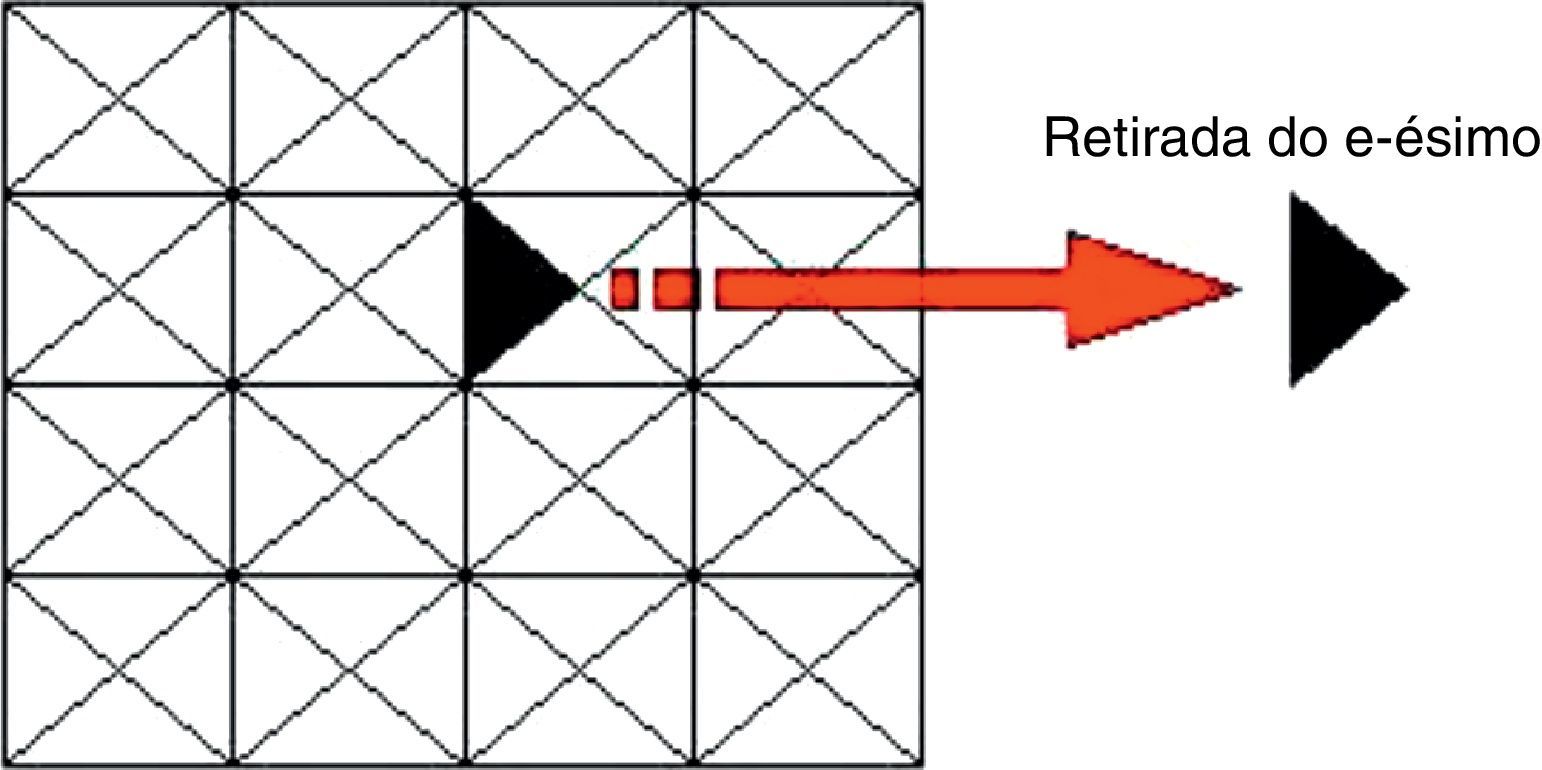
Em cada iteração os elementos que satisfazem a inequação (1) são retirados da estrutura, figura 1. O fator RR é aplicado para controlar o processo da remoção da estrutura (0,0≤ RR ≤1,0). O mesmo ciclo de remoção dos elementos usados pela desigualdade (1) é repetido até que não haja mais elementos que satisfaçam mais esta desigualdade (1). Quando esta situação ocorre, um estado de equilíbrio é alcançado. O processo evolucionário é definido adicionando a RR uma razão de evolução (RE). Assim, um novo ciclo de evolução inicia‐se, até que não existam mais elementos a serem eliminados com esta nova RR. A RR será atualizada conforme a equação (2), até àobtenção de uma configuração otimizada, alcançada pelo controle de um parâmetro de desempenho, denominado de índice de performance (IP). Este procedimento, também é conhecido como um método hard‐kill e pode ser interpretado como segue:
onde Di(j) é a matriz constitutiva do elemento j∈Ω na i‐ésima iteração, D0 é a matriz constitutiva inicial do projeto, a qual é definida pra cada elemento finito, Ω=Γi+Γ¯i é o domínio da estrutura, tal que Γi={Ω/(σe/σVMMAX(Ω))≥RRi} é o conjunto dos elementos que não serão removidos, e Γ¯i=Ω−Γi={Ω/(σe/σVMMAX(Ω))
Na heurística de remoção via ESO, quando o elemento é removido do domínio de projeto durante o processo evolucionário, os elementos que permanecem na estrutura representam uma solução básica, conforme fora demonstrado matematicamente por Tanskanen [17]. Ele demonstra que a função discreta a ser minimizada com restrição por menor peso converge iterativamente, conforme a retirada de um elemento, que significa o encontro de um ponto de minimo.
3Suavização da otimização estrutural evolucionáriaPor outro lado, Tanskanem [17] destaca que a retirada de um elemento pode afetar a convergência do procedimento de otimização, pois o critério de retirada no ESO é indicado pelo atendimento da inequação (1), que muitas vezes pode ser radical, hard‐kill, uma vez que existem elementos que estão na vizinhança da esquerda dessa condição que numericamente são excluídos ou mantidos, mas que deveriam ainda compor ou ser retirados da estrutura, o que afeta o processo evolutivo.
Nesse sentido, é adequado aplicar sobre o método ESO uma condição de relaxação ou de suavização do ESO, apresentando em Simonetti et al. [15] um procedimento soft‐kill, de modo que o material, ou seja, os elementos que deveriam ser removidos pelo critério ESO – seguindo a inequação (1) – são organizados em n grupos e alocados em ordem crescente de tensões sendo ponderados segundo uma função 0≤η(j)≤1.
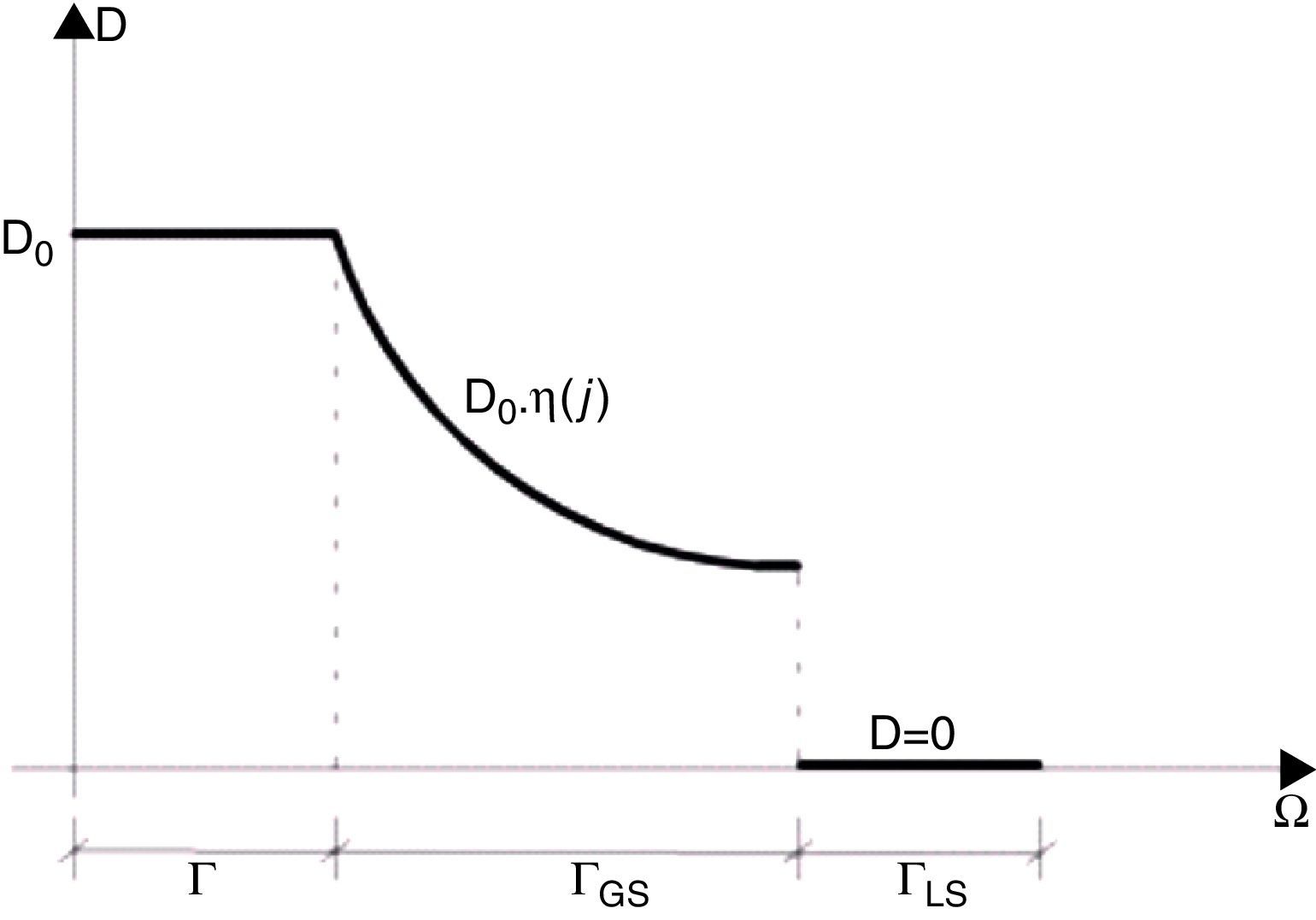
Assim, p% destes n grupos são removidos, os grupos que contém os elementos com menores tensões (domínio ΓLS), e os grupos (1‐p%) são devolvidos a estrutura, domínio ΓGS. Este processo de remoção e devolução de elementos à estrutura pode ser orientado por uma função, linear ou hiperbólica, que pondera a razão σeVM/σVMMAX dentro do domínio Γ¯, isto é, permite que elementos que tenham suas tensões próximas e abaixo da tensão máxima, σVMMAX sejam reintegrados a estrutura a cada iteração. A minimização da função objetivo é atingida mediante o encontro de um ponto ótimo estacionário, conforme [17].
Uma forma alternativa, mais cara computacionalmente, de corrigir esse desvio seria a possibilidade de inserção do elemento na estrutura novamente, destacando que nesse sentido tem‐se uma variante do ESO, o Bidirectional ESO (BESO), Querin [18], que possibilita a entrada e remoção de elementos no domínio de projeto. O SESO vem dessa filosofia, de forma consistente matematicamente e mais eficiente, que pondera a matriz constitutiva, fazendo com que o elemento que a priori seria eliminado no ESO é mantido e recebe uma relaxação, aplicando uma fração de sua rigidez inicial, permanecendo no projeto e naturalmente sua influência contribui para sua permanência ou fortalece a sua retirada por definitivo da malha inicial.
Os elementos que estão próximos ao limite pela esquerda desta tensão máxima são mantidos na estrutura, definindo assim um procedimento de retirada «não radical» e sim, de forma suave. O procedimento soft‐kill usado no SESO pode ser interpretado assim:
onde Γ¯=ΓLS+ΓGS é o domínio dos elementos que atendem a inequação (1), ΓLSi é o domínio dos elementos que devem ser excluídos efetivamente, ΓGSi o domínio dos elementos que são devolvidos a estrutura, 0≤η(Γ¯)≤1 é uma função reguladora que pondera o valor da razão σeVM/σVMMAX dentro do domínio Γ¯.
A proposta da suavização pode ser desempenhada por uma função linear do tipo η(Γ¯)=αj+β ou uma função trigonométrica do tipo η(Γ¯)=sen(αj). Porque as 2 funções são contínuas e podem ser diferenciadas em todo o domínio Γ¯ e tem sua imagem variando de 0‐1, figura 2.
4Índice de performance para a formulação Smooth Evolutionary Structural OptimizationO índice de performance (IP) é um parâmetro adimensional que mede a eficiência da performance da estrutura. O problema consiste na minimização da função objetivo em termos do peso, sujeito a uma restrição de tensão admissível (σprojeto), que é definida como:
onde NE é o número total de elementos finitos.
O IP foi proposto por Liang et al. [5] como:
onde V0 e Vi são o volume inicial e o volume da i‐ésima iteração, σ0,maxvm e σi,maxvm são a tensão inicial e a tensão máxima de Mises na i‐ésima iteração, ρ0 e ρi são o peso específico inicial e o peso específico na i‐ésima iteração, como são iguais para um material incompressível. A suavização gerada devido à equação (4) em termos da matriz constitutiva pode ser escrita em termos de espessura, devido à relação de dependência linear entre elas. Neste contexto, o IP é a equação (7), que leva em conta a expressão (4) em termos de espessura e cada função reguladora do procedimento SESO:
onde t0 é a espessura inicial e tj é a espessura do elemento na iteração j. O controle do ótimo é feito por este IP, pois ele é um fator de «monitoramento» da região ótima de projeto. O controle da maximização deste parâmetro refere‐se ao controle de minimização do volume, assim, caso este índice caia de forma acentuada é uma forte indicação que se passou por uma configuração de ótima ou um ótimo estacionário é alcançado, no entanto, não se pode garantir que este ótimo é um ótimo global, mas sim uma configuração ótima de projeto de engenharia.
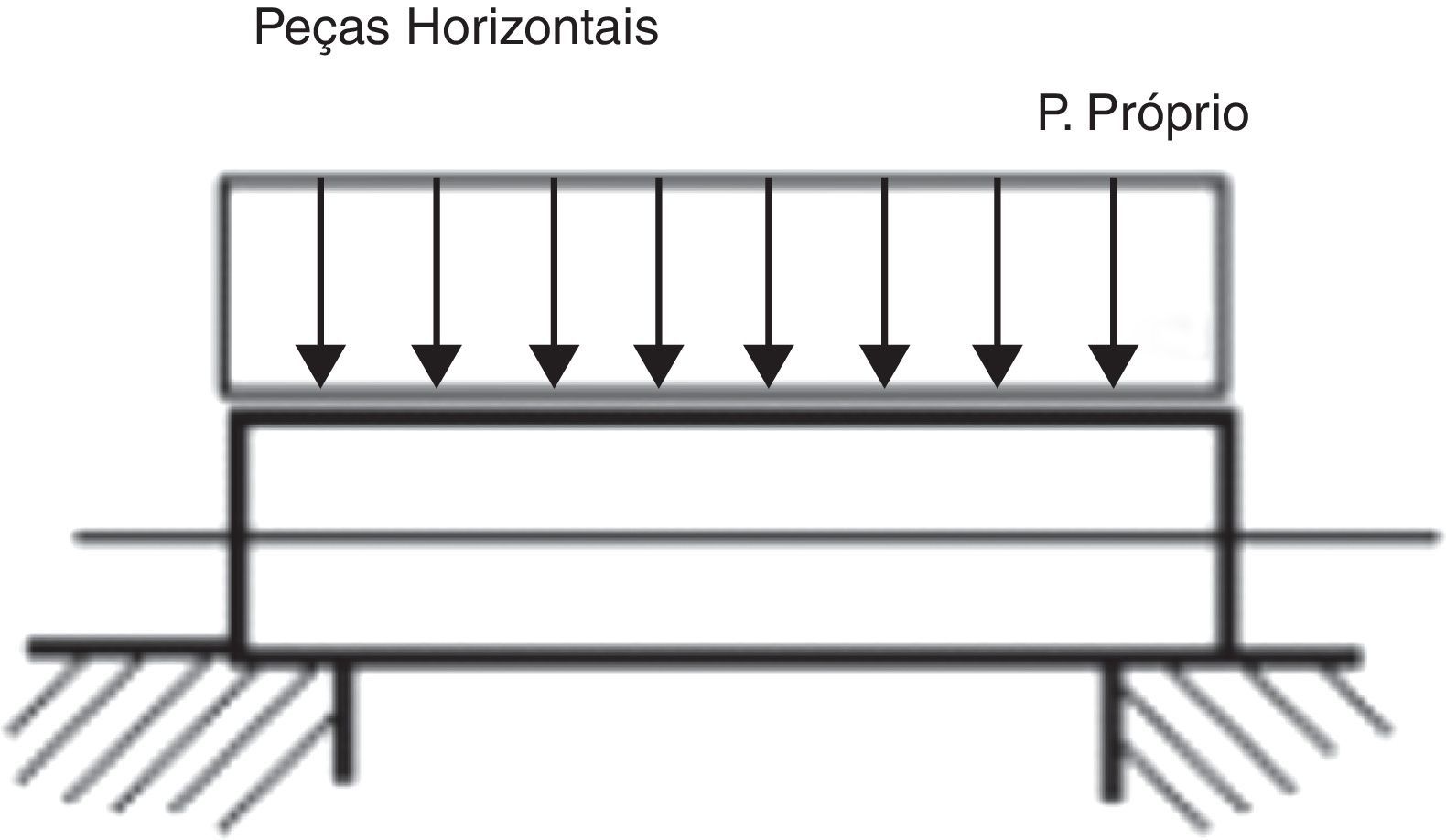
5Peso próprioO peso próprio de elementos estruturais correspondente à ação da gravidade sobre os corpos e constitui‐se em um dos carregamentos que devem ser considerados em seu dimensionamento estrutural. Pode‐se observar na figura 3 como se dá a ação do peso próprio.
Ação do peso próprio [19].
Pode‐se notar que nos elementos estruturais dispostos na posição horizontal o peso próprio constitui‐se em carregamento transversal ao eixo (fig. 3), desenvolvendo os esforços de flexão, momento fletor e esforço cortante.
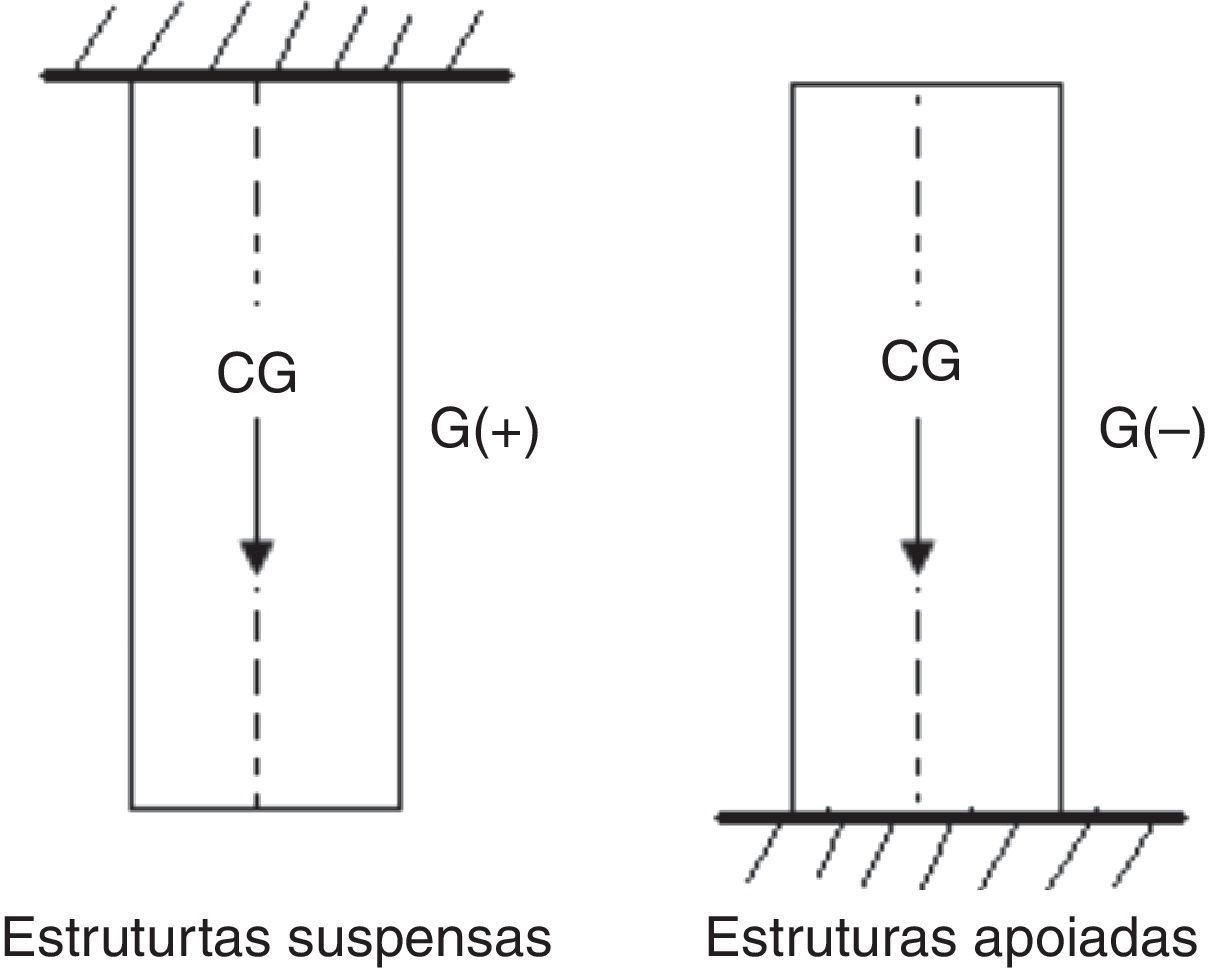
No caso dos elementos dispostos na vertical, o peso próprio (G) atua na direção do eixo longitudinal da peça e provoca esforço axial, que pode ter um efeito diferenciado dependendo da sua vinculação.
Nos elementos suspensos (tirantes, fig. 4a) o efeito do peso é de tração e nas apoiadas (pilares, fig. 4b) este efeito é de compressão. O peso próprio de uma peça (G) pode ser calculado multiplicando‐se o volume da mesma pelo peso específico do material, conforme indica a equação 8:
- ‐
A ‐ área da seção transversal da peça
- ‐
L ‐ comprimento
- ‐
ρ ‐ peso específico do material
Ação do peso próprio [19].
Na tração ou compressão axial a não consideração do peso próprio pode ser eventual e é o caso mais simples.
6Formulação do elemento finito de alta ordemO elemento finito empregado é advindo da formulação livre, destacando‐se que toda a formulação foi baseada no trabalho de Bergan e Felippa [20]. Ele é de geometria triangular com 3 graus de liberdade por vértice: 2 deslocamentos translacionais e uma de rotação azimutal, vetor rotacional ortogonal ao plano do elemento. Inicialmente divide‐se o campo de deslocamentos em 2 modos: Ub e Us, respectivamente modos de deslocamentos básico e superior. O modo básico de deslocamento tem o objetivo de atender as condições de movimento de corpo rígido e de deformação constante com suas funções interpoladoras lineares. O modo de deslocamento superior, ou de alta ordem, são polinômios quadráticos em termos de x e y, levando a campos de tensões de variação lineares. Destarte, a matriz de rigidez final estabelecida como:
A matriz dos modos básicos, Kb, para o caso bidimensional, é dada por:
onde Lj é denominada matriz «amontoadora» (lumped), expressa por:onde xij=xi−xj, xij=xi−xj e i, jek denotam a permutação cíclica de 1,2 e 3. Dm é a matriz constitutiva do elemento. É fundamentalmente a matriz constitutiva da elasticidade, C, integrada ao longo da espessura do elemento. Esta integração reduz o volume V para A, área do elemento.
Para um elemento de espessura t, material com módulo de elasticidade longitudinal E e coeficiente de Poisson ν, a matriz Dm é dada por:
onde C=1t⋅Dm.
O parâmetro α≥0 introduzido na formulação da matriz L aparece como um fator de escala nas funções de forma, multiplicando os termos relacionados com os graus de liberdade rotacionais. O valor de α afeta a matriz dos modos básicos e o cálculo das deformações.
Na equação 11, se α=0, tem‐se a matriz L para o elemento finito triangular com deformação constante (CST). Para este elemento as forças nodais são relacionadas apenas com translações.
A matriz dos modos de alta ordem é dada por:
aqui H=G−1, onde G é a matriz que relaciona os coeficientes associados com os deslocamentos nodais e os parâmetros generalizados q, fazendo‐se as devidas substituições das coordenadas nodais nas funções de forma.
Para um elemento bidimensional, a matriz generalizada de alta ordem é:
onde BS é a matriz de deformação para os modos de alta ordem, definida como:
onde Δ é o operador diferencial para deformações de membrana, expresso por:
e λ é um fator de escala com dimensões iguais ao inverso do comprimento, dada pela equação:
com A, a área do triângulo:
Os outros elementos da matriz Bs são expressos da seguinte maneira:
onde o índice m indica o ponto médio entre j e k com ξm, ηmeμi são as coordenadas adimensionais desse ponto, definidas pelas expressões:
onde i, j e k representam a permutação cíclica entre 1,2 e 3.
A matriz de alta ordem pode ser multiplicada por um escalar positivo β, logo a matriz de rigidez total do elemento é dada por:
que satisfaz ao patch‐test e a condição de ser positiva definida para a convergência, conforme provado por [20]. O parâmetro β≥0 para a matriz de alta ordem é utilizado para calibrar a matriz de rigidez total, K, e com isso aperfeiçoa a convergência. Os valores ótimos sugeridos por [20] para α e β são, respectivamente, 1,5 e 0,5.
7Exemplos numéricosDe posse da formulação descrita nos itens anteriores, desenvolveu‐se um sistema computacional aplicando o SESO em conjunto com o método dos elementos finitos, usando a formulação livre descrita no item 6 baseada em [20]. Introduziu‐se um algoritmo de discretização automática para malhas não estruturadas baseada na triangularização de Delaunay para agilizar o processo e permitir geometria mais complexas, como a formação de poligonais fechadas não convexas e multiplamente conexas. Além disso, devido à necessidade de resolver o sistema linear centenas de vezes no processo iterativo, programou‐se um conjunto de sub‐rotinas em linguagem Fortran otimizadas para resolver sistemas lineares esparsos e simétricos, indicado por Duff e Reid [21]. Adicionalmente, conjugou‐se a metodologia de cálculo do peso próprio gerando automaticamente uma força concentrada equivalente para cada nó do elemento, já computando seu volume e peso específico. Assim, apresentam‐se resultados numéricos para a avaliação e comparação das configurações obtidas pelos modelos clássicos de bielas e tirantes. Os parâmetros de otimização RR e RE, quando não citados, são iguais a 1%, e a função reguladora é definida como η(Γ)=10−4.
7.1Exemplo 1Uma das questões mais intrigantes na natureza ou em estruturas naturais é: «Porque elas são do jeito que são?». Para revelar a resposta desta pergunta, a técnica de otimização pode ser aplicada ao projeto de uma fruta. Especificamente, a intenção é verificar se o algoritmo SESO poderia produzir a mesma forma criada pela natureza de uma maçã, verificando assim se seu formato foi determinado por uma perspectiva genética ou estrutural.
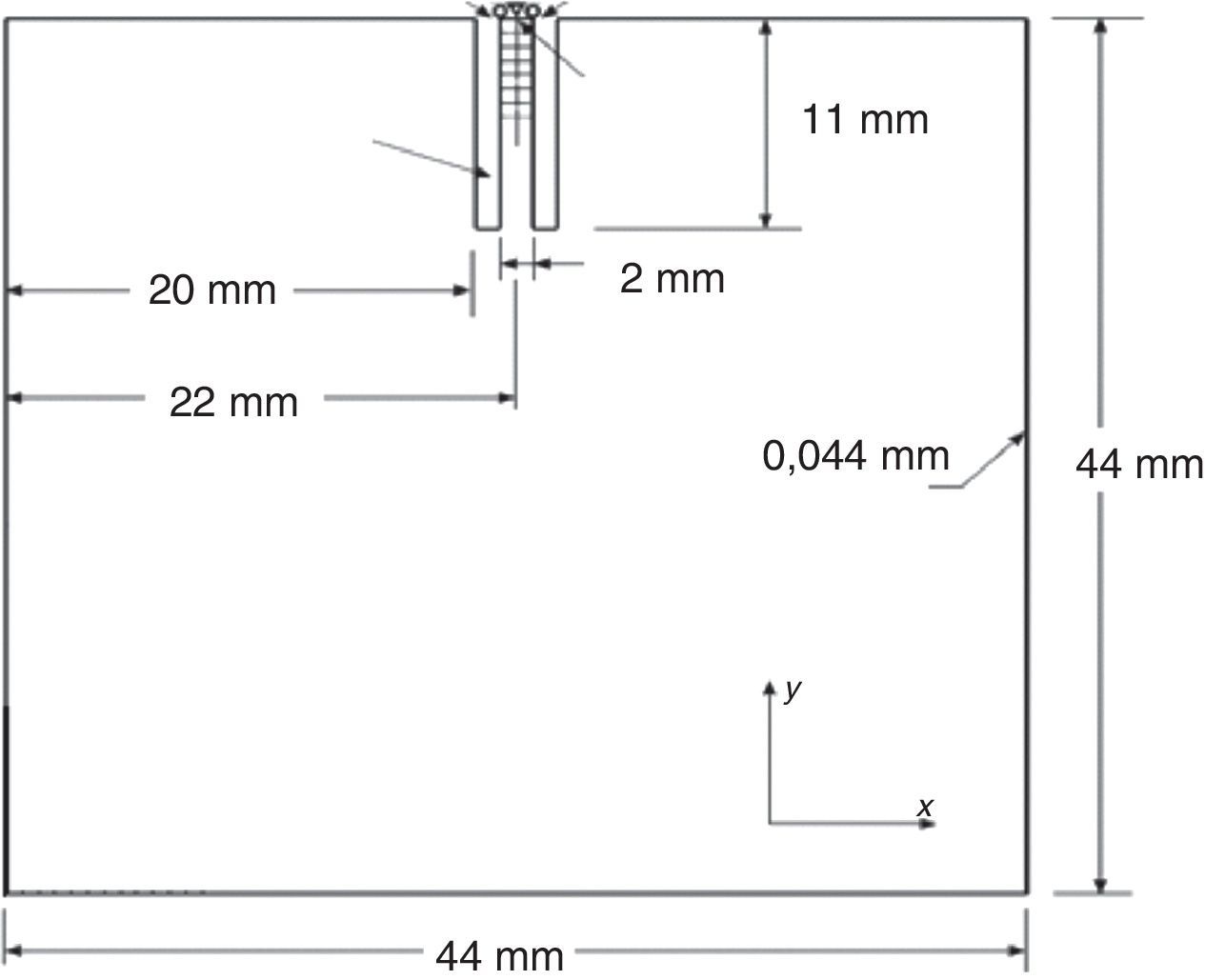
A geometria e as condições de contorno são indicadas na figura 5, a espessura considerada para chapa foi de 0,44mm. O módulo de Young é E=70×103MPa e coeficiente de Poisson é ν=0,3. Utilizou‐se uma razão de rejeição igual a 0%, uma razão evolucionária de 0,5%, e o volume final obtido, com o controle pelo IP, fora igual a 78% do volume inicial e o volume retirado por iteração igual a 5%.
Uma malha refinada de (44x44) totalizando 3.828 elementos finitos triangulares foi utilizada no processo evolucionário. A estrutura está suspensa por um talo em cujos nós extremos permite‐se deslocamento horizontal e o nó central está fixo. A figura 6 ilustra a topologia ótima obtida com a presente formulação, destacando‐se em azul as tensões positivas como devidas à tração que seu peso próprio sobre a estrutura.
Este exemplo foi proposto por Querin [18] e Xie et al. [22], usando ESO. Sua forma ótima está ilustrada na figura 7. A diferença básica entre as formulações utilizadas por estes autores para otimizar a forma desta estrutura está no critério de rejeição, o primeiro usa tensão de Von Mises e o segundo usa a tensão principal ou a soma das tensões principais como critério, obtendo a forma com a uniformidade das tensões na superfície da estrutura.
Topologia semelhante a uma maçã –proposta de Querin [18].
O resultado obtido com a presente formulação mostra que a ação do peso próprio traciona a estrutura fazendo com os elementos próximos ao seu centro de gravidade sejam mais tensionados que os elementos mais próximos ao contorno da estrutura. Nota‐se que o comportamento estrutural é assimétrico, devido a discretização realizada de forma automática por um algoritmo baseado na triangularização de Delaunay, que levou a pequenas assimetrias, mas que não foram significativas para a configuração ótima do problema. Na interface entre os comprimidos e tracionados, respectivamente, vermelho e azul é dentada e descontínua em alguns pontos, características da heurística de remoção dos elementos da malha no procedimento de otimização topológica via SESO.
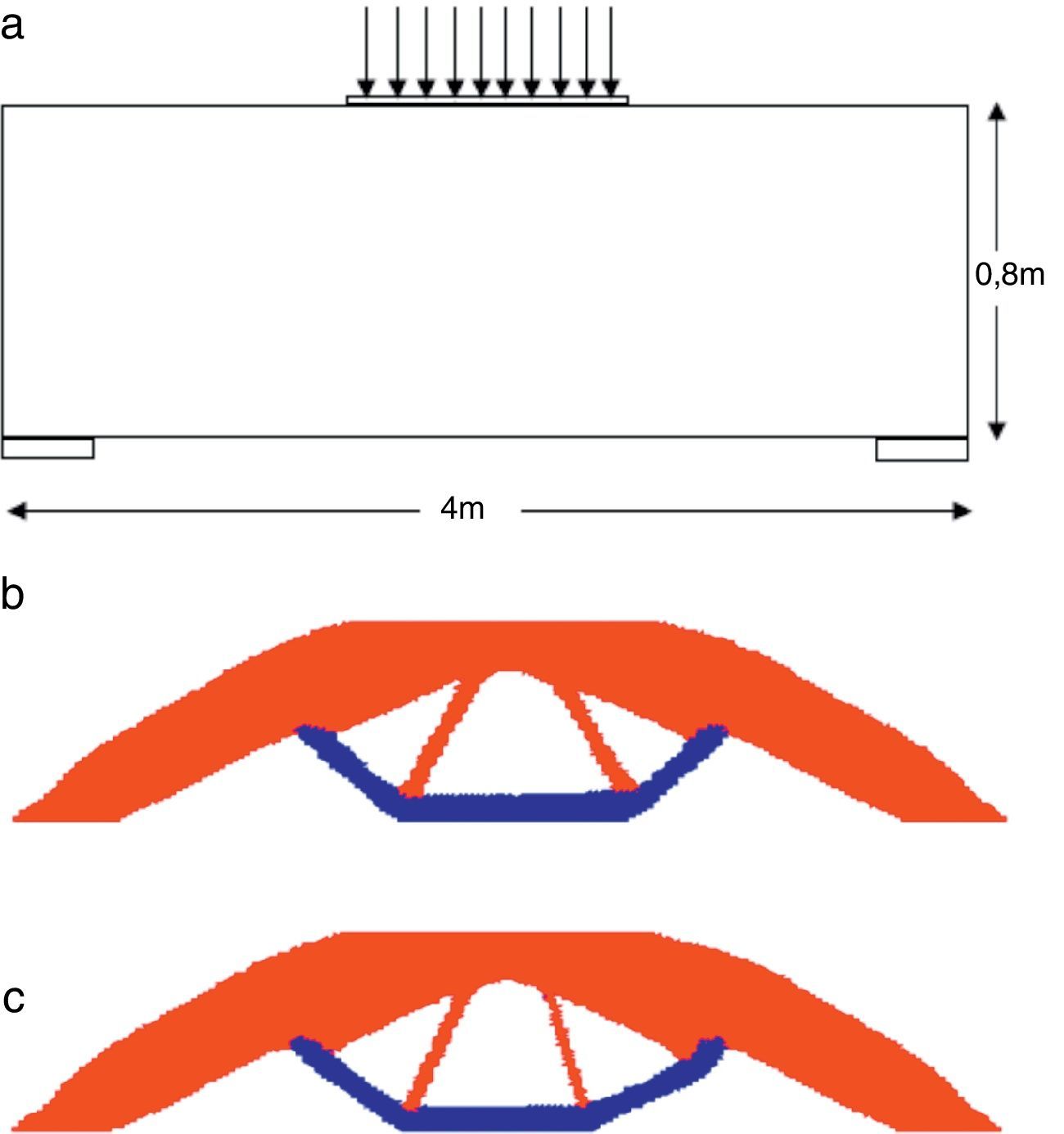
7.2Exemplo 2Este exemplo trata de uma viga baixa biapoiada ilustrada na figura 8a. Os dados utilizados são espessura de 0,50m, módulo de Young E=20820 MPa e coeficiente de Poisson ν=0,3. Aplica‐se a técnica SESO e o critério de parada é realizado em termos do IP da estrutura ou quando o volume desejado é alcançado. Consideraram-se 2 tipos de carregamento, o seu peso próprio e outro de 200kN uniformemente distribuídos em 0,5m, atuando simetricamente no topo da viga, como esquematicamente indicado na figura 8a. Nessa viga baixa utilizou‐se uma razão de rejeição igual a 1%, uma razão evolucionária de 2%. O volume desejado foi de igual 40% do volume inicial e o volume retirado por iteração igual a 1,75%. Durante o procedimento evolucionário o domínio fixo estendido foi definido por uma malha refinada de (160x60) totalizando 19.200 elementos finitos triangulares.
As configurações ótimas obtidas neste problema foram simuladas com as 2 cargas simultaneamente aplicadas durante o processo de otimização. Assim, o algoritmo é capaz de simular melhor o problema físico real. As figuras 8b e c mostram a influência do peso próprio para o modelo de bielas e tirantes, neste problema viga baixa.
Por se tratar de um problema de otimização não convexo, isto é, com vários mínimos locais, optou‐se por uma configuração ótima de projeto com volume de 46,1%, que é um ótimo comum às 2 funções objetivo do problema, destacando‐se que o processo ótimo com o peso próprio chegou a um volume final desejado de 33,4%.
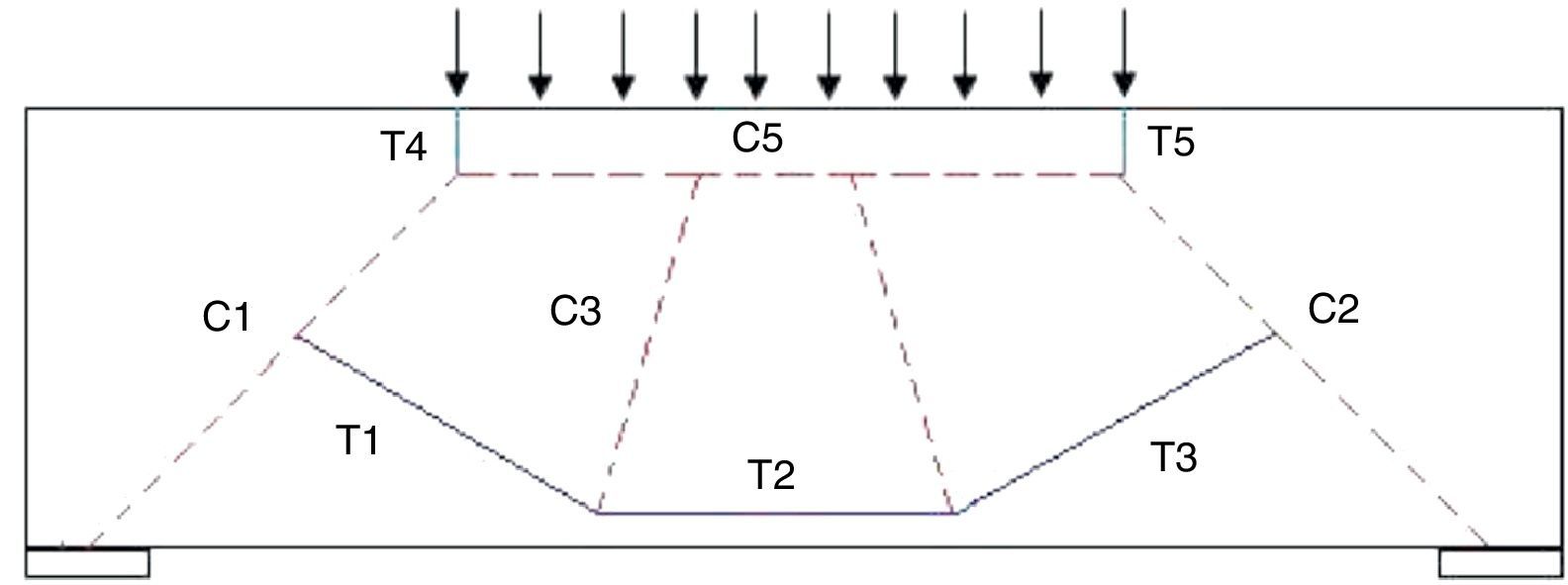
O esquema indicado pela figura 9 mostra os elementos do modelo biela‐tirante elaborados segundo as topologias ótimas de maneira direta. Observa‐se que na proposta esquematizada as semirretas em vermelho e azul indicam, respectivamente, os membros comprimidos, bielas, e os tracionados, tirantes.
Como o peso próprio é pequeno quando comparado com a carga total distribuída, isto é, o seu peso próprio equivale a 5% da carga total distribuída, então, a proposta para o modelo de biela e tirantes com a ação do peso próprio não tem diferenças perceptíveis do modelo indicado na figura 9.
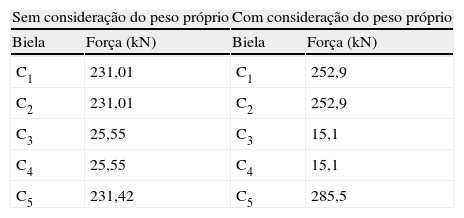
Considerando a teoria de treliça clássica aplicada ao concreto, o modelo demonstra‐se consistente, com o arco superior comprimido (C1, C2 e C5) e bielas inclinadas (C3 e C4) compondo a treliça com os tirantes (T1 e T3) inclinados na ordem de 30 graus com a horizontal e o banzo inferior tracionado (T2). Estes tirantes eram representados por armaduras longitudinais denominadas «cavaletes» mas, hoje em dia, eles são representados pelo conjunto de armaduras longitudinais e estribos verticais.
Indicando‐se os membros onde os fluxos de tensões se destacam, podem‐se calcular os esforços resultantes em cada um por meio das tensões médias calculadas no processo. A força resultante em cada membro é obtida pela multiplicação da tensão média pela respectiva área transversal de cada membro. Já a área da seção do membro é obtida pelo produto da espessura da viga (dado do problema) com a largura média da região do fluxo, medidas na direção transversal à direção das tensões principais e calculadas automaticamente pelo programa computacional.
Calculam‐se assim as áreas das armaduras necessárias na região de tirantes (tabela 1).
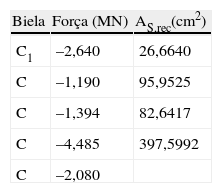
Na tabela 2 apresentam‐se as tensões atuantes no concreto dos membros de bielas. Nota‐se um acréscimo mais significativo de esforços no arco comprimido (banzo superior) de 10‐20%, porém sem alterações importantes nos tirantes.
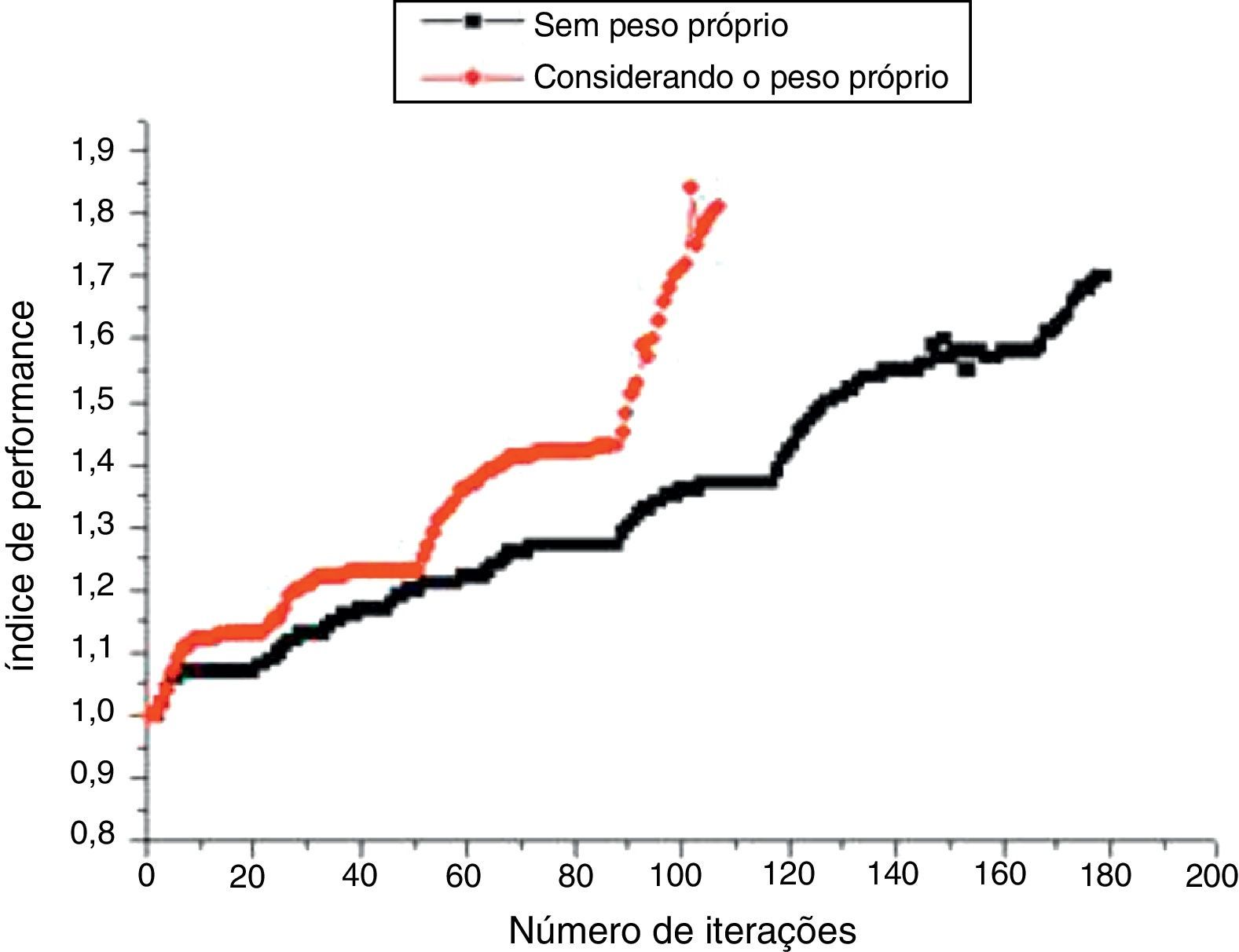
A figura 10 mostra o processo evolucionário e desempenho da estrutura durante este processo. Destaca‐se que o IP máximo obtido com a consideração do peso próprio é de 1,81 e sem o peso próprio é de 1,70. Mostrando que o aumento das tensões médias nos centroides dos elementos finitos proporciona um aumento no número de elementos retirados da estrutura determinando um menor custo computacional.
No procedimento evolucionário considerando o peso próprio é relevante destacar que, mesmo sendo a sua ordem de grandeza menor que o carregamento aplicado à viga, as configurações dos esforços nos elementos do modelo não sofreram alterações significativas, no entanto, a sua consideração proporcionaram maior estabilidade e rapidez ao processo evolucionário.
O procedimento de otimização considerando o peso próprio teve o critério por volume desejado enquanto o IP foi o critério de parada para a viga sem consideração do mesmo. Destaca‐se que o volume desejado no processo evolucionário para ambos os casos foi de 46,6%.
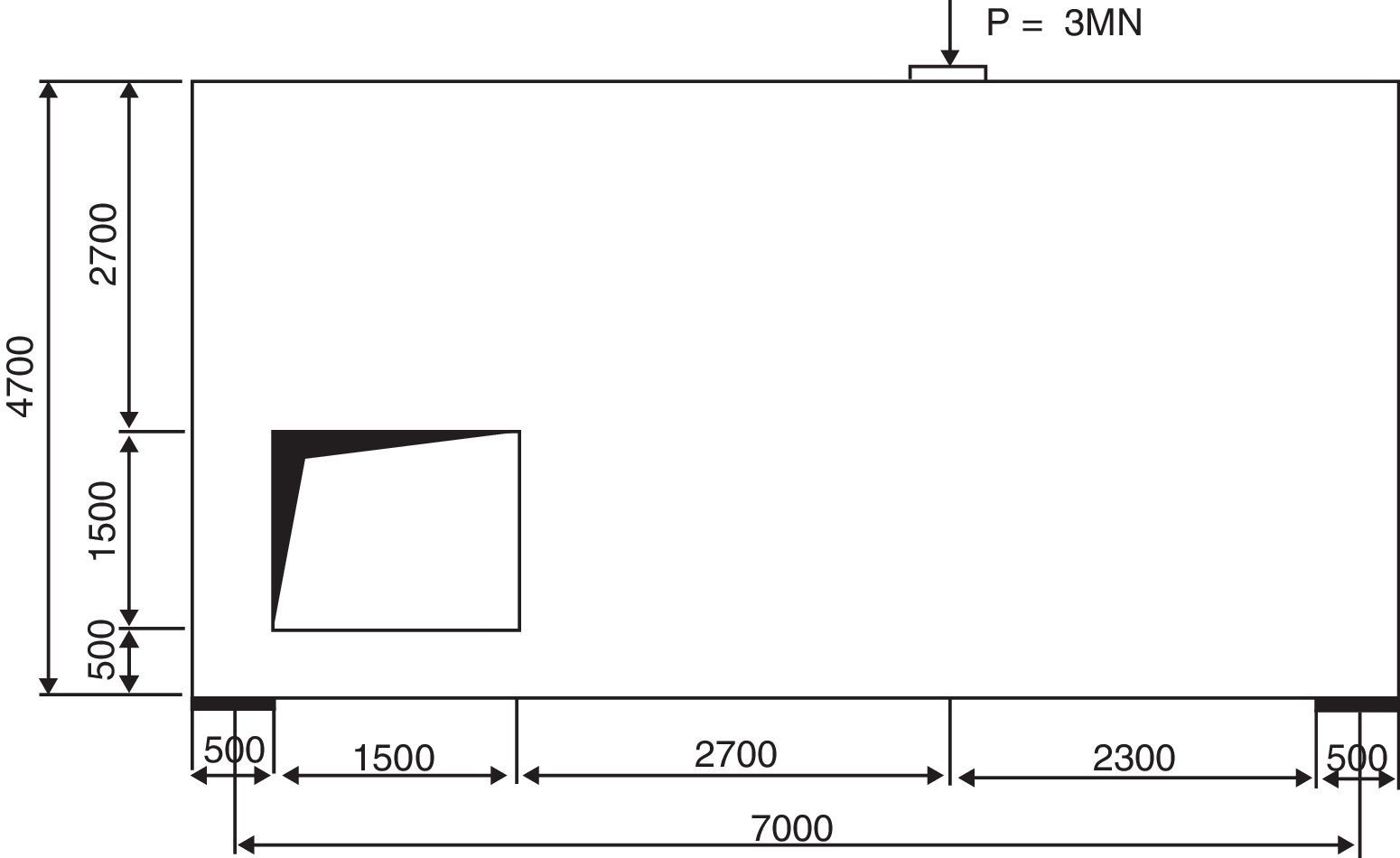
7.3Exemplo 3Este exemplo foi apresentado por [13] que é uma viga biapoiada com uma abertura, onde a geometria e a carga de cálculo (Fd) são apresentadas na figura 11, a qual é usada como domínio estendido para o processo de otimização. Os parâmetros dos materiais utilizados são o módulo de Young E=20820 MPa, coeficiente de Poisson v=0,15 e espessura igual a 0,4m.
Domínio estendido do projeto (mm), [11].
As resistências de cálculo do aço e do concreto são tomadas com valores, respectivamente, de fyd=434MPa e fcd=25 MPa. Essa estrutura possui uma região «D» em virtude da descontinuidade geométrica devido à presença de uma abertura imposta por projeto. Nesse caso, essa região deve ser avaliada usando um modelo de bielas e tirantes.
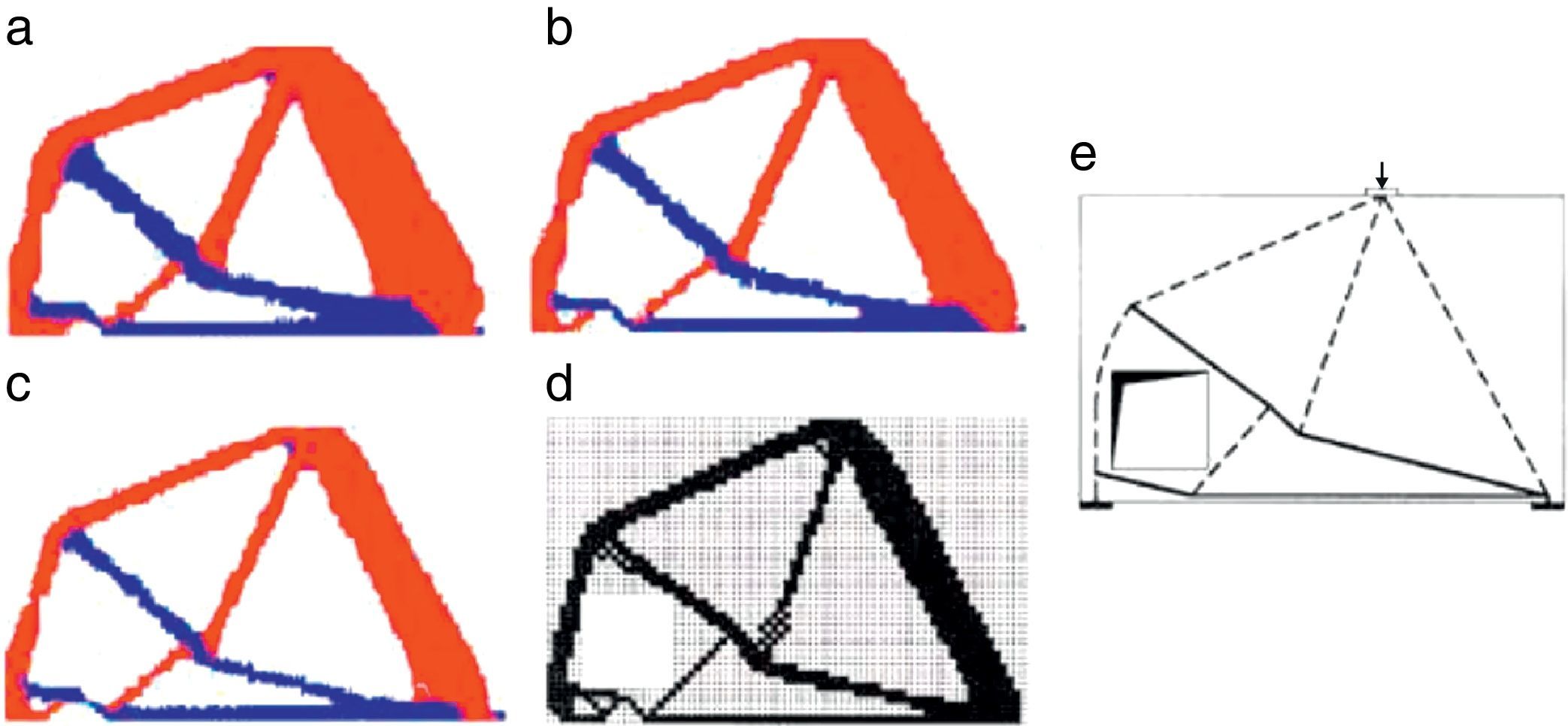
Para a modelagem com a presente formulação, utilizou‐se uma malha de elementos finitos com 13.200 elementos triangulares (150x47) e na figura 12 são mostrados os projetos ótimos obtidos pela presente formulação SESO e comparados com os descritos nos trabalhos de [11] e [13]. A topologia ótima do projeto, indicada na figura 12a, não considera o peso próprio da estrutura.
As figuras 12b e c mostram as configurações ótimas considerando o peso próprio da estrutura em 2 casos diferentes: o primeiro considera uma FR=3, 33MN que é obtida por FR=Fd+PP aplicada no topo da viga, como uma força concentrada, na posição indicada na figura 11, e o segundo, que considera o peso próprio distribuído automaticamente para todos os elementos da estrutura aplicados conjuntamente com a força concentrada Fd.
Neste problema de viga‐parede alta os parâmetros de otimização permaneceram os mesmos para os 3 casos avaliados e a configuração ótima obtida com volume igual a 45,6% sem o peso próprio e, quando se considera peso próprio no topo e distribuído no volume da viga, iguais a 35,1 e 29,9%, respectivamente. Nestas figuras as regiões em vermelho indicam as regiões comprimidas, bielas e as tracionadas, tirantes, em azul. Observa‐se que, mesmo o peso próprio sendo insignificante em relação ao carregamento aplicado à viga, há uma melhor definição dos elementos componentes do modelo e sua configuração.
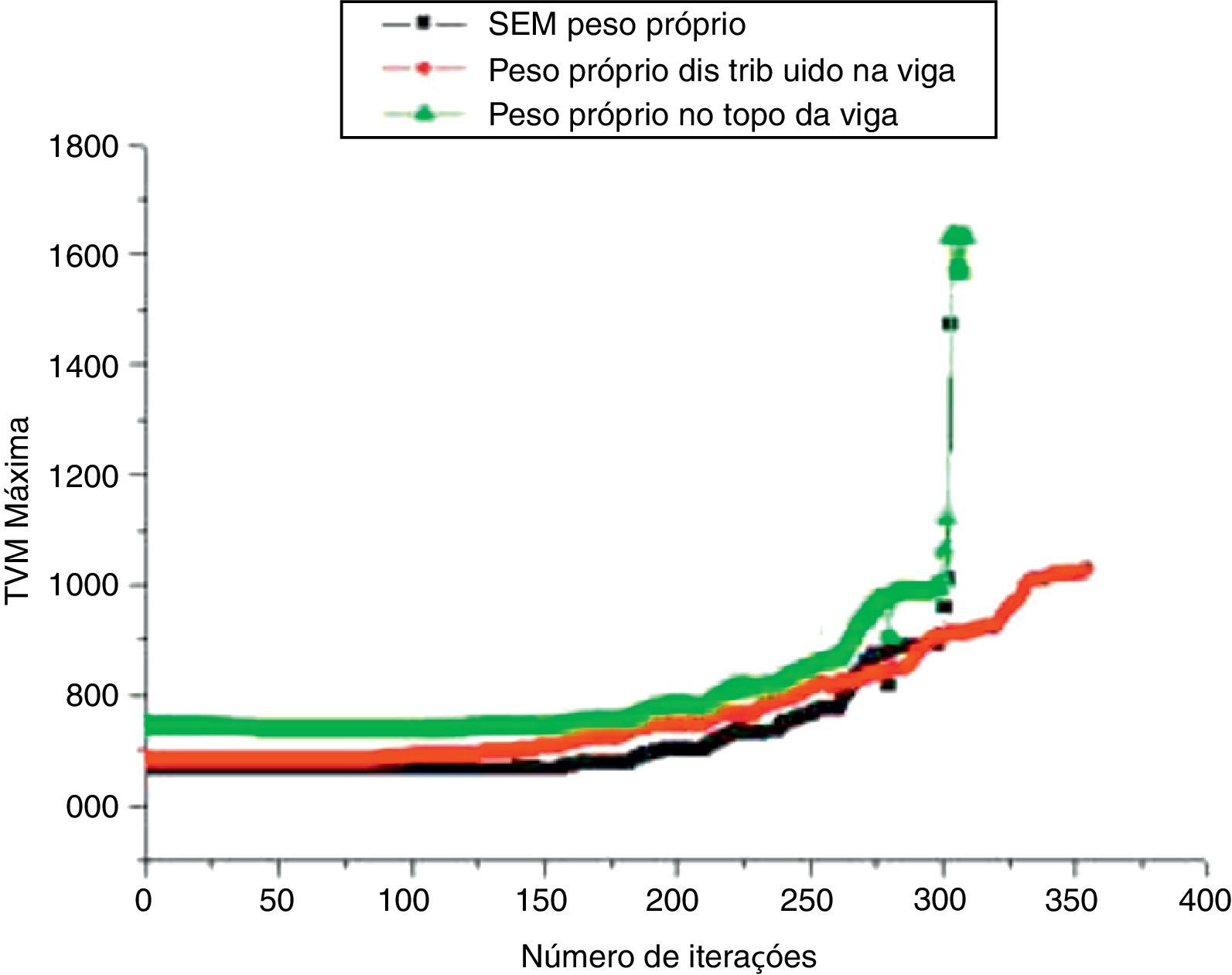
O gráfico da figura 13 mostra as tensões de Von Mises máxima em cada iteração para os 3 casos estudados neste artigo. As tensões médias quando se considera o peso próprio distribuído na viga foram atenuadas representando melhor o modelo real deste problema uma vez que a função objetivo fica mais bem representada neste caso.
O IP atinge um máximo mais rapidamente quando se considera o peso próprio porque é inversamente proporcional ao número de elementos que permanecem na estrutura. Assim, quanto mais elementos são retirados da estrutura pelo critério de otimalidade imposto no processo de otimização maior será o IP.
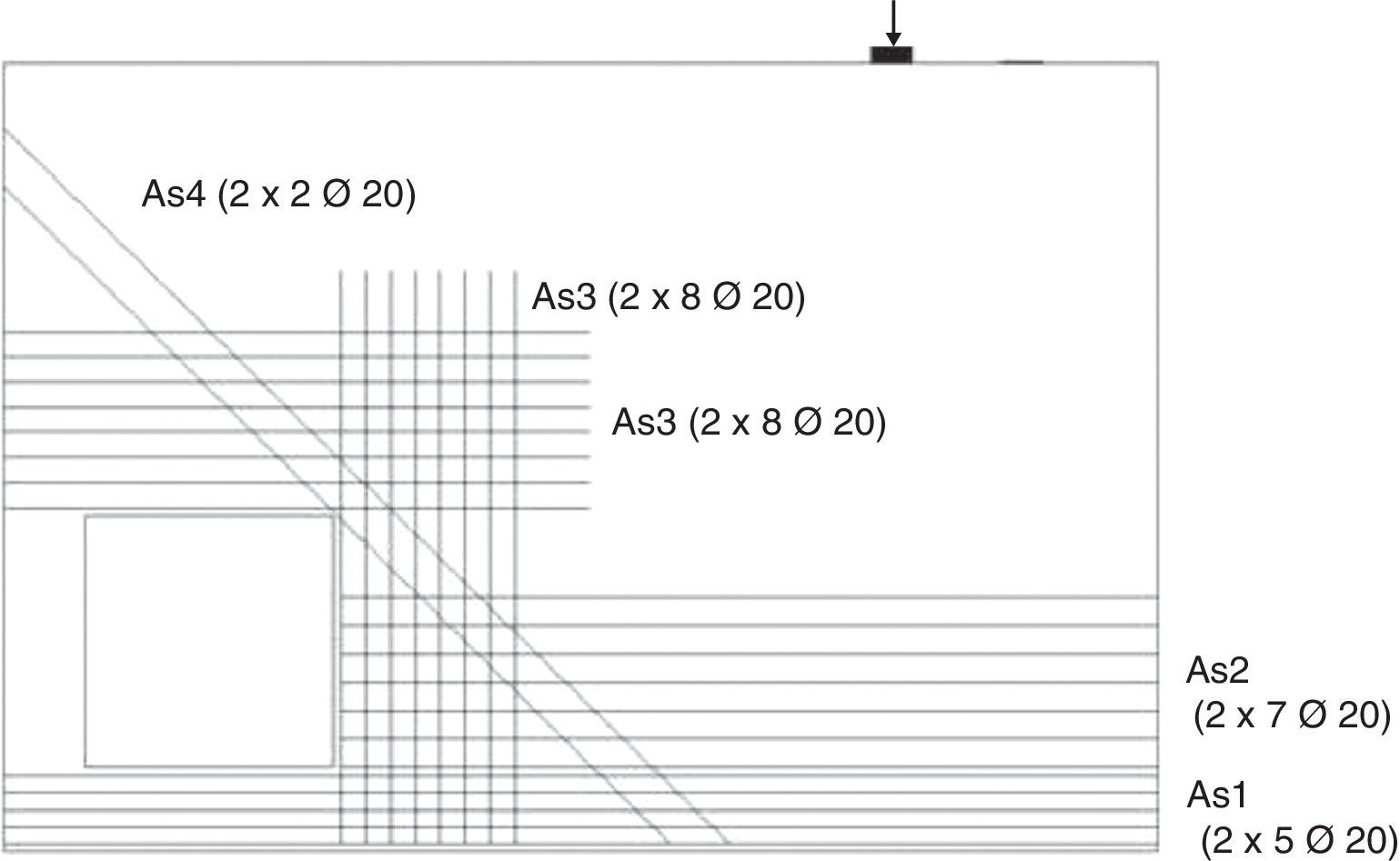
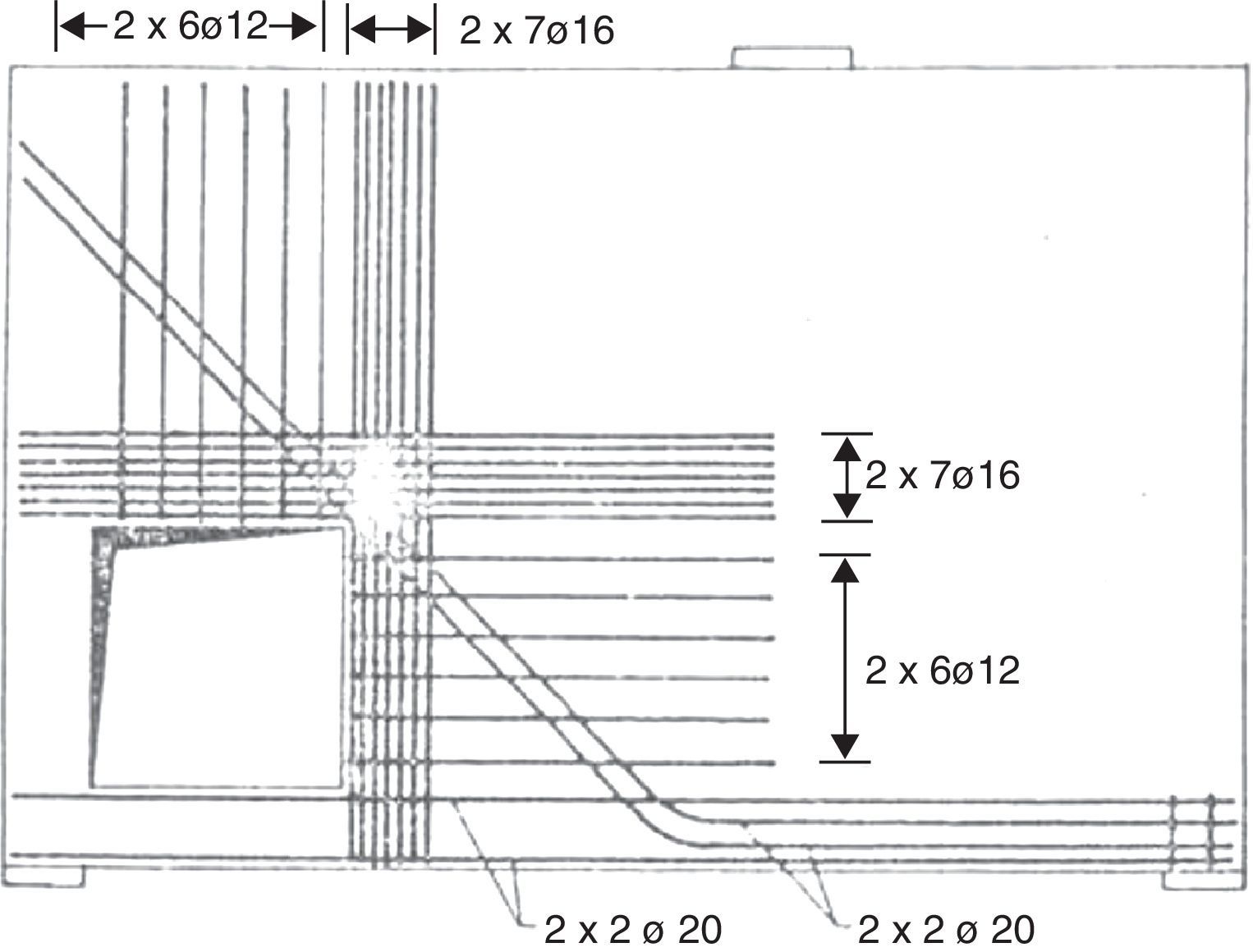
Schlaich et al. [6] apresentam uma proposta de reforço para essa estrutura, denominada de «Deep Beam with a large hole», obtida com o emprego de um modelo de bielas e tirantes advindo da combinação do método dos elementos finitos com um procedimento de se obter os fluxos de forças, usando o método denominado de «load path». De forma que na figura 17 é apresentada a disposição das armaduras propostas pelos autores para reforço da viga com cavidade, entretanto eles não consideram o seu peso próprio.
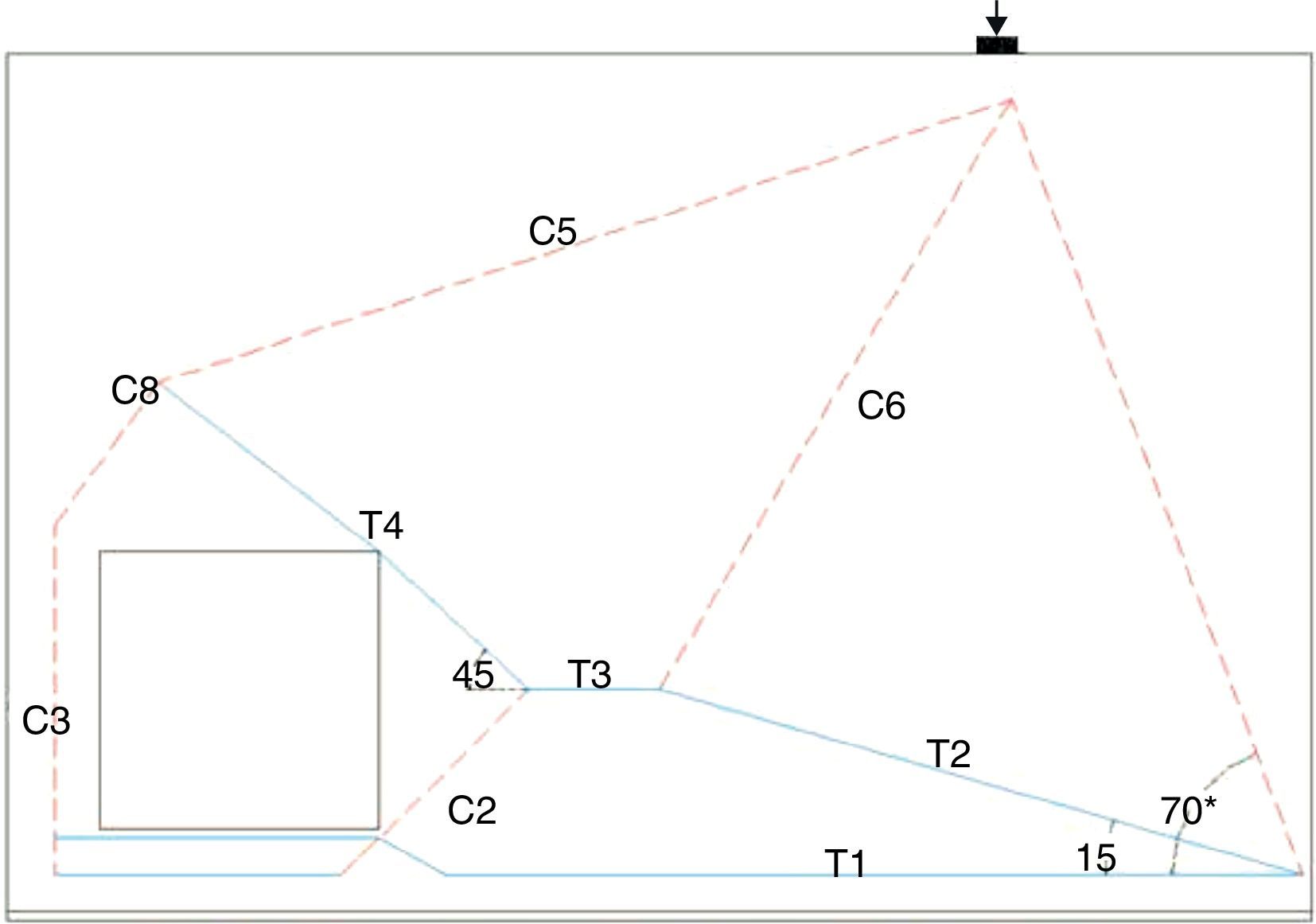
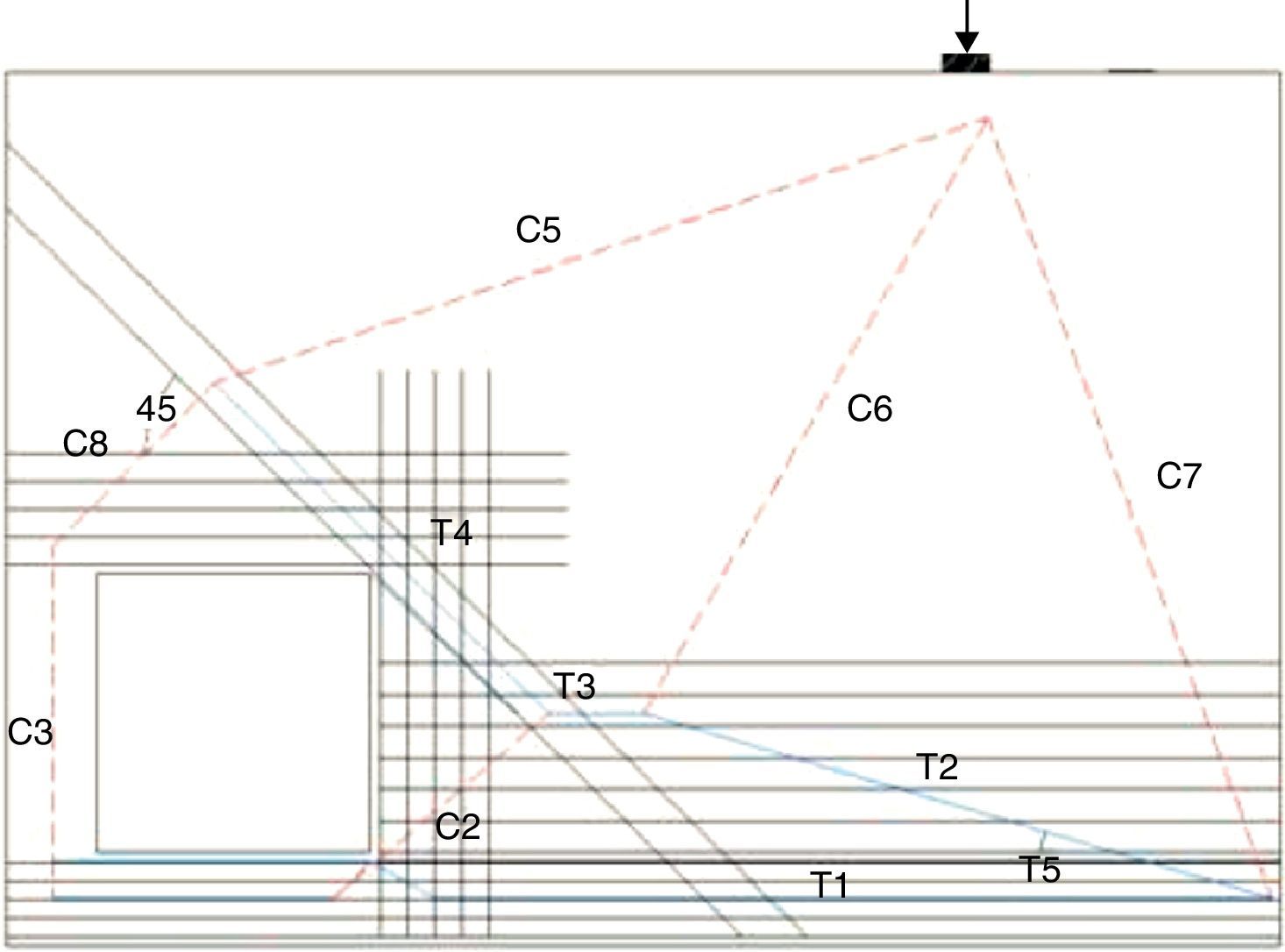
Com a indicação da topologia obtida pela presente formulação é possível definir uma proposta de modelo de biela‐tirante de maneira direta e avaliar a influência de seu peso próprio. Observe‐se a proposta esquematizada na figura 14 onde as semirretas em vermelho e azul indicam, respectivamente, os membros comprimidos, bielas, e os tracionados, tirantes. Indicando‐se os membros onde os fluxos de tensões se destacam, obtendo assim os valores das tensões médias de cada membro e com sua respectiva área, dada pelo produto da espessura da viga com a largura média da região do fluxo.
Deste modo se calculam as áreas das armaduras necessárias na região de tirantes e verifica‐se a resistência do concreto em cada biela.
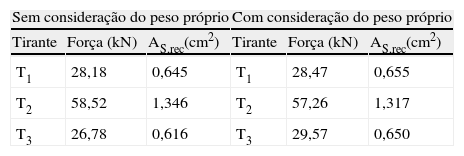
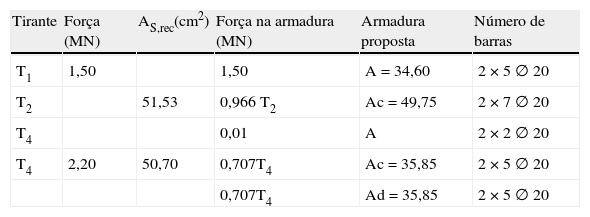
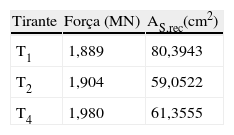
Na tabela 3 são apresentados os valores das forças médias obtidas nos tirantes. Os tirantes T2 e T4 estão inclinados a 15 e 45 graus, respectivamente, da horizontal.
Dimensionamento das armaduras dos tirantes sem consideração do peso próprio
| Tirante | Força (MN) | AS,rec(cm2) | Força na armadura (MN) | Armadura proposta | Número de barras |
| T1 | 1,50 | 1,50 | A=34,60 | 2×5∅20 | |
| T2 | 51,53 | 0,966 T2 | Ac=49,75 | 2×7∅20 | |
| T4 | 0,01 | A | 2×2∅20 | ||
| T4 | 2,20 | 50,70 | 0,707T4 | Ac=35,85 | 2×5∅20 |
| 0,707T4 | Ad=35,85 | 2×5∅20 |
O tirante T2 é representado pela parcela de força decomposta para as barras longitudinais, obtendo‐se assim a área necessária de armadura As2.
O tirante T4 tem sua representação na malha ortogonal, As3, que cobre o trecho junto à borda da cavidade e os encontros de bielas C3 e C8 na extremidade esquerda, e na armadura complementar As4, a 45 graus, cobrindo os encontros de bielas C2, C5 e C8.
Conforme os procedimentos de cálculo admitidos para as armaduras representativas dos tirantes (tabela 3 e fig. 15) apresenta‐se o detalhamento destas armaduras na figura 16, onde nota‐se a extensão das armaduras As3 procurando abranger áreas de encontros de bielas sobre a abertura.
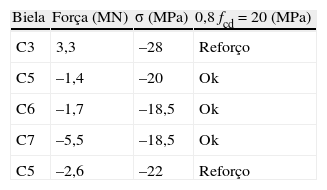
Na tabela 4 apresenta‐se a verificação das tensões atuantes no concreto dos membros de bielas onde nota‐se a não observância do estado último de compressão do concreto nas bielas C3 e C8 (tabelas 5 e 6.).
A proposta para o modelo de bielas e tirantes considerando o peso próprio (de pequena grandeza) da estrutura apresenta configuração semelhante a que não se considera o peso próprio. Nos cálculos para o dimensionamento das armaduras, não houve resultados diferentes das forças resultantes obtidas das tensões médias dos elementos tracionados.
Proposta de disposição de armaduras de para a viga com abertura [6].
O objetivo do artigo é a verificação de um sistema robusto, confiável e automatizado para a obtenção de modelos de bielas e tirantes considerando a influência do peso próprio da estrutura.
Assim, empregou‐se um procedimento de otimização topológica denominado SESO para este fim. Ele, em síntese, emprega o método dos elementos finitos para efetuar a presente análise elástica, de modo a se definir um domínio inicial estendido e, iterativamente, o método busca uma configuração topológica ótima em que, naturalmente, ficam definidos os membros componentes do modelo, bielas e tirantes. Dessa forma, os esforços nos membros podem ser avaliados para possibilitar o dimensionamento e os reforços estruturais necessários para cada trecho.
Os 3 exemplos apresentados demonstraram boa acurácia com as teorias clássicas e os valores descritos por outros autores. Foram propostas também a quantificação e a disposição de armaduras para um exemplo clássico descrito na literatura internacional sobre o assunto e um modelo de bielas e tirantes para uma viga parede baixa com vários casos de carregamento.
Constatou‐se que peso próprio da estrutura influencia positivamente o processo evolucionário e a configuração ótima obtida, mesmo com valores de pequena ordem de grandeza comparados aos carregamentos aplicados aos elementos estruturais. Isto se deve ao fato de que o elemento estrutural passa a ter uma distribuição do peso próprio em cada célula de seu volume proporcionando uma alteração nas tensões internas e no processo suavizado de eliminação que, no entanto, proporciona maior estabilidade e rapidez ao processo evolucionário.
Os autores agradecem ao Departamento de Engenharia de Estruturas e Geotécnica da Escola Politécnica da Universidade de São Paulo (EPUSP), à Universidade Federal de Ouro Preto (UFOP) e à Universidade Estadual Paulista (UNESP) pelo suporte financeiro desta pesquisa.






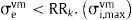
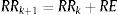
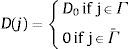

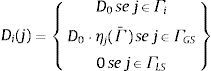

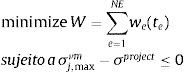
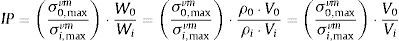
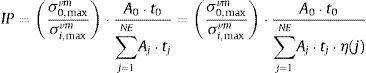
![Ação do peso próprio [19]. Ação do peso próprio [19].](https://static.elsevier.es/multimedia/02131315/0000003000000004/v1_201410050003/S0213131513000722/v1_201410050003/pt/main.assets/thumbnail/gr3.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
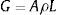
![Ação do peso próprio [19]. Ação do peso próprio [19].](https://static.elsevier.es/multimedia/02131315/0000003000000004/v1_201410050003/S0213131513000722/v1_201410050003/pt/main.assets/thumbnail/gr4.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
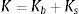
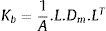
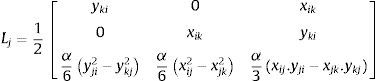
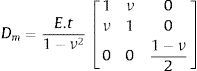
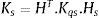
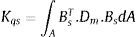
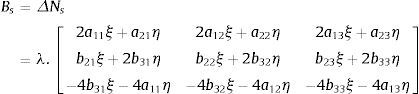
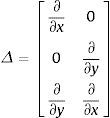
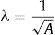
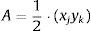
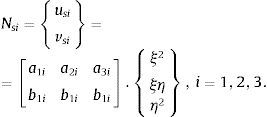
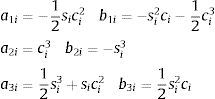
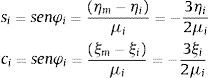
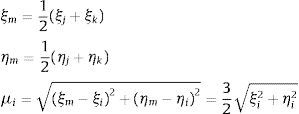
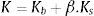


![Topologia semelhante a uma maçã –proposta de Querin [18]. Topologia semelhante a uma maçã –proposta de Querin [18].](https://static.elsevier.es/multimedia/02131315/0000003000000004/v1_201410050003/S0213131513000722/v1_201410050003/pt/main.assets/thumbnail/gr7.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)



![Domínio estendido do projeto (mm), [11]. Domínio estendido do projeto (mm), [11].](https://static.elsevier.es/multimedia/02131315/0000003000000004/v1_201410050003/S0213131513000722/v1_201410050003/pt/main.assets/thumbnail/gr11.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Topologia ótima obtida: a) sem peso próprio, b) peso próprio aplicado no topo, c) peso próprio aplicado em todo corpo da viga (presente modelo), d) [11], e) [13]. Topologia ótima obtida: a) sem peso próprio, b) peso próprio aplicado no topo, c) peso próprio aplicado em todo corpo da viga (presente modelo), d) [11], e) [13].](https://static.elsevier.es/multimedia/02131315/0000003000000004/v1_201410050003/S0213131513000722/v1_201410050003/pt/main.assets/thumbnail/gr12.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)




![Proposta de disposição de armaduras de para a viga com abertura [6]. Proposta de disposição de armaduras de para a viga com abertura [6].](https://static.elsevier.es/multimedia/02131315/0000003000000004/v1_201410050003/S0213131513000722/v1_201410050003/pt/main.assets/thumbnail/gr17.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)