Abolladura de estructuras de barras de sección tipo doble-T

Resumen

En este trabajo se expone una metodología de varias etapas para determinar, con mínimo esfuerzo computacional el factor de carga crítico que produce el fenómeno de inestabilidad local de abolladura de las paredes de los perfiles tipo doble-T. Para ello, se estudia a nivel local como placa delgada cada una de las paredes que forman el perfil. Se constata que es suficiente con analizar las zonas más solicitadas (alas y alma) de la estructura.

Abstract

A stepped methodology for the evaluation, with limited computational effort critical buckling load factor which produces the instability of the walls of double-T sections is proposed in this work. For this purpose, each wall of the cross-section studied in a local level as a thin plate. It is ratified that it is enough to check the most compressed flange and the web of the most loaded beams of the structure.

1

Introducción

Para los elementos estructurales en los que el esfuerzo predominante es el momento flector el mejor aprovechamiento del material se consigue cuando el fallo en el mismo se produce por agotamiento de su capacidad resistente. Sin embargo, también debe considerarse la posibilidad de fallo por pandeo local de los elementos que conforman la viga, es lo que se conoce como fenómeno de abolladura [19,22,23,26].

Las secciones transversales de los elementos a flexión buscan maximizar el valor de su módulo resistente para reducir el valor de las tensiones y desplazamientos máximos. Por estos motivos son muy adecuadas y se emplean con frecuencia las secciones tipo doble-T u otras de pared delgada, bien sean abiertas o cerradas [20,21].

Por lo tanto, resulta de gran interés el estudio de placas planas cargadas en su plano, pues es el caso del alma y de las alas de vigas y pilares de este tipo de perfil y ya que la mayoría de los elementos estructurales se pueden considerar formados por un conjunto de placas planas. De esta manera, cuando una placa se encuentra sometida a esfuerzos de compresión, flexión, cortante o combinación de ellos, puede que se produzca el fallo local por pandeo antes de cualquier otro tipo de fallo.

Timoshenko (1921) fue el primero en presentar una solución para el pandeo local de placas rectangulares simplemente apoyadas en sus cuatro bordes sometidas a cortante. Lo hizo aplicando el método energético, el cual resultó ser una excelente herramienta para resolver un problema que no podía ser resuelto analíticamente como problema de autovalores. En años posteriores diversos investigadores como Southwell y Skan, Seydel, Stein y Neff, Galambos y otros, continuaron con esas investigaciones para obtener tensiones críticas de abolladura más precisas y teniendo en cuenta las diferentes condiciones de contorno de los paneles.

Todas las expresiones deducidas por estos investigadores se fundamentan en que existe una perfecta proporcionalidad entre tensiones y deformaciones de acuerdo a la ley de Hooke generalizada. Sin embargo, estas condiciones se sobrepasan en situaciones de diseño usuales de las estructuras metálicas.

Al contrario del caso del estudio del pandeo de la pieza prismática aislada sometida a compresión axil, no existe una teoría general que estudie el comportamiento de las placas en estas condiciones proporcionando unas relaciones de fácil manejo para el diseño, por ello en lugar de usar teorías más rigurosas como la de Stowell (1948), que utiliza un diagrama tensión-deformación curvo con resultados que se ajustan bien a los de los ensayos, se prefiere en general emplear teorías simplificadas como la de Bleich (1952).

Mientras que en la columna con carga axial la diferencia entre la carga de pandeo y su resistencia posterior es tan pequeña que la carga de pandeo se puede considerar su límite resistente, en el caso de las placas la resistencia post-pandeo puede ser mucho mayor que su carga precrítica. La placa presenta, a diferencia del caso de la columna aislada, un comportamiento totalmente distinto al alcanzar su carga de pandeo, ya que con el aumento de sus deformaciones y desplazamientos modifica su comportamiento mecánico al aparecer en ella el efecto membrana. Por este efecto forma se produce una redistribución de los esfuerzos con la aparición de las fuerzas estabilizadoras de membrana, permitiendo a la placa recuperar su estabilidad en una nueva configuración deformada. Si se siguen aumentando las cargas, la placa en su nueva situación plastifica en las zonas donde su estado tensional es máximo hasta alcanzar su resistencia última [24,25].

En cuanto a la influencia de los rigidizadores longitudinales, diversos han sido los autores que han propuesto soluciones para la variación del coeficiente de abolladura en función del tipo y número de rigidizadores empleados (Crate y Lo (1948), Hoglund (1977) o Beg (2003)). Finalmente, autores como Lee et al. (1996) o Estrada (2005), han estudiado también factores como la influencia del grado de empotramiento que proporcionan las alas en función de los espesores de alas y almas, proponiendo expresiones que toman como base a los resultados clásicos citados anteriormente [18].

Por lo tanto, queda claro que los problemas asociados al fenómeno de pandeo en elementos estructurales de acero son a veces la causa más importante de fallo mecánico [1,3,4,7,9], sobre todo hoy día, que el material cada vez es más resistente y las estructuras proyectadas cada vez más esbeltas.

La formulación matricial del Método Directo de Rigidez (MDR) de estructuras de barras para el caso de no linealidad geométrica en hipótesis de linealidad material facilita la estimación de la carga crítica de pandeo global teórica de forma sistemática con la ayuda del ordenador [10–13]. Sin embargo, lógicamente no permite ningún tipo de comprobación sobre la posible inestabilidad local de los elementos que forman los perfiles de tipo doble-T, las alas y el alma, de las estructuras analizadas. Entre otros motivos, porque la tipología estructural necesaria para realizar dicho análisis es otra, tipo placa en lugar de tipo barra [6,15–17].

Por este motivo, es muy interesante y es el objetivo de este trabajo llevar a cabo dicha comprobación a partir de los resultados disponibles tras un análisis matricial del sistema estructural de barras, desplazamientos y esfuerzos a nivel de sección. Y mediante la teoría de Resistencia de Materiales pasar dichos resultados como condiciones de contorno al problema de placas, con el fin de poder estimar el valor del factor crítico de carga que provoca el fenómeno de abolladura [2,5,8,14].

Este trabajo se ha organizado de la manera siguiente: en primer lugar, tras esta introducción, se presenta la metodología empleada. A continuación, se muestran varios ejemplos de aplicación y en el último apartado se presentan las principales conclusiones obtenidas.

2

Metodología

Se pretende realizar la comprobación a pandeo local de los elementos más comprometidos de cualquier sistema espacial de barras de perfil tipo doble-T. Se asume comportamiento elástico-lineal del material y se adopta un estado proporcional de carga, siendo λ dicho factor de proporcionalidad. Para alcanzar dicho objetivo se establece la siguiente metodología:

• 1)

  Análisis lineal de la estructura. La estructura se modela con elementos tipo barra esbelta y se resuelve mediante MDR. Así, se obtienen los grados de libertad de la estructura, desplazamientos y giros desconocidos en los nudos para el valor nominal de las cargas (λ = 1).

• 2)

  Análisis de estabilidad. Se realiza un análisis no lineal del modelo de barras para calcular el factor de carga crítico de pandeo global (λ_cr,1) y se determina la correspondiente carga crítica asociada a los posibles modos de pandeo del elemento tipo barra: pandeo por flexión, pandeo por flexión y/o torsión, pandeo lateral o vuelco, etc.

• 3)

  Se pasa del modelo de barras al modelo de placas para analizar el elemento más solicitado de la estructura frente a posible abolladura. Para lo cual se trasladan ciertos resultados del modelo de barras obtenidos en el primer análisis, como condiciones de contorno en desplazamientos del modelo de placas.

• 4)

  Análisis para obtener los esfuerzos en el modelo de placas.

• 5)

  Análisis no lineal del modelo de placas, para estimar las cargas críticas asociadas al pandeo local (λ_cr,2) del elemento más solicitado.

3

Resultados y discusión

A continuación se muestran varios ejemplos a los que se aplica la metodología de este trabajo. Los dos primeros ejemplos a modo de validación del método y un tercer ejemplo de aplicación.

Para todos los cálculos los datos son: longitud L=4 m, sección tipo doble-T h=300 mm,b=150 mm,e1=10.7 mm,e=7.1 mm, corresponde al perfil comercial IPE300 (véase fig. 1), de acero E=2.1·1011 Pa,ν=0.3,σy=275 MPa.

Figura 1.

Perfil laminado serie IPE.

3.1

Ejemplo 1. Abolladura del ala comprimida

El primer ejemplo objeto de estudio es un pilar empotrado-libre sometido a un momento concentrado de valor M₀ = 10⁵ N · m en su extremo libre. Para el valor nominal de las cargas (λ = 1) se lleva a cabo un análisis lineal de la estructura mediante un modelo de barras 3D (se emplean 16 elementos) y se obtiene entre otros resultados un desplazamiento máximo de valor δ_MAX = 0.0456 m. A continuación se realiza un análisis de estabilidad global del modelo de barras, que considera flexión según ambos planos y torsión no uniforme, y tras el análisis del equilibrio en la configuración deformada se obtiene un valor crítico del factor de carga de λ_cr,1 = 0.63, que corresponde al nivel de carga que provoca el pandeo global o vuelco de la estructura. Del análisis lineal se conocen los grados de libertad de toda la estructura, por lo tanto se malla el pilar con elementos tipo placa (4x4, 16 elementos placa por pared del perfil, dos alas y el alma, en total 48 elementos placa) y se pasan los resultados de desplazamientos y giros del modelo de barra 3D al modelo placa, con objeto de determinar los esfuerzos de tipo placa. Por último, se hace un análisis no lineal del modelo placa para estimar a qué nivel de carga se pueden producir inestabilidades locales y se comprueba que para un factor de carga de λ_cr,2 = 11.45 se produce la abolladura el ala comprimida tal y como puede verse en la fig. 2.

Figura 2.

Abolladura del ala.

A modo de comprobación, se ha resuelto el problema con el programa comercial de elementos finitos Simulation Mechanical 2015 de Autodesk (abreviado ASM), para ello se ha mallado el pilar completo con elementos placa (plate del software indicado), se ha empleado un total de 1218 elementos y se ha obtenido un valor crítico del factor de carga de λcr,2ASM=11.45 para el fenómeno de inestabilidad por abolladura del ala.

3.2

Ejemplo 2. Abolladura del alma por cortadura

El segundo ejemplo corresponde a un pilar empotrado-libre sometido a una carga transversal puntual de valor P₀ = 10⁵ N en su extremo libre. Del análisis lineal se obtiene un desplazamiento máximo de valor δ_MAX = 0.122 m (se emplean 16 elementos) y del análisis de estabilidad global se obtiene un valor crítico del factor de carga de λ_cr,1 = 1.40, que corresponde al nivel de carga que provoca el pandeo con deformaciones de flexión y/o torsión. Ahora, se malla el pilar con elementos tipo placa (16x4, 16 elementos placa en dirección longitudinal por 4 en dirección transversal y por pared del perfil, en total 192 elementos placa) y se lleva a cabo un análisis lineal del modelo placa para determinar los esfuerzos. A continuación, tras el análisis de estabilidad, se estima que el nivel de carga que puede producir inestabilidad local es de λ_cr,2 = 3.41 y corresponde a la abolladura del alma (véase la fig. 3).

Figura 3.

Abolladura del alma.

De nuevo, y a modo de comprobación, se ha resuelto el problema con el programa ASM (se ha empleado un total de 1218 elementos) y se ha obtenido un valor crítico del factor de carga de λcr,2ASM=3.42 para el fenómeno de inestabilidad por abolladura del alma.

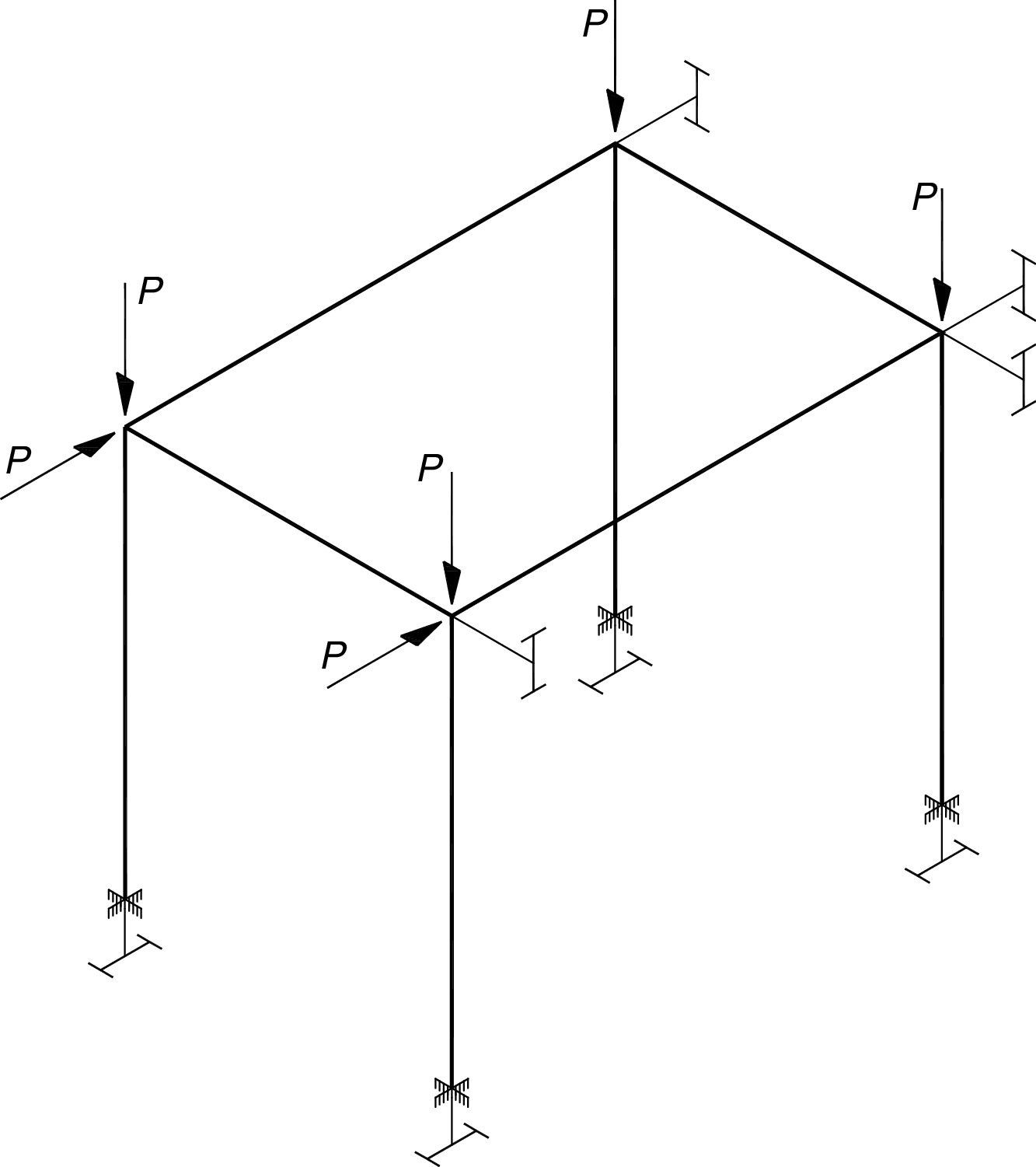
3.3

Ejemplo 3. Pórtico espacial

Como ejemplo de aplicación se resuelve una estructura espacial de barras tipo pórtico 3D (fig. 4). Las cargas aplicadas se suponen concentradas de valor (P). Se asume que todas las barras tienen la misma longitud (L), las bases de los pilares están perfectamente empotradas y todos los nudos son rígidos. Todas las barras son de perfil tipo IPE300 y su disposición espacial es la que se indica.

Figura 4.

Pórtico 3D.

Para resolver este problema lo primero que se lleva a cabo es un análisis lineal de la estructura, modelo de barras (se emplean 16 elementos/barra), mediante MDR y se obtienen los grados de libertad de la estructura, desplazamientos y giros desconocidos en los nudos. Para el valor nominal de carga P0=105 N; λ=1 se obtiene un desplazamiento máximo de valor δ_MAX = 0.0219 m.

En segundo lugar, se realiza un análisis de inestabilidad del modelo de barras para calcular el factor de carga crítico de pandeo global λ_cr,1 = 2.08 y determinar la correspondiente carga crítica.

A continuación, se pasa del modelo de barras al modelo de placas para analizar el pilar más solicitado. Para ello, se trasladan los resultados del modelo de barras obtenidos en el primer análisis como condiciones de contorno en desplazamientos del modelo de placa. Con el modelo placa se hace un análisis lineal para obtener los esfuerzos de placa y después un análisis de inestabilidad para estimar las cargas críticas asociadas al pandeo local. Se emplea una malla de 16x4 elementos placa por pared del pilar analizado (las dos alas y el alma), por lo tanto se emplean 16 elementos placa en dirección longitudinal por 4 en dirección transversal y por pared del perfil, en total 192 elementos placa. Se estima un valor crítico del factor de carga de λ_cr,2 = 10.78 para el fenómeno de abolladura del alma del pilar analizado.

También para este ejemplo de aplicación se ha querido contrastar los resultados con los obtenidos con software ASM de elementos finitos. Para ello se ha mallado toda la estructura con elementos placa (se emplean un total de 9476 elementos) y el programa estima que la abolladura del alma del pilar más solicitado (véase la fig. 5) se produce para un valor del factor de carga de λcr,2ASM=10.83, valor muy próximo al estimado con la metodología de este trabajo.

Figura 5.

Pórtico 3D. Abolladura del alma.

(asociado al valor crítico del factor de carga λ_cr,2 = 10.83).

Por lo tanto, para el pórtico 3D analizado se comprueba que la metodología de este trabajo permite contar con una herramienta útil para la comprobación del fenómeno de inestabilidad local que corresponde a la posibilidad de abolladura del alma del pilar más solicitado.

4

Conclusiones

La principal conclusión consiste en que este trabajo permite analizar un fenómeno de inestabilidad tan complejo como es la abolladura de este tipo de perfiles mediante una metodología sencilla, con mínimos requerimientos computacionales disponibles en cualquier oficina técnica.

Por lo tanto, es suficiente discretizar la estructura mediante elementos barra 1 D y emplear un sencillo método matricial (MDR) para resolver la estructura y posteriormente, en la siguiente etapa del análisis, calcular y comprobar la inestabilidad local de los elementos estructurales aisaldos mediante la metodología expuesta en este trabajo.