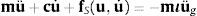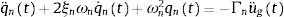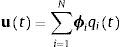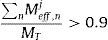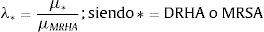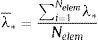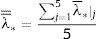En este trabajo se proponen estrategias de análisis y de modelado optimizadas para abordar el estudio sísmico de puentes atirantados que mantienen sus materiales en rango elástico, ofreciendo al diseñador un rango de errores esperables en cada caso en función del tipo de torre de atirantamiento, luz principal y terreno de cimentación, entre otras características. Para ello, se ha realizado un estudio comparativo de diferentes procedimientos de cálculo dinámico aplicados al análisis sísmico elástico de un gran número de puentes atirantados, y se han relacionado las desviaciones observadas con las simplificaciones introducidas en el planteamiento matemático de los mismos. Entre los métodos considerados se encuentra el cálculo modal espectral, el análisis modal dinámico y la integración directa del sistema acoplado de la dinámica. Además, el efecto del impacto del tablero contra las torres en dirección transversal ha sido analizado por medio de elementos de contacto. Se ha concluido que el cálculo modal espectral ofrece resultados que están del lado de la inseguridad, alrededor de un 20%, respecto del cálculo modal dinámico de referencia, el cual es el más preciso.
Several optimized analysis and modelling strategies are provided in this work in order to address the seismic behaviour of cable-stayed bridges in the elastic range, including the expected error ranges in terms of the tower shape, the main span or the stiffness associated with the foundation soil, among other project features. This valuable information for the designer is obtained through the comparative study of different analysis methodologies applied to a large number of cable-stayed bridge models, relating the observed deviations with the simplifications introduced in their mathematical developments. Both the widespread response spectrum analysis, the modal time history analysis and the direct integration of the coupled system of dynamics have been considered. Furthermore, the direct integration has been employed to address the effect of possible contacts and impacts between the deck and the towers during the earthquake in transverse direction. It is concluded that spectrum calculations provide results that are usually 20% lower than the reference modal time history analysis, which is the most precise method.
Debido a la especial importancia social y económica de los puentes atirantados, debe garantizarse su comportamiento elástico ante la acción sísmica de diseño. El proyectista cuenta en la actualidad con varios procedimientos de cálculo; cada uno de ellos presenta sus propias particularidades y es adecuado en determinadas situaciones debido a las simplificaciones asumidas en su formulación matemática. Los puentes atirantados son estructuras ligeras, muy flexibles, con un marcado acoplamiento modal y que, además, presentan un amortiguamiento reducido [1,2], por lo que resulta de vital importancia tener claras las fronteras de aplicabilidad de cada método.
Generalmente se acepta el análisis sísmico elástico y lineal en puentes atirantados con luces principales que no superen los 600 m de luz [3,4], aunque se recomienda que en el análisis estático previo de la situación de equilibrio bajo carga permanente se tenga en cuenta la posible no linealidad geométrica [5]. En líneas generales, existen 3 metodologías de cálculo para analizar la respuesta sísmica de una estructura en rango elástico [6–8], que ordenadas de mayor a menor coste computacional son: a) el cálculo dinámico de la historia de la respuesta mediante la integración directa del sistema acoplado de ecuaciones de la dinámica (DRHA); b) el cálculo modal dinámico de la historia de la respuesta (MRHA), y c) el análisis modal espectral (MRSA) [9].
La mayoría de los trabajos sobre la comparación y crítica de las estrategias de análisis sísmico elástico se centran en estructuras de edificación [6,10] y, generalmente, se ha observado que el cálculo espectral (MRSA) da estimaciones de la respuesta máxima que quedan del lado de la inseguridad respecto de las ofrecidas por el análisis modal dinámico (MRHA). Una de las primeras referencias donde se aborda el análisis de estructuras atirantadas es la de Morris [4], aunque en este trabajo se emplearon modelos bidimensionales y por tanto se ignora el acoplamiento modal característico de dichos puentes en dirección transversal. Ren y Obata [3] analizaron un puente atirantado de 600 m de luz principal y defienden que el principio de superposición que asumen los cálculos basados en la descomposición modal del sistema de la dinámica (MRSA y MRHA) no es aplicable en puentes atirantados de esas dimensiones, incluso admitiendo que su respuesta es lineal, debido al complejo acoplamiento modal. Apoyándose en trabajos de referencia sobre el análisis sísmico de puentes atirantados [1,11], Walker y Stafford [12] contrastaron la fiabilidad de diversas reglas de combinación modal en el método espectral (MRSA), tomando como referencia el cálculo modal dinámico (MRHA) y analizando la respuesta tridimensional de un puente atirantado de luz moderada (Quincy Bayview, USA, luz principal: 274 m). Estos autores observaron que la regla CQC (Complete Quadratic Combination) [13] es la más apropiada a la hora de combinar los valores máximos obtenidos en cada modo de vibración, debido a que tiene en cuenta la correlación (acoplamiento) entre modos de vibración. No obstante, también destacaron que la regla CQC puede llegar a infravalorar en un 20-30% los coeficientes de correlación modal de los modos con más participación en la respuesta. Los autores sugieren que dicho error se debe a fluctuaciones locales en las ordenadas espectrales de los acelerogramas considerados, algo que también apunta Chopra [6], aunque reconocen que deben realizarse más estudios en este sentido.
En la mayoría de los trabajos publicados hasta la fecha se ignora el método de integración directa (DRHA) como posibilidad en el análisis de estructuras en rango elástico, debido a su elevado coste computacional. No obstante, DRHA puede ser la única opción estrictamente válida si se incluyen dispositivos sísmicos o alguna «fuente de no-linealidad»relevante, aunque la estructura se mantenga en rango elástico. Este último es el caso de la respuesta transversal (perpendicular a la dirección del tráfico) de la mayoría de puentes atirantados situados en zona sísmica, que suelen emplear una conexión «flotante»entre el tablero y las torres de atirantamiento con el objetivo reducir los esfuerzos sísmicos. Para ello se dispone de una unión formada por salientes en ambos elementos que liberan el movimiento relativo longitudinal y vertical, mientras que en dirección transversal el tablero contacta teóricamente sin fricción con ambos laterales de las torres [14]; dicho contacto tiene una importancia muy relevante en el comportamiento sísmico del puente [15], y le confiere un carácter intrínsecamente no lineal, incluso ante terremotos de pequeña intensidad o acciones de viento transversal. Por otro lado, la comparación en rango elástico entre el método directo y los procedimientos basados en la descomposición modal resulta interesante para extrapolar resultados al rango inelástico, donde normalmente se asume como referencia «exacta»la solución dada por DRHA a la hora de proponer estrategias simplificadas (e.g. métodos Pushover) [16].
El objetivo de este trabajo es estudiar cómo influyen en la precisión de las estrategias de análisis en rango elástico las diversas decisiones de diseño en un puente atirantado (forma de la torre, tipo de atirantamiento, conexión torre-tablero, etc.), la luz principal y las características del terreno de cimentación. Para ello se han analizado una gran cantidad de puentes atirantados, presentados después de introducir las posibles debilidades de las estrategias de análisis desde el punto de vista de su formulación matemática. Se ha verificado que el cálculo modal espectral (MRSA) ofrece esfuerzos sísmicos en las torres que son típicamente un 20% inferiores a los del MRHA, mientras que DRHA debe evitarse (siempre que el puente se mantenga elástico y no tenga dispositivos sísmicos) modelizando la conexión «flotante»entre el tablero y la torre con un elemento rígido en uno de los lados de la misma.
2Estrategias de análisis sísmicoPlanteando las ecuaciones de equilibrio en una estructura de N grados de libertad sometida a una acción sísmica se obtiene el sistema de N ecuaciones diferenciales, en general acopladas, conocido como sistema de la dinámica:
donde u(t) es el vector de desplazamiento relativo, m y c son respectivamente las matrices de masa y amortiguamiento de la estructura. fS(u,u˙) define la componente del vector de fuerzas debida a la rigidez de la propia estructura, que en general se expresa como una relación no lineal en función del desplazamiento y velocidad relativas; si los materiales se mantienen en rango elástico dicha relación puede linealizarse de la forma: fS=ku, donde k la matriz de rigidez elástica de la estructura. Finalmente, ι es la matriz de influencia, que relaciona los grados de libertad de la estructura con los de las aceleraciones impuestas en las cimentaciones u¨gT(t)=(u¨gX,u¨gY,u¨gZ), siendo u¨gj la componente del acelerograma en dirección j (donde j=X, Y, Z). El lector interesado puede profundizar en la formulación matemática de los procedimientos que se han estudiado por medio textos clásicos de la dinámica estructural [6–8,17].2.1Integración directa en el dominio del tiempo (DRHA)Este procedimiento está basado en la solución directa del sistema de la dinámica (1), actualizando y linealizando la respuesta de la estructura en cada instante por medio de algoritmos de integración «paso a paso». Esta estrategia permite tener en cuenta de un modo realista diferentes causas de no linealidad, como la pérdida de elasticidad en los materiales, la no linealidad geométrica o posibles contactos durante el terremoto, entre otras. Sin embargo, es el método más costoso desde el punto de vista computacional e introduce incertidumbres en la modelización, puesto que se requieren más datos sobre el material o la estructura, algunas veces difíciles de predecir. Además, los algoritmos implícitos de integración introducen un error de fase que aumenta cuanto mayor es el paso de tiempo y/o mayor es la frecuencia de la vibración [17]. En este trabajo se emplea el algoritmo propuesto por Hilber, Hughes y Taylor (HHT) [17], ampliamente aceptado en el ámbito de la dinámica estructural gracias a que se introduce un amortiguamiento numérico (αa) que reduce la contribución de las frecuencias elevadas, despreciable en la respuesta global y que además puede desestabilizar la solución. El algoritmo HHT es implícito y de paso único, con una convergencia cuadrática que es incondicionalmente estable si el análisis es lineal y si los parámetros que lo definen satisfacen ciertas condiciones (e.g. −1/3≤αa≤0). En este estudio se ha empleado un reducido valor de este amortiguamiento, αa=−0.05, para optimizar la estabilidad del análisis [18].
2.2Cálculo modal dinámico (MRHA)El cálculo modal dinámico descompone la respuesta en la contribución de los modos de vibración más importantes y está soportado teóricamente por la ortogonalidad de las matrices que definen el sistema de la dinámica respecto de cualquier autovector que represente un modo de vibración de la estructura, ϕn. A efectos prácticos, las condiciones de ortogonalidad se cumplen si la respuesta es estrictamente elástica y lineal, y si el amortiguamiento es constante para todos los modos de vibración o se define por las distribuciones de Rayleigh o Caughey [6], en ese caso se puede desacoplar el sistema de N grados de libertad en N ecuaciones diferenciales ordinarias que describen los distintos modos de vibración. La ecuación que gobierna la respuesta en el dominio del tiempo del modo n-ésimo, definido por su coordenada generalizada qn, por su frecuencia ωn y por su amortiguamiento ξn característicos, se expresa como:
donde Γn=ϕnTmι/ϕnTmϕn es el factor de participación del modo n-ésimo.La respuesta total (ro) se obtiene agregando de un modo algebraico las repuestas modales obtenidas en el dominio del tiempo, por medio de la expresión:
ϕi y qi siendo respectivamente el autovector y la coordenada generalizada correspondientes al modo de vibración i-ésimo.Una de las ventajas del análisis modal es que no es necesario repetir el estudio en el dominio del tiempo de los N modos de vibración en una estructura de N grados de libertad, que en el caso de los grandes puentes atirantados puede ser muy importante. El peso en la respuesta sísmica de los modos de orden muy elevado, con grandes frecuencias, es despreciable y por tanto se puede truncar el sumatorio en la expresión (3), estudiando los J primeros modos (J<N). Las normativas sísmicas [19] proponen que el número de modos que debe incluirse en el análisis (J) es aquel que permita activar más del 90% de la masa total de la estructura (MT) en todas las direcciones:
siendo Meff,nj la masa activada del modo n en dirección j (j=X, Y, Z), definida como: Meff,nj=Γnj2ϕnTmϕn.Desafortunadamente, el número de modos de vibración necesarios para exceder el 70–80% de la masa de la estructura es muy alto cuando se estudia un puente atirantado [20]; debido a la gran flexibilidad del tablero y del sistema de atirantamiento, únicamente los modos de orden muy elevado son capaces de activar la masa de las torres que se encuentra próxima a la cimentación (la cual supone un importante porcentaje de la masa total del puente), especialmente si el puente tiene torres con diamante inferior (e.g. modelo «YD-LCP»en la figura 3) cimentadas en roca sana [21]. Empleando el criterio del Eurocódigo 8 [19], la frecuencia del último modo incluido en el análisis (referida en adelante como flim) está alrededor de flim≈10 Hz.
2.3Cálculo modal espectral (MRSA)El cálculo modal espectral se olvida de la evolución de la respuesta estructural durante el terremoto para centrarse en los valores máximos de la respuesta de cada modo de vibración (rn,o), evitando por medio del espectro de aceleraciones la integración de las J ecuaciones diferenciales (2). La obtención de la contribución máxima debida a cada modo en la respuesta es exacta, aunque dichos valores no se dan en el mismo instante y no pueden agregarse directamente para obtener la respuesta total como se hace en el método modal dinámico, a través de la expresión (3); en su lugar, se emplean reglas de combinación de naturaleza estadística y basadas en el principio de superposición para obtener la respuesta total (ro); las normativas sísmicas establecen que debe emplearse la regla CQC en el caso de estructuras con un acoplamiento modal significativo, el cual se ha verificado en todos los puentes atirantados estudiados en este trabajo. La formulación de la regla CQC asume que la acción sísmica y la respuesta estructural son estacionarias, pudiendo introducir errores si: a) el terremoto es impulsivo (no es nuestro caso); b) si la aceleración espectral asociada a periodos importantes para la estructura tiene valores no uniformes (en este caso la acción no sería «de banda ancha») [12], y c) si el amortiguamiento es muy reducido (ξ<0.005, que tampoco es el caso que nos ocupa, donde ξ=0.04) [6].
El cálculo modal espectral da como resultado directamente los valores máximos, los cuales son los más interesantes en el diseño sísmico. Además es significativamente más rápido que el resto de procedimientos, puesto que no requiere la integración en el dominio del tiempo de un conjunto de J ecuaciones diferenciales, ni la repetición del análisis para varios acelerogramas, ya que directamente se impone el espectro que define la normativa.
2.4Discusión sobre el método de referenciaSe requiere una medida exacta de la respuesta sísmica para tomarla como referencia y poder contrastar la precisión de los distintos métodos de análisis. Desafortunadamente, son muy pocos los datos que pueden obtenerse de puentes atirantados y en ningún caso el sismo registrado fue de una intensidad importante [20,22,23], por lo que la vibración introducida por acciones de tráfico o viento enmascara la respuesta sísmica registrada, que a su vez se ve muy influenciada por un nivel de amortiguamiento difícil de determinar. Se propone un estudio previo al nivel más elemental: analizaremos la respuesta sísmica de un oscilador masa-resorte de un grado de libertad. En este sistema podemos obtener de un modo exacto la respuesta por medio de la integración numérica de la ecuación diferencial que lo gobierna (2), y para ello se emplea un método basado en la interpolación lineal de la excitación, recomendado cuando se estudia la respuesta sísmica elástica de un oscilador [6].
Se ha realizado un estudio paramétrico variando las propiedades del oscilador para analizar un rango amplio de frecuencias, incluyendo los modos más importantes de los puentes atirantados estudiados: [0, 15−35] Hz. En este análisis se emplea un conjunto de 12 acelerogramas sintéticos cuyo espectro viene dado por el Eurocódigo 8 en terreno blando (en los siguientes apartados se describe con más detalle la acción sísmica). En la figura 1 se presenta la media (μ) de la aceleración absoluta extrema de la masa móvil asociada al resorte en el sistema de un grado de libertad (aceleración espectral), obtenida con diversos procedimientos de análisis. El cálculo MRHA da una respuesta exacta al problema en todo el rango de frecuencias, algo que se esperaba, puesto que la integración en el dominio del tiempo de la respuesta modal resulta exacta si el paso de tiempo en el cálculo coincide con el del acelerograma [8]. DRHA ofrece unos resultados muy próximos al valor exacto, pero cuando el periodo es menor de 0.3 s el error de fase que introduce el método provoca aceleraciones pico ligeramente superiores (ver detalle en la fig. 1). No se presenta el resultado del cálculo espectral, puesto que al tratarse de un sistema con un único modo de vibración su resultado coincide con MRHA y es exacto. Se incluye el espectro del Eurocódigo 8 que sirve para generar los acelerogramas.
Considerando una estructura con múltiples grados de libertad, se podría indicar que al truncar la respuesta de los modos de vibración superiores a cierto umbral se introduce un error del análisis modal que no está presente en el DRHA; no obstante, se han incluido en este trabajo todos los modos por debajo de 35 Hz, y se ha verificado a través de estudios de sensibilidad que ignorar los modos por encima de dicho límite no introduce errores apreciables. Por tanto, se considera el cálculo modal dinámico (MRHA) como el procedimiento más exacto para estudiar la respuesta sísmica de los puentes atirantados, siempre que no tengan dispositivos sísmicos y que se mantengan en rango elástico y lineal (en caso contrario debería emplearse el método directo, DRHA). El cálculo MRHA será la referencia a la hora de comparar resultados entre diversos métodos de análisis en el presente estudio.
3ModeladoUn estudio previo sobre las dimensiones de más de 30 puentes construidos en todo el mundo ha llevado al establecimiento de las secciones y proporciones que definen completamente los modelos de elementos finitos tridimensionales, parametrizados en función de la luz principal, LP, cubriendo un rango entre 200 y 600 m (cada 100 m). La figura 2 ilustra de un modo esquemático el alzado de los puentes estudiados. Las torres de atirantamiento tienen un papel capital en la seguridad de la estructura y por tanto este trabajo se centrará en los esfuerzos sísmicos que se registran en ellas; los resultados se referirán a la torre más próxima al estribo izquierdo de la figura 2.
Se han considerado 5 tipos de torres, las cuales se recogen en la figura 3, junto con el sistema de ejes globales y las palabras clave que se emplean en el trabajo para presentar los resultados. Dos tipos de configuraciones han sido consideradas para el atirantamiento: atirantamiento lateral a ambos lados del tablero (LCP) y atirantamiento central al centro del mismo (CCP); este último ha sido implementado únicamente en las torres con forma de Y invertida (sin diamante inferior y con él). En total se han analizado 35 modelos tridimensionales de elementos finitos, cimentados en 2 terrenos propuestos por el Eurocódigo 8 [19] y radicalmente diferentes: terreno rocoso (TA) y blando (TD), los cuales definen la excitación sísmica (presentada en la siguiente sección) y la flexibilidad de la cimentación. No se ha considerado la interacción suelo-estructura, pero la importancia de este efecto se presume reducida debido a la gran flexibilidad de los puentes atirantados y a su moderado peso, que hace que la energía que transmiten a las cimentaciones no sea excesiva [7].
Las torres son de hormigón (resistencia de 40 MPa) y el tablero es mixto, con sección abierta en puentes con atirantamiento lateral, formada por 2 vigas longitudinales metálicas con perfil en I, sobre las que se conecta la losa de hormigón; la sección es tipo cajón en puentes con atirantamiento central para resistir la torsión que no es capaz de soportar el sistema de cables conectado en el centro de la misma. Se definen propiedades elásticas estándar en los materiales, por medio de los Eurocódigos relevantes.
La conexión entre las torres y el tablero únicamente se realiza en dirección transversal (Y); en los resultados presentados en la sección 5 se soluciona a través de una unión simplificada que relaciona el tablero con uno de los laterales de la torre; en la sección 6 se refina dicha conexión para tener en cuenta el contacto alternante entre ambos elementos. Las pilas intermedias en los vanos de compensación únicamente coaccionan el movimiento vertical del tablero. Dichos apoyos se disponen a una distancia de 0.4LS respecto del estribo correspondiente para mejorar la efectividad del atirantamiento, reduciendo el desplazamiento longitudinal de la parte superior de las torres [14]. La flexibilidad de las cimentaciones se representa por medio de muelles cuyas características varían en función del tipo de terreno considerado. Con el objetivo de facilitar el modelado, se ha empleado un único elemento tipo «barra»(sin resistencia a flexión) en cada cable de atirantamiento. Dicha discretización ignora la interacción cable-estructura; no obstante, los autores de este trabajo han verificado que esta hipótesis se encuentra del lado de la seguridad.
4Acción sísmica y esquema de cálculoLa excitación sísmica empleada se basa en los espectros de diseño del Eurocódigo 8 [19], definidos para terreno rocoso (TA) o blando (TD), adoptando en ambos casos el espectro de tipo 1 y una aceleración de cálculo representativa de zonas de alta sismicidad a nivel mundial: ag=0.5 g. Los periodos fundamentales de los puentes atirantados estudiados con 600 m de luz principal son de aproximadamente 6 s, por lo que se han considerado las prescripciones de esta normativa a la hora de definir los espectros en la zona de periodos elevados, mayores de 4 s. El factor de amortiguamiento es: ξ=4%, para tener en cuenta el pequeño amortiguamiento inherente en estas estructuras [2]. Se adoptan los mismos espectros de diseño en todos los modelos, con independencia de su luz principal.
En los procedimientos basados en la historia de la respuesta (DRHA y MRHA) se requiere la acción impuesta en las cimentaciones en el dominio del tiempo; en este trabajo se han definido acelerogramas sintéticos cuyo espectro es equivalente a los de diseño. Dichas señales sintéticas han sido generadas empleando un algoritmo ad hoc, y validadas por medio de su comparación con las predicciones ofrecidas por modelos empíricos basados en terremotos naturales. En la generación de los acelerogramas se hace variar un ángulo de fase φ para obtener registros independientes entre sí y ajustados al mismo espectro de diseño, imponiendo que la aceleración espectral resultante no sea menor que el 90%, ni mayor del 115% respecto del espectro de diseño en todo el rango de periodos de interés (cumpliendo con el Eurocódigo 8 [19]). Del estudio modal de las estructuras propuestas se ha obtenido el rango [0, 15−35] Hz como intervalo de frecuencias de los modos importantes en la respuesta sísmica de puentes atirantados con luces principales de 200 a 600 m; este rango incluye frecuencias por encima de 10 Hz que serían ignoradas adoptando los rangos propuestos por las normativas sísmicas revisadas, pero que deben tenerse en cuenta por su influencia en el axil sísmico. En la figura 1 se puede apreciar el promedio de los espectros obtenidos con los 12 acelerogramas sintéticos asociados a la acción horizontal en terreno tipo D, destacándose el buen ajuste con el correspondiente espectro objetivo dado por la normativa. La duración total de los acelerogramas es de 20 s, y la intensidad sísmica (intensidad Arias) crece de un modo aproximadamente lineal en el transcurso de los mismos, por lo que se aproximan a la condición de acción estacionaria.
El número mínimo de acelerogramas requeridos por las normativas en el análisis sísmico se encuentra entre 3 o 4 [24], pero la comunidad científica lo suele considerar un número bajo; se ha realizado un estudio de sensibilidad sometiendo un modelo de puente atirantado a 24 acelerogramas sintéticos independientes y de espectro equivalente, verificando que la media de las respuestas obtenidas con 12 registros da un valor suficientemente robusto en todos los esfuerzos sísmicos. Los terremotos se imponen tridimensionalmente pero no se consideran las rotaciones sísmicas impuestas ni efectos de campo cercano. A pesar de la importancia que la variabilidad espacial de la acción sísmica puede tener en los puentes atirantados [1,25], un estudio previo verificó que al considerar la misma acción sísmica en todos los apoyos de los puentes estudiados el error no supera el 20% [21]: la variabilidad espacial no se considera en este trabajo dado que no es dominante en la respuesta y en el diseño de las torres.
En este estudio se realiza el análisis elástico mediante el siguiente esquema, recomendado en puentes atirantados por varios autores [3,5]; a) se obtiene la situación de equilibrio tras la aplicación estática del peso propio, teniendo en cuenta la posible no linealidad geométrica; b) se extraen los modos de vibración a partir de esta configuración deformada, linealizando la respuesta (este paso no es estrictamente necesario en el DRHA); c) se impone la acción sísmica, bien por medio de espectros de aceleraciones (MRSA), o empleando acelerogramas (MRHA o DRHA); en este último caso se repite el análisis con cada uno de los 12 acelerogramas tridimensionales independientes y de espectro equivalente [cada acelerograma tiene 3 componentes: u¨gT(t)=(u¨gX,u¨gY,u¨gZ)]; el cálculo directo considera en este paso la no linealidad geométrica (despreciable según [3]) o de cualquier otro tipo, mientras que los cálculos modales emplean la respuesta linealizada del puente obtenida en el paso anterior, y d) se realiza el post-proceso de los resultados para obtener la respuesta sísmica extrema (suprimiendo el efecto del peso propio); en el cálculo espectral este paso es inmediato, aunque los procesos basados en la historia de la respuesta requieren un estudio de los máximos en cada sección a lo largo del terremoto i-ésimo: ro,i, para luego obtener la respuesta media aritmética: μ=(1/12)∑i=112ro,i. La dispersión de la respuesta sísmica extrema se obtiene por medio de la desviación estándar: σ=(1/12)∑i=112(ro,i−μ)2.
5Comparación entre procedimientos de análisisCada uno de los 35 modelos de puente atirantado propuestos ha sido analizado por medio de los 3 procedimientos de análisis discutidos en la sección 2, comparando la respuesta sísmica extrema (excluyendo los efectos del peso propio) obtenida a lo largo del lateral de las torres que recibe directamente la acción del tablero (lado 1 en la fig. 6b) y de la riostra inferior. Los análisis espectrales (MRSA) se llevan a cabo con 2 criterios a la hora de incluir los modos de vibración: el criterio marcado por las normativas sísmicas y uno más restrictivo, imponiendo que la frecuencia del último modo considerado (flim) sea de 35 Hz (en el cálculo modal dinámico, MRHA, únicamente se adopta esta última opción).
Debido al gran número de modelos estudiados, la figura 4 se limita a mostrar los resultados más destacables. Se incluye la media aritmética de las respuestas (μ) en los procedimientos basados en su evolución en el dominio del tiempo (MRHA y DRHA). No conviene olvidar que dichos procedimientos implican cierta incertidumbre asociada con la acción sísmica, puesto que se imponen acelerogramas de espectro equivalente pero con inevitables variaciones respecto del espectro de diseño dentro de un rango aceptable, como se ha comentado previamente. Con el objetivo de ofrecer una idea de la dispersión, se presenta el promedio de la distancia entre los resultados obtenidos con cada acelerograma y la correspondiente media aritmética a lo largo de la torre en el cálculo MRHA, lo que se realiza a través de una banda sombreada centrada en la media aritmética (μ) y a una distancia igual a la desviación estándar en sentido positivo y negativo ±σ. Se ha observado que tanto MRHA como DRHA presentan típicamente una desviación estándar σ≈10% y que es independiente de la respuesta medida y de la posición de la sección que se está estudiando dentro de la torre. Esto es así siempre que se empleen 12 ternas de acelerogramas sintéticos obtenidos con los criterios de generación presentados en el apartado 4. Por otro lado, en el caso del cálculo espectral (MRSA) no existe dicha incertidumbre asociada a la acción sísmica, puesto que los resultados vienen directamente del espectro de diseño definido unívocamente por la normativa.
Esfuerzos sísmicos extremos obtenidos con distintos procedimientos; cálculo espectral (MRSA) con el número de modos correspondientes al Eurocódigo 8 (EC8), o hasta flim=35 Hz; dinámica directa (DRHA); dinámica modal (MRHA).
(a) Lateral del modelo AD-LCP. LP=200m. Terreno rocoso (TA).
(b) Lateral del modelo YD-LCP. LP=500m. Terreno blando (TD).
(c) Riostra del modelo YD-LCP. LP=600m. Terreno rocoso (TA).
Analizando ahora los valores medios en la figura 4, se observa que el análisis directo normalmente sobrevalora la respuesta en comparación con el cálculo modal dinámico de referencia. El cálculo espectral, por otro lado, ofrece soluciones del lado de la inseguridad en toda la torre. La próxima sección continúa profundizando en estas desviaciones.
El número de modos de vibración considerados en el cálculo espectral, tanto siguiendo las recomendaciones de las normativas (flim≈10 Hz) como imponiendo flim=35 Hz, tiene normalmente una influencia despreciable en la solución, lo cual sugiere que la contribución de los modos con una frecuencia mayor de ≈10 Hz es reducida. Sin embargo, se han observado varias excepciones relacionadas con resultados muy influenciados por la respuesta rígida de las torres: a) el cortante transversal (VY) en el diamante inferior de las torres que poseen este elemento, cuando se trata de puentes con luz principal inferior a 300 m, se incrementa apreciablemente (aproximadamente un 10%) si se incluyen los modos de vibración entre 10 y 35 Hz (para ver la influencia de la luz principal en este sentido basta comparar la fig. 4a con la figura 4b); esto se debe a la mayor importancia de los modos de orden superior causada por la gran rigidez transversal de las pilas formando un diamante, y b) los momentos flectores transversales (MXX) en la parte central de la riostra inferior pueden ser sensibles a los modos de alta frecuencia, probablemente a causa de la reducida esbeltez de este elemento (fig. 4c). Cuando se analizan torres muy rígidas (e.g. estructuras con diamante inferior y luces moderadas), se propone incluir modos hasta una frecuencia máxima de 35 Hz para capturar adecuadamente la flexión transversal. Las torres se deben definir con una malla de elementos finitos suficientemente densa para representar apropiadamente el desplazamiento modal asociado a modos con frecuencias tan altas [18]. La discusión sobre el número de modos de vibración se cierra aquí, continuando con el criterio de imponer flim=35 Hz en todos los resultados asociados a cálculos modales (MRSA y MRHA) presentados en adelante.
El error introducido en el análisis dinámico directo es también mayor si la respuesta se encuentra significativamente influida por los modos superiores, puesto que el error de fase se incrementa cuanto mayor es la frecuencia de la vibración, como pudo observarse en la figura 1. Esto podría explicar el aumento de los errores del método DRHA en términos del axil (N) y cortante transversal sísmico (VY) en modelos con luces principales reducidas.
5.2Promedio de los erroresDebido a la gran cantidad de resultados obtenidos, es conveniente simplificar el estudio de las desviaciones de los mismos; se propone un factor λ que represente el ratio entre la respuesta media (μ) obtenida por medio del análisis directo (DRHA) o del cálculo espectral (MRSA), y el análisis modal dinámico (MRHA) de referencia:
Se asume que el promedio del factor λ a lo largo de la torre es una simplificación aceptable apoyándose en la tendencia uniforme representada en la figura 4:
donde Nelem es el número de elementos en la torre completa, incluyendo tanto sus riostras transversales como sus laterales y la zona de atirantamiento; se ignora el lateral que no recibe la conexión (llamado lado 2 en la fig. 6b) porque sus resultados no son realistas con la conexión simplificada empleada (sección 6).Se ha observado que el error promedio (λ¯*) no está significativamente influido por la luz principal (LP) del puente, dejando al margen el ligero aumento de las desviaciones entre métodos de cálculo al estudiar la flexión transversal de puentes de luz moderada (menor o igual a 300 m), comentado anteriormente. Por tanto, se considera aceptable realizar la media también de las desviaciones obtenidas en las 5 luces estudiadas:
siendo λ¯*|j el error promedio obtenido con la expresión (6), particularizada para puentes de luz j=LP=200 a 600m.La figura 5 recoge los valores de λ¯¯* para todos los modelos estudiados, cimentados en terreno rocoso, considerando los cortantes longitudinales y transversales. Se han obtenido resultados prácticamente idénticos cuando el puente se localiza en terreno blando; este hecho demuestra la influencia marginal del tipo de terreno de cimentación en la precisión de los procedimientos de cálculo cuando la respuesta es elástica, siempre que los acelerogramas empleados sean seleccionados o generados con los mismos criterios sismológicos, siendo especialmente relevante el hecho de que se ajusten al espectro objetivo de un modo adecuado en todo el rango de periodos importantes para la respuesta estructural.
Normalmente los esfuerzos máximos obtenidos con la integración directa (DRHA) son ligeramente superiores a los del cálculo modal dinámico (MRHA), alrededor del 5–10% (λ¯¯DRHA≈1,05-1, 10). Teóricamente, DRHA incluye todos los modos en el análisis, mientras que MRHA ignora las frecuencias superiores a 35 Hz, pero son los errores de fase y no este truncamiento los que explican las desviaciones observadas, puesto que se ha verificado que los resultados apenas varían en el cálculo modal incluyendo modos superiores a 35 Hz. Como excepción, en la fig. 5b se observa que el método directo infravalora la respuesta transversal de referencia, alrededor del 10%, en 2 tipologías especialmente influenciadas por modos de orden superior (según se comprobó en el apartado anterior): a) en puentes con torres en H debido al mayor número de riostras transversales, donde DRHA predice esfuerzos asociados a la flexión transversal menores que MRHA (fig. 4c), y b) en puentes con torres en forma de Y invertida sin diamante inferior, debido a que por sus características geométricas son muy rígidas en dirección transversal [26], lo cual causa su especial sensibilidad a los modos superiores y explicaría, por los errores de fase, el deterioro de los resultados en el método dinámico directo, DRHA.
El análisis espectral (MRSA) conduce a esfuerzos sísmicos que generalmente son inferiores a los del cálculo modal dinámico (MRHA), debido a errores introducidos por a las reglas de combinación de los máximos modales (sección 2.3), quedando las desviaciones en el lado de la inseguridad con valores que oscilan entre el 10 y el 20% (λ¯¯MRSA≈0.83). Este error es similar al observado por Walker y Stafford [12] en los coeficientes de correlación de la regla CQC, y concuerda con el que reporta Chopra [6] en estructuras de edificación. Al igual que fue observado en el procedimiento de integración directa, se registran mayores desviaciones del cálculo espectral respecto del modal dinámico cuando se estudian variables asociadas a la flexión transversal de las torres con forma de H e Y invertida sin diamante. Esto podría deberse de nuevo a que el comportamiento de ambas tipologías se encuentra más influido por modos de orden superior: las fluctuaciones entre frecuencias próximas son mayores en esta zona del espectro debido a las condiciones de generación de los acelerogramas, y por tanto se separa más de las condiciones ideales asumidas por la regla CQC [6,12]. No obstante, debe tenerse en cuenta que los esfuerzos sísmicos (axil y momentos flectores) suelen emplearse en la verificación seccional por medio de diagramas de interacción; en el cálculo espectral se pierde la información de la respuesta en el dominio del tiempo, y se suele considerar que los esfuerzos máximos causados por el terremoto son concomitantes, esto es, que se obtienen en el mismo instante. Esta suposición es errónea pero está del lado de la seguridad, y se ha observado en este estudio que la diferencia puede llegar a ser del 20%, pudiendo por tanto compensar el error en la obtención de los esfuerzos sísmicos por parte del cálculo espectral.
5.3Coste computacionalLa tabla 1 presenta el tiempo de cálculo (CPU) requerido para obtener la respuesta media (μ), en varios modelos cimentados en terreno blando (se han obtenido resultados análogos en terreno rocoso). Se ha empleado en el estudio un ordenador que puede estar disponible en cualquier oficina de proyectos de tamaño pequeño o grande (3 GB de memoria RAM, procesador 2,40 GHz). Debe tenerse en cuenta en la tabla 1 que se requieren 12 análisis independientes para obtener la respuesta media en los procedimientos basados en la historia del comportamiento estructural (MRHA y DRHA), mientras que se necesita un único análisis en el cálculo modal espectral (MRSA). Se verifica que el tipo de torre, de atirantamiento y de terreno de cimentación no influyen apenas en el tiempo de cálculo.
El cálculo espectral es incomparablemente más rápido que los otros 2. Además, los requerimientos de espacio para almacenar la información obtenida y los esfuerzos de post-proceso son mucho menores en el cálculo espectral, representando otra gran ventaja de este procedimiento que normalmente inclina la balanza a su favor frente a otras estrategias de análisis. Por otro lado, el coste computacional del método directo es del orden de 12 veces mayor que el del cálculo modal dinámico, debido a la integración del sistema de la dinámica completo y acoplado (1).
6Conexión entre torres y tableroSiguiendo la tendencia actual en el diseño de puentes atirantados en zona sísmica, la conexión entre torre y tablero se dispone como «flotante», relacionando exclusivamente su desplazamiento transversal (Y) y liberando el resto; este es el caso del puente Rion-Antirion en Grecia, entre otros. Normalmente esta conexión se realiza por medio de salientes unidos a los laterales de la torre y del tablero, que se separan entre sí una mínima distancia δc (obtenida por medio de un panel de poliestireno expandido, u otro material ligero, durante el hormigonado), lo cual evita impactos importantes en dirección transversal y asegura el libre movimiento relativo en dirección vertical y longitudinal. Durante el terremoto el tablero ejerce primero su acción en uno de los laterales, por ejemplo el lado 1 en la figura 6, mientras el lado opuesto está libre de esta acción directa, acto seguido el tablero ejerce su empuje directamente en el lado 2 y así sucesivamente. La simulación realista de esta conexión requiere la definición de contactos entre torre y tablero (fig. 6a), lo cual lleva a métodos de cálculo inherentemente no lineales (incluso permaneciendo los materiales en rango elástico), y por tanto impide utilizar procedimientos de análisis basados en la descomposición modal (MRHA o MRSA). Para evitarlo, se ha propuesto la conexión simplificada representada en la fig. 6b (empleada en la sección anterior); el tablero se une rígidamente a uno de los laterales (lado 1) mientras que la acción del mismo nunca se ejerce directamente en el lado opuesto (lado 2).
En el modelo numérico, ambas conexiones se realizan de la siguiente manera: a) en la simulación realista, el posible contacto entre los elementos tipo «viga»de los laterales de las torres y del tablero se define por medio de elementos tipo gap[18] que únicamente relacionan el movimiento transversal (Y), permitiendo una definición eficaz y robusta del mismo, y b) la conexión simplificada se ha representado por un muelle que actúa únicamente en dirección transversal (Y). En ambos casos se ha asumido una rigidez muy elevada para transmitir la fuerza del tablero al lateral de la torre, correspondiente a la deformabilidad axial del saliente, definido como un bloque de hormigón de 1 m2 de sección transversal y 1 m de profundidad: k=Ec=3.5 GN/m (siendo Ec el módulo de elasticidad del hormigón), y por tanto puede asumirse la conexión como «rígida». En esta sección se emplea el procedimiento dinámico directo (DRHA) en todos los casos, puesto que es el único que permite el estudio de los modelos con la conexión realista, que incluye contactos.
En la figura 7 se presenta el promedio (μ) del máximo cortante transversal sísmico a lo largo del lado 1, empleando las conexiones descritas en la figura 6 en uno de los modelos propuestos; se ha considerado nula la abertura inicial entre los salientes (δc=0) para evitar problemas numéricos, lo cual se acerca a la solución real de proyecto. Queda claro que los resultados obtenidos con ambas conexiones son muy similares en el lado 1 de la torre. Es destacable que el máximo empuje del tablero en las torres debido al sismo, responsable del pico en la distribución de cortantes transversales (correspondiente a la altura adimensionalizada z*≈0.32), es muy parecido con ambas conexiones. Se han obtenido resultados similares en otros puentes atirantados. Por tanto, la conexión simplificada (fig. 6b) se recomienda en el estudio sísmico de puentes atirantados con esta relación flotante entre torre y tablero, empleando en el diseño únicamente los resultados obtenidos en el lado 1 (en el lado 2 la respuesta no es realista) y en las riostras transversales. En los modelos con la conexión torre-tablero realista se ha verificado que la respuesta sísmica en el lado 2 es muy similar a la del lado 1, como se había previsto debido a la simetría del problema, por lo que conociendo esta última se obtiene la respuesta total de la torre.
Cortante transversal sísmico extremo VY en el lado 1, obtenido con las estrategias de conexión propuestas en la figura 6. Integración directa (DRHA).
Se ha contrastado el comportamiento sísmico elástico de una gran cantidad de puentes atirantados por medio de varios métodos de cálculo, obteniendo conclusiones valiosas para el diseñador a la hora de seleccionar el procedimiento de análisis adecuado y definir la conexión entre el tablero y las torres:
- •
Los esfuerzos sísmicos obtenidos por medio del análisis espectral quedan del orden de un 20% del lado de la inseguridad respecto de los del cálculo modal dinámico de referencia, aunque en una segunda etapa del análisis (e.g. verificación de la resistencia de secciones por medio de diagramas de interacción) se pueden compensar estos errores por medio de combinaciones de cargas que están del lado de la seguridad. El cálculo espectral es la forma más rápida y directa de obtener los valores máximos de la respuesta, lo que le convierte en el procedimiento más recomendable en la fase de diseño de puentes atirantados con menos de 600 m de luz, sin dispositivos sísmicos y que se comporten en rango elástico. No obstante, debería verificarse el diseño final de la estructura por medio del análisis modal dinámico, como mínimo con 12 acelerogramas tridimensionales independientes.
- •
El criterio del Eurocódigo 8 [19] para seleccionar el número de modos de vibración incluidos en los procedimientos basados en la descomposición modal ha sido validado en puentes atirantados por debajo de 600 m de luz, excepto si se pretende analizar el cortante o el flector transversal de las torres con diamante inferior y luces moderadas (por debajo de 300 m), donde se recomienda incrementar el número de modos considerados en el análisis hasta que se alcance una frecuencia de 35 Hz.
- •
El método de integración directa del sistema de la dinámica ofrece resultados muy próximos a los de la dinámica modal, excepto en el estudio de torres con forma de H o Y invertida, donde las diferencias son ligeramente superiores. El elevado coste computacional del método directo hace que no se aconseje su uso en puentes atirantados sin dispositivos sísmicos cuya respuesta se prevea elástica. Si se pueden producir impactos en la conexión trasversal entre la torre y el tablero, en el diseño de la torre se recomienda modelizar dicha unión por medio de un elemento rígido que conecte el tablero y un lado de la torre.
- •
La precisión de los distintos métodos de análisis elástico es independiente del tipo de terreno de cimentación, incluso en el caso de que existan grandes diferencias entre las ordenadas espectrales de sus espectros de diseño, siempre que se empleen acelerogramas sintéticos generados con los mismos criterios de ajuste al espectro correspondiente. El tipo de atirantamiento (central o lateral) y la luz principal del puente no son muy relevantes en cuanto a la precisión de los procedimientos de análisis en rango elástico. En cambio, la forma de la torre puede tener influencia; cuanto más rígida es su respuesta, peores resultados son esperables en el análisis dinámico directo y en el cálculo modal espectral.