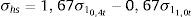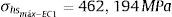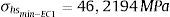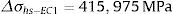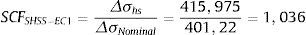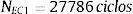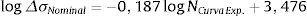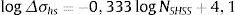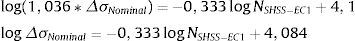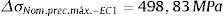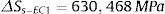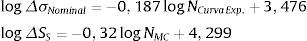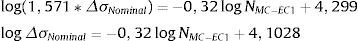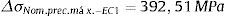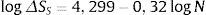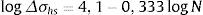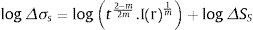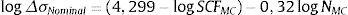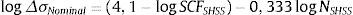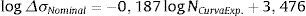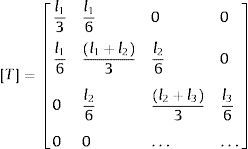Este artigo apresenta um estudo dos métodos da tensão estrutural hot spot e do método da curva mestre (Battelle) para a determinação da vida à fadiga de uma junta soldada do tipo T. Ambos os métodos utilizam o conceito de tensão estrutural, determinada, normalmente, através de modelos de elementos finitos. Utilizando diferentes tipos de modelos de elementos finitos de casca, os resultados obtidos pelos 2 métodos foram comparados com os obtidos experimentalmente, verificando‐se diferenças significativas entre os métodos. Os níveis de carregamento influenciaram decisivamente na precisão de ambas as metodologias, sendo que, para o caso em estudo, o método hot spot demonstrou ser mais preciso. O maior diferencial constatado para o método de Battelle foi a correção do parâmetro da tensão estrutural, visto que, sem essa correção, as tensões no pé da solda foram muito similares às obtidas pelo método hot spot. Comparando a curva mestre de comportamento à fadiga do método de Battelle com a curva do método hot spot, ambas em função da tensão nominal aplicada no ensaio, verificou‐se que o método hot spot é conservador. Para os diferentes modelos numéricos estudados, apenas uma técnica de modelagem forneceu resultados dispersos das demais. Pelo método de Battelle, o comportamento da componente de flexão da tensão variou consideravelmente de um modelo para o outro, denotando que, sobre um carregamento mais complexo, poderá haver uma variabilidade maior na vida à fadiga calculada.
This paper presents a study on the structural hot spot stress method and the master curve method (Battelle) for evaluating the fatigue life of a T‐shaped welded joint. Both methods are based on the concept of structural stress, which is usually determined using finite element models. Using different types of shell finite element models, the results obtained by the two methods were compared to experimental data, verifying significant differences between the studied methods. The loading level had a great deal of influence over the accuracy of both methodologies, but on the other hand the hot spot method revealed to be more precise for the analyzed joint. The main differential for the Batelle method was the correction of the stress amplitude into an equivalent structural stress parameter, since, without this correction, the stresses on the weld toe were very similar between the Battelle and the hot spot methods. Comparing the master curve for the fatigue behavior of the Battelle method to the fatigue curve of hot spot method, with both curves expressed in terms of the nominal stress applied in the experiment, it was verified that the hot spot method is conservative. Among the different modeling techniques used, only one provided results that are not in agreement with the others. Using the Battelle method, the behavior of the bending stress component varied considerably according to the employed numerical model, indicating that can be a greater variability in the expected fatigue life for joints under more complex loading configuration.
Carregamentos cíclicos são capazesde causar a falha de um elemento estrutural em níveis de tensões inferiores ao limite de resistência do material, estando presente em 90% dos casos de falha [1].
A vida à fadiga de uma estrutura é governada pelo comportamento à fadiga de suas juntas [2]. O cálculo da vida em fadiga de uma junta soldada baseia‐se na comparação da geometria e direções de carregamento do caso estudado com uma série de classes de juntas amplamente ensaiadas e padronizadas, selecionando‐se então a curva de fadiga correspondente. Esta comparação pode ser feita de forma global, através da tensão nominal, ou sob um aspecto local, onde efeitos localizados do carregamento são mensurados de forma mais precisa junto ao parâmetro de tensão do diagrama S – N (tensão – número de ciclos), diminuindo‐se, dessa forma, o número de classes normatizadas.
A utilização de ferramentas de modelagem numérica como o método de elementos finitos (MEF) é uma poderosa aliada na determinação de aspectos localizados da junta, possibilitando a aplicação de métodos de análise local no cálculo da vida à fadiga. No entanto, a utilização da técnica de modelagem apropriada torna‐se extremamente importante [3].
A fim de contornar alguns aspectos problemáticos de abordagens locais, em 2001, a comissão XIII do International Institute of Welding (IIW) publicou um guia de utilização de uma abordagem denominada Structural Hot Spot Stress (SHSS), com recomendações para sua utilização a partir de instrumentação da junta ou a partir de ferramentas numéricas como o MEF. O método consiste em obter a tensão na região considerada crítica da junta (pé da solda) a partir da extrapolação de tensões nas regiões vizinhas ou pela linearização de tensões ao longo da espessura [4].
Dong [5], utilizando o MEF como ferramenta, publicou uma abordagem alternativa denominada VerityTMMesh – Insensitive Structural Stress Method (VMISS), onde em vez de se obter a tensão no pé da solda por extrapolação das tensões na região vizinha, a mesma é obtida analiticamente a partir de forças e momentos dados por condições de equilíbrio. Isso permite obter um estado de tensões de membrana e de flexão independente da geometria do cordão ou do nível de discretização do modelo do MEF utilizado para representar a junta. Além disso, o autor sugere, a partir de fatores de correção baseados em conceitos da mecânica da fratura, uma modificação do parâmetro de tensão do diagrama S – N, obtendo uma tensão estrutural equivalente. Com essa modificação, seria possível estabelecer uma faixa de probabilidades do comportamento à fadiga que abrangeria todos os tipos de juntas. Esse diagrama modificado foi nomeado como Master Curve (MC).A aplicação do VMISS em conjunto com o MC compreende o método de Battelle para o cálculo da vida à fadiga.
Com o objetivo de avaliar essa nova metodologia proposta por Dong [5], propõe‐se a comparação da vida calculada pelo método de Battelle e pelo método SHSS, para diferentes modelos de elementos finitos de casca, com os resultados obtidos de uma junta T ensaiada experimentalmente.
2Métodos da tensão estruturalDada a complexidade envolvida na análise de vida em fadiga de estruturas soldadas, esse assunto vem sendo abordado por diversos autores [5–9]. Diversas metodologias são desenvolvidas e normas internacionais são constantemente atualizadas, com o propósito de contrabalançar a minimização de riscos no projeto de um elemento estrutural soldado, com a minimização de custos exigida pelo ambiente industrial altamente competitivo [10].
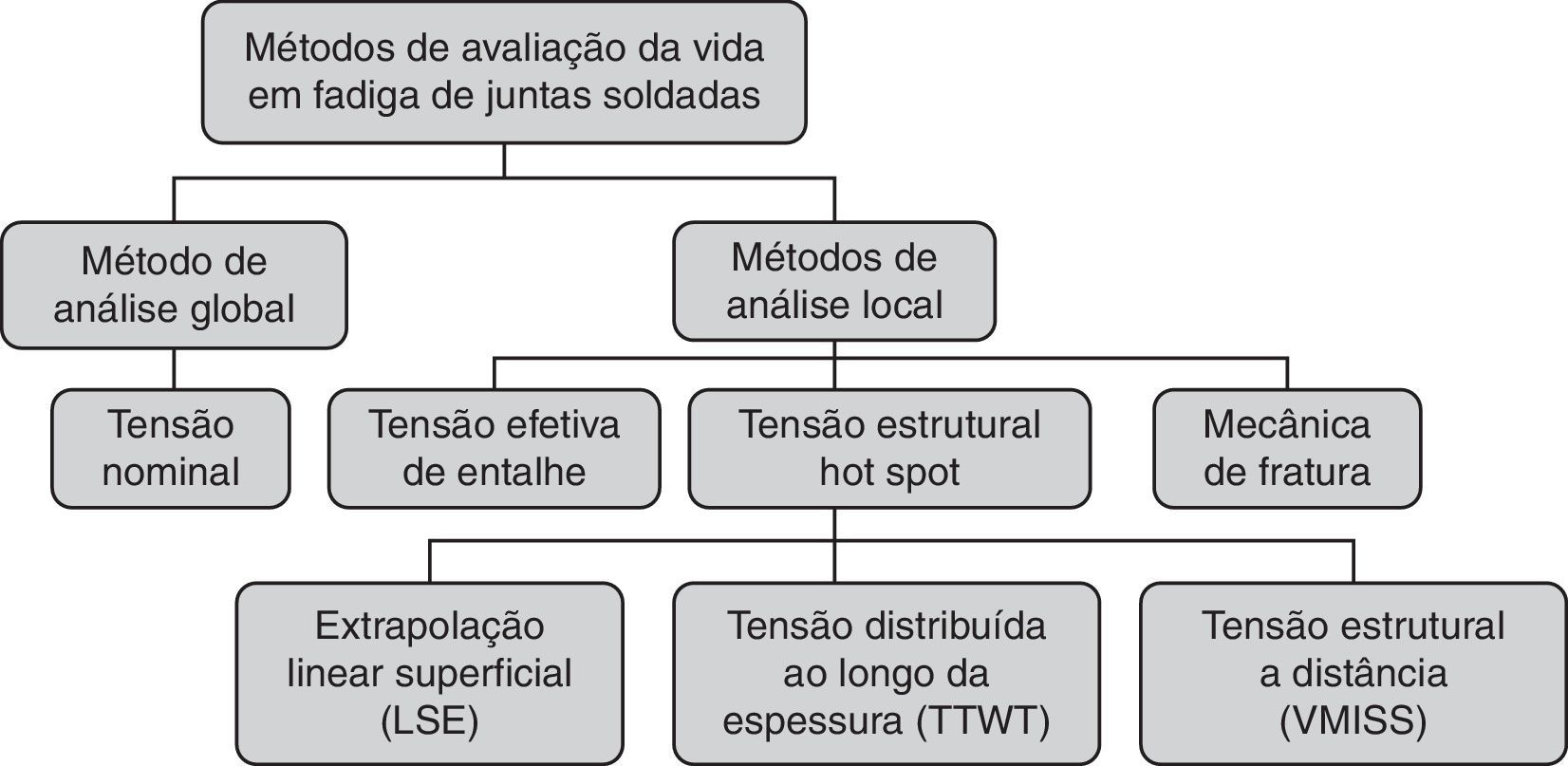
Aygül [3] classifica os diversos métodos de avaliação de vida à fadiga em 2 grandes grupos: métodos de análise global e métodos de análise local. A abordagem global consiste no método da tensão nominal. Métodos como o da tensão efetiva de entalhe, tensão estrutural hot spot e mecânica da fratura, são considerados abordagens locais.
Poutiainen et al. [4] dividem o método da tensão estrutural hot spot em Linear Surface Extrapolation (LSE), Through Thickness at the Weld Toe (TTWT) e VMISS. A figura 1 esquematiza a classificação dos métodos de análise da vida à fadiga. Os 2 primeiros são os utilizados pelo IIW.
Marin e Nicoletto [11] apontam que o VMISS pode ser considerado, também, uma abordagem intermediária entre a global e a local. De qualquer forma, tanto o VMISS como o LSE aplicam‐se adequadamente para o cálculo da tensão estrutural em juntas T como a do presente estudo, onde a tensão principal é perpendicular ao pé da solda e esta, por sua vez, é a região mais provável de nucleação da trinca de fadiga.
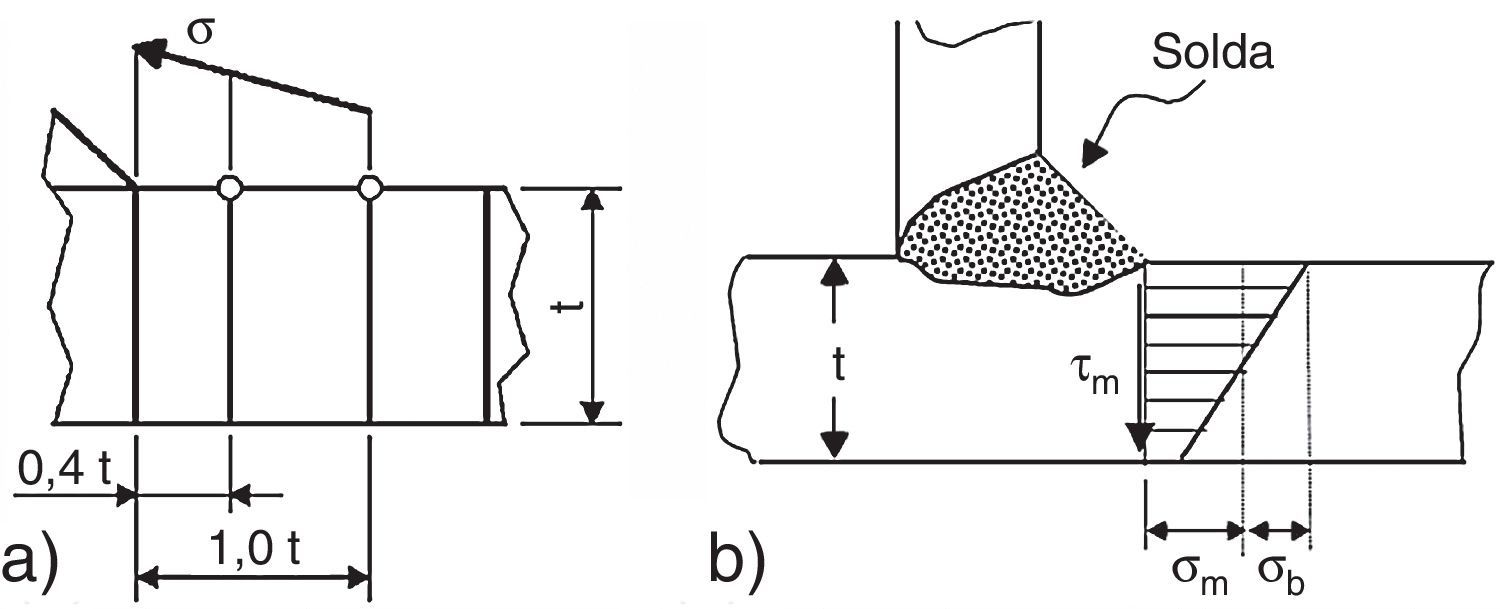
2.1Tensão estrutural hot spot pelo método da extrapolação linear superficialDentre os vários procedimentos para cálculo da tensão estrutural hot spot existentes na literatura, o mais típico é baseado em uma extrapolação linear superficial dos valores de tensão a 0, 4t e 1t de distância do pé da solda, onde t representa a espessura de chapa do membro carregado, conforme ilustra a figura 2(a). O método é válido para diversos detalhes estruturais, desde que o carregamento seja perpendicular ao eixo longitudinal da solda e o início da trinca esperada ocorra no pé da solda [12].
De acordo com Niemi et al. [13], curvas S – N elaboradas através do conceito da tensão estrutural hot spot são expressas da mesma forma que as curvas da tensão nominal, ou seja, os diferentes tipos de juntas são enquadrados em uma classe numerada de acordo com a amplitude de tensões (em N/mm2 ou MPa) para uma vida em fadiga de 2×106 ciclos. Contudo, nesse caso, o valor refere‐se à amplitude da tensão hot spot Δσhs. Como a tensão hot spot já engloba efeitos locais da junta, a quantidade de classes e curvas normatizadas torna‐se consideravelmente menor. A vida à fadiga, nesse caso, é descrita pela equação (1) e o comportamento da curva pode ser observado em [13]
onde, Δσhs = amplitude da tensão hot spot; N=número de ciclos até a falha; m= inclinação da curva S – N; C=valor de projeto da capacidade à fadiga da junta normatizada.Levando‐se em conta que a definição de tensão estrutural é a mesma independente do método de obtenção (LSE ou TTWT), a mesma curva S – N poderá ser utilizada para o cálculo da vida em fadiga [12].
O comportamento da tensão junto ao pé da solda varia conforme o tipo de junta e carregamento, demandando diferentes maneiras de extrapolação, o que caracteriza uma das grandes desvantagens do método. Além disso, como demonstraram Poutiainen et al. [4], para alguns casos, o método da tensão estrutural hot spot é altamente sensível ao tipo de malha de um modelo de elementos finitos. A fim de contornar essas adversidades, Dong [5] propôs uma abordagem diferenciada para o cálculo da tensão estrutural. Em vez de ser obtida por extrapolação junto ao pé da solda, a tensão é calculada a partir dos esforços internos do modelo de elementos finitos.
2.2Método de BattelleUtilizada a partir do MEF, a abordagem VMISS caracterizou‐se por sua insensibilidade quanto ao tamanho e tipo de elementos da malhana simulação numérica de estruturas simples, definindo um diferente conceito de tensão estrutural hot spot: «tensão estrutural insensitiva à malha» [5].
Dong [5] propõe 2 métodos gerais para cálculo da tensão estrutural, através de modelos de casca: (1) utilizando tensões resultantes a partir de um plano afastado ou (2) utilizando esforços nodais dos elementos localizados no pé da solda.
Utilizando a segunda abordagem descrita acima, os esforços internos na região do pé da solda do modelo são obtidos através das condições de equilíbrio. Posteriormente, os valores de tensão são relacionados com os valores dos esforços obtidos, caracterizando um parâmetro insensitivo à malha utilizada. Para modelos de casca, a tensão estrutural é obtida diretamente das forças e dos momentos nodais (F e M) e, para modelos sólidos, é obtida através da linearização da tensão através da espessura da chapa.
Doerk et al. [12] corroboram ao afirmar que, para modelos em casca, a tensão estrutural pode ser avaliada diretamente na região do pé da solda, uma vez que, nesses casos, já é assumida uma distribuição linear da tensão para os elementos. A aplicação do VMISS, por sua vez, torna‐se bastante prática.
Os esforços e momentos nodais (F e M) são transformados em esforços e momentos lineares (f e m) através do produto matricial expresso por Dong [5] nas equações (2) e (3), onde T−1 representa a inversa da matriz das funções de interpolação [T], Appendix A, do elemento de casca utilizado.
Esse produto matricial surge do conceito de que o trabalho realizado pelas cargas distribuídas nos campos de deslocamentos deve ser equivalente ao trabalho dos esforços nodais nos deslocamentos nodais. Para um elemento de casca linear (4 nós), as forças e momentos serão linearmente distribuídos na lateral do elemento.
A partir dos esforços e momentos linearmente distribuídos (f e m), a tensão estrutural σs e suas componentes de membrana σm e de flexão σb, ilustradas na figura 2(b), podem enfim ser calculadas a partir da teoria elementar da mecânica estrutural [15], conforme equação (4)
Na equação (4), fy corresponde ao esforço axial linearmente distribuído na direção de um eixo coordenado y (normal ao pé da solda) e mx corresponde a um momento linearmente distribuído em relação a um eixo coordenado x (na direção do pé da solda).
2.2.1Abordagem da curva mestreA existência de diversas curvas S–N para o cálculo da resistência à fadiga pelo método da tensão nominal e pelo método da tensão hot spot deve‐se à consideração da variação da espessura, geometria e tipo de carregamento. Em alguns casos, também deve ser feita a correção da curva para aspectos não previstos [2].
A definição de um parâmetro de tensão estrutural equivalente ΔSS, expresso pela equação (5), para a definição de uma curva de resistência à fadiga permite considerar, além da amplitude de tensão aplicada, a configuração da junta e efeitos da espessura. Assim, uma única curva (associada a uma faixa de probabilidades) pode descrever o comportamento de diversos detalhes estruturais soldados. Caracteriza‐se então a «curva mestre»[5]
A interpretação da equação (5) pode ser feita da seguinte forma: o termo Δσs corresponde à amplitude da tensão estrutural (σs) calculada pela equação (4), o termo t2−m2m corresponde à correção devido ao efeito da espessura e o termo Ir1m corresponde à correção devido ao modo de carregamento [16]. A constante m=3, 6 representa a declividade expressa no gráfico da lei de Paris [11,17].
Alguns princípios da mecânica da fratura linear elástica (MFLE), como a lei de Paris e o fator de intensidade de tensão K, foram fundamentais na determinação desse parâmetro, capazes de descrever o comportamento à fadiga em função de sua variabilidade estatística expressa pela equação (6), ilustrada em Selvakumar e Hong [15]
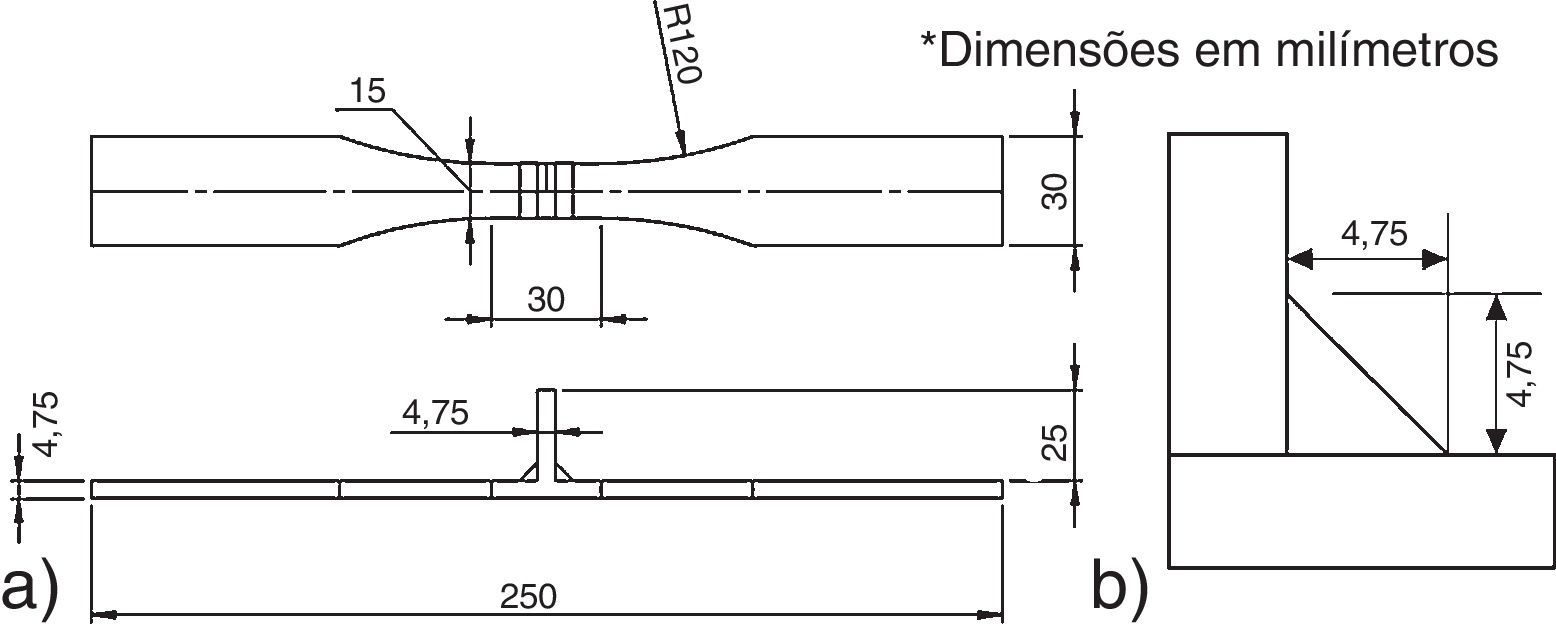
onde, C=constante determinada pela probabilidade de falha; h=0,32 (coeficiente angular da curva mestre).3Descrição do modelo em estudo3.1Descrição geral do ensaio da juntaA junta estudada, fabricada em aço ASTM A514 de alta resistência e baixa liga (ARBL), com tensão de escoamento Sy=743MPa, está ilustrada na figura 3. A mesma foi confeccionada segundo critérios normatizados na ASTM E466 e ensaiada sob carga cíclica do tipo push pull, com freqüência 10Hz e amplitude constante e razão de tensão R=0, 1 [18].
Geometria de junta T ensaiada. (a) Dimensões da junta. (b) Detalhe do cordão de solda [18].
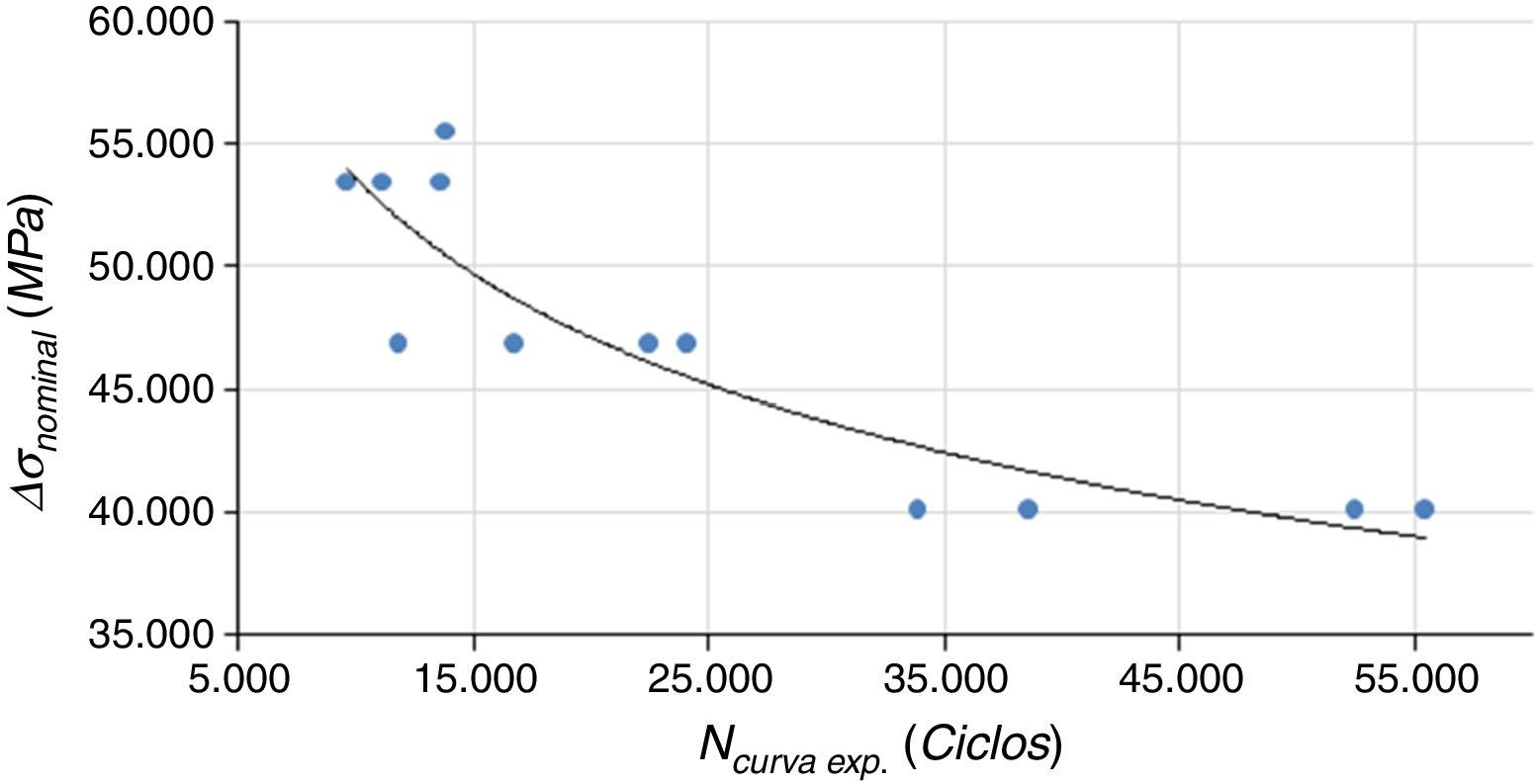
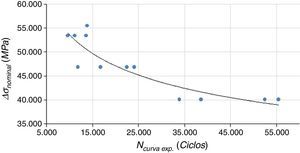
O ensaio foi realizado no laboratório da Universidade de Passo Fundo (UPF), com temperatura controlada em 20° sob 3 níveis distintos de tensão máxima (60, 70e80%Sy). Os resultados experimentais foram tratados estatisticamente, obtendo‐se a curva S–N ilustrada na figura 4, que descreve a resistência à fadiga da junta através da equação (7) [18]
3.2Descrição dos modelos numéricosO processo de modelagem, com o software Ansys 13.0, foi realizado a partir de técnicas exploradas nos trabalhos de [3,11,13,19,20]. Modelos em casca vêm sendo amplamente utilizados e, segundo Dong e Hong [14], se adaptam muito bem ao método de Battelle. Atenção especial deve ser dada, no entanto, às simplificações exigidas para esse tipo de modelagem.
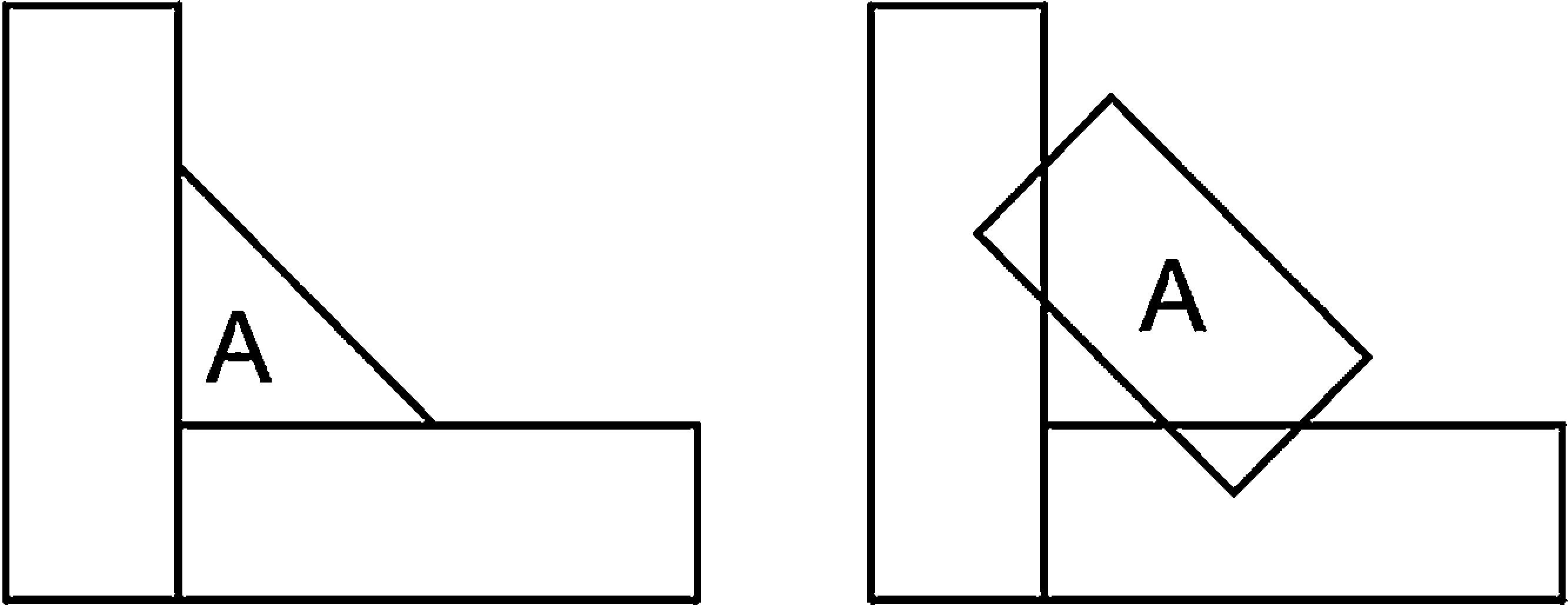
Segundo Aygül [3], modelos em casca podem ser elaborados com ou sem a representação do cordão de solda. Já Marin e Nicoletto [11] salientam o papel da modelagem do filete de solda na correta representação da rigidez da junta, além de algumas estratégias de representação, ilustradas na figura 5, para diferentes tipos e penetrações de cordão. Para juntas de penetração total, a intersecção entre as chapas deve ser representada, conforme figura 5(a) e (c). Além disso, soldas simétricas devem ter seu cordão representado de forma simétrica, conforme figura 5(c) e (d).
Representação numérica da penetração de solda. (a) Penetração total com solda assimétrica (PTSA). (b) Penetração parcial com solda assimétrica (PPSA). (c) Penetração total com solda simétrica (PTSS). (d) Penetração parcial com solda simétrica (PPSS) [11].
De acordo com Niemiet al. [13] e Dong [5], o método SHSS e de Battelle são aplicáveis a juntas nas quais o maior potencial de ruptura por fadiga se dê no pé da solda, ou seja, condição mais provável em juntas com penetração total. Por se tratar de junta T com solda simétrica, adotou‐se a configuração PTSS ilustrada na figura 5(c). A partir dessa definição inicial, existem diferentes possibilidades para a representação do cordão de solda.
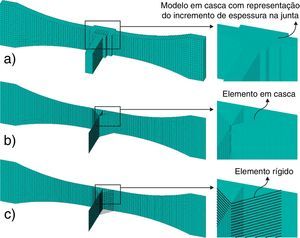
Segundo Aygül [3], a representação do cordão de solda pode ser dada através de elementos rígidos (ER), elementos em casca (EC) ou incremento de espessura (IE). Para modelos do tipo ER e EC, Echer [20] sugere, ainda, 3 técnicas distintas.
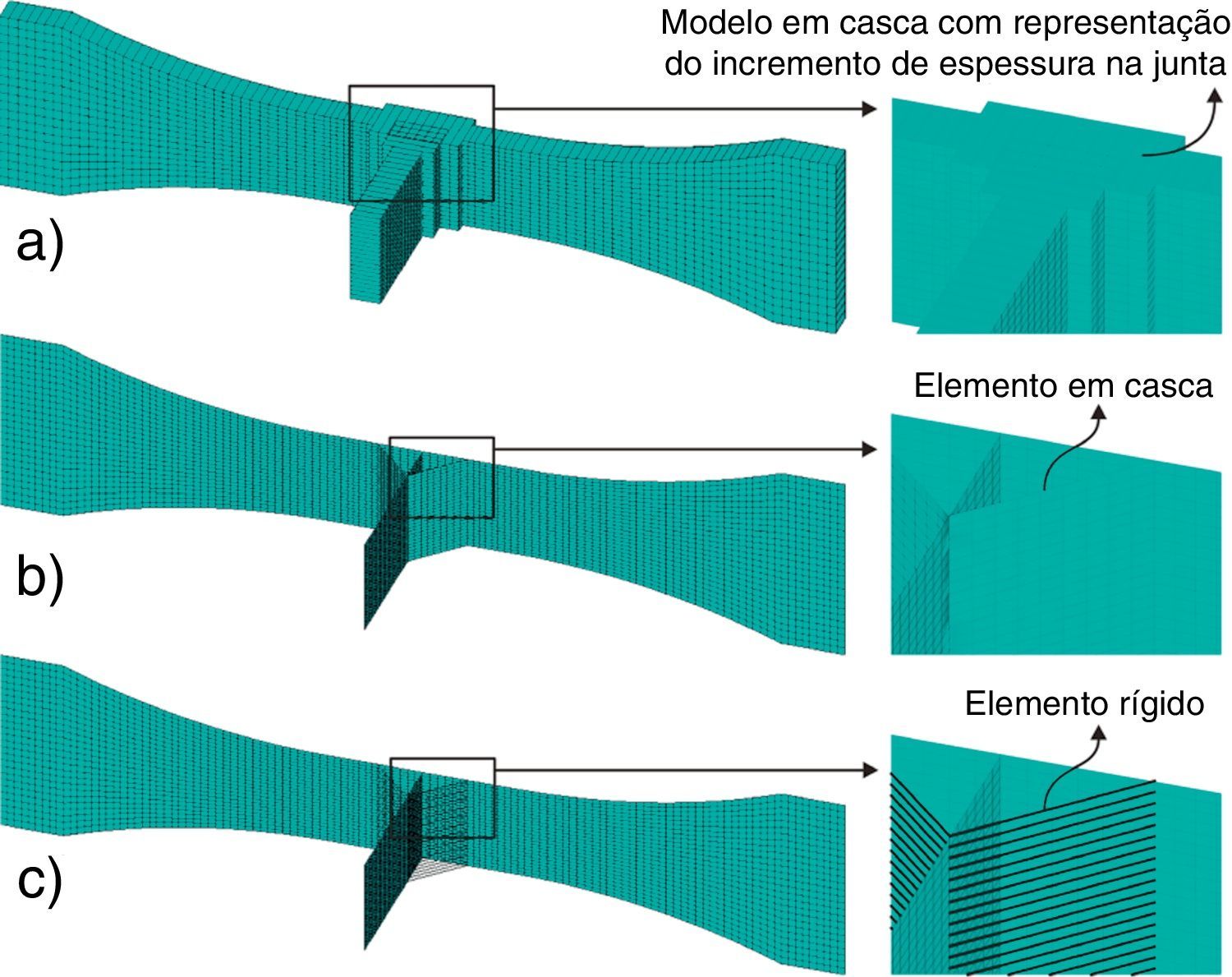
3.1Modelagem numérica de junta com penetração total e solda simétricaA representação do tipo IE, ilustrada na figura 6(a), é a atribuição de um elemento de casca com valor de espessura maior na região de intersecção do cordão de solda. Utilizou‐se, para tanto, a técnica explorada por Aygül [3].
A representação do tipo EC, ilustrada na figura 6(b), consiste em simular o cordão de solda por elementos de casca oblíquos. Recomendada por Niemi et al. [13], essa técnica permite uma representação correta tanto da geometria como da rigidez, mas não deve ser utilizada na previsão de falhas nucleadas a partir da raiz da solda.
A representação do tipo ER consiste em simular o cordão de solda por uma série de elementos unidimensionais oblíquos paralelos entre si, onde cada elemento conecta um nó da chapa principal com um nó da chapa anexa. Os elementos unidimensionais utilizados foram elementos de viga rígidos. O espaçamento entre cada ER será igual à dimensão do EC no qual ele se encontra conectado, conforme figura 6(c).
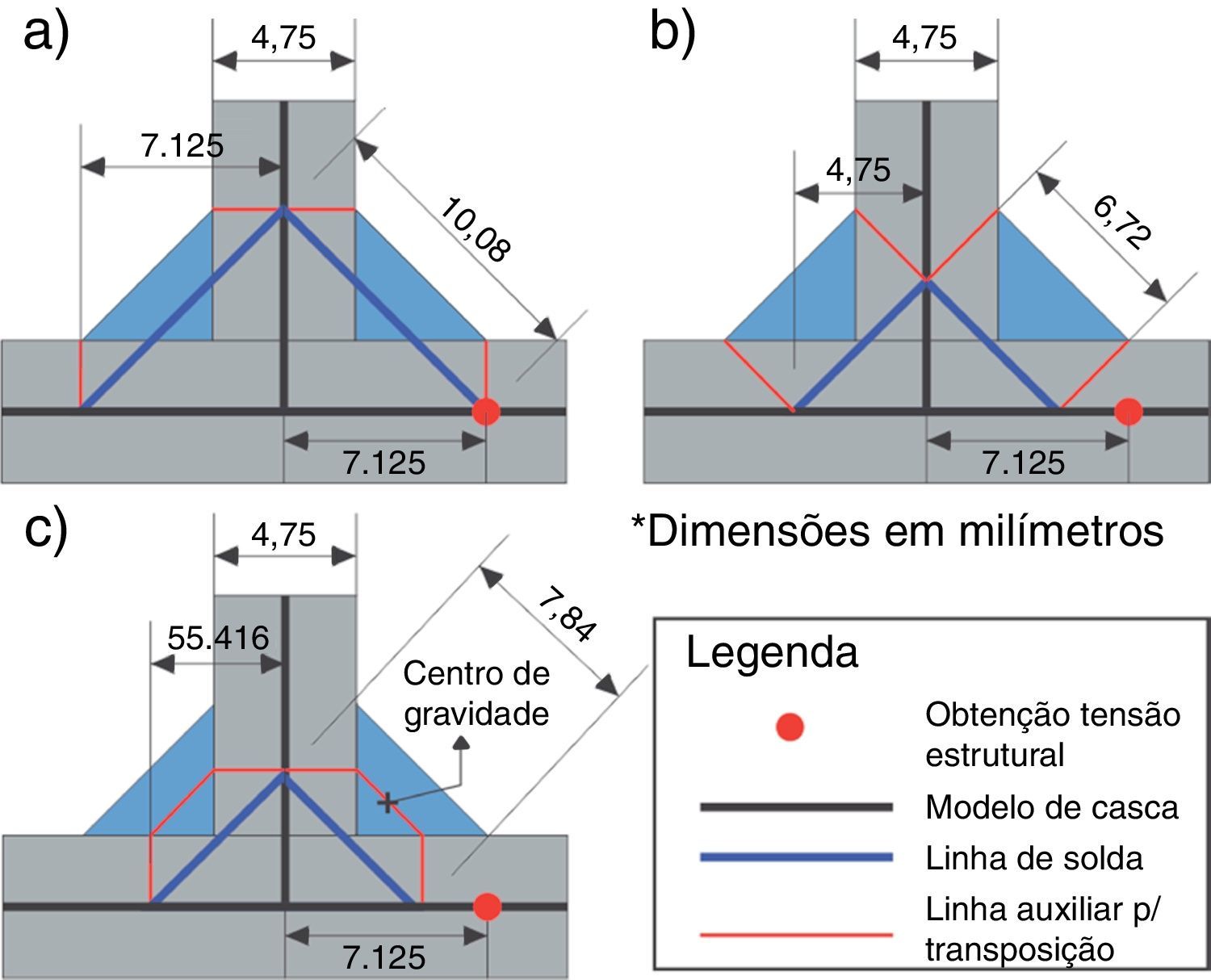
Como mencionado, na modelagem da solda por EC e ER, 3 técnicas exploradas no trabalho de Echer [20] foram utilizadas. As técnicas consistem em posicionar o elemento representativo da solda em 3 diferentes pontos da junta, sem alterar o ponto de obtenção da tensão estrutural, correspondente à projeção do pé da solda de um modelo sólido, como ilustra a figura 7.
Técnicas de representação do cordão de solda em ER e elementos em casca. (a) ER1 ou EC1. (b) ER2 ou EC2. (c) ER3 ou EC3 [20].
Em ER1 ou EC1, a representação do cordão de solda é posicionada de tal forma que sua intersecção com a representação do metal base coincida com o ponto de obtenção da tensão estrutural. Em ER2 ou EC2, a representação do cordão de solda é posicionada de tal forma que sua dimensão coincida com a dimensão do cordão de solda de um modelo sólido. Finalmente, em ER3 ou EC3, a representação do cordão de solda é posicionada de tal forma que sua intersecção com a representação do metal base se dê na projeção de um elemento que passa através do centro de gravidade do cordão de solda de um modelo sólido. A figura 7 ilustra as 3 representações com suas medidas principais [20].
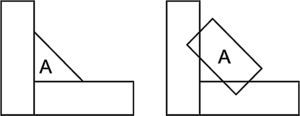
Na definição da espessura dos EC do cordão de solda manteve‐se a área da secção transversal do cordão de solda original (A). Como estes apresentam secção transversal retangular, a espessura do elemento correspondeu à área da secção transversal do cordão original dividido pelo comprimento da garganta de filete obtido em cada uma das técnicas, conforme ilustrado na figura 8.
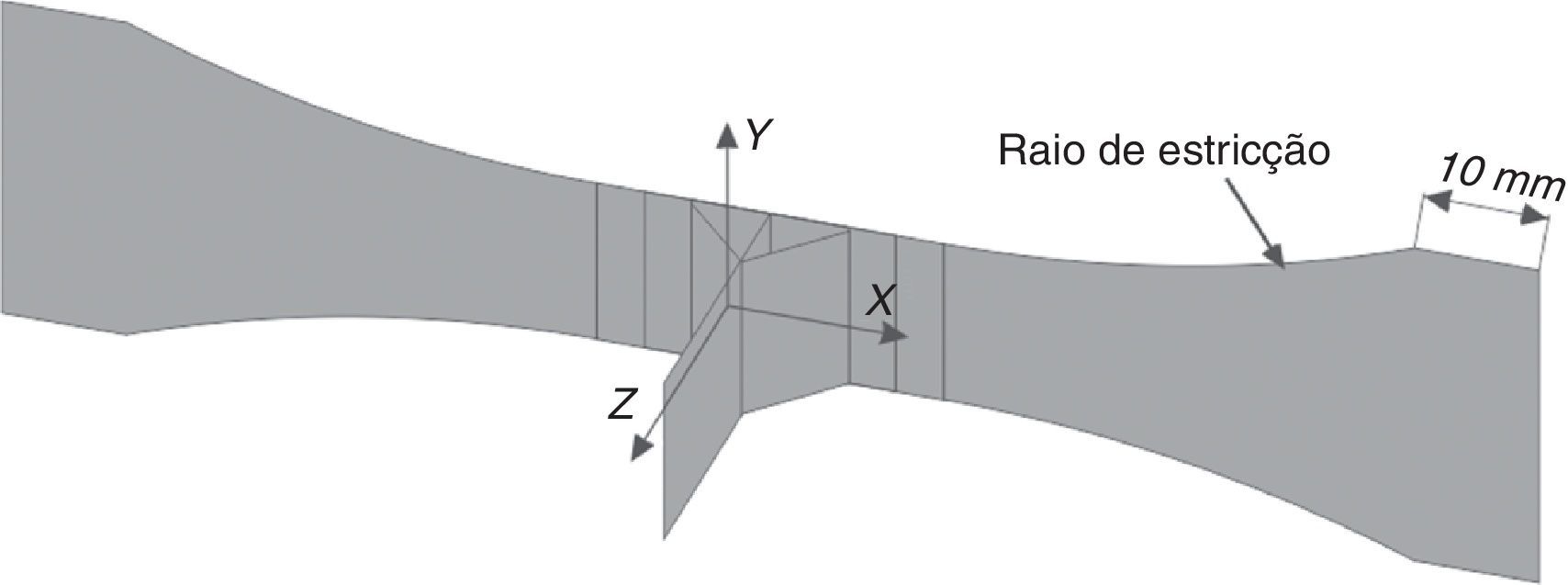
3.2Modelagem numérica da junta T e do ensaioA junta foi modelada centralizada sobre a origem do sistema de referência global, com seu eixo longitudinal na direção do eixo coordenado X e o eixo transversal da chapa principal na direção do eixo coordenado Y.
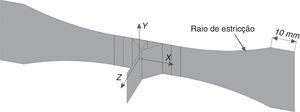
O posicionamento dos corpos de prova na máquina de ensaio de fadiga respeitou o limite imposto pelo raio de estricção da junta, exigido pela norma ASTM E466. Adotou‐se então uma estimativa de 10mm de distância entre o limite do raio de estricção e o ponto de engaste da máquina, modelando‐se apenas a porção sob carregamento do corpo de prova. A figura 9 ilustra as áreas definidas no modelo e seu posicionamento.
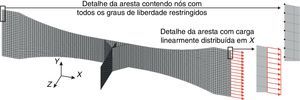
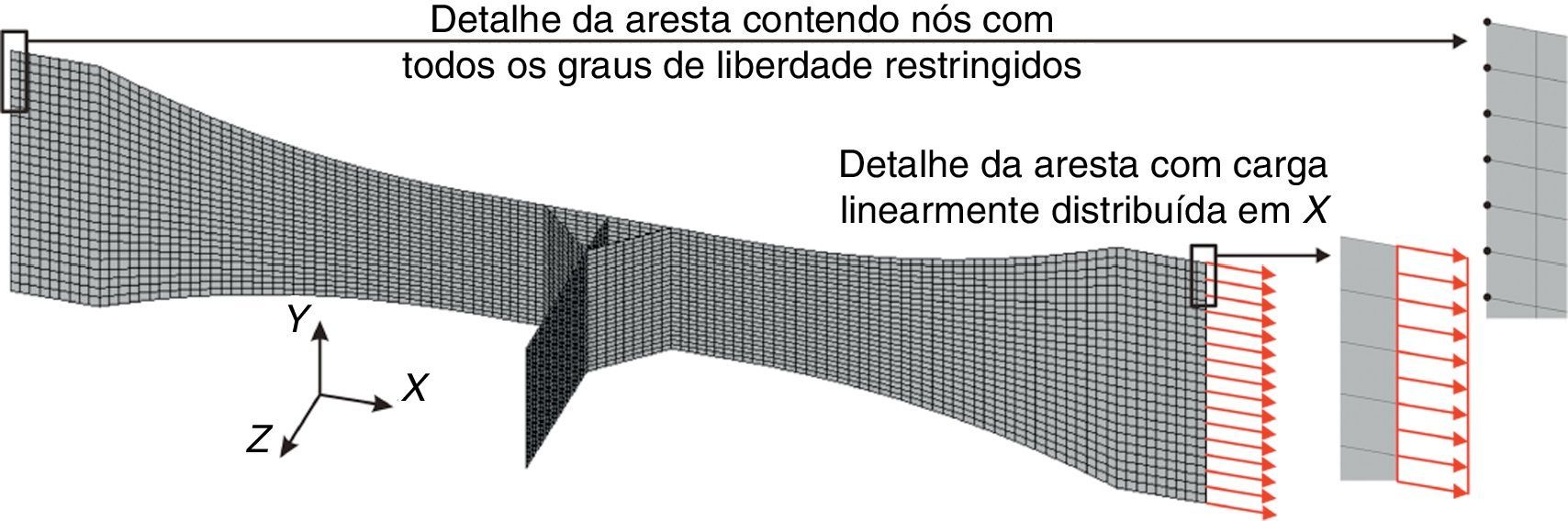
A máquina de fadiga do tipo push‐pull solicita o corpo de prova no sentido axial numa das extremidades e na outra extremidade o corpo de prova é fixado, tal como foi implementado no modelo numérico. Como a pressão do engaste na máquina é uniforme em toda a largura do corpo de prova, o modelo considerou uma carga na direção do eixo da junta linearmente distribuída sobre a aresta carregada. Portanto, na extremidade carregada, restringiram‐se todos os graus de liberdade nodais, exceto os de translação na direção do carregamento. Na aresta oposta, todos os graus de liberdade nodais foram restringidos.
A intensidade do carregamento aplicado ao modelo correspondeu à tensão nominal máxima aplicada (σnominal−máx.) experimentalmente. A figura 10 ilustra o modelo da junta T com as condições de contorno aplicadas.
Diversos autores [4–6,13] apontam a sensibilidade da metodologia SHSS ao grau de discretização da malha, sugerindo, inclusive, um refinamento na região de extrapolação. Como se trata de uma junta com geometria simples, optou‐se por uma malha refinada aplicada de forma integral.
A junta foi discretizada com elemento de casca moderadamente espessa (teoria de Reissner‐Mindlin) de interpolação linear. O elemento possui 4 nós com 6 graus de liberdade em cada. Foi utilizada integração completa e um tamanho máximo de 1, 1875mm, equivalente a um quarto da espessura das chapas. A DNV‐RP‐C203 [21] recomenda o uso de elementos com interpolação quadrática para o método SHSS quando o gradiente de tensões é grande na região da solda. Considerações de Salomaa [22] apontaram diferenças pouco significativas entre os usos de elementos lineares e quadráticos, para juntas cruciformes.
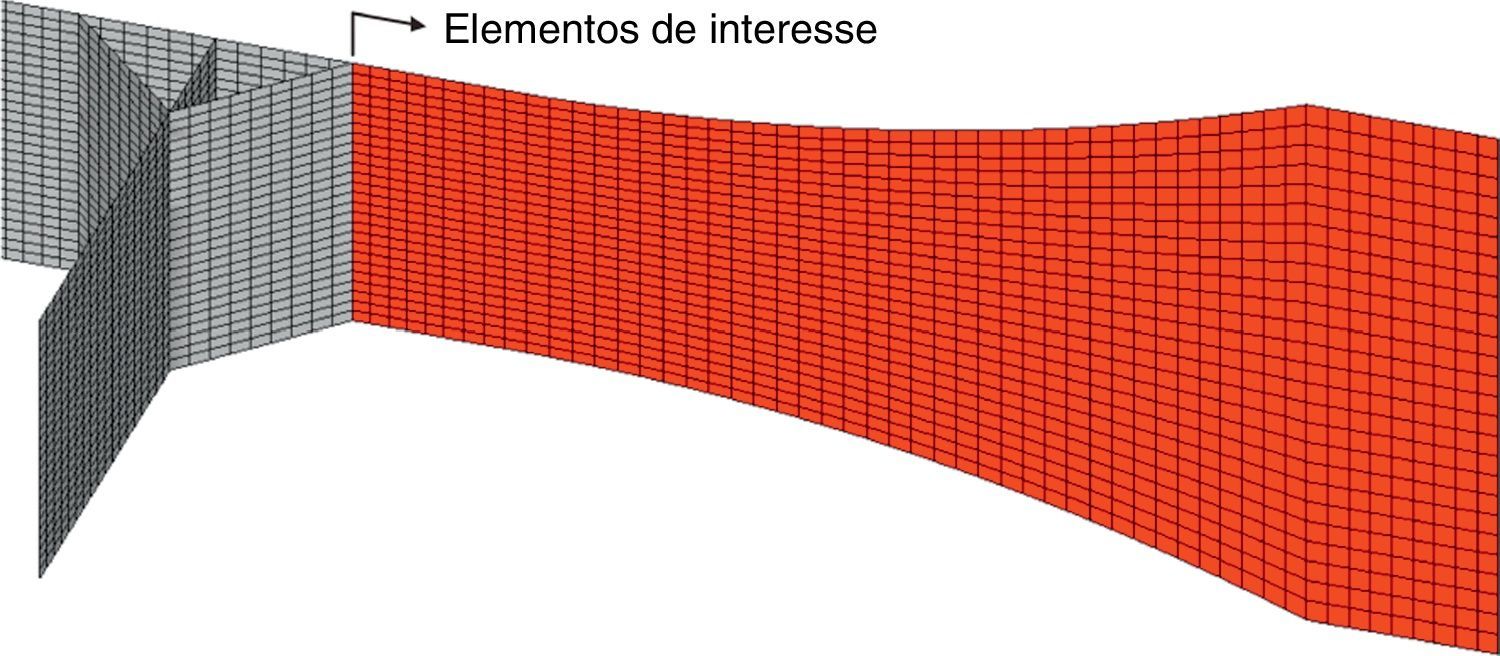
Para modelos em casca, os elementos que representam a solda não se encontram no mesmo plano da chapa, conforme ilustra figura 11. A solução nodal para grandezas calculadas dentro do elemento e extrapoladas para os nós, como as tensões, é dada como a média dos valores fornecidos por todos os elementos que compartilham o nó analisado. Portanto, na região da solda, a solução será dada pela média de tensões vindas de 3 segmentos que se interceptam no pé da solda. As tensões que interessam para o método SHSS são as referentes à chapa principal antes da intersecção supramencionada, representados pelos elementos em vermelho na figura 11.
Para correta aplicação da metodologia SHSS – LSE, esse problema foi contornado a partir da sugestão de Niemi et al. [13]. Apenas os elementos localizados a partir do pé da solda, exemplificado na figura 11 pelos elementos em vermelho, foram selecionados para o cálculo da tensão por extrapolação.
O mesmo procedimento foi necessário para aplicação do VMISS, visto que os esforços e momentos nodais foram obtidos através dos esforços e momentos internos necessários para garantir o equilíbrio em um diagrama de corpo livre com a fronteira na região de interesse (pé da solda).
4Cálculo da vida à fadiga pelo método da tensão estrutural hot spotConforme descrito por Niemi et al. [13], a metodologia SHSS utiliza o conceito de estimar a tensão no pé da solda a partir das tensões nas regiões vizinhas da mesma. Esses pontos, no entanto, são criteriosamente estabelecidos pelos autores a partir de fatores como grau de discretização da malha e ponto de potencial localização de nucleação da trinca de fadiga. A junta T em estudo corresponde a um hot spot do tipo I e, por ser modelada com malha refinada, as tensões principais σ1 devem ser linearmente extrapoladas (LSE) a distâncias de 0, 4t e 1t do pé da solda, através da equação (8)
Convém lembrar nesse ponto que, conforme ilustrado na figura 7, o ponto de obtenção das tensões (hot spot), e, consequentemente os pontos de extrapolação, serão fixos independente da técnica de modelagem.
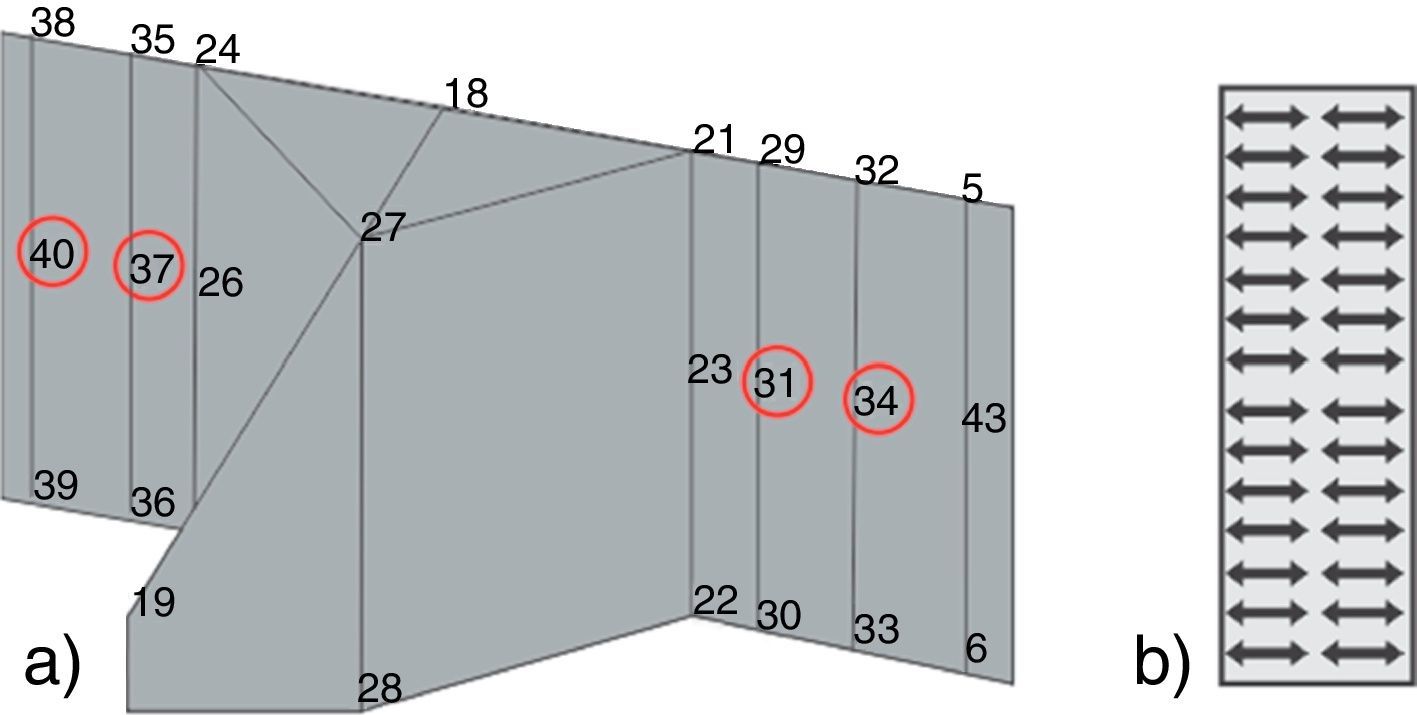
Uma vez estabelecida a distância dos pontos de extrapolação em relação ao pé da solda, resta precisar agora a localização desses pontos em relação ao eixo da mesma. Segundo Niemiet al. [13], os pontos de extrapolação devem estar localizados no eixo de simetria do carregamento, representados na figura 12(a) pelos «keypoints» 31 e 37 (à distância de 0, 4t do pé da solda) e 34 e 40 (à distância de 1, 0t do pé da solda).
A escolha de qual componente de tensão utilizar, segundo Niemi et al. [13] depende da direção das tensões principais em relação ao eixo da solda. Utiliza‐se σ1 (maior tensão principal) nos casos em que sua direção forma um ângulo menor que 60° em relação ao eixo perpendicular ao pé da solda nos pontos de extrapolação, situação característica da junta em análise como mostra a figura 12(b) contendo a representação dos vetores das tensões principais σ1. Como se tem um estado plano de tensões na região de interesse, σ3 torna‐se nula e σ2, por apresentar intensidade muito inferior a σ1, não está representada na imagem.
Ao simular o modelo EC1 sob carregamento nominal máximo σnominal−máx. de 60%Sy tem‐se: σ1−máx0,4t−EC1 e σ1−máx1,0t−EC1 (tensões principais nos pontos a distâncias de 0, 4t e 1t do pé da solda) valendo, respectivamente, 460, 72MPa e 458, 52MPa. Substituindo esses valores na equação (8), encontra‐se o valor da tensão estrutural junto ao pé da solda para modelos do tipo EC1 σhsmáx−EC1 pelo método LSE
Conforme Niemi et al. [13], o método SHSS permite assumir comportamento linear elástico para o material e, como trabalha com a variação de tensão Δσ=σmáx.−σmín., demanda uma análise estática, ao menos, em 2 níveis de carregamento σmáx. e σmín.. Considerando carregamento cíclico de amplitude constante torna‐se possível aplicar a relação de tensão (R) para obter o comportamento σhsmín−EC1 sobre o carregamento mínimo (σnominal−mín.)
A amplitude de tensão no pé da solda para o modelo EC1 Δσhs−EC1 e para o carregamento nominal máximo σnominal−máx. de 60%Sy vale
A análise em regime linear permite estabelecer uma relação constante entre Δσhs e ΔσNominal denominada Stress Concentration Factor (SCF), ou fator concentrador de tensão dada pela equação (9). Para o modelo EC1, tem‐se, em qualquer nível de carregamento
A vida em fadiga prevista através da metodologia SHSS, expressa pela equação (1), para esse modelo sobre carregamento de 60%Sy vale
As constantes m e C valem, respectivamente, 3 e 2×1012 para a junta em estudo.
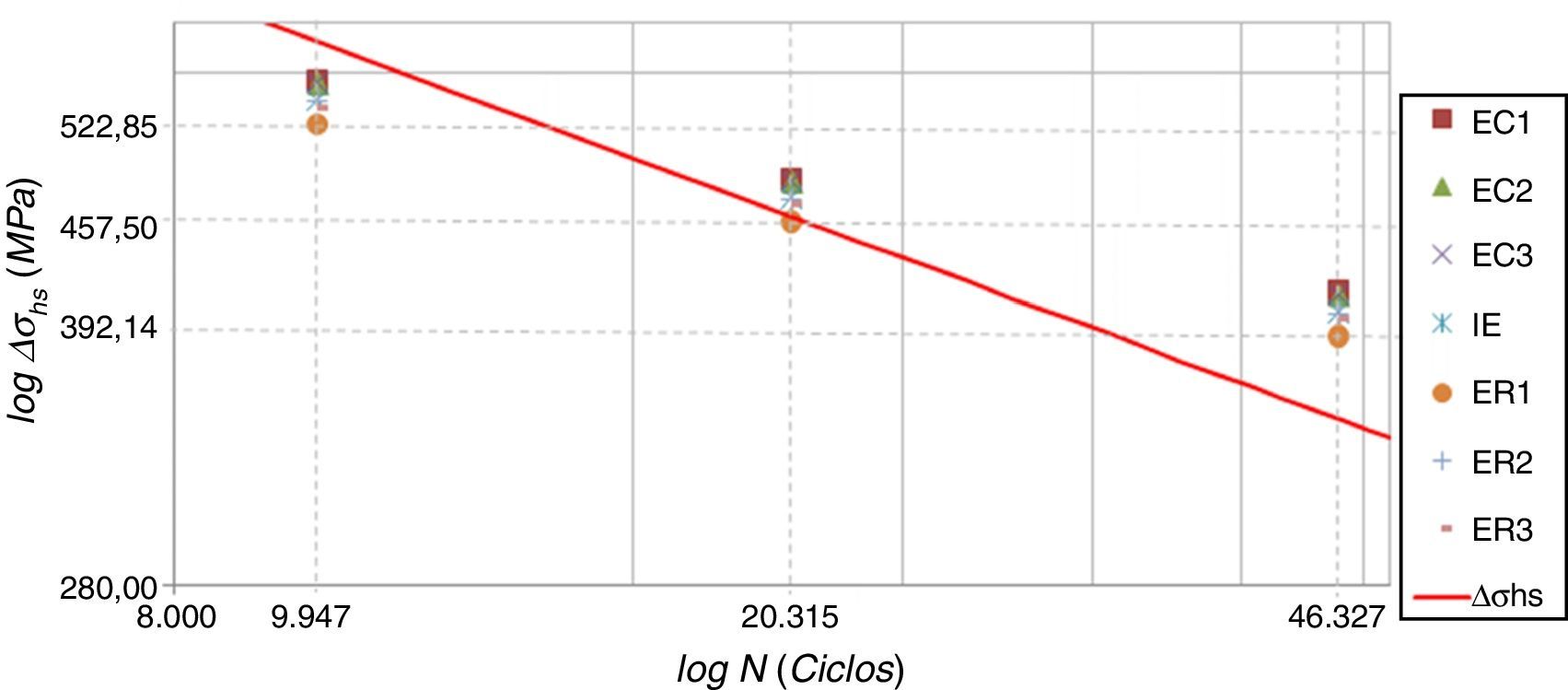
O gráfico da figura 13 apresenta a reta que corresponde ao comportamento da vida NSHSS em relação à amplitude da tensão estrutural no pé da solda Δσhs esperado pela metodologia SHSS. Demais pontos relacionam a vida experimental NCurva Exp. com a amplitude da tensão estrutural no pé da solda Δσhs calculada para cada uma das técnicas de modelagem, em cada nível de carregamento.
Os modelos com níveis mais baixos de carregamento demonstraram‐se conservadores em relação ao parâmetro de vida NSHSS/NCurva Exp., sendo o modelo EC1 com σnominal−máx. de 60%Sy o mais conservador de todos, representando 59, 98% da vida obtida experimentalmente NCurva Exp.. O modelo ER1 com σnominal−máx. de 80%Sy, por outro lado, superestimou em cerca de 40,66% a vida à fadiga, da NCurva Exp.. Essa amplitude de resultados demonstrou uma forte dependência da metodologia SHSS aos níveis de carregamento e ao tipo de modelo utilizado na representação da junta soldada.
O método SHSS pode subestimar a variação de tensão Δσhs no pé da solda. O modelo ER1 é um exemplo disso, pois Δσhs−ER1 apresentou‐se inferior a Δσnominal, ou seja, o fator de concentração de tensão SCF é menor que 1. Como estabelecido na equação (1), na metodologia SHSS, vida e tensão são parâmetros inversa e exponencialmente proporcionais, ou seja, uma subestimação no parâmetro de tensão incrementa exponencialmente a vida prevista. Para o caso em estudo, percebe‐se, então, um notável conservadorismo do método SHSS para o carregamento de 60%Sy, visto que, mesmo com a subestimação de Δσhs−ER1, a vida prevista NER1 foi cerca de 71,59% da vida obtida experimentalmente.
O parâmetro NSHSS/NCurva Exp. apresentou comportamento diretamente proporcional ao nível de carregamento. Isso pode ser compreendido ao comparar a equação (7) ΔσNominal=2991,54NCurva Exp.−0,187 estabelecida por Israel [18] e a equação (1) estabelecida por Niemi et al. [13] na forma linear
Ao considerar o SCFSHSS−EC1=1, 036 e a relação da equação (9) na equação (11), tem‐se, para o modelo EC1
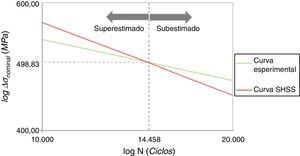
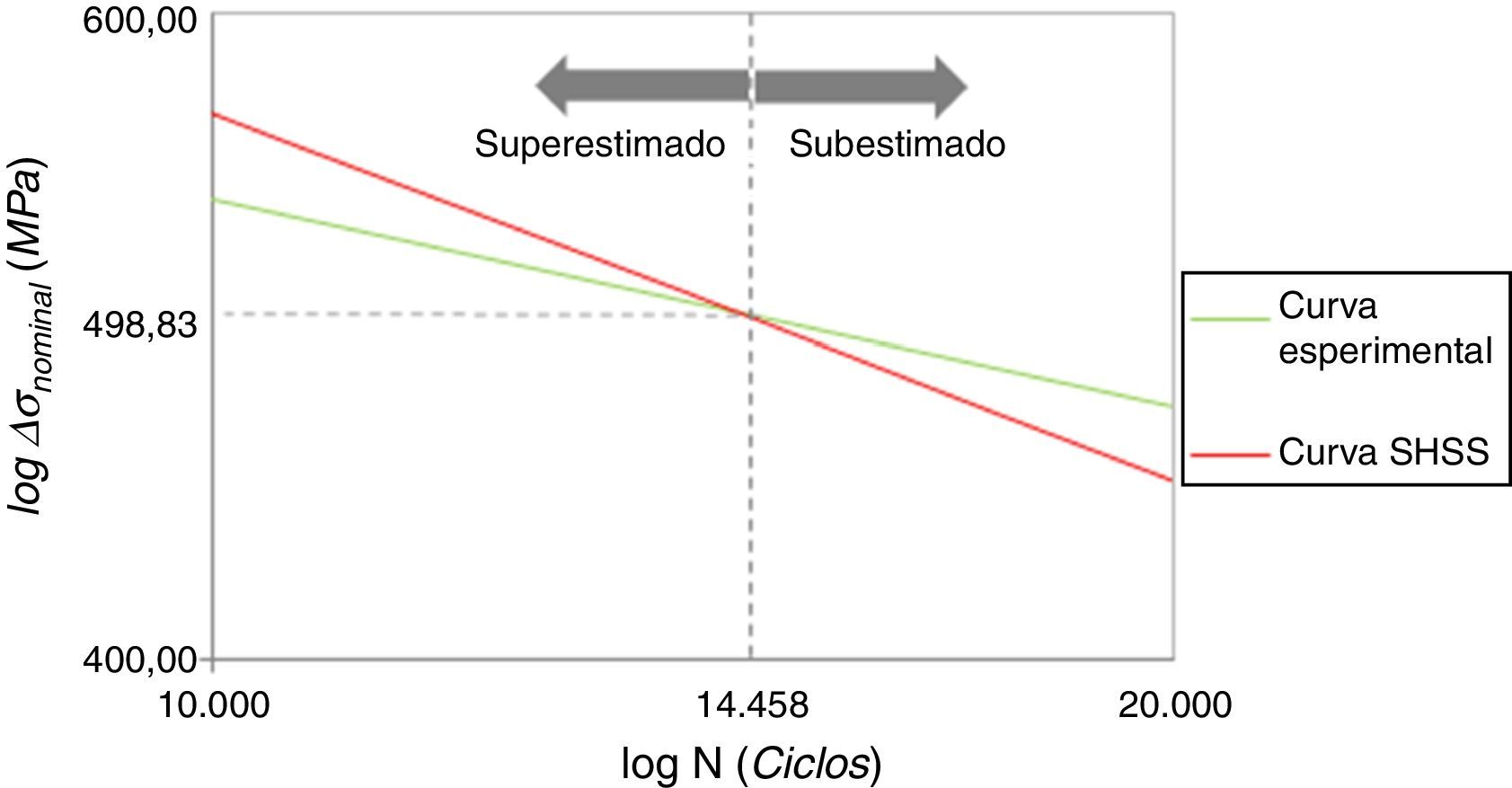
O coeficiente angular da reta, a, vale −0,333 para a curva SHSS e −0,187 para a curva experimental. Isso indica inclinação descendente para ambas, porém, mais acentuado para SHSS, como ilustra a figura 14.
O ponto de intersecção das curvas corresponde à amplitude de tensão nominal ΔσNom.prec.máx.−EC1, onde o método SHSS fornece o máximo de precisão para o cálculo da vida à fadiga. Esse ponto pode ser obtido ao fazer NCurva Exp.=NSHSS−EC1
onde:- •
se ΔσNominal>ΔσNom.prec.máx., NSHSS−EC1 é superestimado;
- •
se ΔσNominal<ΔσNom.prec.máx., NSHSS−EC1 é subestimado.
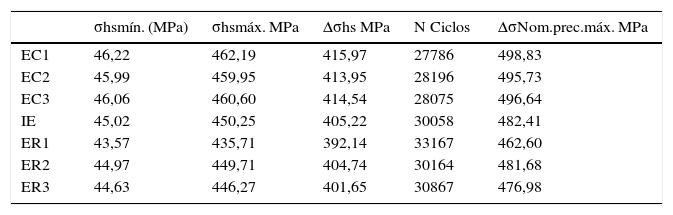
A tabela 1 resume os demais resultados obtidos em todos os modelos numéricos analisados.
Ponto de precisão máxima para todos os modelos analisados pelo método SHSS
| σhsmín. (MPa) | σhsmáx. MPa | Δσhs MPa | N Ciclos | ΔσNom.prec.máx. MPa | |
|---|---|---|---|---|---|
| EC1 | 46,22 | 462,19 | 415,97 | 27786 | 498,83 |
| EC2 | 45,99 | 459,95 | 413,95 | 28196 | 495,73 |
| EC3 | 46,06 | 460,60 | 414,54 | 28075 | 496,64 |
| IE | 45,02 | 450,25 | 405,22 | 30058 | 482,41 |
| ER1 | 43,57 | 435,71 | 392,14 | 33167 | 462,60 |
| ER2 | 44,97 | 449,71 | 404,74 | 30164 | 481,68 |
| ER3 | 44,63 | 446,27 | 401,65 | 30867 | 476,98 |
Nesse método, a vida à fadiga é calculada a partir da amplitude de tensões (Δσ) obtida de um processo de transformação da variação dos esforços nodais (ΔF e ΔM) perpendiculares ao pé da solda [5].
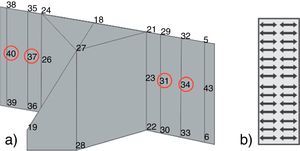
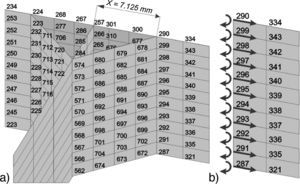
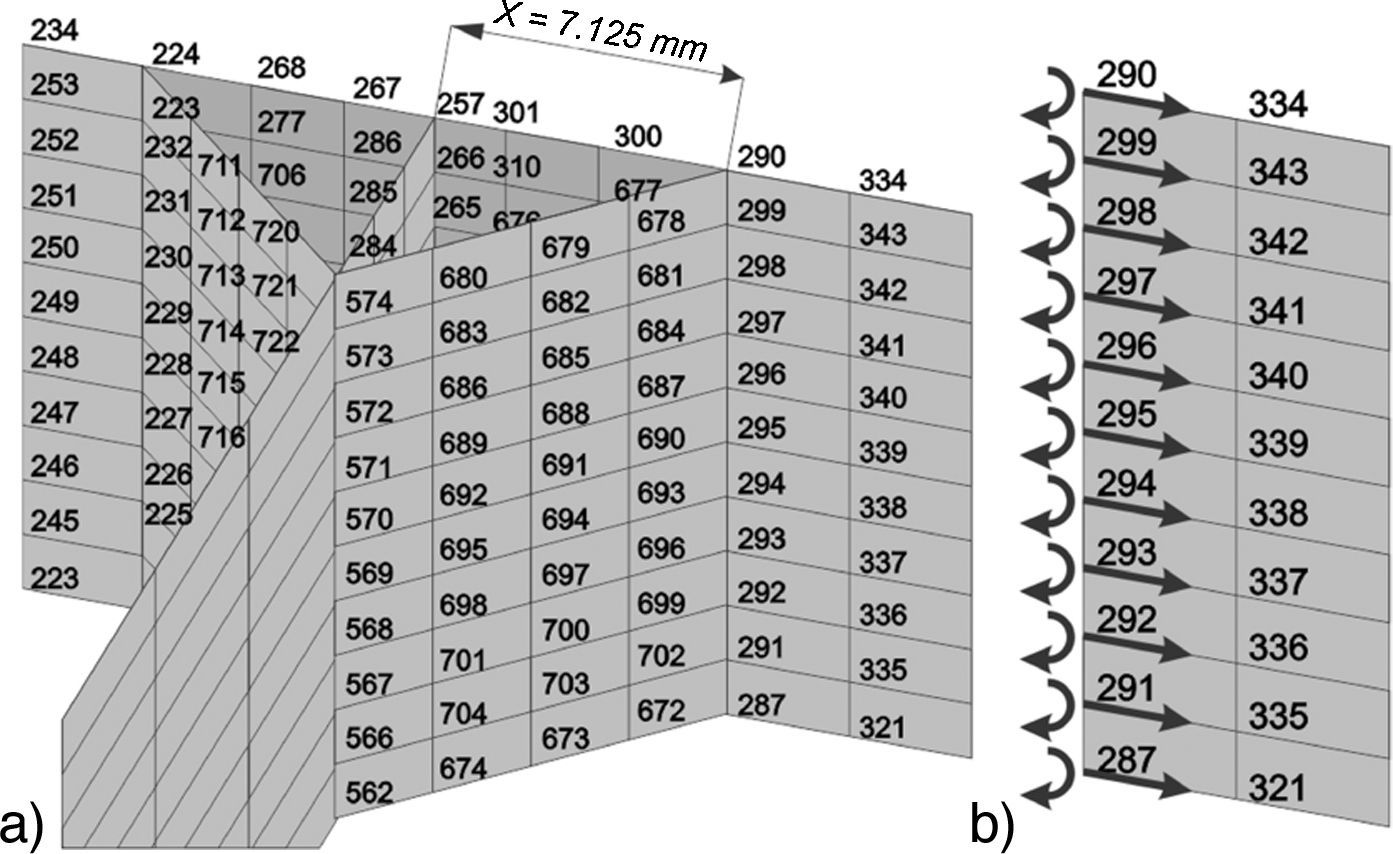
Conforme ilustra a figura 15, a junta em estudo apresenta o pé do cordão de solda na mesma direção do eixo Y do sistema global sob a coordenada X=7, 125mm, logo, é possível usar diretamente as componentes ΔFX (esforços na direção do carregamento) e ΔMY (momentos em relação ao eixo transversal à solda) fornecidas na solução global do modelo.
A variação dos esforços nodais (ΔFX e ΔMY) é transformada em variação de esforços lineares (ΔfX e ΔmY) através do produto matricial expresso por Dong [5] nas equações (2) e (3). Aplicando‐se esses parâmetros na equação (4), obtém‐se a amplitude da tensão estrutural (Δσs), a partir da variação das componentes de membrana (Δσm) e de flexão (Δσb), para cada nó.
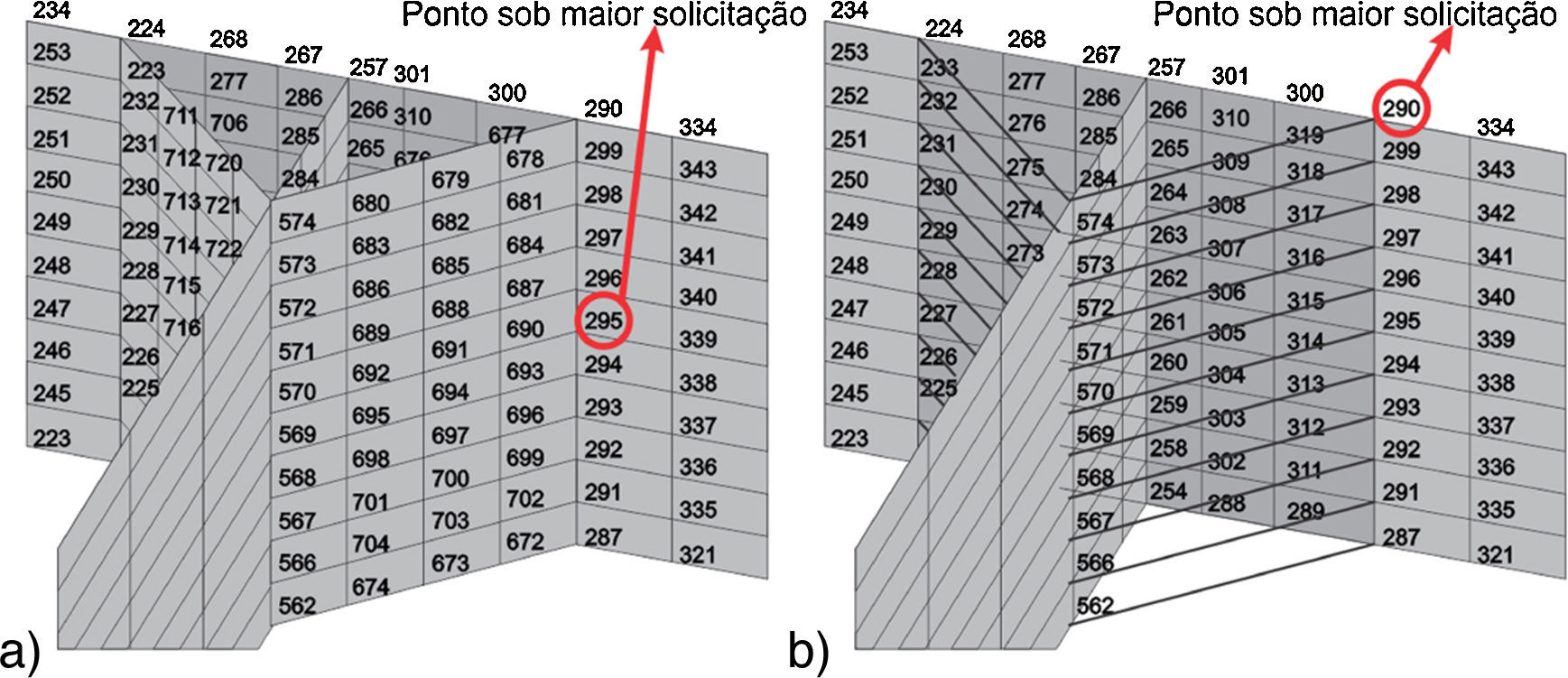
O nó que apresentar o valor Δσs mais intenso indica o ponto de nucleação da trinca e, consequentemente, onde a vida à fadiga deverá ser calculada [5]. Para o modelo EC1 sob carregamento nominal máximo de 60%Sy, o ponto crítico apresentou‐se no eixo longitudinal da chapa principal, como ilustra figura 16(a), com valores de tensão de Δσm=403, 885MPa, Δσb=12, 095MPa e Δσs=415, 979MPa.
Outras técnicas de modelagem como ER1 e IE, no entanto, apontaram o ponto crítico na borda da chapa principal, como ilustra figura 16(b).
A vida à fadiga, segundo Dong [5], é calculada a partir da amplitude da tensão estrutural equivalente (ΔSs), expressa pela equação (5). Adotando‐se os valores de tensão obtidos no ponto crítico, tem‐se, para o modelo EC1
O cálculo da vida prevista, em termos de intervalo de probabilidades, pela equação (6), tem os valores de suas constantes C e h expressos em função do material e, para o caso em estudo, podem ser obtidos na ASME [16].
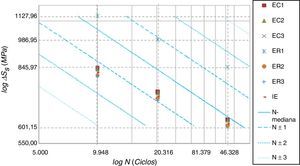
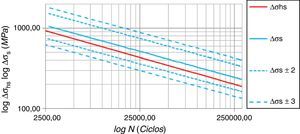
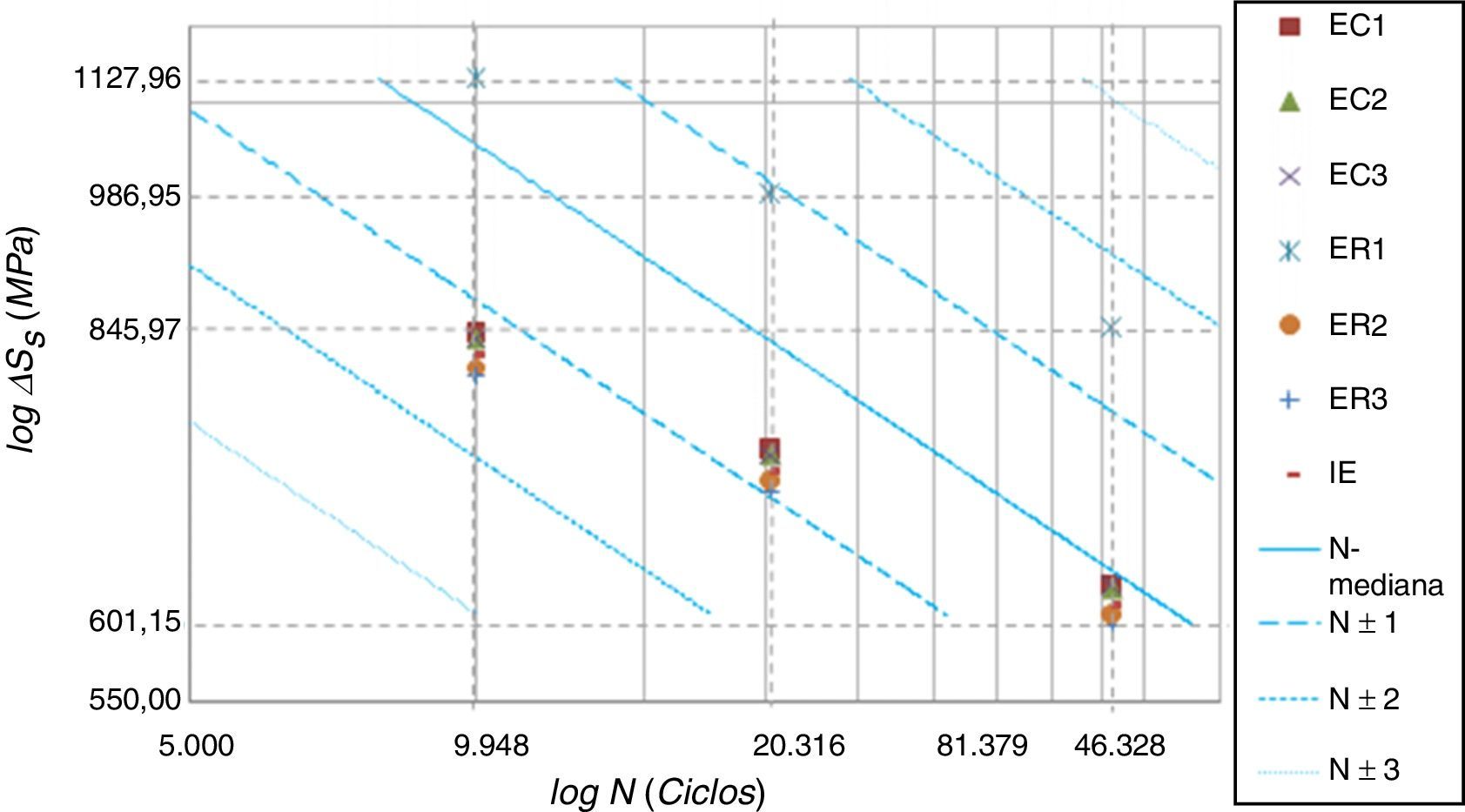
O gráfico da figura 17 apresenta as retas que correspondem ao intervalo de probabilidades para o comportamento da vida à fadiga NMC−Mediana, NMC±1σ, NMC±2σ, NMC±3σ esperado pelo método de Battelle e estabelecido pela equação (6). Demais pontos relacionam a vida obtida da curva experimental NCurva Exp. expressa pela equação (7), com a amplitude da tensão estrutural equivalente no pé da solda ΔSs obtida para cada uma das técnicas de modelagem.
Quase todos os modelos demonstraram‐se não conservadores em relação ao comportamento médio à fadiga NMediana, excetuando‐se apenas os modelos ER1. Vale notar, no entanto, que apesar da variação nos resultados dos modelos, todos eles apresentaram‐se dentro da faixa ±2σ.
Da mesma forma que o método SHSS, o método de Battelle também apresentou comportamento ascendente do parâmetro NMC/NCurva Exp. com o nível de carregamento. Compara‐se, então, equação (7) (ΔσNominal=2991,54NCurva Exp.−0,187) estabelecida por Israel [18] com a equação (6) (ΔSs=CNMCh) estabelecida por Dong [5]
Ao considerar agora o SCFEC1=ΔSs−EC1ΔσNominal=1,571, tem‐se, para o modelo EC1
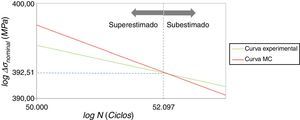
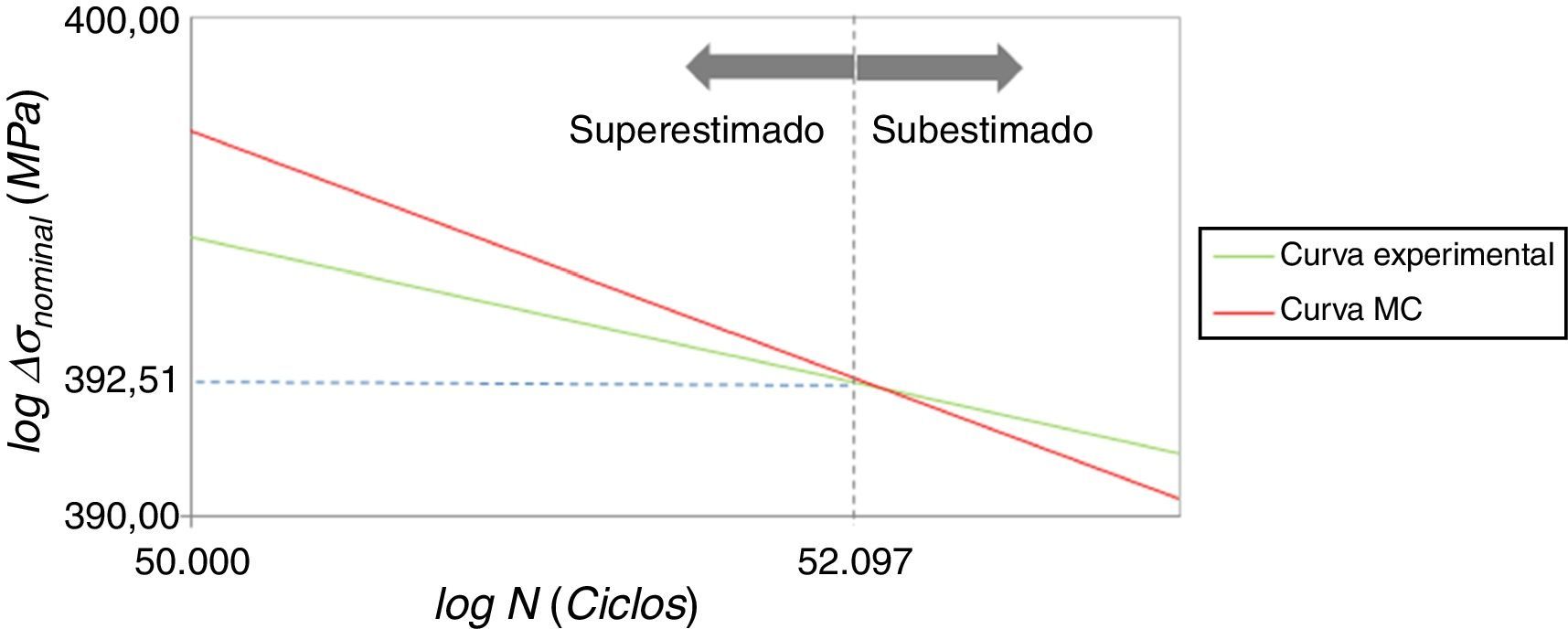
A diferença entre a inclinação da curva do método de Battelle e a curva experimental é, basicamente, a mesma obtida na análise da metodologia SHSS. A diferença mais significativa, nesse caso, reside no ponto de intersecção das curvas, conforme ilustra a figura 18.
O ponto de intersecção das curvas, ou ΔσNom.prec.máx.−EC1, onde o método de Battelle forneceria o máximo de precisão para o cálculo da vida à fadiga para o modelo EC1, obtido da relação NCurva Exp.=NMC−EC1, vale
onde,- •
se ΔσNominal>ΔσNom.prec.máx., NMC−EC1 é superestimado;
- •
se ΔσNominal<ΔσNom.prec.máx., NMC−EC1 é subestimado.
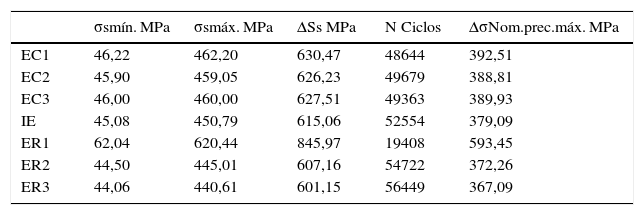
A tabela 2 resume os demais resultados obtidos em todos os modelos numéricos analisados.
Ponto de precisão máxima para todos os modelos analisados pelo método de Battelle
| σsmín. MPa | σsmáx. MPa | ΔSs MPa | N Ciclos | ΔσNom.prec.máx. MPa | |
|---|---|---|---|---|---|
| EC1 | 46,22 | 462,20 | 630,47 | 48644 | 392,51 |
| EC2 | 45,90 | 459,05 | 626,23 | 49679 | 388,81 |
| EC3 | 46,00 | 460,00 | 627,51 | 49363 | 389,93 |
| IE | 45,08 | 450,79 | 615,06 | 52554 | 379,09 |
| ER1 | 62,04 | 620,44 | 845,97 | 19408 | 593,45 |
| ER2 | 44,50 | 445,01 | 607,16 | 54722 | 372,26 |
| ER3 | 44,06 | 440,61 | 601,15 | 56449 | 367,09 |
Analisando‐se os resultados do método de Battelle para os diversos modelos de casca representados no gráfico da figura 17, nota‐se considerável discrepância para os modelos do tipo ER1. O que ocorre é que as conexões dos ER, em todos os nós da linha de solda, funcionam como um engaste para o comportamento membranal dos elementos de casca da porção da junta da linha até o carregamento, provocando uma singularidade no comportamento da tensão dos nós posicionados na borda da chapa principal, deslocando, consequentemente, o ponto crítico para essa região, como observado na figura 16(b).
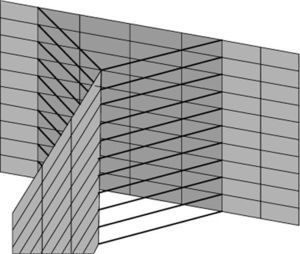
Percebe‐se melhor essa singularidade com o refino da malha, como ilustra a tabela 3, que mostra o comportamento da tensão normal na direção global X.
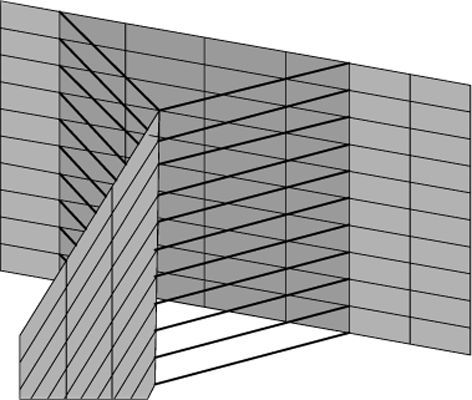
Aygül [3] recomenda que, ao simular o cordão de solda com ER, a intersecção entre as chapas não deve ser representada. Echer [20], em seu estudo, também não o fez. Embora modelos gerados dessa forma ainda apresentem a singularidade supracitada, percebe‐se que esta, para modelos ER1, torna‐se menos sensível ao grau de refinamento da malha, conforme apresentado na tabela 4. A figura 19 ilustra a representação ER1 através dessa técnica.
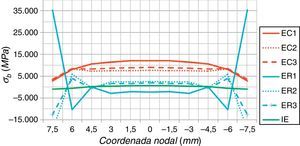
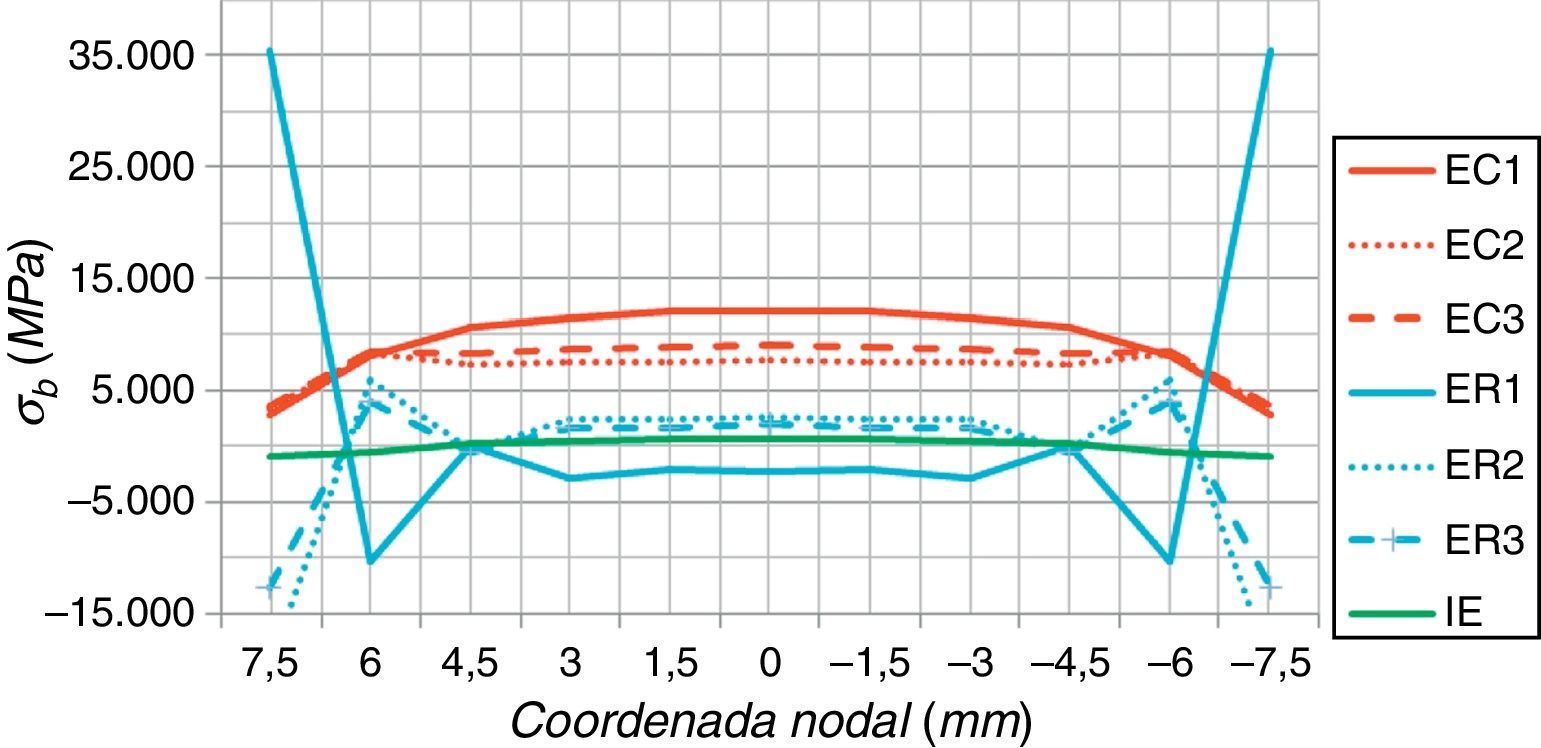
Cálculos para obtenção das componentes da tensão estrutural Δσm e Δσb no pé da solda comprovaram a existência da componente de flexão Δσb em todos os modelos utilizados para a junta T. A variação no comportamento dessa componente para os diferentes modelos, ilustrada na figura 20, pode significar um impacto significativo na tensão estrutural equivalente ΔSs (e, consequentemente, no cálculo da vida à fadiga) para juntas com carregamentos mais complexos, onde o componente de flexão tenha maior participação.
Nos modelos ER3, o ponto de obtenção da tensão encontra‐se afastado do ponto de intersecção do ER e, em ER2, esse afastamento é ainda maior, como ilustrado na figura 7. Apesar desse afastamento, a influência da singularidade gerou um momento em sentido contrário no nó da borda da chapa principal, representado por uma componente negativa da tensão de flexão Δσb com intensidade diretamente proporcional ao valor dessa distância. Essa componente de flexão Δσb, por ter sinal negativo, acaba diminuindo consideravelmente a amplitude da tensão estrutural total Δσs expressa pela equação (4). Isso acaba transferindo, novamente, o ponto crítico para o nó localizado sobre o eixo longitudinal da junta nos modelos ER2 e ER3.
Os nós localizados no eixo da junta não são suscetíveis a essa singularidade. Logo, uma alternativa interessante poderia ser adotar o mesmo critério da metodologia SHSS e aplicar esses valores de tensão no cálculo da vida à fadiga, independente de este ser o mais carregado. A tabela 5 traz dados comparativos das técnicas ER1 ao utilizar as tensões do nó sobre o eixo da junta e sobre o nó mais carregado.
Quadro comparativo geral, método VMISS para técnica ER1 com diferentes pontos críticos sob análise
| σnominal−máx.MPa | 60%Sy | 70%Sy | 80%Sy | |
|---|---|---|---|---|
| Tensões no eixo da junta | Δσs−ER1−ΔσnominalΔσnominal% | −4,03 | −4,03 | −4,03 |
| NER1/NCurva Exp.% | 76,05 | 107,1 | 144,2 | |
| Tensões na borda da junta | Δσs−ER1−ΔσnominalΔσnominal% | 39,17 | 39,17 | 39,17 |
| NER1/NCurva Exp.% | 23,85 | 33,60 | 45,20 | |
Como era de se esperar, ao adotar o nó sobre o eixo longitudinal da junta como nó crítico, a variabilidade dos resultados de ER1 em relação a ER2 e ER3 é menor, pois o efeito da borda da chapa não se faz presente. Em contrapartida, a amplitude da tensão estrutural no pé da solda Δσs foi inferior à amplitude da tensão nominal Δσnominal, superestimando a vida prevista para os níveis de carregamento mais elevados.
6Comparações entre os métodos SHSS e BattelleTrês formas de comparação foram feitas entre os métodos:
S–N: comparação da curva de comportamento à fadiga dos métodos;
ΔSs/Δσhs−N: análise da influência da correção de tensão no método de Battelle;
ΔσNominal−N: comparação do comportamento à fadiga dos métodos SHSS e de Battelle com a curva experimental da junta T.
Os 2 métodos em análise relacionam um parâmetro de tensão S com a vida N de maneira exponencial. Colocando ambas na forma logarítmica, isolando o parâmetro N e substituindo os valores das constantes, tem‐se
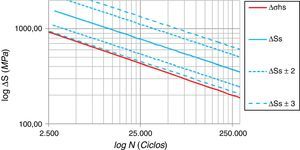
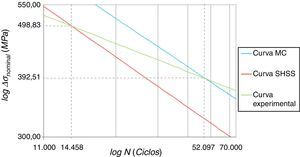
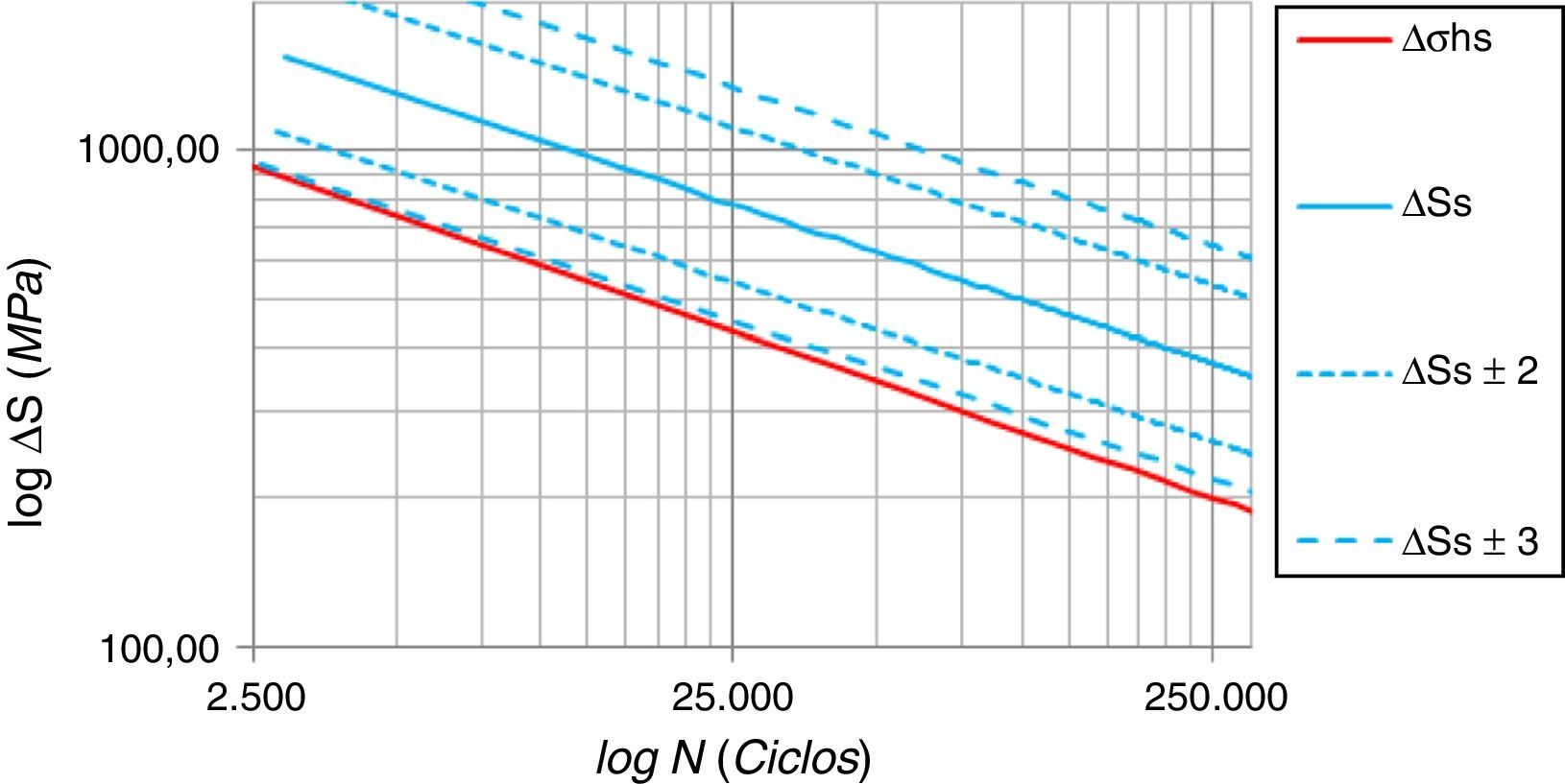
A análise das equações na forma linear permite concluir que, em um diagrama S–N, a inclinação das retas é basicamente a mesma e a diferença no termo independente indica a curva SHSS levemente transladada para baixo em relação à curva do método de Battelle, conforme ilustrado na figura 21.
Niemi et al. [13] já haviam apontado que a curva descrita pelo método SHSS descreve uma probabilidade de 97,7% para o comportamento à fadiga, correspondendo a 2 desvios padrão de afastamento abaixo do comportamento médio. Pela figura 21, é possível perceber que o comportamento da curva SHSS é muito similar ao da curva do método de Battelle subtraída de 3 desvios padrão, ou seja, a metodologia SHSS descreve o comportamento da vida à fadiga de forma mais conservadora que o método de Battelle.
Outra comparação pode ser feita entre as tensões obtidas no pé da solda para cada uma das metodologias, ou seja, entre os parâmetros Δσhs e Δσs. Essa análise permite avaliar a influência da correção de tensão do método de Battelle.
A equação da curva Δσs em função de N pode ser obtida aplicando‐se a equação (5) (ΔSs=Δσst2−m2m.Ir1m) na equação (6)
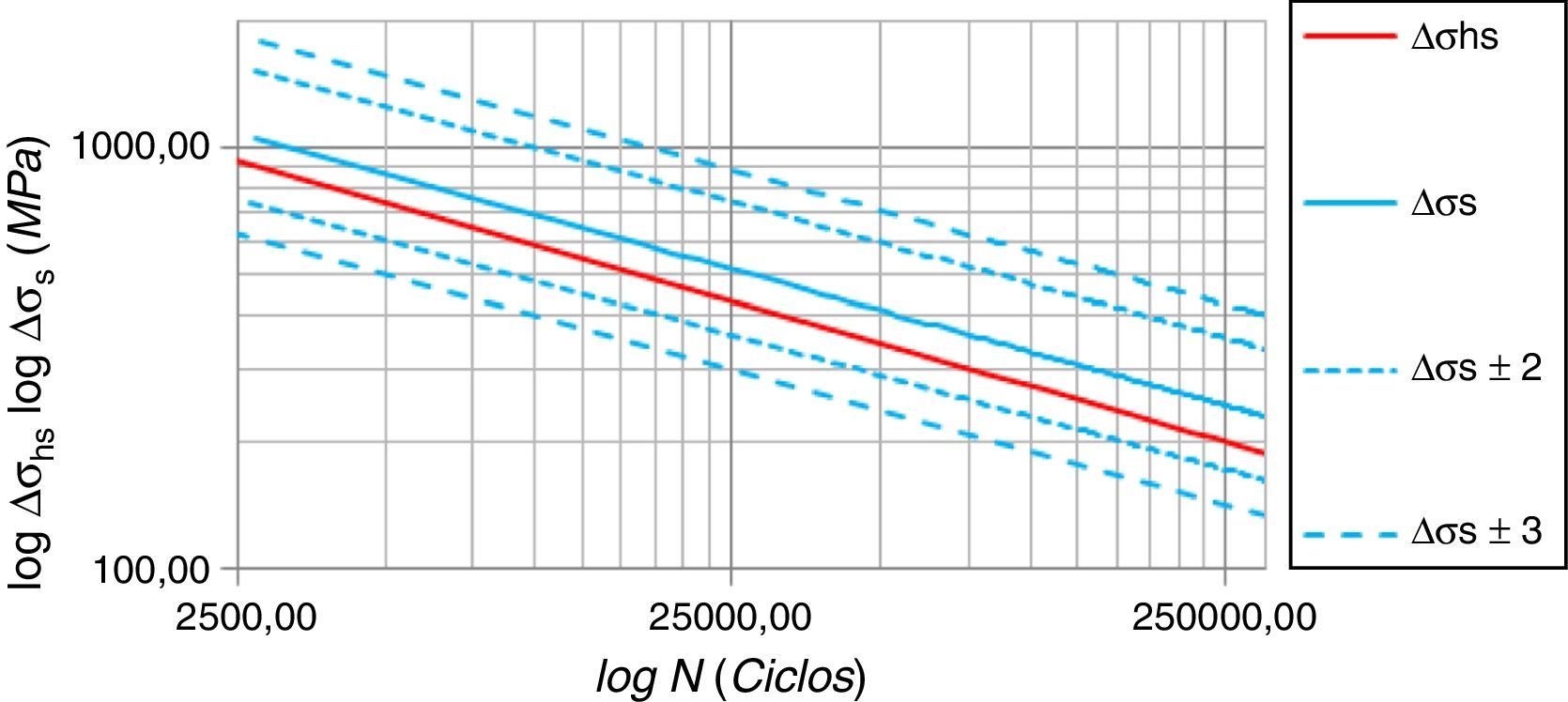
O termo expresso por logt2−m2m.Ir1m é uma constante determinada pela geometria da junta (t2−m2m) e seu modo de carregamento (Ir1m) que, dentro de uma análise linear, também deverá ser constante devido ao parâmetro r. Como m=3, 6 (lei de Paris), o valor desse termo será negativo, justificando, assim, o deslocamento da curva do gráfico da figura 22 em relação ao gráfico da figura 21.
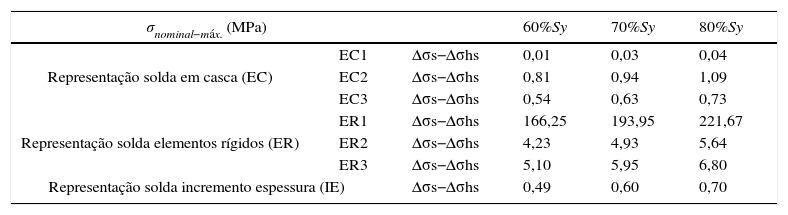
A diferença entre as curvas SHSS e de Battelle torna‐se consideravelmente menor. Percebe‐se que a correção da tensão, de forma específica para um determinado tipo de junta, é o principal diferencial entre as metodologias. Para a junta em estudo, isso foi confirmado através da comparação entre Δσs e Δσhs para os diversos modelos em casca analisados, conforme lista a tabela 6.
Quadro comparativo da tensão estrutural obtida via VMISS e LSE para junta T
| σnominal−máx. (MPa) | 60%Sy | 70%Sy | 80%Sy | ||
|---|---|---|---|---|---|
| Representação solda em casca (EC) | EC1 | Δσs−Δσhs | 0,01 | 0,03 | 0,04 |
| EC2 | Δσs−Δσhs | 0,81 | 0,94 | 1,09 | |
| EC3 | Δσs−Δσhs | 0,54 | 0,63 | 0,73 | |
| Representação solda elementos rígidos (ER) | ER1 | Δσs−Δσhs | 166,25 | 193,95 | 221,67 |
| ER2 | Δσs−Δσhs | 4,23 | 4,93 | 5,64 | |
| ER3 | Δσs−Δσhs | 5,10 | 5,95 | 6,80 | |
| Representação solda incremento espessura (IE) | Δσs−Δσhs | 0,49 | 0,60 | 0,70 | |
Fonte: autor.
As menores diferenças entre Δσs e Δσhs foram encontradas para o modelo EC1, enquanto as maiores para o modelo ER1. Essas diferenças foram provocadas, principalmente, pela singularidade característica da junta T, discutida na secção 5.1.
Por fim, considerando a análise feita em regime linear, é possível aplicar o parâmetro SCF nas equações (15) e (16), deixando‐as em função de ΔσNominal, obtendo‐se as equações (18) e (19)
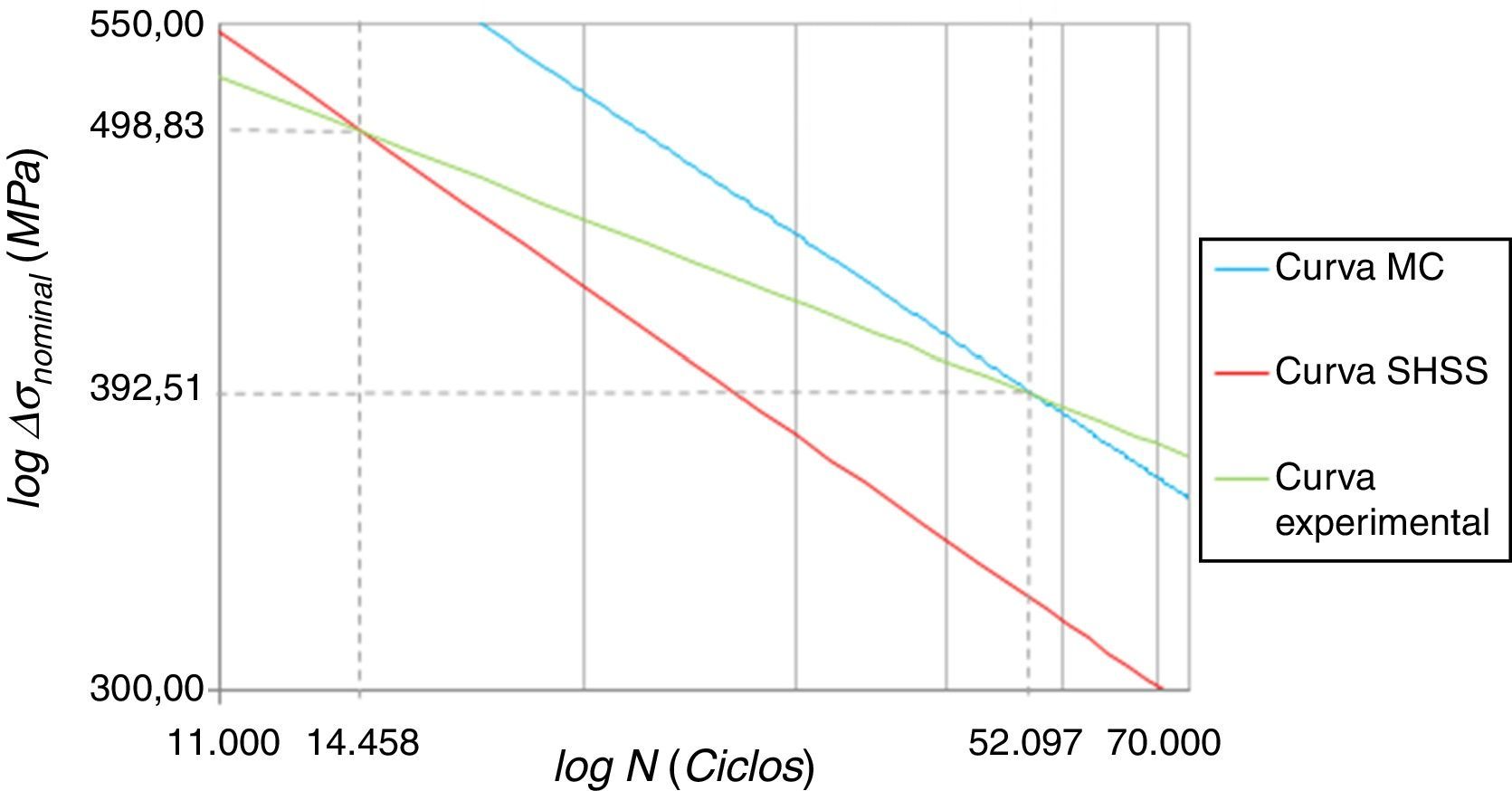
Essa transformação é o que permite a comparação, ilustrada no gráfico da figura 23, entre as curvas SHSS e de Battelle com a curva experimental da junta expressa pela equação (20)
As curvas do método de Battelle e SHSS apresentaram um declive mais acentuado que a curva experimental da junta T. Essa observação permitiu a construção de algumas considerações:
- •
quando a inclinação da curva experimental da junta é maior que a inclinação SHSS/MC, o método MC é mais adequado na análise de fadiga com alta amplitude de tensão, enquanto o método SHSS é mais adequado na análise de fadiga com baixa amplitude de tensão;
- •
quando a inclinação da curva experimental da junta é menor que a inclinação SHSS/MC, o método MC é mais adequado na análise de fadiga com baixa amplitude de tensão, enquanto o método SHSS é mais adequado na análise de fadiga com alta amplitude de tensão;
- •
no caso de juntas em que a curva experimental tiver a mesma inclinação de SHSS/MC, a metodologia mais adequada será determinada pela sua proximidade com a curva experimental. A proximidade das curvas SHSS e MC à curva experimental está diretamente relacionada ao SCF do modelo da junta, conforme expresso nas equações (18) e (19).
Calculou‐se a vida em fadiga de uma junta T utilizando‐se diferentes modelos de elementos finitos de casca através do método de Battelle e SHSS. Os resultados foram comparados com a vida obtida experimentalmente por Israel [18] no laboratório de ensaios mecânicos da UPF.
A diferença entre os modelos numéricos utilizados residiu na técnica de representação do cordão de solda: EC (EC1, EC2 e EC3), ER (ER1, ER2 e ER3) e IE. A adoção dessas técnicas partiu da análise e recomendações de estudos comparativos anteriores [3,20].
Alguns resultados de vida em fadiga obtidos pelo método SHSS foram bastante conservadores, enquanto que, pelo método de Battelle, encontraram‐se dentro da faixa de probabilidades ±2σ da curva mestre (MC).
As técnicas do tipo IE e ER1 caracterizaram‐se pela singularidade apresentada na borda da chapa principal da junta T. A representação da junta sem intersecção entre as chapas (figura 19), no entanto, minimizou esse efeito.
Para o método de Battelle, foi possível verificar que o comportamento da parcela de flexão da tensão mudou significativamente para os diferentes modelos numéricos (figura 20). Isso pode influenciar na determinação da vida à fadiga de outras juntas, com carregamento mais complexo.
A curva do comportamento à fadiga da metodologia SHSS é praticamente coincidente com a curva −3σ do método de Battelle, como ilustra a figura 21. A principal diferença entre os métodos está na correção do parâmetro de tensão (tensão estrutural equivalente). Em outras palavras, os parâmetros Δσhs e Δσs são parâmetros semelhantes, como comprova dados da junta estudada listados na tabela 6.
Como ilustra o gráfico comparativo da figura 23, além da técnica de modelagem, o nível de carregamento é outro fator igualmente importante na precisão dos resultados para ambas as metodologias (Battelle e SHSS). Essa constatação foi construída através da comparação da curva do respectivo método (para o modelo EC1) com a curva experimental da junta. O ponto de intersecção, denominado ΔσNom.prec.máx, indicou o nível de carregamento em que a precisão do método é máxima. Vale ressaltar que a comparação dessas curvas só foi possível a partir da consideração da análise de um regime linear e do conceito de SCF expresso na equação (9).
Nos modelos EC1, a amplitude dos carregamentos aplicados experimentalmente (ΔσNominal) ficou mais próxima do ponto de intersecção da curva experimental com a curva SHSS do que com a curva MC, ou seja, foi mais próxima de ΔσNom.prec.máx−SHSS do que ΔσNom.prec.máx.−MC (comparando figura 14 e figura 18). Esse foi um dos motivos que justificou o fato de os resultados do método SHSS serem mais próximo dos resultados experimentais obtidos na junta analisada.
Como sugestão de assunto a ser abordado em trabalhos futuros, considera‐se pertinente a elaboração e análise de um modelo sólido da junta para comparação com os resultados dos modelos em casca obtidos nesse estudo. Sugestão de assunto a ser abordado em trabalhos futuros.
8Conflito de interessesOs autores declaram não haver conflito de interesses.
A eq. (A.1) mostra a matriz de interpolação do elemento de casca linear de 4 nós, obtida em [14].
Onde l1, l2, l3... correspondem às dimensões das arestas dos elementos 1, 2, 3... ao longo do pé da solda.







![Classificação dos métodos de análise da vida à fadiga (3 e 4], adaptado pelo autor. Classificação dos métodos de análise da vida à fadiga (3 e 4], adaptado pelo autor.](https://static.elsevier.es/multimedia/02131315/0000003300000034/v1_201705221028/S0213131516300335/v1_201705221028/pt/main.assets/thumbnail/gr1.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![(a) Extrapolação linear tensão hot spot[12]. (b) Componentes de membrana (σm) e flexão (σb) da tensão estrutural (σs) no pé da solda [5]. (a) Extrapolação linear tensão hot spot[12]. (b) Componentes de membrana (σm) e flexão (σb) da tensão estrutural (σs) no pé da solda [5].](https://static.elsevier.es/multimedia/02131315/0000003300000034/v1_201705221028/S0213131516300335/v1_201705221028/pt/main.assets/thumbnail/gr2.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
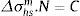
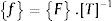
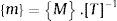
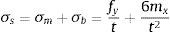
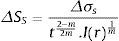

![Geometria de junta T ensaiada. (a) Dimensões da junta. (b) Detalhe do cordão de solda [18]. Geometria de junta T ensaiada. (a) Dimensões da junta. (b) Detalhe do cordão de solda [18].](https://static.elsevier.es/multimedia/02131315/0000003300000034/v1_201705221028/S0213131516300335/v1_201705221028/pt/main.assets/thumbnail/gr3.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
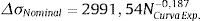
![Representação numérica da penetração de solda. (a) Penetração total com solda assimétrica (PTSA). (b) Penetração parcial com solda assimétrica (PPSA). (c) Penetração total com solda simétrica (PTSS). (d) Penetração parcial com solda simétrica (PPSS) [11]. Representação numérica da penetração de solda. (a) Penetração total com solda assimétrica (PTSA). (b) Penetração parcial com solda assimétrica (PPSA). (c) Penetração total com solda simétrica (PTSS). (d) Penetração parcial com solda simétrica (PPSS) [11].](https://static.elsevier.es/multimedia/02131315/0000003300000034/v1_201705221028/S0213131516300335/v1_201705221028/pt/main.assets/thumbnail/gr5.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Técnicas de representação do cordão de solda em ER e elementos em casca. (a) ER1 ou EC1. (b) ER2 ou EC2. (c) ER3 ou EC3 [20]. Técnicas de representação do cordão de solda em ER e elementos em casca. (a) ER1 ou EC1. (b) ER2 ou EC2. (c) ER3 ou EC3 [20].](https://static.elsevier.es/multimedia/02131315/0000003300000034/v1_201705221028/S0213131516300335/v1_201705221028/pt/main.assets/thumbnail/gr7.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)