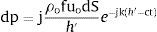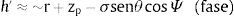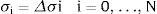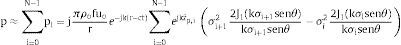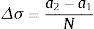Determinación de la presión sonora radiada por pistones circulares y anillos no planos usando un método numérico simplificado

Resumen

Aunque el estudio de la radiación sonora por membranas y placas no es nuevo, recientemente se ha desarrollado una gran cantidad de investigación sobre el tema para abordar aplicaciones actuales y futuras. Se han publicado varios trabajos sobre la radiación por superficies planas generales y algunas geometrías particulares, como las rectangulares, circulares, elípticas y anulares. Sin embargo, el caso de la radiación sonora por anillos axisimétricos no planos que pudieran aplicarse al diseño de altavoces coaxiales no ha recibido la misma atención. En este artículo se presenta un método numérico simplificado para determinar la presión sonora radiada por pistones y anillos no planos con simetría de revolución. El método también puede aplicarse en aquellos casos donde exista una distribución de velocidad con simetría radial.

Abstract

Although the study of the sound pressure radiation from membranes and plates is not new, current and future applications have produced a large body of recent research in the field. Several works have been published on the radiation from general plane surfaces and some particular geometries such as rectangular, circular, elliptic and annular. However, the case of sound radiation from non-planar axisymmetric rings that could be applied to the design of coaxial loudspeakers has not received much attention. In this article, a simplified numerical approach for determining the sound pressure radiated from symmetric non-planar pistons and rings is presented. The method can also include those cases having a radially-symmetric velocity distribution.

1

Introducción

El interés por obtener la presión acústica radiada por placas y membranas no es un problema nuevo [1,2], pero sigue importando en diferentes ámbitos relacionados con la acústica. Existen trabajos clásicos sobre radiación acústica de superficies planas con diferentes geometrías [3–5]. Otros estudios concretan sobre superficies rectangulares de forma genérica [6–8], definen modelos numéricos o propuestas de mejora en los cálculos [9,10], o aplicaciones de estas superficies a la electroacústica [11,12].

Existen trabajos también para pistones circulares [13–15], para superficies elípticas [16], anillos [17,18] e incluso superficies elípticas anulares [19]. Respecto a superficies no planas pueden encontrarse trabajos sobre superficies no planas axisimétricas [20] y aplicaciones de estas superficies a altavoces [21–23]. Sin embargo, es complicado encontrar trabajos específicos que traten el problema de anillos no planos axisimétricos que pudieran aplicarse, por ejemplo, al diseño de altavoces coaxiales.

En este trabajo se propone un método simplificado para poder determinar la presión sonora generada por pistones y anillos no planos con simetría de revolución, incluyendo casos donde exista una distribución de velocidad también con simetría radial. Este método se basa en la generación de un diferencial de anillo que se adapta a diferentes perfiles y patrones de velocidad bajo la limitación de simetría de revolución, que se puede aplicar a la generación de conos para altavoces.

2

Teoría

2.1

Presión radiada por un pistón plano

La forma más utilizada para obtener la presión radiada por un pistón se basa en el modelo de fuente simple. Este modelo parte de la suposición de que una superficie se puede descomponer en un conjunto de fuentes simples de superficie dS [1,24]. La radiación producida por la vibración de una superficie extendida, como por ejemplo un pistón, un diafragma, etc., se puede obtener como la suma de presiones. La presión producida en un punto por una fuente simple viene dada por [1] (fig. 1):

siendo j=−1 la unidad imaginaria, ρ_o la densidad del aire, f la frecuencia de la onda emitida por la fuente simple, u_o la amplitud de velocidad de la superficie vibrante, h la distancia del elemento diferencial al punto en el que se quiere evaluar la presión, c la velocidad de propagación de la onda en el aire, t el tiempo y k el número de onda. El valor de h viene dado por el módulo de la magnitud vectorial, que puede expresarse de diferentes formas. En el caso de geometrías rectangulares suele ser más cómodo utilizar coordenadas cartesianas [9]. Para el caso que nos ocupa es más cómodo trabajar en coordenadas esféricas. El valor de h se puede expresar en función de variables del pistón y del punto de cálculo de la presión:

donde r es la distancia del centro del pistón al punto donde se quiere calcular la presión, σ es la distancia desde el centro del pistón al elemento de superficie, θ es el ángulo que forma el vector formado por el centro del pistón con el punto de cálculo y el eje OZ, Ψ es el ángulo que el vector formado por el centro y el punto donde se sitúa el elemento de superficie forma con el eje OX, y Φ es el ángulo que forma la proyección de r sobre el plano 0XY con el eje X.

Figura 1.

Pistón plano circular.

Para el caso de un pistón circular plano que vibra con movimiento armónico, situado sobre una pared rígida, la expresión compleja de la presión sonora es [1,24]:

donde se ha tomado, por simetría, Φ = 0. La expresión anterior solo tiene solución numérica.

Si se considera el caso de campo lejano, es decir, r >> a, se pueden realizar las siguientes aproximaciones [25]:

que llevan a la siguiente expresión integral:

siendo J₁(x) la función de Bessel de orden 1. Para resolver la expresión integral es importante tener en cuenta las siguientes expresiones integrales de las funciones de Bessel de orden 0 y 1:

Las expresiones (4a) y (4b) para campo lejano se conocen como aproximación de Fraunhofer [26]. Estas se aplican en diferentes ámbitos como la óptica o la acústica. Para el caso de la amplitud de la señal se utiliza la expresión (4a). Esta se obtiene suponiendo que 1/h es prácticamente igual a 1/r, lo que genera un error de primer orden [24–26]. La expresión (5) se transforma a decibelios, por lo que mientras se cumpla que a < r/10, el error por amplitud quedará por debajo de la décima de decibelio, que es la que se suele considerar.

Respecto a la fase, la expresión (4b) se obtiene mediante un desarrollo en serie de Taylor de h, eligiendo hasta el término de primer orden, por lo que el error cometido en esta aproximación es de segundo orden. Esta aproximación permite tener un error menor de 1 radián para frecuencias del rango audible (hasta 20 kHz) en el caso de a < r/10 [26]. Esto es suficiente para el rango de trabajo de altavoces. Para frecuencias más altas (rango de ultrasonidos) u otras relaciones entre a y r, podría considerarse el segundo término del desarrollo de la función.

2.2

Pistón circular no plano

En el caso de un pistón circular con un cierto perfil (no plano), la expresión de la fuente simple ha de modificarse de la siguiente forma (fig. 2) [20]:

donde h’ se puede obtener de la siguiente expresión:

siendo z_p el valor de la variación en el eje z producido por un perfil determinado. Integrando de nuevo (7) obtendríamos la expresión para la presión en un punto. Claramente, la expresión solo tiene solución numérica [3].

Figura 2.

Geometría usada para un pistón circular no plano.

Del mismo modo que en el caso del pistón plano, se puede aplicar la siguiente aproximación válida en campo lejano y para perfiles poco profundos [25], dada por:

que nos llevaría a la siguiente expresión integral:

cuya resolución depende de la forma del perfil y en la mayoría de casos requerirá de integración numérica.

3

Propuesta de cálculo basada en anillos

3.1

Presión sonora radiada por un diferencial de un anillo

La propuesta para obtener la presión sonora radiada por un anillo surge de la aplicación del principio de superposición. Este principio permite sumar las presiones sonoras generadas por diferentes fuentes. Por tanto, se puede plantear que un anillo de radio interior a₁ y exterior a₂ se pueda descomponer en 2 pistones de radio a₁ y a₂, donde la velocidad u_o del pistón de radio a₁ estaría en contrafase con la radiada por el pistón de radio a₂. Por tanto, se obtendría la expresión siguiente para campo lejano:

Esta sencilla expresión permite, por tanto, obtener la presión sonora radiada en campo lejano por un anillo. También puede obtenerse por integración directa de la expresión, teniendo en cuenta los radios interiores y exteriores, y aplicando (6):

En la expresión (12) va implícito un diferencial de anillo de radio σ y espesor dσ:

En el caso de que no fuese plano, este diferencial debería incorporar el efecto del perfil de la siguiente forma:

El término z_p(σ) sería nulo en (14) para el caso de un anillo plano.

3.2

Propuesta de cálculo de pistones circulares no planos con simetría de revolución

Un caso de interés son los pistones no planos con simetría de revolución, que ya se han tratado en trabajos anteriores [22,23]. Estos perfiles son la base de trabajos sobre membranas de altavoces, entre otros. En la figura 3 se muestran algunos perfiles de interés normalizados bajo el parámetro adimensional ka, donde k representa el número de onda y a el radio. En el caso del perfil lineal + circular se ha elegido el radio de valor a/8. A estos perfiles se les asigna una profundidad, p, en función del radio del pistón. En la tabla 1 se muestran las fórmulas de generación de los perfiles, en función del radio σ.

Figura 3.

Perfiles propuestos (en el eje horizontal se representa σ, y en el vertical z_p).

Tabla 1.

Fórmulas para la generación de perfiles

zp=pσa−p Perfil lineal	zp=peσ−eaea−1 Perfil exponencial
zp=pσa2−p   Perfil cuadrático	zp=pσa3−p   Perfil cúbico
zp=pσa−p   Perfil raíz	zp=r2−σ2−pσ

Como ya se ha justificado en el punto 2.2, en estos casos la obtención del campo sonoro pasa por la integración de la expresión diferencial propuesta, que requiere una resolución numérica.

Para realizar la integración se propone descomponer el pistón circular en una suma de N anillos de espesor Δσ. Se cumple que:

Es decir, se construyen anillos de espesor Δσ, de radio interior σ_i y de radio exterior σ_i+1. Una vez realizada esa descomposición se aproxima el valor de z_p en cada anillo por el valor medio de sus extremos en primera aproximación, de forma que se aproxima a una constante en todo el anillo, es decir:

Por tanto, se puede obtener una expresión aproximada del campo sonoro generado por un anillo i-ésimo:

y la suma de todos los anillos proporciona una aproximación del generado por un pistón circular no plano:

La expresión obtenida permite conseguir, por tanto, un valor aproximado del campo sonoro generado por un pistón circular no plano.

La expresión (16), que afecta directamente a la expresión (17), parte de una aproximación del punto medio con un error del orden de Δσ³f”, es decir, de orden 3, siendo f” la derivada segunda de la función por aproximar [27]. Sin embargo, el resultado final de la aproximación dado en (18) y (21) tiene un orden de aproximación global de 2. Si fuese necesario, la expresión (16) podría refinarse utilizando las aproximaciones de Simpson evaluando 3 y 4 puntos, pasando a un error de orden 5 [27].

3.3

Otras modificaciones propuestas

La expresión anterior está pensada para obtener, sobre todo, el campo sonoro de diferentes perfiles de altavoces. En primera instancia puede ser una buena aproximación siempre que se cumpla que [22,24]:

siendo a el radio de la membrana, E el módulo de Young del material del que está compuesto la membrana, ρ la densidad de la membrana y μ el coeficiente de Poisson de la membrana [24]. En esos casos se supone que la velocidad u₀ es constante. En el caso de que la velocidad no sea constante, pero tenga simetría radial (u₀(σ)), se puede proponer también una modificación de la ecuación. Para ello se sustituye, en primera aproximación, la velocidad por su valor medio en los extremos del anillo:

Por tanto:

Esta nueva expresión aproximada se acercará más a la real a medida que los cambios de velocidad sean pequeños en cada anillo. Respecto a la expresión (20), puede hacerse el mismo comentario que en el punto 3.2. con la expresión (16). En Press et al. [27] se puede encontrar información detallada de la generación de diferentes modos para distintas geometrías.

Otra posibilidad de modificación de esta ecuación es la de un anillo no plano. Esta suposición puede servir para modelar altavoces coaxiales, que constan de 2 altavoces concéntricos que ocupan el mismo espacio, y donde el altavoz exterior tendría una membrana en forma de anillo, y el interior de pistón circular. Suponiendo que el radio interior es a₁ y el exterior a₂, se puede utilizar (21) con modificaciones:

4

Resultados

A continuación se presentan algunos resultados obtenidos con las fórmulas propuestas en el apartado 3. Los 2 parámetros de interés que se van a representar son la respuesta en frecuencia y la direccionalidad.

4.1

Respuesta en frecuencia

Se compara la respuesta en frecuencia de diferentes perfiles normalizados según el parámetro adimensional ka y las relaciones de profundidad, p, desde 1 hasta 1/6 del radio a, respecto a la respuesta dada por un pistón circular plano. Se aplica la relación (23) para obtener el nivel de presión sonora en dB, LPS, tanto de los perfiles como del pistón plano circular y se cuantifica la diferencia:

En la figura 4 se presentan los resultados obtenidos para los perfiles de la tabla 1, suponiendo velocidad constante. En el caso del perfil lineal + circular se ha decidido un radio interior de valor a/8. Los resultados se obtienen aplicando la ecuación (18) para los perfiles y la (5) para el pistón plano circular. Se evalúan 4.096 anillos por perfil y 1.000 valores de frecuencia. Los cálculos realizados en Matlab^© en un ordenador de sobremesa con procesador Intel^® Core™ i7-2700k CPU @ 3.5 GHz tardan una media de 0,8 segundos. Con este mallado se asegura que los datos ya convergen. Pueden notarse cambios en función de la profundidad a partir de ka > 1 aproximadamente.

Figura 4.

Resultados de respuesta en frecuencia con los perfiles de la tabla 1.

En la figura 5 se muestran diferentes comparativas. En la figura 5a se comparan los diferentes perfiles entre sí, con una profundidad p = a/2. En la figura 5b se aplica la ecuación (18) modificada con (22), generando un anillo de radio interior r = a/4 (y exterior a). En la figura 5c se valora el caso de que la velocidad no sea constante, introduciendo la velocidad del primer modo radial que se produce en el caso de que el pistón circular tenga condiciones de empotramiento en el borde (es decir, velocidad cero en su perímetro):

Figura 5.

Resultados numéricos de la diferencia de nivel de presión sonora para diferentes perfiles.

Pueden notarse cambios a partir de ka > 2 aproximadamente.

4.2

Direccionalidad

Tomando como base la ecuación (18) se realiza un barrido angular de 0 a 90° (que se puede representar de –90 a 90° por la simetría radial), para obtener la función de direccionalidad en campo lejano, aplicando (23) y normalizando respecto al valor máximo, LPS_max:

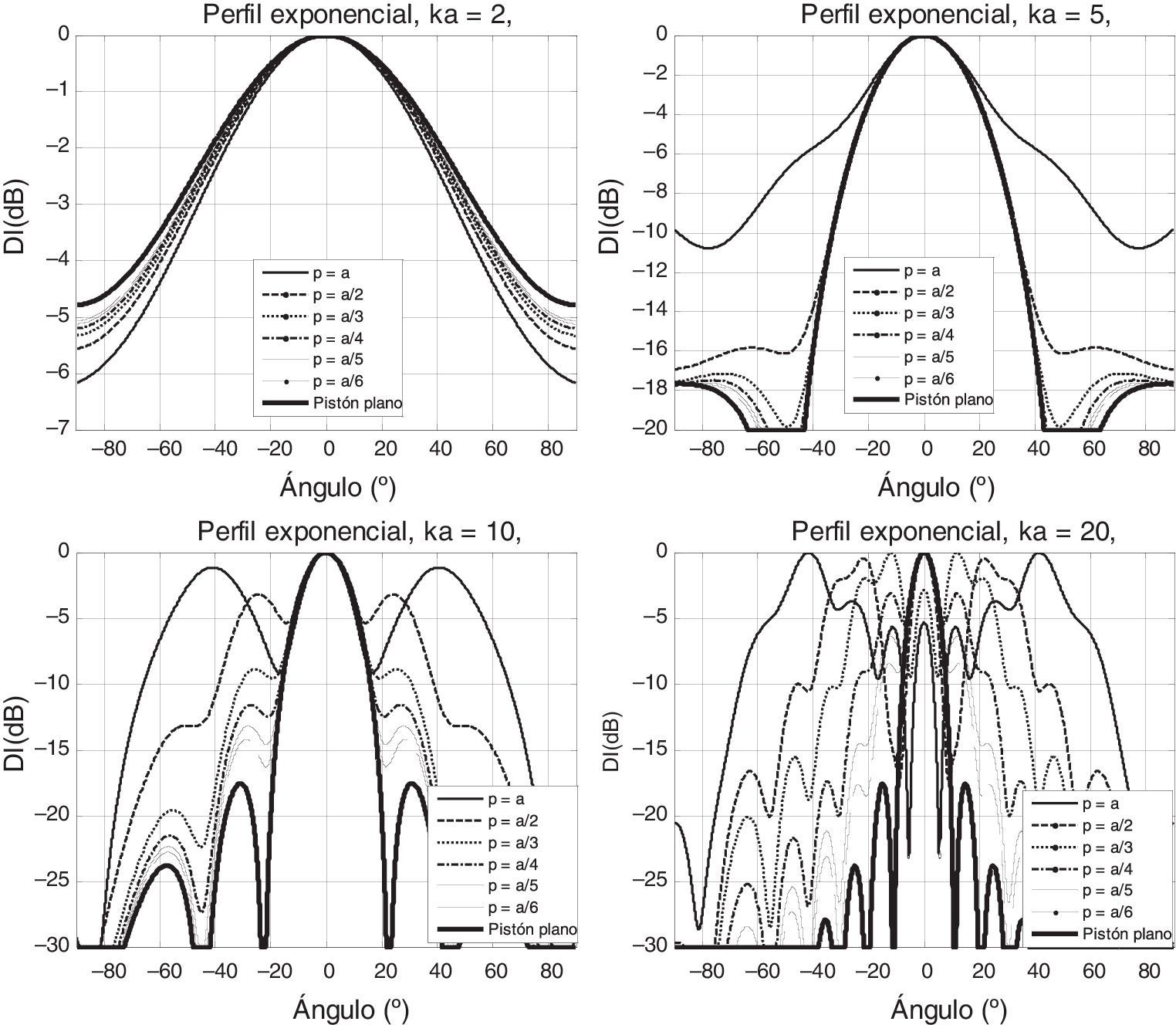
En la figura 6 se muestran los resultados para el perfil lineal, con ka = 0,5, 1, 2, 5, 10 y 20. Puede verse cómo los cambios empiezan a notarse de manera más significativa a partir de ka = 2, siendo estos más evidentes cuanto mayor es la profundidad. El resto de resultados se muestran a partir de ka = 2. Esto también se evidencia en las figuras 4 y 5.

Figura 6.

Direccionalidad computada para el perfil lineal.

En las figuras 7–11 se muestran resultados del perfil exponencial, cuadrático, cúbico, raíz y lineal + circular con radio interior de valor a/8. Se realizan los cálculos en el mismo ordenador con un mallado angular de 16.384 valores y 256 anillos en un tiempo medio de 33 min.

Figura 7.

Direccionalidad computada para el perfil exponencial.

Figura 8.

Direccionalidad computada para el perfil cuadrático.

Figura 9.

Direccionalidad computada para el perfil cúbico.

Figura 10.

Direccionalidad computada para el perfil raíz.

Figura 11.

Direccionalidad computada para el perfil lineal + circular.

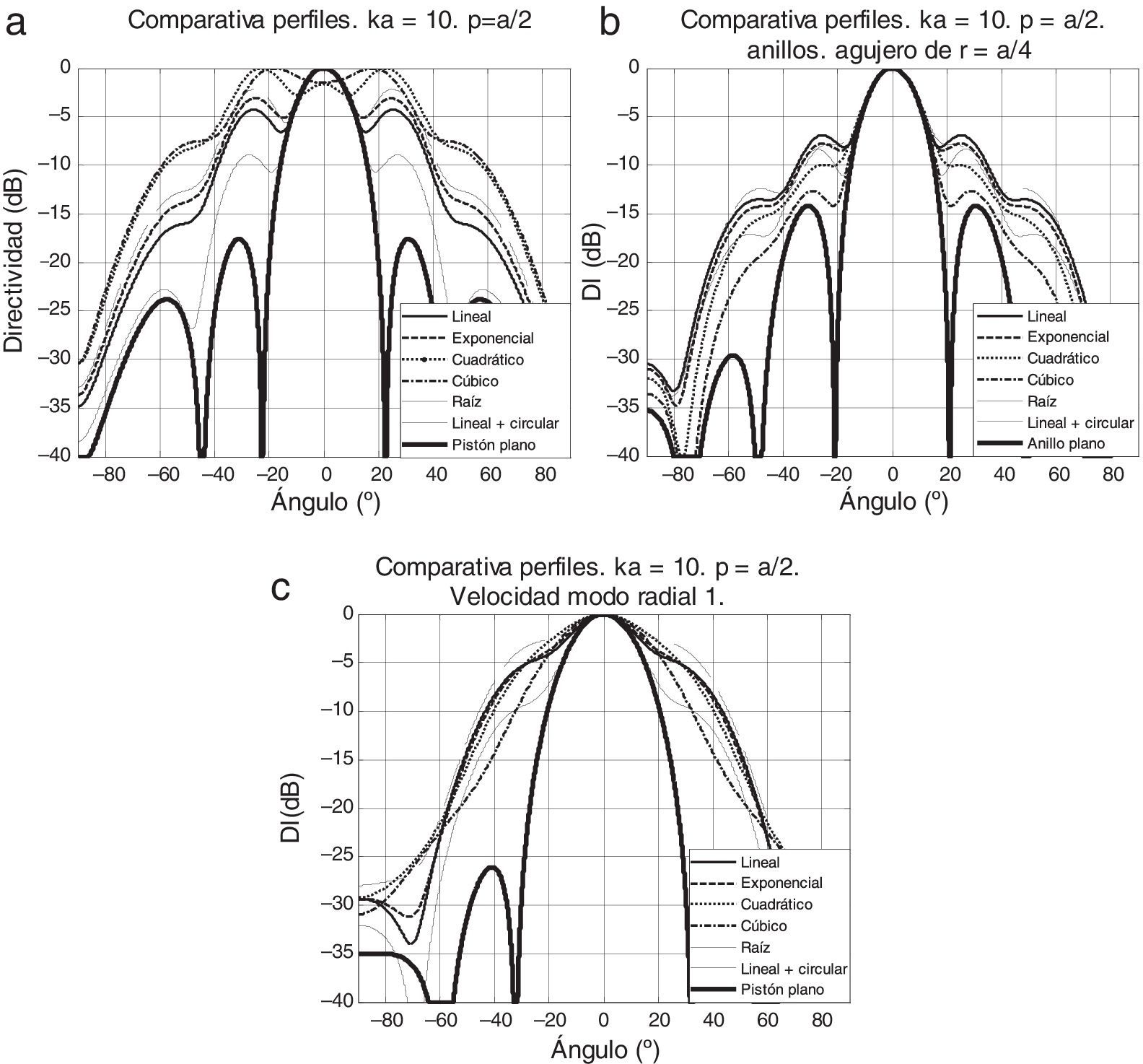
En la figura 12 se muestran diferentes comparativas. En la figura 12a se comparan los diferentes perfiles entre sí, con una profundidad p = a/2. En la figura 12b se aplica la ecuación (18) modificada con (22) generando un anillo de radio interior r = a/4 (y exterior a). En la figura 12c se valora el caso de que la velocidad no sea constante, introduciendo la velocidad del primer modo radial que se produce en el caso de que el pistón circular tenga condiciones de empotramiento en el borde según la ecuación (24).

Figura 12.

Comparativas de la direccionalidad entre perfiles.

En la figura 13 se comparan los resultados del pistón plano (o anillo plano) para el perfil cuadrático con profundidades p = a/2 y p = a. Se combinan los casos de velocidad del modo radial 1 (24), velocidad constante y en forma de anillo con radio interior r = a/4.

Figura 13.

Comparativas de la direccionalidad del perfil cuadrático con el pistón plano y anillo plano.

5

Conclusiones

En este trabajo se propone obtener el campo sonoro de pistones circulares y anillos no planos mediante un diferencial de anillo del que se conoce la expresión del diferencial de presión. La expresión integral que permite la resolución del problema se aproxima a un sumatorio de N anillos en (18), que permite una rápida resolución. Además, también se ofrecen modificaciones para aquellos casos con distribuciones de velocidades no constantes pero de simetría radial (21), o casos donde se consideren anillos no planos a través de la modificación propuesta en (22).

Obviamente, la simplificación del perfil en (16) es una aproximación de primer orden para resolver la integral que podría mejorarse con otras aproximaciones de mayor orden [27]. Sin embargo, se han realizado cálculos para los perfiles de este trabajo utilizando la fórmula de Simpson 3/8 [27] y los resultados no muestran diferencia apreciable. Esto puede deberse a que el error cometido en las aproximaciones de campo lejano es superior, para estos perfiles, a los dados por la aproximación de velocidad. Ese comentario puede extenderse para la aproximación de la velocidad en (20). Los resultados se obtienen en tiempos aceptables, tal y como se ha citado en el apartado de Resultados.

Respecto a los datos de respuesta en frecuencia se puede ver la coherencia de los resultados, puesto que los perfiles pueden considerarse planos si se cumple la relación [24]:

donde λ es la longitud de onda. La ecuación (26) puede expresarse en función de ka y de la relación entre la profundidad p y el radio a:

Aplicando la ecuación (27) en el caso de p = a, la condición deja de cumplirse en ka = 0,63, y para p = a/2 en ka = 1,26. En el caso de p = a/6, ka < 3,77. Esto es visible en las figuras 4 y 5 y en todas las figuras de direccionalidad (fig. 6 en adelante) al comparar en cada figura los resultados del perfil respecto a los obtenidos para el pistón plano. La condición (26) se ve modificada en el caso de algunos perfiles como el raíz (fig. 5), donde la condición se produce a valores de ka algo más elevados. Esto es debido a que, en ese caso, el perfil presenta una profundidad media más baja que los otros casos.

El análisis de las figuras 4 y 5 también muestra cómo se produce una caída en los niveles de presión respecto a la del pistón plano al aumentar ka, y esta se produce antes al aumentar la profundidad. La forma del perfil está influyendo en la rapidez de la caída.

En el caso de los anillos la caída se produce a valores de ka algo más altos y esta es menos pronunciada.

Respecto a la figura 5c, al incorporar el modo radial 1 de velocidad, se produce también ese aumento de ka para la caída y una relajación mayor de esta.

En conclusión, respecto a la respuesta en frecuencia, se cumple de forma generalizada (26), pero hay ciertas desviaciones hacia valores superiores de ka en función de la forma del perfil y de la velocidad.

Respecto a la direccionalidad puede verse que apenas hay cambios con los perfiles para valores de ka < 1. A partir de este valor, y en función de la profundidad, se abre el haz de manera generalizada en todos los casos.

Una variable de análisis y de interés es el ángulo de cobertura a -6 dB, que representa el ángulo respecto al valor de 0° donde el nivel desciende 6 dB multiplicado por 2, debido a la simetría. Puede verse cómo el ángulo de cobertura aumenta de manera general. Ejemplos de esto pueden verse en la figura 12a donde, para profundidades de p = a/2 y ka = 10, el perfil cuadrático ofrece 77,6° de ángulo de cobertura respecto a 25,6° del pistón plano, mejorando los resultados del pistón. Estos aumentos pueden verse también en otras figuras.

En el caso de que se practique una perforación para realizar un anillo puede observarse una pequeña disminución en el ángulo de cobertura de forma generalizada, y un aumento de lóbulos secundarios (figs. 12b y 13). Respecto a los efectos de la velocidad, en la figura 12c puede verse cómo el ángulo de cobertura aumenta y se suavizan las funciones de direccionalidad.

Por tanto, este trabajo sienta las bases para poder trabajar con mayor detalle, utilizando expresiones sencillas y de rápido cálculo, con pistones circulares y anillos no planos. Como futuras líneas de trabajo pueden proponerse, en primer lugar, la mejora de las simplificaciones del perfil (16) y de la velocidad (20). Esto producirá una disminución en el error cometido y un aumento de la velocidad de cálculo [27].

En segundo lugar, puede estudiarse con mayor detalle el efecto de la velocidad, incorporando un conjunto adecuado de modos radiales en el caso de que no se cumpla (19). En este trabajo solo se ha tenido en cuenta el primer modo radial y sería interesante ver el efecto de otros modos superiores y de su conjunto incorporando resultados recogidos en Leissa [28].

Agradecimientos

Este trabajo ha sido posible gracias al proyecto regular FONDECYT 1060117 y al proyecto de Cooperación Internacional FONDECYT 7060073.