En el presente documento se propone una discusión sobre el artículo «Evaluación numérica del efecto del espesor de la placa de contacto en la acción de palanca en conexión de acero tipo T» de L.M. Bezerra, C.S. de Freitas, W.T. Matias y J.E. Carmona. El principal punto que hay que tratar es la definición de los modelos T-equivalente (T-stub). También se han revisado las referencias bibliográficas existentes hasta el momento, así como el procedimiento seguido para el modelado de los componentes.
A discussion is proposed on the paper “Evaluación numérica del efecto del espesor de la placa de contacto en la acción de palanca en conexión de acero tipo T” by L.M. Bezerra, C.S. de Freitas, W.T. Matias and J.E. Carmona. The topics to be discussed are the definition of the T-stub model, the bibliographic references used in the work and the finite element analysis assumptions adopted in the modeling of the components.
Los autores del artículo al que nos referimos [1] desarrollan un modelo numérico mediante elementos finitos para el estudio de la distribución de las fuerzas de apalancamiento en componentes T-equivalente. Desarrollan un estudio que pretende determinar la influencia de ciertos parámetros en la distribución y en el desarrollo de dichas fuerzas de apalancamiento (fuerzas de contacto), así como para establecer el comportamiento final. A continuación se exponen los comentarios que se estima oportuno revisar en el trabajo presentado:
- 1)
Al inicio del artículo se desarrolla un breve estado de la cuestión referente al comportamiento de modelos T-equivalente. Se nombran trabajos relevantes, pero sin embargo no se cita el desarrollado por M. Couchaux ([2–5]), en el que se aborda la distribución de presiones de contacto en modelos T-equivalente desde un punto de vista analítico, basado en la teoría de vigas y considerando la influencia de las deformaciones transversales normales en el comportamiento de placas, desarrollada por G. Z. Voyiadjis, M. H. Baluch y W. K. Chi [6]. Tampoco se cita el trabajo desarrollado por M.E. Lemonis y C.J. Gantes [7], donde se analiza en profundidad el problema del contacto.
- 2)
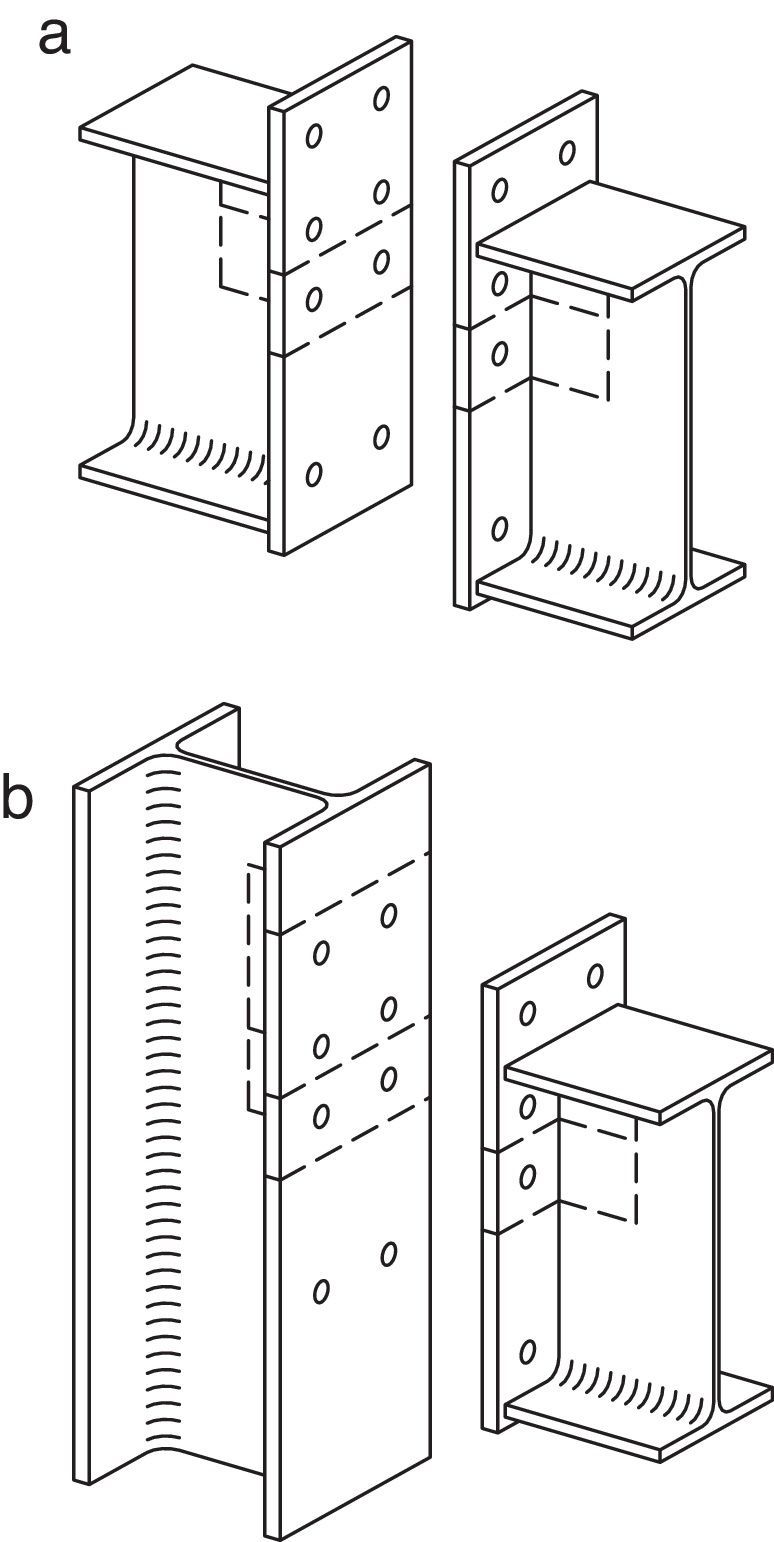
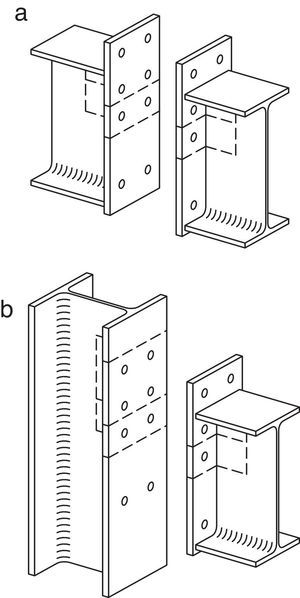
En el punto 1 también se indica que los modelos T-equivalente reales no se corresponden a modelos con simetría respecto al plano inferior del ala. Esta afirmación no es cierta, ya que conexiones tipo uniones viga-viga o viga-pilar, que se pueden observar generalmente en proyectos, tienen esta configuración (fig. 1).
- 3)
No se realiza una comparación del modelo de elementos finitos con ensayos en modelos reales con el fin de calibrar los parámetros de cálculo, como por ejemplo la calidad de la malla o la simplificación del diagrama tensión-deformación para los materiales. Aunque no estuvieran disponibles los datos correspondientes a los ensayos que se citan al final del artículo, en la bibliografía se presentan una gran cantidad de resultados experimentales publicados, entre los que cabe destacar los trabajos de O. Bursi y J.P. Jaspart [8], o los de C. Faella [9].
- 4)
El valor de las fuerzas de apalancamiento no solo depende del nivel de la carga aplicada en el alma de la conexión y de la rigidez de la placa. Un parámetro fundamental en el comportamiento global es la rigidez del tornillo, que depende principalmente de su longitud [10]. La longitud del tornillo considerada es excesiva para los modelos T-equivalente que se reproducen habitualmente en conexiones reales, como las mencionadas en el punto 1.
- 5)
El modelo adoptado supone una simplificación respecto a modelos reales. Según el tipo de tornillo (calidad y norma) es requisito disponer de una o 2 arandelas. No incorporar estos elementos en el modelado induce a estimar una longitud del tornillo equivalente, como se especifica en [11], para que se considere la flexibilidad adicional que aportan.
- 6)
Las condiciones de contorno establecidas en el tornillo no se corresponden con la realidad. Modelos numéricos (fig. 2a) y ensayos experimentales (fig. 2b y [12]) demuestran el comportamiento a flexión más tracción del tornillo y no solo a tracción, como se establece de forma simplificada en [13]. Por tanto, en el modelo debe permitirse el desplazamiento horizontal del vástago del tornillo, pero siempre restringido al espacio en el interior del agujero, por lo que deberá establecerse una condición de contacto adicional vástago del tornillo-agujero. La superficie inferior del tornillo deberá tener coaccionados solo los grados de libertad correspondientes a giros originados por flexión y a desplazamiento vertical.