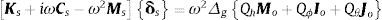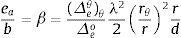Efectos torsionales en estructuras sobre suelo blando

Resumen

En este trabajo se evalúan las vibraciones torsionales de estructuras sobre suelo blando causadas por los efectos combinados de la asimetría estructural y la rotación de la base. Se analiza un sistema suelo-estructura simplificado con 5 grados de libertad. La cimentación se considera enterrada en un estrato uniforme descansando sobre un semiespacio elástico, ante la incidencia inclinada de ondas SH. En lugar de ajustar los máximos momentos torsionantes debidos a los efectos independientes de la asimetría estructural y la rotación de la base, se aplica un nuevo enfoque para el cálculo de la excentricidad de diseño. Específicamente, se obtienen coeficientes de excentricidad torsional compatibles con la máxima respuesta lateral-torsional acoplada, usando un conjunto de temblores de banda angosta característicos de sitios blandos de la Ciudad de México. Se muestra que estos coeficientes no son constantes a lo largo de los ejes principales, sino que dependen de la posición del elemento resistente, por lo que es necesario calcularlos sin asumir una variación lineal como está ocurriendo hasta ahora. Los coeficientes de excentricidad torsional pueden diferir significativamente de los actuales valores reglamentarios, particularmente para estructuras torsionalmente flexibles en las que ambos coeficientes pueden ser negativos. Esto implica que el desplazamiento lateral se reduce por los efectos torsionales.

Abstract

In this work the torsional vibrations of structures on soft soil caused by the combined effects of structural asymmetry and base rotation are evaluated. A simplified soil-structure system with five degrees of freedom is analyzed. The foundation is considered to be embedded into a uniform layer resting on an elastic half-space, under the incidence of inclined SH waves. Instead of matching the maximum torsional moments due to the independent effects of structural asymmetry and base rotation, a new approach for computing the design eccentricity is applied. Specifically, torsional eccentricity coefficients compatible with the peak coupled lateral-torsional response are obtained, using an ensemble of narrow-band earthquake motions typical of soft-soil sites in Mexico City. It is shown that these coefficients are not constant along the principal axes, but they depend on the position of the resistant element. Hence, it is necessary to compute them without assuming a linear variation, as is done nowadays. The torsional eccentricity coefficients can significantly differ from the currently codified values, particularly for torsionally flexible structures for which both coefficients may be negative. This implies that the lateral displacement is reduced by the effects of torsion.

1

Introducción

Para estructuras diseñadas conforme a reglamento, los efectos de torsión se consideran aplicando una fuerza estática equivalente a una distancia e_dis = αe + βb del centro de rigidez, donde e es la excentricidad geométrica dada por la distancia entre los centros de masa y rigidez, y b la dimensión de la planta del edificio perpendicular al movimiento de la excitación. El coeficiente α tiene en cuenta la amplificación dinámica de la respuesta torsional debida a la asimetría de la planta y el coeficiente β es para considerar otras fuentes de torsión, como la rotación de la base por el paso de ondas y las discrepancias existentes entre las excentricidades real y calculada. El paso de ondas puede generar grandes excitaciones torsionales de la base, incluso para estructuras simétricas.

Los valores típicos especificados en las normas de diseño sísmico [1–3] para estos coeficientes son α = 1 o 1,5 y β = 0,05 o 0,1. Estos valores están basados en análisis de estructuras desplantadas sobre base rígida, así como en el juicio ingenieril. Rosenblueth y Elorduy [4] fueron los primeros en definir un factor de amplificación para la excentricidad estática. Asimismo, el concepto de excentricidad accidental fue introducido en primer lugar por Newmark [5] para considerar las vibraciones torsionales inducidas por la rotación de la base. Desde entonces, varios autores han estudiado las excentricidades dinámica [6–8] y accidental [9–11] de estructuras apoyadas sobre base rígida, con el propósito de revisar las recomendaciones de los códigos de diseño.

Algunos estudios han revelado que la flexibilidad de la cimentación influye en el comportamiento a la torsión del sistema [12], si bien los patrones de respuesta siguen siendo similares a los observados en estructuras con base rígida. En particular, la amplificación dinámica de la excentricidad ha sido estudiada por Chandler y Hutchinson [13] suponiendo una excitación uniforme en la base, ignorando así los efectos del paso de las ondas sísmicas [14] y de la incoherencia del movimiento del terreno [15]. Estos autores demostraron que la máxima amplificación ocurre cuando la relación entre las frecuencias naturales desacopladas de torsión y traslación es cercana a la unidad. Al aumentar la flexibilidad de la cimentación, el efecto del acoplamiento entre los movimientos de traslación y torsión se incrementa para estructuras torsionalmente flexibles y se reduce para estructuras torsionalmente rígidas, respecto a los resultados de estructuras con base rígida.

El propósito de este trabajo es evaluar los efectos de torsión natural y accidental en estructuras con base flexible ante la incidencia no vertical de ondas SH. Los efectos combinados de la asimetría estructural y de la rotación de la base se interpretan por medio de coeficientes de excentricidad dinámica y accidental. Estos coeficientes se determinan ajustando el máximo desplazamiento acoplado de traslación y torsión que experimenta la estructura en distintos puntos de control entre el centro de rotación y el borde de la estructura, con el propósito de definir si a lo largo de estos puntos la variación de los desplazamientos máximos es lineal, como se ha supuesto hasta ahora. El método de análisis se describe brevemente, pues el énfasis está puesto en la presentación e interpretación de resultados para el caso particular de temblores de banda angosta característicos de la zona del lago de la Ciudad de México.

2

Ecuaciones de movimiento

Los efectos torsionales en estructuras con base flexible se estudian usando el modelo simplificado con excentricidad de masa mostrado en las figuras 1 y 2. La masa está distribuida de tal manera que el centro de masa se ubica a una distancia e del centro de rigidez. La altura de la estructura se denota con H_e, el radio de la cimentación con r y la profundidad de desplante con D. Las masas de la estructura y cimentación se identifican como M_e y M_c, sus momentos de inercia como I_e e I_c y sus momentos polares como J_e y J_c, respectivamente. La estructura se caracteriza por los periodos desacoplados de traslación y torsión, T_h y T_θ, para la condición de base rígida y sus correspondientes relaciones de amortiguamiento viscoso, ζ_h y ζ_θ. El suelo se idealiza como un estrato uniforme sobre un semiespacio elástico, caracterizados ambos con las velocidades de ondas de corte β_s y β_o, densidades de masa ρ_s y ρ_o, relaciones de Poisson ν_s y ν_o y relaciones de amortiguamiento histerético ζ_s y ζ_o.

Figura 1.

Modelo simplificado para evaluar efectos torsionales.

Figura 2.

Excentricidades dinámica y accidental para representar efectos torsionales.

La excitación del sistema está dada por ondas planas de corte con movimiento paralelo al eje y, propagándose con un ángulo γ respecto al eje z. Con este tipo de excitación, los movimientos de entrada al nivel de desplante de la cimentación son el desplazamiento horizontal Δ_o, el cabeceo ϕ_o respecto al eje x y la torsión θ_o respecto al eje z. Referida al centro de rigidez, la respuesta de la estructura se describe por el desplazamiento lateral Δ_e y la torsión θ_e relativos a la base, mientras que la respuesta de la cimentación se define por el desplazamiento lateral Δ_c, el cabeceo ϕ_c y la torsión θ_c relativos al terreno.

Las ecuaciones que gobiernan el movimiento del sistema en el dominio de la frecuencia pueden escribirse en notación matricial como [16]:

donde i=−1 es la unidad imaginaria y ω la frecuencia circular excitadora. Además, δs=Δe,Δeθ,Δc,Δcϕ,ΔcθT es el vector de amplitudes de los desplazamientos del sistema, siendo Δcϕ=(He+D)ϕc el desplazamiento de cabeceo en la parte superior de la estructura y Δeθ=dθeΔcθ=dθc los desplazamientos de torsión en la estructura y cimentación, respectivamente, en puntos de control ubicados sobre el eje x a una distancia d del centro de rigidez. Las relaciones Q_h = Δ_o/Δ_g, Q_ϕ = (H_e + D)ϕ_o/Δ_g y Q_θ = dθ_o/Δ_g representan las funciones de transferencia de los movimientos de entrada para traslación, cabeceo y torsión, respectivamente, siendo Δ_g el movimiento horizontal de campo libre en la superficie del suelo. En [16] pueden consultarse la forma y los elementos que constituyen los vectores de carga M_o, I_o y J_o, así como las matrices de masa M_s, amortiguamiento C_s y rigidez K_s del sistema.

Un paso fundamental en la solución de la ecuación (1) es el cálculo de las funciones de impedancia del suelo y de los movimientos de entrada de la cimentación. Las funciones de impedancia se calcularon con el método de estrato finito propuesto por Tassoulas y Kaussel [17], basado en modos de propagación del suelo discretos que satisfacen las condiciones de frontera de superficie libre y basamento flexible. Para el tratamiento de las condiciones de frontera absorbentes se utilizó la técnica propuesta por Andrade [18]. Se estudiaron cimentaciones cilíndricas enterradas en un estrato uniforme sobre un semiespacio elástico. Conocidas las funciones de impedancia, los movimientos de entrada se calcularon con el método promediador de Iguchi [19]. Para determinar la respuesta temporal del sistema ante excitación sísmica, se realizó la convolución de las funciones de transferencia Δe/Δg y Δeθ/Δg con sismos reales debidamente seleccionados, aplicando la síntesis de Fourier [20].

3

Coeficientes de excentricidad torsional

En el diseño de estructuras es de especial importancia establecer la forma de combinar los efectos torsionales debidos a la asimetría estructural y la rotación de la base. Un criterio conservador es suponer que las máximas respuestas torsionales independientes ocurren al mismo tiempo y en la misma dirección. Alternativamente, las excentricidades dinámica y accidental pueden definirse tal que el desplazamiento estático del lado flexible de la estructura ocasionado por el cortante basal desacoplado sea igual al desplazamiento dinámico máximo producido por la excitación sísmica. En la figura 2 se ilustra la fuerza estática V_o aplicada excéntricamente para producir el desplazamiento dinámico Δ_p en el punto x = d. Este criterio más racional es una extensión del propuesto por Dempsey y Tso [7] para considerar los efectos de torsión por asimetría de la estructura, y posteriormente ajustado por De la Llera y Chopra [10] para considerar los efectos de torsión por rotación de la base.

De acuerdo con lo anterior, las excentricidades dinámica e_d y accidental e_a satisfacen el siguiente requerimiento:

donde Δp=max|Δe+Δeθ| es el máximo desplazamiento dinámico acoplado. El primer término de la ecuación (2) representa el desplazamiento lateral desacoplado, mientras que el segundo mide el incremento de este debido a los efectos del acoplamiento torsional y de la excitación rotacional. Nótese que Vo=KhΔeo es el cortante basal desacoplado debido a la excitación efectiva de traslación y cabeceo, siendo K_h la rigidez lateral de la estructura y Δeo=max|Δe(e=0)| el máximo desplazamiento dinámico desacoplado.

Para determinar los valores de e_d y e_a, conviene descomponer la ecuación (2) de la siguiente forma:

donde (Δp)hϕ=max|Δe(Qθ=0)+Δeθ(Qθ=0)| es el desplazamiento dinámico máximo debido a la excitación efectiva de traslación y cabeceo. Sustituyendo Vo=KhΔeo en las ecuaciones (3) y (4), las excentricidades dinámica y accidental resultan ser:

donde b = 2r, y:

es la relación de frecuencias desacopladas de torsión y traslación, siendo ωθ=(Kθ/Je)1/2 y ωh=(Kh/Me)1/2; rθ=(Je/Me)1/2 es el radio de giro polar y er=e/r.

La relación (Δp)hϕ/Δeo es una medida de la modificación de la respuesta estructural por efectos del acoplamiento torsional. Nótese que si (Δp)hϕ/Δeo<1, los valores de α serán negativos. Asimismo, la relación [Δp−(Δp)hϕ]/Δeo es una medida de la modificación de la respuesta estructural por efectos de la excitación rotacional. Es evidente que los valores de β serán negativos cuando (Δp)hϕ>Δp. Valores negativos de α y β significan que el desplazamiento lateral se reduce por los efectos torsionales.

En el enfoque conservador se supone que ed=Mn/Vo y ea=Ma/Vo, siendo Mn=max|Δeθ(Qθ=0)|Kθ/d y Ma=max|Δeθ(Qh=Qϕ=0)|Kθ/d los momentos por torsión natural y accidental, respectivamente. Considerando que (Δeθ)hϕ=max|Δeθ(Qθ=0)| y (Δeθ)θ=max|Δeθ(Qh=Qϕ=0)|, se llega a:

Nótese que (Δeθ)hϕ y (Δeθ)θ son los desplazamientos dinámicos máximos debidos a las excitaciones efectivas lateral y torsional, respectivamente.

4

Resultados numéricos

Para fines de análisis estadístico, se usaron 90 movimientos horizontales registrados en 15 estaciones de campo libre localizadas en la Ciudad de México. Estos movimientos corresponden a 3 temblores de subducción con distancia epicentral entre 250 y 300 km. En la tabla 1 se listan las principales características de los movimientos seleccionados en sitios blandos donde se han observado las mayores amplificaciones espectrales. Además de la localización, se indican la magnitud (Mc = de coda, Mb = de ondas de compresión, Ms = de ondas superficiales), el periodo de la excitación (T_ns, Tew) y la aceleración máxima del terreno (A_ns, Aew). Los subíndices ns y ew indican la dirección en la que son consideradas estas variables (norte-sur y este-oeste, respectivamente). Con el propósito de promediar correctamente las respuestas de banda estrecha en sitios blandos [21], los registros sísmicos se normalizaron con el periodo dominante del sitio (para la Ciudad de México, se consideran temblores de banda estrecha los que ocurren en la zona de lago con periodos dominantes de 1 a 5 s).

Tabla 1.

Movimientos sísmicos seleccionados para análisis estadístico

Estación	Temblor: 89/04/25Long. –99,40; Lat. 16,60Mc = 6,5; Mb = 6,3; Ms = 6,9				Temblor: 93/10/24Long. –98,98; Lat. 16,54Mc = 6,5; Mb = 6,2; Ms = 6,6				Temblor: 95/09/14Long. –98,88; Lat. 16,31Mc = 6,4; Mb = 7,2; Ms = 7,3
	Tns (s)	Tew (s)	Ans (gal)	Aew (gal)	Tns (s)	Tew (s)	Ans (gal)	Aew (gal)	Tns (s)	Tew (s)	Ans (gal)	Aew (gal)
01	2,09	2,10	45,8	37,4	1,86	1,08	9,0	9,5	1,89	1,59	41,0	35,2
08	2,00	2,19	32,4	47,3	1,58	1,70	8,4	8,1	2,05	1,97	26,7	28,9
15	1,38	1,48	40,5	27,5	1,23	1,26	12,1	13,9	1,28	1,45	28,7	24,4
19	2,65	2,57	54,6	29,7	2,66	2,67	9,4	7,3	2,72	2,80	51,3	25,0
22	1,41	1,36	23,6	23,7	1,45	1,42	12,0	11,3	1,40	1,57	23,6	28,7
29	2,93	2,88	49,6	47,4	2,50	2,68	13,5	11,5	2,86	2,83	27,7	28,9
39	2,68	2,95	33,5	37,2	2,28	2,75	9,9	13,6	2,22	2,88	30,7	44,0
45	2,28	2,60	42,6	52,3	2,16	2,41	13,0	12,1	2,10	1,97	34,6	32,2
49	3,05	3,07	54,4	58,9	2,44	2,74	14,4	17,7	2,81	2,90	31,8	39,4
51	2,27	2,12	47,0	39,1	1,77	1,91	11,0	11,7	2,00	2,08	40,3	32,3
53	1,36	1,29	39,4	33,0	1,43	1,36	9,7	9,2	1,40	1,26	26,7	30,9
62	2,11	2,15	52,6	45,4	1,82	1,61	9,6	9,5	1,96	2,02	30,0	26,1
84	1,43	1,41	27,0	30,0	1,39	1,36	13,0	10,4	1,42	1,34	27,6	26,7
RO	1,19	1,25	45,7	55,0	1,17	1,37	15,9	14,5	1,38	1,29	29,1	37,3
SC	2,19	2,06	37,5	37,1	1,73	1,83	10,9	11,0	1,52	1,98	26,3	31,8

En todos los cálculos se adoptaron los siguientes valores: Mc/Me=0,25,Ic/Ie=Jc/Je=0,3,βs/βo=0,5,ρs/ρo=0,8,Me/ρsr2He=0,6,ζ_h = ζ_θ = 5%, ν_s = 0, 45, ν_o = 0, 33, ζ_s = 0, 05 y ζ_o = 0, 03. Por su importancia, los demás parámetros del sistema se consideraron variables. Los cálculos se llevaron a cabo para los 90 registros de temblores. Los resultados que se presentan en este estudio corresponden al valor medio de todos los registros, como se ilustra en la figura 3.

Figura 3.

Coeficientes α y β para e_r = 0,1, β_s/c = 0, 05, D/r = 1, r/β_s = 0, 15 y T_h = 1 s, para todos los registros utilizados en el estudio. Las líneas gruesas representan la media (línea continua) y la desviación estándar (línea discontinua).

Para reducir el número de ejemplos, se analizan estructuras bajas (He/r=1) con periodos cortos (T_h = 0, 25 y 0,5 s) y estructuras altas (He/r=3) con periodos largos (T_h = 1 y 2 s), apoyadas sobre cimentaciones superficiales (D/r=0) y enterradas (D/r=0,5 y 1), considerando relaciones de excentricidad e_r = 0,1 y 0,2. Los puntos de control están colocados a distancias d/r=0,2,0,6 y 1 del centro de rotación de la estructura. Los resultados se presentan en términos de valores medios de los coeficientes de excentricidad dinámica y accidental.

Para la caracterización de la excitación sísmica, el ángulo de incidencia se define como sen γ=βs/c, siendo c la velocidad horizontal aparente de onda. Asimismo, la flexibilidad de la cimentación se representa mediante el tiempo de tránsito r/βs. Los valores considerados para estos parámetros son βs/c=0,025 (γ ≈ 1, 5^∘), 0,05 (γ ≈ 3^∘) y 0,1 (γ ≈ 6^∘), así como r/βs=0,15 y 0,3 s.

En las figuras 4 y 5 se muestran comparaciones de los factores α y β calculados con los criterios racional y conservador cuando d/r=1. Como se esperaba, hay grandes diferencias entre los 2 criterios, excepto en los valores de α para periodos T_h ≤ 0,5 s, así como para periodos T_h ≥ 1 s cuando λ > 2. Con el criterio conservador, ambos factores crecen notablemente al aumentar la relación de excentricidad. Con el criterio racional, los valores de estos factores son inferiores a los obtenidos con el criterio conservador; incluso llegan a ser negativos para estructuras torsionalmente flexibles (λ < 1), lo que representa una reducción del cortante basal acoplado respecto al desacoplado usado como referencia. Nótese que esta situación favorable no es posible reproducirla con el criterio conservador. Los valores pico se tienen en λ < 1 (estructuras torsionalmente flexibles) si T_h ≤ 0, 5 s y en λ > 1 (estructuras torsionalmente rígidas) si T_h ≥ 1 s.

Figura 4.

Variación del coeficiente α para e_r = 0,1 (negro) y 0,2 (gris), fijando d/r 1, β_s/c = 0, 025, r/β_s = 0, 15 y D/r=1; criterio racional (—) versus conservador (–––).

Figura 5.

Variación del coeficiente β para e_r = 0, 1 (negro) y 0,2 (gris), fijando d/r=1,β_s/c = 0, 025, r/β_s = 0, 15 y D/r=1; criterio racional (—) versus conservador (–––).

Como se aprecia en la figura 4, las curvas de α obtenidas con el criterio conservador tienen la misma tendencia que las obtenidas con el criterio racional cuando se trata de estructuras bajas (He/r=1 con periodos cortos T_h ≤ 0, 5 s). Sin embargo, para estructuras altas (He/r=3 con periodos T_h ≥ 1 s) los resultados sí muestran una diferencia notable. Es importante señalar que en todos los casos examinados, sin importar el criterio que se utilice, el valor en el reglamento para α (de 1 a 1,5) no es rebasado, por lo que se concluye que los valores de α especificados en las normas de diseño sísmico resultan muy conservadores para sitios blandos de la Ciudad de México.

Los valores de α con el criterio conservador siempre son positivos, mientras que con el criterio racional pueden llegar a ser negativos. Esta situación es evidente para periodos T_h ≥ 1 s cuando λ < 1, y resulta porque los efectos torsionales reducen el cortante basal acoplado respecto al desacoplado usado como referencia.

Los valores de β con el criterio racional son muy inferiores a los del criterio conservador (fig. 5), pudiendo incluso ser negativos debido a la reducción del cortante basal acoplado. Esto último se manifiesta claramente en puntos de control interiores a la periferia de la estructura, como se ilustra posteriormente para d/r=0,2 y 0,6 (fig. 13). El valor acotado en las normas de construcción (β = 0,05 a 0,1) nunca es superado por los valores calculados utilizando el criterio racional, e incluso queda muy por debajo del valor de 0,05. En cambio, al utilizar el criterio conservador, los valores pico sobrepasan por mucho la norma, alcanzando en algunos casos valores superiores a 0,4 (T_h = 0, 5 s), y superando en todos los casos la cota reglamentaria mínima (0,05) para λ mayores después de donde se presenta el pico (cuando la curva tiende a un valor constante).

De acuerdo con los resultados del criterio racional, los valores de α y β especificados en las normas de diseño sísmico resultan muy conservadores para sitios blandos de la Ciudad de México. Es interesante hacer notar que los valores de α no rebasan la unidad, lo que revela una deamplificación dinámica de la excentricidad estática más que una amplificación confirmada solo para temblores de banda ancha.

Aplicando solamente el criterio racional, enseguida se examina la influencia de los principales parámetros del sistema. En la figura 6 puede verse que los valores pico de α para D/r=1 son mayores que para D/r=0, siendo el efecto más notorio cuando T_h = 0, 5 y 1 s. Esto se debe al cambio que sufre el cortante basal desacoplado por el incremento de rigidez en la cimentación al aumentar la profundidad de desplante.

Figura 6.

Variación del coeficiente α para D/r=0 (—), 0,5 (–––) y 1 (········), fijando d/r=1,β_s/c = 0, 1, r/βs=0,3 y e_r = 0, 2.

Por el contrario, en la figura 7 se aprecia que los valores pico de β se reducen cuando crece la relación de enterramiento, notándose el efecto muy claro para T_h = 0, 25 s. Esta situación es consecuencia de la difracción de ondas por las paredes de la cimentación, que altera las excitaciones efectivas lateral y torsional; a mayor profundidad de desplante de la cimentación, mayor es la difracción.

Figura 7.

Variación del coeficiente β para D/r=0 (—), 0,5 (–––) y 1 (········), fijando d/r=1,β_s/c = 0, 1, r/βs=0,3 y e_r = 0, 2.

En las figuras 8 y 9 se muestra el efecto de la flexibilidad de la cimentación en los factores α y β, respectivamente. Los valores de r/βs=0,15 y 0,3 corresponden, por ejemplo, a una cimentación con r = 15 m en un suelo blando con β_s = 100 y 50 m/s, respectivamente. Los efectos debidos a estas variaciones en el tiempo de tránsito son insignificantes para α pero importantes para β. Esto implica que la influencia de r/βs es mayor en la excitación efectiva torsional (responsable de la excentricidad accidental) que en la excitación efectiva lateral (responsable de la excentricidad dinámica).

Figura 8.

Variación del coeficiente α para r/βs=0,15 (—) y 0,3 (········), fijando d/r=1,β_s/c = 0, 025, D/r=1 y e_r = 0, 2.

Figura 9.

Variación del coeficiente β para r/βs=0,15 (—) y 0,3 (········), fijando d/r=1,β_s/c = 0, 025, D/r=1 y e_r = 0, 2.

El parámetro relevante que mide el efecto del paso de las ondas sísmicas en el sistema es la velocidad horizontal aparente (c), debido a que indica el retraso que habrá en la llegada de la excitación de un punto a otro de la cimentación. En otras palabras, la parte iluminada del cimiento es la que empezará a moverse primero y los puntos ubicados en el lado de sombra serán los últimos. Es por ello que la relación βs/c=sen γ (γ es el ángulo de incidencia) es una mejor medida para caracterizar la excitación sísmica. El efecto del paso de las ondas sísmicas en los factores α y β se puede apreciar en las figuras 10 y 11, respectivamente. Se observa que α es insensible a la variación de βs/c, en tanto que β es fuertemente dependiente de este parámetro. La razón es que la excitación efectiva torsional es proporcional a γ, que a su vez es proporcional a βs/c. Nótese que los valores pico de β para T_h = 2 s son muy altos en comparación con los demás periodos estructurales.

Figura 10.

Variación del coeficiente α para βs/c=0,025 (—), 0,05 (–––) y 0,1 (········), fijando d/r=1,r/βs=0,15,D/r=0 y e_r = 0, 1.

Figura 11.

Variación del coeficiente β para βs/c=0,025 (—), 0,05 (–––) y 0,1 (········), fijando d/r=1,r/βs=0,15,D/r=0 y e_r = 0, 1.

Finalmente, la posición del punto de control influye considerablemente en los factores α y β, como se muestra, respectivamente, en las figuras 12 y 13. Esto tiene implicaciones en el diseño de estructuras asimétricas, pues erróneamente suele suponerse que la variación de los desplazamientos máximos a lo largo de los ejes principales es lineal. Puede observarse que los mayores picos negativos de ambos factores ocurren en d/r=0,2, cuando λ < 1. Estos picos se producen para el mismo valor de λ, lo que significa que el desplazamiento generado por torsión va en el sentido opuesto al que ocurre por la traslación. Asimismo, los mayores picos positivos de α ocurren en d/r=1 y los de β en d/r=0,2. Los resultados para T_h ≥ 1 s están mejor perfilados que para T_h ≤ 0, 5 s, independientemente de la posición del punto de control.

Figura 12.

Variación del coeficiente α para d/r = 0,2 (—), 0,6 (–––) y 1 (········), fijando β_s/c = 0, 025, r/βs=0,3,D/r=0 y e_r = 0, 2.

Figura 13.

Variación del coeficiente β para d/r=0,2 (—), 0,6 (–––) y 1 (········), fijando β_s/c = 0, 025, r/βs=0,3,D/r=0 y e_r = 0, 2.

5

Conclusiones

En este trabajo se han evaluado los efectos torsionales en estructuras sobre suelo blando debidos a la asimetría estructural y la rotación de su base. Los efectos combinados se han representado por medio de coeficientes de excentricidad torsional compatibles con la máxima respuesta acoplada en distintos puntos de control entre el centro de rotación y el borde de la estructura.

Se ha mostrado que los factores α y β no tienen definición única, porque dependen de la selección del cortante basal de referencia y de la forma de separar los efectos de torsión por asimetría de la estructura y rotación de la base. Usando un conjunto de temblores de banda angosta característicos de sitios blandos de la Ciudad de México, se han calculado valores medios de estos factores para varias configuraciones del sistema suelo-estructura examinado.

Se han revisado 2 criterios para obtener los valores de α y β: uno que considera que las máximas respuestas torsionales debidas a la asimetría estructural y la rotación de la base ocurren al mismo tiempo, y otro donde se considera el máximo desplazamiento acoplado de traslación y torsión. De este análisis se concluye que las diferencias en los resultados al utilizar uno u otro enfoque pueden ser muy significativas.

Las formas de α y β varían ampliamente con λ, exhibiendo valores que van de pequeños a grandes en comparación con los actuales valores reglamentarios. Los valores observados incluso pueden ser negativos, en cuyo caso los desplazamientos de torsión actúan favorablemente en dirección contraria a los de traslación. Se observa que la excentricidad dinámica es más sensible a los cambios de e_r, mientras que la excentricidad accidental lo es a los cambios de δ_d y βs/c.

Si bien no es práctico seleccionar valores constantes para cubrir cualquier combinación de parámetros del sistema, los máximos valores observados son α = 0, 9 y β = 0, 12. En general, los valores de α crecen al acercarse a la periferia de la estructura, mientras que los valores de β crecen al acercarse al centro de rotación.