Procedimentos experimentais em túneis de vento têm sido tradicionalmente empregados como uma ferramenta fundamental para avaliação dos efeitos aerodinâmicos e aeroelásticos causados pela ação do vento sobre estruturas presentes na engenharia civil, tais como pontes e edifícios esbeltos. Nas últimas décadas, devido à grande versatilidade apresentada pelos métodos numéricos para a variação dos parâmetros físicos e geométricos, a simulação computacional tem‐se tornado uma ferramenta muito atraente. A dinâmica de fluidos computacional (DFC), a dinâmica das estruturas computacional (DEC) e técnicas de interação fluido‐estrutura (IFE) são empregadas para a análise aerodinâmica e aeroelástica em diversos campos da engenharia. Neste trabalho estuda‐se inicialmente a ação do vento no comportamento aerodinâmico e aeroelástico da ponte sobre o rio Guamá, Brasil, cujos estudos experimentais foram conduzidos pelo Laboratório de Aerodinâmica das Construções (LAC) no Túnel de Vento Prof. Joaquim Blessmann, da UFRGS. Procura‐se neste caso simular os ensaios experimentais realizados para a determinação das características aerodinâmicas e aeroelásticas da ponte empregando procedimentos numéricos com modelos seccionais. Finalmente, apresenta‐se a análise aeroelástica de um edifício esbelto flexível. Bons resultados são obtidos através da solução numérica, quando comparados com os resultados experimentais.
Experimental tests in wind tunnels have been traditionally employed as a fundamental tool to evaluate aerodynamic and aeroelastic effects due to wind action on civil engineering structures, such as bridges and slender buildings. In the last decades, due to the versatility presented by numerical methods to change physical as well as geometrical parameters, numerical simulation has become a very attractive tool. Computational Fluid Dynamics (CFD), Computational Structural Dynamics (CSD) together with Fluid‐Structure Interaction (FSI) techniques are employed in aerodynamic and aeroelastic analysis in several engineering fields. Aerodynamic and aeroelastic behavior due to wind action on the Guama River Bridge, located at Pará State, Brazil, is first studied, taking into account experimental tests performed in the Wind Tunnel Joaquim Blessman of the Building Aerodynamic Laboratory, UFRGS. Numerical procedures are used to simulate experimental tests in order to determine aerodynamic and aeroelastic characteristics of the bridge, which is idealized by sectional models. Finally, an aeroelastic analysis of a flexible slender building is presented. Good results are obtained using numerical simulation, when compared with experimental tests.
Por muitos anos os túneis de vento têm sido a única ferramenta disponível para a avaliação da ação do vento sobre as estruturas em geral. No entanto, com o atual estágio tecnológico dos computadores aliado à maturidade dos métodos numéricos já desenvolvidos, a simulação numérica tem‐se tornado atualmente uma ferramenta essencial na análise da ação do vento sobre estruturas. Através da utilização da dinâmica dos fluidos computacional (DFC) foi possível o desenvolvimento da chamada engenharia do vento computacional (EVC), que trata de diversos problemas de interesse na engenharia civil, tais como a aerodinâmica de pontes e prédios, conforto de pedestres, dispersão de poluentes, análise da circulação num meio urbano, entre outros.
No caso de estruturas de pontes de grande vão, a ação do vento pode ser estimada através da identificação das características aerodinâmicas e aeroelásticas da seção. Por meio dos coeficientes aerodinâmicos, tais como os coeficientes de arrastro, de sustentação, de torção e de pressão, é possível determinar‐se as forças que o vento exerce, em termos estáticos, sobre a estrutura. Por outro lado, como consequência da forte interação entre as forças aerodinâmicas e as vibrações apresentadas pela estrutura, podem surgir problemas de instabilidade aeroelástica, como o drapejamento (ou «flutter» na terminologia em inglês), por exemplo, muito comum neste tipo de estrutura devido ao seu baixo amortecimento e a sua baixa rigidez. O drapejamento tem como característica induzir a estrutura a um movimento oscilatório de amplitude crescente, uma vez que a velocidade crítica é atingida. Este fenômeno é considerado como sendo a causa da grande maioria dos acidentes ocorridos até hoje em pontes de grande vão livre. Em edifícios esbeltos, o vento pode provocar desprendimentos de vórtices que geram oscilações crescentes na direção transversal ao escoamento. Para a análise de fenômenos aeroelásticos, além da dinâmica de fluidos computacional (DFC), utilizada na análise aerodinâmica, é necessária a utilização de métodos da dinâmica das estruturas computacional (DEC) e levar em conta a interação fluido‐estrutura (IFE).
Neste trabalho é realizada a análise aerodinâmica e aeroelástica da ação do vento sobre as seções de projeto da ponte sobre o rio Guamá, localizada no estado do Pará, Brasil, simulando, assim, os ensaios realizados. Esta ponte teve os estudos experimentais conduzidos pelo Laboratório de Aerodinâmica das Construções (LAC) da Universidade Federal do Rio Grande do Sul (UFRGS) no Túnel de Vento Prof. Joaquim Blessmann, sendo os resultados apresentados nas XXX Jornadas Sul‐Americanas de Engenharia Estrutural, realizada na Universidade de Brasília, DF, Brasil, no ano de 2002 Souza et al. [1] e Rocha et al. [2]. Os ensaios experimentais foram executados sobre diferentes modelos seccionais, determinando‐se os coeficientes aerodinâmicos em função dos ângulos de ataque, além da determinação de velocidades críticas que provocam instabilidade.
A análise do escoamento de um fluido incompressível é feita utilizando o método dos elementos finitos (MEF) para a discretização espacial e um esquema explícito para a discretização temporal. Um dos primeiros trabalhos na análise aerodinâmica numa seção de uma ponte usando o MEF foi realizado por Kawahara e Hirano [3], sendo que posteriormente Selvam e Bosch [4], Shirai e Ueda [5] e Bruno e Khris [6], entre outros, realizaram um trabalho tratando o mesmo tema. Selvam et al. [7] e Frandsen e Mc Robbie [8] usaram o MEF para a análise aeroelástica de pontes, enquanto Larsen e Walther [9] usaram o método dos vórtices discretos. Morghental e Mc Robie [10] compararam diversos métodos de interação fluido‐estrutura para pontes de grandes vãos.
Também é realizada a análise aeroélástica de um edifício esbelto flexível, realizado experimentalmente no LAC/UFRGS por Miguel [11] e Trein [12]. Numerosos são os trabalhos para analisar os efeitos aerodinâmicos através da simulação numérica, considerando modelos de edifícios rígidos. Entretanto, raramente são encontrados modelos numéricos para tratar fenômenos aeroelásticos em edifícios esbeltos e flexíveis. Como exemplo pode‐se mencionar o trabalho de Swaddiwudhipong e Khan [13].
Emprega‐se uma descrição Arbitrária Lagrangeana‐Euleriana (ALE) no caso da análise do comportamento aeroelástico para descrever o movimento da malha, que acompanha os deslocamentos da estrutura. O modelo de Smagorinsky ou também denominado modelo de simulação de grandes vórtices, conhecido na literatura em inglês por large eddy simulation ou LES (Petry e Awruch [14] e Popiolek et al. [15]), é incluído para simular as escalas de turbulência menores que a da resolução da malha utilizada. Em modelos seccionais, a estrutura é considerada como um corpo rígido com restrições elásticas segundo os componentes de deslocamento horizontal e vertical e segundo a rotação correspondente à torção, já em modelos tridimensionais são considerados corpos elásticos deformáveis. O acoplamento entre o fluido e a estrutura é efetuado aplicando as condições de compatibilidade e de equilíbrio na interface. A análise dinâmica da estrutura é feita utilizando o algoritmo clássico de Newmark ou algoritmos com conservação de energia (em problemas com significativa não linearidade geométrica).
2As equações que governam o escoamentoAs equações que governam o escoamento com as correspondentes condições de contorno, considerando uma descrição ALE, são as seguintes:
- a)
Equações de conservação da quantidade de movimento:
- b)
Equação da conservação de massa:
que é obtida considerando que ∂p∂ρ=c2, sendo Ω o domínio do fluido. - c)
Condições de contorno:
Nas equações apresentadas acima, vi e p (que são, respectivamente, as componentes da velocidade e a pressão) são as incógnitas do problema. As viscosidades cinemática ν e volumétrica λ, a massa específica ρ e a velocidade de propagação de ondas sonoras c, são as propriedades do fluido. Para uma descrição puramente Euleriana, a velocidade de movimento da malha, cujas componentes são wi, é nula. Já para uma descrição puramente Lagrangeana, a velocidade de movimento da malha coincide com a do fluido, ou seja, vi=wi. No caso de uma descrição do tipo ALE, os vetores de velocidade da malha (w→) tomam valores não nulos e intermediários entre 0 (nos contornos do domínio computacional) e a própria velocidade do fluido v→ sobre o corpo imerso. Nos contornos Γcv e Γcp, valores prescritos v→˜ e p˜, respectivamente, devem ser especificados, enquanto que em Γσ as componentes da força de contorno t˜i devem estar em equilíbrio com as componentes do tensor de tensões σij=−pδij+τij. Na eq. (5), nj é o cosseno de direção que a normal a Γσ forma com o eixo coordenado xj. Todas estas equações são acompanhadas de condições iniciais para os campos de velocidade e de pressão no instante t=0.
Como pode ser observado, é incorporado às equações um modelo de turbulência através da viscosidade turbulenta νt, sendo aqui utilizada a simulação de grandes vórtices (denominada «LES» na literatura técnica en inglês) com o modelo de Smagorinsky apresentado por Braun e Awruch [16,17] para as escalas de turbulência inferiores à resolução da malha de elementos finitos. Neste modelo a viscosidade turbulenta fica definida pela seguinte expressão:
sendo Sij=12∂vi∂xj+∂vj∂xi o tensor taxa de deformação e Δ=V13, onde V é o volume do elemento. CS é a chamada constante de Smagorinsky, assumindo usualmente valores no intervalo entre 0,10 e 0,25. Alternativamente, pode‐se usar o modelo dinâmico de Smagorinsky, no qual Cs=Cs (x, y, z, t), também utilizado por Braun e Awruch [16,17].
Aplicando o MEF para o domínio espacial e utilizando um esquema explícito para avançar no tempo, podem ser obtidas as componentes de velocidade e o campo de pressões do fluido. Basicamente, os passos são os seguintes: (a) calculam‐se as componentes da velocidade no tempo atual com a equação de conservação da quantidade de movimento usando variáveis do tempo anterior; (b) calcula‐se o incremento de pressão com a equação da conservação de massa usando as componentes de velocidade do tempo anterior; (c) calculam‐se novamente as componentes da velocidade no tempo atual, corrigindo as mesmas, utilizando o incremento de pressão obtido no tempo anterior; (d) finalmente, a pressão é atualizada com as novas componentes das velocidades calculadas no passo (c) e com o incremento de pressão obtido no passo (b). Em cada um dos passos, as condições prescritas para as variáveis correspondentes são aplicadas. Detalhes do algoritmo são apresentados por Braun e Awruch [16]. A discretização é realizada com elementos isoparamétricos bilineares (no caso de problemas onde a estrutura é representada por um modelo seccional) ou trilineares (em problemas tridimensionais) usando apenas um ponto de integração com controle dos modos espúrios, cujos detalhes também são apresentados por Braun e Awruch [16].
3Cálculo dos coeficientes aerodinâmicosOs coeficientes de arrasto CD, de sustentação CL e de momento torçor CM são definidos, respectivamente, por:
onde pD=0,5(ρV02L0) é a pressão dinâmica, e S1I e S2I são as forças nas direções dos eixos x1 e x2, respectivamente, que atuam sobre a estrutura no nó i, localizado na interface, sendo l1i e l2i as projeções segundo os eixos x1 e x2, respectivamente, da distância do centro de gravidade do corpo ao nó i. NTN é o número total de nós localizados no contorno da estrutura (ou seja, na interface sólido‐fluido). V0 e L0 são a velocidade e a dimensão de referência, respectivamente. As forças S1I e S2I são calculadas a partir das forças S∼I oriundas da eq. (5); que atuam sobre a estrutura em cada lado ou face de um elemento de fluido que pertença à interface. Os coeficientes aerodinâmicos seguem uma convenção de sinais onde o arrasto e a sustentação têm seus eixos positivos considerados de acordo com os eixos que constituem um plano no primeiro quadrante, com o eixo do arrasto estando na direção e sentido do próprio escoamento. Por fim, o coeficiente de torção é considerado positivo quando o momento gerado age no sentido anti‐horário. Os valores instantâneos dos coeficientes dados pela eq. (7) servem para se obter curvas do histórico dos mesmos, assim como um valor médio num certo intervalo de tempo.
4As equações que governam a dinâmica das estruturas de corpos rígidos (utilizadas em modelos seccionais) considerando o acoplamento com o fluidoPara os modelos seccionais, a estrutura é considerada como um corpo rígido bidimensional (ou seja, que sua forma permanece inalterada), que pode ter deslocamentos e rotações no seu plano, restringidos por molas e amortecedores, conforme indicado na figura 1.
A equação de equilíbrio dinâmico da estrutura é dada pela seguinte expressão matricial:
sendo M∼E a matriz de massa, C∼E a matriz de amortecimento, K∼E a matriz de rigidez e U¨∼Ec,U˙∼Ec e U∼Ec os vetores de aceleração, velocidade e deslocamentos generalizados, respectivamente. Finalmente, Q∼Ec é o vetor de cargas. M∼E, C∼E e K∼E são matrizes diagonais de ordem 3×3; os 3 valores de cada propriedade, dados na figura 1, são incluídos na diagonal principal da matriz correspondente. O subíndice E serve para identificar que se trata de matrizes da estrutura e o superíndice C indica que os valores correspondentes são tomados no centro de gravidade do corpo. Convém observar que a hipótese de uma estrutura rígida, que pode deslocar‐se e ter uma rotação, é adequada quando as deformações da seção transversal são muito pequenas frente à magnitude dos componentes de deslocamento e da rotação.
Na interface sólido‐fluido deve ser satisfeita a condição de compatibilidade, ou seja, deve cumprir‐se que as velocidades do fluido e da estrutura sejam iguais nos nós comuns a ambos os meios. Deve também ser satisfeita na interface sólido‐fluido a condição de equilíbrio de forças, ou seja, que a força S∼, dada na eq. (5), e que representa a ação da estrutura sobre o fluido, deve‐se equilibrar com a força ‐ S∼, exercida pelo fluido sobre a estrutura.
A expressão matricial do equilíbrio dinâmico da estrutura fica modificada ao se introduzir os efeitos dos elementos finitos de fluido que tem um lado em comum na interface com a estrutura, e pode ser escrita em forma compacta, depois de considerar o efeito de todos os elementos finitos do fluido com um lado comum na interface com a estrutura, da seguinte forma:
A matriz de amortecimento C¯∼E é não linear e não simétrica. Por outro lado, as matrizes de massa, amortecimento e rigidez, assim como o vetor de cargas, são apresentadas por Braun e Awruch [17].
Neste trabalho não é considerado em nenhum caso um acoplamento monolítico entre o fluido e a estrutura, analisando‐se de forma sequencial ambos os meios.
A eq. (9) é integrada no tempo utilizando‐se o método implícito de Newmark, obtendo‐se U¨∼Ec,U˙∼Ec e U∼Ec em t+Δt correspondente a um novo nível no tempo n+1, de onde pode‐se calcular U˙∼IE=V∼IF (que é a velocidade do fluido em cada nó da interface). Este valor é utilizado como condição prescrita para uma nova análise do escoamento.
5As equações que governam a dinâmica das estruturas de corpos deformáveis e a interação fluido‐estruturaCom base na observação dos problemas estudados pela engenharia do vento, as seguintes hipóteses são consideradas neste trabalho para o modelo analítico de análise da estrutura: (1) consideram‐se apenas materiais elásticos lineares dentro do regime de pequenas deformações com não linearidade geométrica (devida a deslocamentos e rotações finitos); (2) a descrição cinemática da estrutura é feita através de uma formulação Lagrangena atualizada.
As equações de equilíbrio dinâmico são obtidas a partir das equações de conservação de quantidade de movimento (que inclui as forças de inércia), de conservação de massa e da equação constitutiva do material, que neste trabalho é considerada elástica linear. As variáveis da estrutura são as componentes ui do vetor de deslocamentos u (cujas derivadas primeira e segunda em relação ao tempo constituem as componentes da velocidade e da aceleração, respectivamente), as componentes σij do tensor de tensões de Cauchy σ e as componentes ¿ij do tensor de deformações de engenharia ¿. Condições iniciais para os vetores de deslocamento e velocidade, assim como condições de contorno para os vetores de deslocamento e de força atuando na superfície do sólido, devem ser fornecidas para a solução do sistema de equações de equilíbrio dinâmico, a qual é obtida empregando‐se o método implícito de Newmark juntamente com o esquema α‐Generalizado, cujos detalhes são apresentados por Braun e Awruch [18], e que é utilizado para a manutenção da estabilidade numérica em problemas com significativa não linearidade geométrica. A discretização da estrutura no espaço é efetuada usando‐se elementos finitos hexaédricos isoparamétricos de 8 nós com integração reduzida e um esquema para a estabilização de modos espúrios, que foi apresentado por Duarte Filho e Awruch [19].
No presente modelo, a solução do problema aeroelástico é obtida utilizando‐se um esquema de acoplamento fluido‐estrutura particionado com características superiores de conservação, o qual possibilita o uso da técnica de subciclos entre as análises do fluido e da estrutura e de malhas independentes para cada um dos meios físicos existentes. Detalhes sobre o esquema particionado com subciclos e a utilização de malhas de elementos finitos independentes para o fluido e a estrutura com nós não coincidentes podem ser encontrados em Braun e Awruch [16].
Para que o acoplamento fluido‐estrutura seja realizado corretamente, as seguintes condições devem ser impostas ao sistema completo sobre a interface fluido‐estrutura:
(a) Equação de equilíbrio de forças:
(b) Equações de compatibilidade cinemática:
onde σe e ue são o tensor de tensões e o vetor de deslocamentos da estrutura, p e τf são o vetor de pressão e o tensor de tensões viscosas do escoamento, x é o vetor posição da malha do escoamento e n é o vetor de cossenos de direção da normal em um ponto qualquer de Γisf (que representa a interface sólido‐fluido).O algoritmo de solução para um problema de IFE utilizado neste trabalho é descrito na figura 2.
Os próximos passos são os seguintes: (1) transferir o movimento dos contornos da estrutura em contato com o fluido ao sistema de equações do escoamento; (2) atualizar os dados referentes à malha do fluido; (3) avançar a análise do escoamento e computar a carga devido à ação do fluxo sobre os contornos da estrutura em contato com o fluido; (4) avançar a análise da estrutura considerando a ação da carga devido ao escoamento, calculada no passo (3); (5) repetir os passos 1‐4 para o próximo incremento de tempo até que o tempo total seja atingido.
6Atualização da malha em corpos rígidosLevando em conta que o corpo imerso no fluido pode deslocarse e rotacionar em seu plano e que o escoamento é descrito com uma descrição do tipo ALE, é necessária uma lei que governe o movimento da malha, estabelecendo o campo de velocidades w→ no domínio do fluido, de forma tal que a distorção dos elementos seja a menor possível e que respeite as condições de contorno seguintes:
Neste trabalho, o esquema de movimento da malha é similar ao que foi usado por Texeira e Awruch [20]. Considera‐se que i seja um ponto no interior do domínio do fluido e j um nó pertencente a um contorno. Logo, as componentes da velocidade da malha no nó i, segundo a direção do eixo xk, são dadas por:
onde NS é o NTN pertencentes às linhas de contorno e aij são os coeficientes de influência entre os pontos no interior do domínio e os das linhas de contorno, sendo dij a distância entre i e j, e n≥1. O expoente n pode ser ajustado pelo usuário, sendo empregado usualmente n=4. Em problemas tridimensionais, o critério de movimento da malha é o mesmo que o indicado na eq. (13), porém o subíndice k varia de 1‐3.7Aplicações numéricas a problemas de engenharia civil7.1Análise aerodinâmica e aeroelástica da ponte sobre o rio Guamá (estado de Pará‐Brasil)Nesta seção são apresentados os resultados obtidos na simulação numérica dos ensaios realizados para a ponte sobre o rio Guamá. Esta ponte localiza‐se no estado do Pará, Brasil, sendo constituída de um vão central de 320m e 2 vãos de 131m cada, como pode ser observado na figura 3. O tabuleiro apresenta uma largura de 14,2m, suspenso a 31m sobre o espelho do rio. Estruturalmente esta ponte é classificada como sendo do tipo estaiada.
Ponte sobre o rio Guamá: elevação (fonte: ref. [2]).
Nos estudos experimentais foram disponibilizadas 3 diferentes configurações geométricas de seção transversal, com diferenças nas formas dos guarda‐corpos e guarda‐rodas e nas longarinas do tabuleiro. Duas delas foram empregadas para a análise aerodinâmica e a restante foi utilizada para o estudo aeroelástico como indicado em Souza et al. [1] e em Rocha et al. [2]. Na figura 4, onde as medidas são dadas em centímetros, são indicadas as características geométricas dos modelos seccionais usados no túnel de vento e que também são empregados no presente trabalho.
Características geométricas das seções estudadas para as análises aerodinâmica e aeroelástica da ponte sobre o rio Guamá (fonte: ref. [2]).
Na análise aerodinâmica utilizam‐se 2 tipos de modelos seccionais: um modelo, denominado Configuração I, caracterizado pela presença de guarda‐rodas maciços e guarda‐corpos pré‐moldados (detalhes que foram considerados no modelo numérico), enquanto o outro modelo, denominado Configuração II, possui guarda‐rodas vazados e guarda‐corpos em cercado aramado (sendo que este último detalhe não foi considerado no modelo numérico). Na análise aeroelástica é empregada a segunda configuração, porém com uma inclinação das paredes internas das longarinas mais acentuada, sendo este modelo denominado Configuração III. Adotou‐se nas análises, como critério para a malha de elementos finitos, um tamanho mínimo de elemento igual a 1% da dimensão característica do corpo sólido (no caso, a largura da ponte). Entretanto, a dimensão mínima do elemento indicada acima foi reduzida ainda mais para atender a detalhes geométricos das barreiras Jersey e cercas de proteção. A malha de elementos finitos referente à Configuração I tem 23.324 elementos e 23.775 nós com a menor dimensão na ordem de 0,02m. Para a Configuração II a malha tem 19.762 elementos e 20.117 nós e a menor dimensão de malha também ficando por volta de 0,02m. Finalmente, para a Configuração III tem‐se 21.504 elementos, 21.894 nós com a menor dimensão encontrada de 0,01m. Apenas esta última malha é apresentada na figura 5. Como pode se notar, a seção está deslocada verticalmente e possui também um giro inicial (o que também é feito quando se realiza a análise experimental). Isto se deve aos procedimentos de análise usados em problemas de instabilidade.
Neste trabalho é realizada primeiramente uma série de análises para estudar o comportamento aerodinâmico sobre as Configurações I e II, de onde são obtidos os coeficientes aerodinâmicos para ângulos de ataque compreendidos no intervalo entre –8° e +8°. O estudo caracteriza‐se pela análise da ação do vento sobre uma dada seção, rígida e indeslocável, para os vários ângulos de incidência, determinando‐se os coeficientes médios de arrasto (CD), sustentação (CL) e de momento aerodinâmico (ou de torção) (CM) em função destes ângulos e a partir dos históricos obtidos durante o período de tempo analisado.
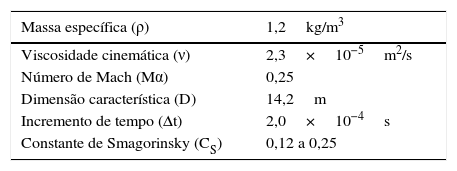
Na tabela 1 estão relacionados os principais dados empregados na caracterização dos problemas analisados. Como indicado na tabela, foram tomados diferentes valores para a constante de Smagorinsky (CS), sendo que os resultados apresentados referemse a constantes usadas que produziram o resultado mais próximo dos ensaios experimentais. Consideram‐se ainda condições de contorno dos bordos externos em função da velocidade de escoamento livre (V0) e dos ângulos de ataque (α), caracterizando assim um escoamento oblíquo de acordo com o caso, com exceção do contorno que representa a saída do domínio, no lado direito da figura, onde não há qualquer valor prescrito. Sobre a superfície da ponte é usada a condição de não deslizamento. Considera‐se ainda o estado de repouso como a condição inicial para os campos de velocidade e pressão.
Os resultados referentes à Configuração I são apresentados na figura 6 abaixo.
Os dados são comparados com aqueles obtidos da análise experimental em túnel de vento e apresentado por Rocha et al. [2]. Como se observa, há uma muito boa concordância entre os trabalhos para o coeficiente de arrasto. Já para o coeficiente de sustentação os resultados mostrados são mais próximos para ângulos de ataque negativos com uma diferença na ordem de 35% para ângulos positivos. Por fim, para o coeficiente de torção, tem‐se uma excelente conformidade entre os resultados para incidência do escoamento positiva, porém verifica‐se uma diferença significativa para ângulos negativos. Quanto às diferenças observadas para a sustentação, poder‐se‐iam justificar através do modelo de turbulência usado onde, devido à grande extensão do corpo imerso, um esquema clássico de Smagorinsky poderia se mostrar insuficiente, sendo que com o uso de um modelo dinâmico, de forma que o coeficiente de Smagorinsky possa variar tanto no espaço como também no domínio do tempo, o mesmo poderia se ajustar aos diferentes regimes de escoamento encontrados na região do corpo imerso. Também podem ser citados como causa destas diferenças alguns aspectos geométricos, como a descrição dos guarda‐corpos, que por sua vez podem ser mais bem representados através de um código tridimensional. Vale lembrar também que ensaios experimentais em túneis de vento não são isentos de erros, já que os dispositivos de medida, bem como as paredes do túnel, podem influenciar consideravelmente os resultados.
Na figura 7 apresentam‐se os resultados obtidos para a Configuração II. Os dados são novamente comparados com o trabalho experimental em túnel de vento obtidos por Rocha et al. [2]. Mais uma vez verifica‐se uma boa concordância para o coeficiente de arrasto. Para o coeficiente de sustentação mantém‐se o quadro visto no estudo anterior, observando‐se, porém, uma diferença bem menor e semelhante em todos os resultados obtidos para ângulos positivos. Por fim, para o coeficiente de torção, é mostrada uma boa conformidade entre os resultados para todas as incidências do escoamento. As mesmas razões apontadas na análise anterior para as diferenças observadas são válidas neste caso. Além disso, como pode ser visto, foi desprezada a existência do cercado aramado no modelo numérico em vista de uma melhor representação do caso analisado em um esquema bidimensional.
Com base nos dados apresentados acima, ficou constatada a boa performance do código proposto para a análise da ação do vento sobre as várias seções de estudo da ponte sobre o rio Guamá.
Da análise aerodinâmica puderam ser observados os seguintes aspectos:
- ‐
Assim como nos resultados experimentais, foi aqui também constatado que os valores de arrasto para a Configuração I são superiores aos da Configuração II. O mesmo ocorre para a sustentação e o momento de torção, onde se inverte o papel, ficando a Configuração II com os maiores valores.
- ‐
Quantitativamente, as maiores diferenças observadas foram nos resultados de sustentação para ângulos positivos extremos e para o momento de torção para ângulos negativos também superiores, ambos referentes à Configuração I. Aspectos geométricos, como a representação do guarda‐corpo e das transversinas, e questões relativas ao modelo de turbulência podem ser as razões para as diferenças observadas. Para isso deve‐se utilizar um código tridimensional a fim de melhor representar estes detalhes e lançar mão de um modelo de turbulência dinâmico, como o utilizado por Braun e Awruch [16], mais apropriado para a análise de corpos imersos com geometrias complexas, verificando ou não a presença destas divergências.
A análise aeroelástica é realizada neste trabalho através da observação das vibrações provocadas pela ação do vento sobre a seção de estudo, que é indeformável, mas que permite deslocamentos segundo os seus graus de liberdade. Usualmente, a identificação dos efeitos aeroelásticos é feita da seguinte forma: são testadas várias velocidades de escoamento observando se as vibrações geradas são amplificadas ou amortecidas, considerando uma estrutura sem amortecimento de forma que o aumento ou o abatimento dos deslocamentos seja de origem puramente aerodinâmica. No primeiro caso, tem‐se uma situação de instabilidade, enquanto que no segundo caso há um movimento estável. A velocidade crítica é obtida através de um gráfico de velocidade versus taxa de incremento/decremento, no momento em que a curva gerada neste gráfico cruza o eixo das velocidades. Esta alternativa foi utilizada em Braun e Awruch [17].
Outra forma, utilizada na análise experimental [2], verifica simplesmente valores estatísticos obtidos dos históricos de deslocamento produzidos nas direções principais da seção, para cada uma das velocidades de escoamento empregadas. Este método visa também a verificação das condições limites de projeto no que se refere aos deslocamentos máximos permitidos. Neste caso obtémse também uma velocidade crítica, sendo, no entanto, necessário uma condição limite de deslocamentos a partir da qual se considera a instabilidade.
No presente trabalho, o estudo das características aeroelásticas da seção é realizada através das 2 técnicas descritas acima. Em ambas as análises, a seção é submetida inicialmente a um escoamento, com a velocidade a ser analisada, como se fosse realizado um estudo aerodinâmico. Partindo desta situação, inicia‐se a análise aeroelástica. Este artifício é usado com a finalidade de acelerar o tempo de análise evitando a necessidade de se aguardar que a carga gerada pelo escoamento vença a inércia do corpo. Após isto, permite‐se que a seção se desloque segundo a ação do vento, produzindo como resultado históricos de deslocamento de onde são extraídos os dados pertinentes para cada um dos 2 procedimentos.
Para a primeira forma de análise, a qual será denominada de Procedimento 1, impõe‐se inicialmente à estrutura um deslocamento prescrito nas direções vertical e rotacional, vibrando a partir desta posição sob a ação do fluido, desenvolvendo assim um histórico de deslocamentos de onde se obtém a taxa de incremento/decremento para cada uma das velocidades estudadas. É construída então uma curva onde cada análise é representada através de um ponto de coordenadas velocidade versus taxa de incremento/decaimento das oscilações. A velocidade crítica é obtida na intersecção entre o eixo das velocidades e o ponto da referida curva para o qual a taxa de incremento/decremento troca de sinal. Foram apenas considerados o deslocamento vertical e a rotação torsional, sendo que a direção horizontal não foi aqui verificada devido a sua pouca importância nestes casos, onde a rigidez é bastante alta em consequência do alto momento de inércia apresentado nesta direção pelas seções de pontes. Este procedimento foi utilizado em Braun e Awruch [17].
Em uma segunda forma de análise, denominada Procedimento 2, utiliza‐se como condição inicial os mesmos campos de velocidade e de pressão desenvolvidos para a análise anterior. Neste caso, no entanto, considera‐se que a estrutura se encontra em seu estado de equilíbrio, ou seja, sem qualquer tipo de deslocamento inicial. A partir daí ela é liberada para vibrar, gerando uma resposta em deslocamentos de onde se calcula a média das amplitudes correspondentes nas direções vertical e angular. Por fim, são apresentados gráficos do tipo velocidade versus amplitude média de onde se obtém a velocidade crítica, conforme o critério de projeto estabelecido.
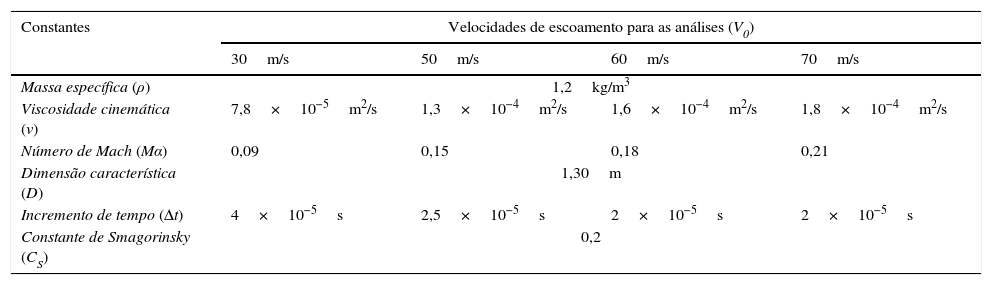
Na tabela 2 são apresentados os dados referentes à representação do vento de acordo com as análises efetuadas. A amplitude inicial empregada nos estudos referentes ao Procedimento 1 é de ‐4° na direção de rotação. Com esta inclinação reproduz‐se a condição experimental usada no túnel de vento, onde foi considerado um ângulo de incidência do escoamento nos mesmos ‐4°. Como condições de contorno tem‐se apenas as condições de bordos externos, através das quais é estabelecido um escoamento horizontal. As condições iniciais correspondem ao escoamento desenvolvido de acordo com os procedimentos descritos anteriormente para a análise aerodinâmica e conforme as velocidades estudadas para a análise aeroelástica. As mesmas condições são usadas para o Procedimento 2, com exceção da condição inicial da estrutura, a qual não tem nenhum deslocamento inicial prescrito.
Constantes físico‐geométricas do escoamento empregadas na análise aeroelástica
| Constantes | Velocidades de escoamento para as análises (V0) | |||
|---|---|---|---|---|
| 30m/s | 50m/s | 60m/s | 70m/s | |
| Massa específica (ρ) | 1,2kg/m3 | |||
| Viscosidade cinemática (ν) | 7,8×10−5m2/s | 1,3×10−4m2/s | 1,6×10−4m2/s | 1,8×10−4m2/s |
| Número de Mach (Mα) | 0,09 | 0,15 | 0,18 | 0,21 |
| Dimensão característica (D) | 1,30m | |||
| Incremento de tempo (Δt) | 4×10−5s | 2,5×10−5s | 2×10−5s | 2×10−5s |
| Constante de Smagorinsky (CS) | 0,2 | |||
Na tabela 3 são relacionadas as constantes mecânicas empregadas na representação da estrutura. Estes dados são os mesmos utilizados nos ensaios experimentais e contidos no trabalho de Rocha et al. [2]. Na análise numérica, realizada segundo o Procedimento 1, foi ignorada a existência de amortecimento estrutural, de forma que o amortecimento observado nas simulações seja puramente aerodinâmico. Este método é usado na grande maioria dos estudos deste tipo, na medida em que esta abstração não representa diferenças consideráveis nos resultados, como é verificado em estudos feitos anteriormente por Braun e Awruch [17]. Ao contrário, no Procedimento 2, usa‐se a mesma taxa de amortecimento empregada nos estudos experimentais (0,3%).
Propriedades mecânicas da estrutura usadas na análise aeroelástica
| Massa translacional | 22.513kg/m |
| Momento de inércia de massa | 566.838 kg/m2/m |
| Frequência natural de sustentação | 0,331Hz |
| Frequência natural de torção | 0,649Hz |
| Taxa de amortecimento estrutural | Procedimento 1: 0% |
| Procedimento 2: 0,3% | |
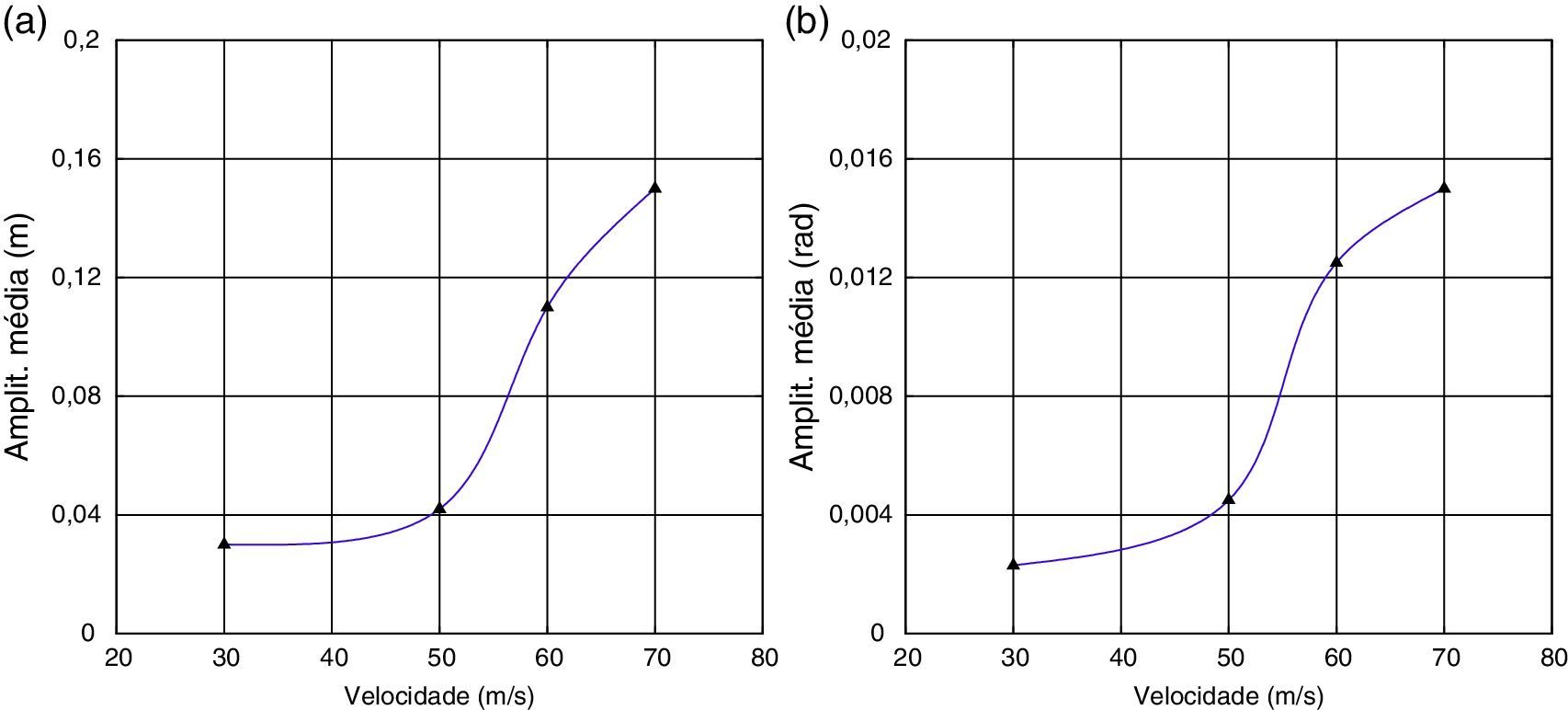
Na figura 8 são mostrados os históricos de deslocamento angular correspondentes às velocidades de vento analisadas para o Procedimento 1. Destes gráficos pode‐se observar que o amortecimento aerodinâmico praticamente inexiste para a faixa de velocidades empregada. As taxas de incremento/decaimento obtidas foram as seguintes: 0,036, 0,042 e 0,056, para V=30m/s, V=50m/s e V=60m/s, respectivamente. O mesmo foi verificado para a direção vertical, onde nenhum tipo de instabilidade foi detectado. De experiências anteriores pode‐se concluir que a velocidade crítica de drapejamento (ou flutter), para as condições de análise utilizadas nesta técnica, está seguramente bem acima dos valores estudados, uma vez que se tem observado que nestes tipos de análise a curva resultante da taxa de incremento/decaimento em função da velocidade de escoamento apresenta‐se inicialmente com valores muito baixos, aumentando depois até um pico, de onde decresce e inverte seu sinal num ponto do eixo de velocidade, passando a ter valores negativos. Esse ponto corresponde ao valor da velocidade crítica. Portanto, considerando mais uma vez as condições de análise para este caso, não foi encontrada a velocidade crítica na faixa de velocidades analisada.
Na figura 9 são apresentados os resultados referentes ao Procedimento 2, onde têm‐se diferentes raízes médias quadráticas das amplitudes para deslocamentos verticais e angulares obtidas conforme os valores de velocidade de vento estudadas. Estes valores das raízes médias quadráticas foram extraídos dos históricos dos deslocamentos vertical e angular fornecidos pelas análises, considerando‐se longos períodos de tempo. O cálculo destes valores é computado quando o fluxo é completamente desenvolvido e a estrutura estabiliza suas oscilações. Como pode ser visto, entre 50 a 60m/s há um aumento significativo tanto nos deslocamentos angulares como também nos deslocamentos verticais. Pode‐se concluir com isso que há efetivamente o acoplamento destes modos de vibração, onde as 2 direções passam a apresentar deslocamentos elevados simultaneamente.
Através da figura 9b, considerando as condições de análise impostas por esta forma de análise e um valor limite de deslocamentos estabelecido no projeto por Rocha et al. [2], determina‐se que a velocidade crítica obtida pelo presente trabalho fica em 56m/s. Segundo Rocha et al. [2], o valor ideal para a condição crítica é uma raiz quadrática média do deslocamento angular igual a 0,5 graus, que corresponde a um pico de deslocamento angular de 1,5 graus. Os resultados observados em túnel de vento, que apresentam curvas semelhantes aos da figura 9, apontam para uma velocidade crítica de 55m/s.
Na figura 10 é apresentada a situação da malha de elementos finitos para um instante de deslocamento extremo, onde pode se observar a boa integridade do sistema, resultado do modelo de movimento de malha e da condição não‐linear de compatibilidade (eq. 15), empregados neste trabalho. É importante destacar que sem estes itens ficaria impossibilitada a análise de problemas onde o corpo analisado apresente grandes rotações.
Com base nos dados apresentados acima, ficou constatada a boa performance do código proposto para a análise aeroelástica devida à ação do vento sobre as várias seções de estudo da ponte sobre o rio Guamá. Além disso, dos resultados apresentados puderam ser tiradas algumas conclusões e também sugestões de aprimoramento do código existente e que serão aqui enumeradas. Da análise aeroelástica pôde‐se observar os seguintes aspectos:
- ‐
A partir das condições de análise construídas para o Procedimento 1 não foi verificada a presença de velocidade crítica na faixa de velocidades analisadas. Deve‐se futuramente estudar a influência da amplitude inicial da estrutura sobre os resultados, utilizando valores menores e, com isso, reduzindo a ação das forças restitutivas (elásticas) nas condições iniciais do sistema dinâmico.
- ‐
Através do Procedimento 2 foi obtida uma velocidade crítica de 56m/s, menos de 2% superior ao maior valor apresentado pelos ensaios experimentais em túnel de vento, que forneceu um valor de 55m/s. Deve‐se aqui também comprovar, através da implementação de um modelo dinâmico para a turbulência, os resultados aqui obtidos.
Nesta seção é realizada numericamente uma análise aeroelástica para a determinação da resposta estrutural de um modelo de edifício alto sob a ação de um escoamento de vento de camada limite atmosférica, o qual foi analisado experimentalmente no túnel de vento do LAC/UFRGS (ver Miguel [11] e Trein [12]). Adotou‐se na análise, como critério para a malha de elementos finitos do fluido, um tamanho mínimo para o elemento de 1% da largura do prédio (dada pelo comprimento da parede frontal). A malha de elementos finitos referente ao escoamento é constituída de 368.800 elementos e 383.613 nós e a malha empregada na discretização da estrutura contém 5×8x25 elementos distribuídos segundo a direção dos eixos globais do domínio de análise e sem qualquer conformidade com os nós do fluido sobre as superfícies de interface (ver figura 11). Ao não ser coincidentes os nós de ambos os meios, o vetor de cargas que o fluido transmite à estrutura, assim como as condições cinemáticas que a estrutura transmite ao fluido, são transportadas aos correspondentes nós das respectivas malhas através de um processo de interpolação similar ao utilizado no MEF. Detalhes ao respeito são apresentados em Braun e Awruch [16].
O escoamento é caracterizado por um número de Reynolds igual a 8×104, calculado com base na dimensão característica da edificação (D=45m) e na velocidade de entrada tomada em Z=180m (v1=100m/s), sendo a integração no tempo do escoamento realizada usando‐se Δt=6,5×10−4 s. O perfil de velocidades na entrada do domínio é gerado de tal forma que a velocidade em Z=180m reproduza a velocidade crítica para o fenômeno de instabilidade aeroelástica por desprendimento de vórtices. A estrutura é caracterizada pelas seguintes propriedades físicas: ρ (massa específica)=1.600 kg/m3, ν (coeficiente de Poisson)=0,2 e E (módulo de elasticidade)=3×108N/m2, o qual leva a uma frequência natural de 0,2Hz. A integração no tempo da análise dinâmica da estrutura é realizada com Δt=1,3×10−2 s. O escoamento é segundo o eixo x.
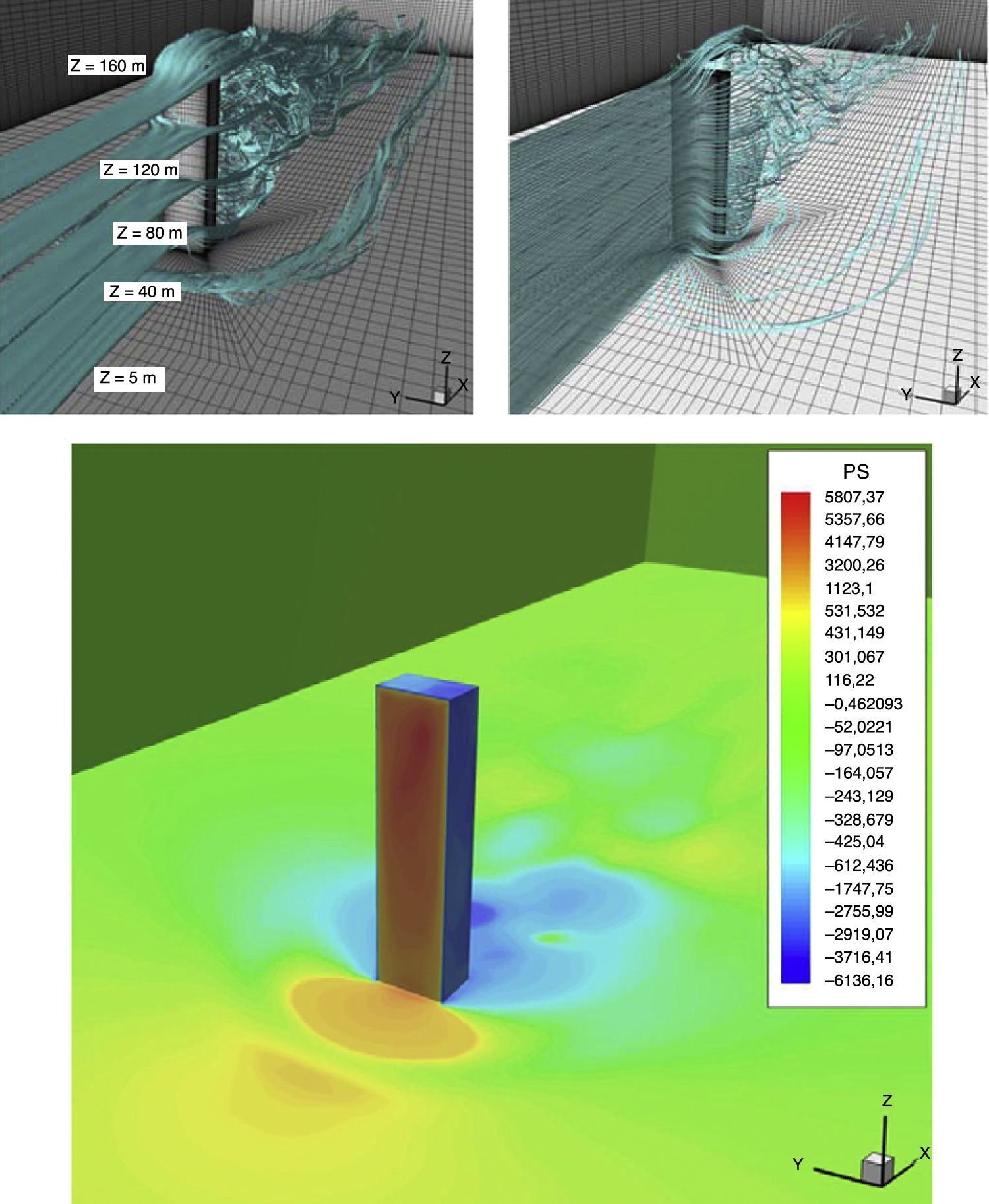
Na figura 12 são apresentados os resultados obtidos em termos dos históricos de deslocamentos avaliados no topo do edifício. Os deslocamentos foram medidos nas 2 direções principais da seção, os quais seguem a orientação dos eixos x (longitudinal) e y (transversal) do domínio de análise. O trabalho experimental de Trein [12] aponta para um deslocamento médio longitudinal em torno de 1,6m, o que vem de encontro com o resultado obtido neste trabalho. Na direção transversal, onde ocorre a instabilidade, Miguel [11] estima uma amplitude de deslocamentos RMS de 11,56m, um valor um pouco superior ao obtido pelo presente trabalho (10,80m). Na mesma figura é mostrada também uma das configurações deformadas da estrutura juntamente com os respectivos vetores de força que agem sobre o edifício devido à ação do escoamento.
O campo de pressão e linhas de corrente instantâneos obtidos neste trabalho são mostrados na figura 13.
Na figura 13 pode‐se verificar a perfeita reprodução dos principais fenômenos físicos do escoamento encontrados neste tipo de análise. Em Peterka et al. [21] apresentam‐se informações detalhadas da circulação em torno de edifícios. Uma grande zona de recirculação é gerada ao nível do solo, na área frontal. Esta zona de recirculação é formada por uma massa de fluido próxima à parede exposta à ação do vento, num intervalo entre 0 e 0,75H, onde H é a altura do prédio. Esta massa de fluido direciona‐se para abaixo numa região próxima à parede frontal, tomando depois uma direção contrária à do vento, contribuindo ao desenvolvimento de vórtices que tomam a forma de uma ferradura. Estes vórtices são caracterizados por uma estrutura helicoidal que atua numa estreita zona próxima do solo, afetando as áreas frontal e lateral a barlavento e sota‐vento. Por outro lado, as massas de fluido atuando nas proximidades da altura do prédio são direcionadas para cima, passando pelo topo e sendo depois lançadas para a região da esteira, por cima da zona de recirculação que se produz na parte posterior do edifício, tomando então novamente uma direção descendente até um nível próximo do solo. Nas paredes laterais formam‐se 2 zonas de separação bem definidas, onde grandes estruturas de vórtices desprendem‐se alternadamente provocando oscilações do prédio na direção normal ao vento. No campo de pressões, a zona de recirculação frontal caracteriza‐se por valores elevados da pressão, enquanto os vórtices em forma de ferradura constituem uma barreira para a massa de fluido próxima do solo com uma ampla zona de pressão elevada que precede a uma estreita zona de sução. As zonas de recirculação na região lateral e atrás do prédio são identificadas por serem zonas com elevada sução.
8ConclusõesNo presente trabalho foram analisados os comportamentos aerodinâmicos e aeroelásticos de alguns dos problemas mais importantes encontrados na engenharia do vento aplicada à engenharia civil empregando modelos numéricos desenvolvidos especialmente para este fim e que foram comparados com testes experimentais realizados num túnel de vento. Como pôde ser verificado, os modelos conseguiram reproduzir adequadamente os principais fenômenos físicos presentes em cada exemplo estudado. Em cada caso, as conclusões foram mencionadas ao final da aplicação correspondente. Faz‐se necessário ainda testar um esquema numérico que introduza as flutuações nos perfis da velocidade de entrada a fim de reproduzir a turbulência na corrente incidente, comumente utilizada nos túneis de vento.
Conflito de interessesOs autores declaram não haver conflito de interesses.
Os autores gostariam de agradecer ao Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) e à Fundação de Amparo à Pesquisa do Estado de Minas Gerais (FAPEMIG) pelos suportes financeiro concedidos para a realização deste trabalho.


















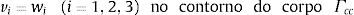











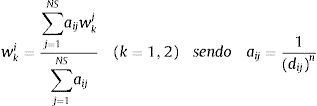
![Ponte sobre o rio Guamá: elevação (fonte: ref. [2]). Ponte sobre o rio Guamá: elevação (fonte: ref. [2]).](https://static.elsevier.es/multimedia/02131315/0000003100000001/v3_201706012355/S0213131514000273/v3_201706012355/pt/main.assets/thumbnail/gr3.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Características geométricas das seções estudadas para as análises aerodinâmica e aeroelástica da ponte sobre o rio Guamá (fonte: ref. [2]). Características geométricas das seções estudadas para as análises aerodinâmica e aeroelástica da ponte sobre o rio Guamá (fonte: ref. [2]).](https://static.elsevier.es/multimedia/02131315/0000003100000001/v3_201706012355/S0213131514000273/v3_201706012355/pt/main.assets/thumbnail/gr4.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)








