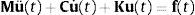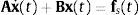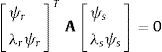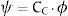Este trabajo se centra en estimar los parámetros modales del sistema dinámico que constituye la pasarela peatonal del Museo de la Ciencia de la ciudad de Valladolid (Spain). El trabajo consiste no sólo en calcular frecuencias propias o naturales y factores de amortiguamiento asociados a cada uno de los modos estimados, como proporcionan muchos programas comerciales a partir de los registros de aceleraciones de ensayos OMA (Operational Modal Analysis) y/o EMA (Experimental Modal Analysis), sino que el objetivo de este articulo es calcular las masas generalizadas correspondientes a cada uno de los modos estimados de la estructura. Para ello, en primer lugar se obtiene una representación del sistema dinámico en el espacio de estados mediante la técnica SSI (Stochastic Subspace Identification), y en segundo lugar se escalan los modos de vibración a partir de la estimación de los residuos de la descomposición en fracciones parciales de la función de respuesta en frecuencia (FRF) de las mediciones. Con este método se consiguen obtener buenas precisiones en los resultados, siempre que se consigan excitar los modos de vibración de los que queramos estimar los parámetros, lo que nos permite simular la respuesta dinámica de la estructura sin tener que recurrir a otros procedimientos como la actualización de un modelo de elementos finitos de la estructura en estudio.
This paper focuses on estimating the modal parameters of the dynamic system that constitutes the pedestrian footbridge of the Science Museum of the city of Valladolid (Spain). The work consists not only of calculating natural frequencies and damping factors associated to each of the estimated modes, as many commercial software provide from acceleration measurements of tests OMA (Operational Modal Analysis) and/or EMA (Experimental modal Analysis), but the aim of this paper is to calculate the generalized masses corresponding to each of the estimated modes of the structure. For this purpose, firstly a representation of the dynamic system is obtained in the state space by SSI technique (Stochastic Subspace Identification), and secondly, vibration modes are scaled from the estimation of the residues of the decomposition in partial fractions of the frequency response function (FRF) measurements. This method gets accurate estimations in the results whose vibration modes are excited, allowing the simulation of the dynamic response of the structure without the need for updating a finite element model of the structure under study.
Hoy en día existen estructuras típicas de proyectos e instalaciones de tipo industrial y de ingeniería civil, tales como chimeneas industriales, torres, edificios altos, puentes, pasarelas o viaductos, que han sido diseñadas y ejecutadas bajo criterios distintos a los actuales. Por otro lado, los nuevos materiales son cada vez más resistentes y permiten el diseño y construcción de estructuras cada vez más esbeltas, complejas y ambiciosas, en las cuales los movimientos pueden ser apreciables. Estos aspectos, junto con las actuales demandas sociales relativas a la percepción de seguridad y confort, en algunos casos recogidas en las normativas y guías, suscitan la necesidad de desarrollar una metodología adecuada para el análisis y diseño asistido por ordenador de estructuras esbeltas, integrando técnicas experimentales que permitan una precisa identificación de los parámetros más relevantes que definen el comportamiento estructural (estático y dinámico).
En el caso concreto de las pasarelas peatonales, generalmente éstas son propensas a ser excitadas por las personas que las ocupan, apareciendo movimientos apreciables que incluso pueden llegar a ser molestos o, en algunos casos, inadecuados o peligrosos desde el punto de vista de la resistencia estructural [1].
Por otro lado, respecto a la metodología de cálculo dinámico, la técnica de análisis modal de estructuras consiste en la recolección de datos, la identificación del sistema y, por último, la estimación de los parámetros modales. La etapa de identificación del sistema juega un papel crucial en los parámetros modales que se derivan, así como en el número de parámetros que se pueden determinar [2]. Los métodos de identificación clásicos se basan en aplicar una excitación al sistema y a continuación registrar la correspondiente respuesta (Experimental Modal Analysis/EMA) [3]. Si los ensayos se realizan en condiciones de uso, en los que la magnitud de las fuerzas excitadoras es desconocida, el análisis se denomina Operational Modal Analysis/OMA y si los ensayos se llevan a cabo en condiciones de operación aplicando una o varias fuerzas artificiales se denomina Operacional Modal Analysis with eXogenous inputs/OMAX.
En el caso de las estructuras civiles y mecánicas se usa en muchas ocasiones el OMA, ya que presentan ventajas económicas y operacionales, sin embargo, debido a que las fuerzas son desconocidas los modos de vibración no pueden ser normalizados y el modelo resulta incompleto lo que no permite simular el sistema. Para solucionar este problema, se han desarrollado algunos métodos de escalado de los modos de vibración que se basan en la actualización de un modelo de elementos finitos de la estructura empleando los parámetros modales estimados en el OMA [4,5]. También se han desarrollado soluciones basadas en la suposición de que la matriz de masa de la estructura (o su inversa) es conocida [6] o modificando el comportamiento dinámico de la estructura variando la masa o la rigidez y realizando un análisis modal operacional tanto en la estructura original como en la modificada [7–13]. Estos métodos requieren un procedimiento experimental más extenso al emplear los parámetros modales de la estructura original y también de la modificada.
Otros métodos de escalado consisten en añadir sistemas de vibración secundarios, midiendo y procesando la respuesta conjunta [14].
La identificación de los parámetros en una formulación diferencial de primer orden también ha recibido considerable atención, pero como es bien sabido, si se parte de un espacio de estados modelo, y se trata de identificar los parámetros del modelo de segundo orden, cuestiones como la no unicidad de la solución complica la resolución del problema inverso [15–21]. Sin embargo se han desarrollado varias metodologías que resuelven el problema imponiendo diferentes restricciones en el número de sensores y actuadores empleados [22–26].
En el presente artículo se retoma el empleo de los resultados del EMA para obtener todos los parámetros modales necesarios para la simulación de una estructura civil, escalando los modos de vibración a partir de la estimación de los residuos de la descomposición en fracciones parciales de la función de respuesta en frecuencia (FRF) de las mediciones. Asimismo se aplica, una vez validada la metodología a través de dos casos teóricos, en una estructura actualmente en uso. La información de partida se obtiene aplicando uno de los métodos más utilizados en la actualidad, el SSI (Stochastic Subspace Identification), y se escoge el escalado de forma que el mayor coeficiente modal sea igual a 1 teniendo el resultado el significado físico de la masa modal (cantidad de masa que participa en cada modo de vibración) [27].
Por último, indicar que el trabajo se ha organizado de la manera siguiente: en primer lugar, tras esta introducción, se presenta la metodología empleada. A continuación, se diserta sobre los resultados obtenidos y en el último apartado se presentan las principales conclusiones que se deducen de este trabajo.
2Metodología2.1Función de transferenciaLa función de transferencia de un sistema amortiguado de multiples grados de libertad puede ser formulada a partir de las ecuaciones del movimiento en términos de las matrices de masa, rigidez y amortiguamiento [28]:
donde u(t) indica el vector de desplazamientos nodales, con (˙) y (¨) que representan la primera y segunda derivada respecto al tiempo, el vector f(t) contiene las excitaciones externas que solicitan el sistema, las magnitudes M, C y K son las matrices simétricas definidas positivas de masa, amortiguamiento y rigidez para un sistema de N grados de libertad.Aplicando la transformada de Laplace a la ecuación (1) y asumiendo condiciones iniciales nulas, resulta:
donde U(s) y F(s) son la transformada de Laplace de la respuesta en desplazamientos y de la fuerza, respectivamente. Se define la matriz dinámica del sistema, como:Y a partir de la matriz dinámica se define la matriz función de transferencia:
En general,
donde p es el grado de libertad de salida y q es el grado de libertad de entrada (orientación y posición física).Por lo tanto, la estimación de una columna de la matriz función de transferencia se lleva a cabo midiendo la respuesta dinámica en distintos puntos para un excitador ubicado en una posición fija.
2.2ResiduosCada uno de los términos de la matriz función de transferencia se puede descomponer en fracciones parciales, tal y como se indica a continuación:
donde Apqr son los residuos asociados al polo λr, y ()* indica el complejo conjugado. En términos de los valores modales del sistema se puede expresar como:siendo Qr el coeficiente de escalado del modo de vibración ψr.2.3Amortiguamiento proporcional (masa modal)Para el caso de amortiguamiento proporcional, el cual incluye el caso sin amortiguamiento, se puede establecer una relación entre el residuo y la masa modal [29].
donde Mr y Kr son la masa modal y la rigidez modal asociada al modo ψr, respectivamente. Y siendo ωr la frecuencia circular (rad/s) natural amortiguada (en el caso de que exista amortiguamiento). Además, se debe tener en cuenta que para los sistemas con amortiguamiento proporcional los vectores modales son siempre modos reales.2.4Amortiguamiento no proporcional (modal A)El propósito del análisis modal es encontrar una transformación de coordenadas que desacople las ecuaciones del movimiento. En un sistema con amortiguamiento no proporcional, las ecuaciones del movimiento se acoplan cuando se formulan en el espacio físico de dimensión N. Afortunadamente, las ecuaciones del movimiento pueden ser desacopladas cuando se formulan en el espacio de estados de dimensión 2N. Este último se representa del siguiente modo [28]:
dondeLa ventaja de escribir las ecuaciones del movimiento de esta forma es que el problema de valores propios asociado es simétrico y puede plantearse en forma matricial como:
donde ψ=[ψ1ψ2…ψ2N] es la matriz que contiene los autovectores del problema complejo de valores propios siguiente:y λi=ςi±jωi los valores propios complejos (siendo j=−1).Al igual que en el caso de los sistemas no amortiguados, son válidos un conjunto de relaciones de ortogonalidad para las matrices del sistema, en este caso A y B.
Los términos modal A y modal B ahora se pueden definir de la siguiente manera:
Se debe tener en cuenta que estas cantidades tienen las mismas propiedades que la masa modal y la rigidez modal para los casos sin amortiguamiento y con amortiguamiento proporcional. Siempre que los vectores modales sean complejos, las magnitudes modal A y modal B deben ser utilizadas para proporcionar el escalado modal.
2.5Identificación del sistema dinámicoLa técnica de identificación consiste en la determinación del modelo de primer orden del sistema dinámico. A partir de los datos de aceleración registrados en los sensores y de la fuerza aplicada mediante el actuador es posible identificar (mediante el método denominado Stochastic Subspace Identification, SSI) una representación en el espacio de estados en una base arbitraria, que se puede expresar como:
donde AC, BC, CC y DC son las matrices del sistema en tiempo continuo.Una vez estimada la matriz AC se procede a calcular sus valores propios λi y los vectores propios asociados ϕ. Y por último, se estiman los parámetros modales: frecuencias, factores de amortiguamiento y modos de vibración según las expresiones:
3Resultados numéricosUna vez expuesta la metodología, se procede a la validación de la misma presentando un primer problema numérico pero suficientemente general (validación), para después aplicar dicha metodología al análisis de un caso general más complejo (ejemplo) y de una estructura real actualmente en uso.
3.1ValidaciónEl problema que se plantea en este apartado es el de una viga biapoyada de longitud L=10.4m, módulo de Young E=2.1·1011Pa, densidad ρ=7850.0kg/m3, inercia Iz=604·10−8m4 y sección transversal de área A=53.8·10−4m2. También se supone un factor de amortiguamiento de 0.5% para cada uno de los modos de vibración de dicha viga. Se simula mediante manipulador simbólico de manera que se obtienen las aceleraciones en las posiciones (1/4, 1/2, 3/4)·L (sensores 1, 2 y 3, respectivamente) cuando se aplica una fuerza externa conocida (f1(t)=102·sin(2πt)) en la misma sección donde se ubica el sensor 1 (para el grado de libertad 1).
A continuación, se sigue la metodología de este trabajo: primero se identifica el sistema en base a un modelo de espacio de estados a partir de los datos de respuesta, en segundo lugar se calculan todos los parámetros modales y, por último, se escalan los modos de vibración a partir de la estimación de los residuos de la descomposición en fracciones parciales de la función de respuesta en frecuencia (FRF) de las mediciones.
En la tabla 1 se recogen los resultados estimados de los parámetros modales: frecuencias propias (fi), factores de amortiguamiento (ζi), modal A (MAi) y masas generalizadas (Mi) asociados a los tres primeros modos de vibración de la viga, así como, también se indica la solución analítica correspondiente.
En la tabla 2 se indican los tres primeros modos de vibración estimados asociados al modal A (MAi) y masa generalizada (Mi) de la tabla 1.
La tabla 3 muestra los modos normalizados respecto de la matriz de masa de la viga biapoyada correspondientes a los tres primeros modos de vibración. Se observa, al igual que en la tabla 1, que los resultados para el tercer modo de vibración son poco precisos, esto se debe a que el tipo de carga aplicada en el ejemplo no es capaz de excitar el tercer modo por lo que resultaría conveniente hacer un barrido en frecuencias.
3.2EjemploA continuación se va a mostrar la metodología de este trabajo para identificar el modelo modal de una viga continua de tres vanos, indicada en la figura 1. La longitud de cada uno de los vanos es: L1=8m, L2=10m y L3=5m. Las propiedades del material y de la sección son respectivamente: módulo de Young E=2.1·1011Pa, densidad ρ=7850kg/m3, área de la sección transversal A=53.8·10−4m2 y momento de inercia Iz=604.0·10−8m4.
De la resolución analítica del problema de análisis modal de dicha viga se obtienen los modos de vibración y frecuencias propias que se muestran a continuación en la figura 2. A continuación, se aplica una fuerza de tipo armónico (f1(t)=102·sin(2πt)) en la sección que indica la figura 1, así mismo, se asume de nuevo un factor de amortiguamiento ζi=0.5% para cada uno de los modos de vibración y se calcula la respuesta dinámica de la estructura mediante el método de superposición modal (se consideran los seis primeros modos calculados anteriormente) con el objeto de generar los registros de aceleraciones en los puntos de la estructura indicados en la figura 1 de un minuto de duración con un tiempo de muestreo Ts=0.005s, para emplear dichos registros, junto con el de la fuerza aplicada, como punto de partida en la aplicación de la metodología objeto de este trabajo.
Es decir, la idea es suponer que solamente contamos con la información recogida en los registros de aceleraciones y el registro de fuerza aplicada, según el esquema de la figura 1. Se identifica el sistema, y con el modelo obtenido en el espacio de estados se aplica la metodología expuesta y se obtienen las estimaciones que se resumen a continuación.
En la tabla 4 se comparan los resultados obtenidos para las frecuencias propias, factores de amortiguamiento, el parámetro modal A y la masa modal asociados a los cuatro primeros modos de vibración de la estructura aplicando la metodología objeto del presente artículo (que se presentan bajo el título “Estimado”) con la solución obtenida resolviendo el problema analíticamente (que se presentan bajo el título “Analítico”).
Ejemplo. Viga continua. Parámetros modales
| Estimado | Analítico | |||||||
|---|---|---|---|---|---|---|---|---|
| modo | fi (Hz) | ζi(%) | MAi | Mi (kg) | fi (Hz) | ζi(%) | MAi | Mi (kg) |
| 1 | 3.75 | 0.5 | 16539.0j | 350.5 | 3.75 | 0.5 | 16526.2j | 350.2 |
| 2 | 5.93 | 0.5 | 17049.0j | 228.7 | 5.93 | 0.5 | 17124.4j | 229.7 |
| 3 | 11.69 | 0.5 | 32444.0j | 220.8 | 11.69 | 0.5 | 35328.1j | 240.4 |
| 4 | 15.68 | 0.9 | 37820.0j | 192.0 | 15.55 | 0.5 | 39528.1j | 202.3 |
En la tabla 5 se muestran los cuatro primeros modos de vibración de la viga continua aplicando la metodología estudiada y los resultados obtenidos analíticamente.
Ejemplo. Viga continua. Modos de vibración
| Estimado | Analítico | |||||||
|---|---|---|---|---|---|---|---|---|
| modo | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| y1 | −0.7398 | 1.0 | 0.1820 | −0.0668 | −0.7395 | 1.0 | 0.1825 | −0.0630 |
| y2 | 1.0 | 0.3279 | 0.7774 | −0.4947 | 1.0 | 0.3279 | 0.7741 | −0.4719 |
| y3 | 0.8962 | 0.5889 | −0.5456 | 0.7022 | 0.8964 | 0.5889 | −0.5415 | 0.6794 |
| y4 | −0.2004 | −0.1775 | 1.0 | 1.0 | −0.2006 | −0.1775 | 1.0 | 1.0 |
La tabla 6 presenta los cuatro modos de vibración anteriormente reflejados en la tabla anterior pero ahora normalizados respecto a la matriz de masa de la viga continua.
Ejemplo. Viga continua. Modos de vibración normalizados
| Estimado | Analítico | |||||||
|---|---|---|---|---|---|---|---|---|
| modo | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| y1 | −0.0395 | 0.0661 | 0.0122 | −0.0048 | −0.0395 | 0.0660 | 0.0118 | −0.0044 |
| y2 | 0.0534 | 0.0217 | 0.0523 | −0.0357 | 0.0534 | 0.0216 | 0.0499 | −0.0332 |
| y3 | 0.0479 | 0.0389 | −0.0367 | 0.0507 | 0.0479 | 0.0389 | −0.0349 | 0.0478 |
| y4 | −0.0107 | −0.0117 | 0.0673 | 0.0722 | −0.0107 | −0.0117 | 0.0645 | 0.0703 |
Se observa en los resultados de los modos de vibración tercero y cuarto una menor precisión debido a que su participación en la respuesta dinámica es pequeña y por lo tanto la incertidumbre es mayor.
3.3Aplicación a un caso realEn esta sección se describe la identificación de los parámetros modales de la pasarela peatonal del Museo de la Ciencia (PMC) de la ciudad de Valladolid. Esta identificación consistió en un análisis modal experimental (EMA) del vano de la estructura más sensible a las vibraciones inducidas por el tránsito de peatones.
3.3.1Descripción de la estructuraLa estructura estudiada, situada en Valladolid, es una pasarela peatonal sobre el río Pisuerga que une el Museo de la Ciencia con el centro de la ciudad. Este puente, construido en el año 2004, es una estructura de 234 metros compuesta de cuatro vanos: tres formados por barras metálicas tubulares y uno de hormigón. Los tres vanos metálicos tienen sección hexagonal, el vano principal (vano 3 en la figura 3) tiene 111 metros y cuenta con un sistema de tendones externos postensados, el segundo vano (vano 2) tiene 51 metros y los otros dos vanos son más cortos y rígidos. El sistema de tendones externo del vano 3 hace que este vano sea suficientemente rígido. Sin embargo, el vano 2 (figura 4), es más sensible a excitaciones dinámicas producidas por humanos. En dicho vano, se alcanzan niveles de vibración que, según la opinión de los usuarios, a veces son molestos, particularmente cuando un corredor cruza el puente.
3.3.2Análisis modal experimentalLa identificación de los parámetros modales de la estructura utilizando el OMA tiene el inconveniente de no identificar la masa modal, parámetro necesario para obtener el modelo modal completo y para realizar las estimaciones de la respuesta utilizando las guías y normativas. Por ello es necesario utilizar otros métodos para estimar este parámetro, lo más inmediato es hacer un EMA en el que la fuerza de excitación sea conocida.
La fuerza de excitación empleada para este caso se generó con un excitador electrodinámico de APS Dynamics modelo 400 en modo inercial colocado en el centro del vano. La fuerza inducida por el excitador se calculó midiendo la aceleración de la masa inercial y multiplicándola por su magnitud (30.4kg). Se utilizó un barrido continuo en frecuencia entre 2.5 y 4.5Hz para excitar el primer modo de vibración. Se utilizaron 3 acelerómetros piezoeléctricos colocados en la línea central de la pasarela en las posiciones (1/3, 1/2, 2/3)·L (siendo L=51m). Este método tiene la ventaja de conocer la excitación y el inconveniente de que se necesita un excitador capaz de hacer vibrar la estructura.
3.3.3Resultados experimentalesSe llevaron a cabo un total de nueve test, en todos ellos el shaker si situó en la sección central del vano de estudio. Los datos concretos de cada test se indican en la tabla 7.
Información de los test realizados
| test | excitación | frecuencias | Burt. | Nivel |
|---|---|---|---|---|
| 1 | Chirp | 1–15Hz | 0.95% | 0.4V |
| 2 | Chirp | 1–15Hz | 0.95% | 0.4V |
| 3 | Chirp | 1–15Hz | 0.95% | 0.4V |
| 4 | Chirp | 2.5–4.5Hz | 0.95% | 1.0V |
| 5 | Chirp | 2.5–4.5Hz | 0.95% | 1.0V |
| 6 | Chirp | 2.5–4.5Hz | 0.95% | 0.1V |
| 7 | Chirp | 2.5–4.5Hz | 0.95% | 0.5V |
| 8 | Chirp | 2.5–4.5Hz | 0.95% | 0.3V |
| 9 | Chirp | 2.5–4.5Hz | 0.95% | 0.7V |
La tabla 8 recoge los valores medios estimados de las frecuencias propias (f¯i), los factores de amortiguamiento (ζ¯i) y las masas generalizadas (M¯i) correspondientes a los tres primeros modos de vibración del vano 2 de la pasarela. Esta misma tabla incluye el valor correspondiente de la desviación típica o estándar de cada una de dichas magnitudes: frecuencias (σfi), factores de amortiguamiento (σζi) y masas generalizadas (σMi), respectivamente. Se comprueba que el método de identificación del sistema dinámico es preciso para estimar frecuencias de vibración, pero respecto a los resultados de amortiguamiento y masas generalizadas hay una dispersión importante.
A continuación, en la tabla 9 se indican los tres primeros modos de vibración asociados a las masas generalizadas estimadas en la tabla anterior (tabla 8), mediante valor medio y desviación de cada una de las coordenadas. Se observa falta de precisión en la estimación de los modos 2 y 3.
Y por último, se indica en la tabla 10 los modos de vibración normalizados respecto de la matriz de masa, en base a valores medios y desviación típica de las coordenadas medidas. Destaca que se obtiene una precisión suficiente desde el punto de vista práctico con los valores estimados en dicha tabla. Por lo tanto, se recomienda trabajar siempre con los modos normalizados respecto de la matriz de masa para simular la respuesta dinámica de la estructura, por ejemplo, aplicando el conocido método de análisis por superposición modal de un número finito y pequeño de modos de vibración.
4ConclusionesAnalizados los resultados experimentales obtenidos, la primera conclusión que merece la pena reseñar (por la relevancia que tiene sobre el resto de las interpretaciones de los datos resultantes) es que sólo se pueden obtener con precisión los parámetros modales que corresponden a los modos de vibración que seamos capaces de excitar. Aunque lógica, esta conclusión ha de estar siempre presente tanto en el análisis como en las aplicaciones de los resultados. También se debe tener en cuenta que la incertidumbre en los resultados será mayor a medida que la participación en la respuesta dinámica de los modos sea menor.
En segundo lugar, a partir de los resultados experimentales de la pasarela peatonal, se concluye que en general mediante los métodos de identificación de sistemas dinámicos se va a conseguir precisión suficiente en la estimación de las frecuencias propias y en los modos de vibración normalizados respecto de la matriz de masa, y no así en otras magnitudes como los factores de amortiguamiento, masas generalizadas y modos de vibración asociados a dichas masas.
También resaltar que estimar los modos de vibración normalizados respecto de la matriz de masa tiene su dificultad a partir de los registros experimentales, ya que en los métodos de identificación de sistemas no se tiene en ningún momento una expresión explícita de dicha matriz de masa.
Y por último, apuntar que la estimación de los parámetros modales permite la simulación de la respuesta dinámica de la estructura sin la necesidad de actualizar un modelo de elementos finitos de la estructura objeto de estudio (método que se conoce en la literatura técnica como FEM Updating). Así mismo, también posibilita predecir su comportamiento dinámico frente a distintos tipos de solicitaciones a partir del modelo modal de la pasarela peatonal, por ejemplo para condiciones usuales o excepcionales de tráfico peatonal.
Este trabajo ha sido realizado en parte con la financiación aportada al proyecto de investigación BIA2011-28493-C02 por el programa de apoyo a Proyectos de Investigación Fundamental No Orientada del Ministerio de Ciencia e Innovación. Los autores agradecen al Ayuntamiento de Valladolid y al Museo de la Ciencia su apoyo en las pruebas de campo.