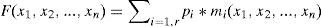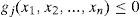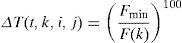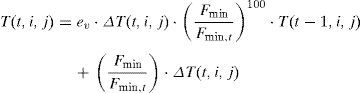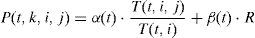Este artículo trata sobre la optimización económica realizada por métodos heurísticos a 15 pilas de sección rectangular hueca de hormigón armado. Las pilas tienen alturas de 20, 30, 40, 50 y 60 m para viaductos de carretera con luces de 40, 50 y 60 metros en los vanos centrales. La optimización se ha realizado mediante una variante del método metaheurístico de la colonia de hormigas. En el trabajo se puede observar cómo van variando en su geometría, hormigón, armado y costes las pilas, tanto en los soportes como en las zapatas, al ir aumentando la altura de las mismas y las longitudes de los vanos.
The present paper deals with the economic optimization of a series of 15 bridge piers with rectangular hollow sections. It combines height columns of 20, 30, 40, 50 and 60m and viaducts of 40, 50 and 60m of main intermediate spans. The optimization uses a variant of the ant colony method. Results show the variation in geometry, concrete quality, reinforcement and cost, both in the footings and in the main column, as the columns gain height and the viaducts grow in span length.
En el diseño de carreteras, una vez definida la ubicación y la longitud de un viaducto la siguiente fase consiste en decidir en cuantos vanos se divide dicho viaducto. Para resolver esto tendrá gran importancia, entre otras cosas, la altura necesaria de las pilas a lo largo del viaducto, es decir, si las pilas son bajas la tendencia será ir a vanos más cortos que si son altas y viceversa. El coste de las pilas suele estar comprendido entre un 20 y un 50% del total del viaducto dependiendo de la altura de las mismas y del tipo de cimentación. En términos generales, se puede decir que vanos de grandes luces y pilas altas serán caros y, por otro lado, vanos cortos y pilas bajas serán más económicos. Por lo que se deberá llegar a la solución de coste óptimo combinando las longitudes de vano y las alturas de alzados que más se adecuen en cada situación. De esta manera se llegará a la solución óptima incluyendo costes de tablero y coste de alzados.
En artículos previos, se ha presentado un modelo para el diseño óptimo de pilas de hormigón armado con sección rectangular hueca para viaductos [1,2]. En estos artículos se describe en detalle el modelo de optimización utilizado incluyendo las restricciones del problema, las variables, los parámetros y el método de optimización utilizado. Una vez el modelo ha sido estudiado y calibrado se ha utilizado para la realización del estudio paramétrico que se presenta en este artículo. Por esto, mientras que las primeras publicaciones trataban sobre el desarrollo de un modelo automatizado de diseño que pueda ser utilizado por una oficina de proyectos, en este artículo se presenta el estudio realizado para pilas óptimas de distintas alturas y vanos de diferente longitud en proyectos de viaductos con tráfico de carretera. Con todo ello se pretende dar una guía de predimensionamiento, además de aumentar el conocimiento sobre este tipo de estructura al presentar cómo se modifican las distintas variables y cómo aumentan los costes de las mismas.
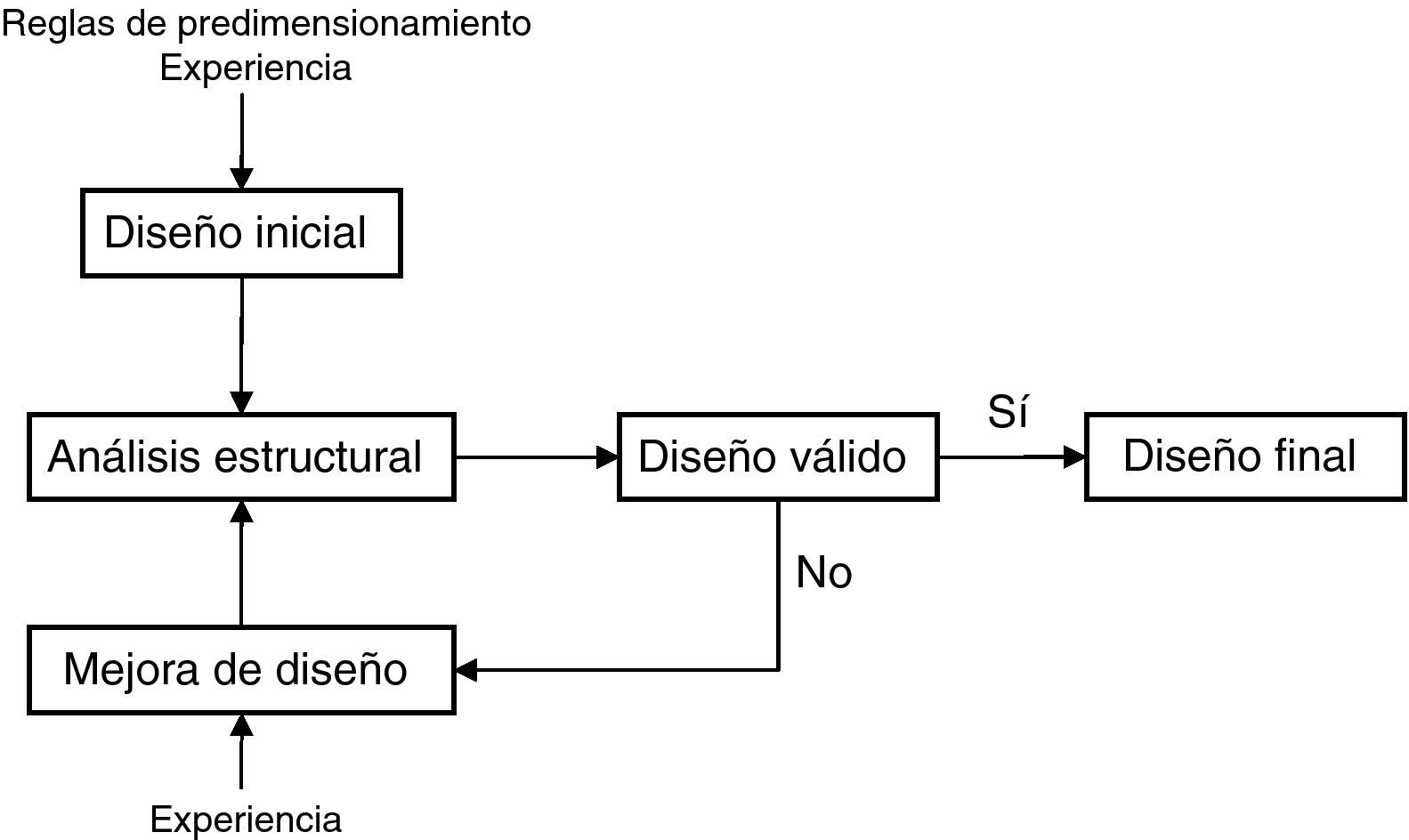
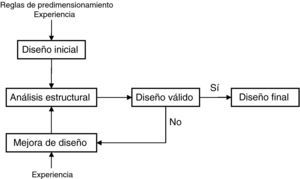
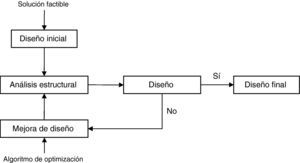
El proceso tradicional de diseño de estructuras se basa en reglas prácticas de predimensionamiento, generalmente aceptadas y sancionadas por la práctica, cuya aplicación permite al proyectista establecer de partida unas geometrías y elegir unos materiales de manera previa al cálculo. Sobre el diseño inicial se van introduciendo ajustes y correcciones, hasta obtener al final la estructura proyectada, siendo el proyecto un proceso iterativo, tal como muestra la figura 1. La normativa proporcionará al proyectista tanto las metodologías de análisis como los niveles de seguridad mínimos que la estructura debe alcanzar. Este proceso incluye etapas en las que un proyectista debe tomar decisiones de carácter subjetivo. Dos proyectistas pueden obtener soluciones estructurales diferentes a un problema concreto, aún cumpliendo estrictamente las normas aplicables, debido al gran número de variables y sus posibilidades para combinarlas. Siendo múltiples las soluciones técnicas posibles, la elección más adecuada deberá incluir criterios de optimización económica entre otros.
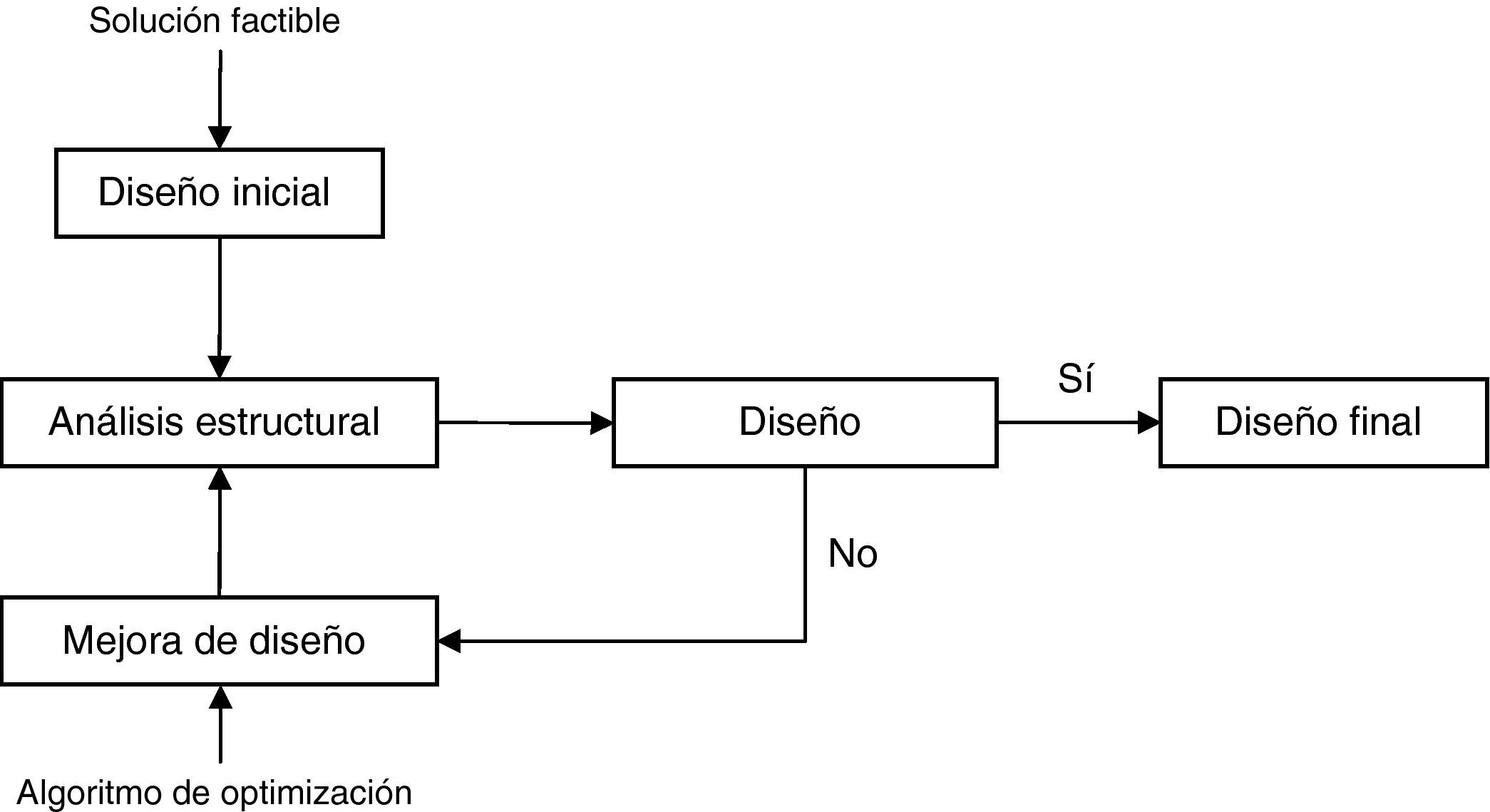
Para obtener los resultados de este artículo se emplea una herramienta de proyecto capaz de diseñar y optimizar una estructura de manera automatizada (fig. 2). En este proceso no son necesarias reglas de predimensionamiento, pues se parten de soluciones iniciales aleatorias, ni de experiencia previa para obtener diseños económicos en un tiempo razonable. En dicho método de diseño automatizado son necesarias dos herramientas principales: la primera el módulo de optimización, que deberá ser capaz de variar la estructura de partida y de evaluar el coste de las nuevas soluciones y la segunda el módulo de comprobación, el cual evaluará los estados límite de manera automatizada según la normativa utilizada [3,4]. Debido a que el propósito de estos métodos es encontrar la estructura de menor coste posible que cumpla los requerimientos de resistencia y estabilidad y de aptitud al servicio, sin unos conocimientos o una experiencia previa, sólo deberán ser usados como una herramienta que aportarán al ingeniero especializado nuevas posibilidades en el diseño de una estructura, pero siempre deberá ser este el que decida si la estructura resultante es válida y cuál es la mejor.
El método heurístico utilizado para realizar la optimización será la colonia de hormigas, ya que parece ser el más eficiente y el que mejor se adapta al propósito buscado según los estudios previos realizados [1,2]. El reciente desarrollo de los métodos heurísticos como colonia de hormigas, algoritmos genéticos, aceptación por umbrales, cristalización simulada, búsqueda tabú, etc. [5–9] ha estado unido al desarrollo de los ordenadores personales. Los primeros trabajos estructurales de optimización heurística con métodos poblaciones fueron aplicados a estructuras metálicas y entre ellos se encuentran los desarrollados por Goldberg y Samtami [10] a finales de la década de los 80 que abordaron la optimización de una celosía articulada de 10 barras empleando algoritmos evolutivos. Ya en la década de los noventa Jenkins [11], Rajeev y Krishnamoorthy [12] y Adeli y Cheng [13–15] resolvieron estructuras metálicas con algoritmos genéticos intentando minimizar el peso de las mismas. Respecto a la aplicación de algoritmos poblacionales en estructuras de hormigón armado, una de las primeras aplicaciones destacables fue publicada en 1997 y corresponde a Coello et al. [16] que aplicaron algoritmos genéticos a la optimización económica de una viga biapoyada. A continuación, Rafiq y Southcombe [17] optimizaron mediante algoritmos genéticos el armado de pilares sometidos a flexocompresión esviada. Rajeev y Krishnamoorthy [18] aplicaron algoritmos genéticos en la optimización de dos pórticos de hormigón armado planos, destacando la utilización de variables discretas. Ya en el 2000, Leps y Sejnoha [19] optimizaron una viga continua de dos vanos simétrica de hormigón armado, teniendo en cuenta el armado de flexión y el de cortante. Lee y Ahn [20] y Camp et al. [21] utilizaron algoritmos genéticos para la optimización de estructuras planas de hormigón armado. Govindaraj y Ramasamy [22] optimizaron en 2005 vigas de hormigón armado mediante algoritmos genéticos, destacar que en el cálculo tienen en cuenta condiciones de rotura, servicio, ductilidad, durabilidad y constructibilidad de las soluciones. Más recientemente, nuestro grupo de investigación ha aplicado distintos algoritmos a la optimización de muros, pórticos, marcos, bóvedas y pilas de puente [1,2,23–26]. El objetivo de todas estas publicaciones de estructuras de hormigón armado es que las soluciones sean construibles, para lo que se dispone variable discreta y se cumplen todas las especificaciones de la normativa a aplicar en cada caso. Según la experiencia de los autores con distintos tipos de estructuras de hormigón, la optimización heurística conduce a ahorros económicos de no menos de un 10%.
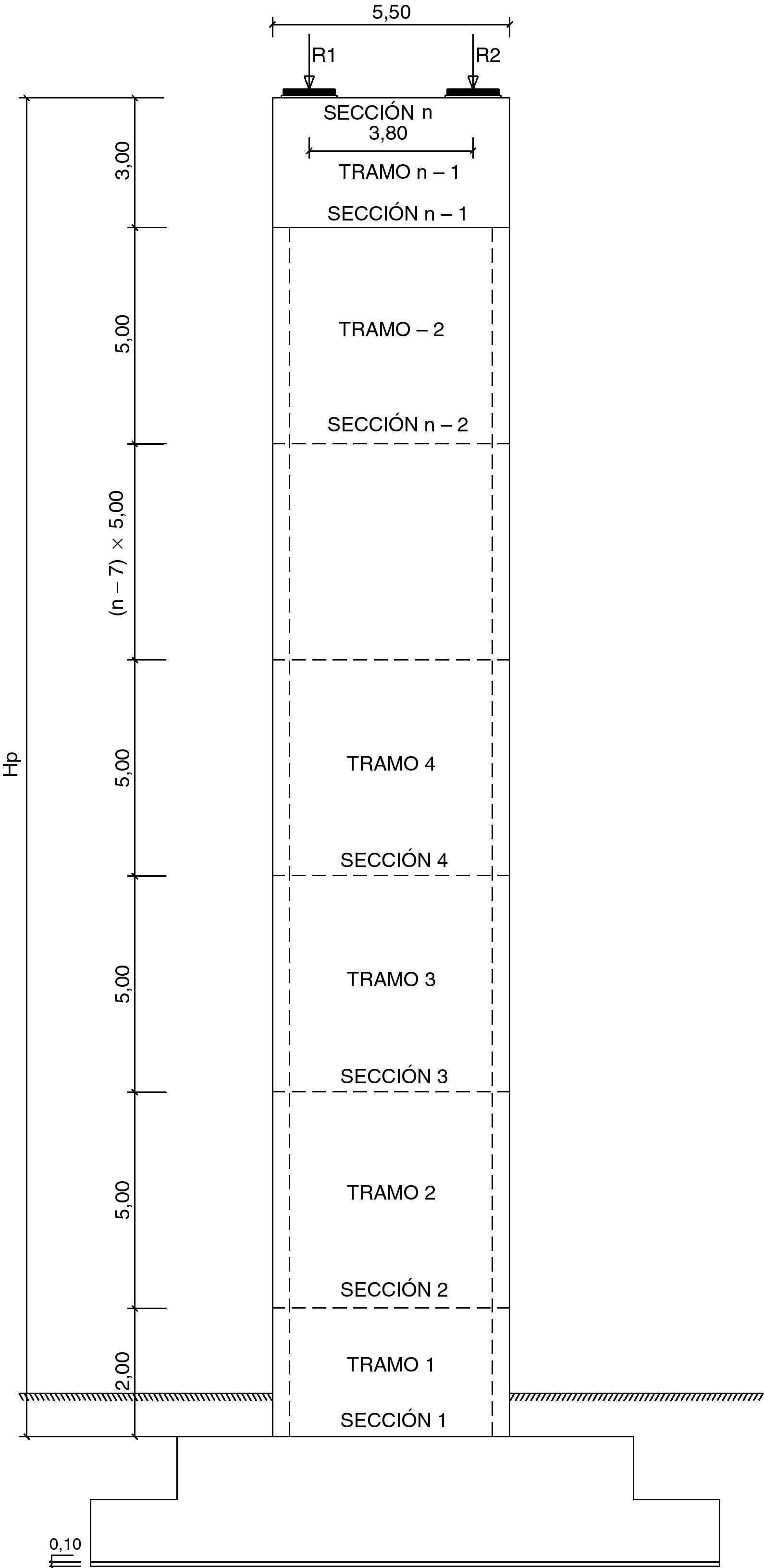
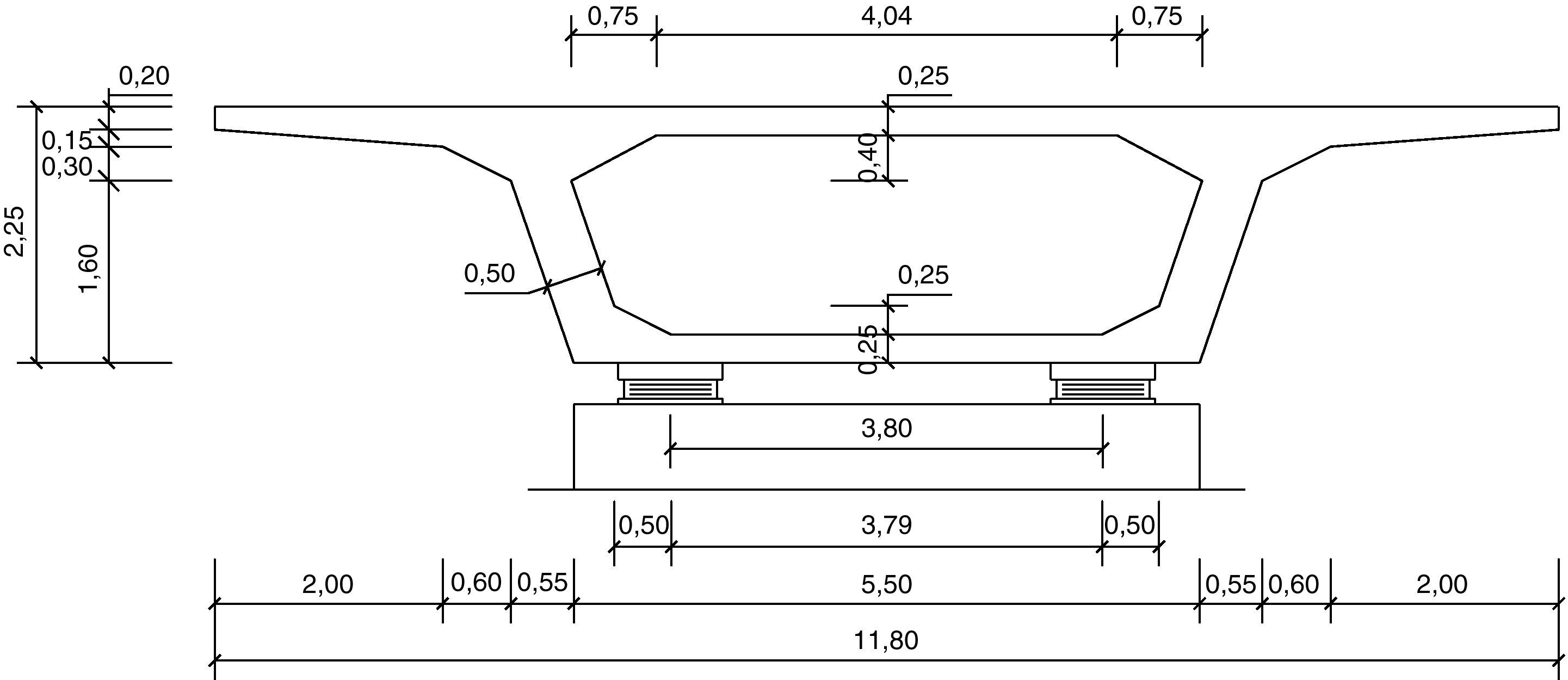
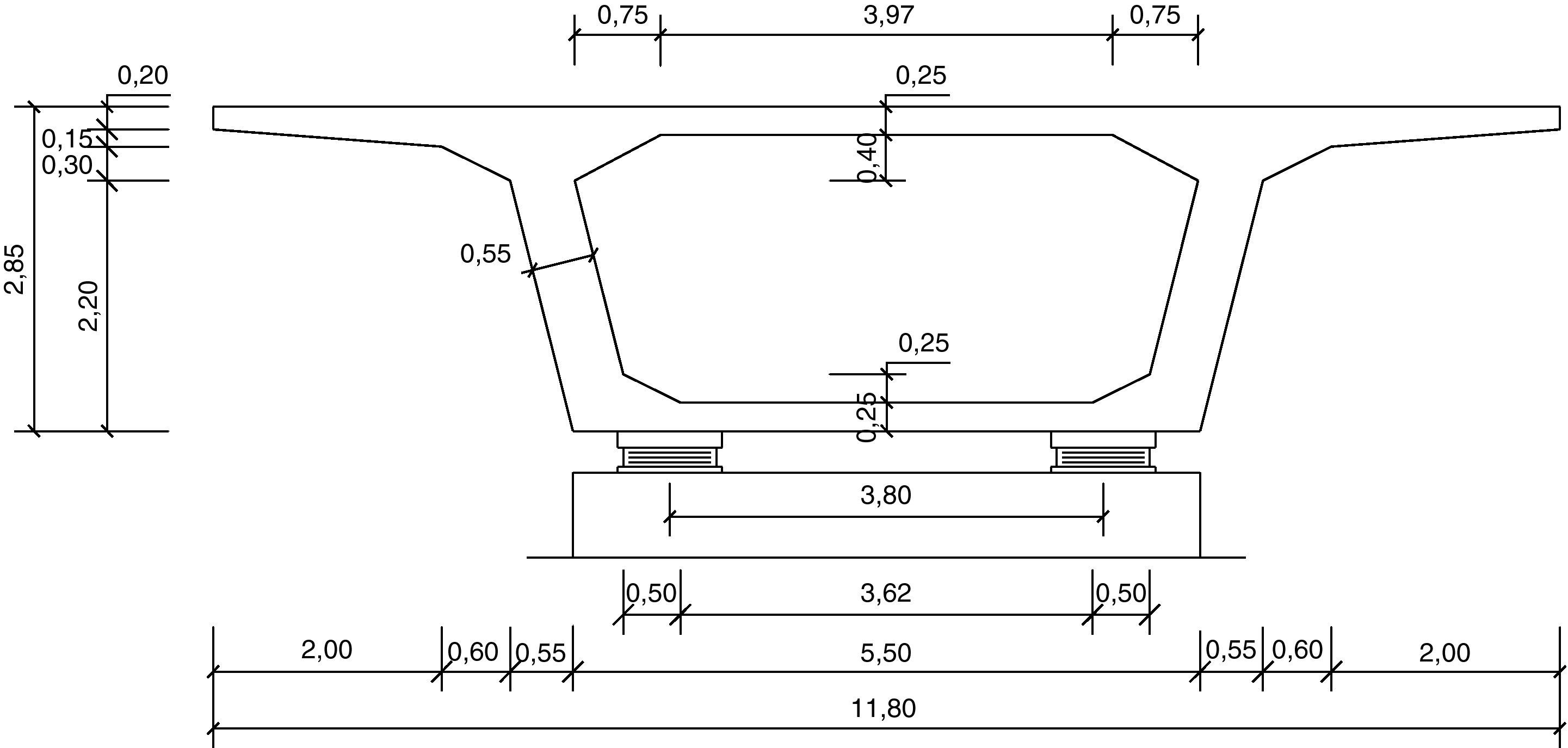
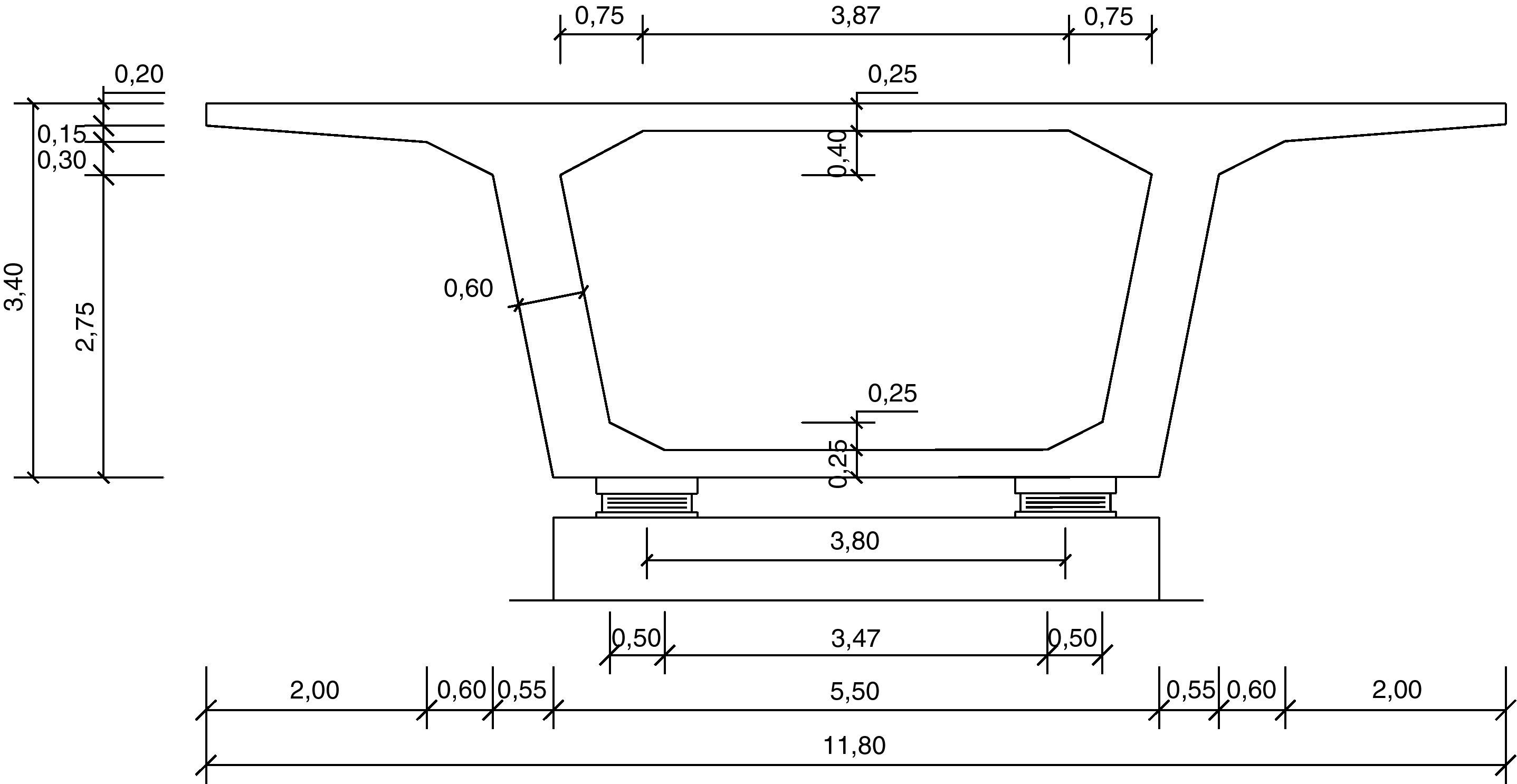
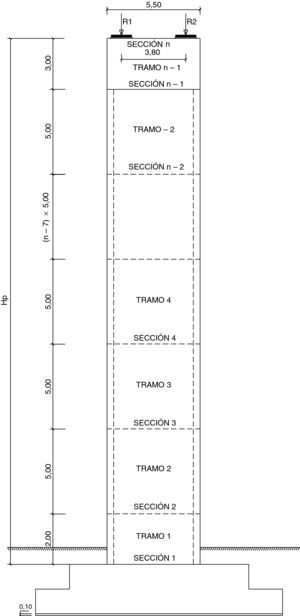
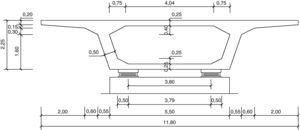
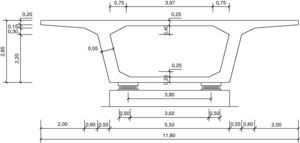
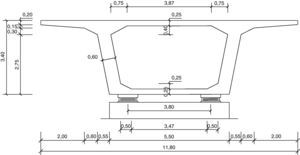
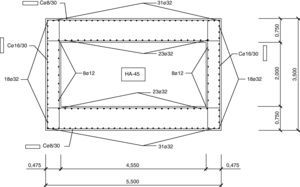
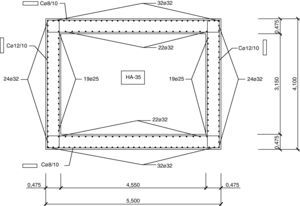
2Definición del problema de optimización2.1Pilas a optimizarLas pilas de hormigón armado con sección rectangular hueca parametrizadas son un total de 15 (fig. 3). Las alturas consideradas son 20, 30, 40, 50 y 60m. Los viaductos estudiados son tableros rectos continuos de hormigón pretensado con cargas de carretera. Estos viaductos tienen 10 vanos y longitudes de 384, 480 y 576m. La secuencia de longitudes de los 10 tramos son 32-8x40-32=384m, 40-8x50-40=480m y 48-8x60-48=576m. Las longitudes de los 8 vanos intermedios resultan ser de 40, 50 y 60m, respectivamente. Las pilas a estudio son las de los vanos intermedios y se supone que todas tienen alturas iguales. Las figuras 4–6 mostrarán las secciones transversales de los tableros de estos viaductos, en los cuales se ha dispuesto un ancho total del tablero de 11,80m dejando los 7,00m centrales de la sección para dos carriles de 3,50m cada uno y 2,40m a cada lado para los arcenes y disposición de la barrera de protección. Al tener los viaductos diferentes luces en los vanos interiores (40, 50 y 60m) variará el canto de la sección transversal de los mismos, manteniéndose relaciones canto/luz similares, y el ancho de las almas por tener que disponer de un mayor pretensado. Como los vanos son de luz elevada los viaductos tendrán una longitud suficiente para ser necesario disponer apoyos tipo POT guiados en sentido longitudinal (avance de PK). Disponiendo un punto fijo en el estribo de menor altura que será donde se resistan las reacciones horizontales longitudinales. En sentido transversal, uno de los dos apoyos de las pilas será guiado y el otro fijo de manera que se permita tanto la libre dilatación del tablero en esta dirección, como que sean capaces de transmitir las reacciones horizontales del tablero a la pila.
2.2Definición del problemaEl problema a resolver será de optimización condicionada con función multivariable, variables discretas y restricciones. La función objetivo F (expresión 1) utilizada es económica y viene dada por los costes unitarios que llevan asociados cada uno de los materiales y operaciones realizadas para la construcción de la pila. Estos costes unitarios pi se multiplicarán por su correspondiente medición, mi dando un coste total que habrá que minimizar. Además la solución deberá ser factible, es decir, verificar las restricciones del problema (expresión 2) que en este caso serán los diferentes estados límite de servicio y últimos según la normativa aplicada.
En la expresión (1), x1, x2,...,xn son las variables del problema que se describirán en el siguiente epígrafe y servirán para definir la estructura y por tanto poderla evaluar. La expresión (2) se refiere a las restricciones explícitas del problema, que serán los distintos estados límite que marca la normativa. Además de las restricciones explícitas, la estructura deberá de satisfacer otras restricciones implícitas a la definición del modelo y a las variables de diseño y sus rangos. El propósito de estas restricciones implícitas será que la pila resultante sea construible en la práctica.2.3Variables de diseñoLas variables son valores necesarios para definir la estructura y serán modificadas por el algoritmo de búsqueda durante el proceso de optimización. Se adoptarán discretas, ya que lo que se pretende es que las pilas resultado del proceso sean construibles. Se pueden dividir, tanto para el soporte como para la zapatas, en tres grandes grupos: geométricas, relacionadas con la calidad del hormigón y relacionadas con el armado.
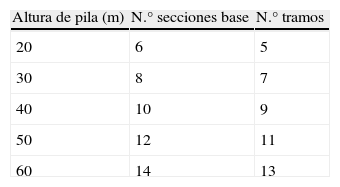
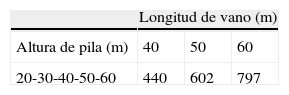
Las variables del soporte dependerán de la altura de los mismos, ya que las pilas se dividirán en tramos para construirlas. Estos tramos estarán limitados por dos secciones base y medirán 5,00m (medida del encofrado) en la parte central del soporte (fig. 3), 3,00m en la cabeza del soporte, que será maciza, y 2,00m en el tramo inicial. El número de tramos y secciones base será diferente según la altura de la pila (tabla 1).
Las variables geométricas del soporte son su dimensión longitudinal en cabeza y los dos espesores interiores del soporte en cada puesta. La dimensión longitudinal en cabeza se mantendrá constante a lo largo de todo el soporte y podrá variar de 1,00 a 5,00m con incrementos de 0,05m lo que dará un total de 81 posibilidades. Esta dimensión deberá ser igual o superior a la de los apoyos en esta dirección más 0,20m.
Los soportes tendrán doble simetría en todas sus secciones, tanto geométrica como de armado. Por lo que sólo se considerarán dos espesores interiores del soporte, uno el de la dirección transversal y el otro el de la longitudinal. Estos espesores podrán cambiar para cada una de las secciones huecas tomadas en el estudio de la misma. La restricción que ha sido adoptada consiste en que el ancho de la sección base superior deberá ser como máximo igual al de la inferior, pero nunca mayor. Los valores que pueden tomar estas variables van desde 0,25 a 0,75m variando de 0,025m en 0,025m, por lo que el número total de espesores posibles será de 21 en la sección base 1 para cada dirección. En el resto de secciones los valores posibles serán menores y dependerán del adoptado en la sección inferior para esa dirección.
La cimentación, que constará de zapata inferior y plinto, podrá adoptar un canto total que irá desde 1,00 hasta 4,00m. La variación entre valores de cantos será de 0,100m, por lo que habrá 31 posibles. El canto total se dividirá entre la zapata inferior y el plinto adoptando cada uno la mitad del mismo.
Las dimensiones en planta de la zapata, para cada lado, será mayor al ancho del soporte en su sección de arranques más un canto útil por cada lado. Las dimensiones posibles irán desde 8,00 a 25,00m, siendo la variación de 0,25m y el número de posibilidades de 69, en cada dirección. Las dimensiones del plinto, que serán como mucho las de la zapata, deberán ser mayores al ancho del soporte en su sección de arranques más un canto útil por cada lado. Las dimensiones posibles irán de 4,00 a 25,00m, siendo la variación de 0,25m y el número de posibilidades de 85.
2.3.2Variables relacionadas con la calidad del hormigónRespecto a las variables relacionadas con la calidad del hormigón podrán variar de resistencia en el soporte en cada una de las puestas (tramos) siempre que se cumpla que el de la puesta superior sea de igual o menor resistencia al de la inferior. Se dispondrán como posibles 6 tipos de hormigón armado diferentes, según su resistencia a compresión simple a 28 días. Estas 6 posibilidades serán HA-25, HA-30, HA-35, HA-40, HA-45, HA-50.
En la cimentación el hormigón a disponer será el mismo para toda ella y los posibles tipos serán los mismos que para el soporte.
2.3.3Variables relacionadas con el armadoRespecto a las variables relacionadas con el armado se dispondrán, a lo largo del soporte, barras longitudinales en el paramento exterior de la sección y en el interior. Las barras en caras paralelas serán iguales en número y diámetro en cada tramo, de tal manera que todas las secciones se mantengan simétricas respecto a los dos ejes. El número de barras longitudinales a disponer dependerá de las dimensiones del paramento que cubren y de la separación de las mismas. Suponiendo conocidas las dimensiones de las caras, las posibles separaciones de las barras en el primer tramo serán de 0,100m a 0,300m tomando una variación de la misma de 0,002m, por lo que se tendrán 101 posibilidades en este tramo. El número de barras a disponer en los tramos superiores será el mismo que el del tramo inferior o la mitad (si el de la inferior es impar la mitad más una), limitando la separación máxima de las mismas a 0,300m.
Los posibles diámetros de las barras longitudinales del soporte serán 12, 16, 20, 25 y 32 expresados en milímetros. El diámetro de las barras en el tramo superior será igual o menor al del tramo inferior para cada cara. Por lo tanto, en la sección base 1 se tendrá la posibilidad de disponer 6 diámetros diferentes en cada una de las caras y los diámetros de los tramos superiores dependerán de los inferiores.
En el soporte se podrán montar dos tipos de cercos, independientes unos de otros, en una determinada sección: los que van en dirección longitudinal y los que van en transversal. Estos cercos podrán ser de diferente diámetro en un mismo tramo, según la dirección de los mismos, siendo la separación entre ambos igual. Cuando se dispongan cercos en un tramo, los que van en la misma dirección en el superior tendrán que ser de igual o menor diámetro y la separación de los mismos en el tramo superior tendrá que ser igual o mayor.
Los posibles diámetros que se pueden disponer para armadura de cortante del soporte serán 12, 16 y 20mm. Además, existirá la posibilidad de no disponer armadura aunque en todos los casos se dispondrán barras de diámetro 8mm que sujeten las barras verticales. Las posibles separaciones de cercos irán de 0,100m a 0,300m, variando de 0,025m en 0,025m.
Para el armado de la cimentación se dispondrán un número determinado de barras en su parte inferior, tanto en la dirección longitudinal como en la transversal. Dicho número dependerá de las dimensiones y de la separación de las mismas que irá de 0,100m a 0,300m variando de 0,025m en 0,025m, por lo que se tendrán 9 posibilidades. Además, el número de capas posibles para cada una de las direcciones podrá tener uno de los siguientes valores: 1, 2, 3 o 4. El número de barras dispuesto en la parte superior de la zapata será el mismo que en su parte inferior en una capa, para cada dirección. Este número de barras en la parte superior de la zapata será nulo si la zapata tiene las mismas dimensiones que el plinto, en cuyo caso se tendrá una zapata sin plinto y la armadura superior del plinto pasará a ser la de la zapata. Las barras dispuestas en la parte superior del plinto serán la parte proporcional de las de la zapata en su parte inferior en relación con la dimensión del mismo. Los posibles diámetros de las barras de armado de la cimentación serán los mismos que en la armadura longitudinal del soporte. En la cimentación no se ha considerado la posibilidad de disponer armadura de cortante, ya que es poco frecuente en la práctica para este tipo de cimentaciones y aumentaría significativamente los costes de las mismas debido a la gran cantidad de acero que habría que disponer.
En la cabeza del soporte se dispondrá un armado que dependerá del hormigón dispuesto en dicho tramo, de las reacciones en los apoyos y de los anchos de las paredes del soporte en el tramo inferior al mismo.
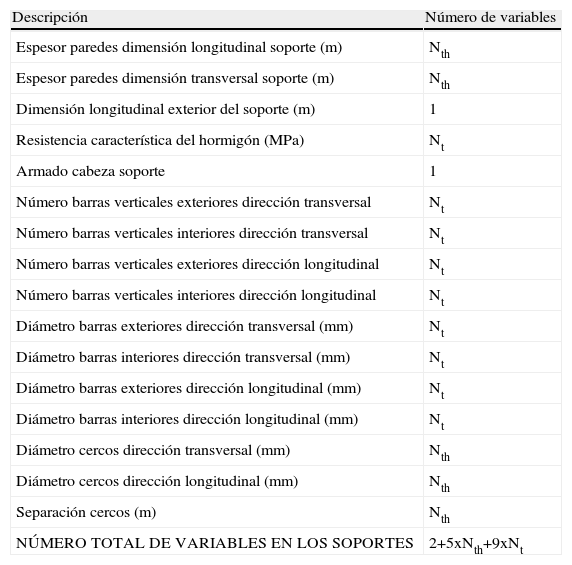
Con todo lo anterior, el número total de variables para las pilas de 20, 30, 40, 50 y 60m de altura serán 83, 111, 139, 167 y 195, respectivamente. Correspondiendo 16 variables a la zapata, en todos los casos, y el resto al soporte. En la tabla 2 se detallan las distintas variables del soporte, siendo Nth el número de tramos de soporte huecos, y Nt el número total de tramos.
Número variables soporte
| Descripción | Número de variables |
| Espesor paredes dimensión longitudinal soporte (m) | Nth |
| Espesor paredes dimensión transversal soporte (m) | Nth |
| Dimensión longitudinal exterior del soporte (m) | 1 |
| Resistencia característica del hormigón (MPa) | Nt |
| Armado cabeza soporte | 1 |
| Número barras verticales exteriores dirección transversal | Nt |
| Número barras verticales interiores dirección transversal | Nt |
| Número barras verticales exteriores dirección longitudinal | Nt |
| Número barras verticales interiores dirección longitudinal | Nt |
| Diámetro barras exteriores dirección transversal (mm) | Nt |
| Diámetro barras interiores dirección transversal (mm) | Nt |
| Diámetro barras exteriores dirección longitudinal (mm) | Nt |
| Diámetro barras interiores dirección longitudinal (mm) | Nt |
| Diámetro cercos dirección transversal (mm) | Nth |
| Diámetro cercos dirección longitudinal (mm) | Nth |
| Separación cercos (m) | Nth |
| NÚMERO TOTAL DE VARIABLES EN LOS SOPORTES | 2+5xNth+9xNt |
Los parámetros son todos aquellos datos necesarios para definir un problema concreto que serán invariantes durante el proceso de cálculo. Los distintos tipos de parámetros serán: geométricos, de carga, de armado, de normativa y de exposición (tablas 3–6).
Diversos parámetros de cálculo
| Parámetros | Valores |
| Dimensión transversal del soporte | 5,50m |
| Altura zona maciza del soporte | 3,00m |
| Altura trepa encofrado | 5,00m |
| Número de apoyos | 2 |
| Separación de apoyos | 3,80m |
| Densidad de las tierras | 20,00kN/m3 |
| Tensión admisible del terreno | 500,00kN/m2 |
| Tipo de acero (B-500-S) | 500MPa |
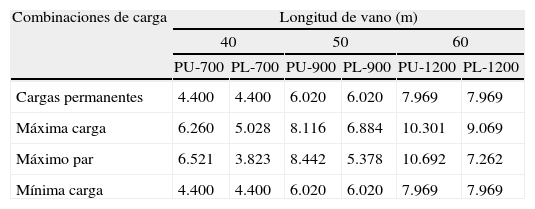
Reacciones verticales del tablero (kN)
| Combinaciones de carga | Longitud de vano (m) | |||||
| 40 | 50 | 60 | ||||
| PU-700 | PL-700 | PU-900 | PL-900 | PU-1200 | PL-1200 | |
| Cargas permanentes | 4.400 | 4.400 | 6.020 | 6.020 | 7.969 | 7.969 |
| Máxima carga | 6.260 | 5.028 | 8.116 | 6.884 | 10.301 | 9.069 |
| Máximo par | 6.521 | 3.823 | 8.442 | 5.378 | 10.692 | 7.262 |
| Mínima carga | 4.400 | 4.400 | 6.020 | 6.020 | 7.969 | 7.969 |
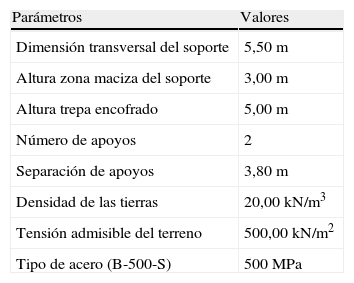
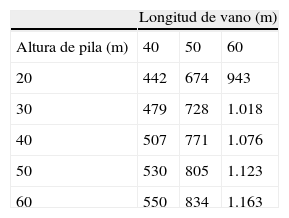
Los parámetros de geometría son la dimensión transversal del soporte (5,50m), la altura del soporte en cada caso (20, 30, 40, 50 y 60m), la dimensión de la parte maciza del soporte bajo apoyos (3,00m) en la cual se realizará el armado de cabeza, la altura de trepa con la que se construirá (5,00m) y el número, separación y dimensión de los apoyos. Los parámetros de carga y terreno son: la densidad de las tierras sobre la zapata, la tensión admisible del terreno, las reacciones sobre los apoyos y el resto de acciones que actúan sobre la pila. Los parámetros de armado son: el tipo de acero utilizado (B-500S) y el armado de las caras laterales de la zapata y del plinto, que se ha dispuesto Ø12/20. Los parámetros de normativa se corresponden con las normas aplicadas que han sido la EHE-08, Eurocódigo 2, IAP-98 y NCSP-07 [3,4,27,28]. Por último, los parámetros de exposición contemplarán los diferentes ambientes en los que se encuentra construida la estructura: interior, exterior y enterrado.
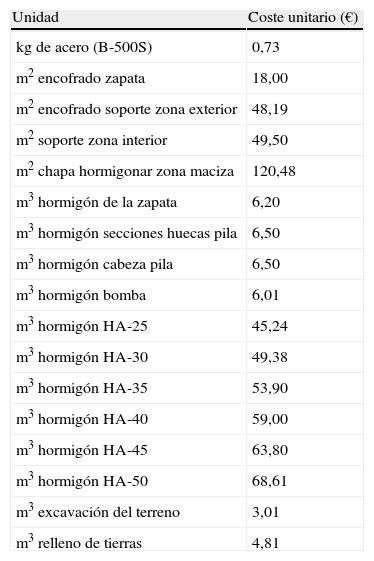
2.5Función objetivoLa función objetivo utilizada es económica y viene dada por los costes unitarios (tabla 7) que llevan asociados cada uno de los materiales y trabajos realizados para la construcción de la pila. Estos costes unitarios pi se multiplicarán por su cantidad correspondiente mi y la suma dará un coste total que habrá que minimizar. Los costes unitarios son los reales de mercado en el año 2007 e incluirán todo lo necesario para la ejecución de la pila, es decir, en el armado vendrá incluido el suministro, doblado, montaje y puesta en obra según normativa [3], incluso despuntes, atado y solapes. El encofrado incluirá el suministro del mismo, la colocación con los medios necesarios, desencofrado y limpieza, incluso la parte proporcional de cuñas, apuntalamiento y desencofrante. El coste del hormigonado variará, según el tipo de hormigón que se esté empleando y el elemento a hormigonar, disponiéndose de bomba para hormigonar tanto el soporte como la zapata. El coste unitario incluirá la fabricación, el transporte, puesta en obra, vibrado y curado del mismo. La excavación del terreno incluirá el despeje, desbroce y excavación con medios mecánicos, incluso extracción, carga y transporte a vertedero o al lugar de empleo del mismo. El relleno se realizará con material procedente de la excavación o de otra parte de la obra y se compactará en tongadas de espesor hasta 25cm utilizando bandeja vibrante.
Costes unitarios de las pilas
| Unidad | Coste unitario (€) |
| kg de acero (B-500S) | 0,73 |
| m2 encofrado zapata | 18,00 |
| m2 encofrado soporte zona exterior | 48,19 |
| m2 soporte zona interior | 49,50 |
| m2 chapa hormigonar zona maciza | 120,48 |
| m3 hormigón de la zapata | 6,20 |
| m3 hormigón secciones huecas pila | 6,50 |
| m3 hormigón cabeza pila | 6,50 |
| m3 hormigón bomba | 6,01 |
| m3 hormigón HA-25 | 45,24 |
| m3 hormigón HA-30 | 49,38 |
| m3 hormigón HA-35 | 53,90 |
| m3 hormigón HA-40 | 59,00 |
| m3 hormigón HA-45 | 63,80 |
| m3 hormigón HA-50 | 68,61 |
| m3 excavación del terreno | 3,01 |
| m3 relleno de tierras | 4,81 |
Las restricciones del problema se derivan de la aptitud al servicio y de las exigencias de resistencia y estabilidad y se expresarán mediante los estados límite de servicio y últimos que deberá de satisfacer el soporte y la zapata de acuerdo con los artículos de la EHE [3]. Adicionalmente, el problema incluirá restricciones implícitas como las explicadas anteriormente debidas a la geometría, armado, materiales y constructibilidad de las soluciones.
Las restricciones estructurales para este tipo de pilas han sido ampliamente descritas en una publicación previa [1]. El soporte debe verificar los ELU de inestabilidad, agotamiento frente solicitaciones normales, agotamiento frente a cortante y fatiga y el ELS de fisuración, además de tener un armado superior a los mínimos mecánicos y geométricos. Dichas restricciones se comprobarán en cada una de las secciones base definidas, excepto la de inestabilidad que será global del soporte. Para la comprobación del ELU de inestabilidad será necesario la mayor parte del tiempo computacional debido a la gran cantidad de procesos iterativos, para su comprobación se ha utilizado el método de rigidez propuesto por Manterola [29]. La zapata deberá verificar: las tensiones en el terreno, la armadura mínima geométrica y mecánica, los ELU de cortante, flexión y fatiga y el ELS de fisuración. Las comprobaciones se realizarán en las dos direcciones: longitudinal y transversal. El método utilizado para la integración de las secciones es el propuesto por Bonet et al. [30], que realizará la integración de tensiones por el método de la cuadratura de Gauss-Legendre.
3Método de optimizaciónPara llegar a las pilas óptimas en cada caso se ha utilizado una variante del método metaheurístico de la colonia de hormigas. La colonia de hormigas fue inicialmente propuesta por Dorigo et al. y Bonabeau et al. [31,32]. Este algoritmo está basado en el establecimiento de una analogía entre el procedimiento natural que utilizan las hormigas para encontrar y explotar una fuente de alimentos. Una hormiga por sí sola no es capaz de hacer nada, pero todas unidas funcionan como un sistema inteligente. Cuando un conjunto de H hormigas salen del hormiguero en busca de alimento la trayectoria seguida por cada una de ellas será, en principio, aleatoria. De las H hormigas habrá un número de ellas que se perderán sin encontrar o encontrando comida y no regresarán al hormiguero (soluciones no factibles). Las hormigas que encuentran comida y regresan al hormiguero (soluciones factibles) dejarán un rastro de feromona. Cuando un nuevo conjunto de H hormigas vuelve a salir del hormiguero la selección de la trayectoria dependerá de la intensidad de la traza dejada por las anteriores y de una componente aleatoria. Esta traza se reforzará en función del número de hormigas que pasen por él, por lo que si para alcanzar una fuente de comida hay varios caminos las hormigas que vayan por el más corto volverán antes por lo que pasarán más veces dejando mayor rastro. Otro factor es la evaporación de la feromona que irá reduciendo la intensidad de las trazas con el paso del tiempo. El algoritmo deberá diversificar en fases iniciales intensificando en la búsqueda de soluciones de mayor calidad alrededor de las mejores encontradas. El proceso de búsqueda del algoritmo adoptado en este trabajo viene definido por las expresiones (3) a (6):
En el problema planteado optimizarán diversas pilas tipo con distintas alturas, lo que dará lugar a problemas con diferente número de variables. Además, como los rangos de las variables son los mismos, se tendrán factibilidades distintas para cada uno de ellos. Por lo anterior y para que no existan etapas, en alguno de los problemas, en las que el número de hormigas factibles sea nulo se ha utilizado un número H de hormigas factibles generadas en cada etapa que serán igual a 50. El número total de etapas será igual a 100.
El proceso de cálculo partirá de un valor nulo de las trazas de las variables, por lo que el sistema no tendrá ninguna información inicialmente. En la primera etapa las soluciones se buscan de manera aleatoria, llegando a H soluciones. A partir de la segunda etapa, las soluciones dependerán de la información dejada en el sistema por las hormigas de las etapas anteriores y de un valor aleatorio. Las hormigas constituirán la matriz de trazas T(t,i,j) (expresiones [3] a [5]) para una etapa t, una variable i y una determinada posición de la variable j dejarán un rastro, que será mayor o menor en función de la calidad de la solución encontrada por cada una de ellas, dejando rastro cero si no pasan por esa posición. Cada hormiga k dejará en una etapa t un incremento de rastro (ΔT(t,k,i,j)) (expresión [3]) para cada posición de las variables por las que pase que dependerá de Fmin, menor coste de todas las hormigas encontradas hasta el momento, de F(k) coste de la hormiga k a evaluar y de un exponente de valor 100 utilizado para que las hormigas con coste más parecido al Fmin dejen mayor rastro. La expresión (4) dará como resultado la suma de las trazas de todas las hormigas en la etapa t. Finalmente en la expresión (5) se obtendrá la traza total T(t,i,j) para la etapa t que dependerá, entre otros, de un factor de evaporación ev que se ha tomado igual a la unidad, de Fmin,t hormiga de mínimo coste de la etapa y del resto de factores de costes y trazas. La construcción de las nuevas soluciones H en una etapa t se hará de manera separada para el soporte y para la zapata y según una matriz de probabilidades (expresión 6) que dependerá de los valores de la matriz de trazas T(t,i,j), de T(t,i) que representará los valores de las sumas de las trazas para todas las posiciones de la variable i y de un factor aleatorio R con valores entre 0 y 1, multiplicados ambos por sus coeficientes α y β. A α y β se les darán unos valores iniciales comprendidos entre 0 y 1 y conforme avanza el algoritmo α aumentará y β disminuirá proporcionalmente en función de la etapa en que se encuentre el experimento y del número total de etapas, de manera que en la etapa final α=1 y β=0 y en todo el proceso α+β=1. Los valores iniciales dados para α y β han sido 0,9 y 0,1, respectivamente, para la columna y 0,8 y 0,2 para la zapata, dando más peso a la información dejada por el sistema que a la parte aleatoria, ya que fue como se obtuvieron mejores resultados en trabajos previos [1].
Para determinar el número de experimentos requeridos en cada ejecución se ha utilizado la distribución t de Student con un intervalo de confianza del 95% respecto a la media. El error estimado dado por la expresión tN−12.5sN, donde tN−12.5 es el coeficiente de la distribución t de Student, s la desviación típica de la muestra y N el tamaño de muestra, deberá ser menor del 0,5% al menor coste obtenido de la población de soluciones de la etapa inicial.
El algoritmo ha sido programado en Compaq Visual Fortran Edición Profesional 6.6.0. El ordenador utilizado ha sido un ordenador convencional con procesado Core 2 Duo de 1,86GHz.
4Análisis de los resultadosEn este punto se presentarán y discutirán los resultados obtenidos del proceso de optimización de las 15 pilas de hormigón armado con sección rectangular hueca. Las figuras 7–20 mostrarán los resultados de las diferentes características de las pilas. Los tiempos de computación de cada ejecución varían desde un mínimo de 1,23horas para la menor pila (vanos de 40m y altura de 20m), hasta un tiempo de 24,38horas para la mayor pila (vanos 60m y altura de 60m).
Las figuras 7–14 se referirán a distintas características geométricas, de armado y de hormigón del soporte. La figura 7 muestra como varía la dimensión longitudinal exterior del soporte en función de la altura del soporte y de la luz de vano. Se observará la necesidad de una mayor dimensión longitudinal del soporte en cuanto se aumentan las luces de los vanos o la altura del mismo, esto será debido a que las fuerzas y momentos aplicados en la base serán mayores por lo que se necesitará mayor sección para resistirlos de la manera más eficiente posible.
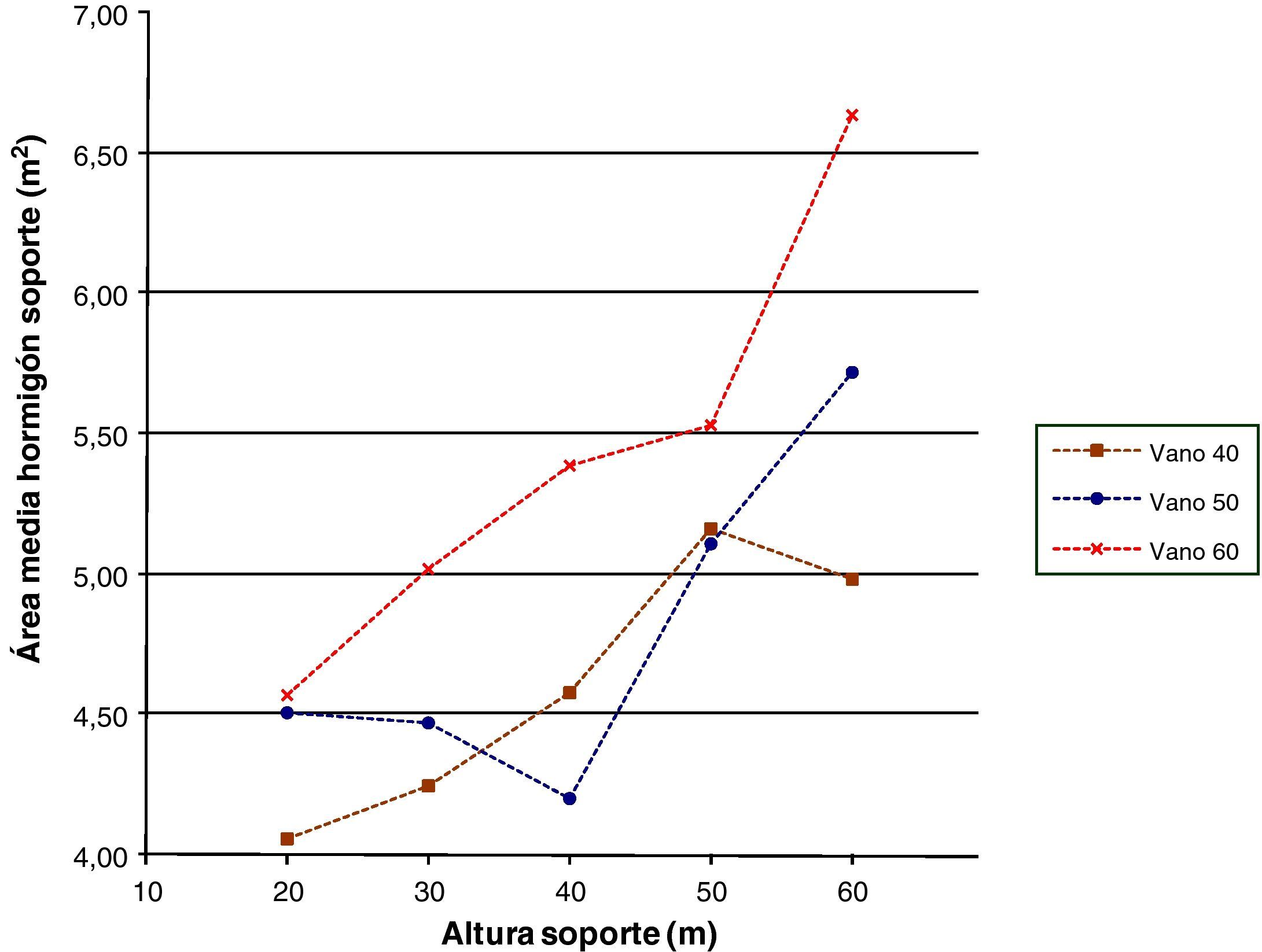
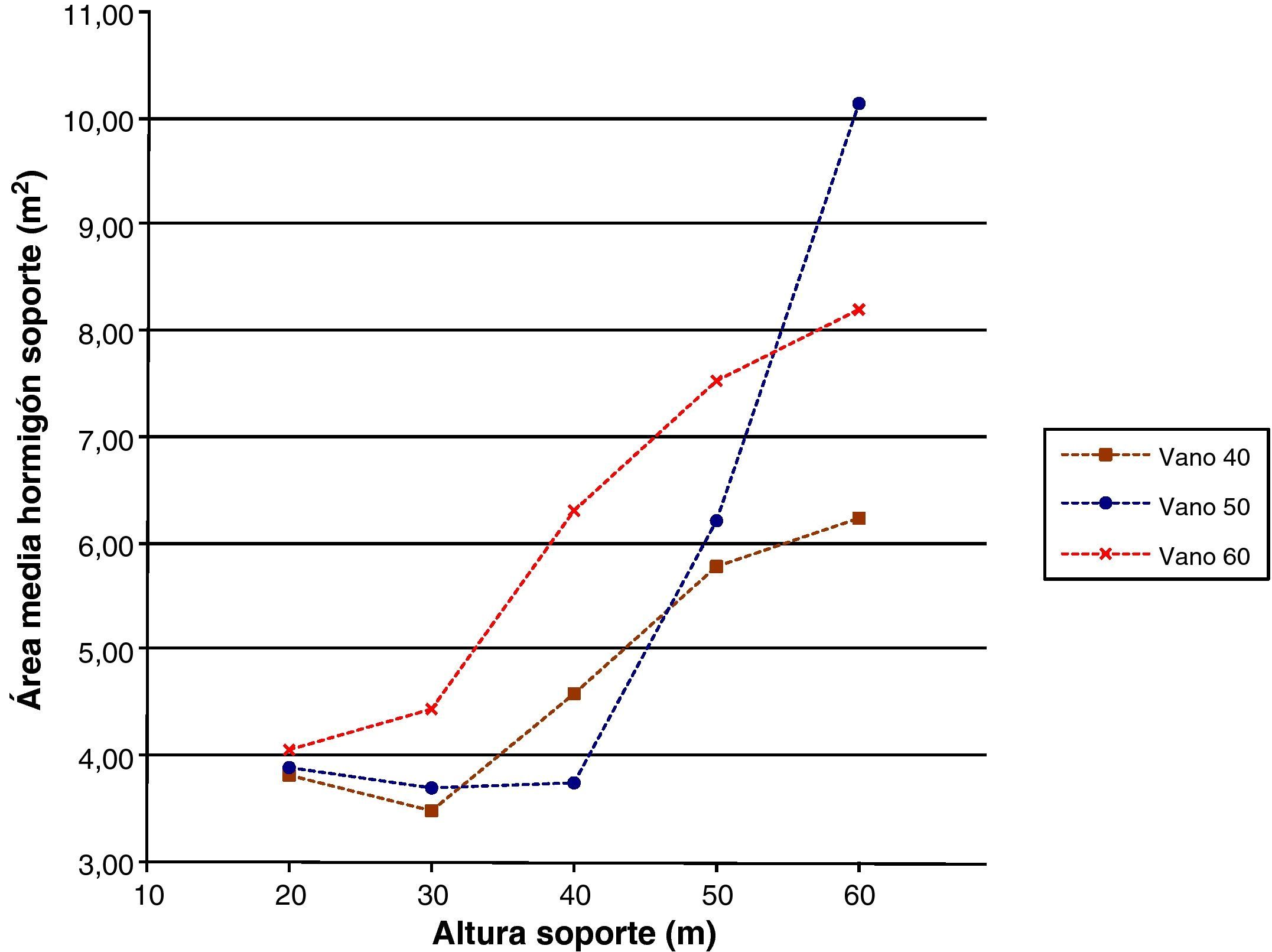
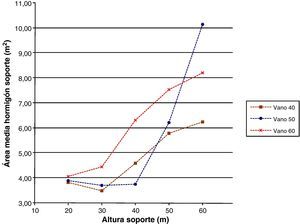
Las figuras 8 y 10 se referirán a los m3 de hormigón del soporte por metro lineal del mismo, lo que dará el área media de hormigón en las secciones del mismo y el área de hormigón en las secciones de arranque. El volumen de hormigón en los soportes será creciente conforme aumenta la altura del mismo. Esta misma tendencia se mantendrá en caso de que el volumen total se divida por la altura del mismo obteniendo el área media y poniendo de manifiesto la necesidad de secciones mayores conforme aumenta la altura de la pila. Sin embargo, aunque la tendencia de las curvas sea la misma la figura 10 tendrá un área superior a la de la figura 8 poniendo de manifiesto la disminución de los anchos de las secciones en un soporte conforme se aumenta en altura.
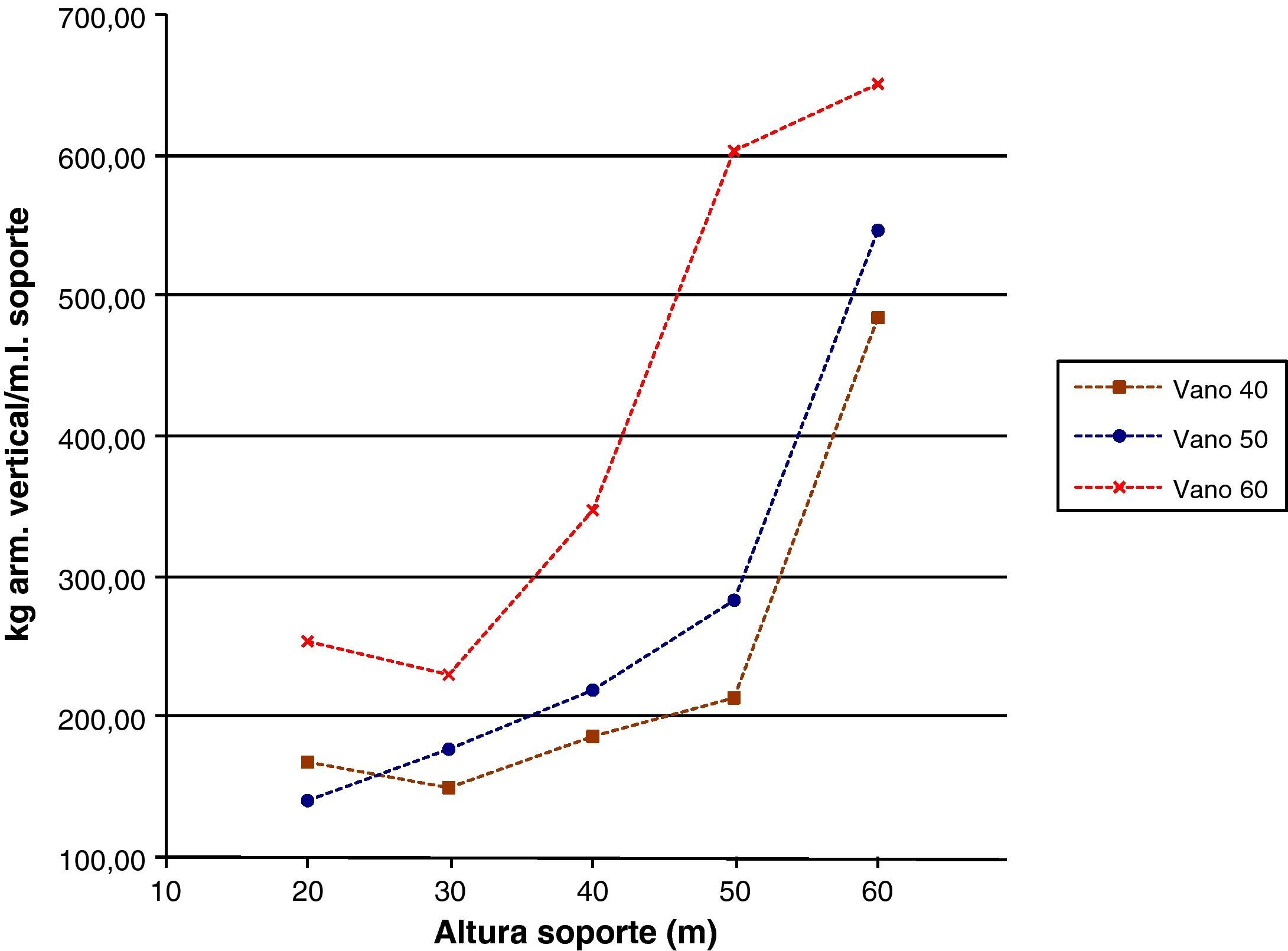
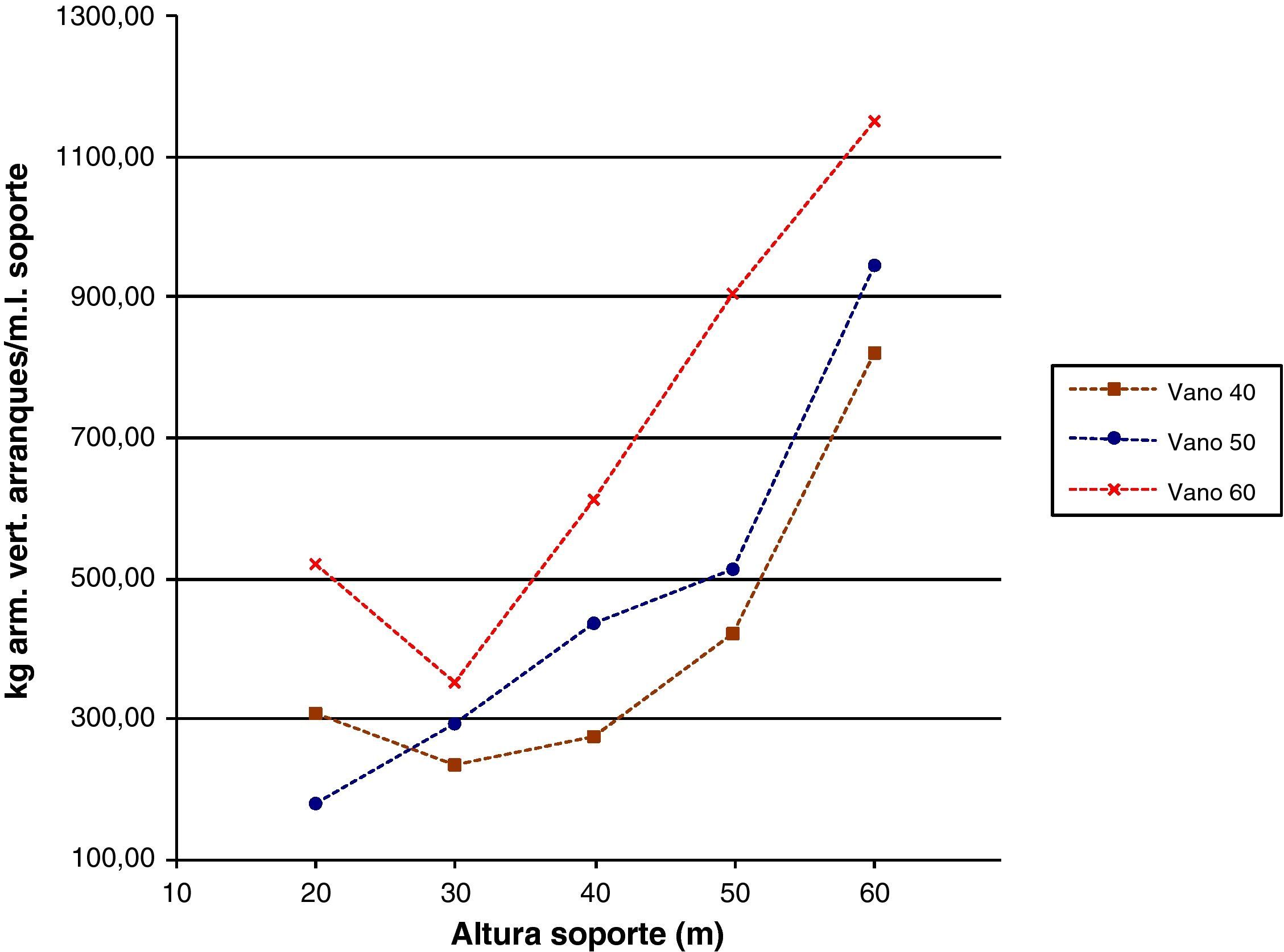
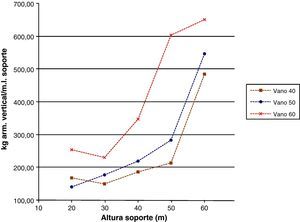
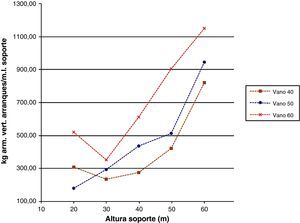
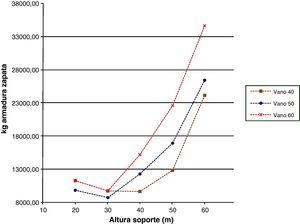
Las figuras 9 y 11 se referirán a los kilogramos de armadura vertical en los soportes por metro lineal de los mismos y al armado vertical en arranques por metro lineal, todo ello en función de la luz de vano y de la altura de soporte. La tendencia de las curvas será, en general, creciente con la altura y la luz de vano en ambas figuras. No obstante, en la figura 11 las cuantías serán superiores, ya que las secciones de arranques estarán sometidas a mayores esfuerzos. Sin embargo, se observa que en los soportes de 20 a 30m disminuye la cuantía de armadura para a continuación aumentar en las de más altura. Esto se producirá debido a que la sección del soporte en dirección transversal es constante en todos los casos, y aunque en longitudinal varía no deja de ser una sección transversal con dimensiones demasiado grandes para las menores alturas de soporte. Esto producirá que el armado vertical dispuesto sea por mínimos y no por la necesidad de verificar los distintos estados límite. Conforme se aumenta la altura del soporte las secciones vendrán dimensionadas por los estados límite, lo cual llevará a mostrar una tendencia creciente de armado por metro lineal cuando se aumenta la altura.
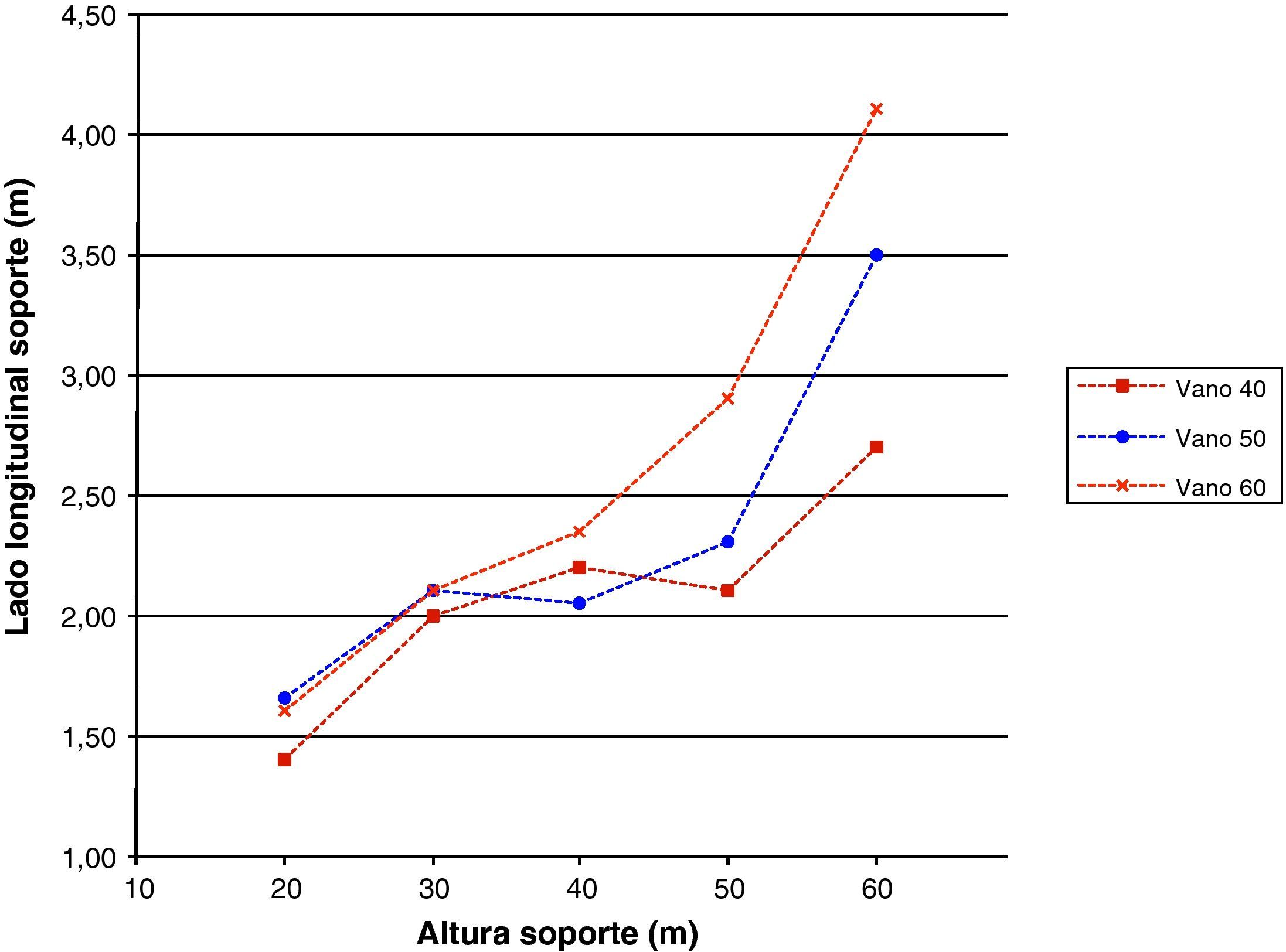
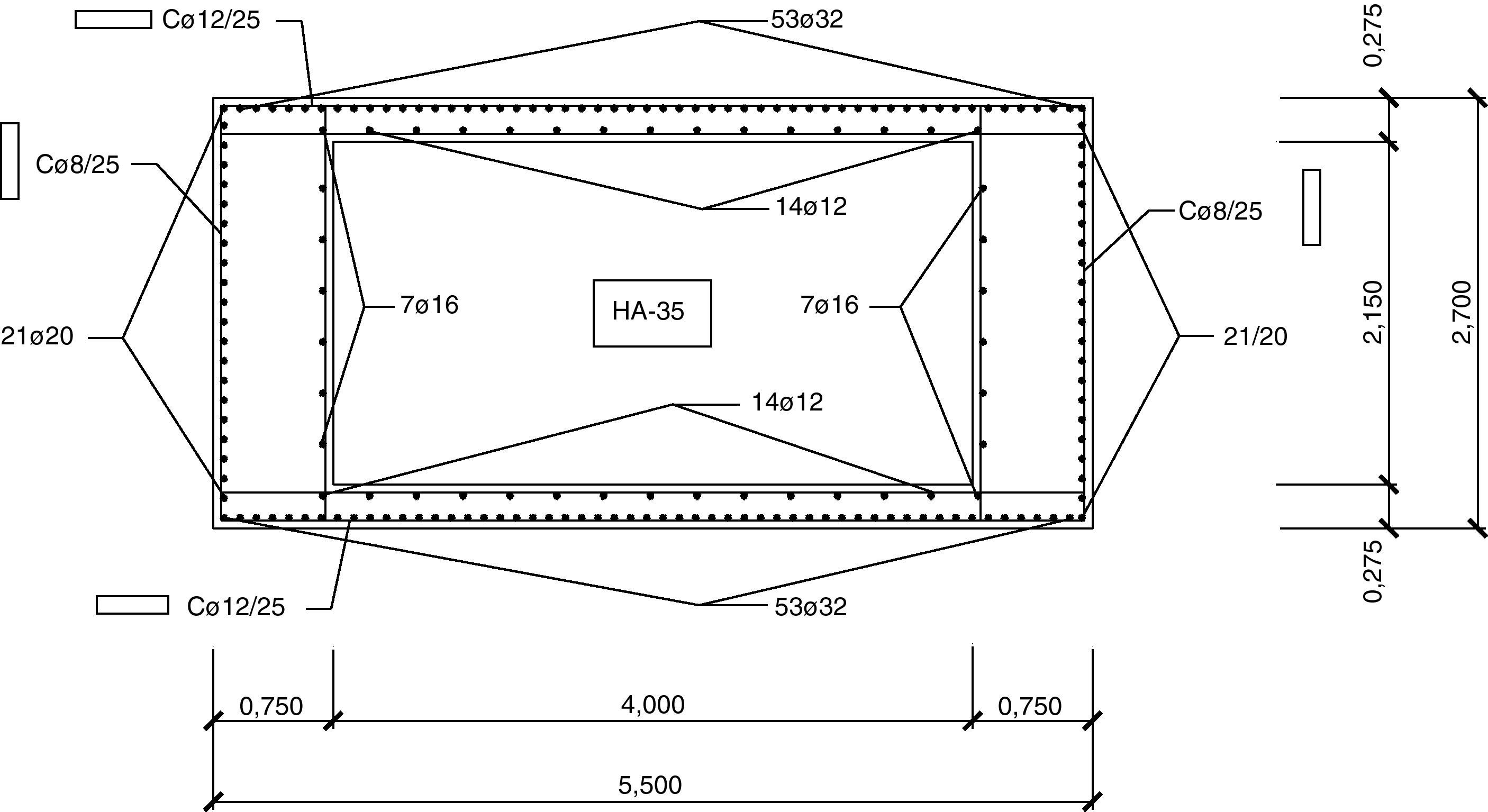
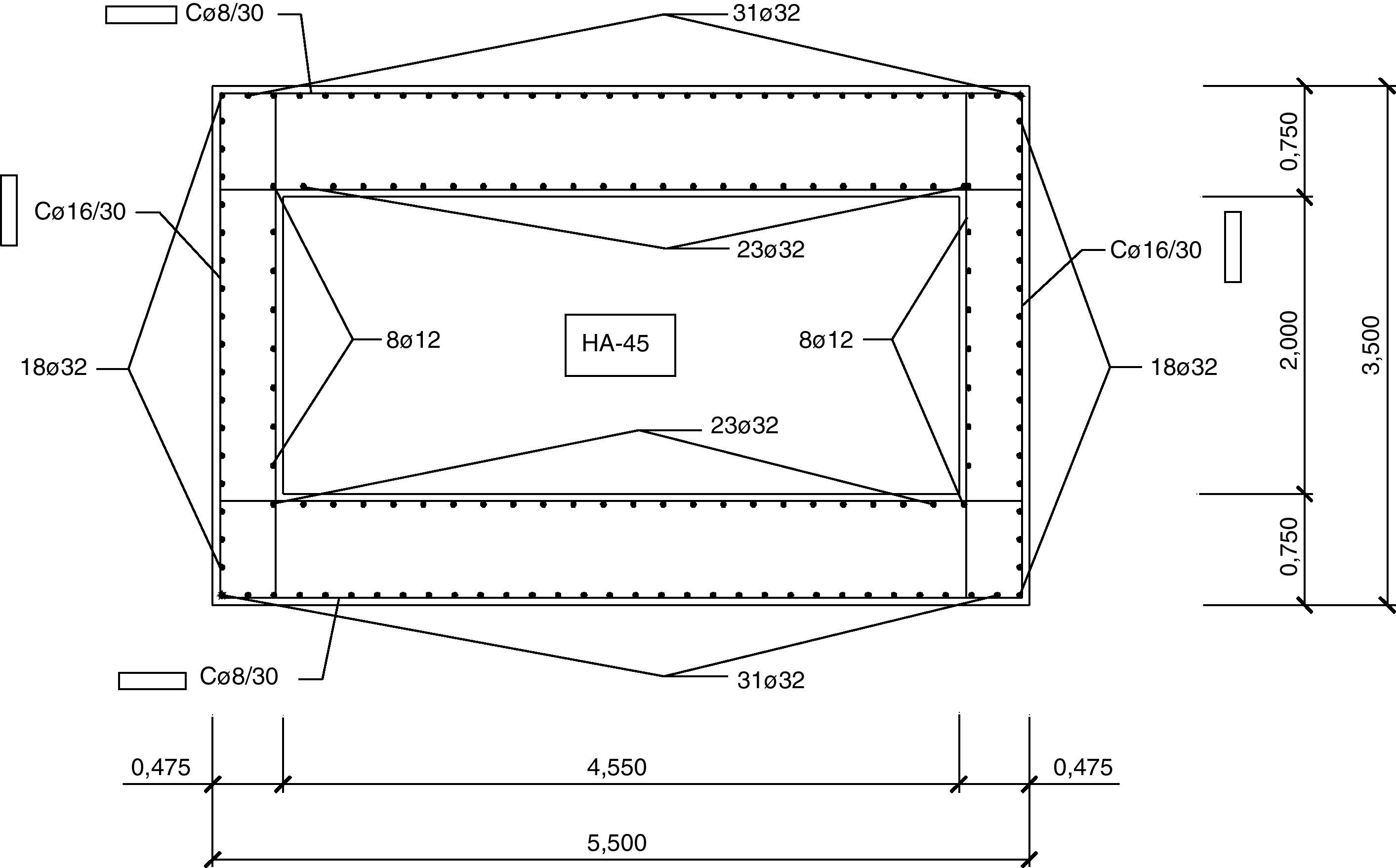
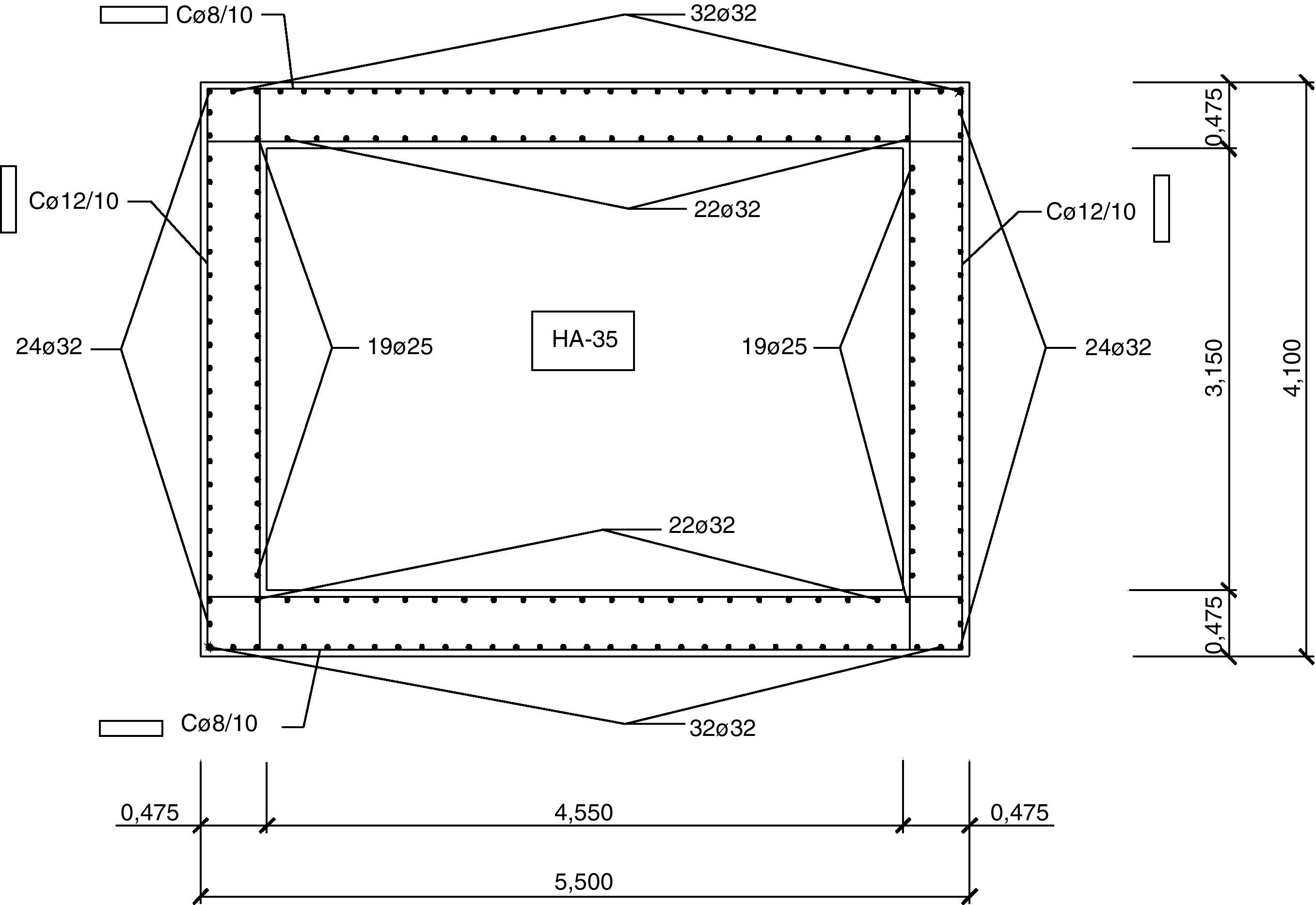
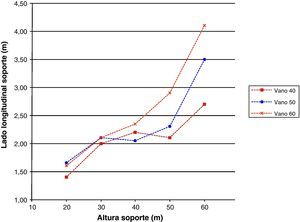
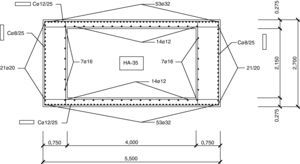
Las figuras 12–14 mostrarán las secciones base de arranques para los soportes de 60 metros de altura. Se puede observar que la dimensión del lado longitudinal aumentará con la luz de vano dando lugar a secciones de mayor medida debido a que los esfuerzos a resistir serán superiores. Además, también aumentará el armado para estas secciones con la luz de vano.
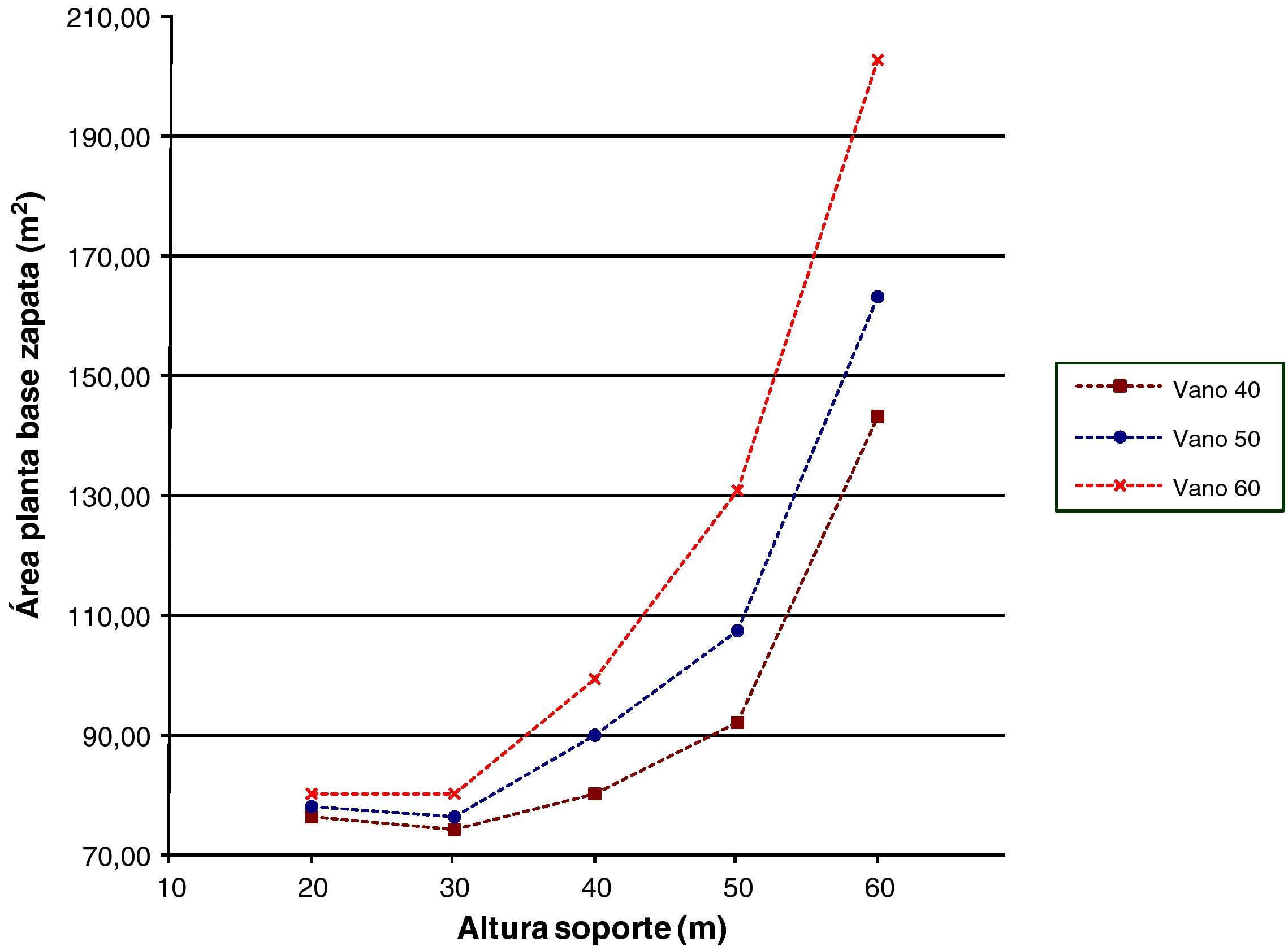
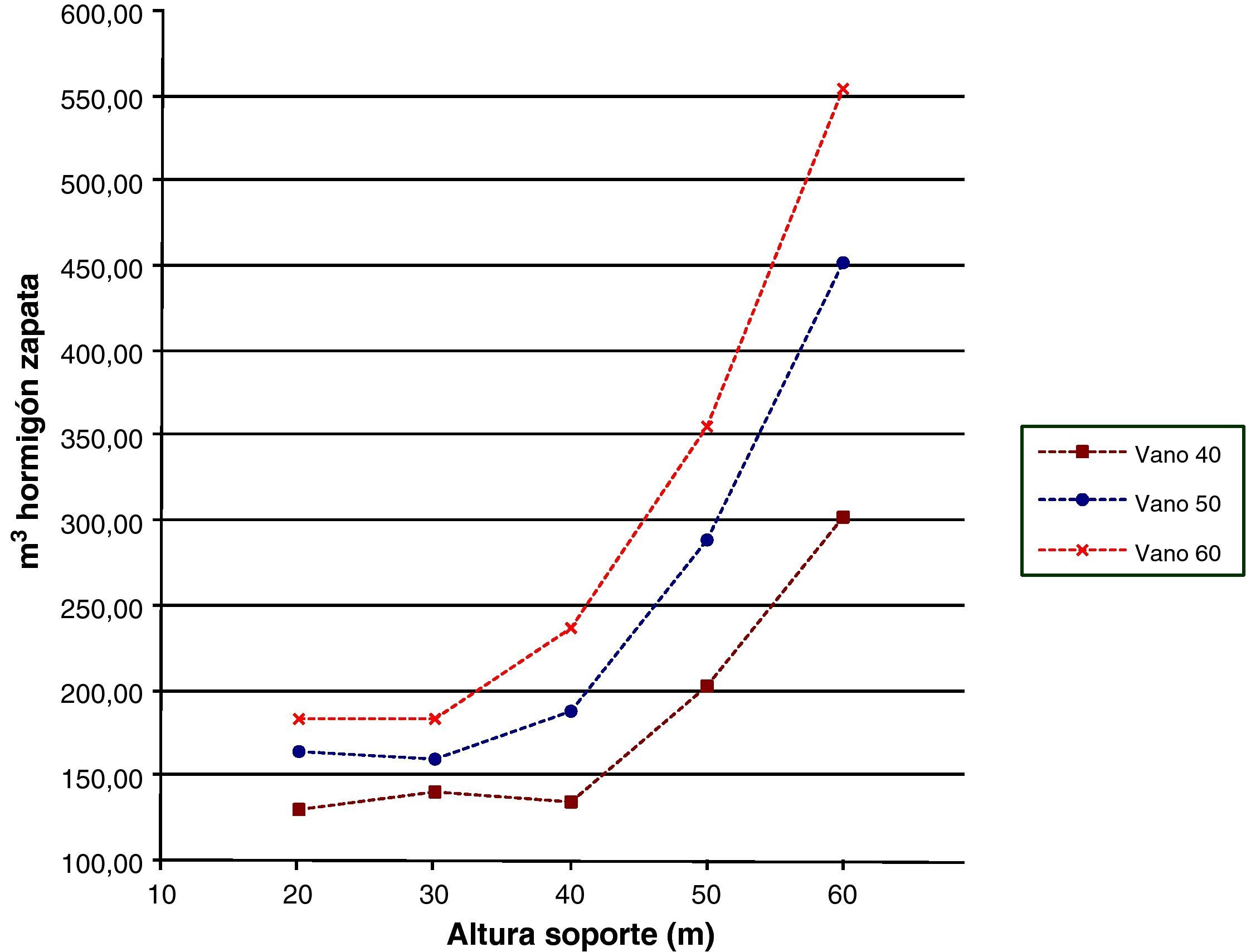
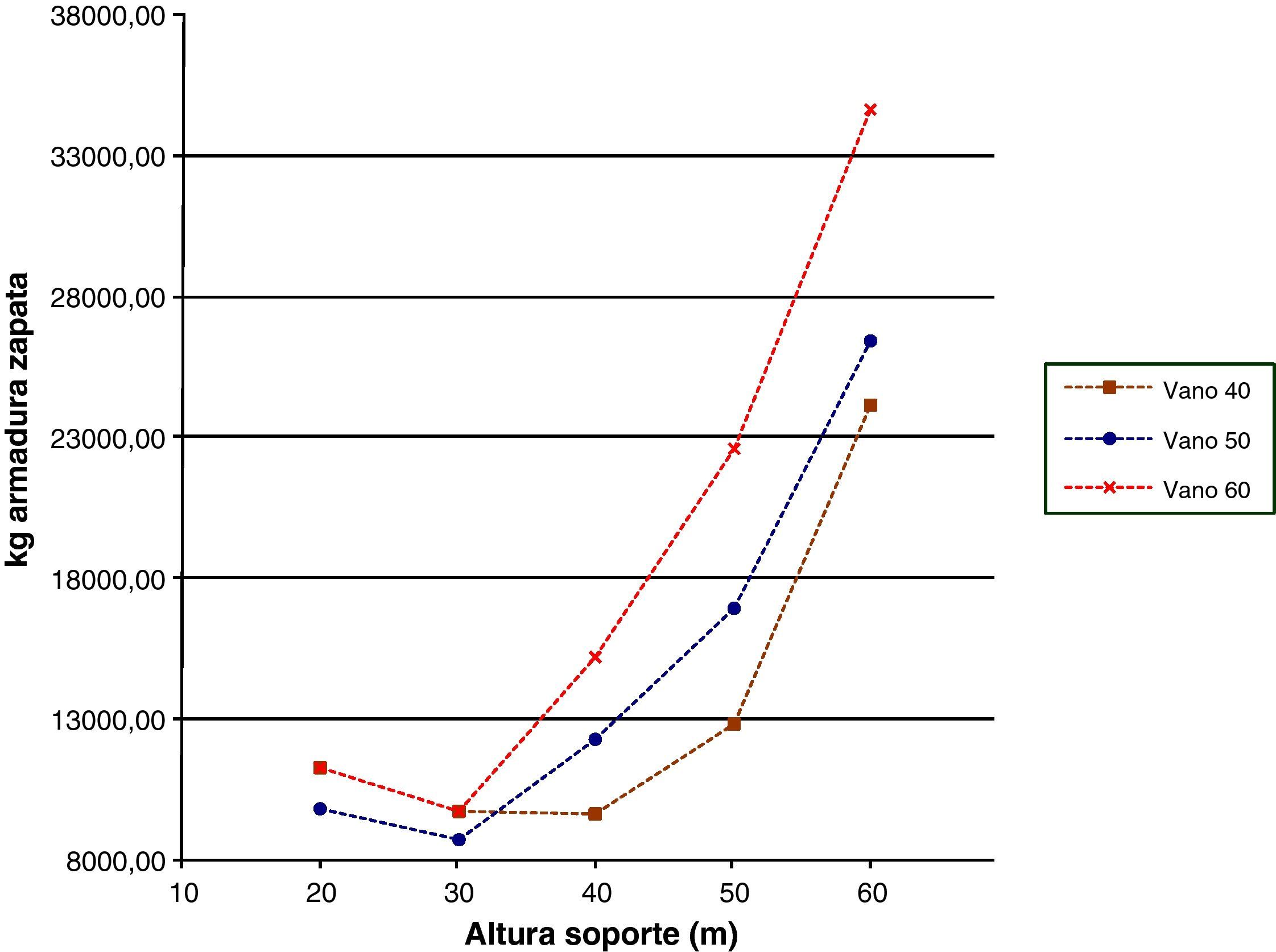
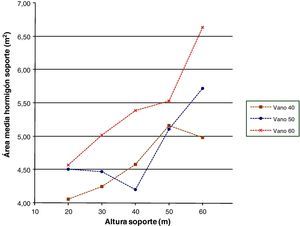
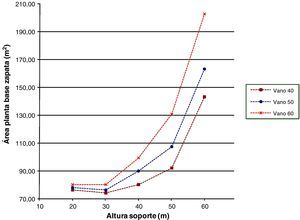
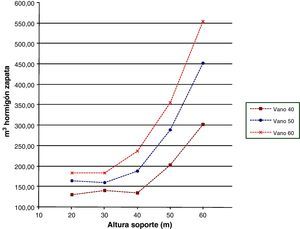
Las figuras 15–17 representarán las distintas características de las zapatas. La figura 15 mostrará el área de las plantas, la figura 16 el volumen de hormigón y la figura 17 los kilogramos de armadura todo ello en función de las distintas alturas de soporte y longitudes de vano. El área de las plantas de las zapatas para alturas de soporte de 20 y 30m serán similares, esto se debe a que con alturas bajas los esfuerzos que se producen en la base de las zapatas son pequeños y producirán tensiones pequeñas que se podrán resistir con las dimensiones mínimas de zapata. Sin embargo, conforme aumenta la altura de los soportes los esfuerzos en la base de la zapata serán mayores, por lo que la forma de la zapata se tendrá que ir adaptando de manera que se ajuste a la tensión máxima admisible que permite el terreno. Lo anterior se verá incrementado al aumentar la luz de los vanos, ya que las fuerzas horizontales serán superiores. Por otro lado, las dimensiones superiores de zapata serán las transversales al ser las acciones horizontales mayores en esta dirección. Respecto al volumen de hormigón dispuesto en las zapatas pasará algo similar a las áreas de las plantas, siendo similar en las pilas de menores alturas y aumentando conforme aumenta la altura del soporte. Por último, en lo que se refiere al armado de las zapatas la tendencia de las curvas será similar a las de las curvas de área de las plantas y volumen de hormigón, ya que cuanta mayor dimensión tengan las zapatas debido a la necesidad de verificar las tensiones en el terreno mayores esfuerzos se producirán en las mismas y será necesario mayor armado y canto de las secciones para resistirlos.
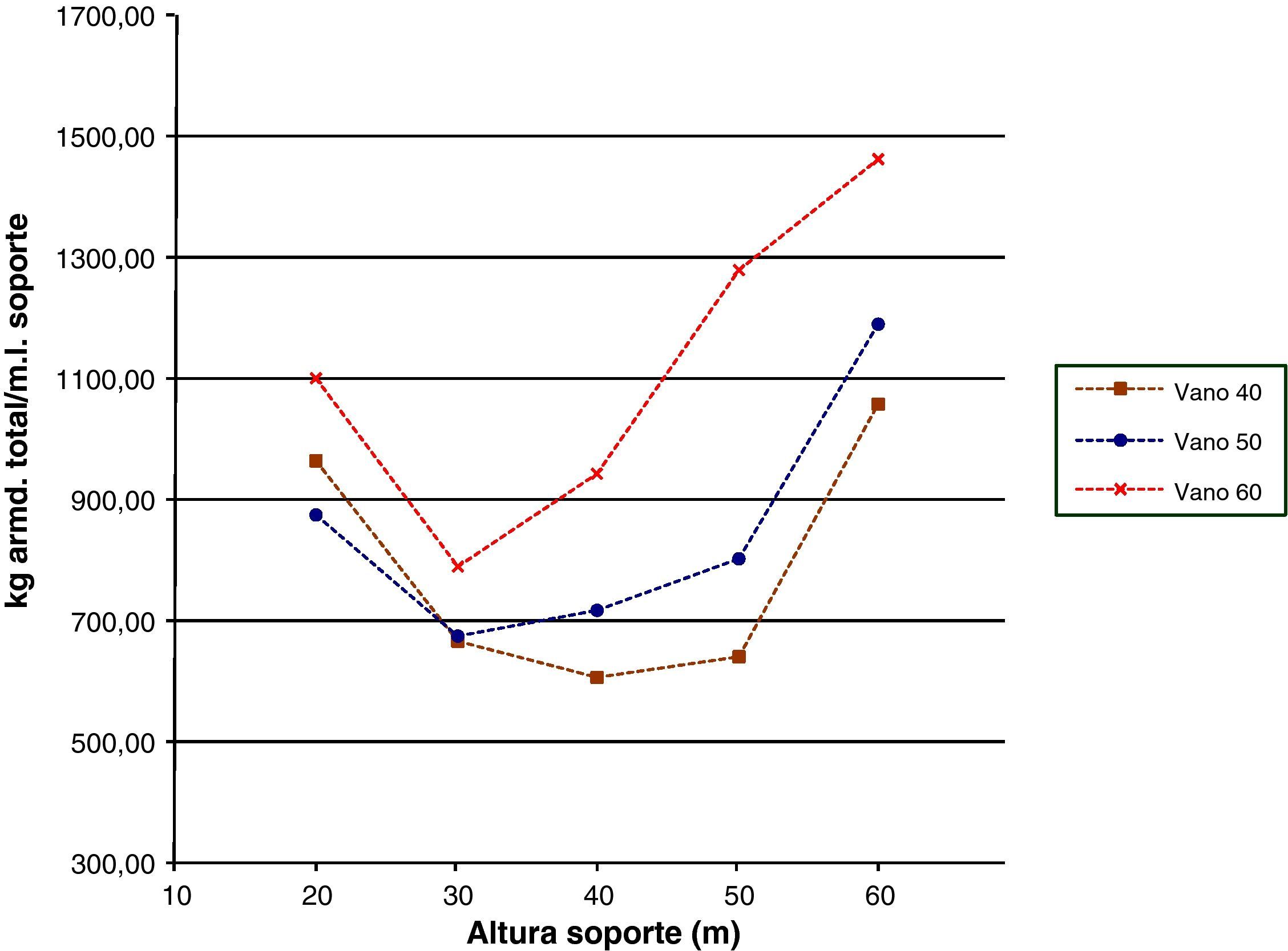
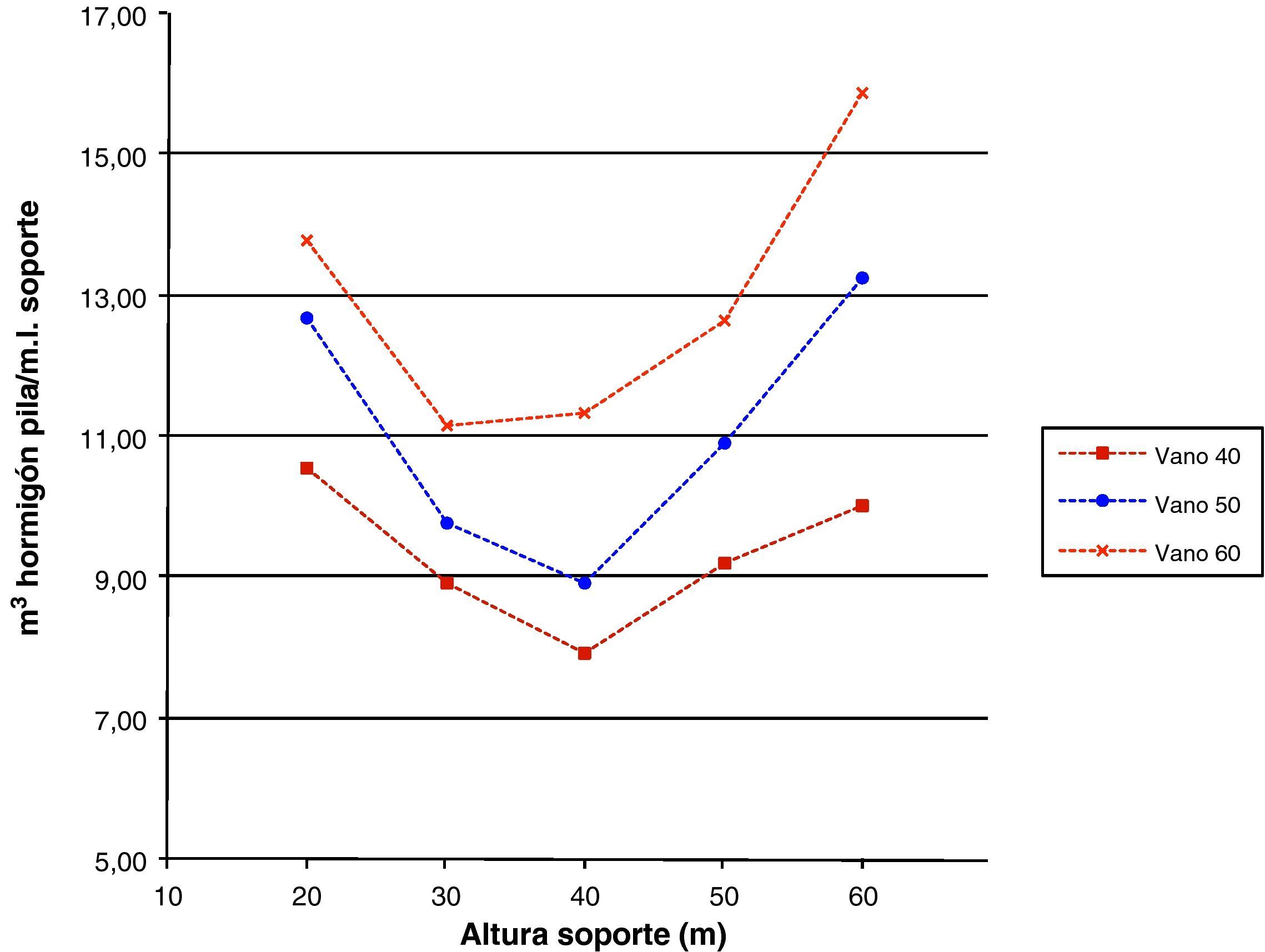
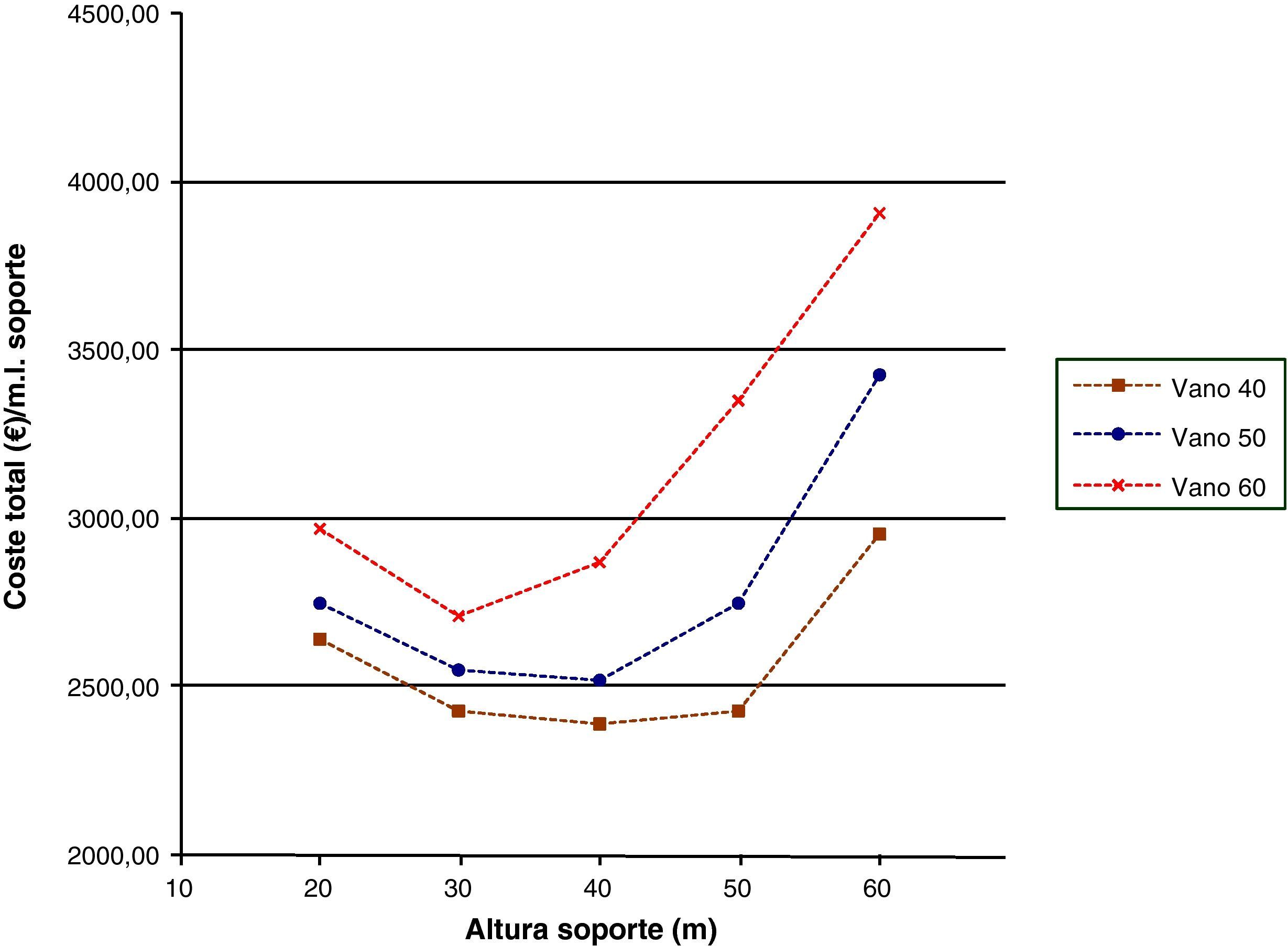
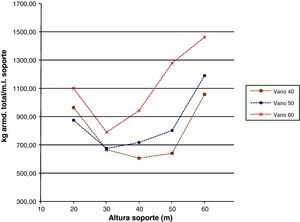
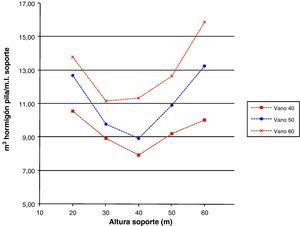
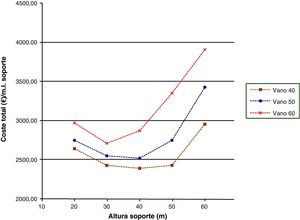
Las figuras 18–20 se referirán, respectivamente, a las cuantías por metro lineal de soporte de los kilogramos totales de armadura dispuestos en la pila, al volumen total de hormigón y a los costes totales. La tendencia de las tres figuras es similar disminuyendo hasta una cierta altura de soporte para a continuación aumentar. Aunque los kilogramos totales de armado y el volumen total de hormigón aumenten con la altura de soporte y con la luz de vano no aumentarán tanto como para hacer creciente la cuantía hasta una cierta altura de pila. Esto se debe, principalmente, a que estas mediciones en las zapatas de las pilas de menores alturas son similares y a que el valor de las mediciones de las zapatas es importante dentro del total de la pila. Por otro lado, la tendencia de las curvas del coste total por metro lineal de soporte (fig. 20) será similar a la tendencia de las curvas de las mediciones de armado y hormigón, ya que el coste de la pila es directamente proporcional al material dispuesto en la misma.
5ConclusionesSe han estudiado 15 pilas de sección rectangular hueca de hormigón armado con diferentes alturas (20, 30, 40, 50 y 60m) para viaductos de carretera con luces de 40, 50 y 60 metros en los vanos interiores. Las pilas a estudio pertenecerán a los vanos interiores y se supondrán de igual altura a lo largo de todo el viaducto.
Para obtener las pilas que minimicen la función objetivo verificando todas las restricciones del problema se ha utilizado una variante del algoritmo de la colonia de hormigas. Este algoritmo requerirá la definición de los valores iniciales de α y β (expresión [6]), el número de hormigas en cada etapa y el número total de etapas. Los resultados se obtuvieron con valores iniciales de α y β de 0,9-0,1 para el soporte y 0,8-0,2 para la zapata. Los valores de α y β al final del proceso de búsqueda valdrán 1 y 0, mientras que a lo largo de todo el proceso se cumplirá que α+β=1. El número de hormigas consideradas para cada etapa ha sido de 50, que coincidirá para la variante de colonia de hormigas utilizada con el número de soluciones factibles, y el número total de etapas de 100.
Respecto a los resultados obtenidos, destacar que conforme se aumenta la altura de las pilas y las luces de vano de los viaductos los esfuerzos a los que se verán sometidas las diferentes secciones serán mayores. Esto dará lugar a mayores geometrías y armados para resistirlos, tanto en la zapata como en el soporte, lo que aumentará los costes en estas estructuras. Sin embargo, en las curvas de cuantías se observa una tendencia decreciente hasta una cierta altura de pila para a continuación cambiar a creciente. Esto se debe a que en las pilas de menores alturas muchas geometrías y armados se han dispuesto por mínimos por lo que no aumentarán al ser mayor la altura de pila llevando a relaciones menores.