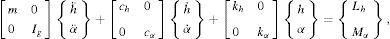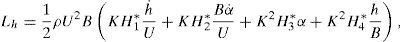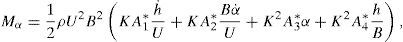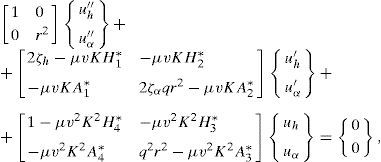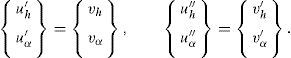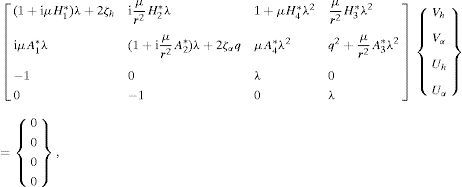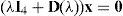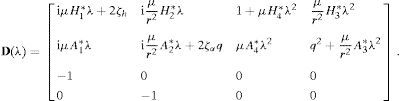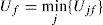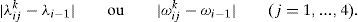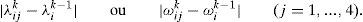Neste artigo estuda-se a ocorrência de instabilidade aerodinâmica por flutter em estruturas prismáticas esbeltas de secção retangular. Considera-se um modelo com 2 graus de liberdade e obtém-se a sua formulação adimensional identificando-se um número mínimo de parâmetros adimensionais que regem a ocorrência de instabilidade por flutter. Obtém-se uma muito boa concordância entre os resultados do modelo de 2 graus de liberdade e os resultados existentes na literatura. Este artigo tem 2 objetivos: (i) definir as condições para as quais estruturas esbeltas com secções retangulares podem instabilizar por flutter sob a ação do vento e (ii) fornecer uma coleção alargada de resultados sob a forma de tabelas ou gráficos prontos a usar, cobrindo um largo número de casos, que proporciona aos projetistas de estruturas uma ferramenta que estes podem utilizar, a nível de pré-dimensionamento, para prever as velocidades críticas do vento que provocam a instabilidade por flutter.
This paper is dedicated to the study of the occurrence of flutter instability in slender prismatic structures of rectangular cross section. A two degree of freedom model is considered and its non dimensional formulation is derived so that a minimum number of non dimensional parameters governing the occurrence of flutter instability are put in evidence. A very good agreement has been obtained by comparing the results of the two degree of freedom model with the results available in the literature. The goal of this document is twofold: (i) to summarize the conditions for which slender structures with rectangular cross sections may get unstable by flutter under the action of steady wind conditions and (ii) to supply a broad collection of data in the form of ready-to-use tables or graphics covering a wide range of cases, that provide a basis for designers to predict the critical wind velocities at the onset of flutter instability.
A necessidade e a vontade de vencer grandes vãos tem levado ao projeto e construção de pontes cada vez mais leves e esbeltas. Este facto também tem sido encorajado pelo uso de novos materiais e de novas técnicas computacionais de cálculo. Neste tipo de estruturas o vento tem uma ação dominante: a grande flexibilidade de algumas pontes, especialmente as suspensas, tem levado à crescente preocupação dos projetistas com os fenómenos de instabilidade causados pelo vento. Pontes atirantadas são também particularmente vulneráveis à ação do vento, especialmente durante a fase construtiva [1]. Apesar dos grandes avanços feitos nas últimas décadas na compreensão da interação vento-estrutura, este assunto continua na ordem do dia.
Foi em 1940, com o colapso da ponte de Tacoma, que surgiram as primeiras preocupações com o potencial efeito instabilizante do vento. Inicialmente alguns investigadores pensaram que as causas do acidente tinham sido as grandes amplitudes do movimento geradas por ressonância: defendiam que o vento tinha produzido uma ação externa (excitação externa por «destacamento de vórtices») com uma frequência semelhante a uma das frequências naturais da estrutura. Na realidade o que aconteceu não foi um fenómeno de ressonância, de facto os registos indicam que, na altura do colapso da estrutura, o vento atuava com uma velocidade constante (68 km/h) e a frequência de destacamento de vórtices era 1 Hz enquanto a frequência de oscilação era 0,2Hz (5 vezes menor) [2]. O fenómeno que originou o colapso da ponte de Tacoma foi uma autoexcitação aerodinâmica, usualmente designada como flutter, que pode ser interpretada como devida a um «amortecimento efectivo negativo» (no grau de liberdade de torção).
O cálculo das condições que definem a ocorrência de instabilidade por flutter em estruturas (tridimensionais) elásticas, prismáticas e esbeltas tem sido objeto de vários estudos, alguns deles baseados (parcialmente) em cálculos analíticos e outros completamente baseados no método dos elementos finitos.
Nos estudos semianalíticos admite-se que o movimento do tabuleiro pode ser decomposto numa soma finita de modos. As equações que regem o movimento podem ser escritas em função das coordenadas modais generalizadas. As forças aerodinâmicas generalizadas são definidas por integrais ao longo do vão das forças aerodinâmicas seccionais que se admite dependerem linearmente do estado (posição e velocidade) de cada secção transversal; os coeficientes destas funções lineares são as derivadas seccionais de flutter, determinadas experimentalmente, que caracterizam as propriedades de rigidez e de amortecimento da interação vento-estrutura. Investiga-se a ocorrência de instabilidade por flutter num único modo ou por coalescência de 2 modos de vibração (ambos os casos conduzem a um movimento oscilatório de amplitude crescente fisicamente associado à ocorrência de um amortecimento modal efetivo negativo). Os trabalhos [1,3–8] seguem esta orientação analítica.
Um método alternativo consiste na análise de um modelo simplificado (com 2 graus de liberdade) que se pode considerar um caso particular do método referido no parágrafo anterior [8]. Estes modelos simplificados permitem obter boas aproximações para as velocidades críticas do vento, como também se conclui no presente artigo, e têm sido utilizados em variados estudos [9–14].
Outros autores preferem resolver um problema de valores e vetores próprios baseado num modelo de elementos finitos 3D da estrutura. O tabuleiro da ponte é discretizado em elementos finitos e as forças aerodinâmicas nodais são calculadas da forma usual. As forças aerodinâmicas dependem linearmente dos deslocamentos e velocidades generalizados, pelo que contribuem com matrizes aerodinâmicas de rigidez e de amortecimento (dependentes da velocidade do vento e da frequência de oscilação através das derivadas seccionais de flutter) que se subtraem às suas homólogas estruturais. Admitindo pequenas amplitudes das oscilações dinâmicas no início da ocorrência da instabilidade por flutter, obtém-se um problema de valores e vetores próprios simétrico, mas que é não linear uma vez que os operadores matriciais dependem não linearmente dos valores próprios (frequências de oscilação). Agar [15] estudou o efeito do refinamento da malha de elementos finitos no valor da velocidade crítica do vento. Namibi et al. [16] mostraram que as menores velocidades críticas podem ser obtidas para valores não nulos do ângulo de incidência do vento e compararam a aproximação obtida pelo método dos elementos finitos com a obtida pelo método semianalítico [1]. Em [17] fez-se uma descrição pormenorizada e analisaram-se várias pontes atirantadas ou suspensas. Ge e Xiang [18] prestaram especial atenção às várias maneiras possíveis de obter as derivadas seccionais de flutter. Mendes e Semião [19,20] calcularam a velocidade crítica do vento para vários modelos de elementos finitos de pontes e compararam os resultados com os obtidos por meio de fórmulas simplificadas.
Vários autores têm continuado a dedicar-se à simulação numérica da aerodinâmica de pontes. Entre outros referem-se (i) os trabalhos de Fourestey e Piperno [21] e de Patro et al. [22] que resolvem numericamente as equações de Navier-Stokes para estudar o escoamento em torno de secções transversais de pontes, (ii) o trabalho de Lazzari [23] que analisa modelos de 2 ou 3 graus de liberdade de secções transversais de pontes no domínio do tempo e (iii) o de Diana et al. [24] que analisa numericamente modelos tridimensionais de uma ponte pelo método dos elementos finitos em que as forças aerodinâmicas atuantes no modelo se obtêm mediante testes apropriados realizados em túnel de vento.
O objetivo deste artigo é o de apresentar e discutir os resultados numéricos de um algoritmo [17] que permite obter as condições para a ocorrência de instabilidade aerodinâmica por flutter em estruturas esbeltas. Implementa-se o algoritmo num modelo com 2 graus de liberdade. Utilizando o respetivo programa, constroem-se ábacos que permitem avaliar a suscetibilidade à instabilidade por flutter de estruturas prismáticas com secções retangulares. Os resultados obtidos com o presente modelo de 2 graus de liberdade são comparados com os existentes na literatura obtidos em modelos com 2 ou 3 graus de liberdade. Uma das conclusões deste estudo é a consistência de resultados entre os modelos bi e tridimensionais existentes na literatura e o presente modelo simplificado de 2 graus de liberdade que permite validar os resultados numéricos obtidos para utilização no pré-dimensionamento de estruturas prismáticas esbeltas com secções retangulares.
Tanto quanto é do conhecimento dos autores, este estudo é o primeiro estudo numérico sistemático sobre a ocorrência de instabilidade por flutter em estruturas esbeltas com secções retangulares sob a ação do vento. Determina-se a dependência da velocidade crítica do vento com (i) a esbelteza, (ii) o amortecimento estrutural, (iii) a razão entre as frequências naturais relevantes, (iv) o momento polar de inércia da secção transversal e (v) a massa da estrutura por unidade de comprimento. Este artigo oferece um conjunto de ábacos e tabelas que permitem determinar a velocidade crítica do vento que conduz à instabilidade por flutter e que são úteis para o pré-dimensionamento deste tipo de estruturas.
Este artigo está organizado do seguinte modo: na Secção 2 apresenta-se a formulação adimensional de um modelo aeroelástico 2D identificando-se um conjunto de parâmetros adimensionais que controlam a ocorrência da instabilidade por flutter e comparam-se as velocidades críticas obtidas com o algoritmo implementado com as existentes na literatura obtidas para o aerofólio de Theodorsen [25] e para pontes reais ou projetadas. Na Secção 3 apresentam-se os resultados de um grande número de simulações numéricas realizadas com valores dos parâmetros adimensionais na gama de valores correspondentes a pontes reais ou projetadas. Na Secção 4 trata-se da adequação dos modelos 2D para análise de flutter em estruturas reais e sobre a influência dos vários parâmetros adimensionais relevantes no valor das velocidades críticas.
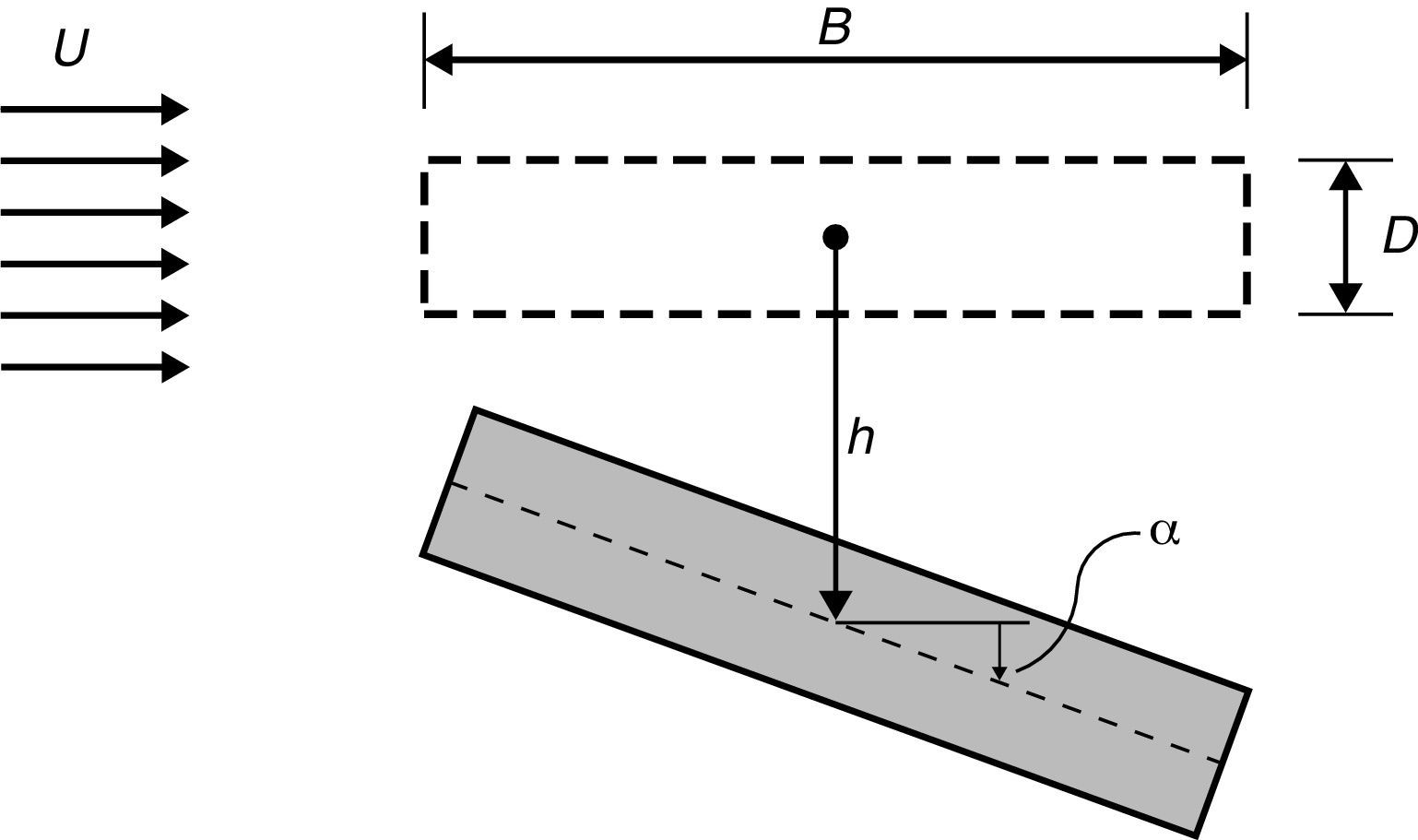
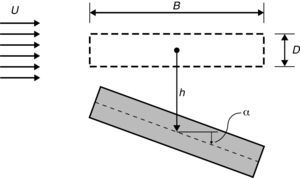
2Modelos aeroelásticos 2D de prismas 3D2.1FormulaçãoNuma análise bidimensional (fig. 1) consideram-se 2 graus de liberdade parametrizados pelo deslocamento vertical h e pela rotação α. Neste caso particular a equação que rege o movimento do modelo pode ser escrita na forma
Seguidamente transforma-se (1, 2, 3) num sistema de 2 equações diferenciais de segunda ordem adimensionais em termos dos deslocamentos generalizados adimensionais uh=hB e uα=α. Utilizam-se as definições clássicas:
- •
i=Igm: raio de giração em relação ao centro de gravidade (a unidade imaginária i que satisfaz i2=−1 não tem qualquer relação com i),
- •
ωh=khm, ωα=kαIg: frequências angulares naturais, para velocidade do vento nula (U=0), do movimento de translação vertical e de rotação, respetivamente.
Para além disso, utilizando as seguintes definições
- •
τ=ωht: tempo adimensionalizado,
- •
q=ωαωh: razão entre as 2 frequências naturais,
- •
r=iB: raio de giração adimensionalizado,
- •
μ=ρB22m: coeficiente de massa adimensionalizado,
- •
ζh=ch2mωh, ζα=cα2Igωα: fatores de amortecimento associados ao movimento vertical e ao movimento de rotação, respetivamente,
- •
v=UBωh: velocidade do vento adimensionalizada.
obtém-se o sistema de equações adimensionais que regem o movimento do modelo
em função dos 6 parâmetros adimensionais q, r, μ, ζh, ζα, v, da frequência reduzida K=ωBU=1vωωh e das 8 derivadas seccionais de flutterAi*, Hi* (i=1, ..., 4). As derivadas de primeira e de segunda ordem em ordem ao tempo adimensionalizado τ designam-se por ()′ e ()′′, respetivamente. O sistema dinâmico (4) pode ser transformado num sistema apenas com derivadas de primeira ordem se definirmosSe em (4) efetuarmos as substituições indicadas anteriormente obtemos então um sistema de 4 equações diferenciais ordinárias de primeira ordem nas variáveis (vh(τ),vα(τ),uh(τ),uα(τ)). Admitindo uma solução exponencial do tipo (Vh, Vα, Uh, Uα)exp(λτ) obtém-se o problema não linear de valores e vetores próprios
a partir do qual se obtêm as velocidades críticas do vento utilizando o algoritmo incremental/iterativo indicado por exemplo em [17]. O problema anterior pode ser escrito na forma
em que I4 designa a matriz identidade de 4 por 4 e a matrizNo problema de valores e vetores próprios (6) ou {(7), (8)}, λ=iωωh. O caráter não linear de (6) (ou {(7), (8)}) resulta do facto de as derivadas seccionais de flutter serem funções não lineares da frequência reduzida K=−iλv que, por sua vez, é função do valor próprio λ. As soluções de (1) são instáveis quando [28]:
- 1.
A parte real de um dos valores próprios com parte imaginária nula se torna positiva (pelo menos um Re(λj)>0). Neste caso o movimento cresce exponencialmente sem oscilação (Im(λj)=0), isto é, ocorre instabilidade por divergência.
- 2.
A parte real de um dos valores próprios com parte imaginária não nula se torna positiva (pelo menos um Im(λj)≠0 com Re(λj)>0). Neste caso o movimento cresce exponencialmente com oscilação (Im(λj)≠0), isto é, ocorre instabilidade por flutter.
Na prática o flutter em tabuleiros de pontes resulta da autoexcitação de um modo de oscilação, geralmente um modo de torção de baixa frequência. Envolve interação entre as forças elásticas, de amortecimento, de inércia e aerodinâmicas, que atuam fornecendo energia ao tabuleiro aumentando a amplitude da sua oscilação até níveis catastróficos.
2.2Algoritmo incremental-iterativoO problema de valores e vetores próprios não linear {(7), (8)} terá de ser resolvido de forma incremental e iterativa como se indica seguidamente:
A. Resolver o problema de valores e vetores próprios correspondente às vibrações livres amortecidas na ausência de vento (U=0), o que corresponde a anular todas as derivadas seccionais de flutterAl* e Hl* (l=1, ..., 4) e a resolver o problema de vetores próprios clássico (λI4+D(0))x=0. Do espetro do problema anterior importa reter os valores de λ que correspondam a frequências naturais com parte real positiva, as únicas com significado físico. Recordar que ω=−iωhλ (nota: i2=−1). Inicialização do contador de soluções: j=0.
B. Atualização do contador de soluções: j=j+1.
Para λj com Im(λj)>0 (correspondentes a frequências naturais com parte real positiva) inicia-se um processo incremental em que se aumenta a velocidade do vento U de 1 km/h em 1 km/h (de 0, 2(7) m/s em 0, 2(7) m/s) até um valor máximo UM de 486 km/h (135 m/s). Os incrementos de U designam-se por ΔU.
B.1 Atualização do índice de incremento: i←i+1. Incremento da velocidade do vento Ui=Ui−1+ΔU.
Calcular o par (λ, ω)i para a velocidade do vento Ui que corresponde a (λ, ω)0=(λj, ωj) para a velocidade do vento nula (este passo será pormenorizado mais adiante).
B.2 Verificar se Re(λi)>0⇔Im(ωi)<0.
Se Re(λi)>0⇔Im(ωi)<0 pára-se o processo iterativo pois já se atravessou a fronteira de flutter da solução j:
Se Re(λi)<0⇔Im(ωi)>0 retorna-se ao passo B.1.
C. Se j<4 regressar ao passo B com o objetivo de determinar a fronteira de flutter das soluções m≥j.
D. A velocidade crítica de flutter será então:
Pormenorização do passo B.1:
Inicialização do índice de iteração: k=0.
B.1. Atualização do índice de iteração: k=k+1. Para a velocidade Ui, calcular Al* e Hl* (l=1, ..., 4) e formar a matriz dinâmica D (8) incluindo todos os termos aerodinâmicos.
B.1.1. Usando o programa Matlab, calcular os 4 valores próprios λijk (j=1, ..., 4). Calcular também as frequências naturais complexas ωijk=−iλijk (o índice i pretende apenas relembrar que essas quantidades correspondem à velocidade do vento Ui).
B.1.2. Comparar cada um dos λijk (j=1, ..., 4) ou ωijk (j=1, ..., 4) com o último λ ou ω obtido.
Se k=1 a comparação é:
Se k>1 a comparação é:
Selecionar o valor de λijk (ou ωijk) que corresponda à menor diferença das comparações anteriores e designá-lo por λik (ou ωik).
B.1.3. Comparar λik com λik−1 ou ωik com ωik−1.
Se |λik−λik−1| Se |λik−λik−1|>TOL=10−6 então regressar a B.1 para actualizar os Al*, Hl* e a matriz D com λik.
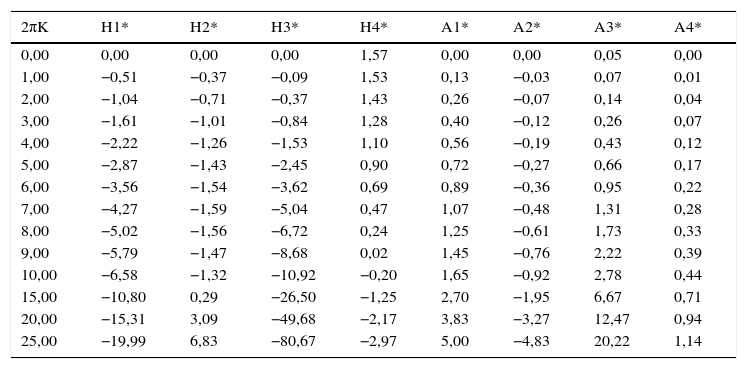
A análise começou pelo caso clássico da secção de um aerofólio para a qual os coeficientes (derivadas seccionais de flutter) que caracterizam as forças aerodinâmicas (membro da direita da equação (1)) têm expressões analíticas [25,27]. Os valores numéricos dessas derivadas seccionais de flutter usados no cálculo do valor Ucrit=44,40 m/s da primeira linha da tabela 2 encontram-se listados na tabela Apêndice A.1.
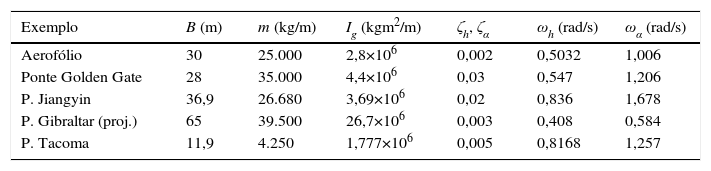
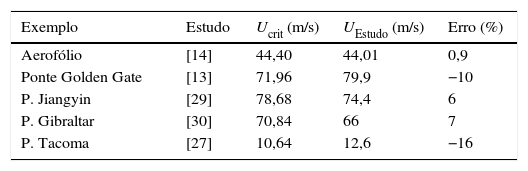
Testaram-se igualmente várias secções de tabuleiros de pontes cujas derivadas seccionais de flutter existem na literatura; na tabela 1 indicam-se as propriedades mecânicas e geométricas utilizadas e nas tabelas Apêndice A.2 a Apêndice A.5 do Apêndice A encontram-se os valores numéricos usados nos cálculos dos valores de Ucrit da tabela 2. Nessa tabela comparam-se as velocidades críticas do vento obtidas com o presente algoritmo (Ucrit) com as existentes na literatura UEstudo.
Propriedades dos casos considerados na tabela 2
| Exemplo | B (m) | m (kg/m) | Ig (kgm2/m) | ζh, ζα | ωh (rad/s) | ωα (rad/s) |
|---|---|---|---|---|---|---|
| Aerofólio | 30 | 25.000 | 2,8×106 | 0,002 | 0,5032 | 1,006 |
| Ponte Golden Gate | 28 | 35.000 | 4,4×106 | 0,03 | 0,547 | 1,206 |
| P. Jiangyin | 36,9 | 26.680 | 3,69×106 | 0,02 | 0,836 | 1,678 |
| P. Gibraltar (proj.) | 65 | 39.500 | 26,7×106 | 0,003 | 0,408 | 0,584 |
| P. Tacoma | 11,9 | 4.250 | 1,777×106 | 0,005 | 0,8168 | 1,257 |
Analisando a tabela 2 conclui-se que o presente algoritmo conduziu a velocidades críticas do vento bastante próximas dos valores existentes na literatura; isto valida o algoritmo que foi usado para obter os ábacos referidos na próxima secção com o propósito de proporcionar aos projetistas uma ferramenta que estes possam utilizar, a nível de pré-dimensionamento, no estudo da estabilidade aerodinâmica de pontes. O facto de por vezes o erro relativo atingir os 10% pode dever-se a uma menos boa aproximação das derivadas seccionais de flutter, especialmente nos casos em que estas foram obtidas experimentalmente. O método utilizado neste estudo para aproximar as derivadas seccionais de flutter no algoritmo incremental/iterativo usa a função de interpolação interna do software Matlab [31]. No caso do aerofólio em que as derivadas seccionais de flutter têm expressões analíticas a velocidade crítica de flutter obtida neste estudo é muito semelhante ao valor da literatura [32,14].
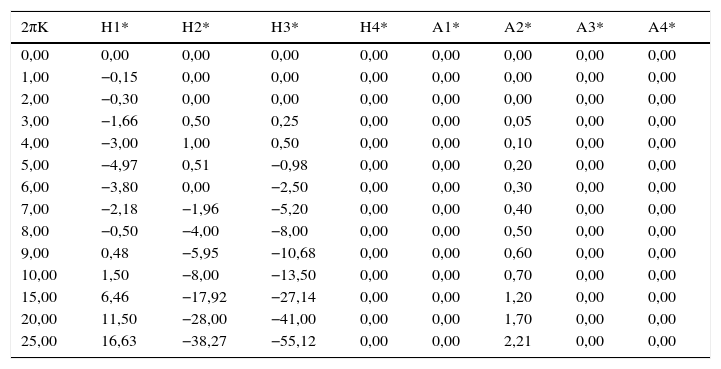
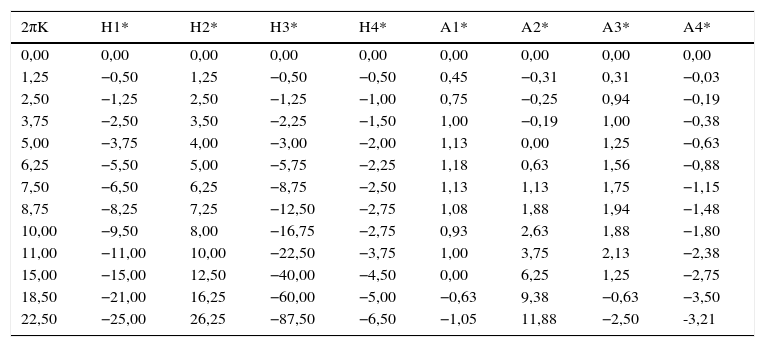
3Instabilidade por flutter de prismas com secções transversais retangularesNesta secção mostra-se a variação das velocidades críticas do vento no instante em que se inicia a instabilidade por flutter com os parâmetros adimensionais que regem o problema de valores e vetores próprios (6). Este estudo baseia-se nas referências [33,34] onde se registam as derivadas seccionais de flutter, obtidas experimentalmente, para prismas de secção retangular de esbelteza BD variável (ver a fig. 1). Nas tabelas Apêndice B.1 a Apêndice B.3 registam-se os valores numéricos das 8 derivadas seccionais de flutter para 3 valores diferentes da esbelteza BD=5,10,20, em função da velocidade reduzida do vento 2πK, obtidos a partir de [33]. Neste estudo admitiu-se que os fatores de amortecimento estrutural dos movimentos de translacção vertical e de rotação são iguais: ζh=ζα.
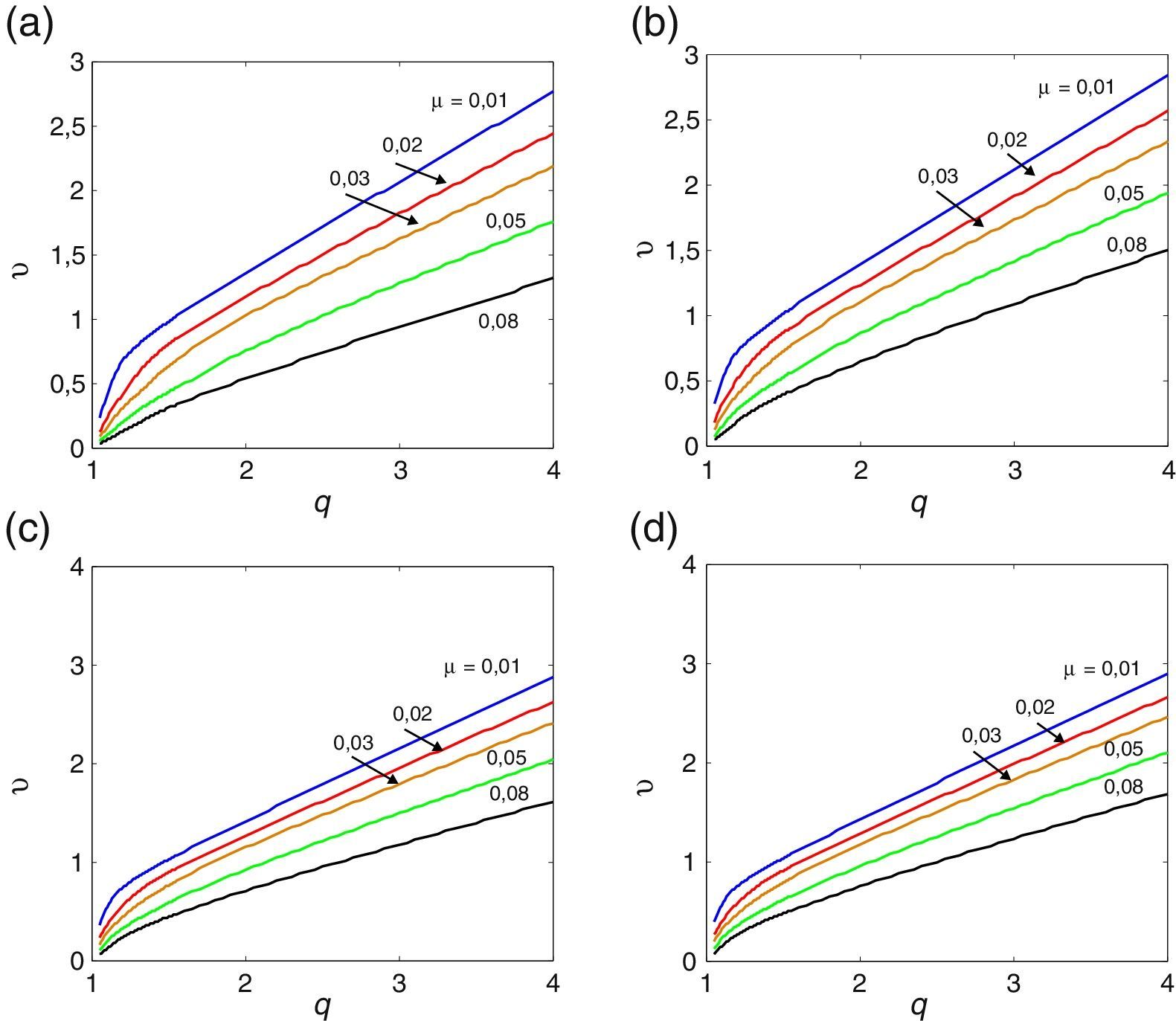
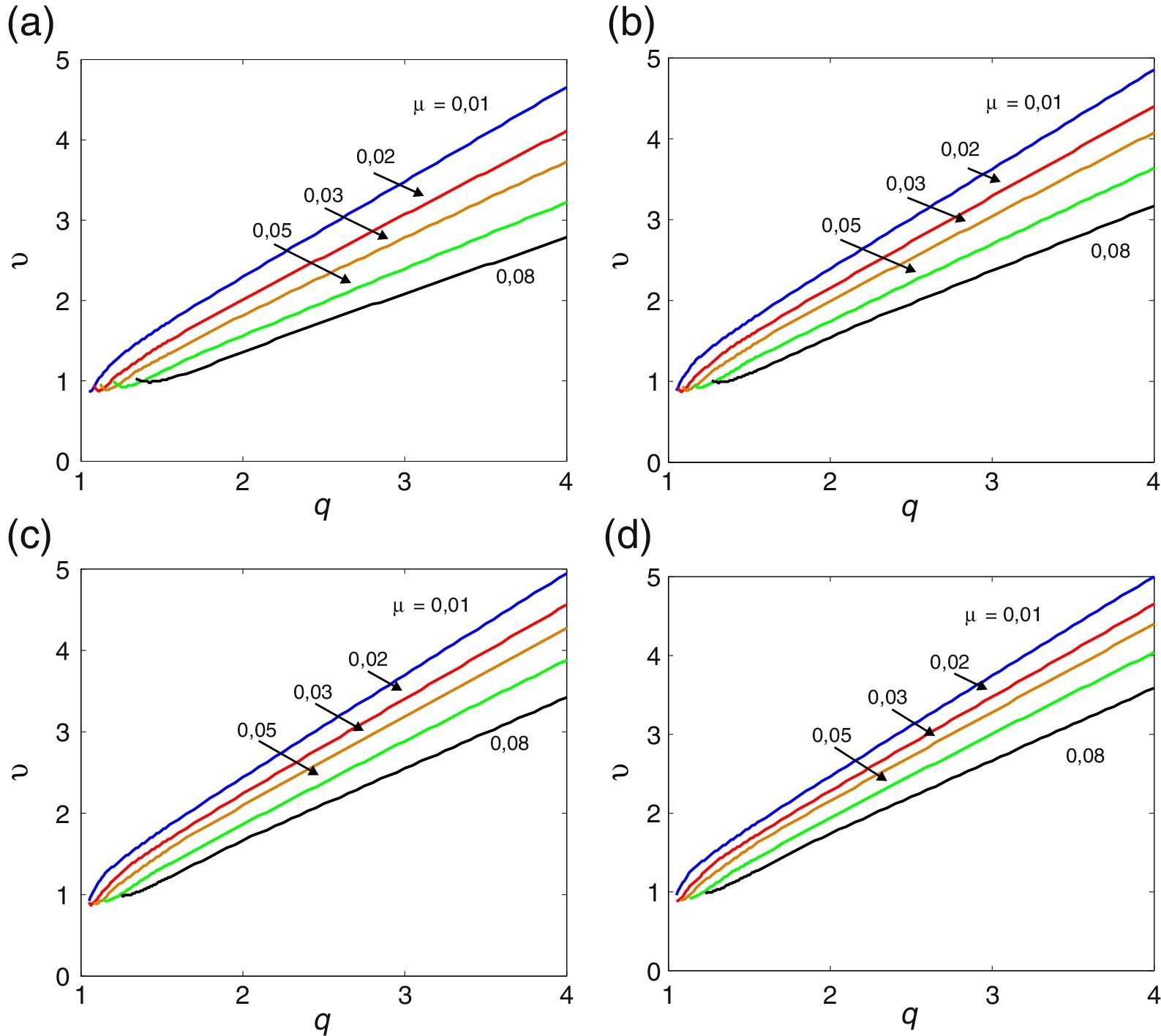
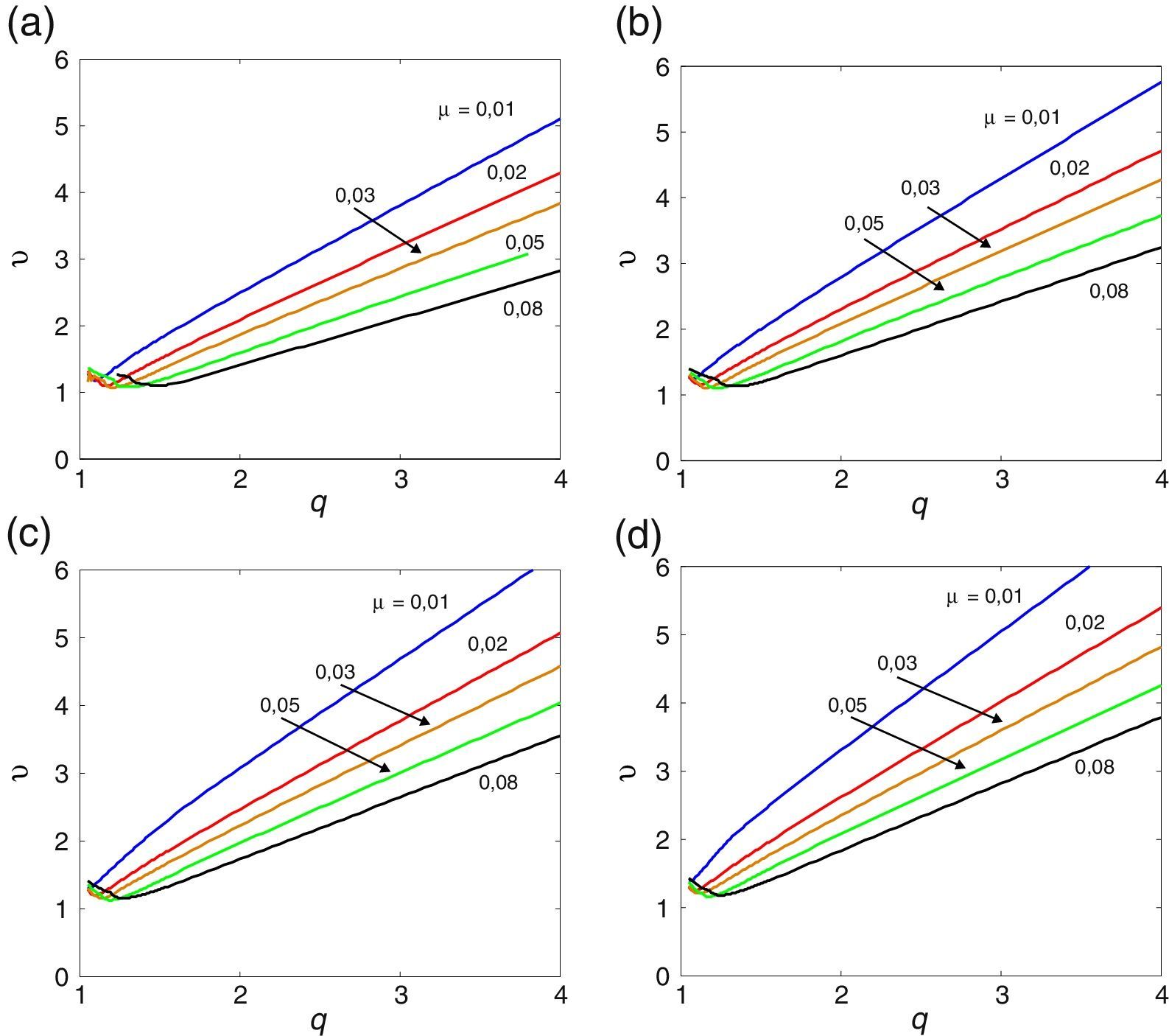
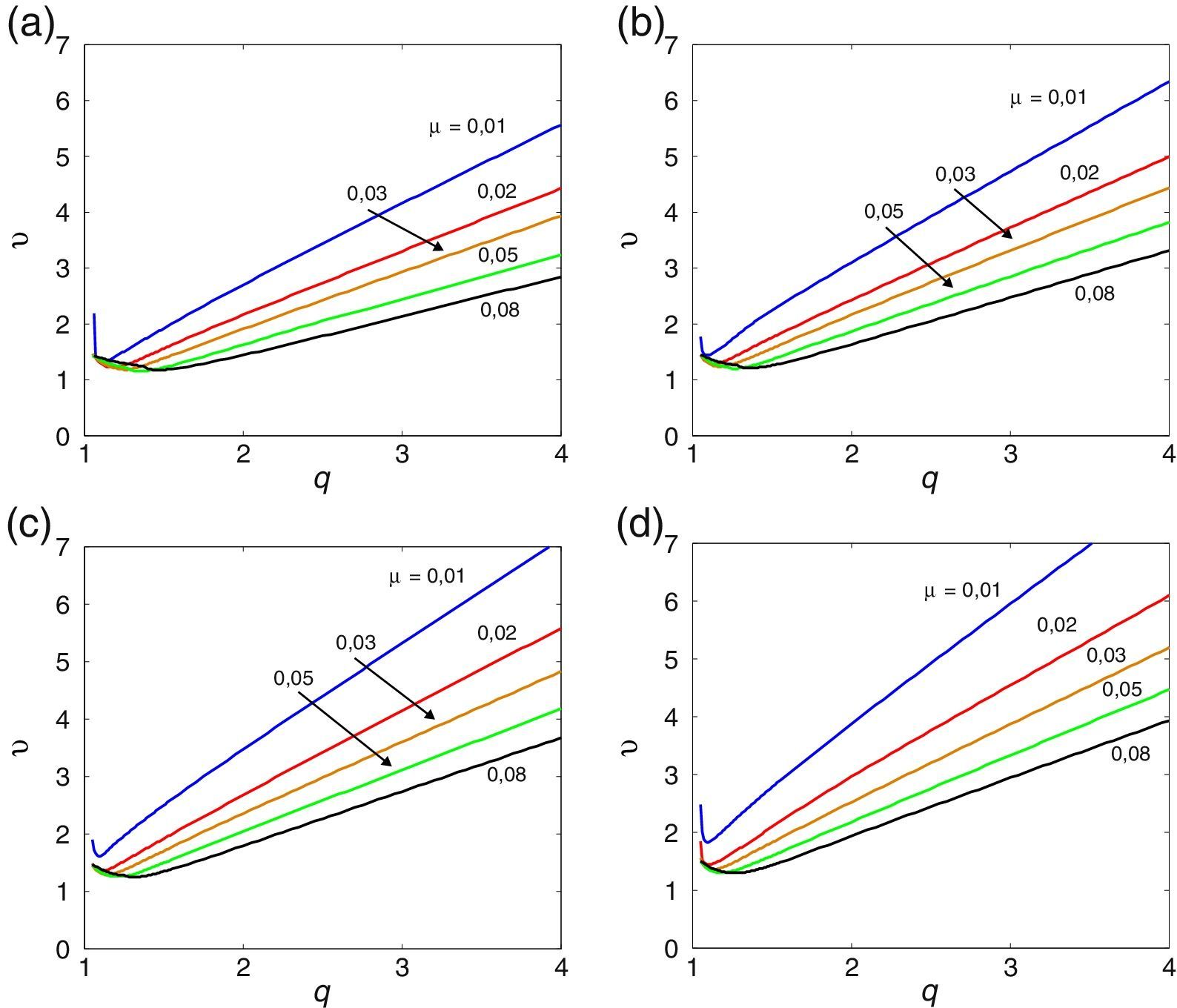
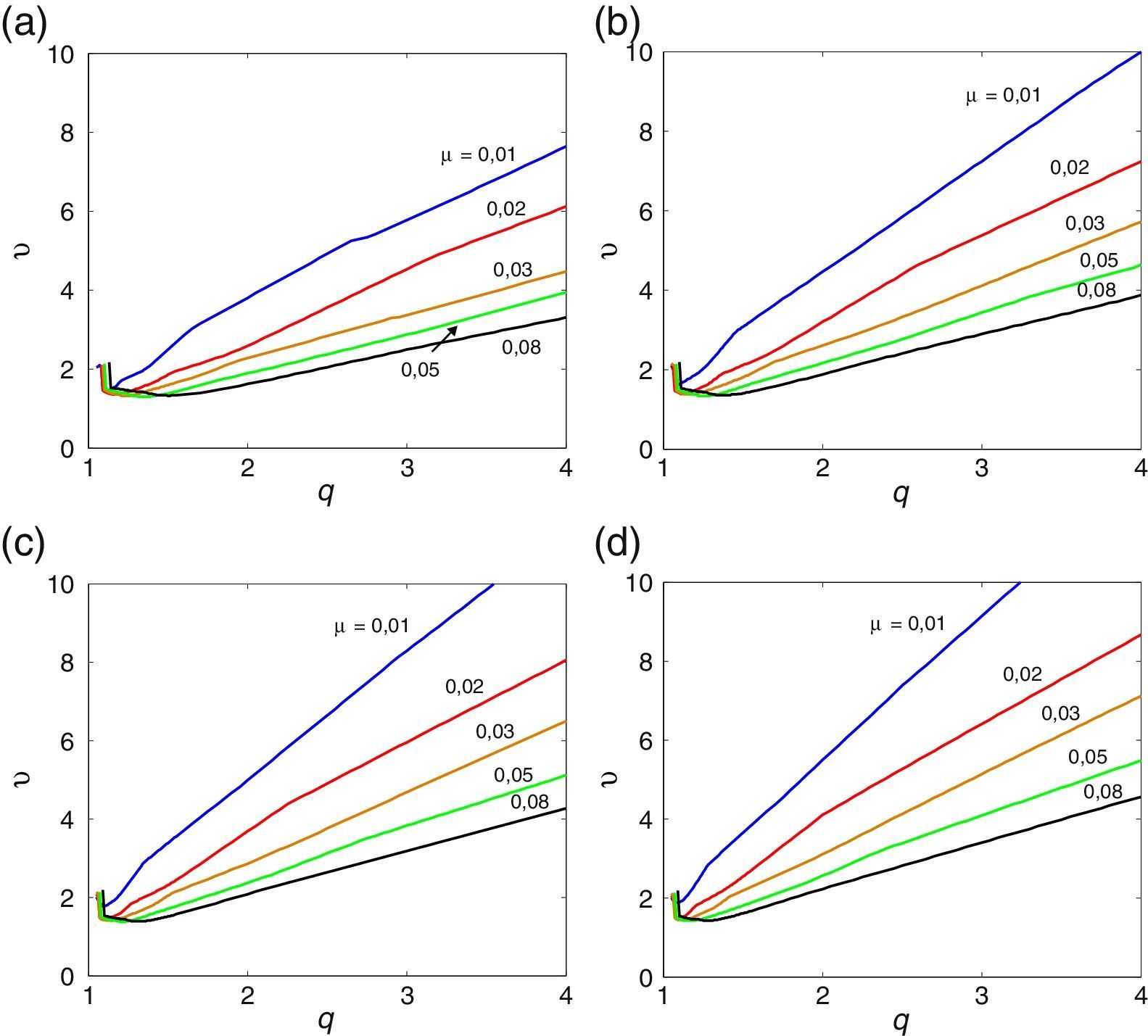
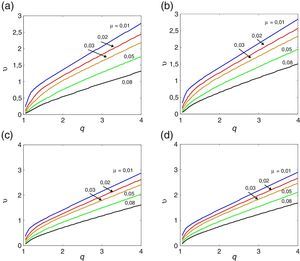
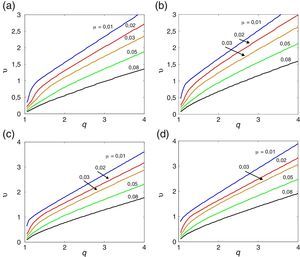
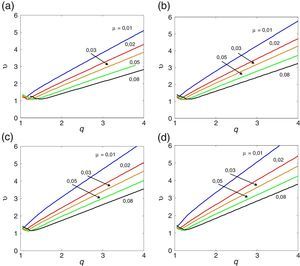
3.1Esbelteza BD=5A tabela Apêndice B.1 regista os valores numéricos das derivadas seccionais de flutter, utilizados pelo programa desenvolvido no presente estudo no seu processo de interpolação, para a menos esbelta das secções retangulares (BD=5). Realizando a análise numérica incremental/iterativa indicada na Secção 2.1, obtiveram-se os gráficos das velocidades críticas de flutter do vento representados nas figuras 2, 3 e 4 para diferentes valores do coeficiente de amortecimento estrutural. Para esta esbelteza observa-se claramente que o aumento do amortecimento estrutural atrasa a ocorrência da instabilidade por flutter uma vez que a partir das curvas homólogas das figuras 2, 3 e 4 se obtêm maiores velocidades críticas à medida que se aumenta o amortecimento desde 0 na figura 2 até 2% na figura 4 (ver também [35]); no entanto, este efeito é mais pronunciado quando o coeficiente de massa adimensionalizado μ é menor.
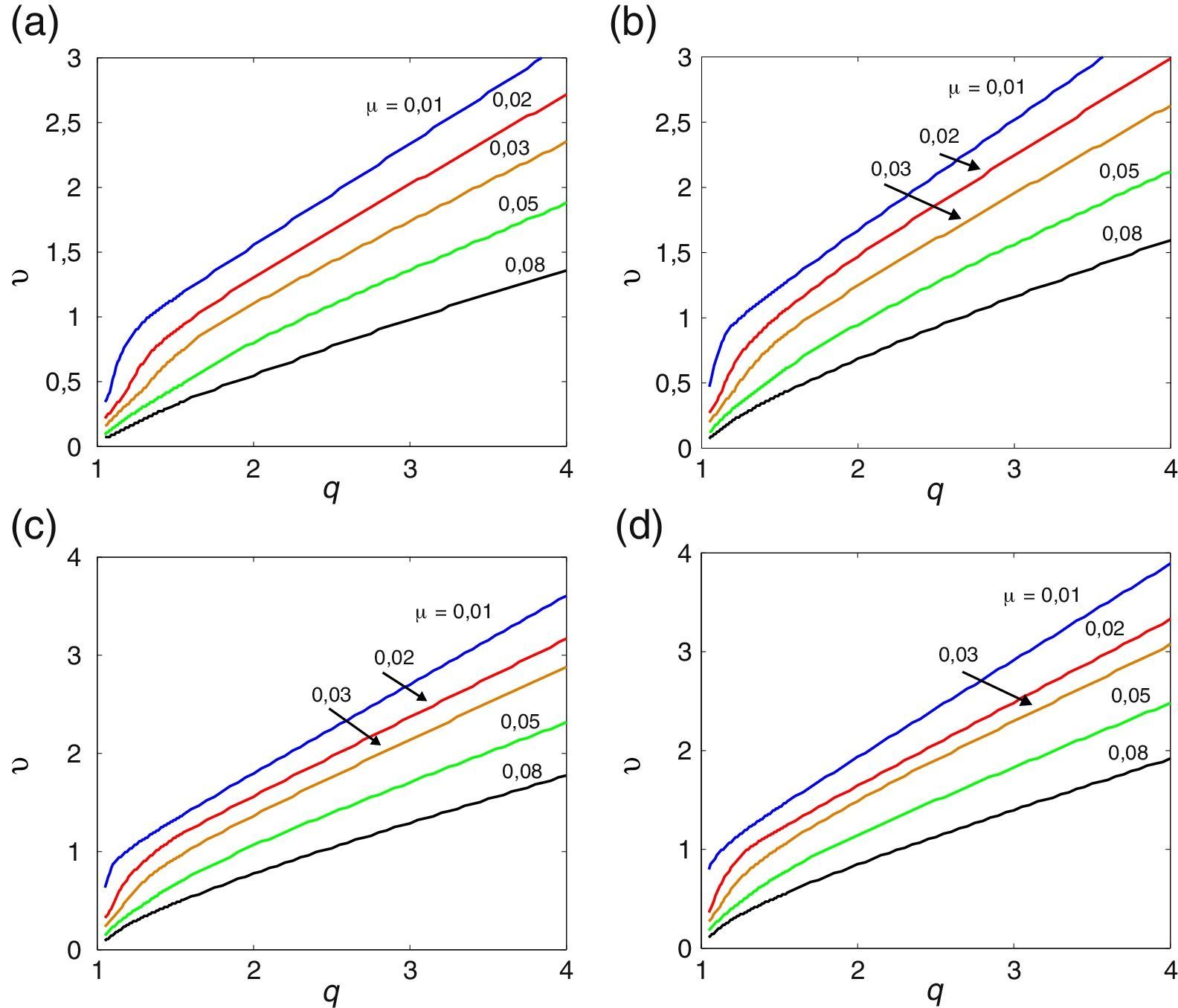
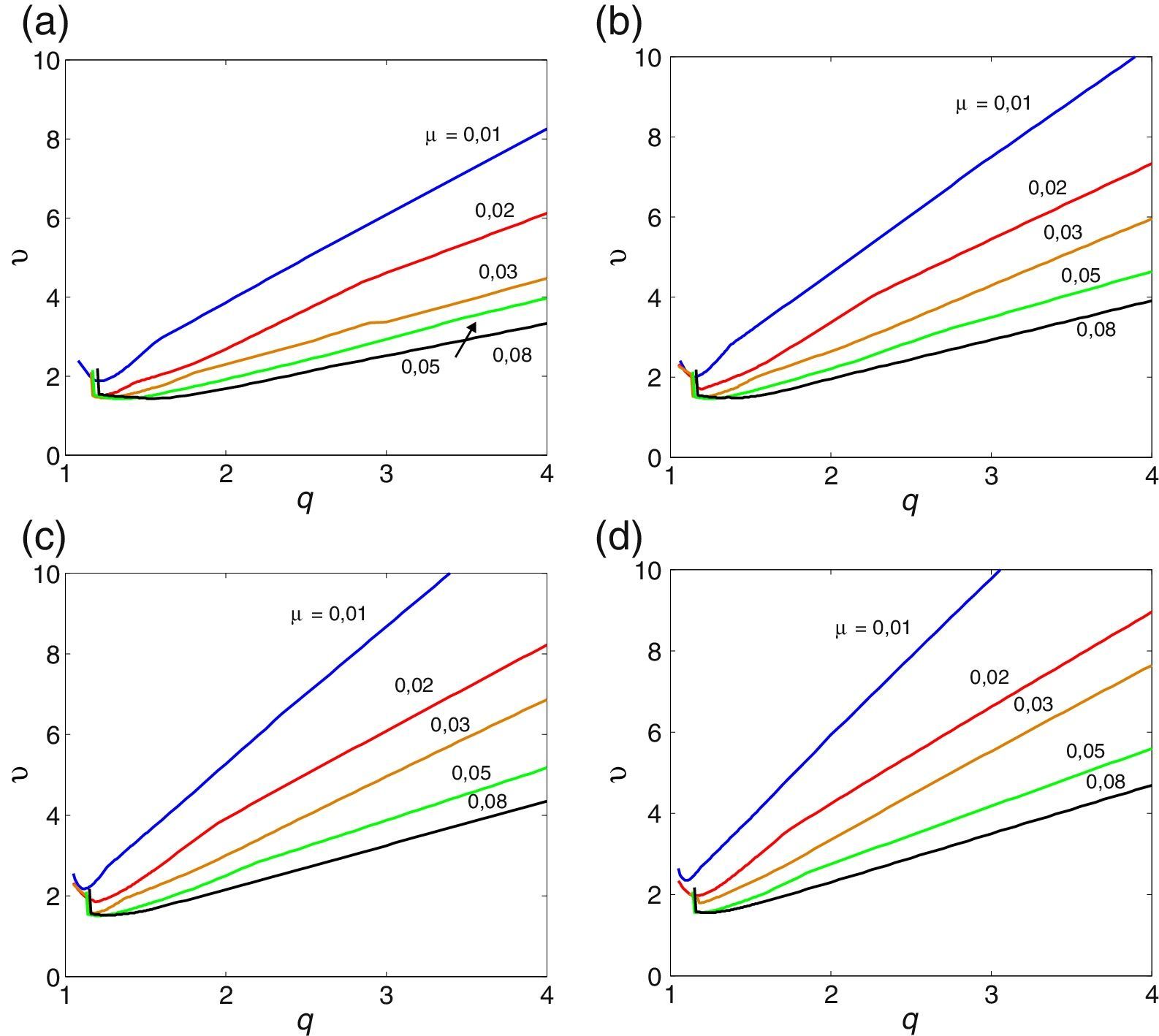
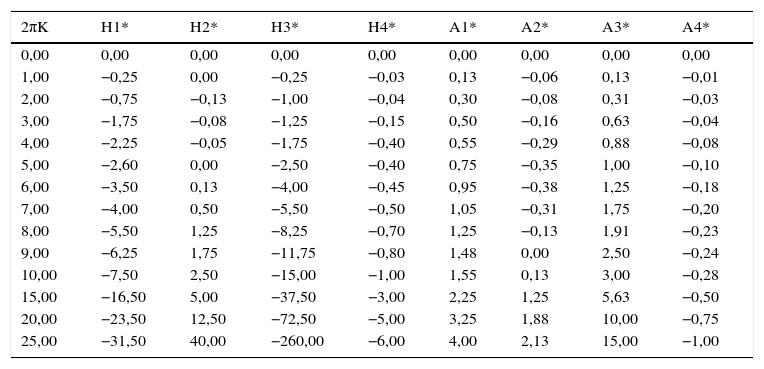
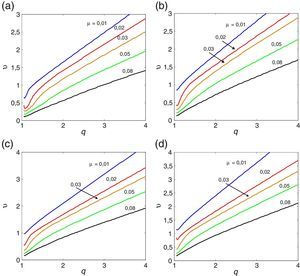
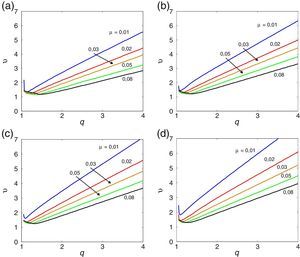
A tabela Apêndice B.2 regista os valores numéricos das derivadas seccionais de flutter enquanto nas figuras 5, 6 e 7 se representam os gráficos das velocidades críticas do vento em função dos vários parâmetros adimensionais, para uma esbelteza intermédia. Observa-se igualmente o efeito estabilizador do amortecimento estrutural.
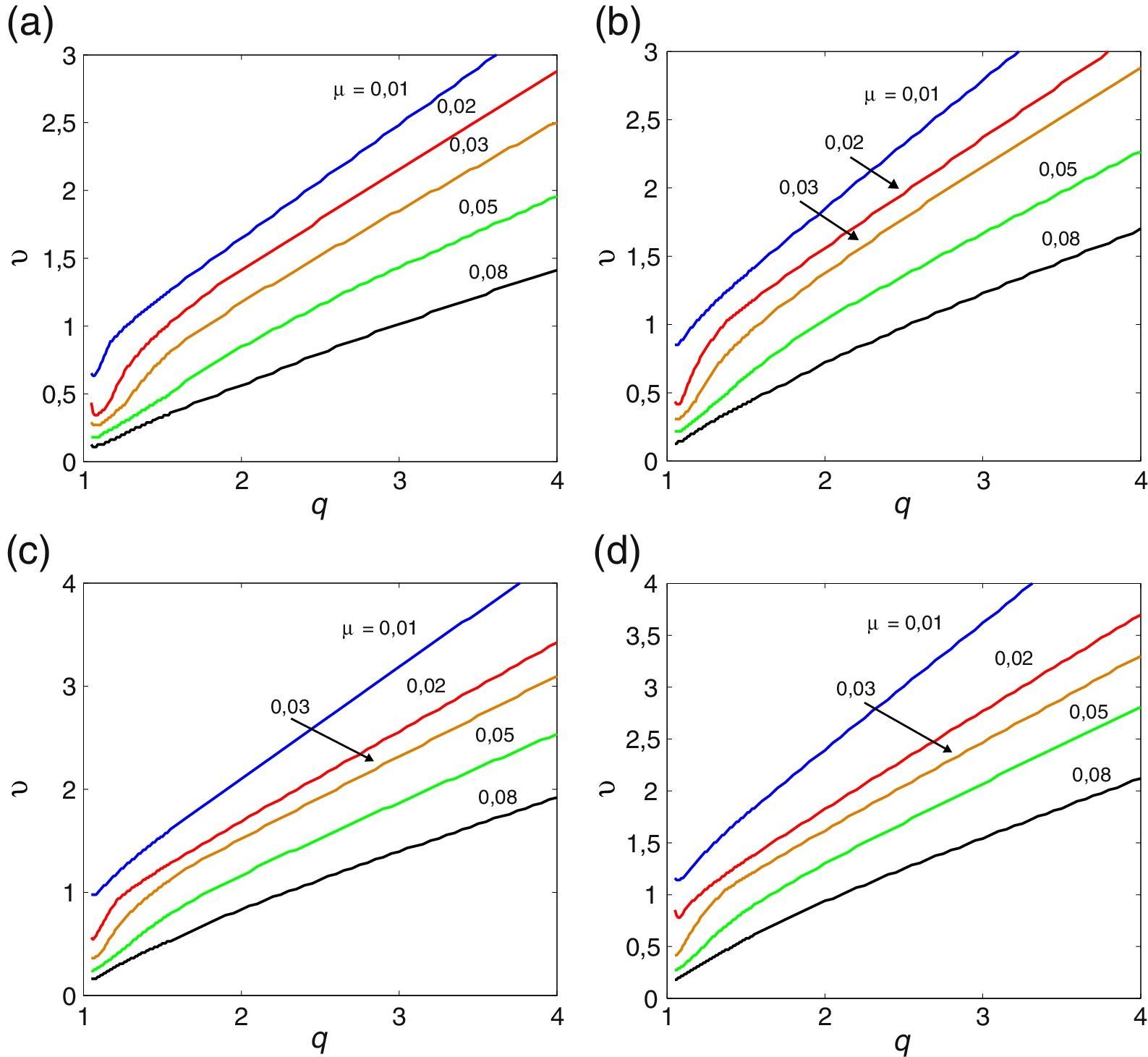
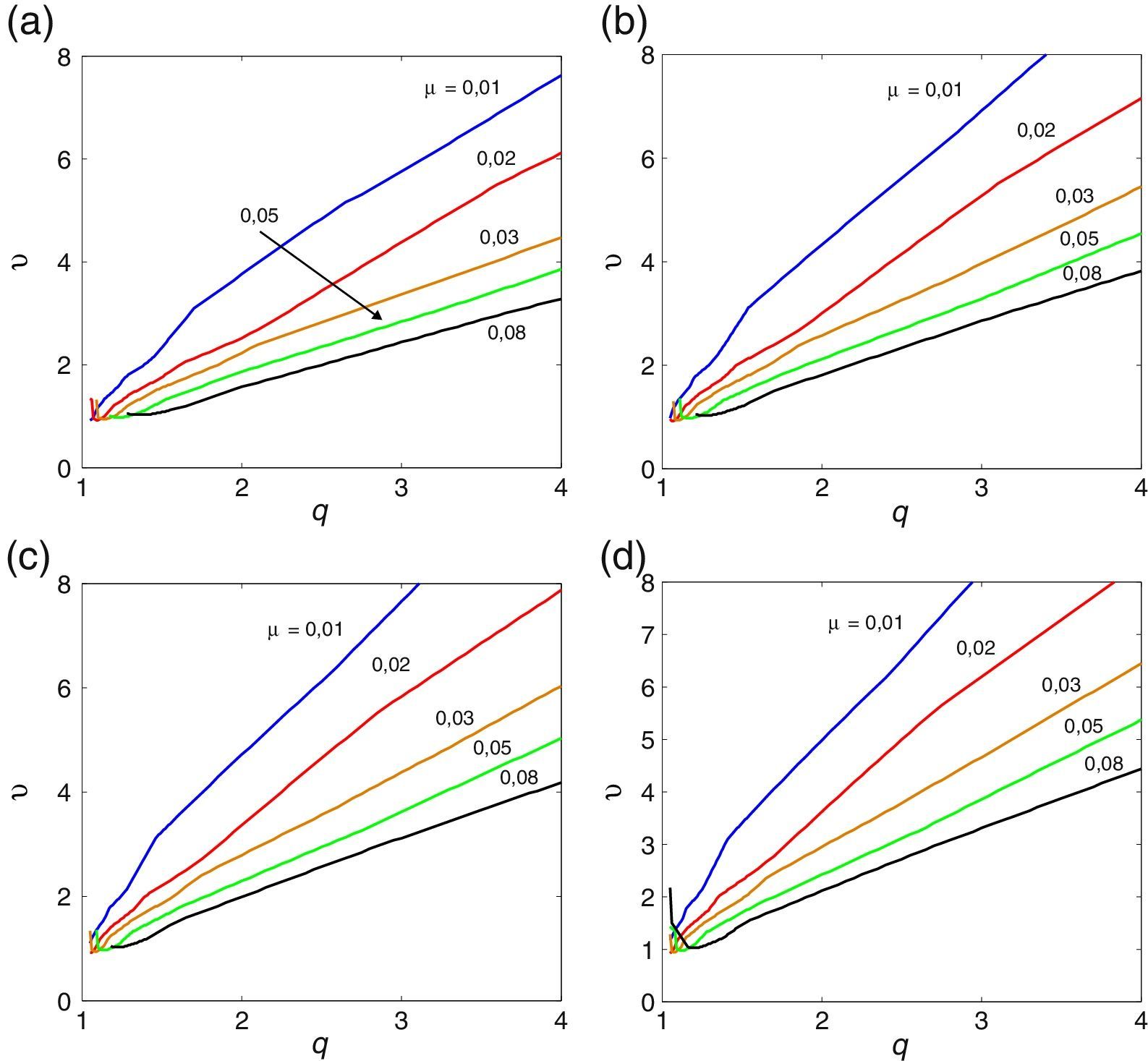
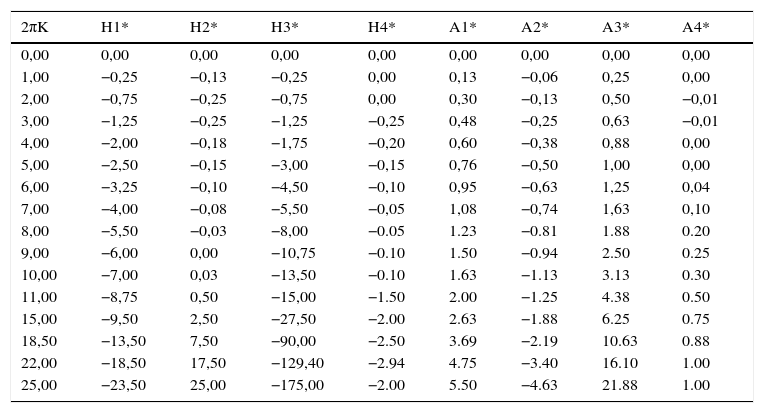
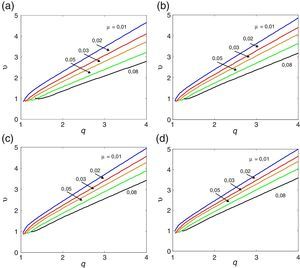
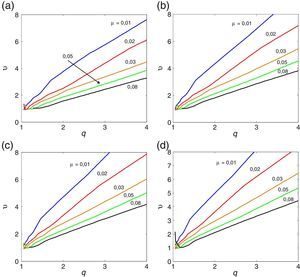
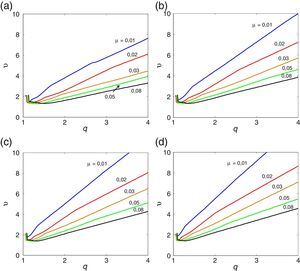
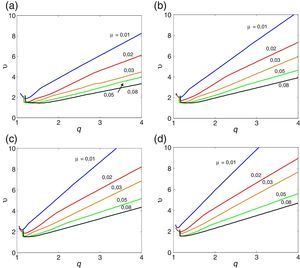
Nesta secção apresentam-se os resultados obtidos para a secção retangular mais esbelta de todas as consideradas em [33]. A razão BD=20 é a que aproxima melhor a esbelteza de uma ponte real. A tabela Apêndice B.3 regista o valor das correspondentes derivadas seccionais de flutter. As figuras 8, 9 e 10 mostram os ábacos que permitem caraterizar a suscetibilidade à instabilidade por flutter de prismas retangulares esbeltos; obtiveram-se figuras homólogas (não mostradas neste artigo) para aerofólios, utilizando o mesmo algoritmo, mas com derivadas seccionais de flutter iguais às expressões analíticas de Theodorsen. Claramente, quando se vai de BD=5 para BD=20 as curvas aproximam-se das correspondentes ao aerofólio sendo as curvas para BD=20 já muito próximas das curvas correspondentes ao aerofólio. No entanto, as velocidades críticas de um aerofólio são maiores do que as da secção retangular com esbelteza B/D=20, o que sugere que a partir da formulação de Theodorsen se podem obter resultados não conservativos para pontes reais. O efeito benéfico do amortecimento estrutural também se verifica para esta esbelteza.
Neste artigo estuda-se a ocorrência da instabilidade por flutter em estruturas prismáticas esbeltas sujeitas à ação do vento. O artigo fornece um alargado conjunto de resultados computacionais que são úteis para o pré-dimensionamento deste tipo de estruturas. Apresentam-se e discutem-se os resultados do algoritmo implementado. Realizam-se análises bidimensionais e comparam-se os respetivos resultados com os resultados existentes na literatura obtidos em simulações bi e tridimensionais. Apesar de na tabela 2 se registarem erros relativos de cerca de 10%, deve-se realçar a consistência e a validade dos resultados obtidos no presente estudo:
- •
Como seria de esperar, a velocidade crítica de flutter diminui à medida que a estrutura se torna mais leve.
- •
O amortecimento estrutural tem um efeito estabilizador aumentando a velocidade crítica do vento (mais pronunciado para estruturas mais pesadas).
- •
A velocidade crítica de flutter das secções retangulares diminui à medida que a sua esbelteza decresce.
- •
No caso bidimensional, a velocidade crítica de flutter diminui à medida que a razão entre as frequências naturais de rotação e de translação se aproximam de um. Esta observação justifica o princípio utilizado em dimensionamento que consiste em afastar estas frequências.
Os autores declaram não haver conflito de interesses.
Os autores agradecem ao doutor Arno Kirch da Universidade de Braunschweig, Alemanha, os esclarecimentos que permitiram melhorar o manuscrito.
See tabela Apêndice Apêndice A.1–Apêndice A.5.
Derivadas seccionais de flutter para o aeroflio [14]
| 2πK | H1* | H2* | H3* | H4* | A1* | A2* | A3* | A4* |
|---|---|---|---|---|---|---|---|---|
| 0,00 | 0,00 | 0,00 | 0,00 | 1,57 | 0,00 | 0,00 | 0,05 | 0,00 |
| 1,00 | −0,51 | −0,37 | −0,09 | 1,53 | 0,13 | −0,03 | 0,07 | 0,01 |
| 2,00 | −1,04 | −0,71 | −0,37 | 1,43 | 0,26 | −0,07 | 0,14 | 0,04 |
| 3,00 | −1,61 | −1,01 | −0,84 | 1,28 | 0,40 | −0,12 | 0,26 | 0,07 |
| 4,00 | −2,22 | −1,26 | −1,53 | 1,10 | 0,56 | −0,19 | 0,43 | 0,12 |
| 5,00 | −2,87 | −1,43 | −2,45 | 0,90 | 0,72 | −0,27 | 0,66 | 0,17 |
| 6,00 | −3,56 | −1,54 | −3,62 | 0,69 | 0,89 | −0,36 | 0,95 | 0,22 |
| 7,00 | −4,27 | −1,59 | −5,04 | 0,47 | 1,07 | −0,48 | 1,31 | 0,28 |
| 8,00 | −5,02 | −1,56 | −6,72 | 0,24 | 1,25 | −0,61 | 1,73 | 0,33 |
| 9,00 | −5,79 | −1,47 | −8,68 | 0,02 | 1,45 | −0,76 | 2,22 | 0,39 |
| 10,00 | −6,58 | −1,32 | −10,92 | −0,20 | 1,65 | −0,92 | 2,78 | 0,44 |
| 15,00 | −10,80 | 0,29 | −26,50 | −1,25 | 2,70 | −1,95 | 6,67 | 0,71 |
| 20,00 | −15,31 | 3,09 | −49,68 | −2,17 | 3,83 | −3,27 | 12,47 | 0,94 |
| 25,00 | −19,99 | 6,83 | −80,67 | −2,97 | 5,00 | −4,83 | 20,22 | 1,14 |
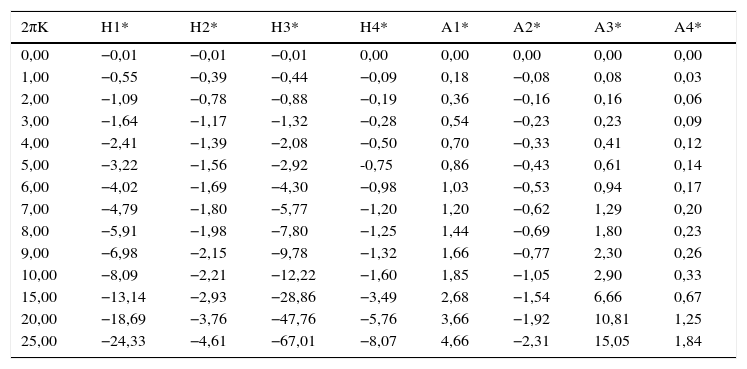
Derivadas seccionais de flutter para a ponte Golden Gate [13]
| 2πK | H1* | H2* | H3* | H4* | A1* | A2* | A3* | A4* |
|---|---|---|---|---|---|---|---|---|
| 0,00 | −0,01 | −0,01 | −0,01 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
| 1,00 | −0,55 | −0,39 | −0,44 | −0,09 | 0,18 | −0,08 | 0,08 | 0,03 |
| 2,00 | −1,09 | −0,78 | −0,88 | −0,19 | 0,36 | −0,16 | 0,16 | 0,06 |
| 3,00 | −1,64 | −1,17 | −1,32 | −0,28 | 0,54 | −0,23 | 0,23 | 0,09 |
| 4,00 | −2,41 | −1,39 | −2,08 | −0,50 | 0,70 | −0,33 | 0,41 | 0,12 |
| 5,00 | −3,22 | −1,56 | −2,92 | -0,75 | 0,86 | −0,43 | 0,61 | 0,14 |
| 6,00 | −4,02 | −1,69 | −4,30 | −0,98 | 1,03 | −0,53 | 0,94 | 0,17 |
| 7,00 | −4,79 | −1,80 | −5,77 | −1,20 | 1,20 | −0,62 | 1,29 | 0,20 |
| 8,00 | −5,91 | −1,98 | −7,80 | −1,25 | 1,44 | −0,69 | 1,80 | 0,23 |
| 9,00 | −6,98 | −2,15 | −9,78 | −1,32 | 1,66 | −0,77 | 2,30 | 0,26 |
| 10,00 | −8,09 | −2,21 | −12,22 | −1,60 | 1,85 | −1,05 | 2,90 | 0,33 |
| 15,00 | −13,14 | −2,93 | −28,86 | −3,49 | 2,68 | −1,54 | 6,66 | 0,67 |
| 20,00 | −18,69 | −3,76 | −47,76 | −5,76 | 3,66 | −1,92 | 10,81 | 1,25 |
| 25,00 | −24,33 | −4,61 | −67,01 | −8,07 | 4,66 | −2,31 | 15,05 | 1,84 |
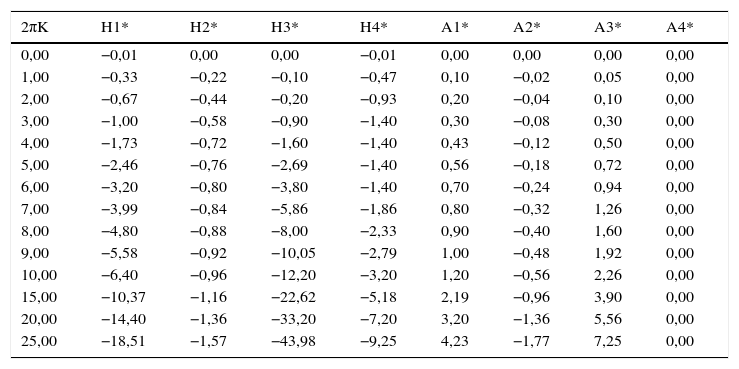
Derivadas seccionais de flutter para a ponte de Jiangyin [29]
| 2πK | H1* | H2* | H3* | H4* | A1* | A2* | A3* | A4* |
|---|---|---|---|---|---|---|---|---|
| 0,00 | −0,01 | 0,00 | 0,00 | −0,01 | 0,00 | 0,00 | 0,00 | 0,00 |
| 1,00 | −0,33 | −0,22 | −0,10 | −0,47 | 0,10 | −0,02 | 0,05 | 0,00 |
| 2,00 | −0,67 | −0,44 | −0,20 | −0,93 | 0,20 | −0,04 | 0,10 | 0,00 |
| 3,00 | −1,00 | −0,58 | −0,90 | −1,40 | 0,30 | −0,08 | 0,30 | 0,00 |
| 4,00 | −1,73 | −0,72 | −1,60 | −1,40 | 0,43 | −0,12 | 0,50 | 0,00 |
| 5,00 | −2,46 | −0,76 | −2,69 | −1,40 | 0,56 | −0,18 | 0,72 | 0,00 |
| 6,00 | −3,20 | −0,80 | −3,80 | −1,40 | 0,70 | −0,24 | 0,94 | 0,00 |
| 7,00 | −3,99 | −0,84 | −5,86 | −1,86 | 0,80 | −0,32 | 1,26 | 0,00 |
| 8,00 | −4,80 | −0,88 | −8,00 | −2,33 | 0,90 | −0,40 | 1,60 | 0,00 |
| 9,00 | −5,58 | −0,92 | −10,05 | −2,79 | 1,00 | −0,48 | 1,92 | 0,00 |
| 10,00 | −6,40 | −0,96 | −12,20 | −3,20 | 1,20 | −0,56 | 2,26 | 0,00 |
| 15,00 | −10,37 | −1,16 | −22,62 | −5,18 | 2,19 | −0,96 | 3,90 | 0,00 |
| 20,00 | −14,40 | −1,36 | −33,20 | −7,20 | 3,20 | −1,36 | 5,56 | 0,00 |
| 25,00 | −18,51 | −1,57 | −43,98 | −9,25 | 4,23 | −1,77 | 7,25 | 0,00 |
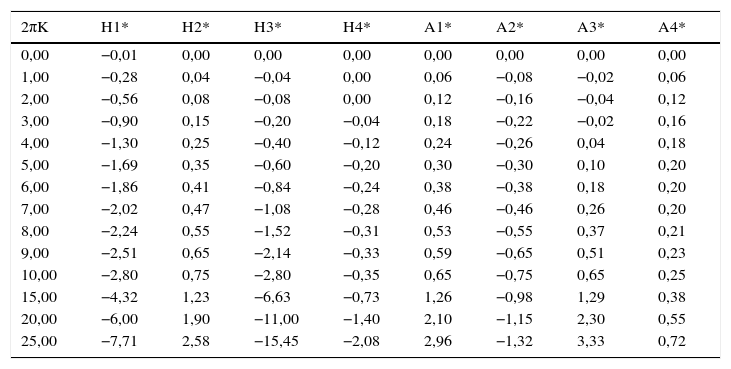
Derivadas seccionais de flutter para a ponte de Gibraltar [30]
| 2πK | H1* | H2* | H3* | H4* | A1* | A2* | A3* | A4* |
|---|---|---|---|---|---|---|---|---|
| 0,00 | −0,01 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
| 1,00 | −0,28 | 0,04 | −0,04 | 0,00 | 0,06 | −0,08 | −0,02 | 0,06 |
| 2,00 | −0,56 | 0,08 | −0,08 | 0,00 | 0,12 | −0,16 | −0,04 | 0,12 |
| 3,00 | −0,90 | 0,15 | −0,20 | −0,04 | 0,18 | −0,22 | −0,02 | 0,16 |
| 4,00 | −1,30 | 0,25 | −0,40 | −0,12 | 0,24 | −0,26 | 0,04 | 0,18 |
| 5,00 | −1,69 | 0,35 | −0,60 | −0,20 | 0,30 | −0,30 | 0,10 | 0,20 |
| 6,00 | −1,86 | 0,41 | −0,84 | −0,24 | 0,38 | −0,38 | 0,18 | 0,20 |
| 7,00 | −2,02 | 0,47 | −1,08 | −0,28 | 0,46 | −0,46 | 0,26 | 0,20 |
| 8,00 | −2,24 | 0,55 | −1,52 | −0,31 | 0,53 | −0,55 | 0,37 | 0,21 |
| 9,00 | −2,51 | 0,65 | −2,14 | −0,33 | 0,59 | −0,65 | 0,51 | 0,23 |
| 10,00 | −2,80 | 0,75 | −2,80 | −0,35 | 0,65 | −0,75 | 0,65 | 0,25 |
| 15,00 | −4,32 | 1,23 | −6,63 | −0,73 | 1,26 | −0,98 | 1,29 | 0,38 |
| 20,00 | −6,00 | 1,90 | −11,00 | −1,40 | 2,10 | −1,15 | 2,30 | 0,55 |
| 25,00 | −7,71 | 2,58 | −15,45 | −2,08 | 2,96 | −1,32 | 3,33 | 0,72 |
Derivadas seccionais de flutter para a ponte de Tacoma [27]
| 2πK | H1* | H2* | H3* | H4* | A1* | A2* | A3* | A4* |
|---|---|---|---|---|---|---|---|---|
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
| 1,00 | −0,15 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
| 2,00 | −0,30 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
| 3,00 | −1,66 | 0,50 | 0,25 | 0,00 | 0,00 | 0,05 | 0,00 | 0,00 |
| 4,00 | −3,00 | 1,00 | 0,50 | 0,00 | 0,00 | 0,10 | 0,00 | 0,00 |
| 5,00 | −4,97 | 0,51 | −0,98 | 0,00 | 0,00 | 0,20 | 0,00 | 0,00 |
| 6,00 | −3,80 | 0,00 | −2,50 | 0,00 | 0,00 | 0,30 | 0,00 | 0,00 |
| 7,00 | −2,18 | −1,96 | −5,20 | 0,00 | 0,00 | 0,40 | 0,00 | 0,00 |
| 8,00 | −0,50 | −4,00 | −8,00 | 0,00 | 0,00 | 0,50 | 0,00 | 0,00 |
| 9,00 | 0,48 | −5,95 | −10,68 | 0,00 | 0,00 | 0,60 | 0,00 | 0,00 |
| 10,00 | 1,50 | −8,00 | −13,50 | 0,00 | 0,00 | 0,70 | 0,00 | 0,00 |
| 15,00 | 6,46 | −17,92 | −27,14 | 0,00 | 0,00 | 1,20 | 0,00 | 0,00 |
| 20,00 | 11,50 | −28,00 | −41,00 | 0,00 | 0,00 | 1,70 | 0,00 | 0,00 |
| 25,00 | 16,63 | −38,27 | −55,12 | 0,00 | 0,00 | 2,21 | 0,00 | 0,00 |
See tabela Apêndice Apêndice B.1–Apêndice B.3.
Valores de Hi* e Ai* para secções retangulares de esbelteza B/D=5
| 2πK | H1* | H2* | H3* | H4* | A1* | A2* | A3* | A4* |
|---|---|---|---|---|---|---|---|---|
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
| 1,25 | −0,50 | 1,25 | −0,50 | −0,50 | 0,45 | −0,31 | 0,31 | −0,03 |
| 2,50 | −1,25 | 2,50 | −1,25 | −1,00 | 0,75 | −0,25 | 0,94 | −0,19 |
| 3,75 | −2,50 | 3,50 | −2,25 | −1,50 | 1,00 | −0,19 | 1,00 | −0,38 |
| 5,00 | −3,75 | 4,00 | −3,00 | −2,00 | 1,13 | 0,00 | 1,25 | −0,63 |
| 6,25 | −5,50 | 5,00 | −5,75 | −2,25 | 1,18 | 0,63 | 1,56 | −0,88 |
| 7,50 | −6,50 | 6,25 | −8,75 | −2,50 | 1,13 | 1,13 | 1,75 | −1,15 |
| 8,75 | −8,25 | 7,25 | −12,50 | −2,75 | 1,08 | 1,88 | 1,94 | −1,48 |
| 10,00 | −9,50 | 8,00 | −16,75 | −2,75 | 0,93 | 2,63 | 1,88 | −1,80 |
| 11,00 | −11,00 | 10,00 | −22,50 | −3,75 | 1,00 | 3,75 | 2,13 | −2,38 |
| 15,00 | −15,00 | 12,50 | −40,00 | −4,50 | 0,00 | 6,25 | 1,25 | −2,75 |
| 18,50 | −21,00 | 16,25 | −60,00 | −5,00 | −0,63 | 9,38 | −0,63 | −3,50 |
| 22,50 | −25,00 | 26,25 | −87,50 | −6,50 | −1,05 | 11,88 | −2,50 | -3,21 |
Valores de Hi* e Ai* para secções retangulares de esbelteza B/D=10
| 2πK | H1* | H2* | H3* | H4* | A1* | A2* | A3* | A4* |
|---|---|---|---|---|---|---|---|---|
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
| 1,00 | −0,25 | 0,00 | −0,25 | −0,03 | 0,13 | −0,06 | 0,13 | −0,01 |
| 2,00 | −0,75 | −0,13 | −1,00 | −0,04 | 0,30 | −0,08 | 0,31 | −0,03 |
| 3,00 | −1,75 | −0,08 | −1,25 | −0,15 | 0,50 | −0,16 | 0,63 | −0,04 |
| 4,00 | −2,25 | −0,05 | −1,75 | −0,40 | 0,55 | −0,29 | 0,88 | −0,08 |
| 5,00 | −2,60 | 0,00 | −2,50 | −0,40 | 0,75 | −0,35 | 1,00 | −0,10 |
| 6,00 | −3,50 | 0,13 | −4,00 | −0,45 | 0,95 | −0,38 | 1,25 | −0,18 |
| 7,00 | −4,00 | 0,50 | −5,50 | −0,50 | 1,05 | −0,31 | 1,75 | −0,20 |
| 8,00 | −5,50 | 1,25 | −8,25 | −0,70 | 1,25 | −0,13 | 1,91 | −0,23 |
| 9,00 | −6,25 | 1,75 | −11,75 | −0,80 | 1,48 | 0,00 | 2,50 | −0,24 |
| 10,00 | −7,50 | 2,50 | −15,00 | −1,00 | 1,55 | 0,13 | 3,00 | −0,28 |
| 15,00 | −16,50 | 5,00 | −37,50 | −3,00 | 2,25 | 1,25 | 5,63 | −0,50 |
| 20,00 | −23,50 | 12,50 | −72,50 | −5,00 | 3,25 | 1,88 | 10,00 | −0,75 |
| 25,00 | −31,50 | 40,00 | −260,00 | −6,00 | 4,00 | 2,13 | 15,00 | −1,00 |
Valores de Hi* e Ai* para secções retangulares de esbelteza B/D=20
| 2πK | H1* | H2* | H3* | H4* | A1* | A2* | A3* | A4* |
|---|---|---|---|---|---|---|---|---|
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
| 1,00 | −0,25 | −0,13 | −0,25 | 0,00 | 0,13 | −0,06 | 0,25 | 0,00 |
| 2,00 | −0,75 | −0,25 | −0,75 | 0,00 | 0,30 | −0,13 | 0,50 | −0,01 |
| 3,00 | −1,25 | −0,25 | −1,25 | −0,25 | 0,48 | −0,25 | 0,63 | −0,01 |
| 4,00 | −2,00 | −0,18 | −1,75 | −0,20 | 0,60 | −0,38 | 0,88 | 0,00 |
| 5,00 | −2,50 | −0,15 | −3,00 | −0,15 | 0,76 | −0,50 | 1,00 | 0,00 |
| 6,00 | −3,25 | −0,10 | −4,50 | −0,10 | 0,95 | −0,63 | 1,25 | 0,04 |
| 7,00 | −4,00 | −0,08 | −5,50 | −0,05 | 1,08 | −0,74 | 1,63 | 0,10 |
| 8,00 | −5,50 | −0,03 | −8,00 | −0.05 | 1.23 | −0.81 | 1.88 | 0.20 |
| 9,00 | −6,00 | 0,00 | −10,75 | −0.10 | 1.50 | −0.94 | 2.50 | 0.25 |
| 10,00 | −7,00 | 0,03 | −13,50 | −0.10 | 1.63 | −1.13 | 3.13 | 0.30 |
| 11,00 | −8,75 | 0,50 | −15,00 | −1.50 | 2.00 | −1.25 | 4.38 | 0.50 |
| 15,00 | −9,50 | 2,50 | −27,50 | −2.00 | 2.63 | −1.88 | 6.25 | 0.75 |
| 18,50 | −13,50 | 7,50 | −90,00 | −2.50 | 3.69 | −2.19 | 10.63 | 0.88 |
| 22,00 | −18,50 | 17,50 | −129,40 | −2.94 | 4.75 | −3.40 | 16.10 | 1.00 |
| 25,00 | −23,50 | 25,00 | −175,00 | −2.00 | 5.50 | −4.63 | 21.88 | 1.00 |